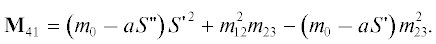1. На главную
  2. Электронные версии
  3. Радиотехника и электроника
  4. T. 66, № 2, 2021

Радиотехника и электроника, 2021, T. 66, № 2, стр. 190-198

Микрополосковый полосно-пропускающий фильтр четвертого порядка со смешанной перекрестной связью

А. В. Захаров a, *, С. А. Розенко a, С. Н. Литвинцев a

a Национальный технический университет Украины “Киевский политехнический институт им. Игоря Сикорского”
03056 Киев, просп. Победы, 37, Украина

* E-mail: azakharov217@gmail.com

Поступила в редакцию 01.07.2020
После доработки 14.07.2020
Принята к публикации 14.08.2020

Полный текст (PDF)

Аннотация

Приведено решение прямой и обратной задачи для полосно-пропускающего фильтра (ППФ) четвертого порядка, у которого перекрестная связь между крайними резонаторами K14 является смешанной. Решение прямой задачи позволяет по заданным коэффициентам связи определить нули передачи (полюсы затухания) фильтра. В обратной задаче задаются нули передачи, исходя из которых находятся коэффициенты связи фильтра. В основе решений лежит матрица проводимостей [Ỹ] ППФ и ее минор M41, а также особая форма представления коэффициента смешанной перекрестной связи в этой матрице. Установлены всевозможные варианты размещения нулей передачи рассматриваемого фильтра. Представлен образец микрополоскового экспериментального фильтра, а также его измеренные и промоделированные частотные характеристики, соответствующие двум различным его состояниям.

ВВЕДЕНИЕ

В последние годы значительное внимание уделялось полосно-пропускающим фильтрам (ППФ) со смешанными связями [1–13]. Использование в фильтрах смешанных связей, содержащих магнитную и электрическую компоненты K = Km + Ke, делает их частотные характеристики более разнообразными. Это обусловлено тем, что смешанные связи вносят дополнительные нули передачи на комплексной плоскости s = σ + jΩ. Такие связи также называют “резонансными” [1, 3] или “частотно зависимыми” [7, 8]. Наиболее часто упоминается использование смешанных связей в ППФ третьего [1–6] и четвертого [7–10] порядков. Смешанные связи могут быть реализованы в различных конструкциях линий передачи, таких как коаксиальная [2], многослойная [3], микрополосковая [4–6], интегрированная в волновод [7–10], полосковая [11–13].

ППФ третьего порядка со смешанными связями изучены наиболее полно [1–6]. Установлено [6], что они могут иметь два нуля передачи, расположенных эквидистантно относительно S = 0. В одном случае S1,2 = σ1,2 (σ2 = ‒ σ1) и ППФ третьего порядка является фильтром задержки. Во втором случае S1,2 = jΩ1,2 (jΩ2 = ‒ jΩ1) и фильтр обладает квазиэллиптической частотной характеристикой. Фильтры третьего порядка с обычными связями, включая перекрестную, не могут воспроизвести подобные частотные характеристики, поскольку обладают единственным нулем передачи на вещественных частотах [14, 15]. Если все связи обычные, то для реализации подобных частотных характеристик потребуется использование ППФ четвертого порядка [16, 17].

Отметим, что ППФ четвертого порядка со смешанными связями [7–10] обладают тремя нулями передачи, подобно фильтрам пятого порядка с обычными связями [18]. Тем не менее эти ППФ изучены недостаточно. В цитируемых работах нули передачи этих ППФ определяются различным образом. В работах [9, 10] для этого использовано компьютерное электромагнитное моделирование, которое приводит к частным результатам, правомерным лишь для заданного типа линии передачи. В работах [7, 8] для этого используется оптимизационный процесс, основанный на многократном построении частотных характеристик на основе матрицы связи. В работе [7] использована линейная форма представления смешанной связи, позволяющая внести ее в матрицу связи и осуществить последующую оптимизацию. Процесс оптимизации ППФ на основе построения частотных характеристик с использованием матрицы связи впервые предложен в [19]. Отметим, что термин “оптимизация” в данном случае подразумевает перебор всевозможных состояний с целью определения наиболее приемлемого. Иначе говоря, это настройка фильтра. Оптимизационный процесс может быть реализован и при использовании программ линейного моделирования [20].

В данной статье исследуются возможности микрополоскового фильтра четвертого порядка со смешанной перекрестной связью К14. Предполагается установить всевозможные варианты расположения нулей передачи ППФ четвертого порядка со смешанной перекрестной связью, а также определить те из вариантов, которыми может обладать рассматриваемый фильтр. Это задача анализа ППФ. Следует отметить, что несмотря на имеющиеся публикации [7–10] до сих пор не установлены упомянутые выше всевозможные варианты размещения нулей передачи. Не менее важной является и обратная задача, когда задается набор нулей передачи, по которому следует определить параметры ППФ со смешанной перекрестной связью. Эти задачи и составляют предмет данной статьи. Предполагается получить аналитические выражения, которые связывают нули передачи и коэффициенты связи упомянутых фильтров.

1. НУЛИ ПЕРЕДАЧИ ППФ ЧЕТВЕРТОГО ПОРЯДКА СО СМЕШАННОЙ ПЕРЕКРЕСТНОЙ СВЯЗЬЮ

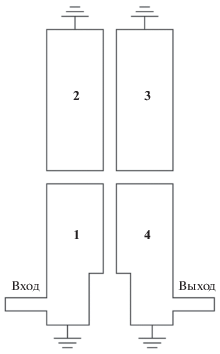
Предметом изучения является микрополосковый ППФ четвертого порядка со смешанной перекрестной связью, который показан на рис. 1. Такой фильтр характеризуется основными K12= = K34, K23 и перекрестным K14 коэффициентами связи, внешней добротностью крайних резонаторов Qe, центральной частотой полосы пропускания f0, шириной полосы пропускания BW, относительной шириной полосы пропускания FBW = BW/f0. Для описания фильтра используются нормированные коэффициенты связи

(1)
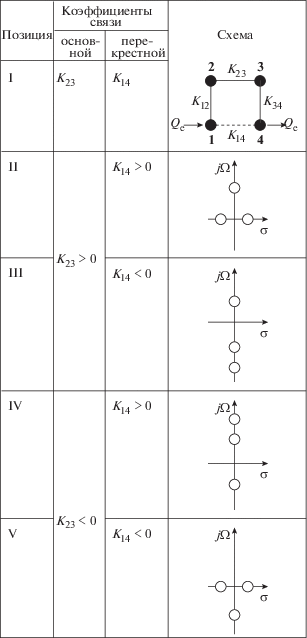
${{m}_{{ij}}} = {{{{K}_{{ij}}}} \mathord{\left/ {\vphantom {{{{K}_{{ij}}}} {{\text{FBW}}}}} \right. \kern-0em} {{\text{FBW}}}}$
Рис. 1.

Микрополосковый ППФ четвертого порядка со смешанной перекрестной связью.

и внешняя добротность крайних резонаторов qe = = QeFBW, а также комплексная частота S = σ + jΩ, где Ω = (f/f0 – f0/f)/FBW является нормированной частотой. Структура связей такого фильтра показана в табл. 1, позиция I . Пунктирной линией проведена перекрестная связь.

Таблица 1.

ППФ четвертого порядка со смешанной перекрестной связью и его нули передачи

1.1. Уравнение для определения нулей передачи

Нормированная матрица проводимостей ППФ четвертого порядка [$\tilde {Y}$] записывается в виде [20]

(2)
$\left[ {\tilde {Y}} \right] = \left[ {\begin{array}{*{20}{c}} {{1 \mathord{\left/ {\vphantom {1 {{{q}_{1}}}}} \right. \kern-0em} {{{q}_{1}}}} + S}&{ - j{{m}_{{12}}}}&{ - j{{m}_{{13}}}}&{ - j{{m}_{{14}}}} \\ { - j{{m}_{{21}}}}&S&{ - j{{m}_{{23}}}}&{ - j{{m}_{{24}}}} \\ { - j{{m}_{{31}}}}&{ - j{{m}_{{32}}}}&S&{ - j{{m}_{{32}}}} \\ { - j{{m}_{{41}}}}&{ - j{{m}_{{42}}}}&{ - j{{m}_{{43}}}}&{{1 \mathord{\left/ {\vphantom {1 {{{q}_{4}}}}} \right. \kern-0em} {{{q}_{4}}}} + S} \end{array}} \right].$

Минор M41 элемента матрицы (2), расположенного на пересечении четвертой строки и первого ряда, представляет собой определитель

(3)
$\begin{gathered} {{M}_{{41}}} = \left| {\begin{array}{*{20}{c}} {{{m}_{{12}}}}&{{{m}_{{13}}}}&{{{m}_{{14}}}} \\ {S{\kern 1pt} '}&{{{m}_{{23}}}}&{{{m}_{{24}}}} \\ {{{m}_{{32}}}}&{S{\kern 1pt} '}&{{{m}_{{34}}}} \end{array}} \right| = \\ = {{m}_{{14}}}S{\kern 1pt} {{'}^{2}}\,\, + {{m}_{{12}}}{{m}_{{23}}}{{m}_{{34}}} - {{m}_{{14}}}{{m}_{{23}}}{{m}_{{32}}}. \\ \end{gathered} $

В (3) S ' = S/j, характерно, что S  ′2 = ‒ S 2. Приравнивая минор (3) нулю [14], получаем уравнение

(4)
${{S}^{{'2}}} + {{{{m}_{{12}}}{{m}_{{23}}}{{m}_{{34}}}} \mathord{\left/ {\vphantom {{{{m}_{{12}}}{{m}_{{23}}}{{m}_{{34}}}} {{{m}_{{14}}}}}} \right. \kern-0em} {{{m}_{{14}}}}} - {{m}_{{23}}}{{m}_{{32}}} = 0,$

которое определяет нули передачи рассматриваемого фильтра со всеми простыми связями. Учитывая, что S ′2 = ‒ S 2, находим корни этого уравнения

(5a)
${{S}^{2}} = ({{{{m}_{{12}}}{{m}_{{23}}}{{m}_{{34}}}} \mathord{\left/ {\vphantom {{{{m}_{{12}}}{{m}_{{23}}}{{m}_{{34}}}} {{{m}_{{14}}}}}} \right. \kern-0em} {{{m}_{{14}}}}}) - m_{{23}}^{2},$

или

(5б)
${{S}_{{12}}} = \pm \sqrt {{{{{m}_{{12}}}{{m}_{{23}}}{{m}_{{34}}}} \mathord{\left/ {\vphantom {{{{m}_{{12}}}{{m}_{{23}}}{{m}_{{34}}}} {{{m}_{{12}}}}}} \right. \kern-0em} {{{m}_{{12}}}}} - m_{{23}}^{2}} .$

Выражения (4) впервые установлено в работе [14]. Поскольку всегда выполняется условие |m12m23m34/m14| > $m_{{23}}^{2}$, то знак подкоренного выражения (5б) определяется знаком первого слагаемого. Здесь действует правило знаков: если произведение знаков всех коэффициентов связи соответствует “+”, то нулями передачи будут вещественные числа S12 = σ12 (σ1 = ‒ σ2) и этот фильтр является фильтром задержки. Если же указанное произведение знаков соответствует “‒”, то два нуля передачи будут расположены на вещественных частотах S12 = jΩ12 (jΩ1 = ‒ jΩ2) и этот фильтр будет квазиэллиптическим фильтром.

1.2. Смешанная связь между резонаторами

Cмешанный коэффициент связи K представляет собой сумму магнитной Km и электрической Ke компонент

(6)
$K = {{K}_{m}} + {{K}_{e}} = {{K}_{m}} - \left| {{{K}_{e}}} \right|.$

Магнитной компоненте Km приписывается знак “+”, а электрической компоненте Ke знак “‒”. Основная особенность смешанной связи заключается в том, что она генерирует нуль передачи, расположенный на частоте fz [21, 22]

(7)
${{f}_{z}} = {{f}_{0}}\sqrt {{{{{K}_{m}}} \mathord{\left/ {\vphantom {{{{K}_{m}}} {\left| {{{K}_{e}}} \right|}}} \right. \kern-0em} {\left| {{{K}_{e}}} \right|}}} .$

Расположение fz (7) характеризуется следующей закономерностью. Если К > 0 (Km > |Ke|), то нуль передачи является правосторонним fz > f0. Если же К < 0 (Km < |Ke|), то нуль передачи является левосторонним fz < f0.

Использование нормировки (1) m = K/FBW при внесения смешанной связи в матрицу связи не отражает физической картины, а именно появления нуля передачи. Для этого может быть использована линейная форма представления смешанной связи в плоскости (m, Ω) [7]

(8)
$m(\Omega ) = {{m}_{0}} - a\Omega ,\,\,\,\,a > 0,$
где m0 = (Km + Ke)/FBW представляет нормированный коэффициент связи на центральной частоте f0 (Ω = 0), параметр a является крутизной, которая характеризует наклон прямой линии (8).

Закономерность (7) приводит к нормированному значению нуля передачи

(9)
$\begin{gathered} {{{\Omega }}_{z}} = \frac{{{{{{f}_{z}}} \mathord{\left/ {\vphantom {{{{f}_{z}}} {{{f}_{0}} - {{{{f}_{0}}} \mathord{\left/ {\vphantom {{{{f}_{0}}} {{{f}_{z}}}}} \right. \kern-0em} {{{f}_{z}}}}}}} \right. \kern-0em} {{{f}_{0}} - {{{{f}_{0}}} \mathord{\left/ {\vphantom {{{{f}_{0}}} {{{f}_{z}}}}} \right. \kern-0em} {{{f}_{z}}}}}}}}{{{\text{FBW}}}} = \\ = \frac{{\sqrt {{{{{K}_{m}}} \mathord{\left/ {\vphantom {{{{K}_{m}}} {\left| {{{K}_{e}}} \right|}}} \right. \kern-0em} {\left| {{{K}_{e}}} \right|}}} - {1 \mathord{\left/ {\vphantom {1 {\sqrt {{{{{K}_{m}}} \mathord{\left/ {\vphantom {{{{K}_{m}}} {\left| {{{K}_{e}}} \right|}}} \right. \kern-0em} {\left| {{{K}_{e}}} \right|}}} }}} \right. \kern-0em} {\sqrt {{{{{K}_{m}}} \mathord{\left/ {\vphantom {{{{K}_{m}}} {\left| {{{K}_{e}}} \right|}}} \right. \kern-0em} {\left| {{{K}_{e}}} \right|}}} }}}}{{{\text{FBW}}}} = {{{{m}_{0}}} \mathord{\left/ {\vphantom {{{{m}_{0}}} {\sqrt {{{K}_{m}}\left| {{{K}_{e}}} \right|} }}} \right. \kern-0em} {\sqrt {{{K}_{m}}\left| {{{K}_{e}}} \right|} }}. \\ \end{gathered} $

Поскольку a = m0/Ωz, то подстановка (9) в знаменатель этого равенства, дает

(10)
$a = \sqrt {{{K}_{m}}\left| {{{K}_{e}}} \right|} .$

Параметр крутизны a (10) следует из закономерности (7) расположения fz относительно f0. Значение a (10) всегда положительное, а наклон прямой (8) отрицательный. Представление смешанной связи в линейной форме (8) было рассмотрено в [7]. При этом предполагалось, что значения a могут быть отрицательными, а прямая (8) может иметь положительный наклон, что противоречит закономерности (7).

Обратный переход от формы представления смешанной связи (8) к (6) осуществляется по формулам

(11)
$K = {{m}_{0}}{\text{FBW}},\,\,\,{{K}_{m}},\;{{K}_{e}} = {K \mathord{\left/ {\vphantom {K 2}} \right. \kern-0em} 2} \pm \sqrt {{{{\left( {{K \mathord{\left/ {\vphantom {K 2}} \right. \kern-0em} 2}} \right)}}^{2}} + {{a}^{2}}} .$

Правое из выражений (11) имеет два значения, положительное и отрицательное, положительное значение относится к Km, а отрицательное – к Ke.

1.3. ППФ четвертого порядка со смешанной перекрестной связью

Рассмотрим симметричный ППФ К12 = К34 (m12 = = m34) четвертого порядка. При использовании смешанной перекрестной связи в выражении (3) надо заменить m14 на m(S ′) = m0 – aS ':

(12)

Приравнивая минор (12) нулю, получаем алгебраическое уравнение третьей степени, определяющее нули передачи:

(13)
$S{\kern 1pt} {{'}^{3}}\,\, - \frac{{{{m}_{0}}}}{a}S{\kern 1pt} {{'}^{2}}\,\, - m_{{23}}^{2}S{\kern 1pt} '\,\, - \frac{{m_{{12}}^{2}{{m}_{{23}}}}}{a} = 0.$

Знак второго слагаемого в (13) зависит только от знака смешанной связи m0. Знак свободного члена в (13) зависит только от знака основного коэффициента связи m23. Расположение корней многочлена (13) зависит от соотношения между знаками указанных коэффициентов связи m0 и m23. Возможно четыре варианта, которые систематизированы в табл. 1. Симметричный ППФ четвертого порядка со смешанной перекрестной связью К14 имеет четыре различных состояния (II–V), которые характеризуются тремя нулями передачи и особым их расположением.

1. Первые два состояния (II и III) имеют место при положительном значении К23 > 0. Если К14 > 0, то два нуля передачи располагаются на оси σ, а один располагается на положительной полуоси jΩ (позиция II). Это состояние соответствует фильтру задержки с повышенной правосторонней избирательностью. Если К14 < 0, то два нуля передачи располагаются на отрицательной полуоси jΩ, а один нуль передачи — на положительной полуоси jΩ (позиция III).

2. Вторые два состояния (IV и V) имеют место при отрицательном значении основной связи К23 < 0. Если К14 > 0, то три его нуля передачи располагаются на оси jΩ различным образом: два из них на положительной полуоси jΩ, а один нуль передачи на отрицательной полуоси jΩ (позиция V). При К14 < 0 (позиция V) два нуля передачи располагаются на оси σ, а один нуль передачи на отрицательной полуоси jΩ. Это состояние соответствует фильтру задержки с повышенной левосторонней избирательностью.

2. ПОСТРОЕНИЕ ППФ С ЗАДАННЫМИ НУЛЯМИ ПЕРЕДАЧИ

Задача определения нулей передачи $S_{1}^{'}$, $S_{2}^{'}$ и $S_{3}^{'}$ ППФ четвертого порядка заключается в определении корней алгебраического уравнения (13). Обратная задача заключается в определении компонентов смешанной перекрестной связи по заданным значениям $S_{1}^{'}$, $S_{2}^{'}$ и $S_{3}^{'}$ при известных основных (m12 и m23) коэффициентах связи между резонаторами.

Представим уравнение (13) в стандартной форме:

(14)
${{S}^{{'2}}} + {{А}_{2}}{{S}^{{'2}}} + {{А}_{3}}S{\kern 1pt} '\,\, + {{А}_{4}} = 0.$

Связь между нулями $S_{i}^{'}$ (14) и коэффициентами полинома (14) третьей степени выражается формулами Виета [23]

(15)
$\begin{gathered} {{A}_{2}} = - \left( {S_{1}^{'} + S_{2}^{'} + S_{3}^{'}} \right), \\ {{A}_{3}} = S_{1}^{'}S_{2}^{'} + S_{1}^{'}S_{3}^{'} + S_{2}^{'}S_{3}^{'},\,\,\,\,{{A}_{4}} = - S_{1}^{'}S_{2}^{'}S_{3}^{'}. \\ \end{gathered} $

Сопоставляя выражения (13) и (14), запишем три равенства:

(16a)
${{A}_{2}} = - {\text{ }}(S_{1}^{'} + S_{2}^{'} + S_{3}^{'}) = - ({{{{m}_{0}}} \mathord{\left/ {\vphantom {{{{m}_{0}}} a}} \right. \kern-0em} a}),$
(16б)
${{A}_{3}} = S_{1}^{'}S_{1}^{'} + S_{1}^{'}S_{3}^{'} + S_{2}^{'}S_{3}^{'} = - m_{{23}}^{2},$
(16в)
${{A}_{4}} = - S_{1}^{'}S_{2}^{'}S_{3}^{'} = {{ - m_{{12}}^{2}{{m}_{{23}}}} \mathord{\left/ {\vphantom {{ - m_{{12}}^{2}{{m}_{{23}}}} a}} \right. \kern-0em} a}.$

Равенства (16) выражают взаимосвязь между нулями передачи и коэффициентами связи ППФ четвертого порядка со смешанной перекрестной связью m14 = m0 ‒ аΩ .

Два параметра смешанной перекрестной связи m0 и a могут быть определены из системы уравнений (16), включающей три нуля передачи. Для определения m0 и a достаточно использовать два уравнения (16а) и (16в). Из уравнения (16в) можно определить а, затем подставить это значение в (16а) и определить m0. Уравнение (16б) не содержит определяемых величин m0, a и может показаться избыточным. Но это не так, равенство (16б) свидетельствует о том, что три нуля передачи ППФ четвертого порядка со смешанной перекрестной связью являются взаимозависимыми. Мы можем задать только два из них, а третий нуль передачи должен быть доопределен из условия связи (16б).

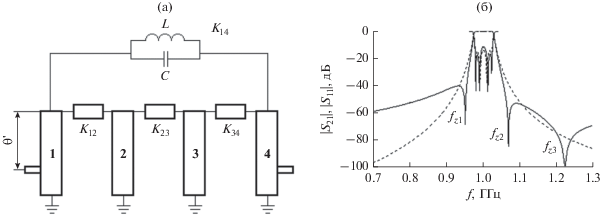
Рассмотрим пример дизайна симметричного (K12 = K34) ППФ четвертого порядка, схема которого показана на рис. 2а. Фильтр имеет один левосторонний и два правосторонних нуля передачи. Как показал анализ (см. табл. 1, позиция V), в этом случае основная связь К23 должна быть отрицательной К23 < 0, а перекрестная смешанная связь должна быть положительной К14 > 0.

Рис. 2.

Полосно-пропускающий фильтр четвертого порядка со смешанной перекрестной связью: (а) схема, (б) ее частотные характеристики для случая К23 < 0, K14 > 0 с перекрестной связью (сплошная кривая ) и без перекрестной связи (штриховая).

В качестве исходного выберем Чебышевский прототип с величиной пульсаций LAr = 0.2 дБ, N = 4, FBW = 0.05 и f0 = 1 ГГц. Ему соответствуют параметры низкочастотного прототипа [24]: g0 = 1, g1 = = 1.3028, g2 = 1.2814, g3 = 1.9761, g4 = 0.8468. Используя формулы из работы [24], определяем основные коэффициенты связи K12 = К34 = 0.0387 (m12 = 0.774), К23 = ‒0.0314 (m23 = ‒0.628) и внешнюю добротность крайних резонаторов Qe = 26.056.

В фильтре использованы четвертьволновые резонаторы с характеристическим импедансом Z0 = 10 Ом, которые характеризуются параметром крутизны b = π/4Z0 [24]. Авторы работ [25, 26] ввели в рассмотрение идеальный инвертор проводимости (J-inverter), который представляет собой четырехполюсник и характеризуется параметром проводимости J. При соединении J-инвертором двух резонаторов параллельного типа с одной и той же резонансной частотой f0 обеспечивается коэффициент связи

(17)
$K = {J \mathord{\left/ {\vphantom {J {\sqrt {{{b}_{1}}{{b}_{2}}} }}} \right. \kern-0em} {\sqrt {{{b}_{1}}{{b}_{2}}} }},$

где b1 и b2 – параметры крутизны проводимости этих резонаторов.

В качестве инвертора проводимости использованы четвертьволновые отрезки линий передачи с характеристическим сопротивлением Zi,i + 1. В этом случае J = 1/Zi,i + 1, а $\sqrt {{{b}_{1}}{{b}_{2}}} = {{\pi } \mathord{\left/ {\vphantom {{\pi } {4{{Z}_{0}}}}} \right. \kern-0em} {4{{Z}_{0}}}}$, подстановка этих значений в (17) дает

(18)
${{K}_{{i,\,i + 1}}} = {{4{{Z}_{0}}} \mathord{\left/ {\vphantom {{4{{Z}_{0}}} {{\pi }{{Z}_{{i,\,i + 1}}}}}} \right. \kern-0em} {{\pi }{{Z}_{{i,\,i + 1}}}}}.$

С помощью выражения (18) находим характеристические сопротивления четвертьволновых отрезков, осуществляющих связь между резонаторами Z12 = Z34 = 329 Ом, Z23 = ‒409.49 Ом. Нагрузки фильтра RL = 50 Ом подключаются кондуктивно к крайним резонаторам. Требуемое значение внешней добротности обеспечивается координатой θ′ подключения нагрузки, которая отсчитывается от разомкнутого конца четвертьволнового резонатора

${{Q}_{e}} = {{R}_{L}}b = {{R}_{L}}{{\pi } \mathord{\left/ {\vphantom {{\pi } {4{{Z}_{0}}{{{\cos }}^{2}}{\theta }{\kern 1pt} {\text{'}}}}} \right. \kern-0em} {4{{Z}_{0}}{{{\cos }}^{2}}{\theta }{\kern 1pt} {\text{'}}}}.$

Из этого равенства определяем, что значение Qe = = 26.056 обеспечивается при θ′ = 67.15°. На рис. 2б штриховыми линиями показаны промоделированные частотные отклики этого фильтра.

Внесем в характеристику вносимых потерь этого фильтра три нуля передачи. При этом можем задать только два из них, например, $S_{1}^{'}$ = ‒ 2 (fz1 = 950 MГц) и $S_{3}^{'}$ = 8 (fz3 = 1200 MГц). Чтобы доопределить $S_{2}^{'}$, обратимся к выражению (16б), которое запишем в виде

(19)
$S_{2}^{'} = {{ - (m_{{23}}^{2} + S_{1}^{'}S_{3}^{'})} \mathord{\left/ {\vphantom {{ - (m_{{23}}^{2} + S_{1}^{'}S_{3}^{'})} {(S_{1}^{'} + S_{3}^{'})}}} \right. \kern-0em} {(S_{1}^{'} + S_{3}^{'})}}.$

Подстановка в правую часть исходных значений дает $S_{2}^{'}$ = 2.6 (fz2 = 1065 MГц).

Используя значения трех нулей передачи и выражения (16а), (16в), составим два равенства:

(20а)
$ - \left( {{{{{m}_{0}}} \mathord{\left/ {\vphantom {{{{m}_{0}}} a}} \right. \kern-0em} a}} \right) = - \left( {S_{1}^{'} + S_{2}^{'} + S_{3}^{'}} \right) = - 8.6;$
(20б)
${{ - m_{{12}}^{2}{{m}_{{23}}}} \mathord{\left/ {\vphantom {{ - m_{{12}}^{2}{{m}_{{23}}}} a}} \right. \kern-0em} a} = - S_{1}^{'}S_{2}^{'}S_{3}^{'} = 41.6{\text{ }}.$

Из (20б) определяем параметр a = 0.009044, подстановка которого в (20а) дает значение m0 = = 0.0778. По известным значениям m0, $a = \sqrt {{{K}_{m}}\,\left| {{{K}_{e}}} \right|} $ и формулам обратного перехода (11) определяем смешанный коэффициент связи K13 = 0.0039 и его компоненты Km = 0.0112, Ke = ‒ 0.0073.

У фильтра на рис. 2а для реализации смешанной связи используется LC-контур, элементы которого связаны с компонентами Km, Ke соотношениями

(21)
${{K}_{m}} \approx {1 \mathord{\left/ {\vphantom {1 {2\pi {{f}_{0}}L\sqrt {{{b}_{1}}{{b}_{2}}} }}} \right. \kern-0em} {2\pi {{f}_{0}}L\sqrt {{{b}_{1}}{{b}_{2}}} }};\,\,\,\,{{K}_{e}} \approx - {{2\pi {{f}_{0}}C} \mathord{\left/ {\vphantom {{2\pi {{f}_{0}}C} {\sqrt {{{b}_{1}}{{b}_{2}}} }}} \right. \kern-0em} {\sqrt {{{b}_{1}}{{b}_{2}}} }},$

что следует из (17). Подставляя в (21) исходные величины, получаем значения L и C, которые обеспечивают заданные компоненты смешанной связи L = 180.9 нГ, C = 0.091 пФ. На рис. 2б показаны промоделированные частотные характеристики ППФ четвертого порядка со смешанной перекрестной связью, который имеет предписанные нули передачи.

3. МИКРОПОЛОСКОВАЯ РЕАЛИЗАЦИЯ

Полученные в предыдущих разделах результаты позволяют определить потенциальные возможности микрополоскового ППФ четвертого порядка со смешанной перекрестной связью (см. рис. 1). Для изготовления фильтра была использована диэлектрическая подложка ТММ-10i (Rogers), εr = 9.8, tg δ = 0.002, h = 1.905 мм. Рассмотрим два случая, когда смешанная перекрестная связь является отрицательной K14 < 0 и когда положительной К14 > 0. В обоих случаях занимаемая фильтром площадь составляет 38 × 17.4 мм. При построении фильтра использованы закономерности коэффициентов связи между резонаторами в планарных линиях передачи [27, 28].

3.1. ППФ с отрицательным коэффициентом перекрестной связи

Топология этого фильтра с указанием размеров представлена на рис. 3а. На рис. 3б дана фотография фильтра. Фильтр содержит два ступенчато-импедансных резонатора (1 и 4), а также два модифицированных четвертьволновых резонатора (2 и 3), резонансная частота которых f0 = 1.74 ГГц. Все резонаторы короткозамкнуты на одном конце с помощью металлизированных отверстий диаметром 0.6 мм. В области короткого замыкания резонаторов 1 и 4 из их центральных проводников удалены прямоугольники размером 6.2 × 1.2 мм, что сделало эти резонаторы ступенчато-импедансными. Резонаторы 1, 4 связаны с резонаторами 2, 3 через емкостные зазоры, поэтому основные коэффициенты связи К12 = К34 между резонаторами отрицательные. Основной коэффициент связи между резонаторами 2 и 3 является положительным K23 > 0.

Рис. 3.

Экспериментальный микрополосковый ППФ четвертого порядка со смешанной перекрестной связью: (а) топология, принятые размеры L1 = 14 мм; w1 = 3.6 мм; L2 = 15.8 мм; w2 = 2.4 мм; S12 = 1.3 мм; S14 = 0.8 мм; S23 = 2.4 мм; (б) фотография; (в) характерные частоты связанных резонаторов 1 и 4 для случая K14 < 0; (г) экспериментальные (сплошная кривая) и расчетные (штриховая) частотные характеристики ППФ для случая К23 > 0, K14 < 0.

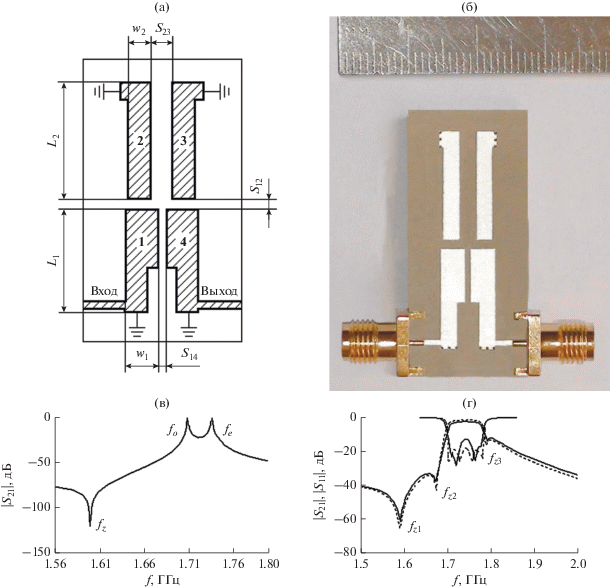
Для определения коэффициентов связи между резонаторами используется известное выражение [20]

(22)
$K = {{(f_{o}^{2} - f_{e}^{2})} \mathord{\left/ {\vphantom {{(f_{o}^{2} - f_{e}^{2})} {(f_{o}^{2} + f_{e}^{2})}}} \right. \kern-0em} {(f_{o}^{2} + f_{e}^{2})}},$

где fe и fo представляют собой четную и нечетную моды двух связанных резонаторов. Частоты fe и fo определяются компьютерным моделированием при слабой связи резонаторов с нагрузками. Для моделирования была использована компьютерная программа Microwave Office (AWR).

Рассматриваемый фильтр при приведенных на рис. 3а параметрах имеет основные коэффициенты связи K12 = K34 = –0.0330, K23 = 0.0319. Резонаторы 2 и 3 являются модифицированными, поскольку короткое замыкание выполнено нестандартным образом, как показано на рис. 3а. Такой прием позволил при использовании толстой (h = = 1.905 мм) подложки и сравнительно малом зазоре между резонаторами S23 = 2.4 мм получить малое значение коэффициента связи K23 = 0.0319.

На рис. 3в представлены характерные частоты двух связанных ступенчато-импедансных резонаторов 1 и 4 при их слабой связи с нагрузками. Наличие полюса fz указывает на то, что связь между этими резонаторами смешанная. Измеренные значения: fo = 1.709 ГГц; fe = 1.736 ГГц; fz = 1.60 ГГц. Расположение fz позволяет идентифицировать две частоты связи, указав, какая из них является четной, а какая нечетной модой связанных колебаний. Нуль передачи fz всегда расположен по соседству с нечетной модой fо.

Подставляя измеренные значения fe и fo в (22), определяем смешанный коэффициент связи K14 = ‒0.0157. Используя выражение (10), в котором f0 = (fe + fo)/2, и значение смешанного коэффициента связи К14, несложно определить ее компоненты: Кm = 0.0989; Ке = ‒0.1146.

Внешняя добротность крайних резонаторов Qe определяется расположением микрополосковых линий на входе и выходе фильтра, ширина которой 1.2 мм. Используя выражение [20]

(23)
${{Q}_{e}} = {{\pi {{f}_{0}}{{\tau }_{{{{S}_{{11}}}}}}({{f}_{0}})} \mathord{\left/ {\vphantom {{\pi {{f}_{0}}{{\tau }_{{{{S}_{{11}}}}}}({{f}_{0}})} 2}} \right. \kern-0em} 2},$

можно определить значение Qe путем компьютерного моделирования. В выражении (23) ${{\tau }_{{{{S}_{{11}}}}}}({{f}_{0}})$ – время группового запаздывания параметра S11 для резонатора с односторонней нагрузкой на частоте f0. В данном случае Qe = 26.

Измеренные и промоделированные частотные характеристики рассматриваемого фильтра приведены на рис. 3г. Поскольку основной коэффициент связи К23 положительный, а перекрестный смешанный коэффициент связи К14 отрицательный, то фильтр имеет три нуля передачи на вещественных частотах, как было предсказано в табл. 1, позиция II. Фильтр имеет следующие измеренные параметры: центральная частота f0 = 1740 MГц; ширина полосы пропускания BW = 75 MГц; вносимые потери на центральной частоте IL0 = 1.5 дБ; обратные потери RL ≤ –13 дБ. Нули передачи расположены на частотах fz1 = 1590 МГц, fz2 = 1674 МГц, fz3 = 1788 МГц.

3.2. ППФ с положительным коэффициентом перекрестной связи

Если зазор S14 между крайними резонаторами фильтра (см. рис. 3) увеличить на 0.4 мм, с S14 = = 0.8 мм до S14 = 1.2 мм, то смешанный коэффициент перекрестной связи К14 превратится из отрицательного в положительный. Основные коэффициенты связи фильтра К12 = К34 и К23 остаются неизменными. На рис. 4а показаны характерные частоты связанных ступенчато-импедансных резонаторов 1 и 4 при их слабой связи с нагрузками: fe = = 1.7193 ГГц; fo = 1.722 ГГц; fz = 1.747 ГГц. Поскольку нуль передачи fz является правосторонним, то ближайшая к нему частота связи является нечетной модой колебаний fo, а смешанная связь К14 является положительной.

Рис. 4.

Экспериментальный микрополосковый фильтр задержки с повышенной правосторонней избирательностью: а) характерные частоты связанных резонаторов 1 и 4 для случая K14 > 0; б) экспериментальные (сплошная кривая) и расчетные (штриховая) частотные характеристики фильтра для случая К23 > 0, K14 < 0.

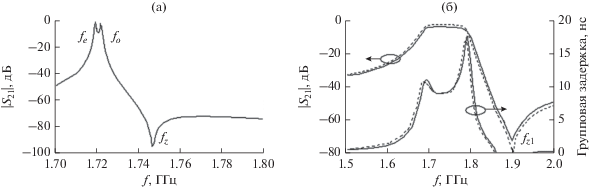
Подставляя измеренные значения fe и fo в (22), определяем смешанный коэффициент связи K14 = 0.00157. Используя выражение (10) и значение К14, находим компоненты смешанной связи: Кm = 0.05221; Ке = ‒0.05064.

Частотные характеристики фильтра изображены на рис. 4б. Поскольку основной коэффициент связи К23 > 0, а перекрестная смешанная связь превратилась из отрицательной в положительную – К14 > 0, то фильтр стал обладать постоянным временем задержки с повышенной правосторонней избирательностью, как было предсказано в табл. 1, позиция III. Фильтр имеет следующие измеренные параметры: центральная частота f0 = 1740 MГц; ширина полосы пропускания BW = 75 MГц; вносимые потери на центральной частоте IL0 = 1.5 дБ. Нуль передачи расположен на частоте fz = 1890 МГц. Время задержки фильтра τ = 9.2 ± 0.2 нс в полосе частот 38 МГц, которая составляет половину полосы пропускания. Поскольку этот фильтр является фильтром задержки, то степень его согласования с нагрузками была улучшена, что нашло отражение в показателе обратных потерь RL ≤ –18 дБ (прежний показатель RL ≤ –13 дБ). Для улучшения согласования микрополосковые отрезки на входе и выходе фильтра, подключенные кондуктивно к крайним резонаторам, были несколько смещены в сторону разомкнутых концов. Это привело к понижению значения внешней добротности этих резонаторов Qe = 21.

Частотные характеристики предложенного микрополоскового фильтра четвертого порядка со смешанной перекрестной связью достаточно разнообразны и полезны для практического применения. В то же время рассмотренный фильтр обладает ограниченными возможностями. Он реализует лишь два из четырех представленных в табл. 1 состояний. Это обусловлено тем, что в предложенной конструкции знак основного коэффициента связи К23 не может быть отрицательным, он всегда положительный, К23 > 0.

Соотношение между возможным числом нулей передачи и количеством резонаторов N в ППФ представляет определенный интерес. Ответ на этот вопрос получить достаточно просто, распространив выражения (2)–(4) и (12), (13) на случай произвольного N. В этом случае минор MN1 ППФ представляет собой определитель квадратной матрицы (3) размером (N ‒ 1) × (N ‒ 1). Из условия MN1 = 0 получаем алгебраическое уравнение относительно комплексной частоты S = σ + jΩ. Степень полинома левой части этого уравнения зависит от типа используемых в ППФ коэффициентов связи. Если все связи ППФ простые, то максимальная степень полинома MN1(S) равна (N ‒ 2), столько же может быть и нулей передачи. Если в ППФ есть смешанные связи, то максимальная степень полинома MN1(S) равна (N ‒ 1), таким же количеством нулей передачи может обладать ППФ. Эта закономерность относится к ППФ с отсутствующей перекрестной связью между входом и выходом, которая добавляет еще два нуля передачи на вещественных частотах (оси jΩ).

Приведенное обобщение сделано на основе использования классической матрицы проводимости (2), которая выражает в матричной форме законы Кирхгофа. В свою очередь, законы Кирхгофа справедливы для электрических цепей с двухполюсными элементам R, L, C. Если электрическая цепь содержит элемент с двумя парами зажимов (отрезок линии передачи, включенный на проход), то уравнения Кирхгофа становятся неприменимыми к этой цепи, так же как и матрица проводимости [$\tilde {Y}$] (2).

Примером таких цепей являются ППФ с резонаторами полуволного типа, которые могут быть ступенчато-импеданстными резонаторами. Таким фильтрам присущи иные закономерности, которые строго не определены еще до сих пор. В работе [29] проведен обзор микрополосковых ППФ с резонаторами полуволного типа, которые могут иметь П-образную форму. Резонаторы расположены рядом друг с другом, поэтому кроме магнитной связи между ними действует и электрическая связь, что приводит к смешанному коэффициенту связи К = Km + Ke. Рассматриваемые в [29] микрополосковые ППФ являются чрезвычайно сложными для аналитического описания из-за использования резонаторов полуволнового типа, смешанных связей между резонаторами и паразитных перекрестных связей. Эффект образования нулей передачи в таких фильтрах был рассмотрен в более ранней работе [30]. Он поясняется различными фазовыми скоростями четной и нечетной волн, распространяющихся в отрезках линий передачи.

В работе [29] высказано предположение, что число нулей передачи в подобных фильтрах может быть равно N + 1. Это предположение подтверждено результатами 3D-моделирования и данными экспериментальных измерений. Это также совпадает с результатами других авторов, изложенными в [31], где ППФ с N = 3 имел четыре нуля передачи на вещественных частотах.

Отметим, что поведение ППФ с резонаторами полуволнового типа может иметь двойственный характер, как, например, у микрополоскового решетчатого ППФ третьего порядка [5] со смешанной перекрестной связью К13. Если его порты расположены ближе к одной паре разомкнутых концов, то этот фильтр является фильтром задержки с нулями передачи на оси σ. Если его порты переместить ближе к другой паре разомкнутых концов, то фильтр становится квазиэллиптическим с нулями передачи на ось jΩ.

Полосно-пропускающие фильтры с полуволновыми резонаторами [29–31] являются весьма перспективными. Они могут обладать значительным числом нулей передачи. В этих фильтрах еще многое предстоит изучить, чтобы установить аналитическую взаимосвязь между нулями передачи и коэффициентами связи.

ЗАКЛЮЧЕНИЕ

Рассмотрен микрополосковый полосно-пропускающий фильтр четвертого порядка со смешанной перекрестной связью между крайними резонаторами K14 = Km + Ke, который при одной и той же топологии обладает двумя состояниями, с существенно отличающимися друг от друга частотными характеристиками. При положительном значении коэффициента перекрестной связи K14 > 0 этот фильтр является фильтром задержки с повышенной правосторонней избирательностью, обусловленной нулем передачи, расположенным с правой стороны от полосы пропускания. При отрицательном значении коэффициента перекрестной связи K14 < 0 этот фильтр имеет на вещественных частотах три нуля передачи. Два нуля передачи расположены слева от полосы пропускания, а один нуль передачи находится справа от полосы пропускания. Рассмотренный фильтр может оказаться полезным в некоторых технических приложениях.

Список литературы

  1. Levy R. // IEEE MTT-S Int. Microw. Symp. Dig., Jun. 6–11, 2004. Fort Worth, TX, USA. V. 2. P. 447.

  2. Zhu F., Hong W., Chen J.-X., Wu K. // IEEE Microwave and Wireless Components Lett. 2014. V. 24. № 2. P. 90.

  3. Hoft M., Shimamura T. // IEEE Trans. 2010. V. MTT-58. № 1. P. 165.

  4. Захаров А.В., Розенко С.А., Захарова Н.А. // РЭ. 2012. Т. 57. № 3. С. 342.

  5. Zakharov A., Rozenko S., Litvintsev S., Ilchenko M. // IEEE Microwave and Wireless Components Lett. 2020. V. 30. № 1. P. 12.

  6. Захаров А.В., Розенко С.А. // РЭ. 2012. Т. 57. № 6. С. 713.

  7. Szydlowski L., Lamecki A., Mrozowski M. // IEEE Microwave and Wireless Components Lett. 2012. V. 22. № 6. P. 312.

  8. Szydlowski L., Leszczynska N., Mrozowski M. // IEEE Microwave and Wireless Components Lett. 2014. V. 24. № 1. P. 32.

  9. Shen W., Wu L.-S., Sun X.-W. et al. // IEEE Microwave and Wireless Components Lett. 2009. V. 19. № 11. P. 701.

  10. Gong K., Hong W., Zhang Y. et al. // IEEE Trans. 2012. V. MTT-60. № 10. P. 3071.

  11. Zakharov A.V., Ilchenko M.Y., Karnau, V.Y., Pinchuk L.S. // Radioelectronics and Communications Systems. 2011. V. 54. № 3. P. 163.

  12. Захаров А.В., Ильченко М.Е. // РЭ. 2013. Т. 58. № 7. С. 716.

  13. Зaxapoв A.B. // PЭ. 2013. T. 58. № 3. C. 300.

  14. Kurzrok R.M. // IEEE Trans. 1966. V. MTT-14. № 1. P. 46.

  15. Hong J.-S., Lancaster M.J. // IEE Proc. – Microwaves Antennas Propag. 1999. V. 146. № 1. P. 84.

  16. Kurzrok R.M. // IEEE Trans. 1966. V. MTT-14. № 6. P. 295.

  17. Levy R. // IEEE Trans. 1976. V. MTT-24. № 4. P. 172.

  18. Cameron R.J., Kudsia C.M., Mansour R.R. Microwave Filters for Communication Systems: Fundamentals, Design and Applications. Hoboken (NJ): Wiley, 2007.

  19. Atia W., Zaki K., Atia A. // 1998 IEEE MTT-S Int. Microw. Symp. Dig. 7-12 Jun. 1998. V. 2. P. 821.

  20. Hong J.-S., Lancaster M.J. // Microstrip Filters for RF/Microwave Application. N.-Y.: Wiley, 2001.

  21. Wang H., Chu Q.-X. // IEEE Trans. 2009. V. MTT-57. № 3. P. 667.

  22. Chu Q.-X., Wang H. // IEEE Trans. 2008. V. MTT-56. № 2. P. 431.

  23. Korn G.A., Korn T.M. Mathematical handbook for scientists and engineers: definitions, theorems, and formulas for reference and review. N.-Y.: McGraw-Hill, 1961.

  24. Matthaei G.L., Young L., Jones E.M.T. Microwave Filters, Impedance-Matching Network and Coupling Structures. Norwood (MA): Artech House, 1980.

  25. Cohn S.B. // Proc. IRE. 1957. V. 45. № 2. P. 187.

  26. Matthaei G.L. // 1958 IRE National Convention Record. V. 6. Pt. 1. P. 98.

  27. Zakharov A.V., Il’chenko M.Ye., Pinchuk L.S. // Radioelectronics and Communications Systems. 2015. V. 58. № 6. P. 284.

  28. Захаров А.В., Ильченко М.Е., Корпач В.Н. // РЭ. 2014. Т. 59. № 6. С. 602.

  29. Aristarkhov G.M., Grebennikov A., Zvezdinov N.V. // IEEE Microwave Mag. 2019. V. 20. № 11. P. 22.

  30. Аристархов Г.М., Вершинин Ю.П. // РЭ. 1983. Т. 28. № 9. С. 1714.

  31. Hsu C.-L., Yu C.-H., Kuo J.-T. // 2012 4th Intern. High Speed Intelligent Communication Forum. 2012. P. 1.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал