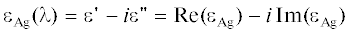Радиотехника и электроника, 2021, T. 66, № 3, стр. 245-252

ВВЕДЕНИЕ

Как известно, дифракция электромагнитных волн наноструктурами из благородных металлов (серебра, золота) в световом диапазоне волн сопровождается как образованием поверхностных волн (плазмон-поляритонов), так и существованием их резонансов. При этом интерес к исследованию свойств плазмон-поляритонов связан главным образом с высокой локализацией электромагнитного поля вблизи поверхности наноструктур, которая позволяет использовать их в субволновом и ближнепольном зондировании. Известно, что нанопровода из серебра и золота широко применяются в качестве сенсоров [1]. Отметим, что плазмонные резонансы в цилиндрических наноструктурах (нитях) с круглым сечением реализуются в ультрафиолетовой части спектра. Используя нанотрубки, можно сместить частоты плазмонных резонансов в видимую область светового диапазона [1–3]. В [4] исследованы плазмонные резонансы в кварцевой нанонити, покрытой слоем золота переменной толщины в предположении, что границами оболочки являются круговые цилиндры со смещенными центрами. Различные геометрии оболочек из серебра и кварца, контуры поперечного сечения которых образованы круговыми или круговыми и эллиптическими цилиндрами, рассматривались в работах [5–7].

Цель данной работы состоит в исследовании особенностей плазмонных резонансов в 2D-наноструктурах из серебра (золота) в случае, когда контур поперечного сечения структуры представляют собой круг, переходящий в эллипс. Из близких по тематике работ отметим [8–11].

1. ФОРМУЛИРОВКА ЗАДАЧИ

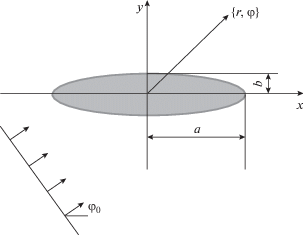
Рассматрим двумерную задачу дифракции плоской электромагнитной линейно-поляризованной ТМ-волны на двумерной цилиндрической диэлектрической структуре, поперечное сечение которой представляет собой эллипс с полуосями $a$ и $b$, ($a > b$) (рис. 1)

Рис. 1.

Геометрия задачи.

Если в (1) принять $a = b$, то поперечное сечение структуры будет представлять собой круг.

Плоская волна распространяется в направлении единичного вектора ($\cos {{\varphi }_{0}},\sin {{\varphi }_{0}},0$) и характеризуется следующими компонентами электромагнитного поля:

Зависимость от времени выбрана в виде $\exp (i\omega t)$, где $\omega = kc$ – круговая частота, $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$ – волновое число свободного пространства, $c - $ скорость света в вакууме, $\lambda $ − длина волны, $\eta = \sqrt {{{{{\mu }_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}}} = 120\pi \,\,Ом$ − волновое сопротивление вакуума, ${{\mu }_{0}},{{\varepsilon }_{0}}$ – магнитная и диэлектрическая проницаемости вакуума.

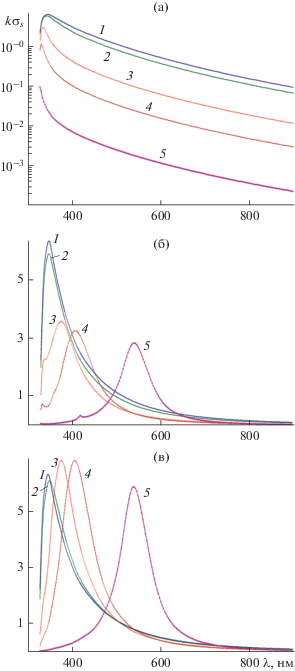
Считается, что среда структуры представляет собой серебро (или золото). При этом частотная зависимость относительной диэлектрической проницаемости серебра

(или золота – ${{\varepsilon }_{{{\text{Au}}}}}(\lambda )$) рассчитывалась на основе интерполяции экспериментальных данных работы [12] кубическими сплайнами. Отметим, что использование результатов работы [12] (как и теории Друде [1]) ограничивает максимальный размер рассеивателя ${\text{min}}(a,b) \geqslant 10\,\,{\text{нм}}$, поскольку при меньших значениях $a$ или $b$ необходимо учитывать явления пространственной дисперсии серебра (золота) [1].

Пространственное распределение диэлектрической проницаемости для структуры, изображенной на рис. 1, имеет вид

Исследование сформулированной задачи дифракции удобнее проводить, используя $z$-компоненту $U(x,y) = {{H}_{z}}(x,y)$ магнитного поля, так как краевая задача для функции $U(x,y)$ является скалярной. Полное поле $U(x,y)$ в кусочно-постоянной среде (3) удовлетворяет уравнению Гельмгольца

Компоненты электрического поля могут быть выражены через функцию $U(x,y)$

На границе структуры должны быть непрерывны величины $U$ и $\frac{1}{\varepsilon }\frac{{\partial U}}{{\partial N}}$, где $\frac{{\partial U}}{{\partial N}}$ обозначает производную по направлению нормали к границе раздела сред. Полное поле $U(x,y)$ вне структуры (1) представим в виде суперпозиции падающего ${{U}^{0}}(x,y)$ и рассеянного ${{U}^{S}}(x,y)$ полей

где падающее поле задано функцией

Полное поле внутри структуры (1) обозначим ${{U}^{P}}(x,y)$.

Рассеянное поле в цилиндрической системе координат ($r,\varphi $), где $x = r\cos \varphi $ и $y = r\sin \varphi $, в дальней зоне ($kr \to \infty $) должно удовлетворять условию излучения

где $\Phi (\varphi )$ − диаграмма рассеяния.

Полное сечение рассеяния ${{\sigma }_{s}}$ и сечение поглощения ${{\sigma }_{a}}$ определяются формулами

2. КВАЗИСТАТИЧЕСКОЕ ПРИБЛИЖЕНИЕ

Рассмотрим сначала случай, когда максимальный размер структуры (1) $ka \ll 1$. Тогда внутри структуры (1) и в статической близости от нее ($kr \ll 1$) волновое поле $U(x,y)$ будет приближенно удовлетворять уравнению Лапласа

Далее будем использовать координаты эллиптического цилиндра $\nu ,\;\mu $ [13]. Как известно, они связаны с декартовыми координатами $x,y$ формулами

Отметим, что при ν ⪢ 1 связь между координатами $\nu ,\mu $ и цилиндрическими координатами $r,\varphi $ имеет вид

В координатах эллиптического цилиндра границы раздела сред определяются формулой

где

В переменных $\nu ,\mu $ уравнение Лапласа (11) сохраняет свою каноническую форму

На границе $\nu = {{\nu }_{1}}$ условия непрерывности величин $U$ и $\frac{1}{\varepsilon }\frac{{\partial U}}{{\partial N}}$ приобретают вид

Покажем, что при некоторых дискретных значениях диэлектрической проницаемости оболочки ε_m существуют убывающие при $\nu \to \infty $ решения однородной краевой задачи (16), (17).

Исследуемая структура симметрична относительно плоскости $y = 0$. Поэтому искомые собственные колебания можно разделить на два класса, которым будут соответствовать четные и нечетные по координате $y$ функции ${{U}^{ + }}(\nu ,\mu )$ и ${{U}^{ - }}(\nu ,\mu )$. Используя метод разделения переменных, получим следующие выражения для полей собственных колебаний:

Граничные условия (17), примененные к выражениям (18), (19), приводят к системам однородных линейных алгебраических уравнений для неизвестных коэффициентов $A_{m}^{ \pm },\;B_{m}^{ \pm }$. Приравняв к нулю детерминанты этих систем, получим характеристические уравнения для резонансных значений $\varepsilon _{m}^{ \pm }$. Используя формулы (15), характеристические уравнения можно представить в виде

Таким образом, круговая симметрия приводит к вырождению колебаний ${{U}^{ + }}$ и ${{U}^{ - }}$. Более того, для кругового цилиндра (когда $a = b$) из (20) следует, что все мультипольные резонансы для серебряного цилиндра вырождаются и имеют место при $\varepsilon _{m}^{ \pm } = - 1$ для любого $m$.

Наличие нетривиальных решений однородного уравнения Лапласа означает, что для структур малых электрических размеров дифракционное поле, найденное из уравнения Гельмгольца, будет резко возрастать при приближении комплексной диэлектрической проницаемости $\varepsilon (\lambda )$ к вещественным собственным значениям $\varepsilon _{m}^{ \pm }$. Величины $\varepsilon _{m}^{ \pm }$ удовлетворяют уравнению (20). Следовательно, значение функции $\varepsilon (\lambda )$ в некоторой точке исследуемого диапазона длин волн может приблизиться к этому корню.

Вне области резонансного рассеяния квазистатический подход позволяет получить простое явное выражение для диаграммы рассеяния $\Phi (\varphi )$. Поле падающей плоской волны (6) при $kx \ll 1$ и $ky \ll 1$ будем аппроксимировать выражением

Очевидно, что первое слагаемое в (21) можно не принимать во внимание, так как оно не дает вклада в электрическое поле. Перейдем в (21) к координатам $\nu ,\mu $

Решение задачи возбуждения структуры внешним полем (22) можно получить в явном виде методом разделения переменных. При этом потребуются лишь дипольные гармоники $\cos \mu $ и $\sin \mu $. В частности, для рассеянного поля получим

где

Выразим в (23) координаты $\nu ,\mu $ через полярные координаты $r,\varphi $ и положим $r \to \infty $

Продолжив при помощи функции Ганкеля $H_{1}^{{(2)}}(kr)$ статическое поле (25) в дальнюю зону, получим следующее выражение для диаграммы рассеяния:

Заметим, что выражение для диаграммы рассеяния кругового цилиндра радиусом $a$ следует из (26)

Подставив (26) в (9), найдем полное сечение рассеяния

3. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Численное решение сформулированной задачи проводилось модифицированным методом дискретных источников [14, 15]. При этом точность решения задачи контролировалась путем вычисления невязки $\delta $ граничных условий в линейной норме в точках, расположенных в середине между точками, где граничные условия выполняются точно (в таких точках граничные условия выполняются наихудшим образом [11]). Во всех приведенных ниже расчетах максимальная невязка граничных условий не превышает величину $\delta < {{10}^{{ - 3}}}$.

Рассмотрим сначала поведение нормированного поперечника рассеяния $k{{\sigma }_{s}}$ в зависимости от длины волны $\lambda $ для случая серебряной структуры (см. рис. 1) при различных углах падения ${{\varphi }_{0}}$ плоской волны. Отметим, что во всех представленных ниже результатах, $\lambda $ изменяется в пределах 300 нм < < λ < 600 нм, для серебра и $300\,\,{\text{нм}} < \lambda < 900\,\,{\text{нм}}$ для золота.

На рис. 2а–2в представлены зависимости нормированных сечений рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ для эллиптической структуры с различными соотношениями полуосей а/b (нм): 50/50, 50/45, 50/25, 50/15, 50/5, и для трех значениях угла падения плоской волны ${{\varphi }_{0}} = 0$ (а), π/4 (б) и π/2 (в).

Рис. 2.

Зависимости нормированных сечений рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ при угле падения плоской волны ${{\varphi }_{0}} = 0$ (а), ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ (б), ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ (в) для структуры из серебра с соотношением полуосей: а = 50 нм (1–5), b = 50 (1), 0.9а (2), 0.5а (3), 0.3а (4), 0.1а нм (5).

Из рис. 2а–2в видно, что при различных углах падения плоской волны и указанных выше параметрах структуры нормированное сечение рассеяния $k{{\sigma }_{s}}$ имеет только один максимум. При этом расположение максимума $k{{\sigma }_{s}}$ на оси длин волн $\lambda $ зависит от отношенияи полуосей ${b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a}$ – чем оно меньше, тем больше и дальше он сдвигается по оси длин волн. Заметим, что существование такого максимума объясняется наличием дипольного резонанса поверхностных плазмонов.

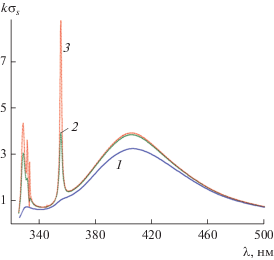
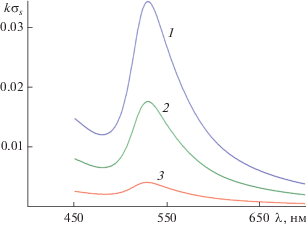
Рисунок 3 иллюстрирует влияние потерь серебра на зависимость полных сечений рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ для структуры с соотношением полуосей $a = 50\,\,{\text{нм}};b = 0.3a$ и угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$. Кривая 1 этого рисунка соответствует случаю реальных потерь серебра, которые определяются значениями мнимой части относительной диэлектрической проницаемости серебра $\operatorname{Im} ({{\varepsilon }_{{{\text{Ag}}}}})$ (см. рис. 2а), кривая 2 – случаю, когда мнимая часть относительной диэлектрической проницаемости серебра равна $0.1\operatorname{Im} (\varepsilon )$, а кривая 3 – случаю, когда мнимая часть относительной диэлектрической проницаемости серебра равна $0.001\operatorname{Im} (\varepsilon )$. Из рис. 3 следует, что при малых потерях серебра наблюдается серия максимумов $k{{\sigma }_{s}}$, связанных как с дипольным резонансом (в окрестности $\lambda \approx 406\,\,{\text{нм}}$), так и мултипольными резонансами (в окрестности $\lambda \approx 330...360$ нм). Однако реальные потери серебра приводят не только к уменьшению амплитуд максимумов резонансов $k{{\sigma }_{s}}$, но к фактическому исчезновению мультипольных резонансов.

Рис. 3.

Зависимости нормированных сечений рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ при угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ для структуры из серебра с соотношением полуосей $a = 50\,\,{\text{нм}};\,\,\,b = 0.3a$; кривая 1 – $\operatorname{Im} ({{\varepsilon }_{{{\text{Ag}}}}})$, кривая 2 – 0.1$\operatorname{Im} ({{\varepsilon }_{{{\text{Ag}}}}})$, кривая 3 – 0.001$\operatorname{Im} ({{\varepsilon }_{{{\text{Ag}}}}})$.

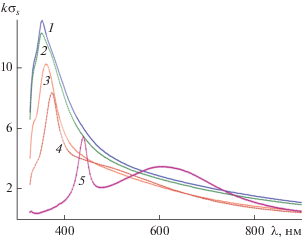
На рис. 4 изображены зависимости нормированных сечений рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ для эллиптической структуры из серебра, большая полуось $a$ которой в два раза превышает размеры большой полуоси предыдущей структуры. Угол падения плоской волны был равен ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$. При этом соотношение полуосей а/b (нм) полагались равными: 100/100, 100/90, 100/50, 100/15, 100/10. Из рис. 4 видно, что при a = 100 нм; $b = 10\,\,{\text{нм}}$ (кривая 5) нормированное сечение рассеяния $k{{\sigma }_{s}}$ имеет два максимума, а при больших значениях отношения полуосей ${b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a}$ только один максимум $k{{\sigma }_{s}}$.

Рис. 4.

Зависимости нормированных сечений рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ при угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ для структуры из серебра с соотношением полуосей: а = 100 нм (1–5), b = 100 (1), 0.9а (2), 0.5а (3), 0.3а (4), 0.1а нм (5).

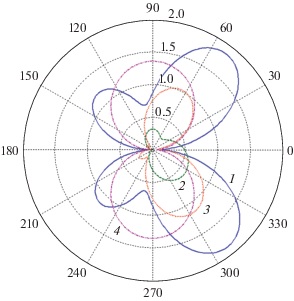
На рис. 5а и 5б представлены соответственно результаты расчетов нормированных сечений рассеяния $k{{\sigma }_{s}}$ и поглощения $k{{\sigma }_{a}}$ для разных длин волн $\lambda $ в случае эллиптической структуры из серебра при угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$, у которой малая полуось равнялась $b = 10\,\,{\text{нм}}$ и оставалась постоянной, а большая полуось $a$ принимала соответственно значения 200, 150 и 100 нм. Из рис. 5а (кривые 1 и 2) следует, что при $a = 200\,\,{\text{нм}}$ и $a = 150\,\,{\text{нм}}$ имеет место как дипольный резонанс, так и два мультипольных резонанса. Уменьшение размера большой полуоси приводит к уменьшению числа мультипольных резонансов (кривая 3, $a = 100\,\,{\text{нм}}$).

Рис. 5.

Зависимости нормированных сечений рассеяния (а) и поглощения (б) $k{{\sigma }_{s}}$ от длины волны $\lambda $ при угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ для структуры из серебра при фиксированном значении малой полуоси $b = 10\,\,{\text{нм}}$ и различных значениях большой полуоси: а = 200 (1), 150 (2) и 100 нм (3).

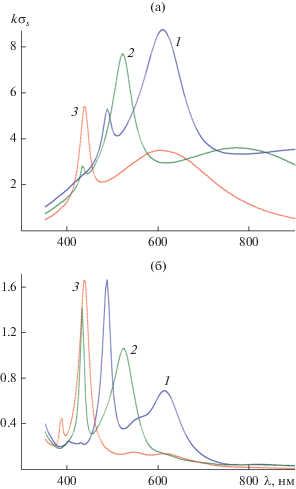
Сравнение результатов, представленных на рис. 5а и 5б показывает приблизительное соответствие в расположении максимумом соответствующих кривых.

На рис. 6 представлены зависимости нормированных сечений рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ для эллиптической структуры из золота. Угол падения плоской волны равнялся ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ при различных соотношениях полуосей а/b (нм) : 50/5, 100/10, 150/15, 200/20. Из рис. 6 следует, что структуры из золота также имеют максимумы, расположение которых зависит от отношения ${b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a}$. При этом дипольный резонанс наблюдается при больших значениях $\lambda $, чем у соответствующих структур из серебра.

Рис. 6.

Зависимости нормированных сечений рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ при угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ для структуры из золота с соотношением полуосей а/b (нм): 50/5 (1), 100/10 (2), 150/15 (3), 200/20 (4).

На рис. 7 и 8 изображены результаты расчетов нормированных нормированных сечений рассеяния $k{{\sigma }_{s}}$ для различных длин волн $\lambda $ в случае эллиптической структуры из золота, полученные в результате строгого численного решения задачи дифракции и приближенного решения (28). При расчетах считалось, что структура из золота имела размеры $a = 20\,\,{\text{нм}},\,\,b = 5\,\,{\text{нм}}$, а угол падения плоской волны φ₀ равнялся π/2, π/4 и π/10. Сравнение результатов, представленных на этих рисунках показывает, что квазистатическое приближение не только качественно, но и довольно хорошо количественно описывает поперечник рассеяния структуры.

Рис. 7.

Результаты строгого расчета зависимости нормированного сечения рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ для структуры из золота с соотношением полуосей $a = 20\,\,{\text{нм,}}\,\,b = 6\,\,{\text{нм}}$ и углах падения плоской волны φ₀ = π/2 (1), π/4 (2) и π/10 (3).

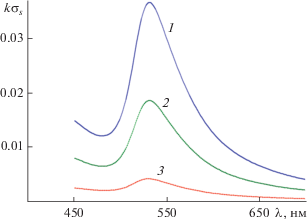
Рис. 8.

Результаты квазистатического расчета по формуле (28) зависимости нормированных сечений рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ для структуры из золота с соотношением полуосей $a = 20\,\,{\text{нм,}}\,\,b = 6\,\,{\text{нм}}$ и углах падения плоской волны φ₀ = π/2 (1), π/4 (2) и π/10 (3).

Наконец, на рис. 9 показаны результаты расчета диаграммы рассеяния структуры из серебра. При этом считалось, что структура из серебра имеет размеры $a = 100\,\,{\text{нм}},\,\,b = 10\,\,{\text{нм}}$, а угол падения плоской волны был равен ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ при длинах волн λ = 440, 336.7, 410 и 610 нм. Отметим, что при $\lambda = 440\,\,{\text{нм}}$ имеет место квадрупольный резонанс плазмонов, а при $\lambda = 610\,\,{\text{нм}}$ – дипольный. Из рисунка следует, что длина волны и потери среды существенно влияют на характер диаграммы рассеяния.

Рис. 9.

Диаграмма рассеяния эллиптической структуры из серебра при $a = 100\,\,{\text{нм}};\,\,b = 10\,\,{\text{нм}}$, ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ и различных длинах волн: λ = 440 (1), 336.7 (2), 410 (3) и 610 нм (4).

ЗАКЛЮЧЕНИЕ

Рассмотрена дифракция плоской волны на цилиндрической 2D-структуре, представляющей собой круговой или эллиптический наноцилиндр из серебра (золота). Строгими численными методами рассчитаны спектральные и пространственные характеристики рассеянного поля. Исследовано влияние потерь среды, геометрических размеров структуры и угла падения плоской волны на поперечник рассеяния и диаграмму рассеяния. Установлено, что положение дипольного резонанса и число мультипольных резонансов для серебряной (золотой) наноструктуры зависит от среды структуры, толщины и длины структуры, а также угла падения плоской волны. Показано, что реальные потери серебра (золота) делают невозможным существование высших мультипольных резонансов.