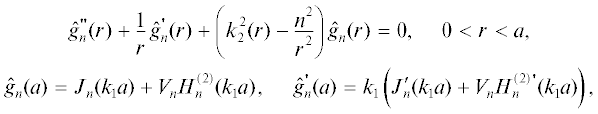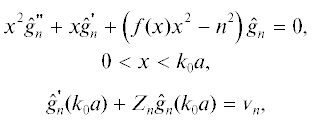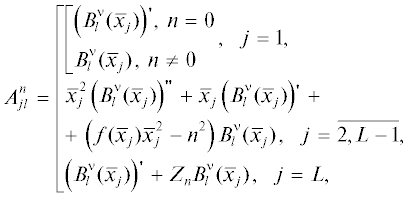Радиотехника и электроника, 2021, T. 66, № 3, стр. 236-244

Решение задачи дифракции на круговом неоднородном цилиндре, частично покрытом отражающим экраном

Д. В. Крысанов^a, А. Г. Кюркчан^a, b, c, С. А. Маненков^a, *

^a Московский технический университет связи и информатики
111024 Москва, ул. Авиамоторная, 8а, Российская Федерация

^b Фрязинский филиал Института радиотехники и электроники им. В.А. Котельникова РАН
141190 Фрязино, Московской обл., пл. Введенского, 1, Российская Федерация

^c Центральный научно-исследовательский институт связи
111141 Москва, 1-й проезд Перова поля, 8, Российская Федерация

^* E-mail: mail44471@mail.ru

Поступила в редакцию 04.05.2020
После доработки 04.05.2020
Принята к публикации 15.06.2020

DOI: 10.31857/S0033849421030128

Полный текст (PDF)

Аннотация

На основе метода продолженных граничных условий разработан алгоритм численного решения двумерной задачи дифракции на диэлектрическом цилиндре с волновым числом, зависящим от радиальной координаты, который частично покрыт идеально отражающим экраном. Метод протестирован для случая однородной среды внутри диэлектрического цилиндра. Проведена проверка точности выполнения оптической теоремы для различных зависимостей волнового числа от радиальной координаты и построены угловые зависимости диаграммы рассеяния для различных углов раскрыва отражающего экрана.

ВВЕДЕНИЕ

Частицы, покрытые тонкими экранами (в частности, частицы Януса), представляют большой интерес в антенной технике, медицине и биологии. Они используются также в качестве основных элементов для разработки новых материалов с интересными новыми свойствами. Однако рассеяние волн на таких структурах исследовано достаточно слабо (см., например, [1, 2]). Для решения данной задачи дифракции использовались, например, метод интегральных уравнений [1] и метод T-матриц [2].

В данной работе рассмотрена двумерная задача дифракции плоской волны на бесконечном круговом диэлектрическом цилиндре, частичнопокрытом бесконечно тонким круговым экраном. При этом предполагается, что материальные характеристики среды цилиндра зависят от радиальной координаты. Отметим, что насколько известно авторам, в литературе рассмотрены задачи дифракции на однородных цилиндрических и сферических частицах, покрытых экранами, т.е. не исследуется более сложный случай неоднородной среды внутри тела, который рассмотрен в данной работе. Задача рассеяния на покрытом цилиндре решалась методом продолженных граничных условий (МПГУ), который успешно применялся ранее к решению широкого круга задач теории дифракции [3–6]. Для решения задачи дифракции с помощью МПГУ в работе использована функция Грина (ФГ) неоднородного кругового цилиндра. При этом исходная краевая задача сводится к решению интегрального уравнения первого рода относительно тока на поверхности экрана с ядром, выражающимся через ФГ цилиндра. Основной трудностью при решении рассматриваемой задачи дифракции является расчет ФГ неоднородного кругового цилиндра. Для преодоления этой трудности в работе применялась методика, аналогичная технике, предложенной в работах [7, 8], в которых рассмотрена задача дифракции на теле, расположенном в плоскослоистом волноводе с переменным волновым числом и на неоднородной диэлектрической сфере соответственно.

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим математическую постановку задачи. Пусть бесконечный диэлектрический круговой цилиндр радиусом a покрыт бесконечно тонким экраном $S$ с углом раскрыва $2\gamma $. Введем цилиндрическую систему координат, причем ось z направим вдоль оси цилиндра. Геометрия задачи изображена на рис. 1. Предполагаем, что относительные значения материальных параметров среды внутри цилиндра ${{\mu }_{2}} = {{\mu }_{2}}(r)$ и ${{\varepsilon }_{2}} = {{\varepsilon }_{2}}(r)$, а снаружи – ${{\mu }_{1}},\;{{\varepsilon }_{1}}$. Будем рассматривать случай Е-поляризации, когда вектор напряженности электрического поля $\vec {E}$ имеет только одну составляющую ${{E}_{z}}$ (далее – $U$), параллельную образующей цилиндрического тела. Тогда будут иметь место следующие граничные условия (для упрощения выкладок будем считать, что магнитная проницаемость всюду равна единице):

(1)

${{\left. U \right|}_{{r = a}}} = 0,\,\,\,\,\varphi \in [ - \gamma ,\gamma ],$

(2)

${{\left. {\left[ U \right]} \right|}_{{r = a}}} = 0,\,\,\,{{\left. {\left[ {\frac{{\partial U}}{{\partial r}}} \right]} \right|}_{{r = a}}} = 0,\,\,\,\,\varphi \notin [ - \gamma ,\gamma ],$

Рис. 1.

Геометрия задачи.

где квадратные скобки означают скачок соответствующей величины. Поле внутри и вне кругового цилиндра удовлетворяет уравнениям Гельмгольца:

(3)

$\begin{gathered} \Delta U + k_{1}^{2}U = 0,\,\,\,r > a, \\ \Delta U + k_{2}^{2}(r)U = 0,\,\,\,\,{\text{0}} < r < a, \\ \end{gathered} $

где ${{k}_{1}} = \omega \sqrt {{{\varepsilon }_{1}}} $, ${{k}_{2}}(r) = \omega \sqrt {{{\varepsilon }_{2}}(r)} $ – волновое число среды вне и внутри цилиндра ($\omega $ – круговая частота). Предполагаем, что структура облучается плоской волной:

(4)

${{U}_{{{\text{пад}}}}} = \exp ( - i{{k}_{1}}r\cos (\varphi - {{\varphi }_{0}})).$

На бесконечности предполагаются выполненными стандартные условия излучения для рассеянного поля.

2. РЕШЕНИЕ ЗАДАЧИ МЕТОДОМ ПРОДОЛЖЕННЫХ ГРАНИЧНЫХ УСЛОВИЙ

Применим МПГУ для решения поставленной задачи дифракции. С этой целью представим поле вне и внутри диэлектрического цилиндра в виде

(5)

$U(\vec {r}) = {{U}^{0}}(\vec {r}) + \int\limits_S {j(\vec {r}{\kern 1pt} ')G(\vec {r},\vec {r}{\kern 1pt} ')ds{\kern 1pt} '} ,$

где ${{U}^{0}}(\vec {r})$ – первичное поле, определяемое из решения задачи дифракции на цилиндре в отсутствие экрана, $j(\vec {r}{\kern 1pt} ') = {{\left[ {\frac{{\partial U}}{{\partial r{\kern 1pt} '}}} \right]}_{\begin{subarray}{l} r = a \\ \left| \varphi \right| < \gamma \end{subarray} }}$ – неизвестный ток на поверхности экрана. В формуле (5) $G(\vec {r},\vec {r}{\kern 1pt} ')$ – функция Грина кругового цилиндра, которая имеет вид

(6)

$G(\vec {r},\vec {r}{\kern 1pt} ') = \left\{ \begin{gathered} \frac{i}{4}\left( {H_{0}^{{(2)}}({{k}_{1}}\left| {\vec {r} - \vec {r}{\kern 1pt} '} \right|) + \sum\limits_{n = - \infty }^\infty {{{V}_{n}}H_{n}^{{(2)}}({{k}_{1}}r{\kern 1pt} ')H_{n}^{{(2)}}({{k}_{1}}r)\exp \left( {in(\varphi - \varphi {\kern 1pt} ')} \right)} } \right),\,\,\,r > a, \hfill \\ \frac{i}{4}\sum\limits_{n = - \infty }^\infty {H_{n}^{{(2)}}({{k}_{1}}r{\kern 1pt} '){{{\hat {g}}}_{n}}(r)\exp \left( {in(\varphi - \varphi {\kern 1pt} ')} \right)} ,{\text{ 0}} < r < a. \hfill \\ \end{gathered} \right.$

Здесь величины ${{V}_{n}}$ и функции ${{\hat {g}}_{n}}(r)$ определяются из решения следующей краевой задачи [8]:

(7)

где $n = 0, \pm 1, \pm 2,....$ Заметим, что первичное поле вне цилиндра имеет вид

(8)

$\begin{gathered} {{U}^{0}}(\vec {r}) = \exp ( - i{{k}_{1}}r\cos (\varphi - {{\varphi }_{0}})) + \\ + \,\,\sum\limits_{n = - \infty }^\infty {{{i}^{{ - n}}}{{V}_{n}}H_{n}^{{(2)}}({{k}_{1}}r)\exp (in(\varphi - {{\varphi }_{0}}))} . \\ \end{gathered} $

В соответствии с МПГУ подставим далее формулу (5) в граничное условие вида (1) на вспомогательном контуре ${{S}_{\delta }}$, смещенном на малое расстояние $\delta $ от экрана [3–6]. В результате задача сведется к решению одномерного интегрального уравнения первого рода относительно функции $j(\vec {r}{\kern 1pt} ') \equiv j(\varphi {\kern 1pt} ')$:

(9)

$\int\limits_{ - \gamma }^\gamma {{{G}_{\delta }}(\varphi ,\varphi {\kern 1pt} ')j(\varphi {\kern 1pt} ')ad\varphi {\kern 1pt} '} = - {{U}^{0}}(a + \delta ,\varphi ),\,\,\,\varphi \in \left[ { - \gamma ,\gamma } \right],$

где

(10)

$\begin{gathered} {{G}_{\delta }}(\varphi ,\varphi {\kern 1pt} ') = \frac{i}{4}\left( {H_{0}^{{(2)}}({{k}_{1}}{{R}_{\delta }})} \right. + \\ \left. { + \,\,\sum\limits_{n = - \infty }^\infty {{{V}_{n}}H_{n}^{{(2)}}({{k}_{1}}a)H_{n}^{{(2)}}({{k}_{1}}(a + \delta ))\exp (in(\varphi - \varphi {\kern 1pt} '))} } \right), \\ \end{gathered} $

(11)

${{R}_{\delta }} = \sqrt {{{{(a + \delta )}}^{2}} + {{a}^{2}} - 2(a + \delta )a\cos (\varphi - \varphi {\kern 1pt} ')} .$

Интегральное уравнение (9) решаем методом Крылова–Боголюбова. С этой целью введем сетку на интервале $\left[ { - \gamma ,\gamma } \right]$:

(12)

${{\varphi }_{p}} = - \gamma + \Delta \left( {p - \frac{1}{2}} \right){\text{,}}\,\,\,\,\Delta = \frac{{2\gamma }}{N},\,\,\,\,p = 1,2,...,N.$

Далее запишем неизвестную токовую функцию $j(\varphi {\kern 1pt} ')$ в виде

(13)

$j(\varphi {\kern 1pt} ') = \sum\limits_{q = 1}^N {{{c}_{q}}{{\psi }_{q}}(\varphi {\kern 1pt} ')} ,$

где ${{\psi }_{q}}(\varphi {\kern 1pt} ')$ – импульсные функции:

(14)

${{\psi }_{q}}(\varphi {\kern 1pt} ') = \left\{ \begin{gathered} 1,\,\,\,\,\varphi {\kern 1pt} ' \in [{{\varphi }_{q}} - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2},\,\,{{\varphi }_{q}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}], \hfill \\ 0,\,\,\,\,\varphi {\kern 1pt} ' \notin [{{\varphi }_{q}} - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2},\,\,{{\varphi }_{q}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}]. \hfill \\ \end{gathered} \right.$

Подставив (13) в интегральное уравнение (9) и приравняв левую и правую части в точках коллокации ${{\varphi }_{p}}$, выбранных на вспомогательном контуре $S_{\delta }^{{}}$, получим следующую систему алгебраических уравнений относительно величин $c_{q}^{{}}$:

(15)

$\sum\limits_{q = 1}^N {{{G}_{{pq}}}c_{q}^{{}}} = b_{p}^{{}},\,\,\,\,p = \overline {1,N} ,$

в которой матричные элементы и правые части имеют вид

(16)

$\begin{gathered} {{G}_{{pq}}} = \int\limits_{{{\varphi }_{q}}\, - \,\,\frac{\Delta }{2}}^{{{\varphi }_{q}}\, + \,\,\frac{\Delta }{2}} {{{G}_{\delta }}({{\varphi }_{p}},\varphi \,')ad\varphi {\kern 1pt} '} , \\ {{b}_{p}} = - {{U}^{0}}(a + \delta ,{{\varphi }_{p}}),\,\,\,\,p,q = \overline {1,N} . \\ \end{gathered} $

Учитывая, что второе слагаемое в формуле (10) является медленно меняющейся функцией переменных $\varphi $ и $\varphi {\kern 1pt} '$, матричные элементы можно приближенно вычислять по формуле

(17)

$\begin{gathered} {{G}_{{pq}}} \approx \frac{i}{4}\int\limits_{{{\varphi }_{q}}\, - \,\,\,\,\frac{\Delta }{2}}^{{{\varphi }_{q}}\, + \,\,\frac{\Delta }{2}} {H_{0}^{{(2)}}({{k}_{1}}{{R}_{{\delta ,pq}}})ad\varphi {\kern 1pt} '} + \\ + \,\,\frac{i}{4}\Delta a\sum\limits_{n = - \infty }^\infty {{{V}_{n}}H_{n}^{{(2)}}({{k}_{1}}a)H_{n}^{{(2)}}\left( {{{k}_{1}}(a + \delta )} \right) \times } \\ \times \,\,\exp (in({{\varphi }_{p}} - {{\varphi }_{q}})), \\ \end{gathered} $

где

${{R}_{{\delta ,pq}}} = \sqrt {{{{(a + \delta )}}^{2}} + {{a}^{2}} - 2a(a + \delta )\cos ({{\varphi }_{p}} - {{\varphi }_{q}})} .$

После нахождения коэффициентов $c_{q}^{{}}$ из системы (15) можно найти диаграмму рассеяния, которая определяется соотношением

(18)

${{U}^{1}}(r,\varphi ) \sim \sqrt {\frac{2}{{\pi {{k}_{1}}r}}} g(\varphi )\exp \left( { - i{{k}_{1}}r + i\frac{\pi }{4}} \right),$

где

(19)

$g(\varphi ) = {{g}_{0}}(\varphi ) + {{g}_{1}}(\varphi ),$

(20)

${{g}_{0}}(\varphi ) = \sum\limits_{n = - \infty }^\infty {{{V}_{n}}\exp (in(\varphi - {{\varphi }_{0}}))} ,$

(21)

$\begin{gathered} {{g}_{1}}(\varphi ) = \frac{{ia\Delta }}{4}\sum\limits_{q = 1}^N {{{c}_{q}}\left[ {\exp (i{{k}_{1}}a\cos (\varphi - {{\varphi }_{q}})) + \frac{{^{{}}}}{{}}} \right.} \\ \left. { + \,\,\sum\limits_{n = - \infty }^\infty {{{i}^{n}}{{V}_{n}}H_{n}^{{(2)}}({{k}_{1}}a)\exp (in(\varphi - {{\varphi }_{q}}))} } \right]. \\ \end{gathered} $

3. ЧИСЛЕННЫЙ АЛГОРИТМ НАХОЖДЕНИЯ ФУНКЦИИ ГРИНА ЦИЛИНДРА

Рассмотрим вопрос о вычислении ядра интегрального уравнения (9), т.е. вычисление ФГ $G(\vec {r},\vec {r}{\kern 1pt} ')$. Отметим, что в случае постоянного волнового числа внутри цилиндра функцию ${{\hat {g}}_{n}}(r)$ следует искать в виде

(22)

${{\hat {g}}_{n}}(r) = {{W}_{n}}{{J}_{n}}({{k}_{2}}r),$

где величина ${{W}_{n}}$ имеет смысл “коэффициента прохождения” цилиндрической волны при решении задачи дифракции поля нити тока на круговом цилиндре (без экрана). Тогда из второй и третьей формул (7) получим

(23)

${{V}_{n}} = \frac{{{{\kappa }_{{12}}}J_{n}^{'}({{k}_{1}}a){{J}_{n}}({{k}_{2}}a) - {{J}_{n}}({{k}_{1}}a)J_{n}^{'}({{k}_{2}}a)}}{{H_{n}^{{(2)}}({{k}_{1}}a)J_{n}^{'}({{k}_{2}}a) - {{\kappa }_{{12}}}H_{n}^{{(2)}}({{k}_{1}}a){{J}_{n}}({{k}_{2}}a)}},$

где ${{\kappa }_{{12}}} = {{{{k}_{1}}} \mathord{\left/ {\vphantom {{{{k}_{1}}} {{{k}_{2}}}}} \right. \kern-0em} {{{k}_{2}}}}$. В случае, когда волновое число ${{k}_{2}}$ зависит от радиальной координаты, приходится находить ФГ численно. С этой целью удобно применить подход, изложенный в работах [7, 8]. Сделаем замену $x = {{k}_{0}}r$, где ${{k}_{0}} = {{k}_{2}}(0)$, и обозначим $k_{2}^{2}(r) = k_{0}^{2}f(x)$, причем $f(0) = 1$. Тогда для ${{\hat {g}}_{n}}(x)$ получаем краевую задачу

(24)

где

(25)

$\begin{gathered} {{Z}_{n}} = - {{\kappa }_{{10}}}\frac{{H_{n}^{{(2)'}}({{k}_{1}}a)}}{{H_{n}^{{(2)}}({{k}_{1}}a)}},\,\,\,\,{{v}_{n}} = \frac{{2i{{\kappa }_{{10}}}}}{{\pi {{k}_{1}}aH_{n}^{{(2)}}({{k}_{1}}a)}}, \\ {{\kappa }_{{10}}} = \frac{{{{k}_{1}}}}{{{{k}_{0}}}},\,\,\,\,n = 0, \pm 1, \pm 2,.... \\ \end{gathered} $

При этом

(26)

${{V}_{n}} = \frac{{{{{\hat {g}}}_{n}}({{k}_{0}}a) - {{J}_{n}}({{k}_{1}}a)}}{{H_{n}^{{(2)}}({{k}_{1}}a)}}.$

Далее решаем краевую задачу (24) с помощью сплайнов. Выберем точки коллокации на интервале $\left[ {0,{{k}_{0}}a} \right]$:

(27)

${{\bar {x}}_{j}} = \frac{{{{k}_{0}}a(j - 1)}}{{L - 1}},\,\,\,\,j = \overline {1,L} .$

Затем введем сетку на рассматриваемом интервале:

(28)

${{x}_{j}} = \left[ \begin{gathered} \frac{{{{k}_{0}}a(j - \nu )}}{{L - 1}},\,\,\,\,j = 1,2,...,\nu , \hfill \\ {{{\bar {x}}}_{{j - {\nu \mathord{\left/ {\vphantom {\nu 2}} \right. \kern-0em} 2}}}},\,\,\,\,j = \nu + 1,...,L, \hfill \\ {{k}_{0}}a\left( {1 + \frac{{j - L - 1}}{{L - 1}}} \right),\,\,\,j = L + 1,...,L + \nu . \hfill \\ \end{gathered} \right.$

В формуле (28) $\nu $– порядок сплайнов, причем $\nu $ – четное число. Данный выбор узлов сетки соответствует условию в концевых точках интервала $\left[ {0,{{k}_{0}}a} \right]$ типа “нет узла” [9]. Далее запишем

(29)

${{g}_{n}}(x) = \sum\limits_{l = 1}^L {a_{l}^{n}B_{l}^{\nu }(x)} ,$

где $B_{l}^{\nu }(x)$ – В-сплайн порядка $\nu $, $a_{l}^{n}$ – неизвестные коэффициенты. Коэффициенты $a_{l}^{n}$ при базисных функциях удовлетворяют линейной системе, получаемой методом коллокации:

(30)

$\sum\limits_{l = 1}^L {A_{{jl}}^{n}a_{l}^{n} = w_{j}^{n}} ,\,\,\,\,j = \overline {1,L} ,\,\,\,\,n = 0, \pm 1, \pm 2, \ldots ,$

где

(31)

(32)

$w_{j}^{n} = \left[ \begin{gathered} 0,\,\,\,\,j = \overline {1,L - 1} , \hfill \\ {{v}_{n}},\,\,\,\,{\text{ }}j = L. \hfill \\ \end{gathered} \right.$

Видно, что матричные элементы данной системы зависят от значений сплайнов и их производных в точках коллокации. Поэтому, вычислив заранее значения сплайнов и их производных, можно существенно сократить время вычислений на ЭВМ.

Одним из критериев правильности полученных результатов является оптическая теорема, которая записывается в виде [10]

(33)

$\sigma = - \operatorname{Re} (g(\varphi = {{\varphi }_{0}})),$

где

(34)

$\sigma = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {{{{\left| {g(\varphi )} \right|}}^{2}}d\varphi } .$

В качестве оценки точности выполнения оптической теоремы будем рассчитывать величину, которая представляет собой относительную разность левой и правой частей в формуле (33):

(35)

${{\Delta }_{{{\text{отн}}}}} \equiv \frac{{\left| {\sigma + \operatorname{Re} (g({{\varphi }_{0}}))} \right|}}{\sigma }.$

4. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Рассмотрим результаты численного моделирования. Как уже было указано выше, будем считать, что относительная магнитная проницаемость всюду равна единице. Относительную диэлектрическую проницаемость среды вне цилиндра ${{\varepsilon }_{1}}$ также примем равной единице. Диэлектрическую проницаемость среды внутри цилиндра возьмем равной ${{\varepsilon }_{2}} = 2.25$.

В табл. 1 приведены результаты проверки точности выполнения оптической теоремы для случая однородной среды внутри цилиндра для указанных материальных параметров сред. Параметр $k\delta $ всюду брали равным $k\delta = {{10}^{{ - 4}}}$, где $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$ ($\lambda $ – длина волны). Угол раскрыва отражающего экрана был равен 2γ = π/2, угол падения первичной волны ${{\varphi }_{0}} = 0$. Рассматривались два различных радиуса кругового цилиндра. Из таблицы видно, что относительная разность правой и левой частей равенства (33) – величина ${{\Delta }_{{{\text{отн}}}}}$ – уменьшается с ростом числа базисных функций $N$ и имеет достаточно малое значение. При одинаковых $N$ для тела малых размеров точность выполнения оптической теоремы на порядок выше.

Таблица 1.

Точность выполнения оптической теоремы для случая однородной среды внутри цилиндра

N	${{\sigma }_{s}}$	$ - \operatorname{Re} (g({{\varphi }_{0}}))$	${{\Delta }_{{{\text{отн}}}}}$
ka = 4
50	4.422194	4.420111	4.712 × 10^–4
100	4.415870	4.415245	1.416 × 10^–4
200	4.412940	4.412680	5.878 × 10^–5
400	4.411528	4.411360	3.805 × 10^–5
ka = 20
50	21.684342	21.433267	1.158 × 10^–2
100	21.467725	21.406531	2.851 × 10^–3
200	21.423223	21.407659	7.265 × 10^–4
400	21.416396	21.412148	1.984 × 10^–4

На рис. 2а, 2б приведены угловые зависимости диаграммы рассеяния для случая однородной среды внутри кругового цилиндра при различных значениях параметров геометрии задачи, указанных выше. Сравнивались результаты, полученные с использованием формул (22), (23), с результатами, найденными при помощи сплайн-аппроксимации ФГ (при этом принимаем, что$f(x) = 1$, т.е. ${{k}_{0}} \equiv {{k}_{2}}$). Порядок сплайнов брали равным $\nu = 6$, число точек коллокации $L = 100$. В табл. 2 приведены относительные разности модуля диаграммы рассеяния для указанного случая, полученные с помощью аналитического представления ФГ и численной методики. Как видно из табл. 2, разность результатов при увеличении числа используемых точек коллокации быстро уменьшается. Из приведенных данных также следует, что для тел малых волновых размеров сходимость результатов будет более быстрой.

Рис. 2.

Угловые зависимости диаграмм рассеяния однородного кругового цилиндра малых ka = 4 (а) и больших ka = 20 (б) волновых размеров, полученные с использованием аналитического метода нахождения ФГ (кривые 1) и численного алгоритма на основе сплайнов (кривые 2).

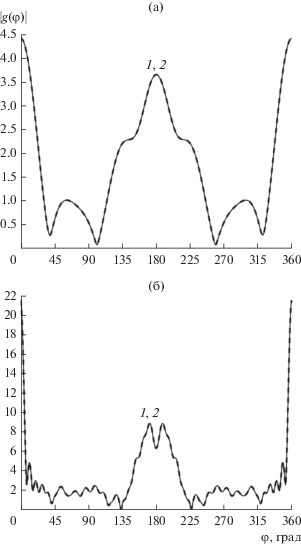
Таблица 2.

Относительная разность (%) между диаграммами рассеяния, полученными двумя методами. Случай однородной среды внутри цилиндра

L	ka=4	ka=8	ka = 16	ka = 20
50	0.014	0.028	0.886	2.445
100	0.0009	0.001	0.031	0.111
200	0.00004	0.00005	0.0011	0.004

На рис. 3, 4 приведены угловые зависимости диаграммы рассеяния для случая неоднородной среды внутри кругового цилиндра различных размеров при различных углах раскрыва отражающего экрана. Функция, описывающая изменение волнового числа внутри диэлектрического цилиндра от радиальной координаты, имела вид $f(x) = 1 - 0.1{{{{x}^{2}}} \mathord{\left/ {\vphantom {{{{x}^{2}}} {{{{({{k}_{0}}a)}}^{2}}}}} \right. \kern-0em} {{{{({{k}_{0}}a)}}^{2}}}}$. Порядок сплайнов и числа точек коллокации для нахождения ФГ и для решения интегрального уравнения выбирали следующими: $\nu = 6,{\text{ }}L = 200,{\text{ }}N = 400$. Для сравнения на рисунках представлена диаграмма рассеяния для идеально отражающего кругового цилиндра тех же волновых размеров. Как следует из приведенных рисунков, для исследуемых геометрий имеются максимумы угловых зависимостей диаграммы рассеяния в направлении прямого рассеяния. Из графиков также следует, что при угле падения φ₀ = 180° и при больших углах раскрыва диаграмма рассеяния цилиндра с экраном мало отличается от диаграммы идеально отражающего цилиндра (кривые 1). В случае угла падения ${{\varphi }_{0}} = 0^\circ $ соответствующие зависимости различаются существенно (кривые 1 и 2). Из рис. 4 видно, что для тела больших размеров зависимость диаграммы имеет осциллирующий характер, более выраженный при ${{\varphi }_{0}} = 180^\circ $. В случае малого волнового размера тела, не полностью покрытого экраном (при ${{\varphi }_{0}} = 0^\circ $), на всех графиках наблюдается максимум зависимости диаграммы в направлении обратного рассеяния. Его величина возрастает с уменьшением угла раскрыва экрана. В случае большого волнового размера тела (при ${{\varphi }_{0}} = 0^\circ $) для углов раскрыва $\gamma = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ и $\gamma = {\pi \mathord{\left/ {\vphantom {\pi {10}}} \right. \kern-0em} {10}}$ имеется провал графика диаграммы в окрестности $\varphi = 180^\circ $.

Рис. 3.

Угловые зависимости диаграмм рассеяния неоднородного кругового цилиндра радиусом ka = 4 для двух углов падения плоской волны: ${{\varphi }_{0}} = 0^\circ $ (а) и ${{\varphi }_{0}} = 180^\circ $ (б); угол раскрыва отражающего экрана: $\gamma = {{9\pi } \mathord{\left/ {\vphantom {{9\pi } {10}}} \right. \kern-0em} {10}}$ (кривые 2), $\gamma = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ (кривые 3), $\gamma = {\pi \mathord{\left/ {\vphantom {\pi {10}}} \right. \kern-0em} {10}}$ (кривые 4); кривые 1 соответствуют случаю идеально отражающего цилиндра. Зависимость f(x) = $ = 1 - {{0.1{{x}^{2}}} \mathord{\left/ {\vphantom {{0.1{{x}^{2}}} {{{{({{k}_{0}}a)}}^{2}}}}} \right. \kern-0em} {{{{({{k}_{0}}a)}}^{2}}}}$.

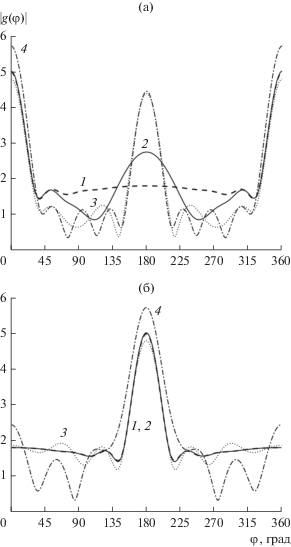
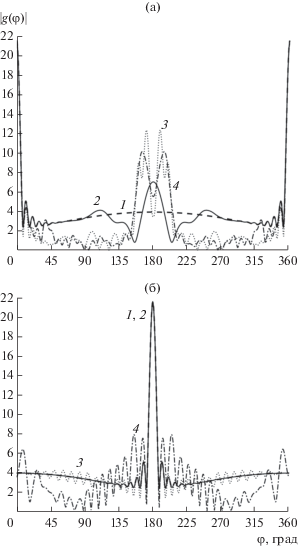
Рис. 4.

Угловые зависимости диаграмм рассеяния неоднородного кругового цилиндра радиусом ka = 20 для двух углов падения плоской волны: ${{\varphi }_{0}} = 0^\circ $ (а) и ${{\varphi }_{0}} = 180^\circ $ (б); угол раскрыва отражающего экрана: $\gamma = {{9\pi } \mathord{\left/ {\vphantom {{9\pi } {10}}} \right. \kern-0em} {10}}$ (кривые 2), $\gamma = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ (кривые 3), $\gamma = {\pi \mathord{\left/ {\vphantom {\pi {10}}} \right. \kern-0em} {10}}$ (кривые 4); кривые 1 соответствуют случаю идеально отражающего цилиндра. Зависимость f(x) = $ = 1 - {{0.1{{x}^{2}}} \mathord{\left/ {\vphantom {{0.1{{x}^{2}}} {{{{({{k}_{0}}a)}}^{2}}}}} \right. \kern-0em} {{{{({{k}_{0}}a)}}^{2}}}}$.

На рис. 5, 6 приведены диаграммы рассеяния частично покрытого цилиндра для тех же параметров задачи, но при $f(x) = 1 - 0.5{{{{x}^{2}}} \mathord{\left/ {\vphantom {{{{x}^{2}}} {{{{({{k}_{0}}a)}}^{2}}}}} \right. \kern-0em} {{{{({{k}_{0}}a)}}^{2}}}}$. Из рисунков следует, что характер полученных зависимостей в основном аналогичен предыдущим результатам. Однако имеются некоторые существенные отличия. Во-первых, в случае $ka = 4$ и φ₀ = 0° у зависимости диаграммы рассеяния, соответствующей углу раскрыва экрана γ = 9π/10, отсутствует максимум в направлении обратного рассеяния. Во-вторых, в случае $ka = 20$ и ${{\varphi }_{0}} = 0^\circ $ у зависимостей диаграммы рассеяния, соответствующих углам раскрыва экрана $\gamma = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ и $\gamma = {\pi \mathord{\left/ {\vphantom {\pi {10}}} \right. \kern-0em} {10}}$, имеются резкие максимумы в направлении обратного рассеяния. При этом у зависимости, соответствующей углу раскрыва $\gamma = {\pi \mathord{\left/ {\vphantom {\pi {10}}} \right. \kern-0em} {10}}$, в направлении обратного рассеяния максимум отсутствует.

Рис. 5.

Угловые зависимости диаграмм рассеяния неоднородного кругового цилиндра радиусом ka = 4 для двух углов падения плоской волны: ${{\varphi }_{0}} = 0^\circ $ (а) и ${{\varphi }_{0}} = 180^\circ $ (б); угол раскрыва отражающего экрана: $\gamma = {{9\pi } \mathord{\left/ {\vphantom {{9\pi } {10}}} \right. \kern-0em} {10}}$ (кривые 2), $\gamma = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ (кривые 3), $\gamma = {\pi \mathord{\left/ {\vphantom {\pi {10}}} \right. \kern-0em} {10}}$ (кривые 4); кривые 1 соответствуют случаю идеально отражающего цилиндра. Зависимость f(x) = $ = 1 - {{0.5{{x}^{2}}} \mathord{\left/ {\vphantom {{0.5{{x}^{2}}} {{{{({{k}_{0}}a)}}^{2}}}}} \right. \kern-0em} {{{{({{k}_{0}}a)}}^{2}}}}$.

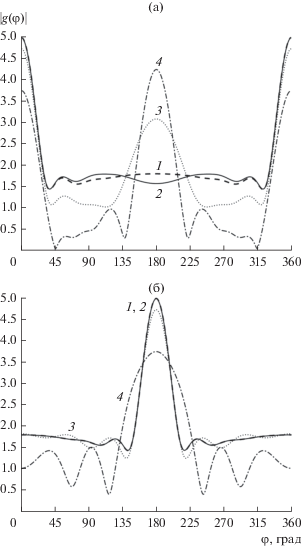
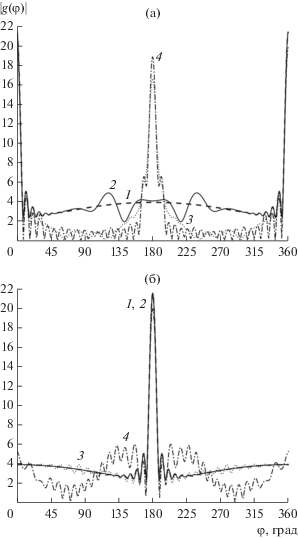
Рис. 6.

Угловые зависимости диаграмм рассеяния неоднородного кругового цилиндра радиусом ka = 20 для двух углов падения плоской волны: ${{\varphi }_{0}} = 0^\circ $ (а) и ${{\varphi }_{0}} = 180^\circ $ (б); угол раскрыва отражающего экрана: $\gamma = {{9\pi } \mathord{\left/ {\vphantom {{9\pi } {10}}} \right. \kern-0em} {10}}$ (кривые 2), $\gamma = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ (кривые 3), $\gamma = {\pi \mathord{\left/ {\vphantom {\pi {10}}} \right. \kern-0em} {10}}$ (кривые 4); кривые 1 соответствуют случаю идеально отражающего цилиндра. Зависимость f(x) $ = 1 - {{0.5{{x}^{2}}} \mathord{\left/ {\vphantom {{0.5{{x}^{2}}} {{{{({{k}_{0}}a)}}^{2}}}}} \right. \kern-0em} {{{{({{k}_{0}}a)}}^{2}}}}$.

В табл. 3 приведены результаты проверки точности выполнения оптической теоремы для рассмотренных на рис. 3–6 случаев. Из таблицы следует, что величина относительной погрешности ${{\Delta }_{{{\text{отн}}}}}$ не превышает 2.5 × 10^–3. Видно также, что точность значительно выше при меньших углах раскрыва отражающего экрана. Для тела больших размеров наблюдается резкий скачок улучшения точности выполнения оптической теоремы при малом угле раскрыва экрана (в случае $\gamma = {\pi \mathord{\left/ {\vphantom {\pi {10}}} \right. \kern-0em} {10}}$).

Таблица 3.

Точность выполнения оптической теоремы для случая неоднородной среды внутри цилиндра

${{\Delta }_{{{\text{отн}}}}}$	${{\varphi }_{0}} = 0$		${{\varphi }_{0}} = \pi $
${{\Delta }_{{{\text{отн}}}}}$	ka = 4	ka = 20	ka = 4	ka = 20
$f(x) = 1 - 0.1\frac{{{{x}^{2}}}}{{{{{({{k}_{0}}a)}}^{2}}}},{\text{ }}0 \leqslant x \leqslant {{k}_{0}}a$
$\gamma = {{9\pi } \mathord{\left/ {\vphantom {{9\pi } {10}}} \right. \kern-0em} {10}}$	1.518 × 10^–4	2.129 × 10^–3	7.033 × 10^–5	1.241 × 10^–3
$\gamma = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$	8.157 × 10^–5	1.133 × 10^–3	2.843 × 10^–5	3.654 × 10^–4
$\gamma = {\pi \mathord{\left/ {\vphantom {\pi {10}}} \right. \kern-0em} {10}}$	1.086 × 10^–5	1.111 × 10^–6	3.138 × 10^–6	3.271 × 10^–6
$f(x) = 1 - 0.5\frac{{{{x}^{2}}}}{{{{{({{k}_{0}}a)}}^{2}}}},{\text{ }}0 \leqslant x \leqslant {{k}_{0}}a$
$\gamma = {{9\pi } \mathord{\left/ {\vphantom {{9\pi } {10}}} \right. \kern-0em} {10}}$	8.053 × 10^–5	1.867 × 10^–3	5.473 × 10^–5	1.234 × 10^–3
$\gamma = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$	7.699 × 10^–5	4.379 × 10^–4	1.148 × 10^–5	3.562 × 10^–4
$\gamma = {\pi \mathord{\left/ {\vphantom {\pi {10}}} \right. \kern-0em} {10}}$	4.792 × 10^–5	4.197 × 10^–5	1.251 × 10^–5	1.335 × 10^–6

ЗАКЛЮЧЕНИЕ

Таким образом, с помощью метода продолженных граничных условий разработан численный алгоритм решения двумерной задачи дифракции на диэлектрическом цилиндре с волновым числом, зависящим от радиальной координаты, который частично покрыт идеально отражающим экраном. Разработан эффективный алгоритм вычисления ФГ неоднородного кругового цилиндра, основанный на использовании В-сплайнов. Проведено тестирование методики расчета ФГ на основе сплайнов для случая однородной среды внутри кругового цилиндра. Построены угловые зависимости диаграммы рассеяния для различных углов раскрыва отражающего экрана для случая неоднородной среды внутри диэлектрического цилиндра. Проведена проверка точности выполнения оптической теоремы для квадратичной зависимости волнового числа от радиальной координаты. Показано, что погрешность получаемых результатов не превосходит 2.5 × 10^–3.

Список литературы

Kim D., Avital E.J., Miloh T. // Advances in Acoustics and Vibration. 2014. V. 2014. Article ID 392138.
Gillman A. // Advances Comput. Math. 2017. V. 43. P. 351.
Кюркчан А.Г., Анютин А.П. // Докл. АН. 2002. Т. 385. № 3. С. 309.
Maнeнкoв C.A. // PЭ. 2007. T. 52. № 12. C. 1413.
Кюркчан А.Г., Смирнова Н.И. Математическое моделирование в теории дифракции с использованием априорной информации об аналитических свойствах решения. М.: ИД Медиа Паблишер, 2014.
Кюркчан А.Г., Маненков С.А. // РЭ. 2020. Т. 65. № 7. С. 644.
Maнeнкoв C.A. // PЭ. 2009. T. 54. № 5. C. 541.
Maнeнкoв C.A. // PЭ. 2018. T. 63. № 1. C. 3.
Де Бор К. Практическое руководство по сплайнам. М.: Радио и связь, 1985.
Шендеров Е.Л. Излучение и рассеяние звука. Л.: Судостроение, 1989.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал