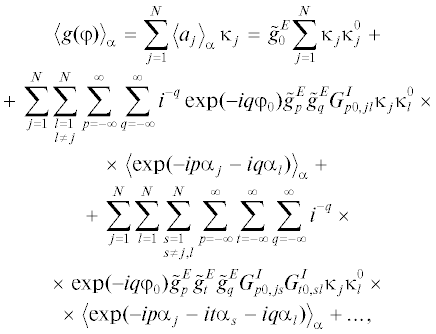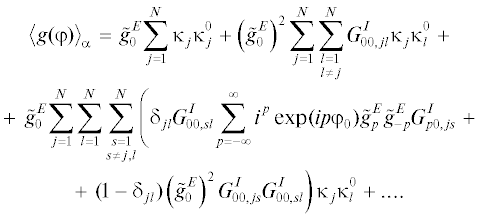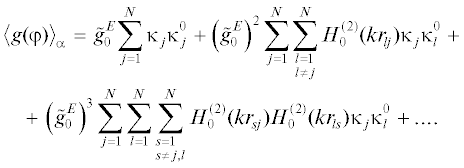Радиотехника и электроника, 2021, T. 66, № 3, стр. 226-235
Применение метода диаграммных уравнений к задаче дифракции на группе случайно расположенных малых рассеивателей
А. Г. Кюркчан a, b, c, С. А. Маненков a, *
a Московский технический университет связи и информатики
111024 Москва, ул. Авиамоторная, 8а, Российская Федерация
b Фрязинский филиал Института радиотехники и электроники им. В.А. Котельникова РАН
141190 Фрязино, Московской обл., пл. Введенского, 1, Российская Федерация
c Центральный научно-исследовательский институт связи
111141 Москва, 1-й проезд Перова поля, 8, Российская Федерация
* E-mail: mail44471@mail.ru
Поступила в редакцию 07.07.2020
После доработки 07.07.2020
Принята к публикации 01.08.2020
Аннотация
На основе метода диаграммных уравнений и метода малых возмущений предложена методика расчета усредненной диаграммы рассеяния на группе одинаковых бесконечных идеально отражающих цилиндров, имеющих случайные координаты и случайную ориентацию. Задача решена в предположении, что размеры сечений рассеивателей малы по сравнению с длиной волны и средним расстоянием между телами. Предполагается также, что среднеквадратическое отклонение координат рассеивателей мало по сравнению с длиной волны. Для тестирования метода произведено сравнение результатов расчета, полученных при помощи метода малых возмущений, с результатами, полученными при помощи непосредственного усреднения диаграммы рассеяния, для небольшого числа тел.
ВВЕДЕНИЕ
В литературе имеется большое количество публикаций, посвященных дифракции волн в случайно-неоднородных средах [1–4]. В данной работе исследуется двумерная задача дифракции волн на нескольких одинаковых рассеивателях в виде бесконечных цилиндров произвольного сечения, которые имеют случайные координаты и случайные углы поворота. Предполагается, что размеры сечений тел малы по сравнению с длиной волны и средним расстоянием между телами. Для решения задачи использован метод диаграммных уравнений (МДУ), который разработан ранее [5–7] и затем применялся к решению задач рассеяния волн одиночным телом [5], периодической решеткой [6], группой тел [7] и другим задачам. Преимуществом этого метода является то, что исходная задача дифракции сводится к нахождению диаграммы рассеяния волнового поля, а не к поиску токов на поверхности рассеивателей, как, например, в методе токовых интегральных уравнений [5–8], что позволяет получать более быстродействующие и более устойчивые алгоритмы.
Рассматриваемая задача дифракции решалась при помощи МДУ в так называемом одномодовом приближении [7, 9]. В такой формулировке задача может быть сведена к решению алгебраической системы относительно диаграмм рассеяния каждого тела, которые в данном приближении (точнее, в случае малости размеров сечения тела по сравнению с длиной волны) не зависят от угла наблюдения. При условии, что размеры сечений тел малы, удается аналитически произвести усреднение диаграммы рассеяния по углам ориентации тел, которые предполагаются независимыми в совокупности случайными величинами (не зависящими от координат центров тел). При этом задача сводится к решению алгебраической системы, матрица которой и правая часть аналогичны матрице и правой части, соответствующим случаю дифракции на группе круговых рассеивателей с некоторым множителем, учитывающим форму тел.
Отметим, что даже в указанном одномодовом приближении усреднение диаграммы рассеяния по координатам центров тел с помощью непосредственного решения возникающей алгебраической системы относительно парциальных диаграмм, является трудно осуществимой задачей из-за очень большого объема требуемых вычислений. Например, при усреднении диаграммы группы из десяти тел потребовалось бы вычисление двадцатикратных интегралов (без учета усреднения по углам ориентации тел). Поэтому приходится делать дополнительное предположение относительно малости отклонений координат центров тел от их средних значений. Для усреднения диаграммы рассеяния группы тел по координатам центров тел применялся метод малых возмущений (ММВ), аналогичный методу, изложенному в монографии [10]. С использованием указанного метода удается получить усредненную диаграмму рассеяния с точностью до второго порядка относительно малого параметра $k\sigma $, где $k$ – волновое число, а $\sigma $ – среднеквадратическое отклонение координат центров тел от их средних значений. При таком подходе удается добиться высокой скорости вычислений.
1. ВЫВОД ОСНОВНЫХ СООТНОШЕНИЙ
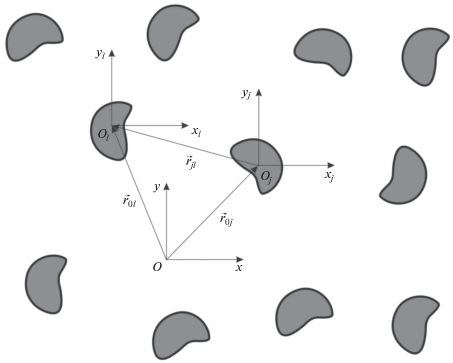
Рассмотрим математическую постановку задачи. Пусть имеется группа из N случайно расположенных одинаковых бесконечно длинных цилиндров произвольного сечения, образующие которых параллельны оси z (см. рис. 1). Предположим, что электромагнитное поле имеет только одну составляющую, параллельную этой оси: $u = {{E}_{z}}(x,y)$. Будем считать, что на контурах, ограничивающих сечения тел, поле удовлетворяет однородному условию Дирихле:
где ${{S}_{j}}$ – контур, ограничивающий сечение j-го тела. При этом координаты “центров” $({{x}_{{0j}}},{{y}_{{0j}}})$ рассеивателей являются независимыми случайными величинами, которые распределены по усеченному нормальному закону [4]
(2)
${{w}_{j}}({{x}_{{0j}}},{{y}_{{0j}}}) = \left\{ \begin{gathered} {{C}_{j}}\exp \left( { - {{\left( {{{{({{x}_{{0j}}} - {{{\bar {x}}}_{{0j}}})}}^{2}} + {{{({{y}_{{0j}}} - {{{\bar {y}}}_{{0j}}})}}^{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{({{x}_{{0j}}} - {{{\bar {x}}}_{{0j}}})}}^{2}} + {{{({{y}_{{0j}}} - {{{\bar {y}}}_{{0j}}})}}^{2}}} \right)} {2{{\sigma }^{2}}}}} \right. \kern-0em} {2{{\sigma }^{2}}}}} \right),\,\,\,\,\left| {{{x}_{{0j}}}} \right| \leqslant {{L}_{1}},\,\,\,\,\left| {{{y}_{{0j}}}} \right| \leqslant {{L}_{2}}, \hfill \\ {\text{0,}}\,\,\,\,{\text{в}}\,\,{\text{других}}\,\,{\text{случаях,}} \hfill \\ \end{gathered} \right.$где $j = 1,2,...,N$. Величины ${{C}_{j}}$ определяются из условия нормировки. В дальнейшем будем считать, что ${{L}_{{1,2}}} \gg \sigma $ и значения величин ${{L}_{{1,2}}}$ таковы, что границы группы тел расположены “далеко” от точек с координатами $({{\bar {x}}_{{0j}}},{{\bar {y}}_{{0j}}})$. В результате закон распределения (2) будет близок к нормальному закону и $\left\langle {{{x}_{{0j}}}} \right\rangle \approx {{\bar {x}}_{{0j}}},\,\,\,\,\left\langle {{{y}_{{0j}}}} \right\rangle \approx {{\bar {y}}_{{0j}}}$, $j = 1,2,...,N$. Предположим также, что контуры ${{S}_{j}}$ повернуты на случайные углы ${{\alpha }_{j}}$, распределенные равномерно на интервале $[0,2\pi ]$, которые независимы между собой и независимы от координат $({{x}_{{0j}}},{{y}_{{0j}}})$. Таким образом, в полярной системе координат, связанной с j-м телом, уравнение контура цилиндра имеет вид
где вид функции $\rho (\varphi )$ не зависит от номера тела и $\rho (\varphi )$ не является случайной величиной. В качестве первичного поля рассмотрим плоскую волну
где ${{\varphi }_{0}}$ – угол падения волны, $k$ – волновое число.
В соответствии с МДУ запишем полное поле вне рассматриваемых цилиндрических тел в виде
где $u_{j}^{1}$ – поле, рассеянное j-м телом. При этом рассеянные поля $u_{j}^{1}$ могут быть представлены в виде [5, 8]
(6)
$\begin{gathered} u_{j}^{1}({{r}_{j}},{{\varphi }_{j}}) = \\ = \frac{1}{\pi }\int\limits_{ - \frac{\pi }{2} - i\infty }^{\frac{\pi }{2} + i\infty } {{{g}_{j}}(\psi + {{\varphi }_{j}})\exp ( - ik{{r}_{j}}\cos \psi )} d\psi . \\ \end{gathered} $Парциальная диаграмма j-го тела имеет вид [5, 8]
(7)
$g_{j}^{{}}({{\varphi }_{j}}) = \sum\limits_{n = - \infty }^\infty {{{a}_{{jn}}}\exp (in{{\varphi }_{j}})} ,$где
(8)
$\begin{gathered} {{a}_{{jm}}} = \frac{i}{4}\int\limits_0^{2\pi } {{{v}_{j}}({{\varphi }_{j}}){{J}_{m}}(k{{\rho }_{j}}({{\varphi }_{j}}))\exp \left( { - im\left( {{{\varphi }_{j}} - \frac{\pi }{2}} \right)} \right)d{{\varphi }_{j}}} , \\ {{v}_{j}} = {{\left. {\left[ {{{\rho }_{j}}\frac{{\partial u}}{{\partial {{r}_{j}}}} - \frac{{\rho {{{_{j}^{'}}}_{{}}}}}{{{{\rho }_{j}}}}\frac{{\partial u}}{{\partial {{\varphi }_{j}}}}} \right]} \right|}_{{{{r}_{j}} = {{\rho }_{j}}({{\varphi }_{j}})}}}. \\ \end{gathered} $Подставив далее формулы (5) и (6) в соотношения (8), c учетом (7) получим следующую алгебраическую систему относительно коэффициентов ${{a}_{{jm}}}$ [7, 8]:
(9)
$\begin{gathered} {{a}_{{jm}}} = a_{{jm}}^{0} + \sum\limits_{l = 1}^N {\sum\limits_{n = - \infty }^\infty {G_{{mn,jl}}^{{}}{{a}_{{ln}}}} } ,j = 1,...,N, \\ m = 0, \pm 1, \pm 2,..., \\ \end{gathered} $где
(10)
$G_{{mn,jl}}^{{}} = G_{{mn,jj}}^{\infty }{{\delta }_{{jl}}} + \sum\limits_{p = - \infty }^\infty {G_{{mp,jj}}^{E}G_{{pn,jl}}^{I}} (1 - {{\delta }_{{jl}}}),$(11)
$\begin{gathered} G_{{mn,jj}}^{\infty } = \frac{{{{i}^{{m - n}}}}}{4}\int\limits_0^{2\pi } {{{J}_{m}}(k{{\rho }_{j}})\left[ {ik{{\rho }_{j}}({{\varphi }_{j}})H{{{_{n}^{{(2)}}}}^{'}}(k{{\rho }_{j}}) + \frac{{^{{^{{}}}}}}{{_{{_{{}}}}}}} \right.} \\ + \,\,\left. {n\frac{{\rho _{j}^{'}({{\varphi }_{j}})}}{{{{\rho }_{j}}({{\varphi }_{j}})}}H_{n}^{{(2)}}(k{{\rho }_{j}})} \right]\exp \left( {i(n - m){{\varphi }_{j}}} \right)d{{\varphi }_{j}}, \\ \end{gathered} $(12)
$\begin{gathered} G_{{mp,jj}}^{E} = \frac{{{{i}^{m}}}}{4}\int\limits_0^{2\pi } {{{J}_{m}}(k{{\rho }_{j}})\left[ {ik{{\rho }_{j}}({{\varphi }_{j}})J_{p}^{'}(k{{\rho }_{j}}) + \frac{{^{{^{{}}}}}}{{}}} \right.} \\ + \,\,\left. {p\frac{{\rho _{j}^{'}({{\varphi }_{j}})}}{{{{\rho }_{j}}({{\varphi }_{j}})}}{{J}_{p}}(k{{\rho }_{j}})} \right]\exp \left( {i(p - m){{\varphi }_{j}}} \right)d{{\varphi }_{j}}, \\ \end{gathered} $(13)
$G_{{pn,jl}}^{I} = {{i}^{{ - n}}}H_{{n - p}}^{{(2)}}(k{{r}_{{lj}}})\exp \left( {i(n - p){{\varphi }_{{lj}}}} \right),\,\,\,\,j \ne l,$(14)
$a_{{mj}}^{0} = \sum\limits_{p = - \infty }^\infty {G_{{mp,jj}}^{E}{{i}^{{ - p}}}\exp ( - ip{{\varphi }_{0}})} \kappa _{j}^{0},$(15)
$\kappa _{j}^{0} = \exp ( - ik{{x}_{{0j}}}\cos {{\varphi }_{0}} - ik{{y}_{{0j}}}\sin {{\varphi }_{0}}).$В формулах (10)–(15) ${{r}_{{lj}}}$ – расстояние между рассеивателями с номерами j и l, ${{\varphi }_{{jl}}}$ – полярный угол в l -й системе координат начала координат j-го тела, ${{\delta }_{{jl}}}$ – символ Кронекера.
В предположении, что все тела имеют малое сечение по сравнению с длиной волны, можно считать, что парциальные диаграммы не зависят от угла наблюдения, т.е. [7, 9]
Действительно, если, например, рассматривается задача дифракции на тонком круговом бесконечном цилиндре радиусом a ($ka \ll 1$), то, как хорошо известно, диаграмма рассеяния имеет вид
где ${{c}_{n}} = - \frac{{{{J}_{n}}(ka)}}{{H_{n}^{{(2)}}(ka)}}$.
Из асимптотик функций Бесселя следует, что ${{с}_{n}} = O({{(ka)}^{{2|n|}}}),\;n = \pm 1, \pm 2...$ Таким образом, в разложении диаграммы можно ограничиться только нулевым членом. Назовем данный подход одномодовым приближением. Отметим, что одномодовое приближение позволяет моделировать характеристики рассеяния тел (в том числе с учетом взаимодействия между ними) с приемлемой точностью при характерных размерах рассеивателя до $kd \sim 1$ [8, 9]. Более жесткие ограничения на размеры рассеивателя накладывает ММВ [10].
Итак, рассмотрим решение задачи в одномодовом приближении. В результате система (9) примет вид
(18)
${{a}_{j}} = a_{j}^{0} + G_{0}^{\infty }{{a}_{j}} + \sum\limits_{l = 1}^N {G_{{jl}}^{{}}{{a}_{l}}} ,\,\,\,\,j = 1,...,N,$(19)
$G_{0}^{\infty } = \frac{i}{4}\int\limits_0^{2\pi } {k\rho (\varphi ){{J}_{0}}(k\rho )H{{{_{0}^{{(2)}}}}^{'}}(k\rho )} d\varphi ,$(20)
$G_{{jl}}^{{}} = \sum\limits_{p = - \infty }^\infty {G_{{0p,jj}}^{E}G_{{p0,jl}}^{I}} (1 - {{\delta }_{{jl}}}),$(21)
$a_{j}^{0} = \sum\limits_{p = - \infty }^\infty {G_{{0p,jj}}^{E}{{i}^{{ - p}}}\exp ( - ip{{\varphi }_{0}})} \kappa _{j}^{0},$(22)
$\begin{gathered} G_{{0p,jj}}^{E} = \frac{1}{4}\int\limits_0^{2\pi } {{{J}_{0}}(k\rho )\left[ {ik\rho (\varphi )J_{p}^{'}(k\rho )} \right.} + \\ + \,\,\left. {p\frac{{\rho {\kern 1pt} '(\varphi )}}{{\rho (\varphi )}}{{J}_{p}}(k\rho )} \right]\exp \left( {ip\varphi } \right)d\varphi \exp ( - ip{{\alpha }_{j}}) \equiv \\ \equiv g_{p}^{E}\exp ( - ip{{\alpha }_{j}}). \\ \end{gathered} $Здесь мы учли, что выполняется равенство (3), т.е. контуры всех тел отличаются поворотом на некоторый угол. Далее при условии $ka \ll 1$ ($a$ – характерный радиус сечения тел в группе) имеем
(23)
$\begin{gathered} g_{p}^{E} = \frac{1}{4}\int\limits_0^{2\pi } {{{J}_{0}}(k\rho )\left[ {ik\rho (\varphi )J_{p}^{'}(k\rho ) + \frac{{^{{}}}}{{}}} \right.} \\ + \,\,\left. {p\frac{{\rho {\kern 1pt} '(\varphi )}}{{\rho (\varphi )}}{{J}_{p}}(k\rho )} \right]\exp \left( {ip\varphi } \right)d\varphi \approx \\ \approx \frac{1}{{p!{{2}^{{p + 2}}}}}\int\limits_0^{2\pi } {{{J}_{0}}(k\rho )p{{{(k\rho )}}^{p}}\left[ {i + \frac{{\rho {\kern 1pt} '(\varphi )}}{{\rho (\varphi )}}} \right]} \times \\ \times \,\,\exp \left( {ip\varphi } \right)d\varphi = \frac{1}{{p!{{2}^{{p + 2}}}}} \\ \times \,\,\int\limits_0^{2\pi } {k\rho {\kern 1pt} '{{J}_{1}}(k\rho )} {{(k\rho )}^{p}}\exp \left( {ip\varphi } \right)d\varphi . \\ \end{gathered} $Последний интеграл получен интегрированием по частям. В результате величины $g_{p}^{E}$ имеют порядок $O({{(ka)}^{{|p| + 2}}})$.
Перейдем к нахождению усредненной диаграммы всей группы случайно расположенных тел. Перепишем систему (18) в виде
где
(25)
${{b}_{j}} = \frac{{a_{j}^{0}}}{{1 - G_{0}^{\infty }}},\,\,\,\,{{Q}_{{jl}}} = \frac{{G_{{jl}}^{{}}}}{{1 - G_{0}^{\infty }}}.$Для нахождения усредненной диаграммы запишем систему (24) в матричной форме:
где ${\mathbf{Q}} = \left\| {{{Q}_{{jl}}}} \right\|,$ ${\mathbf{b}} = \left\| {{{b}_{j}}} \right\|,$ ${\mathbf{a}} = \left\| {{{a}_{j}}} \right\|,$ $j,l = \overline {1,N} .$ Усредним вначале искомую диаграмму рассеяния по углам ориентации тел ${{\alpha }_{j}}$. Для этого применим метод итераций к системе (26). В результате получим
Отметим, что, например, третье слагаемое в этой сумме соответствует двукратному рассеянию на группе тел [11]. Далее, диаграмма всей группы тел имеет вид
где ${{\kappa }_{j}} = \exp (ik{{x}_{{0j}}}\cos \varphi + ik{{y}_{{0j}}}\sin \varphi )$. Подставим выражения для коэффициентов ${{a}_{j}}$ из формулы (27) в соотношение (28). В результате усреднения по углам ориентации полученного выражения будем иметь
где $\tilde {g}_{p}^{E} = \frac{{g_{p}^{E}}}{{1 - G_{0}^{\infty }}}$. Учтем, что случайные величины ${{\alpha }_{j}}$ и ${{\alpha }_{l}}$ независимы при $j \ne l$. Тогда
С использованием формулы (23) имеем $g_{p}^{E}g_{{ - p}}^{E} = $ $ = O({{(ka)}^{{2|p| + 4}}})$ и поэтому при малых $ka$ члены ряда с индексами $p = \pm 1$ в третьей сумме в формуле (30) на два порядка меньше нулевого члена ряда, а остальные члены ${\text{c}}$ большими значениями индекса p будут иметь еще больший порядок малости. Очевидно, что в последующих суммах аналогичные слагаемые также будут малы. Поэтому, пренебрегая этими величинами в формуле (30), получим
Нетрудно видеть, что усредненная диаграмма получается подстановкой в формулу (28) коэффициентов ${{a}_{j}}$, удовлетворяющих алгебраической системе вида (24), в которой
(32)
${{Q}_{{jl}}} = \tilde {g}_{0}^{E}H_{0}^{{(2)}}(k{{r}_{{lj}}})(1 - {{\delta }_{{jl}}}),\,\,\,{{b}_{j}} = \tilde {g}_{0}^{E}\kappa _{j}^{0}.$Здесь мы не стали вводить новые обозначения для усредненных по углам ориентации коэффициентов ${{a}_{j}}$, матричных элементов и правых частей. В полученной системе случайными являются величины ${{r}_{{lj}}}$ и $\kappa _{j}^{0}$, которые зависят от координат центров тел.
Рассмотрим теперь вопрос об усреднении диаграммы рассеяния по координатам центров тел. Предположим, что выполняются два условия. Во-первых, размер сечений тел $a$ в группе мал по сравнению с длиной волны и, во-вторых, $k\sigma \ll 1$, т.е. величина среднего отклонения координат центров тел мала по сравнению с длиной волны. Предположим также, что $a \ll \sigma $. Для нахождения средней диаграммы применим подход, основанный на методе малых возмущений. Этот метод близок к методу возмущений, разработанному в монографии [10] применительно к задаче дифракции на статистически неровной поверхности. Будем вновь исходить из матричной записи (26) алгебраической системы вида (24) для усредненных по углам ориентации тел коэффициентов ${{a}_{j}}$. Разложим следующие величины по степеням малого параметра $k\sigma $ до второго порядка включительно:
(33)
$\begin{gathered} {\mathbf{a}} = {\mathbf{a}}_{{}}^{{(0)}} + {\mathbf{a}}_{{}}^{{(1)}} + {\mathbf{a}}_{{}}^{{(2)}}, \\ {\mathbf{Q}} = {\mathbf{Q}}_{{}}^{{(0)}} + {\mathbf{Q}}_{{}}^{{(1)}} + {\mathbf{Q}}_{{}}^{{(2)}}, \\ {\mathbf{b}} = {\mathbf{b}}_{{}}^{{(0)}} + {\mathbf{b}}_{{}}^{{(1)}} + {\mathbf{b}}_{{}}^{{(2)}}, \\ \kappa = \kappa _{{}}^{{(0)}} + \kappa _{{}}^{{(1)}} + \kappa _{{}}^{{(2)}}, \\ \end{gathered} $где $\kappa = \left\| {{{\kappa }_{j}}} \right\|,\,\,j = \overline {1,N} .$ При этом первые слагаемые ${{{\mathbf{Q}}}^{{(0)}}},\,\,{{{\mathbf{b}}}^{{(0)}}},\,\,{{\kappa }^{{(0)}}}$ берутся при ${{x}_{{0j}}} = \left\langle {{{x}_{{0j}}}} \right\rangle ,$ ${{y}_{{0j}}} = \left\langle {{{y}_{{0j}}}} \right\rangle $ и т.д. Вторые и третьи слагаемые в формуле (33) получаются с помощью разложения величин ${\mathbf{Q}},\;\;{\mathbf{b}}$ и κ в ряд Тейлора по координатам ${{x}_{{0j}}},{{y}_{{0j}}},{{x}_{{0l}}},{{y}_{{0l}}}$ в окрестности ${{x}_{{0j}}} = \left\langle {{{x}_{{0j}}}} \right\rangle ,$ ${{y}_{{0j}}} = \left\langle {{{y}_{{0j}}}} \right\rangle $ и т.д., до членов второго порядка.
Подставим далее первые три выражения в формуле (33) в систему вида (26) относительно усредненных по углам ориентации тел коэффициентов ${{a}_{j}}$ и приравняем в полученном равенстве величины одинаковых порядков. В результате получим
(34)
$\begin{gathered} {\mathbf{a}}_{{}}^{{(0)}} = {{{\mathbf{b}}}^{{(0)}}} + {{{\mathbf{Q}}}^{{(0)}}}{\mathbf{a}}_{{}}^{{(0)}}, \\ {\mathbf{a}}_{{}}^{{(1)}} = {{{\mathbf{b}}}^{{(1)}}} + {{{\mathbf{Q}}}^{{(0)}}}{\mathbf{a}}_{{}}^{{(1)}} + {{{\mathbf{Q}}}^{{(1)}}}{\mathbf{a}}_{{}}^{{(0)}}, \\ {\mathbf{a}}_{{}}^{{(2)}} = {{{\mathbf{b}}}^{{(2)}}} + {{{\mathbf{Q}}}^{{(0)}}}{\mathbf{a}}_{{}}^{{(2)}} + {{{\mathbf{Q}}}^{{(1)}}}{\mathbf{a}}_{{}}^{{(1)}} + {{{\mathbf{Q}}}^{{(2)}}}{\mathbf{a}}_{{}}^{{(0)}}. \\ \end{gathered} $Далее заменим во втором и третьем уравнении в (34) величину ${\mathbf{a}}_{{}}^{{(0)}}$ на величину $\left\langle {\mathbf{a}} \right\rangle = {\mathbf{a}}_{{}}^{{(0)}} + \left\langle {{\mathbf{a}}_{{}}^{{(2)}}} \right\rangle $. При этом мы допускаем погрешность порядка ${{(k\sigma )}^{3}}$ и ${{(k\sigma )}^{4}}$ соответственно. Отметим, что мы неявно предполагаем, что средние от величин первого порядка малости равны нулю. Это будет соблюдаться, например, при условии, что координаты тел распределены по нормальному закону или близкому к нему (см. Введение). Усредняя первое и третье уравнения в формуле (34) по координатам и складывая полученные равенства, найдем
(35)
$\left\langle {\mathbf{a}} \right\rangle = \left\langle {\mathbf{b}} \right\rangle + \left\langle {\mathbf{Q}} \right\rangle \left\langle {\mathbf{a}} \right\rangle + \left\langle {{\mathbf{Q}}_{{}}^{{(1)}}{\mathbf{a}}_{{}}^{{(1)}}} \right\rangle ,$(36)
${\mathbf{a}}_{{}}^{{(1)}} = {\mathbf{L}}\left( {{\mathbf{b}}_{{}}^{{(1)}} + {\mathbf{Q}}_{{}}^{{(1)}}\left\langle {\mathbf{a}} \right\rangle } \right),$где мы обозначили
(37)
$\begin{gathered} \left\langle {\mathbf{Q}} \right\rangle = \left\langle {{\mathbf{Q}}_{{}}^{{(0)}}} \right\rangle + \left\langle {{\mathbf{Q}}_{{}}^{{(2)}}} \right\rangle ,\,\,\,\,\left\langle {\mathbf{b}} \right\rangle = \left\langle {{\mathbf{b}}_{{}}^{{(0)}}} \right\rangle + \left\langle {{\mathbf{b}}_{{}}^{{(2)}}} \right\rangle , \\ {\mathbf{L}} = {{({\mathbf{E}} - {{{\mathbf{Q}}}^{{(0)}}})}^{{ - 1}}}. \\ \end{gathered} $В последней формуле через ${\mathbf{E}}$ обозначена единичная матрица. Подставим далее равенство (36) в формулу (35). В результате получим алгебраическую систему для вектора усредненных коэффициентов диаграммы
(38)
$\left\langle {\mathbf{a}} \right\rangle = \left\langle {{\mathbf{\tilde {b}}}} \right\rangle + \left\langle {{\mathbf{\tilde {Q}}}} \right\rangle \left\langle {\mathbf{a}} \right\rangle ,$в которой
(39)
$\left\langle {{\mathbf{\tilde {Q}}}} \right\rangle = \left\langle {\mathbf{Q}} \right\rangle + \left\langle {{\mathbf{Q}}_{{}}^{{(1)}}{\mathbf{LQ}}_{{}}^{{(1)}}} \right\rangle ,$(40)
$\left\langle {{\mathbf{\tilde {b}}}} \right\rangle = \left\langle {\mathbf{b}} \right\rangle + \left\langle {{\mathbf{Q}}_{{}}^{{(1)}}{\mathbf{Lb}}_{{}}^{{(1)}}} \right\rangle .$Таким образом, матрица этой системы и ее правая часть не случайны, что позволяет легко найти усредненную диаграмму с точностью до величин второго порядка малости относительно $k\sigma $. Действительно, для усредненной диаграммы имеем (см. формулу (28)):
(41)
$\begin{gathered} \left\langle {g(\varphi )} \right\rangle = \left\langle {{{\kappa }^{T}}{\mathbf{a}}} \right\rangle \approx \left\langle {{{\kappa }^{T}}} \right\rangle \left\langle {\mathbf{a}} \right\rangle + \left\langle {{{\kappa }^{{(1)T}}}{{{\mathbf{a}}}^{{(1)}}}} \right\rangle = \\ = \left\langle {{{\kappa }^{{(1)T}}}{\mathbf{L}}{{{\mathbf{b}}}^{{(1)}}}} \right\rangle + \left( {\left\langle {{{\kappa }^{T}}} \right\rangle + \left\langle {{{\kappa }^{{(1)T}}}{\mathbf{L}}{{{\mathbf{Q}}}^{{(1)}}}} \right\rangle } \right)\left\langle {\mathbf{a}} \right\rangle , \\ \end{gathered} $где $\left\langle \kappa \right\rangle = \kappa _{{}}^{{(0)}} + \left\langle {\kappa _{{}}^{{(2)}}} \right\rangle $, T – операция транспонирования. Отметим, что в формуле (41) мы использовали приближенное равенство
(42)
$\left\langle {{{{({{\kappa }^{{(0)}}} + {{\kappa }^{{(2)}}})}}^{T}}({{{\mathbf{a}}}^{{(0)}}} + {{{\mathbf{a}}}^{{(2)}}})} \right\rangle \approx \left\langle {{{\kappa }^{T}}} \right\rangle \left\langle {\mathbf{a}} \right\rangle .$При такой замене левой части в формуле (42) мы делаем ошибку порядка ${{(k\sigma )}^{4}}$. Аналогично, в силу того что мы заменили в формулах (34) ${\mathbf{a}}_{{}}^{{(0)}}$ на величину $\left\langle {\mathbf{a}} \right\rangle $, также допускаем погрешность порядка ${{(k\sigma )}^{4}}$в формуле (42). Таким образом, формулы (38)–(41) дают решение рассматриваемой задачи с точностью до второго порядка малости по параметру $k\sigma $.
Отметим, что поскольку закон распределения координат центров тел близок к нормальному закону, а также из определения величин $Q_{{jl}}^{{(1)}},b_{j}^{{(1)}}$ и т.д. вытекает, что все средние величины, входящие в формулы (38)–(41) линейно выражаются через дисперсии $\sigma _{{xj}}^{2},\;\sigma _{{yj}}^{2}$ координат ${{x}_{{0j}}},{{y}_{{0j}}}$, которые приближенно равны ${{\sigma }^{2}}$. Мы не приводим здесь соответствующие формулы. В результате при расчете усредненной диаграммы по формулам (38)–(41) не требуется вычислять многократные интегралы, которые возникали бы при непосредственном усреднении диаграммы рассеяния, с использованием строгого решения системы (9) или (18). Поэтому скорость вычисления усредненной диаграммы, очевидно, будет существенно выше, при применении рассматриваемого подхода.
2. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ
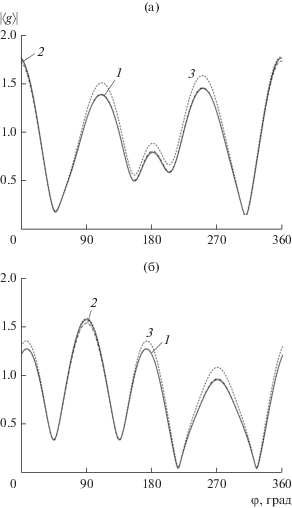
Рассмотрим результаты численного моделирования. На рис. 2 изображены угловые зависимости модуля усредненной диаграммы рассеяния, полученные при помощи непосредственного решения алгебраической системы (9) и при помощи ММВ, изложенного выше. Рассматривалась дифракция на группе из трех случайно расположенных круговых цилиндров радиусом $ka = 0.1$. Максимальные размеры “облака” составляли $2k{{L}_{1}} = 2k{{L}_{2}} = 10$. Параметр $k\sigma = 0.25$. Средние значения координат $({{\bar {x}}_{{0j}}},{{\bar {y}}_{{0j}}})$ центров тел были выбраны так, чтобы цилиндры образовали равносторонний треугольник, а именно $k{{\bar {x}}_{{01}}} = - 2.5,$ $k{{\bar {x}}_{{02}}} = 0,$ $k{{\bar {x}}_{{03}}} = 2.5,$ $k{{\bar {y}}_{{01}}} = k{{\bar {y}}_{{03}}} = 0,$ $k{{\bar {y}}_{{02}}} = {{5\sqrt 3 } \mathord{\left/ {\vphantom {{5\sqrt 3 } 2}} \right. \kern-0em} 2}$. Штриховой кривой на рисунке изображена угловая зависимость “невозмущенной” диаграммы рассеяния, которая соответствует дифракции на группе цилиндров, имеющих неслучайные координаты, равные средним значениям $({{\bar {x}}_{{0j}}},{{\bar {y}}_{{0j}}})$. Отметим, что усреднение диаграммы производилось непосредственно при помощи решения алгебраической системы (9), причем мы брали максимально три первых члена в разложении парциальной диаграммы (7). Как видно из рисунков, результаты усреднения диаграммы с использованием точного решения системы (9) и ММВ практически совпадают.
Рис. 2.
Угловая зависимость усредненной диаграммы рассеяния группы из трех круговых цилиндров для двух углов падения ${{\varphi }_{0}} = 0^\circ $ (а) и ${{\varphi }_{0}} = 90^\circ $(б): 1– строгое решение задачи, 2 – метод на основе ММВ, 3 – зависимость “невозмущенной” диаграммы.
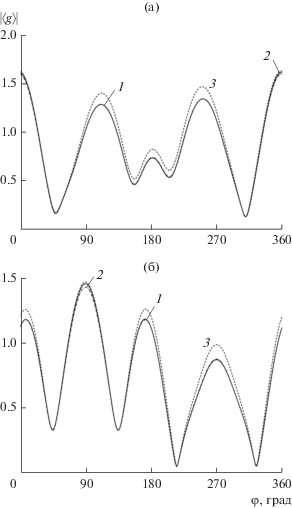
На рис. 3 представлены угловые зависимости модуля усредненной диаграммы рассеяния для “облака”, образованного тремя случайно расположенными эллиптическими цилиндрами с полуосями $ka = 0.1,\,\,kb = 0.05$. Остальные параметры задачи были такие же, как и для рис. 2. Штриховой кривой на рисунке изображена зависимость “невозмущенной” диаграммы ${{\left\langle {g(\varphi )} \right\rangle }_{\alpha }}$, усредненной по углам ориентации тел (при этом координаты центров тел выбирались равными $({{\bar {x}}_{{0j}}},{{\bar {y}}_{{0j}}})$). В рассматриваемом случае усреднение диаграммы по координатам центров тел и по углам ориентации вновь осуществлялось непосредственно при помощи решения алгебраической системы (9), причем для усреднения диаграммы требовалось вычисление девятикратных интегралов. Как видно из приведенных рисунков, имеется хорошая точность при использовании ММВ как в случае “осевого” падения (при ${{\varphi }_{0}} = 90^\circ $), так и в случае падения плоской волны перпендикулярно оси симметрии указанного выше треугольника.
Рис. 3.
Угловая зависимость усредненной диаграммы рассеяния группы из трех эллиптических цилиндров для двух углов падения ${{\varphi }_{0}} = 0^\circ $ (а) и ${{\varphi }_{0}} = 90^\circ $(б): 1 – строгое решение задачи, 2 – метод на основе ММВ, 3 – зависимость “невозмущенной” диаграммы ${{\left\langle {g(\varphi )} \right\rangle }_{\alpha }}$.
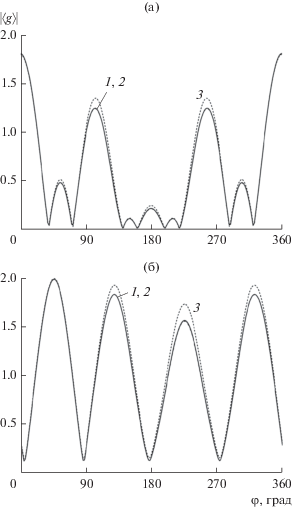
На рис. 4 показаны угловые зависимости модуля усредненной диаграммы рассеяния для группы из четырех случайно расположенных круговых (радиуса $ka = 0.1$), а на рис. 5 – эллиптических цилиндров (с полуосями $ka = 0.1,\,\,kb = 0.05$). Максимальные размеры “облака” составляли $2k{{L}_{1}} = 2k{{L}_{2}} = 10$, параметр $k\sigma = 0.25$. Средние значения координат центров тел были равны $k{{\bar {x}}_{{01}}} = k{{\bar {x}}_{{03}}} = - 2.5,$ $k{{\bar {x}}_{{02}}} = k{{\bar {x}}_{{04}}} = 2.5,$ $k{{\bar {y}}_{{01}}} = $ $ = k{{\bar {y}}_{{02}}} = - 2.5,$ $k{{\bar {y}}_{{03}}}$ = $k{{\bar {y}}_{{04}}} = 2.5$. Сплошная кривая иллюстрирует поведение усредненной диаграммы, полученной в одномодовом приближении с помощью непосредственного усреднения решения системы (18). Штриховой кривой на рисунке изображена угловая зависимость “невозмущенной” диаграммы рассеяния (полученной также в одномодовом приближении), которая соответствует дифракции на группе цилиндров, имеющих неслучайные координаты, равные средним значениям $({{\bar {x}}_{{0j}}},{{\bar {y}}_{{0j}}})$. В силу большого объема вычислений мы не сравнивали решение, полученное с использованием ММВ, и точное решение исходной системы (9), а ограничились одномодовым приближением. Как видно, кривые 1 и 2 практически совпадают.
Рис. 4.
Угловая зависимость усредненной диаграммы рассеяния группы из четырех круговых цилиндров для двух углов падения ${{\varphi }_{0}} = 0^\circ $ (а) и ${{\varphi }_{0}} = 45^\circ $ (б): 1 – решение задачи, основанное на использовании системы (18), 2 – метод на основе ММВ, 3 – зависимость “невозмущенной” диаграммы. Одномодовое приближение.
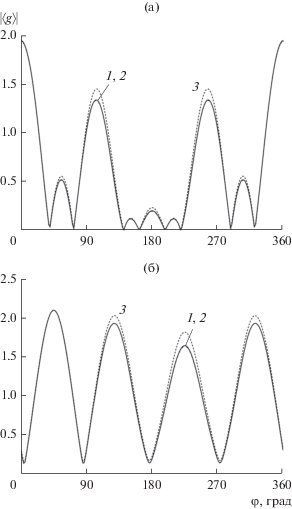
Рис. 5.
Угловая зависимость усредненной диаграммы рассеяния группы из четырех эллиптических цилиндров для двух углов падения ${{\varphi }_{0}} = 0^\circ $ (а) и ${{\varphi }_{0}} = 45^\circ $ (б): 1 – решение задачи, основанное на использовании системы (18), 2 – метод на основе ММВ, 3 – зависимость “невозмущенной” диаграммы. Одномодовое приближение.
Рассмотрим результаты расчетов для большего количества тел в “облаке”. В связи с тем, что для большого количества тел практически невозможно непосредственное усреднение диаграммы рассеяния (как решение систем (9) или (18)), мы сравнили реализацию диаграммы рассеяния для некоторого фиксированного набора значений координат центров тел в группе. На рис. 6 приведены угловые зависимости модуля диаграммы рассеяния группы из 16 круговых цилиндров радиусом $ka = 0.1$, полученные с использованием ММВ и решением алгебраической системы (9) (учитывали три первых члена в разложении парциальной диаграммы (7)). Максимальные размеры “облака” составляли $2k{{L}_{1}} = 2k{{L}_{2}} = 20$. Координаты центров тел были выбраны равными
(43)
$\begin{gathered} k{{x}_{{01}}} = - 7.5 - k\sigma ,\,\,\,\,k{{x}_{{02}}} = - 2.5 + k\sigma , \\ k{{x}_{{03}}} = 2.5 - k\sigma ,\,\,\,\,k{{x}_{{04}}} = 7.5 + k\sigma , \\ k{{x}_{{05}}} = - 7.5 + k\sigma ,\,\,\,\,k{{x}_{{06}}} = - 2.5 - k\sigma , \\ k{{x}_{{07}}} = 2.5 + k\sigma ,\,\,\,\,k{{x}_{{08}}} = 7.5 - k\sigma , \\ k{{x}_{{09}}} = - 7.5 - k\sigma ,\,\,\,\,k{{x}_{{010}}} = - 2.5 + k\sigma , \\ k{{x}_{{011}}} = 2.5 - k\sigma ,\,\,\,\,k{{x}_{{012}}} = 7.5 + k\sigma , \\ k{{x}_{{013}}} = - 7.5 + k\sigma ,\,\,\,\,k{{x}_{{014}}} = - 2.5 - k\sigma , \\ k{{x}_{{015}}} = 2.5 + k\sigma ,\,\,\,\,k{{x}_{{016}}} = 7.5 - k\sigma , \\ \end{gathered} $(44)
$\begin{gathered} k{{y}_{{01}}} = - 7.5 - k\sigma ,\,\,\,\,k{{y}_{{02}}} = - 7.5 + k\sigma , \\ k{{y}_{{03}}} = - 7.5 - k\sigma ,\,\,\,\,k{{y}_{{04}}} = - 7.5 + k\sigma , \\ k{{y}_{{05}}} = - 2.5 + k\sigma ,\,\,\,\,k{{y}_{{06}}} = - 2.5 - k\sigma , \\ k{{y}_{{07}}} = - 2.5 + k\sigma ,\,\,\,\,k{{y}_{{08}}} = - 2.5 - k\sigma , \\ k{{y}_{{09}}} = 2.5 - k\sigma ,\,\,\,\,k{{y}_{{010}}} = 2.5 + k\sigma , \\ k{{y}_{{011}}} = 2.5 - k\sigma ,\,\,\,\,k{{y}_{{012}}} = 2.5 + k\sigma , \\ k{{y}_{{013}}} = 7.5 + k\sigma ,\,\,\,\,k{{y}_{{014}}} = 7.5 - k\sigma , \\ k{{y}_{{015}}} = 7.5 + k\sigma ,\,\,\,\,k{{y}_{{016}}} = 7.5 - k\sigma , \\ \end{gathered} $Рис. 6.
Угловая зависимость диаграммы рассеяния группы из 16 круговых цилиндров: 1 –метод на основе ММВ, 2 – строгое решение задачи.
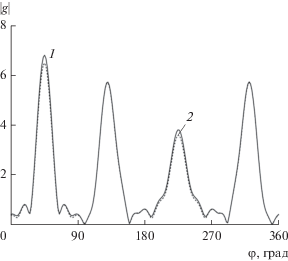
где $k\sigma = 0.25$. Угол падения плоской волны ${{\varphi }_{0}} = 45^\circ $. Заметим, что, так как в данном случае рассматривается не усредненная диаграмма, для применения ММВ необходимо изменить алгоритм решения задачи. А именно мы исходим вновь из формул (34). Однако теперь применяем “стандартный” ММВ, решая сначала систему из первого равенства в (34), т.е.
Затем подставляем это решение в следующую формулу в (34), откуда
(46)
${\mathbf{a}}_{{}}^{{(1)}} = {\mathbf{Lb}}_{{}}^{{(1)}} + {\mathbf{LQ}}_{{}}^{{(1)}}{{{\mathbf{a}}}^{{(0)}}} = {\mathbf{Lb}}_{{}}^{{(1)}} + {\mathbf{LQ}}_{{}}^{{(1)}}{\mathbf{L}}{{{\mathbf{b}}}^{{(0)}}}.$Наконец из третьего уравнения получим
(47)
$\begin{gathered} {\mathbf{a}}_{{}}^{{(2)}} = {\mathbf{L}}{{{\mathbf{b}}}^{{(2)}}} + {\mathbf{L}}{{{\mathbf{Q}}}^{{(1)}}}{\mathbf{a}}_{{}}^{{(1)}} + {\mathbf{L}}{{{\mathbf{Q}}}^{{(2)}}}{\mathbf{a}}_{{}}^{{(0)}} = \\ = {\mathbf{L}}{{{\mathbf{Q}}}^{{(1)}}}{\mathbf{Lb}}_{{}}^{{(1)}} + {\mathbf{L}}{{{\mathbf{b}}}^{{(2)}}} + {\mathbf{LQ}}_{{}}^{{(1)}}{\mathbf{LQ}}_{{}}^{{(1)}}{\mathbf{L}}{{{\mathbf{b}}}^{{(0)}}} + {\mathbf{L}}{{{\mathbf{Q}}}^{{(2)}}}{\mathbf{Lb}}_{{}}^{{(0)}}. \\ \end{gathered} $При таком подходе получаем диаграмму, по крайней мере, с ошибкой порядка ${{(k\sigma )}^{3}}$. Учитывая, что число тел в группе достаточно велико, ошибка может иметь большие значения. Рисунок 6 иллюстрирует это утверждение. Однако при усреднении диаграммы ошибка должна быть существенно меньше, что показывают рис. 2–5.
На рис. 7 приведены угловые зависимости модуля усредненной диаграммы группы из 16 круговых цилиндров, описанной выше. При этом средние значения координат центров тел получаются из формул (43) и (44) при $\sigma = 0$. Штриховой кривой показана зависимость модуля “невозмущенной” диаграммы рассеяния, т.е. для значений координат центров тел, равных средним значениям $({{\bar {x}}_{{0j}}},{{\bar {y}}_{{0j}}})$.
ЗАКЛЮЧЕНИЕ
На основе одномодового приближения в рамках МДУ разработан подход для нахождения усредненной диаграммы рассеяния группы одинаковых идеально проводящих цилиндров произвольного сечения. Произведено усреднение диаграммы как по углам, на которые повернуты контуры сечений тел, так и по координатам центров цилиндров. Показана хорошая точность нахождения диаграммы на примере дифракции на группе из трех и четырех круговых и эллиптических цилиндров, имеющих случайную ориентацию и случайные координаты. Проведено сравнение “реализации” диаграммы для группы из 16 круговых цилиндров, полученной при помощи ММВ, с решением задачи, основанным на точном решении соответствующей алгебраической системы. Показана удовлетворительная точность поученных результатов. Приведены угловые зависимости модуля усредненной диаграммы рассеяния для группы из 16 случайно расположенных круговых цилиндров.
Список литературы
Газарян Ю.Л. // ЖЭТФ. 1969. Т. 56. Вып. 6. С. 1856.
Абрамович Б.С., Гурбатов С.Н., Рыжов Ю.А. // Изв. вузов. Радиофизика. 1979. Т. 22. № 5. С. 566.
Заборонкова Т.М., Коган Л.П., Тамойкин В.В. // РЭ. 2005. Т.50. № 5. С. 552.
Григорьев Г.И., Заборонкова Т.М., Коган Л.П. // РЭ. 2017. Т. 62. № 10. С. 945.
Kюpкчaн A.Г. // PЭ. 1993. T. 38. № 1. C. 48.
Kюpкчaн A.Г., Coлoвeйчик A.Л. // PЭ. 2000. T. 45. № 4. C. 389.
Кюркчан А.Г., Маненков С.А. // РЭ. 2002. Т. 47. № 11. С. 1322.
Кюркчан А.Г., Смирнова Н.И. Математическое моделирование в теории дифракции с использованием априорной информации об аналитических свойствах решения. М.: ИД Медиа Паблишер, 2014.
Демин Д.Б., Клеев А.И., Кюркчан А.Г. // РЭ. 2018. Т. 63. № 6. С. 507.
Басс Ф.Г., Фукс И.М. Рассеяние волн на статистически неровной поверхности. М.: Наука, 1972.
Рытов С.М., Кравцов Ю.А., Татарский В.И. Введение в статистическую радиофизику. М.: Наука, 1978. Ч. 2.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника