Радиотехника и электроника, 2021, T. 66, № 4, стр. 333-338

ВВЕДЕНИЕ

Проблема дифракции плоской электромагнитной волны на полупрозрачной полуплоскости является актуальной задачей теории дифракции. Ее решение расширяет множество структур, для которых рассеянное поле может быть записано в строгой и достаточно простой аналитической форме. Кроме того, оно расширяет область применения асимптотических методов теории дифракции, включая в нее полупрозрачные рассеиватели с острыми кромками.

Среди аналитических методов решения граничных задач для полубесконечных структур, таких как полуплоскости, полупластины и клинья, следует отметить два основных подхода: метод Винера-Хопфа и метод Малюжинца. Метод Малюжинца часто называют также методом интеграла Малюжинца или Зоммерфельда–Малюжинца. Оба метода неоднократно и весьма успешно применялись для анализа указанных выше структур. Строгое решение задачи рассеяния плоской волны на полуплоскости с идеально проводящими граничными условиями и импедансными граничными условиями Леонтовича получено методом интеграла Зоммерфельда–Малюжинца соответственно в работах [1] и [2]. Задача рассеяния плоской волны полупрозрачной полуплоскостью исследовалась в [3–11]. В работе [3] предложено использовать метод интеграла Зоммерфельда–Малюжинца для решения задачи рассеяния плоской волны на диэлектрических пластинах. Метод Винера–Хопфа используется в [4–8, 11] для опредения интегрального представления рассеянного поля. В работе [11] также приводятся эвристические формулы для опредения диаграммы направленности цилиндрической волны, рассеянной краем полупрозрачной полуплоскости. Метод интеграла Зоммерфельда–Малюжинца используется в [9] для определения решения задачи рассеяния Е-поляризованной плоской волны на полупрозрачной полуплоскости с граничными условиями частного вида, которое выражается через специальные функции Малюжинца. Решение, полученное в [9], непригодно для расчета рассеянного поля, так как в нем отсутствует информация о виде специальной функции Малюжинца. Как будет показано в данной работе, для корректного вычисления данной функции для произвольного комплексного аргумента, необходимо использовать ее представление через двойное бесконечное произведение. Метод интеграла Зоммерфельда–Малюжинца используется также в [10] для определения решения задачи рассеяния Е-поляризованной плоской волны на сочленении импедансного клина и полупрозрачной полуплоскости. Несмотря на то, что формулы, полученные в [10], могут быть модифицированны для случая рассеяния Е-поляризованной плоской волны на полупрозрачной полуплоскости, решения такой задачи в [10] не представлено.

Таким образом, можем сделать вывод, что в настоящее время решение для полупрозрачной полуплоскости с граничными условиями достаточно общего вида получено только методом Винера–Хопфа. Основной целью нашего исследования является развитие метода Малюжинца в направлении применения его для анализа полупрозрачных структур. В данной работе рассматриваем задачу рассеяния плоской волны, падающей под произвольным углом на полупрозрачную полуплоскость. Для решения граничной задачи используется метод интеграла Зоммерфельда–Малюжинца для двух поляризаций падающего поля. При помощи указанного строгого решения, мы найдем аналитическое представление для диаграммы направленности поля, рассеянного полупрозрачной полуплоскостью. Верификация полученного решения проводится путем сравнения численных результатов по методу Малюжинца с известным решением по методу Винера–Хопфа.

1. ГРАНИЧНЫЕ УСЛОВИЯ

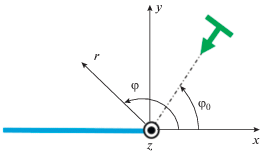
Рассмотрим полупрозрачную бесконечно тонкую полуплоскость, расположенную при y = 0, x ≤ 0 (рис. 1). Граничные условия на поверхности полуплоскости имеют вид

Рис. 1.

Геометрия задачи.

Здесь, $\vec {E}_{{}}^{ \pm }$ ($\vec {H}_{{}}^{ \pm }$) – вектор напряженности электрического (магнитного) поля на поверхности полуплоскости при φ = ±π; $\vec {n}$ – единичный вектор нормали к освещенной стороне полуплоскости; ${{\vec {j}}^{e}}$ – электрический ток на полуплоскости; ${\mathbf{Z}}$ – тензор импеданса. Условия (1) могут быть записаны через компоненты векторов напряженности электрического ($E_{{x,z}}^{ \pm }$) и магнитного ($H_{{x,z}}^{ \pm }$) полей и компоненты электрического тока ($j_{{x,z}}^{e}$) в декартовых координатах (x, y, z):

где Z_xx, Z_xz, Z_zx, и Z_zz – компоненты тензора импеданса, которые характеризуют свойства полуплоскости. В общем случае, данные компоненты являются комплексными числами с аргументами, лежащими в интервале [−π/2; π/2].

Рассмотрим раздельно возбуждение полуплоскости волнами электрической (H_z = 0) и магнитной (E_z = 0) поляризаций. При этом взаимодействие между ортогональными компонентами тока $j_{x}^{e}$ и $j_{z}^{e}$ отсутствует, т.е. Z_zx = Z_xz = 0. Тогда условия (2) могут быть выражены через скалярные функции u_E,H, которые представляют компоненты E_z или H_z для электрической (E) или магнитной (H) поляризаций соответственно. Используя соотношения, следующие из уравнений Максвелла:

можем записать условия (2) в цилиндрических координатах (r, φ, z) через соотношение ∂u/∂y = = −∂u/(r∂φ) следующим образом:

Здесь Z₀ – волновой импеданс падающей волны; k = 2π/λ; λ – длина волны в вакууме; i – мнимая единица. Условия (4) становятся условиями u_E = 0 и ∂u_H/∂φ = 0 для идеально проводящей полуплоскости при Z_xx,zz = 0.

2. МЕТОД МАЛЮЖИНЦА

Рассмотрим падающую волну в форме

в полярных координатах (r, φ), распространяющуюся из верхнего полупространства при 0 ≤ φ₀ < π. Предполагаем зависимость от времени вида exp(iωt), где ω – круговая частота, t – время. Как известно, решение уравнения Гельмгольца Δu_{E, H} + $ + \,\,{{k}^{2}}{{u}_{{{\text{E,H}}}}} = 0$ было использовано Зоммерфельдом [1] для решения задачи рассеяния плоской волны идеально проводящей полуплоскостью в следующем виде:

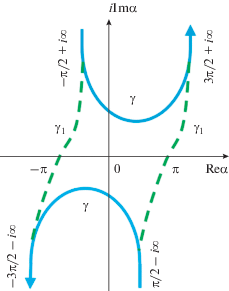
где γ – контур интегрирования в комплексной плоскости α (рис. 2); S_E,H – амплитуды парциальных плоских волн. Контур γ и подынтегральная функция S_E,H определяются таким образом, чтобы удовлетворить условию сходимости интеграла (5), граничным условиям, а также условиям излучения на бесконечности. Для определения диаграммы направленности цилиндрической волны, рассеянной краем идеально проводящей полуплоскости, в [1] используется метод перевала применительно к интегралу (5). Контур интегрирования γ деформируется так, что он преобразуется в контур γ₁ (см. рис. 2), имеющий две ветви, которые проходят через точки перевала α = ±π. Ветви контура γ₁ определяются как Re α = ±π + gd(Im α), где gd(x) = arcsin(thx) – функция Гудермана. Применение метода перевала при условии kr $ \gg $ 1 позволяет представить (5) как сумму геометрооптического поля и поля цилиндрической волны, рассеянной краем полуплоскости. Рассеянное идеально проводящей полуплоскостью поле для электрической ($u_{E}^{{{\text{рп}}}}$) и магнитной ($u_{H}^{{{\text{рп}}}}$) поляризаций падающей волны имеет вид:

Рис. 2.

Контуры интегрирования γ и γ₁.

Здесь ξ_E, H равно 1 или –1 для E- и H-поляризации соответственно.

Интеграл вида (5) также используется в [2] для строгого решения задачи рассеяния плоской волны непрозрачной полуплоскостью, на которой заданы импедансные граничные условия Леонтовича (полуплоскость – это частный случай клина, рассмотренного в [2]). Данные граничные условия имеют вид

Отметим, что в [3] показано, что в записи граничных условий в [2] допущена опечатка. Перед ik в формуле (1) работы [2] должно быть $ \mp $ вместо ±). Параметры $\vartheta _{{E,H}}^{ \pm }$, характеризующие свойства поверхностей при φ = ±π, являются углами Брюстера, при которых коэффициент отражения $R_{{E,H}}^{z}$ от бесконечной плоскости с граничными условиями Леонтовича обращается в нуль:

Углы Брюстера связаны с импедансами непрозрачной поверхности полуплоскости (Z_L±) как $\sin \vartheta _{{E,H}}^{ \pm } = {{\left( {{{{{Z}_{{L \pm }}}} \mathord{\left/ {\vphantom {{{{Z}_{{L \pm }}}} {{{Z}_{0}}}}} \right. \kern-0em} {{{Z}_{0}}}}} \right)}^{{ - {{\xi }_{{E,H}}}}}}$. Подынтегральное выражение в (5), соответствующее импедансным граничным условиям, имеет вид

где Ψ выражается через специальную функцию Малюжинца Ψ_π:

Наиболее общий вид функции Малюжинца Ψ_π(α), который позволяет определить ее для любых, в том числе комплексных значений аргумента α, выражается через двойное бесконечное произведение [2]:

Другое представление Ψ_π, выраженное через экспоненциальную функцию с интегралом в показателе, также имеется в [2]. Однако данное представление содержит опечатки. Корректное выражение Ψ_π через экспоненциальную функцию с интегралом в показателе имеет следующий вид [10]:

Представление функции Ψ_π через выражение (9) пригодно только для значений аргумента, лежащих в пределах |Reα| ≤ 5π/2. Для вычисления функции Ψ_π через выражение (9) для аргумента α вне указанного интервала необходимо использовать следующие рекуррентные соотношения [2]:

Применение метода перевала к интегралу (5) с подынтегральной функцией (7) дает представление поля в дальней зоне как сумму геометрооптической части, поля цилиндрической волны, рассеянной краем импедансной полуплоскости, и поля поверхностных волн, возбуждаемых на поверхностях полуплоскости [2]. Выражение поля цилиндрической волны, рассеянной краем импедансной полуплоскости, для электрической ($u_{E}^{{{\text{ри}}}}$) и магнитной ($u_{H}^{{{\text{ри}}}}$) поляризации падающей волны имеет вид:

3. РЕШЕНИЕ ДЛЯ ПОЛУПРОЗРАЧНОЙ ПОЛУПЛОСКОСТИ

Рассмотрим задачу рассеяния плоской волны, падающей на полуплоскость с полупрозрачными граничными условиями (4). Симметрия структуры относительно оси x позволяет представить полное поле $u_{{E,H}}^{t}$ как суперпозицию симметричного $u_{{E,H}}^{{\text{с}}}$ и антисимметричного $u_{{E,H}}^{{\text{а}}}$ полей:

где

Поля $u_{{E,H}}^{{\text{с}}}$ и $u_{{E,H}}^{{\text{а}}}$ возбуждаются падающими (п) плоскими волнами соответственно

и

Функции $u_{{E,H}}^{{{\text{с,а}}}}$ удовлетворяют уравнению Гельмгольца $\Delta u_{{E,H}}^{{{\text{с,а}}}} + {{k}^{2}}u_{{E,H}}^{{{\text{с,а}}}} = 0$ везде, кроме поверхности полуплоскости. На поверхности полуплоскости данные функции удовлетворяют следующим условиям, полученным после подстановки (12) в (4):

Из (14) следует, что для Е-поляризации симметричное и антисимметричное поля удовлетворяют при x < 0 с учетом обозначения ${\text{sin}}\vartheta _{E}^{ \pm }$ = Z₀/(2Z_zz) импедансному граничному условию Леонтовича и граничному условию идеальной проводимости соответственно. Для Н-поляризации, антисимметричное и симметричное поля удовлетворяют импедансному граничному условию Леонтовича при замене ${\text{sin}}\vartheta _{H}^{ \pm }$ = 2Z_xx/Z₀ и граничному условию идеальной проводимости соответственно. Однако видно, что для Е- и Н-поляризаций граничные условия 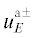= 0 и 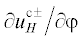= 0 удовлетворяются для падающего поля автоматически. Поэтому рассеянное антисимметричное поле Е-поляризации или симметричное поле Н-поляризации отсутствует, а полное поле совпадает с полем падающей волны. Таким образом, строгое решение задачи рассеяния плоской волны полупрозрачной полуплоскостью сводится к следующей сумме:

где

Применение метода перевала к интегралам в (15) позволяет представить полное поле в дальней зоне как сумму геометрооптической части ($u_{{E,H}}^{{{\text{ГО}}}}$) и поля цилиндрической волны, рассеянное краем полуплоскости. Геометрооптическое поле вычисляется через коэффициенты отражения ($R_{{E,H}}^{{st}}$) и прохождения ($T_{{E,H}}^{{st}}$) E- или H-поляризованной плоской волны, падающей на бесконечную полупрозрачную плоскость, следующим образом:

Выражение поля цилиндрической волны, рассеянной краем полупрозрачной полуплоскости, для электрической ($u_{E}^{{{\text{рпп}}}}$) и магнитной ($u_{H}^{{{\text{рпп}}}}$) поляризации падающей волны имеет вид

где $u_{{E,H}}^{{{\text{ри}}}}\left( {r,\varphi ,{{\varphi }_{0}},\vartheta _{{E,H}}^{{st}},\vartheta _{{E,H}}^{{st}}} \right)$ определяется выражением (11).

Отметим, что применение метода перевала к интегралам в (15) дает также член, соответствующий поверхностной волне, возбуждаемой на полуплоскости при некоторых значениях угла Брюстера. Однако можно показать, что амплитуда данной поверхностной волны убывает как exp(−ζr) (ζ – положительная постоянная) при r → ∞, в то время как амплитуда поля цилиндрической волны, рассеянной краем полуплоскости, убывает как r^−1/2. Поэтому амплитуда поля поверхностной волны в дальней зоне много меньше амплитуды $u_{{E,H}}^{{{\text{рпп}}}}$, и мы не рассматриваем ее вклад в формирование диаграммы направленности.

4. ЧИСЛЕННАЯ ПРОВЕРКА РЕШЕНИЯ

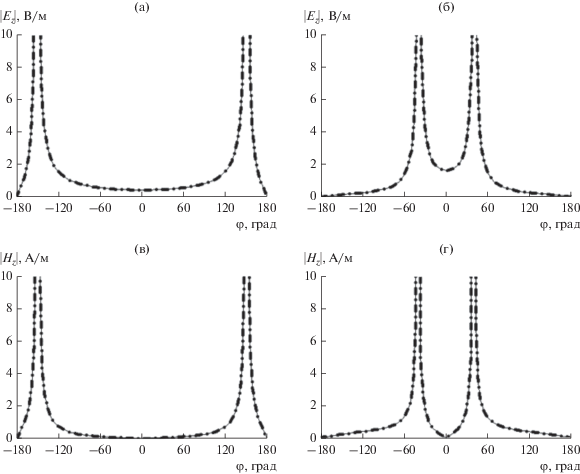
Для проверки точности полученного решения, сравним графики диаграмм направленности волны, рассеянной краем полупрозрачной полуплоскости, построенные по формуле (17) и с помощью метода Винера–Хопфа [11]. Модули компонент электрического и магнитного рассеянного полей, построенные для k = π/10 и различных значений импедансов полуплоскости и углов падения плоской волны, представлены на рис. 3. Кривые получены методом интеграла Зоммерфельда–Малюжинца и Винера–Хопфа и рассчитаны для двух вариантов: Z_xx,zz = –100i, φ₀ = 30° и Z_xx,zz = 200i, φ₀ = 140°. Структура возбуждается в случае как Е-, так и Н-поляризации волной единичной амплитуды, $\left| {u_{{E,H}}^{{\text{п}}}} \right|$ = 1. Из рис. 3 видно, что амплитудные диаграммы направленности, полученные двумя методами, совпадают для всех углов наблюдения. Дополнительный анализ показывает, что фазовые диаграммы также совпадают для всех углов наблюдения для обеих поляризаций.

Рис. 3.

Диаграммы направленности компонент |E_z| (а, б) и |H_z| (в, г), построенные с использованием метода интеграла Зоммерфельда–Малюжинца (сплошная кривая) и метода Винера–Хопфа (штрих-пунктирная) для следующих параметров: a, в) Z_xx,zz = –100i, φ₀ = 30°; б, г) Z_xx,zz = 200i, φ₀ = 140°.

ЗАКЛЮЧЕНИЕ

Таким образом, получено строгое решение задачи дифракции плоской волны на полупрозрачной полуплоскости методом интеграла Зоммерфельда–Малюжинца для двух поляризаций падающего поля. Используя данное строгое решение, мы получаем аналитическое выражение для поля цилиндрической волны, рассеянной краем полуплоскости, которое выражается через специальную функцию Малюжинца. Результаты соспоставления полученного решения с методом Винера–Хопфа показали хорошее совпадение двух подходов, что является подтверждением правильности приведенных в работе соотношений.