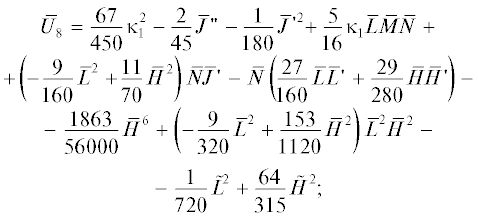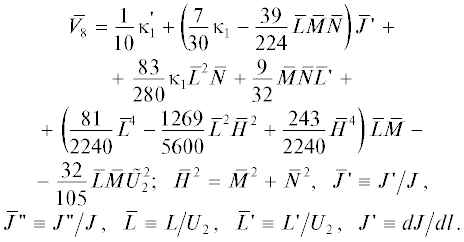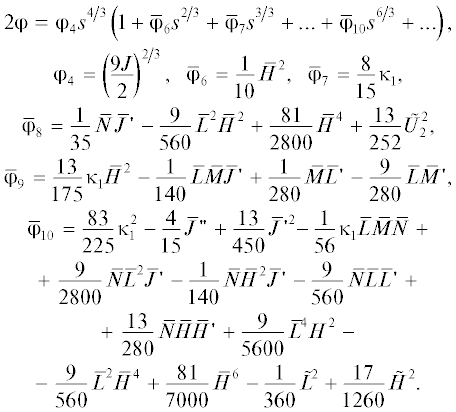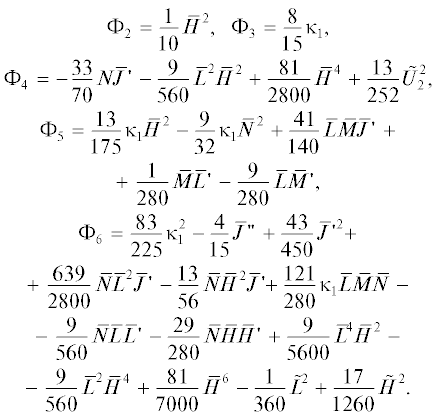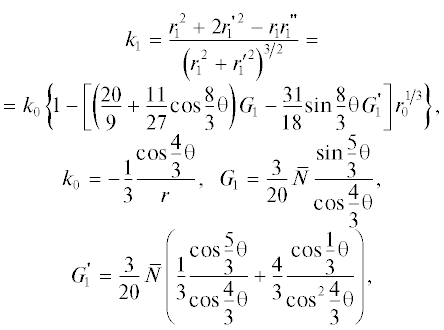Радиотехника и электроника, 2021, T. 66, № 4, стр. 402-409
Структура электрического поля вблизи кромки катода при эмиссии в ρ-режиме
В. А. Сыровой *
ВЭИ – филиал ФГУП “РФЯЦ-ВНИИТФ им. акад. Е.И. Забабахина”
111250 Москва, ул. Красноказарменная, 12, Российская Федерация
* E-mail: red@cplire.ru
Поступила в редакцию 17.01.2020
После доработки 17.01.2020
Принята к публикации 22.02.2020
Аннотация
На основе теории антипараксиальных разложений для ленточного релятивистского пучка исследована структура электрического поля вблизи кромки катода при эмиссии в ρ-режиме и наличии внешнего неоднородного магнитного поля. Описаны формы боковой поверхности катода и отрицательных эквипотенциалей, позволяющие сформировать профилированный тепловой зазор, который не нарушает принятую гидродинамическую модель потока.
ВВЕДЕНИЕ
Концепция синтезированного теплового зазора сформулирована в работе [1] на примере формирования цилиндрического пучка, потенциал в котором соответствует закону ${4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}$ плоского диода. Противоречащее теории интенсивных пучков задание теплового зазора при использовании двумерных и трехмерных программ траекторного анализа является одним из основных фактов, вызывающих сомнение в адекватности расчетов как в случае осесимметричных потоков с высокой компрессией, так и при рассмотрении электронных пучков с прямоугольным сечением, часто аппроксимируемым эллипсом. Анализ подходов такого рода приведен в работе [2], вопрос о конфигурации теплового зазора и возможности управлять сходимостью потока за счет наклона нулевого формирующего электрода рассматривался в работах [3, 4].
В последней из них [4] на основе теории антипараксиальных разложений [5] рассчитана боковая форма катода и отрицательные эквипотенциали при эмиссии в ρ-режиме для электростатических потоков. В работе [6] выполнен расчет теплового зазора для планарного гиротрона при эмиссии в Т-режиме. Локальное решение уравнения Лапласа вблизи кромки катода для того же прибора в геометризованной постановке построено в работе [7]. Конфигурация теплового зазора для магнетронно-инжекторной пушки на основе точного решения для плоского магнетрона исследована в [8].
Цель работы – решение в общей постановке задачи формирования ленточного релятивистского пучка в окрестности кромки искривленного катода с неоднородным токоотбором при эмиссии в ρ-режиме при наличии внешнего неоднородного магнитного поля. Рассмотрение ведется в нормировках, исключающих из уравнений пучка все физические константы используемой системы единиц.
1. ПАРАМЕТРЫ ЭЛЕКТРОННОГО ПОТОКА ПРИ ЭМИССИИ В ρ-РЕЖИМЕ
Компоненты скорости. Решение вблизи катода $s = 0$ при эмиссии в ρ-режиме имеет вид координатных разложений по параметру $\sqrt[3]{s}$, где s – расстояние по нормали к катоду в системе s, l, x (l – длина дуги кривой, определяющей форму стартовой поверхности, х – циклическая координата) [5, 9]:
(1)
$\begin{gathered} {{U}_{s}} = {{U}_{2}}{{s}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}\left( {1 + {{{\bar {U}}}_{4}}{{s}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + {{{\bar {U}}}_{5}}{{s}^{{{3 \mathord{\left/ {\vphantom {3 3}} \right. \kern-0em} 3}}}} + ...} \right), \\ {{U}_{l}} = {{U}_{2}}{{s}^{{{3 \mathord{\left/ {\vphantom {3 3}} \right. \kern-0em} 3}}}}\left( {{{{\bar {V}}}_{3}} + {{{\bar {V}}}_{4}}{{s}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} + {{{\bar {V}}}_{5}}{{s}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + ...} \right). \\ \end{gathered} $Коэффициенты в (1), являющиеся функциями l, следующим образом выражаются через кривизну катода ${{\kappa }_{1}}$, плотность тока эмиссии J и компоненты напряженности магнитного поля $\vec {H} = \left\{ {L,\,M,\,N} \right\}$ при s = 0:
Выражение для потенциала. Потенциал электрического поля ${\varphi }$ описывается разложением
Члены, исчезающие в нерелятивистском пределе, отмечены символом тильда.
Уравнение трубки тока. Дифференциальное уравнение трубки тока имеет вид
где ${{h}_{k}}$ – коэффициенты Ляме системы s, l, x:
Решение уравнения (4) определяется формулой
(6)
$\bar {l} = l - {{l}_{0}} = {{{\alpha }}_{4}}{{s}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + {{{\alpha }}_{5}}{{s}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + ... + {{{\alpha }}_{9}}{{s}^{{{9 \mathord{\left/ {\vphantom {9 3}} \right. \kern-0em} 3}}}} + ...,$причем при сохранении члена с коэффициентом ${{{\alpha }}_{9}}$ в (6) функции ${{\bar {V}}_{3}}$, ${{\bar {V}}_{4}}$ должны быть разложены в окрестности точки старта $l = {{l}_{0}}$:
(7)
$\begin{gathered} {{{\bar {V}}}_{3}}\left( l \right) = {{{\bar {V}}}_{3}}\left( {{{l}_{0}}} \right) + \bar {V}_{3}^{'}\left( {{{l}_{0}}} \right)\bar {l} = \\ = - \bar {N} + \left( {\frac{1}{3}\bar {N}\bar {J}{\kern 1pt} '\,\, - \frac{2}{9}\tilde {U}_{2}^{2}} \right)\left( {{{{\alpha }}_{4}}{{s}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + {{{\alpha }}_{5}}{{s}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}}} \right), \\ {{{\bar {V}}}_{4}}\left( l \right) = {{{\bar {V}}}_{4}}\left( {{{l}_{0}}} \right) + \bar {V}_{4}^{'}\left( {{{l}_{0}}} \right)\bar {l} = \frac{3}{4}\bar {L}\bar {M} + \\ + \,\,\frac{3}{4}\left( { - \frac{2}{3}\bar {L}\bar {M}\bar {J}{\kern 1pt} '\,\, + \bar {M}\bar {L}{\kern 1pt} '\,\, + \bar {L}\bar {M}{\kern 1pt} '} \right){{{\alpha }}_{4}}{{s}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}. \\ \end{gathered} $Коэффициенты ${{{\alpha }}_{k}}$ в (6) и выражения в правых частях (7) являются константами, соответствующими точке старта ${{l}_{0}}$:
(8)
$\begin{gathered} {{{\alpha }}_{4}} = - \frac{3}{4}\bar {N},\,\,\,\,{{{\alpha }}_{5}} = \frac{9}{{20}}\bar {L}\bar {M}, \\ {{{\alpha }}_{6}} = \frac{1}{{10}}\bar {J}{\kern 1pt} '\,\, + \frac{9}{{40}}\left( {{{{\bar {L}}}^{{{\kern 1pt} 2}}} - {{{\bar {H}}}^{2}}} \right)\bar {N}, \\ {{{\alpha }}_{7}} = - \frac{{37}}{{70}}{{\kappa }_{1}}\bar {N} + \left( {\frac{{27}}{{112}}{{{\bar {H}}}^{2}} - \frac{{27}}{{280}}{{{\bar {L}}}^{{{\kern 1pt} 2}}}} \right)\bar {L}\bar {M}, \\ {{{\alpha }}_{8}} = \frac{{21}}{{40}}{{\kappa }_{1}}\bar {L}\bar {M} + \left( { - \frac{9}{{560}}{{{\bar {L}}}^{{{\kern 1pt} 2}}} + \frac{{81}}{{1400}}{{{\bar {H}}}^{2}} - \frac{3}{{224}}{{{\bar {N}}}^{{{\kern 1pt} 2}}}} \right)\bar {J}{\kern 1pt} '\,\, + \\ + \,\,\frac{9}{{112}}\bar {L}\bar {L}{\kern 1pt} '\,\, - \frac{{81}}{{560}}\bar {H}\bar {H}{\kern 1pt} '\,\, + \\ + \,\,\left( { - \frac{{81}}{{2240}}{{{\bar {L}}}^{4}} + \frac{{1269}}{{5600}}{{{\bar {L}}}^{{{\kern 1pt} 2}}}{{{\bar {H}}}^{2}} - \frac{{243}}{{2240}}{{{\bar {H}}}^{{{\kern 1pt} 4}}}} \right)\bar {N} + \frac{{31}}{{336}}\bar {N}\tilde {U}_{2}^{2}, \\ {{{\alpha }}_{9}} = \frac{1}{{30}}\kappa _{1}^{'} + \frac{{19}}{{150}}{{\kappa }_{1}}\bar {J}{\kern 1pt} '\,\, + \frac{{353}}{{3360}}\bar {L}\bar {M}\bar {N}\bar {J}{\kern 1pt} '\,\, + \frac{{877}}{{420}}{{\kappa }_{1}}{{{\bar {L}}}^{{{\kern 1pt} 2}}}\bar {N} - \\ - \,\,\frac{{363}}{{1400}}{{\kappa }_{1}}\bar {N}{{{\bar {H}}}^{2}} - \frac{{361}}{{1120}}\bar {M}\bar {N}\bar {L}{\kern 1pt} '\,\, + \frac{{143}}{{560}}\bar {L}\bar {N}\bar {M}{\kern 1pt} '\,\, + \\ + \,\,\frac{{27}}{{2240}}{{{\bar {L}}}^{{{\kern 1pt} 5}}}\bar {M} - \frac{{837}}{{5600}}{{{\bar {L}}}^{{{\kern 1pt} 3}}}{{{\bar {H}}}^{2}}\bar {M} + \\ + \,\,\frac{{1593}}{{11{\kern 1pt} 200}}{{{\bar {H}}}^{4}}\bar {L}\bar {M} - \frac{1}{{21}}\bar {L}\bar {M}\tilde {U}_{2}^{2}. \\ \end{gathered} $Введем локальные декартовы координаты X, Y, направленные по нормали и касательной к катоду в точке старта. С криволинейными координатами s, $\bar {l}$ с необходимой точностью они связаны соотношениями
(9)
$\begin{gathered} s = X - \frac{1}{2}{{\kappa }_{1}}{{Y}^{2}} - \frac{1}{2}\kappa _{1}^{2}X{{Y}^{2}}, \\ \bar {l} = \left( {1 + {{\kappa }_{1}}X + \kappa _{1}^{2}{{X}^{2}}} \right)Y. \\ \end{gathered} $Уравнение трубки тока в координатах X, Y описывается формулами
(10)
$\begin{gathered} Y = {{a}_{4}}{{X}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + {{a}_{5}}{{X}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + ... + {{a}_{9}}{{X}^{{{9 \mathord{\left/ {\vphantom {9 3}} \right. \kern-0em} 3}}}}; \\ {{a}_{4}} = {{{\alpha }}_{4}},\,\,\,\,{{a}_{5}} = {{{\alpha }}_{5}},\,\,\,\,{{a}_{6}} = {{{\alpha }}_{6}},\,\,\,\,{{a}_{7}} = {{{\alpha }}_{7}} + \frac{3}{4}{{\kappa }_{1}}\bar {N}, \\ {{a}_{8}} = {{{\alpha }}_{8}} - \frac{9}{{20}}{{\kappa }_{1}}\bar {L}\bar {M},\,\,\,\,{{a}_{9}} = {{{\alpha }}_{9}} + \frac{9}{{32}}{{\kappa }_{1}}{{{\bar {N}}}^{3}}. \\ \end{gathered} $2. ЛОКАЛЬНОЕ РЕШЕНИЕ УРАВНЕНИЯ ЛАПЛАСА
Распрямляющее отображение. Перейдем от X, Y к криволинейной системе u, v, в которой граница пучка описывается уравнением v = 0:
(11)
$\begin{gathered} Z \equiv X + iY = w + i\left( {{{a}_{4}}{{w}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + {{a}_{5}}{{w}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + ...} \right), \\ w = u + iv. \\ \end{gathered} $Обратное отображение определено формулой
(12)
$\begin{gathered} w = Z - i{{a}_{4}}{{Z}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} - \left( {i{{a}_{5}} + \frac{4}{3}a_{4}^{2}} \right){{Z}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + \\ + \,\,\left( { - i{{a}_{6}} - 3{{a}_{4}}{{a}_{5}} + 2ia_{4}^{3}} \right){{Z}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}} + \\ + \,\,\left( { - i{{a}_{7}} - \frac{{10}}{3}{{a}_{4}}{{a}_{6}} - \frac{5}{3}a_{5}^{2} + i\frac{{65}}{9}a_{4}^{2}{{a}_{5}} + \frac{{268}}{{81}}a_{4}^{4}} \right){{Z}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0em} 3}}}}; \\ w = M\exp \left( {iT} \right),\,\,\,\,Z = r\exp \left( {i\theta } \right), \\ {{M}^{2}} = {{u}^{2}} + {{v}^{2}},\,\,\,\,{\text{tg}}T = {v \mathord{\left/ {\vphantom {v u}} \right. \kern-0em} u}, \\ {{r}^{2}} = {{X}^{2}} + {{Y}^{2}},\,\,\,\,{\text{tg}}\theta = {Y \mathord{\left/ {\vphantom {Y X}} \right. \kern-0em} X}. \\ \end{gathered} $Связь координат u, v и X, Y описывается выражениями
(13)
$\begin{gathered} u = r\cos \theta + {{r}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}{{\alpha }_{{4s}}}\sin \frac{4}{3}\theta + \\ + \,\,{{r}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}}\left( {{{\alpha }_{{5c}}}\cos \frac{5}{3}\theta + {{\alpha }_{{5s}}}\sin \frac{5}{3}\theta } \right) + \\ + \,\,{{r}^{2}}\left( {{{\alpha }_{{6c}}}\cos 2\theta + {{\alpha }_{{6s}}}\sin 2\theta } \right) + \\ + \,\,{{r}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0em} 3}}}}\left( {{{\alpha }_{{7c}}}\cos \frac{7}{3}\theta + {{\alpha }_{{7s}}}\sin \frac{7}{3}\theta } \right), \\ v = r\sin \theta - {{r}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}{{\alpha }_{{4s}}}\cos \frac{4}{3}\theta + \\ + \,\,{{r}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}}\left( { - {{\alpha }_{{5s}}}\cos \frac{5}{3}\theta + {{\alpha }_{{5c}}}\sin \frac{5}{3}\theta } \right) + \\ + \,\,{{r}^{2}}\left( { - {{\alpha }_{{6s}}}\cos 2\theta + {{\alpha }_{{6c}}}\sin 2\theta } \right) + \\ + \,\,{{r}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0em} 3}}}}\left( { - {{\alpha }_{{7s}}}\cos \frac{7}{3}\theta + {{\alpha }_{{7c}}}\sin \frac{7}{3}\theta } \right); \\ X = u - {{a}_{4}}{{M}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\sin \frac{4}{3}T - {{a}_{5}}{{M}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}}\sin \frac{5}{3}T - \\ - \,\,{{a}_{6}}{{M}^{2}}\sin 2T - {{a}_{7}}{{M}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0em} 3}}}}\sin \frac{5}{3}T, \\ Y = v + {{a}_{4}}{{M}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\cos \frac{4}{3}T + {{a}_{5}}{{M}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}}\cos \frac{5}{3}T + \\ + \,\,{{a}_{6}}{{M}^{2}}\cos 2T + {{a}_{7}}{{M}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0em} 3}}}}\cos \frac{7}{3}T. \\ \end{gathered} $Коэффициенты в (13) вычисляются в точке старта ${{l}_{0}}$ и определены формулами
(14)
$\begin{gathered} {{{\alpha }}_{{4s}}} = - \frac{3}{4}\bar {N},\,\,\,\,{{{\alpha }}_{{5c}}} = - \frac{3}{4}{{{\bar {N}}}^{2}},\,\,\,\,{{{\alpha }}_{{5s}}} = \frac{9}{{20}}\bar {L}\bar {M}, \\ {{{\alpha }}_{{6c}}} = \frac{{81}}{{80}}\bar {L}\bar {M}\bar {N},\,\,\,\,{{{\alpha }}_{{6s}}} = \frac{1}{{10}}\bar {J}{\kern 1pt} '\,\, + \\ + \,\,\frac{9}{{40}}\left( {{{{\bar {L}}}^{{{\kern 1pt} 2}}} - {{{\bar {H}}}^{2}}} \right)\bar {N} + \frac{{27}}{{32}}{{{\bar {N}}}^{3}}, \\ {{{\alpha }}_{{7c}}} = \frac{1}{4}\bar {N}\bar {J}{\kern 1pt} '\,\, - \frac{{27}}{{80}}{{{\bar {L}}}^{{{\kern 1pt} 2}}}{{{\bar {M}}}^{2}} + \frac{9}{{16}}\left( {{{{\bar {L}}}^{{{\kern 1pt} 2}}} - {{{\bar {H}}}^{2}}} \right){{{\bar {N}}}^{2}} + \frac{{67}}{{64}}{{{\bar {N}}}^{4}}, \\ {{{\alpha }}_{{7s}}} = \frac{{31}}{{140}}{{\kappa }_{1}}\bar {N} - \frac{{27}}{{280}}{{{\bar {L}}}^{{{\kern 1pt} 3}}}\bar {M} + \frac{{27}}{{112}}\bar {L}\bar {M}{{{\bar {H}}}^{2}} - \frac{{117}}{{64}}\bar {L}\bar {M}{{{\bar {N}}}^{2}}. \\ \end{gathered} $Потенциал на трубке тока. При сохранении члена порядка ${{s}^{{{{10} \mathord{\left/ {\vphantom {{10} 3}} \right. \kern-0em} 3}}}}$ в выражении (3) для потенциала необходимо провести разложение в окрестности точки $l = {{l}_{0}}$ функций ${{{\varphi }}_{4}}$ и ${{{\varphi }}_{6}}$:
(15)
$\begin{gathered} 2{{{\varphi }}_{e}} = {{\left( {\frac{{9J}}{2}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}{{s}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\left[ {1 + \frac{2}{3}\bar {J}{\kern 1pt} '\left( {{{{\alpha }}_{4}}{{s}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + {{{\alpha }}_{5}}{{s}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + {{{\alpha }}_{6}}{{s}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}}} \right)} \right] \times \\ \times \,\,\left\{ {1 + \frac{1}{{10}}\left[ {{{{\bar {H}}}^{2}} + \left( { - \frac{2}{3}{{{\bar {H}}}^{2}}\bar {J}{\kern 1pt} '\,\, + 2\bar {H}\bar {H}{\kern 1pt} '} \right){{{\alpha }}_{4}}{{s}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}} \right]{{s}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + } \right. \\ \left. {\frac{{}}{{}}\, + \,\,{{{{\bar {\varphi }}}}_{7}}s + {{{{\bar {\varphi }}}}_{8}}{{s}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + {{{{\bar {\varphi }}}}_{9}}{{s}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + {{{{\bar {\varphi }}}}_{{10}}}{{s}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}}} \right\}, \\ \end{gathered} $где индексом e отмечено значение функции на границе.
На основании формулы для s из (9) координата s на трубке тока выражается через Х следующим образом:
(16)
$s = X\left( {1 - \frac{2}{3}{{\kappa }_{1}}{\alpha }_{4}^{2}{{X}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} - \frac{4}{3}{{\kappa }_{1}}{{{\alpha }}_{4}}{{{\alpha }}_{5}}{{X}^{2}}} \right).$В результате для функции ${{{\varphi }}_{e}}$ получаем
Нормальная производная потенциала на трубке тока. Для вычисления производной $\left( {{{\partial {\varphi }} \mathord{\left/ {\vphantom {{\partial {\varphi }} {\partial v}}} \right. \kern-0em} {\partial v}}} \right)$ служат соотношения
(18)
$\begin{gathered} \frac{{\partial {\varphi }}}{{\partial v}} = \frac{{\partial {\varphi }}}{{\partial s}}\frac{{\partial s}}{{\partial v}} + \frac{{\partial {\varphi }}}{{\partial l}}\frac{{\partial l}}{{\partial v}},\,\,\,\,\frac{{\partial s}}{{\partial v}} = \frac{{\partial s}}{{\partial X}}\frac{{\partial X}}{{\partial v}} + \frac{{\partial s}}{{\partial Y}}\frac{{\partial Y}}{{\partial v}}, \\ \frac{{\partial l}}{{\partial v}} = \frac{{\partial l}}{{\partial X}}\frac{{\partial X}}{{\partial v}} + \frac{{\partial l}}{{\partial Y}}\frac{{\partial Y}}{{\partial v}}. \\ \end{gathered} $Формулы (3), (9), (13) позволяют вычислить входящие в (18) производные. В результате получим
(19)
$\begin{gathered} {{{\varphi }}_{{ve}}} \equiv {{\left( {{{\partial {\varphi }} \mathord{\left/ {\vphantom {{\partial {\varphi }} {\partial v}}} \right. \kern-0em} {\partial v}}} \right)}_{e}} = {{{\varphi }}_{4}}\left( {{{{\bar {F}}}_{2}}{{X}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + {{{\bar {F}}}_{3}}{{X}^{{{3 \mathord{\left/ {\vphantom {3 3}} \right. \kern-0em} 3}}}}} \right. + \\ \left. { + \,\,{{{\bar {F}}}_{4}}{{X}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + {{{\bar {F}}}_{5}}{{X}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + {{{\bar {F}}}_{6}}{{X}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}} + {{{\bar {F}}}_{7}}{{X}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0em} 3}}}}} \right); \\ {{{\bar {F}}}_{2}} = - \frac{{16}}{9}{{a}_{4}},\,\,\,\,{{{\bar {F}}}_{3}} = - \frac{{20}}{9}{{a}_{5}}, \\ {{{\bar {F}}}_{4}} = - \frac{8}{3}{{a}_{6}} - \frac{8}{3}{{a}_{4}}{{{{\bar {\varphi }}}}_{6}} + {\bar {\varphi }}{{_{4}^{'}}_{4}}, \\ {{{\bar {F}}}_{5}} = - \frac{{28}}{9}{{a}_{7}} - \frac{4}{3}{{\kappa }_{1}}{{a}_{4}} - \frac{{10}}{3}{{{{\bar {\varphi }}}}_{6}}{{a}_{5}} - \frac{{28}}{9}{{{{\bar {\varphi }}}}_{7}}{{a}_{4}}, \\ {{{\bar {F}}}_{6}} = - \frac{{32}}{9}{{a}_{8}} - \frac{4}{3}{{\kappa }_{1}}{{a}_{5}} - 4{{{{\bar {\varphi }}}}_{6}}{{a}_{6}} - \frac{{35}}{9}{{{{\bar {\varphi }}}}_{7}}{{a}_{5}} - \frac{{32}}{9}{{{{\bar {\varphi }}}}_{8}}{{a}_{4}}, \\ {{{\bar {F}}}_{7}} = - 4{{a}_{9}} - \frac{4}{3}{{\kappa }_{1}}{{a}_{6}} - \frac{{14}}{3}{{{{\bar {\varphi }}}}_{6}}{{a}_{7}} - \\ - \,\,\frac{{14}}{3}{{{{\bar {\varphi }}}}_{7}}{{a}_{6}} - \frac{{40}}{9}{{{{\bar {\varphi }}}}_{8}}{{a}_{5}} + {{\kappa }_{1}}{\bar {\varphi }}{{_{4}^{'}}_{4}}. \\ \end{gathered} $При сохранении выписанных в (19) членов ряда после вычисления производных из (18) на границе потока имеем
Выпишем несколько первых коэффициентов в явном виде:
(21)
$\begin{gathered} {{{\bar {F}}}_{2}} = \frac{4}{3}\bar {N},\,\,\,\,{{{\bar {F}}}_{3}} = - \bar {L}\bar {M},\,\,\,\,{{{\bar {F}}}_{4}} = \frac{2}{5}\bar {J}{\kern 1pt} '\,\, - \frac{3}{5}{{{\bar {L}}}^{{{\kern 1pt} 2}}}\bar {N} + \\ + \,\,\frac{4}{5}\left( {{{{\bar {M}}}^{2}} + {{{\bar {N}}}^{2}}} \right)\bar {N};\,\,\,\,{\bar {\varphi }}{{_{4}^{'}}_{4}} \equiv {{{\varphi }_{4}^{'}} \mathord{\left/ {\vphantom {{{\varphi }_{4}^{'}} {{{{\varphi }}_{4}}}}} \right. \kern-0em} {{{{\varphi }}_{4}}}} = \frac{2}{3}\bar {J}{\kern 1pt} '. \\ \end{gathered} $Решение уравнения Лапласа. Точное решение уравнения Лапласа описывается формулой
(22)
$2{\varphi }\left( {u,v} \right) = \operatorname{Re} {{{\varphi }}_{e}}\left( w \right) + \operatorname{Im} \int {{{{\varphi }}_{{ve}}}\left( w \right)dw} .$В окрестности кромки катода выражение (22) приобретает вид
(23)
$\begin{gathered} \frac{{2{\varphi }\left( {u,v} \right)}}{{{{{\varphi }}_{4}}}} = \left[ {{{M}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\cos \frac{4}{3}T} \right] + \left[ {\frac{3}{5}{{M}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}}{{{\bar {F}}}_{2}}\sin \frac{5}{3}T} \right] + \\ + \,\,\left[ {{{\Phi }_{2}}\left( {{{u}^{2}} - {{v}^{2}}} \right) + {{{\bar {F}}}_{3}}uv} \right] + \\ + \,\,\left[ {{{M}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0em} 3}}}}\left( {{{\Phi }_{3}}\cos \frac{7}{3}T + \frac{3}{7}{{{\bar {F}}}_{4}}\sin \frac{7}{3}T} \right)} \right] + \\ + \,\,\left[ {{{M}^{{{8 \mathord{\left/ {\vphantom {8 3}} \right. \kern-0em} 3}}}}\left( {{{\Phi }_{4}}\cos \frac{8}{3}T + \frac{3}{8}{{{\bar {F}}}_{5}}\sin \,\frac{8}{3}T} \right)} \right] + \\ + \,\,\left[ {{{\Phi }_{5}}\left( {{{u}^{3}} - 3u{{v}^{2}}} \right) + \frac{1}{3}{{{\bar {F}}}_{6}}\left( {3{{u}^{2}}v - {{v}^{3}}} \right)} \right] + \\ + \,\,\left[ {{{M}^{{{{10} \mathord{\left/ {\vphantom {{10} 3}} \right. \kern-0em} 3}}}}\left( {{{\Phi }_{6}}\cos \frac{{10}}{3}T + \frac{3}{{10}}{{{\bar {F}}}_{7}}\sin \frac{{10}}{3}T} \right)} \right]. \\ \end{gathered} $3. РАСЧЕТ ЭКВИПОТЕНЦИАЛЕЙ
Эквипотенциаль $\varphi = \varphi * < 0$. Выразим функции М, Т через полярные координаты r, θ в плоскости X, Y, пользуясь для этого формулами (13)
(24)
$\begin{gathered} + \,\,2{{{\alpha }}_{{4s}}}\left( { - {{{\alpha }}_{{6c}}}\sin \frac{2}{3}\theta + {{{\alpha }}_{{6s}}}\cos \frac{2}{3}\theta } \right) + {\alpha }_{{5c}}^{2} + {\alpha }_{{5s}}^{2}; \\ {\text{tg}}T = \frac{{v}}{u} = {\text{tg}}\theta \left( {1 + {{T}_{1}}{{r}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} + {{T}_{2}}{{r}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + ...} \right), \\ {{T}_{1}} = - {{{\alpha }}_{{4s}}}\frac{{\cos \frac{1}{3}\theta }}{{\sin \,\theta \cos \theta }},\,\,\,\, \\ {{T}_{2}} = \left( {{{{\alpha }}_{{5c}}}\sin \,\frac{2}{3}\theta - {{{\alpha }}_{{5s}}}\cos \frac{2}{3}\theta + {\alpha }_{{4s}}^{2}\frac{{\sin \,\frac{4}{3}\theta \cos \frac{1}{3}\theta }}{{\cos \theta }}} \right) \times \\ \times \,\,\frac{1}{{\sin \theta \cos \theta }},\,\,\,\,{{T}_{3}} = \frac{{{{{\alpha }}_{{6c}}}}}{{\cos \theta }} - \frac{{{{{\alpha }}_{{6s}}}}}{{\sin \theta }} + \\ + \,\,\frac{1}{2}\left[ {{{{\alpha }}_{{4s}}}{{{\alpha }}_{{5c}}}\left( { - \sin \theta \sin \frac{1}{3}\theta + \cos 2\theta } \right)} \right. + \\ \end{gathered} $Явные выражения для нескольких первых коэффициентов описываются формулами
(25)
$\begin{gathered} {{M}_{1}} = - \frac{3}{4}\bar {N}\sin \frac{1}{3}\theta , \\ {{M}_{2}} = \left( {\frac{9}{{16}} - \frac{3}{2}\cos \frac{2}{3}\theta } \right){{{\bar {N}}}^{2}} + \frac{9}{{10}}\bar {L}\bar {M}\sin \frac{2}{3}\theta , \\ {{\Theta }_{1}} = \frac{3}{4}\bar {N}\cos \frac{1}{3}\theta , \\ {{\Theta }_{2}} = - \frac{{15}}{{32}}{{{\bar {N}}}^{2}}\sin \frac{2}{3}\theta - \frac{9}{{20}}\bar {L}\bar {M}\cos \frac{2}{3}\theta . \\ \end{gathered} $При сохранении членов порядка r2уравнение (23) имеет вид
(26)
$\begin{gathered} \frac{{2{\varphi }}}{{{{{\varphi }}_{4}}}} = {{r}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\left[ {1 + \frac{2}{3}{{M}_{1}}{{r}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} + \left( {\frac{2}{3}{{M}_{2}} - \frac{1}{9}M_{1}^{2}} \right){{r}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}} \right] \times \\ \times \,\,\left[ {\cos \frac{4}{3}\theta - \frac{4}{3}{{\Theta }_{1}}\sin \frac{4}{3}\theta {\kern 1pt} \,{{r}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} - } \right. \\ - \,\,\left. {\left( {\frac{4}{3}{{\Theta }_{2}}\sin \frac{4}{3}\theta + \frac{8}{9}\Theta _{1}^{2}\cos \frac{4}{3}\theta } \right){{r}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}} \right] + \\ + \,\,\frac{3}{5}{{{\bar {F}}}_{2}}\left( {1 + \frac{5}{6}{{M}_{1}}{{r}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} \right)\left( {\sin \frac{5}{3}\theta + \frac{5}{3}{{\Theta }_{1}}\cos \frac{5}{3}\theta \,{{r}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} \right){{r}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + \\ + \,\,\left( {{{\Phi }_{2}}\cos 2\theta + \frac{1}{2}{{{\bar {F}}}_{3}}\sin 2\theta } \right){{r}^{2}}. \\ \end{gathered} $Для эквипотенциали ${\varphi } = {\varphi *}$ уравнению (26) может быть придана следующая форма:
(27)
$\begin{gathered} {{r}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\cos \frac{4}{3}\theta = {\bar {\varphi }*} + {{R}_{5}}{{r}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + {{R}_{6}}{{r}^{2}},\,\,\,\,{\bar {\varphi }}* \equiv {{2{\varphi *}} \mathord{\left/ {\vphantom {{2{\varphi *}} {{{{\varphi }}_{4}}}}} \right. \kern-0em} {{{{\varphi }}_{4}}}}; \\ {{R}_{5}} = \frac{1}{5}\bar {N}\sin \frac{5}{3}\theta , \\ {{R}_{6}} = \frac{1}{2}{{{\bar {N}}}^{2}}\left( { - \cos 4\theta + \frac{3}{4}\cos 2\theta - 2\cos \theta \cos \frac{1}{3}\theta } \right) + \\ + \,\,\frac{3}{{10}}\bar {L}\bar {M}\left( {\sin 4\theta - \frac{2}{3}\sin 2\theta + 2\sin \theta \cos \frac{1}{3}\theta } \right). \\ \end{gathered} $Разрешая (27) относительно r(θ) итеративно, получаем соотношения, описывающие отрицательную эквипотенциаль в нулевом, первом и втором приближениях:
(28)
$\begin{gathered} {{r}_{0}} = {{\left( {{{{\bar {\varphi }*}} \mathord{\left/ {\vphantom {{{\bar {\varphi }*}} {\cos \frac{4}{3}\theta }}} \right. \kern-0em} {\cos \frac{4}{3}\theta }}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}},\,\,\,\,{{r}_{1}} = {{r}_{0}}\left( {1 + {{G}_{1}}r_{0}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} \right), \\ {{r}_{2}} = {{r}_{0}}\left( {1 + {{G}_{1}}r_{0}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}} + {{G}_{2}}r_{0}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} \right); \\ {{G}_{1}} = {{\frac{3}{4}{{R}_{5}}} \mathord{\left/ {\vphantom {{\frac{3}{4}{{R}_{5}}} {\cos \frac{4}{3}\theta }}} \right. \kern-0em} {\cos \frac{4}{3}\theta }},\,\,\,\,{{G}_{2}} = {{\frac{3}{4}{{R}_{6}}} \mathord{\left/ {\vphantom {{\frac{3}{4}{{R}_{6}}} {\cos \frac{4}{3}\theta }}} \right. \kern-0em} {\cos \frac{4}{3}\theta }} + \frac{3}{2}G_{1}^{2}. \\ \end{gathered} $В нулевом приближении поверхность φ = $ = {\varphi *} < 0$ соответствует плоскому диоду, в первом приближении решение возмущается за счет компоненты $\bar {N}$ магнитного поля, во втором приближении свой вклад вносят ${{\bar {N}}^{2}}$ и комбинация $\bar {L}\bar {M}$, отличная от нуля для вихревого течения.
Вычислим кривизну эквипотенциали φ = $ = {\varphi *} < 0$ в первом приближении
где k0 – кривизна эквипотенциали для плоского диода.
На линии симметрии $\theta = {{3{\pi }} \mathord{\left/ {\vphantom {{3{\pi }} 4}} \right. \kern-0em} 4}$ одномерного решения имеем
(30)
$\begin{gathered} {{k}_{1}}\left( {\frac{{3{\pi }}}{4}} \right) = {{k}_{0}}\left( {1 - \frac{{71}}{{180\sqrt 2 }}Nr_{0}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} \right) \approx \\ \approx {{k}_{0}}\left( {1 - 0.279\bar {N}r_{0}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} \right). \\ \end{gathered} $Отрицательные значения потенциала по модулю возрастают на ней по закону
(31)
$\begin{gathered} 2{\varphi }\left( {\frac{{3{\pi }}}{4}} \right) = {{{\varphi }}_{4}} \times \\ \times \,\,\left[ { - {{r}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + \frac{1}{{5\sqrt 2 }}\bar {N}{{r}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + \left( {{{{\bar {N}}}^{2}} + \frac{1}{2}\bar {L}\bar {M}} \right){{r}^{2}}} \right]. \\ \end{gathered} $При $\bar {N}$, $\bar {L}\bar {M} > 0$ магнитное поле замедляет этот процесс.
Нулевая эквипотенциаль. Запишем уравнение эквипотенциали ${\varphi } = 0$ в координатах u, v и X, Y в следующем виде:
В силу конформности отображений (11), (12) коэффициенты ${{{\beta }}_{3}}$ и ${{b}_{3}}$ равны и имеют смысл тангенса угла наклона кривой ${\varphi } = 0$ к границе пучка в точке старта:
Выпишем разложения для первых комплексов из (23), заключенных в квадратные скобки, на линии ${\varphi } = 0$:
(34)
$\frac{v}{u} = {{{\beta }}_{3}} + {{{\beta }}_{4}}{{u}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} + {{{\beta }}_{5}}{{u}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + ...$Главным членом в уравнении ${\varphi } = 0$ является
(35)
${{u}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}{{a}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}\cos \frac{4}{3}\vartheta = 0,\,\,\,\,a = 1 + {\beta }_{3}^{2}.$Уравнение (35) имеет два корня, соответствующие ветвям эквипотенциали ${\varphi } = 0$ в первом и третьем квадрантах, причем второй корень определяет боковую поверхность катода
(36)
$\cos \frac{4}{3}\vartheta = 0,\,\,\,\,\vartheta = \frac{{3{\pi }}}{8},\,\,\,\,\frac{{9{\pi }}}{8};\,\,\,\,\sin \frac{4}{3}\vartheta = \sigma = \pm 1.$Для функции Т имеем следующее разложение:
(37)
$\begin{gathered} T = \vartheta + \bar {x}, \\ \bar {x} = \frac{1}{a}x - \frac{{{{{\beta }}_{3}}}}{{{{a}^{2}}}}{{x}^{2}} + \frac{{3{\beta }_{3}^{2} - 1}}{{{{a}^{3}}}}{{x}^{3}} + \frac{{{{{\beta }}_{3}} - {\beta }_{3}^{3}}}{{{{a}^{4}}}}{{x}^{4}}, \\ x = {{{\beta }}_{4}}{{u}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} + {{{\beta }}_{5}}{{u}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + {{{\beta }}_{6}}{{u}^{{{3 \mathord{\left/ {\vphantom {3 3}} \right. \kern-0em} 3}}}} + {{{\beta }}_{7}}{{u}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}. \\ \end{gathered} $Первый комплекс в (23) с учетом соотношений (36), (37) приобретает вид
(38)
$\begin{gathered} {{M}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\cos \frac{4}{3}\theta = {\sigma }{{u}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}{{a}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} \times \\ \times \,\,\left\{ { - \frac{4}{3}\frac{{{{{\beta }}_{4}}}}{a}{{u}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} + \left( { - \frac{4}{3}\frac{{{{{\beta }}_{5}}}}{a} - \frac{4}{9}\frac{{{{{\beta }}_{3}}{\beta }_{4}^{2}}}{{{{a}^{2}}}}} \right)} \right.{{u}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + \\ + \,\,\left[ { - \frac{4}{3}\frac{{{{{\beta }}_{6}}}}{a} - \frac{8}{9}\frac{{{{{\beta }}_{3}}{{{\beta }}_{4}}{{{\beta }}_{5}}}}{{{{a}^{2}}}} + \frac{{28}}{{27}}\frac{{{\beta }_{3}^{2}{\beta }_{4}^{3}}}{{{{a}^{3}}}}} \right. + \\ \left. {\left. { + \,\,\frac{1}{{{{a}^{3}}}}\left( {\frac{{68}}{{81}} - \frac{8}{9}a} \right){\beta }_{4}^{3}} \right]{{u}^{{{3 \mathord{\left/ {\vphantom {3 3}} \right. \kern-0em} 3}}}}} \right\}. \\ \end{gathered} $Для второго комплекса имеем
(39)
$\begin{gathered} \frac{3}{5}{{{\bar {F}}}_{2}}{{M}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}}\sin \frac{5}{3}T = \frac{3}{5}{{{\bar {F}}}_{2}}{{u}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}}{{a}^{{{5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-0em} 6}}}} \times \\ \times \,\,\left\{ {\sin \frac{5}{3}\vartheta + } \right.\left( {\frac{5}{3}\frac{{{{{\beta }}_{4}}}}{a}\cos \frac{5}{3}\vartheta + \frac{5}{3}\frac{{{{{\beta }}_{3}}{{{\beta }}_{4}}}}{a}\sin \frac{5}{3}\vartheta } \right){{u}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} + \\ \,\, + \left[ {\left( {\frac{5}{3}\frac{{{{{\beta }}_{5}}}}{a} + \frac{{10}}{9}\frac{{{{{\beta }}_{3}}{\beta }_{4}^{2}}}{{{{a}^{2}}}}} \right)\cos \frac{5}{3}\vartheta } \right. + \\ \left. {\left. { + \,\,\left( {\frac{5}{6}\frac{{2{{{\beta }}_{3}}{{{\beta }}_{5}} + {\beta }_{4}^{2}}}{a} - \frac{5}{{18}}\frac{{{\beta }_{3}^{2}{\beta }_{4}^{2}}}{{{{a}^{2}}}} - \frac{{25}}{{18}}\frac{{{\beta }_{4}^{2}}}{{{{a}^{2}}}}} \right)\sin \frac{5}{3}\vartheta } \right]{{u}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}} \right\}. \\ \end{gathered} $Третий и четвертый комплексы определены формулами
(40)
$\begin{gathered} {{\Phi }_{2}}\left( {{{u}^{2}} - {{v}^{2}}} \right) + {{{\bar {F}}}_{3}}uv = \\ = {{u}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}}\left\{ {\left[ {{{\Phi }_{2}}\left( {1 - {\beta }_{3}^{2}} \right) + {{{\bar {F}}}_{3}}{{{\beta }}_{3}}} \right] + \left( { - 2{{\Phi }_{2}}{{{\beta }}_{3}}{{{\beta }}_{4}} + {{{\bar {F}}}_{3}}{{{\beta }}_{4}}} \right){{u}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} \right\}, \\ {{M}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0em} 3}}}}\left( {{{\Phi }_{3}}\cos \frac{7}{3}\theta + \frac{3}{7}{{{\bar {F}}}_{4}}\sin \frac{7}{3}\theta } \right) = \\ = {{u}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0em} 3}}}}{{a}^{{{7 \mathord{\left/ {\vphantom {7 6}} \right. \kern-0em} 6}}}}\left( {{{\Phi }_{3}}\cos \frac{7}{3}\vartheta + \frac{3}{7}{{{\bar {F}}}_{4}}\sin \frac{7}{3}\vartheta } \right). \\ \end{gathered} $Записывая балансы членов порядка ${{u}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}$, ${{u}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}}$, ${{u}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}}$, ${{u}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0em} 3}}}}$в (23), получаем уравнения для определения коэффициентов ${{{\beta }}_{k}}$ из (32):
(41)
$\begin{gathered} {{{\beta }}_{4}} = \frac{3}{5}{{a}^{{{7 \mathord{\left/ {\vphantom {7 6}} \right. \kern-0em} 6}}}}\bar {N}\cos \frac{1}{3}\vartheta , \\ {{{\beta }}_{5}} = {\sigma }{{a}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}\left[ {\frac{3}{{40}}\left( {1 - {\beta }_{3}^{2}} \right){{{\bar {H}}}^{2}} - \frac{3}{4}{{{\beta }}_{3}}\bar {L}\bar {M}} \right] - \\ - \,\,{{a}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}{{{\bar {N}}}^{2}}\cos \frac{1}{3}\vartheta \left( {\frac{{12}}{{25}}{{{\beta }}_{3}}\cos \frac{1}{3}\vartheta - \frac{3}{5}\sin \frac{1}{3}\vartheta } \right), \\ {{{\beta }}_{6}} = {\sigma }{{a}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\bar {N}\cos \frac{1}{3}\vartheta \left( { - \frac{9}{{100}}{{{\beta }}_{3}}{{{\bar {H}}}^{2}} - \frac{9}{{20}}\bar {L}\bar {M}} \right) + \\ + \,\,{{a}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\left[ { - \frac{2}{5}{{\kappa }_{1}}\sin \vartheta } \right. + \\ \left. { + \,\,\left( {\frac{9}{{70}}\bar {J}{\kern 1pt} '\,\, - \frac{{27}}{{140}}{{{\bar {L}}}^{{{\kern 1pt} 2}}}\bar {N} + \frac{9}{{35}}\bar {N}{{{\bar {H}}}^{2}}} \right)\cos \vartheta } \right] + \\ + \,\,\frac{3}{5}{{a}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}{{{\beta }}_{5}}\bar {N}\frac{{\sin \frac{2}{3}\vartheta }}{{\cos \vartheta }} + \frac{3}{5}{{a}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}{\beta }_{4}^{2}\bar {N} \times \\ \times \,\,\left( { - \frac{{10}}{9}\frac{{{{{\beta }}_{3}}}}{a}\sin \frac{1}{3}\vartheta + \frac{5}{9}{\sigma }\sin \frac{2}{3}\vartheta \cos \frac{1}{3}\vartheta } \right). \\ \end{gathered} $Переход к локальным декартовым координатам. Для вычисления коэффициентов ${{b}_{k}}$ в (32), определяющих конфигурацию эквипотенциали ${\varphi } = 0$ в системе X, Y, необходимо записать функции u, v из (13) на этой линии:
(42)
$\frac{Y}{X} = {{b}_{3}} + {{b}_{4}}{{X}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} + {{b}_{5}}{{X}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + {{b}_{6}}{{X}^{{{3 \mathord{\left/ {\vphantom {3 3}} \right. \kern-0em} 3}}}}.$Для первой из них получаем
(43)
$\begin{gathered} u = X + {{u}_{4}}{{X}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + {{u}_{5}}{{X}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + {{u}_{6}}{{X}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}}, \\ {{u}_{4}} = {\sigma }{{a}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}{{a}_{4}},\,\,\,\,{{u}_{5}} = {{a}^{{{5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-0em} 6}}}}{{a}_{5}}\sin \frac{5}{3}\vartheta + \\ + \,\,\frac{4}{3}{\sigma }{{a}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}}}}{{b}_{3}}{{b}_{4}}{{a}_{4}} - \frac{4}{3}{{a}^{{{5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-0em} 6}}}}a_{4}^{2}\cos \frac{5}{3}\vartheta , \\ {{u}_{6}} = 2{{b}_{3}}\left( {{{a}^{6}} - 2a_{4}^{3}} \right) - 3{{a}_{4}}{{a}_{5}}\left( {1 - b_{3}^{2}} \right) + \\ + \,\,\frac{5}{3}{{a}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 6}} \right. \kern-0em} 6}}}}{{b}_{4}}{{a}_{5}}\frac{{\cos \frac{2}{3}\vartheta }}{{\cos \vartheta }} + \\ + \,{\sigma }{{a}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}}}}\left[ {\frac{2}{3}\left( {2{{b}_{3}}{{b}_{5}} + b_{4}^{2}} \right) - \frac{4}{9}\frac{{b_{3}^{2}b_{4}^{2}}}{a} - \frac{8}{9}\frac{{b_{4}^{2}}}{a}} \right]{{a}_{4}} + \\ + \,\,\frac{{20}}{9}{{a}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 6}} \right. \kern-0em} 6}}}}{{b}_{4}}a_{4}^{2}\frac{{\sin \frac{2}{3}\vartheta }}{{\cos \vartheta }}. \\ \end{gathered} $Переменная v из (13) на границе потока (42) имеет вид
(44)
$\begin{gathered} v = Y + {{v}_{4}}{{X}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + {{v}_{5}}{{X}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + {{v}_{6}}{{X}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}}, \\ {{v}_{4}} = 0,\,\,\,\,{{v}_{5}} = - {{a}^{{{5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-0em} 6}}}} \times \\ \times \,\,\left( {{{a}_{5}}\cos \frac{5}{3}\vartheta + a_{4}^{2}\sin \frac{5}{3}\vartheta } \right) + \frac{4}{3}{\sigma }{{a}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}}}}{{b}_{4}}{{a}_{4}}, \\ {{{v}}_{6}} = \left( { - {{a}_{6}} + 2a_{4}^{3}} \right)\left( {1 - b_{3}^{2}} \right) - 6{{a}_{4}}{{a}_{5}}{{b}_{3}} + \\ + \,\,\frac{5}{3}{{a}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 6}} \right. \kern-0em} 6}}}}{{b}_{4}}{{a}_{5}}\frac{{\sin \frac{2}{3}\vartheta }}{{\cos \vartheta }} + {\sigma }{{a}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}}}}\left( {\frac{4}{3}{{b}_{5}} + \frac{4}{9}\frac{{b_{3}^{{}}b_{4}^{2}}}{a}} \right){{a}_{4}} - \\ - \,\,\frac{{20}}{9}{{a}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 6}} \right. \kern-0em} 6}}}}{{b}_{4}}a_{4}^{2}\frac{{\cos \frac{2}{3}\vartheta }}{{\cos \vartheta }}. \\ \end{gathered} $Приравнивая функции v в (32) и (44), получаем уравнения для определения коэффициентов ${{b}_{k}}$:
(45)
$\begin{gathered} v = Y + {{v}_{5}}{{X}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + {{v}_{6}}{{X}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}} = \\ = \left( {{{b}_{3}}X + {{b}_{4}}{{X}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + {{b}_{5}}{{X}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + {{b}_{6}}{{X}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}}} \right) + \\ + \,\,\left( {{{v}_{5}}{{X}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + {{v}_{6}}{{X}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}}} \right) = \\ = {{{\beta }}_{3}}\left( {X + {{u}_{4}}{{X}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + {{u}_{5}}{{X}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + {{u}_{6}}{{X}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}}} \right) + \\ + \,\,{{{\beta }}_{4}}{{X}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\left[ {1 + \frac{4}{3}{{u}_{4}}{{X}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}} \right. + \left. {\left( {\frac{4}{3}{{u}_{5}} + \frac{2}{9}u_{4}^{2}} \right){{X}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}} \right] + \\ + \,\,{{{\beta }}_{5}}{{X}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}}\left( {1 + \frac{5}{3}{{u}_{4}}{{X}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} \right) + {{{\beta }}_{6}}{{X}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}}, \\ \end{gathered} $В явном виде коэффициенты ${{b}_{k}}$ имеют вид
(46)
$\begin{gathered} {{b}_{4}} = - \frac{3}{{20}}{\sigma }{{{\beta }}_{3}}{{\left( {1 + {\beta }_{3}^{2}} \right)}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\bar {N},\,\,\,\,1 + {\beta }_{3}^{2} = \frac{1}{{{{{\cos }}^{2}}\vartheta }}, \\ {{b}_{5}} = {{\left( {1 + {\beta }_{3}^{2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}\left\{ {\frac{3}{{40}}{\sigma }\left( {1 - {\beta }_{3}^{2}} \right)\left( {\bar {L} + \bar {M}} \right)} \right.\bar {M} + \\ + \,\,\left[ {\frac{3}{{40}}{\sigma } - \frac{{51}}{{100}}{{{\beta }}_{3}} - \frac{3}{{40}}{\sigma \beta }_{3}^{2} - \frac{{21}}{{100}}{\beta }_{3}^{3} + } \right. \\ \left. { + \,\,\frac{1}{{\sqrt 2 }}\,\left. {\left( {\frac{9}{{40}} + \frac{9}{{56}}{\sigma }{{{\beta }}_{3}} + \frac{9}{{20}}{\beta }_{3}^{3} + \frac{6}{{25}}{\sigma \beta }_{3}^{3}} \right)} \right]{{{\bar {N}}}^{2}}} \right\}, \\ {{b}_{6}} = - \frac{2}{5}{{{\beta }}_{3}}\left( {1 + {\beta }_{3}^{2}} \right){{\kappa }_{1}} + \frac{8}{{35}}\left( {1 + {\beta }_{3}^{2}} \right)\bar {J}{\kern 1pt} '\,\, + \\ + \,\,\frac{9}{{280}}\left( {1 + {\beta }_{3}^{2}} \right){{{\bar {L}}}^{{{\kern 1pt} 2}}}\bar {N} + \left[ {\left( {\frac{{27}}{{160}} + \frac{9}{{100}}{\sigma }} \right){\beta }_{3}^{4}} \right. + \\ \left. { + \,\,\left( {\frac{9}{{280}} + \frac{9}{{100}}{\sigma }} \right){\beta }_{3}^{2} - \frac{{153}}{{1120}} + \frac{{27}}{{200}}{\sigma }\left( {1 - {\beta }_{3}^{4}} \right)\frac{1}{{\sqrt 2 }}} \right]{{{\bar {M}}}^{2}}\bar {N} + \\ + \,\,\left[ {\left( {\frac{9}{{160}}{\sigma \beta }_{3}^{4} + \frac{9}{{40}}{\beta }_{3}^{3} - \frac{{171}}{{40}}{{{\beta }}_{3}} + \frac{{99}}{{800}}{\sigma }} \right)} \right. - \\ - \,\,\frac{1}{{\sqrt 2 }}\left( {\frac{{81}}{{160}}{\beta }_{3}^{4} + \frac{{27}}{{80}}{\sigma \beta }_{3}^{3} + \frac{9}{{10}}{\beta }_{3}^{2}} \right. + \left. {\left. {\frac{{27}}{{80}}{\sigma }{{{\beta }}_{3}} + \frac{{171}}{{80}}} \right)} \right] \times \\ \times \,\,\bar {L}\bar {M}\bar {N} + \left[ {\left( { - \frac{{267}}{{50}} + \frac{{411}}{{400}}{\sigma }} \right){\beta }_{3}^{5} - \frac{{201}}{{4000}}{\beta }_{3}^{4}} \right. + \\ + \,\,\left( { - \frac{{57}}{{25}} + \frac{{81}}{{1000}}{\sigma }} \right){\beta }_{3}^{3} + \left( { - \frac{{727}}{{28{\kern 1pt} 000}} + \frac{3}{{100}}{\sigma }} \right){\beta }_{3}^{2} + \\ + \,\,\left( {\frac{{153}}{{50}} - \frac{{393}}{{2000}}{\sigma }} \right){{{\beta }}_{3}} + \frac{{4411}}{{7000}} + \frac{1}{{\sqrt 2 }}\left( { - \frac{{153}}{{500}}{\beta }_{3}^{5}} \right. + \\ \left. {\left. { + \,\,\frac{9}{{100}}{\sigma \beta }_{3}^{4} - \frac{{213}}{{250}}{\beta }_{3}^{3} + \frac{9}{{50}}{\sigma \beta }_{3}^{2} - \frac{{273}}{{500}}{{{\beta }}_{3}} + \frac{9}{{100}}{\sigma }} \right)} \right]{{{\bar {N}}}^{3}}. \\ \end{gathered} $4. ЧАСТНЫЕ СЛУЧАИ ОРИЕНТАЦИИ МАГНИТНОГО ПОЛЯ
Магнитное сопровождение. В работе [10] показано, что в случае криволинейных траекторий идеальное магнитное сопровождение, при котором частицы движутся по силовым линиям магнитного поля, в принципе невозможно, так как выполнение этого условия переопределяет систему уравнений, описывающих пучок. Максимально близким к идеальному варианту является отсутствие поперечных компонент поля на одной траектории (оси пучка) и на стартовой поверхности. В рассматриваемой локальной задаче при M = N = 0, $L \ne 0$ справедливы результаты рассмотрения электростатических течений [4].
Планарный гиротрон. В случае плоского магнитного поля
отрицательные эквипотенциали определены уравнением
(48)
$\begin{gathered} r = \frac{{{\bar {\varphi }*}}}{{\cos \frac{4}{3}\vartheta }}\left[ {1 + \frac{9}{{40}}\frac{{\bar {L}\bar {M}}}{{\cos \frac{4}{3}\vartheta }}} \right. \times \\ \times \,\,\left. {\left( {\sin 4\theta - \frac{2}{3}\sin 2\theta + 2\sin \theta \cos \frac{1}{3}\vartheta } \right)\sqrt {\frac{{{\bar {\varphi }*}}}{{\cos \frac{4}{3}\vartheta }}} } \right]. \\ \end{gathered} $Кривые ${\varphi } = 0$ описываются соотношением
(49)
$\begin{gathered} Y = {{{\beta }}_{3}}X + {{\left( {1 + {\beta }_{3}^{2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}\left\{ {\frac{3}{{40}}{\sigma }\left( {1 - {\beta }_{3}^{2}} \right)\left( {\bar {L} + \bar {M}} \right)\bar {M}{{X}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + } \right. \\ + \,\,\left. {\left[ { - \frac{2}{5}{{{\beta }}_{3}}\left( {1 + {\beta }_{3}^{2}} \right){{\kappa }_{1}} + \frac{8}{{35}}\left( {1 + {\beta }_{3}^{2}} \right)\bar {J}{\kern 1pt} '} \right]{{X}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}}} \right\}. \\ \end{gathered} $Эквипотенциаль в первом квадранте описывается формулой
(50)
$\begin{gathered} Y = 2.414X + 0.687\left( {\bar {L} + \bar {M}} \right)\bar {M}{{X}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + \\ + \,\,\left( { - 6.594{{\kappa }_{1}} + 1.561\bar {J}{\kern 1pt} '} \right){{X}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}},\,\,\,\,X > 0. \\ \end{gathered} $Для боковой формы катода имеем
(51)
$\begin{gathered} Y = 0.414X - 0.687\left( {\bar {L} + \bar {M}} \right)\bar {M}{{X}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} + \\ + \,\,\left( { - 6.594{{\kappa }_{1}} + 1.561\bar {J}{\kern 1pt} '} \right){{X}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}},\,\,\,\,X < 0. \\ \end{gathered} $ЗАКЛЮЧЕНИЕ
Реализация профилированного теплового зазора в соответствии с требованиями теории улучшает качество пучка, приводит к уменьшению токоперехвата на элементы конструкции, что особенно важно для мощных приборов, используемых в технологических установках различного профиля.
Выполнение зазора в виде щели постоянной ширины, параллельной оси потока, ставит под сомнение результаты математического моделирования при использовании программ траекторного анализа, особенно при расчетах пучков с высокой компрессией. Установившаяся практика задания теплового зазора, как и предложение управлять сходимостью потока за счет уменьшения угла наклона нулевого формирующего электрода, является абсурдной и подобна замене закона ${\varphi } \sim {{x}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}$ вблизи эмитирующей поверхности произвольной функцией, не имеющей физического смысла, например, ${\varphi } = 1 - \exp \left( { - {{x}^{2}}} \right)$ [2].
Полученные выше соотношения позволяют синтезировать профилированный тепловой зазор, образованный эквипотенциалью ${\varphi } = {\varphi *} < 0$ и второй ветвью эквипотенциали ${\varphi } = 0$ в третьем квадранте, определяющей боковую поверхность катода.
Список литературы
Данилов В.Н., Сыровой В.А. // РЭ. 1976. Т. 21. № 2. С. 418.
Акимов П.И., Никитин А.П., Сыровой В.А. // Электрон. техника. Сер. 1. СВЧ-техника. 2018. № 1. С. 32.
Cыpoвoй B.A. // PЭ. 2006. T. 51. № 7. C. 879.
Акимов П.И., Невский П.В., Сыровой В.А. // РЭ. 2009. Т. 54. № 1. С. 98.
Сыровой В.А. Теория интенсивных пучков заряженных частиц. М.: Энергоатомиздат, 2004.
Сапронова Т.М., Сыровой В.А. // РЭ. 2017. Т. 62. № 11. С. 1106.
Cыpoвoй B.A. // PЭ. 2016. T. 61. № 3. C. 263.
Сапронова Т.М., Сыровой В.А. // РЭ. 2017. Т. 62. № 11. С. 1116.
Сыровой В.А. Введение в теорию интенсивных пучков заряженных частиц. М.: Энергоатомиздат, 2004.
Cыpoвoй B.A. // PЭ. 2001. T. 46. № 5. C. 617.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника