Радиотехника и электроника, 2021, T. 66, № 4, стр. 339-344
Влияние слоистости литосферы на возбуждение крайне низкочастотных электромагнитных волн горизонтальным диполем
Е. Д. Терещенко a, П. Е. Терещенко b, c, *
a Полярный геофизический институт РАН
183010 Мурманск, ул. Халтурина, 15, Российская Федерация
b Санкт-Петербургский филиал Института земного магнетизма,
ионосферы и распространения радиоволн им. Н.В. Пушкова РАН
199034 Санкт-Петербург, Университетская набережная, 5Б, Российская Федерация
c Санкт-Петербургский научный центр РАН
199034 Санкт-Петербург, Университетская набережная, 5, Российская Федерация
* E-mail: tereshchenko@gmail.com
Поступила в редакцию 11.06.2020
После доработки 26.08.2020
Принята к публикации 01.09.2020
Аннотация
Получено аналитическое решение задачи возбуждения электромагнитных волн горизонтальным диполем, расположенным на границе раздела между вакуумом и проводящей двуслойной средой, опирающееся на малость длины волны в проводящей среде по сравнению с вакуумом. Проведены численные расчеты, позволившие оценить эффективность такого подхода и показать, что приближенные формулы описывают поведение поля с высокой точностью. Получено асимптотическое представление для магнитного поля на границе раздела между плоскослоистой Землей и атмосферой, имеющее вид волны в однородном полупространстве с коэффициентом возбуждения, зависящим от эффективной проводимости нижнего полупространства, что полезно для определения электропроводности литосферы на основе экспериментальных данных регистрации электромагнитного поля активного источника. Отмечена большая чувствительность к проводимости среды вертикальной компоненты магнитного поля по сравнению с горизонтальными.
ВВЕДЕНИЕ
Задача возбуждения электромагнитного поля диполем, расположенным на границах двух сред, анализировалась в ряде работ [1–5]. Исследования, начатые Зоммерфельдом, были дополнены Фоком, получившим аналитические решения, удобные для практического использования. В [2] было введено понятие “квазистационарное приближение” (волновое число в вакууме ${{k}_{0}} = 0$), в рамках которого решение задачи было представлено в виде модифицированных функций Бесселя. При этом обобщение на случай ${{k}_{0}} \ne 0$ имело вид разложения по параметру $q = {{\left( {k_{0}^{2} - k_{1}^{2}} \right)} \mathord{\left/ {\vphantom {{\left( {k_{0}^{2} - k_{1}^{2}} \right)} {\left( {k_{0}^{2} + k_{1}^{2}} \right)}}} \right. \kern-0em} {\left( {k_{0}^{2} + k_{1}^{2}} \right)}}$, где ${{k}_{1}}$ – волновое число, относящееся к проводящему полупространству. В дальнейшем результаты и выводы, полученные в [2], использовались для обоснования многих работ, связанных с дистанционным электромагнитным зондированием глубинной структуры Земли [6, 7].
В практике генерации электромагнитного поля сверх- и крайне низкочастотного диапазона используют антенны с горизонтальным током [8, 9], возбуждающие поле, которое не обладает азимутальной симметрией. Это приводит к необходимости даже для изотропной среды определять две составляющие электрического вектор-потенциала.
Ниже рассмотрим возбуждение низкочастотного электромагнитного поля горизонтальным заземленным диполем с гармонической зависимостью от времени. Считаем, что Земля состоит из плоских слоев разной проводимости, расположенных друг над другом. В отличие от традиционного подхода при построении аналитического решения будем использовать малость параметра $\left| {{{{{k}_{0}}} \mathord{\left/ {\vphantom {{{{k}_{0}}} {{{k}_{j}}}}} \right. \kern-0em} {{{k}_{j}}}}} \right|$, где ${{k}_{j}}$ – волновое число в j-слое. Такое предположение является вполне естественным в свете реальной проводимости литосферы для частот $f < {{10}^{5}}$ Гц [4].
1. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим возбуждение горизонтальным заземленным вибратором поля в плоской трехслойной среде. Одну среду будем считать практически вакуумом, а две другие – проводящими средами с различными значениями проводимости. Вибратор с током, меняющимся по монохроматическому закону exp(–iωt), где t – время, ω – циклическая частота, расположим на границе между вакуумом и проводящей областью. Для решения такой задачи можно использовать подход, описанный ранее [10], отличием от прежней работы будет отсутствие ионосферы и учет конечности ${{k}_{0}}$.
Введем декартову систему координат $\left( {x,y,z} \right)$ с центром в середине диполя, осью $Ox$, направленной вдоль диполя, осью $Oy$ – в перпендикулярном горизонтальном направлении, осью $Oz$ – перпендикулярной границе раздела. Тогда для электрического вектор-потенциала $\vec {A}$, относящегося к области над Землей $\left( {z \geqslant 0} \right)$, можно написать следующее представление:
(1)
$\begin{gathered} \vec {A} = {{A}_{x}}\overrightarrow {{{e}_{x}}} + {{A}_{z}}\overrightarrow {{{e}_{z}}} , \\ {{A}_{x}} = \frac{{J\Delta x}}{{4\pi }}\int\limits_0^\infty {\left( {\frac{\lambda }{{{{\nu }_{0}}}} + {{\alpha }_{0}}} \right)} \exp {\text{\;}}( - {{\nu }_{0}}z){{J}_{0}}\left( {\lambda \rho } \right)d\lambda , \\ {{A}_{z}} = - \frac{{J\Delta x}}{{4\pi }}\frac{\partial }{{\partial x}}\int\limits_0^\infty {{{\eta }_{0}}} \exp {\text{\;}}( - {{\nu }_{0}}z)\frac{1}{\lambda }{{J}_{0}}\left( {\lambda \rho } \right)d\lambda , \\ \end{gathered} $где $\overrightarrow {{{e}_{x}}} $, $\overrightarrow {{{e}_{z}}} $ – орты, направленные вдоль осей $Ox$ и $Oy$, $i{{\nu }_{j}} = \sqrt {k_{j}^{2} - {{\lambda }^{2}}} = i\sqrt {\kappa _{j}^{2} + {{\lambda }^{2}}} $, $\operatorname{Re} {\text{\;}}{{\nu }_{j}} > 0$, $j = 0,1,2$ – указывает на среду, ${{\kappa }_{j}} = - i{{k}_{j}}$, ${{k}_{j}} = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c} \times $ $ \times \,\sqrt {{{{{\varepsilon }_{j}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{j}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}} + {{i{{\sigma }_{j}}} \mathord{\left/ {\vphantom {{i{{\sigma }_{j}}} {\left( {\omega {{\varepsilon }_{0}}} \right)}}} \right. \kern-0em} {\left( {\omega {{\varepsilon }_{0}}} \right)}}} $ – волновое число в j-й среде, ${{\varepsilon }_{0}} \simeq {{{{{10}}^{{ - 9}}}} \mathord{\left/ {\vphantom {{{{{10}}^{{ - 9}}}} {\left( {36\pi } \right)}}} \right. \kern-0em} {\left( {36\pi } \right)}}$ Ф/м , ${{\varepsilon }_{j}}$ и ${{\sigma }_{j}}$ – диэлектрическая проницаемость и проводимость, $J{\Delta }x$ – момент тока, ${{J}_{0}}\left( {\lambda \rho } \right)$ – функция Бесселя первого рода, $\rho $ – расстояние между элементарным диполем и проекцией точки, в которой вычисляется потенциал, на плоскость $\left( {x,y,0} \right)$.
Коэффициенты ${{\alpha }_{0}}$ и ${{\eta }_{0}}$ находятся из граничных условий для потенциала. Для трехслойной среды получаем
где
$d$ – толщина первого слоя, примыкающего к вакууму.
Выражение для η0 имеет более сложную структуру и может быть представлено для трехслойной среды в следующем виде:
(2)
$\begin{gathered} {{\eta }_{0}} = {{D}_{\eta }}\left( {\frac{\lambda }{{{{\nu }_{0}}}} + {{\alpha }_{0}}} \right) + \\ + \,\,\frac{{8{{\lambda }^{2}}k_{0}^{2}\nu _{1}^{2}}}{{D\left( {{{\nu }_{0}}} \right){{D}_{z}}}}\left( {k_{1}^{2} - k_{2}^{2}} \right)\exp {\text{\;}}( - 2{{\nu }_{1}}d), \\ \end{gathered} $где
Из формулы (2) следуют предельные соотношения. Для однородной Земли $d \to \infty $ или ${{k}_{1}} = {{k}_{2}}$
(3)
${{\eta }_{0}} = \frac{{2\left( {\kappa _{0}^{2} - \kappa _{1}^{2}} \right){{\lambda }^{2}}}}{{\left( {{{\nu }_{0}} + {{\nu }_{1}}} \right)\left( {\kappa _{0}^{2}{{\nu }_{1}} + \kappa _{1}^{2}{{\nu }_{0}}} \right)}}$и приближение, справедливое для малых значений $\left| {{{k_{0}^{2}} \mathord{\left/ {\vphantom {{k_{0}^{2}} {{{k}_{j}}}}} \right. \kern-0em} {{{k}_{j}}}}} \right| \ll 1$ $(j = 1,2$), имеет вид
(4)
${{\eta }_{0}} = - \frac{\lambda }{{{{\nu }_{0}}}}\left( {\frac{\lambda }{{{{\nu }_{0}}}} + {{\alpha }_{0}}} \right).$Подстановка (4) в (1) показывает, что такое приближение эквивалентно выполнению в области $z \geqslant 0$ условия ${\text{div\;}}\vec {A} = 0$.
Магнитное поле $\vec {H}\left( {\rho ,z} \right)$ связано с вектором-потенциалом формулой $\vec {H} = {\text{rot\;}}\vec {A}$. Воспользовавшись соотношением (1), получаем
(5)
${{H}_{x}}\left( {\rho ,z} \right) = \frac{\partial }{{\partial y}}{{A}_{z}},\,\,\,\,{{H}_{y}}\left( {\rho ,z} \right) = \frac{\partial }{{\partial z}}{{A}_{x}} - \frac{\partial }{{\partial x}}{{A}_{z}}.$В качестве первого шага воспользуемся полученными результатами для обоснования возможности использования приближения $\left| {{{k_{0}^{2}} \mathord{\left/ {\vphantom {{k_{0}^{2}} {k_{1}^{2}}}} \right. \kern-0em} {k_{1}^{2}}}} \right| \ll 1$ при вычислении поля на границе двух сред.
2. ГОРИЗОНТАЛЬНЫЕ КОМПОНЕНТЫ МАГНИТНОГО ПОЛЯ НА ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД ДЛЯ ОДНОРОДНОЙ ЗЕМЛИ
Подстановка в (5) выражения (3) для ${{\eta }_{0}}$ позволяет представить выражение для ${{H}_{x}}$-компоненты магнитного поля на границе раздела в следующем виде:
(6)
$\begin{gathered} {{H}_{x}}\left( {\rho ,0} \right) = \frac{{J\Delta x}}{{2\pi }}\left( {1 - \frac{{k_{0}^{2}}}{{k_{1}^{2}}}} \right)\frac{\partial }{{\partial x}}\frac{\partial }{{\partial y}} \times \\ \times \,\,\int\limits_0^\infty {\frac{{{\text{exp}}~( - {{\nu }_{0}}z)}}{{\left( {{{\nu }_{1}} + {{\nu }_{0}}} \right)\left( {{{\nu }_{0}} + {{k_{0}^{2}} \mathord{\left/ {\vphantom {{k_{0}^{2}} {k_{1}^{2}{{\nu }_{1}}}}} \right. \kern-0em} {k_{1}^{2}{{\nu }_{1}}}}} \right)}}} {{J}_{0}}\left( {\lambda \rho } \right)\lambda d\lambda ,\,\,\,z \to + 0. \\ \end{gathered} $Здесь знак плюс 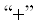 указывает, что подходим к границе между вакуумом и проводящей средой сверху. Учитывая,
что
указывает, что подходим к границе между вакуумом и проводящей средой сверху. Учитывая,
что
выполним дифференцирование по y в формуле (6). В результате получим
(7)
${{H}_{x}}\left( {\rho ,0} \right) = - \frac{{J\Delta x}}{{2\pi {{\kappa }_{1}}}}\frac{\partial }{{\partial x}}\frac{y}{{{{\rho }^{3}}}}{{F}_{x}},$где обозначено
Здесь ${{J}_{1}}\left( {\lambda \rho } \right)$ – функция Бесселя с индексом, равным единице. Если ввести безразмерные величины ${{r}_{1}} = \rho {{\kappa }_{1}}$, ${{r}_{0}} = \rho {{\kappa }_{0}}$, $s = \lambda \rho $ и ${{\tau }_{j}} = \sqrt {{{s}^{2}} + r_{j}^{2}} $, $j = \left( {0,1} \right)$, то в этих обозначениях ${{F}_{x}}$ можно записать следующим образом:
(8)
$\begin{gathered} {{F}_{x}} = {{r}_{1}}\left( {1 - \frac{{r_{0}^{2}}}{{r_{1}^{2}}}} \right) \times \\ \times \,\,\mathop \smallint \limits_0^\infty \frac{1}{{\left( {{{\tau }_{1}} + {{\tau }_{0}}} \right)\left( {{{\tau }_{0}} + {{r_{0}^{2}} \mathord{\left/ {\vphantom {{r_{0}^{2}} {r_{1}^{2}{{\tau }_{1}}}}} \right. \kern-0em} {r_{1}^{2}{{\tau }_{1}}}}} \right)}}{{J}_{1}}\left( s \right){{s}^{2}}ds. \\ \end{gathered} $Пренебрегая членами, содержащими ${{r_{0}^{2}} \mathord{\left/ {\vphantom {{r_{0}^{2}} {r_{1}^{2}}}} \right. \kern-0em} {r_{1}^{2}}} = $ $ = {{k_{0}^{2}} \mathord{\left/ {\vphantom {{k_{0}^{2}} {k_{1}^{2}}}} \right. \kern-0em} {k_{1}^{2}}}$, получим приближенную формулу для ${{F}_{x}}$, связанную с ${{H}_{x}}$ компонентой магнитного поля:
В отличие от функции ${{F}_{x}}$ для ${{\tilde {F}}_{x}}$ несложно найти аналитическое представление, выполнив интегрирование по $s$. Воспользовавшись схемой, предложенной в работе [2], после ряда преобразований можно получить
(9)
$\begin{gathered} {{{\tilde {F}}}_{x}} = {{r}_{1}}{{I}_{1}}\left( {\frac{{{{r}_{1}} - {{r}_{0}}}}{2}} \right){{K}_{1}}\left( {\frac{{{{r}_{1}} + {{r}_{0}}}}{2}} \right) + \frac{{{{r}_{1}}{{r}_{0}}}}{2} \times \\ \times \,\,\left[ {{{I}_{0}}\left( {\frac{{{{r}_{1}} - {{r}_{0}}}}{2}} \right){{K}_{1}}\left( {\frac{{{{r}_{1}} + {{r}_{0}}}}{2}} \right) + {{I}_{1}}\left( {\frac{{{{r}_{1}} - {{r}_{0}}}}{2}} \right){{K}_{0}}\left( {\frac{{{{r}_{1}} + {{r}_{0}}}}{2}} \right)} \right], \\ \end{gathered} $где ${{I}_{0}}$, ${{I}_{1}}$, ${{K}_{0}}$, ${{K}_{1}}$ – цилиндрические функции мнимого аргумента. Для квазистационарного приближения ${{r}_{0}} = 0$ и, соответственно,
Если ${{\left| {{{r}_{1}} \pm {{r}_{0}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{r}_{1}} \pm {{r}_{0}}} \right|} 2}} \right. \kern-0em} 2} \gg 1$, то имеет место асимптотическое представление:
(10)
${{\tilde {F}}_{x}} \sim \left( {1 + {{r}_{0}}} \right)\exp {\text{\;}}( - {{r}_{0}}),\,\,\,\,{{\left| {{{r}_{1}} \pm {{r}_{0}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{r}_{1}} \pm {{r}_{0}}} \right|} 2}} \right. \kern-0em} 2} \gg 1,$т.е. функция, имеющая структуру волны в верхнем полупространстве, не зависящая от проводимости нижнего полупространства, определяемая расстоянием до точки наблюдения и частотой.
Оценим возможность замены функции Fx на ее приближение ${{\tilde {F}}_{x}}$ в сверхнизкочастотном и крайне низкочастотном (СНЧ-КНЧ) и более низкочастотном диапазоне. С этой целью выполним численные расчеты по формуле (8) и сравним их с результатами, определяемыми выражением (9). Результаты сравнения ${{F}_{x}}$ и ${{\tilde {F}}_{x}}$ удобно представить в виде зависимости от параметра $\left| {{{r}_{0}}} \right|$. При этом для рассматриваемого диапазона можно представить ${{r}_{1}}$ в следующем виде:
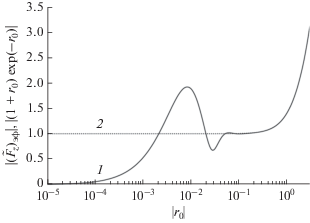
На рис. 1, 2 приведены результаты расчета модуля и фазы функций ${{F}_{x}}$, ${{\tilde {F}}_{x}}$ и $\left( {1 + {{r}_{0}}} \right)\exp {\text{\;}}( - {{r}_{0}})$. Значение ${{\sigma }_{1}}\rho = 6$ См близко к реальной ситуации в эксперименте FENIСS-2014 [10] при регистрации поля в обсерватории Ловозеро. Из графиков видно совпадение функций ${{F}_{x}}$ и ${{\tilde {F}}_{x}}$ во всем диапазоне изменения ${{r}_{0}}$.
Рис. 1.
Зависимость от безразмерного расстояния $\left| {{{r}_{0}}} \right|$ функции $\left| {{{F}_{x}}} \right|$ (1), аппроксимации $\left| {{{{\tilde {F}}}_{x}}} \right|$ (2) и функции $\left| {\left( {1 + {{r}_{0}}} \right)\exp ( - {{r}_{0}})} \right|$ (3) для горизонтального диполя на границе двух однородных сред.
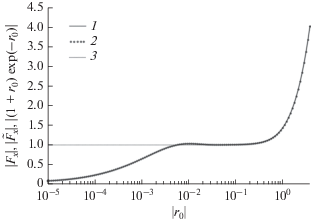
Рис. 2.
Зависимость от безразмерного расстояния $\left| {{{r}_{0}}} \right|$ функции $\arg ({{F}_{x}})$ (1), аппроксимации $\arg ({{\tilde {F}}_{x}})$ (2) и функции $\arg (\left( {1 + {{r}_{0}}} \right)\exp ( - {{r}_{0}}))$ (3) для горизонтального диполя на границе двух однородных сред.
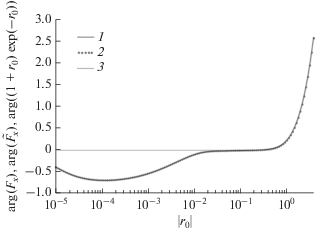
Следующий шаг – анализ ${{H}_{y}}\left( {\rho ,z} \right)$. Запишем эту компоненту магнитного поля в виде
где ${{F}_{x}}$ определена формулой (8), а
Выполняя интегрирование по $s$, получим
(11)
$\begin{gathered} {{F}_{y}} = \frac{{\left( {r_{1}^{2} - r_{0}^{2}} \right){{r}_{1}}}}{8} \times \\ \times \,\,\left[ {{{I}_{0}}\left( {\frac{{{{r}_{1}} - {{r}_{0}}}}{2}} \right){{K}_{0}}\left( {\frac{{{{r}_{1}} + {{r}_{0}}}}{2}} \right) - {{I}_{2}}\left( {\frac{{{{r}_{1}} - {{r}_{0}}}}{2}} \right){{K}_{2}}\left( {\frac{{{{r}_{1}} + {{r}_{0}}}}{2}} \right)} \right]. \\ \end{gathered} $При совместном выполнении ограничений $\left| {{{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} {{{r}_{1}}}}} \right. \kern-0em} {{{r}_{1}}}}} \right| \ll 1$ и $\left| {{{\left( {{{r}_{1}} \pm {{r}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{r}_{1}} \pm {{r}_{0}}} \right)} 2}} \right. \kern-0em} 2}} \right| > 1$ формула (11) имеет асимптотическое представление, аналогичное ${{\tilde {F}}_{x}}:$
Подводя итог, можно сказать, что для однородного полупространства приближенные формулы, полученные в предположении $\left| {{{{{k}_{0}}} \mathord{\left/ {\vphantom {{{{k}_{0}}} {{{k}_{1}}}}} \right. \kern-0em} {{{k}_{1}}}}} \right| < 1$, достаточно полно описывают поведение поля и дают хорошее количественное согласие с точными формулами. Причиной такого совпадения являются осциллирующие функции Бесселя в подынтегральных выражениях, из-за которых вклад в интеграл областей с большими значениями переменной интегрирования мал. Поэтому в задаче со слоистой Землей возможен переход от точного выражения для ${{\eta }_{0}}$ к его приближению (3).
3. МАГНИТНОЕ ПОЛЕ ДЛЯ ДВУХСЛОЙНОЙ МОДЕЛИ ЗЕМЛИ
Рассмотрим возбуждение горизонтальным диполем магнитного поля для модели Земли в виде двух слоев с различной проводимостью. Используя приближение $\left| {{{k_{0}^{2}} \mathord{\left/ {\vphantom {{k_{0}^{2}} {{{k}_{j}}}}} \right. \kern-0em} {{{k}_{j}}}}} \right| \ll 1$, $j = 1,~2$, для низкочастотного диапазона из (5) с учетом (4) получим
Выполняя дифференцирование по $y$, находим
(12)
${{H}_{x}}\left( {\rho ,0} \right) = - \frac{{J\Delta x}}{{2\pi {{\kappa }_{{{\text{эф}}}}}}}\frac{\partial }{{\partial x}}\frac{y}{{{{\rho }^{3}}}}{{({{\tilde {F}}_{x}})}_{{{\text{эф}}}}},$где
Для аналогии с (7) ввели коэффициент ${{\kappa }_{{{\text{эф}}}}}$. Выберем его так, а соответственно, и проводимость, чтобы ${{\tilde {F}}_{{{\text{эф}}}}}$ как при $d \to \infty $, $\left| {{{{{r}_{1}}} \mathord{\left/ {\vphantom {{{{r}_{1}}} 2}} \right. \kern-0em} 2}} \right| > 1$, так и при $d \to 0$, $\left| {{{{{r}_{2}}} \mathord{\left/ {\vphantom {{{{r}_{2}}} 2}} \right. \kern-0em} 2}} \right| > 1,$ совпадало с асимптотическим значением ${{\tilde {F}}_{x}}$, определяемым формулой (10). Если взять значение ${{\sigma }_{{{\text{эф}}}}}$, следующее из выражения для импеданса плоской волны для двухслойной среды [4]
то с учетом того, что ${{\kappa }_{{{\text{эф}}}}} = {{\left( {1 - i} \right)} \mathord{\left/ {\vphantom {{\left( {1 - i} \right)} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}\sqrt {\omega {{\mu }_{0}}{{\sigma }_{{{\text{эф}}}}}} $, несложно показать справедливость высказанного требования.
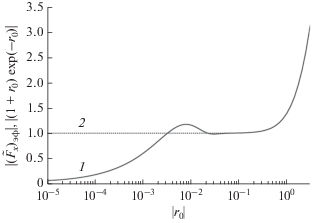
Рассмотрим поведение функции ${{({{\tilde {F}}_{x}})}_{{{\text{эф}}}}}$ в случае конечной, не равной нулю, толщины первого слоя. На рис. 3 представлены результаты расчета модуля и фазы функции ${{({{\tilde {F}}_{x}})}_{{{\text{эф}}}}}$ для двухслойной модели Земли с проводимостью ${{\sigma }_{1}} = {{10}^{{ - 4}}}$ См/м, ${{\sigma }_{2}} = {{10}^{{ - 5}}}$ См/м и толщиной первого слоя $d = 12 \times {{10}^{3}}$ м. Для сравнения на этих графиках показаны значения функции (1 + r0)exp(–r0). Видим, что при $\left| {{{r}_{0}}} \right| > 8 \times {{10}^{{ - 2}}}$, функция ${{({{\tilde {F}}_{x}})}_{{{\text{эф}}}}}$ хорошо аппроксимируется этим выражением. Преобразуем (12) следующим образом
Рис. 3.
Сравнение функций $\left| {{{{({{{\tilde {F}}}_{x}})}}_{{{\text{эф}}}}}} \right|$ (1) и $\left| {\left( {1 + {{r}_{0}}} \right)\exp ( - {{r}_{0}})} \right|$ (2) при двухслойной среде под диполем.
При равенстве функций ${{({{\tilde {F}}_{x}})}_{{{\text{эф}}}}}$ и ${{\tilde {F}}_{x}}$ получаем
(13)
$\begin{gathered} {{H}_{x}}\left( {\rho ,0} \right) = \frac{{{{Z}_{g}}}}{{{{Z}_{1}}}}{{\left. {{{H}_{x}}\left( {\rho ,0} \right)} \right|}_{{{{\sigma }_{1}} = {{\sigma }_{2}}}}}, \\ \frac{{{{Z}_{g}}}}{{{{Z}_{1}}}} = \frac{{1 - R\exp ~( - {{\kappa }_{1}}d)}}{{1 + R\exp ~( - {{\kappa }_{1}}d)}}, \\ \end{gathered} $т.е. произведение отношения импедансов двухслойного и однородного полупространства и поля, возбуждаемого диполем, расположенным на границе между вакуумом и проводящей средой.
Для компоненты ${{H}_{y}}\left( {\rho ,0} \right)$ вычисления подобны сделанным для ${{H}_{x}}\left( {\rho ,0} \right)$. Так как второе слагаемое в (5) сводится к составляющей поля ${{H}_{x}}\left( {\rho ,0} \right)$, то рассмотрим ${\partial \mathord{\left/ {\vphantom {\partial {\partial z{{A}_{x}}}}} \right. \kern-0em} {\partial z{{A}_{x}}}}$. Для двухслойной среды представим в виде
где
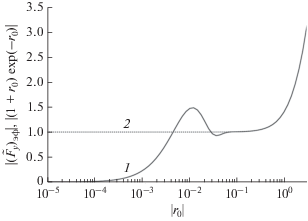
На рис. 4 приведены результаты расчета модуля и фазы функций ${{({{F}_{y}})}_{{{\text{эф}}}}}$ и $\left( {1 + {{r}_{0}}} \right)\exp {\text{\;}}( - {{r}_{0}})$ с теми же параметрами, что и для рис. 3. Видим поведение ${{({{F}_{y}})}_{{{\text{эф}}}}}$ подобно ранее рассмотренному для ${{({{F}_{x}})}_{{{\text{эф}}}}}$. При этом ${{({{F}_{y}})}_{{{\text{эф}}}}}$ идентична $\left( {1 + {{r}_{0}}} \right)\exp {\text{\;}}( - {{r}_{0}})$ при $\left| {{{r}_{0}}} \right| > 8 \times {{10}^{{ - 2}}}$. Поэтому и составляющую ${{H}_{y}}\left( {\rho ,0} \right)$ можно записать аналогично (13), а значит, и для тангенциальной составляющей будет иметь место соотношение
(14)
${{\vec {H}}_{\tau }}\left( {\rho ,0} \right) = \frac{{{{Z}_{g}}}}{{{{Z}_{1}}}}{{\left. {{{{\vec {H}}}_{\tau }}\left( {\rho ,0} \right)} \right|}_{{{{\sigma }_{1}} = {{\sigma }_{2}}}}}.$Рис. 4.
Сравнение функций $\left| {{{{({{{\tilde {F}}}_{x}})}}_{{{\text{эф}}}}}} \right|$ (1) и $\left| {\left( {1 + {{r}_{0}}} \right)\exp ( - {{r}_{0}})} \right|$ (2) при двухслойной среде под диполем.
Такие же преобразования можно применить и к вертикальной составляющей магнитного поля. В результате можно прийти к следующему выражению:
(15)
$\begin{gathered} {{H}_{z}}\left( {\rho ,0} \right) = - \frac{{J\Delta x}}{{2\pi \kappa _{{{\text{эф}}}}^{2}}}\frac{\partial }{{\partial y}}\frac{{{{{({{F}_{z}})}}_{{{\text{эф}}}}}}}{{{{\rho }^{3}}}}, \\ {{({{F}_{z}})}_{{{\text{эф}}}}} = r_{{{\text{эф}}}}^{2}\mathop \smallint \limits_0^\infty \frac{{{{\tau }_{1}} + {{\tau }_{2}} + \left( {{{\tau }_{1}} - {{\tau }_{2}}} \right)\exp ~({{ - 2{{\tau }_{1}}d} \mathord{\left/ {\vphantom {{ - 2{{\tau }_{1}}d} \rho }} \right. \kern-0em} \rho })}}{{\left( {{{\tau }_{0}} + {{\tau }_{1}}} \right)\left( {{{\tau }_{1}} + {{\tau }_{2}}} \right) + \left( {{{\tau }_{0}} - {{\tau }_{1}}} \right)\left( {{{\tau }_{1}} - {{\tau }_{2}}} \right)\exp ~({{ - 2{{\tau }_{1}}d} \mathord{\left/ {\vphantom {{ - 2{{\tau }_{1}}d} \rho }} \right. \kern-0em} \rho })}}{{J}_{0}}\left( s \right)sds. \\ \end{gathered} $На рис. 5 приведен результат сравнения ${{({{F}_{z}})}_{{{\text{эф}}}}}$ и $\left( {1 + {{r}_{0}}} \right)\exp {\text{\;}}( - {{r}_{0}})$. Видно, что с ростом $\left| {{{r}_{0}}} \right|$ происходит совпадение этих функций. Наличие $\kappa _{{{\text{эф}}}}^{2}$ в (15), в отличие от горизонтальных составляющих, где в определяющие их выражения входит ${{\kappa }_{{{\text{эф}}}}}$ в первой степени, указывает на большую чувствительность к проводимости среды вертикальной компоненты магнитного поля, что отмечалось и в экспериментальных данных [11].
ЗАКЛЮЧЕНИЕ
Таким образом, решение задачи возбуждения электромагнитных волн горизонтальным диполем, расположенным на границе раздела между вакуумом и проводящей двухслойной средой, позволило оценить эффективность подхода к определению поля, опирающегося на малость длины волны в проводящей среде по сравнению с вакуумом. Сравнение численных расчетов по точным и приближенным формулам показало целесообразность такого подхода как в задаче с однородным полупространством, так и для слоистой среды.
Для расстояний от источника, превышающих величину скин-слоя любого из проводящих слоев, найдено асимптотическое представление для магнитного поля на границе раздела между плоскослоистой Землей и атмосферой, имеющее вид волны в однородном полупространстве с коэффициентом возбуждения, зависящим от эффективной проводимости нижнего полупространства.
Этот результат полезен для интерпретации данных экспериментов с активным источником, где известны параметры источника и геометрия эксперимента, а требуется определить электропроводность Земли. Используя формулу (14), легко перейти от поля диполя к полю реальной антенны. Результат интегрирования по длине антенны будет зависеть лишь от поля диполя, расположенного на границе двух сред.
Список литературы
Sommerfeld A. // Ann. Phys. 1909. V. 333. № 4. P. 665. https://doi.org/10.1002/andp.19093330402
Fock V. // Ann. Phys. 1933. V. 409. № 4. P. 401. https://doi.org/10.1002/andp.19334090405
Wait J.R. Electromagnetic Waves in Stratified Media. N.Y.: Pergamon press, 1962.
Макаров Г.И., Новиков В.В., Рыбачек С.Т. Распространение электромагнитных волн над земной поверхностью. М.: Наука, 1991.
Терещенко Е.Д., Терещенко П.Е. // РЭ. 2018. Т. 63. № 4. С. 323. https://doi.org/10.7868/S0033849418040034
Ваньян Л.Л. Электромагнитные зондирования. М.: Научный мир, 1997.
Ковтун А.А. Строение коры и верхней мантии на северо-западе Восточно-Европейской платформы по данным магнитотеллурического зондирования. Л.: Изд-во ЛГУ, 1989.
Bannister P.B. // Radio Sci. 1986. V. 21. № 3. P. 529. https://doi.org/10.1029/RS021i004p00605
Велихов Е.П., Кононов Ю.М., Шорин В.И. и др. Способ электромагнитного зондирования земной коры с использованием нормированных источников поля // Пат. РФ № 2093863. Опубл. офиц. бюл. “Изобретения. Полезные модели” № 30 от 20.10.1997.
Терещенко Е.Д., Сидоренко А.Е., Терещенко П.Е. // ЖТФ. 2019. Т. 89. № 7. С. 1098. https://doi.org/10.21883/JTF.2019.07.47805.388-18
Терещенко Е.Д., Григорьев В.Ф., Терещенко П.Е., Юрик Р.Ю. // Вестн. Кольского науч. центра РАН. Апатиты: Кольский научный центр РАН, 2013. № 3. С. 34.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника