Радиотехника и электроника, 2021, T. 66, № 5, стр. 468-475
Однопозиционная пассивная локация и навигация с учетом эволюции периода радиосигнала в точке приема
Ю. Г. Булычев a, *, А. А. Мозоль b, c
a Всероссийский научно-исследовательский институт “Градиент”
344000 Ростов-на-Дону, просп. Соколова, 96, Российская Федерация
b Северо-Кавказский филиал Московского технического университета связи и информатики
344000 Ростов-на-Дону, ул. Серафимовича, 62, Российская Федерация
c Краснодарское высшее военное училище им. генерала армии С.М. Штеменко
350000 Краснодар, ул. Красина, 4, Российская Федерация
* E-mail: profbulychev@yandex.ru
Поступила в редакцию 19.08.2020
После доработки 10.11.2020
Принята к публикации 25.11.2020
Аннотация
Развит однопозиционный метод пассивной локации и навигации с учетом периодичности излучаемого радиосигнала (период может быть не известен), когда в паре источник излучения-наблюдатель один из объектов является стационарным, а второй движется по кусочно-линейной траектории с неизвестной скоростью. Измеряемым параметром является временная невязка между периодами излучаемого и принимаемого радиосигналов. Рассмотрены вопросы, связанные с оценкой доплеровских поправок частоты на основе этой невязки, с наблюдаемостью метода для разных частных случаев, оценкой его точностных характеристик и практическими рекомендациями. Приведен численный пример.
ВВЕДЕНИЕ
Вопросы, связанные с однопозиционными методами пассивного определения местоположения и параметров движения различных типов объектов, остаются актуальными до настоящего времени. В большинстве случаев эти методы оперируют с пеленгами, разностями фаз, доплеровскими частотами, относительной мощностью радиосигналов и их различными производными, при этом зачастую используется дополнительная информация от различных источников подсвета, отражателей естественного и искусственного происхождения, внешних управляющих систем, а также априорные данные о структуре и некоторых параметрах излучаемого радиосигнала, скорости объекта, начальной или конечной точке его маршрута, наличии участков барражирования, возможности маневра и др. (см., например, [1–20]). При этом наибольший интерес представляют методы, для реализации которых не используются измерения пеленгов, поскольку достижение требуемой точности в пеленгаторных системах (особенно мобильных и связанных с осуществлением специального маневра), как правило, сопряжено с существенными техническими сложностями, большими габаритами и экономическими затратами.
Известны методы однопозиционной пассивной локации и навигации (ОПЛН), не использующие пеленги, но оперирующие с периодическими радиосигналами и ориентированные на возможность измерения непрерывного смещения доплеровской частоты принимаемого радиосигнала в точке наблюдения, обусловленного движением либо источника излучения (ИИ), либо наблюдателя (Н) в паре ИИ–Н (в работе [6] на с. 169–173 дан исчерпывающий список литературы по данному вопросу, доступной в открытой печати). При этом измерения могут осуществляться на любой характерной частоте из спектра излучаемого периодического радиосигнала (например, на центральной), либо модулирующей функции, а также путем сопоставления моментов прихода фронтов последовательных импульсов с учетом известного периода. По эволюции периода (в точке наблюдения) удается определять параметры движения одного из объектов пары ИИ–Н, не прибегая к пеленгационным измерениям. Все методы ОПЛН основаны на идее “синтеза базы”, что приводит в конечном итоге к формированию нескольких точек наблюдения на траектории движения и возможности использования известных методов многопозиционной локации (например, триангуляционного, разностно-дальномерного, трилатерационного и их комбинаций [21, 22]).
В известных методах ОПЛН, как правило, рассматриваются такие траектории, которые на участке наблюдения либо известны (например, орбитальные с известными параметрами движения), либо с достаточной для практики точностью аппроксимируются моделью прямолинейного равномерного движения (как с известными, так и неизвестными параметрами движения). При этом принципиальным моментом для всех методов ОПЛН является учет априорной информации о величине скорости движущегося объекта (либо ИИ, либо Н) (см., например, [2, разд. 7] и [6, разд. 3]), что для практики зачастую является неприемлемым. Кроме того, в известных работах, посвященных методам ОПЛН, отсутствуют результаты какого-либо эксперимента, подтверждающие возможность эффективного применения этих методов с учетом периодичности излучаемого радиосигнала для некоторых характерных условий радиоконтакта.
Цель данной статьи состоит в разработке метода определения параметров движения объекта (Н) из пары ИИ–Н в условиях отсутствия априорной информации о величине скорости его движения. При этом в качестве пути достижения цели предполагается использовать (по аналогии с [6]) измерения эволюции периода радиосигнала, излучаемого стационарным ИИ.
1. ПОСТАНОВКА ЗАДАЧИ
Ограничимся рассмотрением задачи навигации, поскольку развиваемый ниже метод без труда переносится на задачу локации. Пусть в прямоугольной декартовой системе координат $XYZ$, которую свяжем с ИИ, движение Н является кусочно-линейным, при этом на $i$-м участке используется следующая модель:
где ${{\vec {r}}_{i}}\left( t \right) = {{\left[ {{{x}_{i}}\left( t \right),{{y}_{i}}\left( t \right),{{z}_{i}}\left( t \right)} \right]}^{T}},$ ${{\vec {r}}_{i}} = {{\vec {r}}_{i}}\left( {{{t}_{i}}} \right)$ = $ = {{\left[ {{{x}_{i}},{{y}_{i}},{{z}_{i}}} \right]}^{T}},$ ${{{\vec {v}}}_{i}} = {{\left[ {{{V}_{{xi}}},{{V}_{{yi}}},{{V}_{{z\,i}}}} \right]}^{T}} = {\text{const}}$ $\forall t \in \left[ {{{t}_{i}},{{t}_{{i + 2}}}} \right]$, ${{V}_{i}} = \left\| {{{{\vec {v}}}_{i}}} \right\|$ – модуль вектора скорости; ${{R}_{i}}\left( t \right) = \left\| {{{{\vec {r}}}_{i}}\left( t \right)} \right\| - $ дальность до Н в момент времени $t$; ${{t}_{i}}$,${{t}_{{i + 1}}}$ и ${{t}_{{i + 2}}}$ – три основных узла (крупной временной сетки), с которыми связан “синтез базы” и определение параметров движения Н на $i$-м участке. Несколько забегая вперед, отметим, что при неизвестном периоде радиосигнала нам в дальнейшем потребуется и четвертый узел ${{t}_{{i + 3}}}$, при этом ${{t}_{{i + 3}}} > {{t}_{{i + 2}}}$.
Стационарный ИИ вырабатывает периодический радиосигнал с периодом ${{T}_{i}}$ (может быть неизвестен) и длительностью mi + 2Ti, где mi + 2 – количество формируемых периодов.
В качестве типовых значений параметров радиосигналов, излучаемых, например, многофункциональными радиолокационными станциями, можно рассматривать следующие:
– частота следования импульсов 1…100 кГц;
– длительность импульсов 0.1…100 мкс;
– несущая частота 3…18 ГГц.
При этом наличие гармонической внутриимпульсной модуляции обеспечивает дополнительный информационный параметр. Режимы и параметры обзора пространства должны обеспечивать выполнение энергетического и информационного критериев по обнаружению и распознаванию сигнала.
Вследствие движения Н некоторая характерная мгновенная частота (о которой говорилось ранее) в точке наблюдения может быть представлена в виде ${{f}_{i}}\left( t \right) = {{f}_{{i0}}} - {{F}_{i}}\left( t \right)$, где $t \in \left[ {{{t}_{i}},{{t}_{{i + 2}}}} \right]$, ${{F}_{{i\,}}}\left( t \right)$ – частота Доплера, которая зависит от выбора ${{f}_{{i0}}}$. Если ${{f}_{{i0}}} = T_{i}^{{ - 1}}$, то речь идет о частоте следования импульсов модулирующей функции; также под ${{f}_{{i0}}}$ может пониматься частота несущего колебания.
Введем на интервале $\left[ {{{t}_{i}},{{t}_{{i + 2}}}} \right]$ мелкую сетку $\left\{ {{{t}_{{ij}}}} \right\}$, где $j = \overline {1,{{J}_{i}}} $, ${{t}_{{i\,1}}} = {{t}_{i}}$ и ${{t}_{{i\,{{J}_{i}}}}} \leqslant {{t}_{{i + 2}}}$, при этом ${{t}_{{i\,,j + 1}}} = {{t}_{{i\,1}}} + {{\Delta }_{{i,j + 1}}} = {{t}_{{i\,1}}} + {{m}_{{i,j + 1}}}{{T}_{i}} + {{\delta }_{{i,j + 1}}},$ $j \in \{ 1,2,...,$ ${{J}_{i}} - 1\} $; ${{m}_{{i,j + 1}}}$ – число подсчитываемых (в точке наблюдения) периодов излучаемого радиосигнала между узлами ${{t}_{i}} = {{t}_{{i\,1}}}$ и ${{t}_{{i,j + 1}}}$; ${{\delta }_{{i,j + 1}}} = {{c}^{{ - 1}}} \times $ $ \times \,\,\left( {{{R}_{{i,j + 1}}} - {{R}_{i}}} \right) = {{c}^{{ - 1}}}\Delta {{R}_{{i,j + 1}}}$ – информационная невязка (именно в ней содержится полезная информация о параметрах движения Н), обусловленная эволюцией ${{m}_{{i,j + 1}}}$ периодов радиосигнала на интервале $\left[ {{{t}_{i}},\;{{t}_{{i\,,j + 1}}}} \right]$. Здесь ${{R}_{i}} = {{R}_{i}}\left( {{{t}_{i}}} \right)$ и ${{R}_{{i,j + 1}}} = {{R}_{i}}\left( {{{t}_{{ij}}}} \right)$, $c$ – скорость света. В непрерывном времени эволюцию невязки, обусловленную движением Н, можно описать некоторой функцией
где ${{\delta }_{i}}({{t}_{i}}) = {{\delta }_{i}} = 0$. Применительно к сетке $\left\{ {{{t}_{{ij}}}} \right\}$ имеем ${{\delta }_{i}}({{t}_{{ij}}}) = {{\delta }_{{ij}}}$.
Узлы ${{t}_{k}}$ ($k \in \left\{ {i,i + 1} \right\}$) представим в виде ${{t}_{{k + 1}}} = {{t}_{k}} + {{\Delta }_{{k + 1}}}$, где ${{\Delta }_{{k + 1}}} = {{t}_{{k + 1}}} - {{t}_{i}}$ $ = {{m}_{{k + 1}}}{{T}_{i}} + {{\delta }_{{k + 1}}}$; ${{m}_{{k + 1}}}$ – максимально возможное целое число периодов радиосигнала, заполняющих интервал $\left[ {{{t}_{i}},{{t}_{{k + 1}}}} \right]$; ${{\delta }_{{k + 1}}}$ – невязка, обусловленная эволюцией ${{m}_{{k + 1}}}$ периодов радиосигнала в точке наблюдения на интервале $\left[ {{{t}_{i}},{{t}_{{k + 1}}}} \right]$. В терминах функции ${{\delta }_{i}}(t)$ имеем ${{\delta }_{i}}({{t}_{{i + 1}}}) = {{\delta }_{{i + 1}}}$ и ${{\delta }_{i}}({{t}_{{i + 2}}}) = {{\delta }_{{i + 2}}}$.
Далее полагаем, что доступны измерения ${{h}_{{i\left( {i + 1,\,i + 2} \right)}}}$ $ = {{\delta }_{{i\left( {i + 1,\,i + 2} \right)}}} + {{\xi }_{{i\left( {i + 1,\,i + 2} \right)}}}$ и ${{h}_{{ij}}} = {{\delta }_{{ij}}} + {{\xi }_{{ij}}}$ величин ${{\delta }_{{i + 1}}}$, ${{\delta }_{{i + 2}}}$ и ${{\delta }_{{ij}}}$ соответственно, при этом случайные погрешности измерений ${{\xi }_{{i\left( {i + 1,\,i + 2} \right)}}}$ и ${{\xi }_{{ij}}}$ распределены по нормальному закону с нулевыми математическими ожиданиями и известными корреляционными матрицами ${{{\mathbf{K}}}_{{i2}}}$ и ${{{\mathbf{K}}}_{{i,{{J}_{i}} - 1}}}$ (здесь индексы 2 и ${{J}_{i}} - 1$ указывают на размерности матриц). Размер ${{J}_{i}}$ мелкой сетки $\left\{ {{{t}_{{ij}}}} \right\}$ выбирается таким, чтобы в рамках развиваемого метода обеспечивались необходимые точность и устойчивость применяемых вычислительных процедур.
Для принятых моделей движения и измерения на интервале $\left[ {{{t}_{i}},{{t}_{{i + 2}}}} \right]$ требуется оценить частоту Доплера ${{F}_{{i\,}}}\left( t \right)$, дальности ${{R}_{{i\;\left( {i + 1,\;i + 2} \right)}}}$ и курсовые углы ${{\theta }_{{i\;\left( {i + 1,\;i + 2} \right)}}}$ в узлах ${{t}_{{i\;\left( {i + 1,\;i + 2} \right)}}}$, а также скорость ${{V}_{i}}$ наблюдателя для данного интервала.
Близкая (по сути) постановка задачи рассматривалась в [6, с. 153–158], однако теперь скорость Н полагается априорно неизвестной и модель движения принята кусочно-линейной, при этом рассматриваются два принципиально разных случая: период радиосигнала известен (случай 1) и неизвестен (случай 2).
2. РЯД УТВЕРЖДЕНИЙ. ОЦЕНИВАНИЕ ЧАСТОТЫ ДОПЛЕРА
Применительно к рассмотренной постановке задачи далее будем пользоваться следующими легко доказываемыми утверждениями.
Утверждение 1: справедливо строгое равенство $R_{i}^{2}\left( t \right) = {{a}_{{i0}}} + {{a}_{{i1}}}t + {{a}_{{i2}}}{{t}^{2}}$, где $\left\{ {{{a}_{{i0}}},{{a}_{{i1}}},{{a}_{{i2}}}} \right\}$ – некоторые действительные коэффициенты, соответствующие модели движения Н.
Утверждение 2: если только Н не движется на ИИ, то функция ${{\delta }_{i}}(t)$ является гладкой (дифференцируемой) и выпуклой (не содержит точек перегиба) на всем интервале $\left[ {{{t}_{i}},{{t}_{{i + 2}}}} \right]$.
Утверждение 3: если Н движется на ИИ (в этом случае курсовой угол равен нулю), то ${{F}_{{i\,}}}\left( t \right) = $ $ = {{F}_{i}} = {\text{const}}$ и $\mathop {{{\delta }_{i}}}\limits^\centerdot \left( t \right) = {\text{сonst}}$ на всем интервале $\left[ {{{t}_{i}},{{t}_{{i + 2}}}} \right]$ (здесь и далее точка сверху означает дифференцирование по $t$), следовательно, ${{R}_{i}}\left( t \right)$ и ${{\delta }_{i}}(t)$ – линейные функции времени на этом интервале.
Утверждение 4: условие ${{F}_{i}} = 0$ возможно только при попадании Н в точку траверза.
Развиваемый метод предполагает знание доплеровских поправок частоты ${{F}_{{i\,}}} = {{F}_{{i\,}}}\left( {{{t}_{i}}} \right)$, ${{F}_{{i + 1\,}}} = {{F}_{{i\,}}}\left( {{{t}_{{i + 1}}}} \right)$ и ${{F}_{{i + 2\,}}} = {{F}_{{i\,}}}\left( {{{t}_{{i + 2}}}} \right)$ в узлах ${{t}_{i}}$, ${{t}_{{i + 1}}}$ и ${{t}_{{i + 2}}}$, поэтому в данном разделе предлагаем эффективный алгоритм оценивания этих величин с использованием мелкой сетки {tij} и наблюдений {hij}. Он основан на возможности представления частоты Доплера в виде ${{F}_{i}}\left( t \right) = {{c}^{{ - 1}}}{{f}_{{i0}}}\mathop {{{R}_{i}}}\limits^\centerdot \left( t \right) = {{f}_{{i0}}}\mathop {{{\delta }_{i}}}\limits^\centerdot \left( t \right)$. Поскольку функция ${{\delta }_{i}}(t)$ является гладкой (утверждение 2), то путем соответствующего выбора объема сетки $\left\{ {{{t}_{{ij}}}} \right\}$ можно добиться достаточно высокой точности представления производной $\mathop {{{\delta }_{i}}}\limits^\centerdot \left( t \right)$ на базе инвариантно-несмещенного алгоритма оптимального оценивания производных при наличии не только флуктуационных, но и сингулярных погрешностей [23]. В простейшем случае достаточно ограничиться традиционным методом наименьших квадратов, если предположить, что по результатам измерений ${{h}_{{ij}}}$ сформированы частные оценки ${{\hat {\delta }}_{{ij}}} = {{h}_{{ij}}} - {{m}_{{ij}}}{{T}_{i}}$ величин ${{\delta }_{{ij}}}$. Используя сглаживающий полином ${{\alpha }_{i}}\left( t \right) = {\mathbf{b}}_{i}^{T}{{{\mathbf{\Psi }}}_{i}}\left( t \right)$ (с заданным вектором ${{{\mathbf{\Psi }}}_{i}}\left( t \right)$ базисных функций), путем минимизации соответствующей невязки, например
Подобную оценку можно найти, используя общее правило:
где под $\left[ \centerdot \right]_{k}^{{\left( 1 \right)}}$ понимается оператор дифференцирования в точке $t = {{t}_{k}}$, $k \in \left\{ {i,\;i + 1,\;i + 2} \right\}$. Как показано далее в численном примере, эффекты накопления и сглаживания существенно повышают точность вычисления доплеровских поправок частоты согласно предложенному подходу.
Далее с учетом того, что ${{F}_{{i\,}}}$, ${{F}_{{i + 1\,}}}$ и ${{F}_{{i + 2\,}}}$ нам известны, рассмотрим вопрос определения параметров движения Н для двух случаев: период радиосигнала известен (случай 1) и неизвестен (случай 2).
3. РЕШЕНИЕ ЗАДАЧИ ДЛЯ РАДИОСИГНАЛА С ИЗВЕСТНЫМ ПЕРИОДОМ
Для первой производной $\mathop {{{R}_{{i + 1}}}}\limits^\centerdot $ дальности ${{R}_{i}}\left( t \right)$ в точке ${{t}_{{i + 1}}}$ справедливо
(1)
$\mathop {R_{{i + 1}}^{{}}}\limits^\centerdot = R_{{i + 1}}^{{ - 1}}\vec {r}_{{i + 1}}^{T}{{\vec {v}}_{i}} = R_{{i + 1}}^{{ - 1}}\left( {\vec {r}_{i}^{T}{{{\vec {v}}}_{i}} + V_{i}^{2}{{\Delta }_{{i + 1}}}} \right).$Так как для движущегося Н мгновенная частота ${{f}_{i}}\left( t \right)$ входного радиосигнала является функцией времени (вследствие эффекта Доплера), то для точки ${{t}_{{i + 1}}}$ справедлива запись ${{f}_{i}}\left( {{{t}_{{i + 1}}}} \right) = {{f}_{{i0}}} - {{F}_{{i + 1}}}$, где ${{F}_{{i + 1}}} = {{c}^{{ - 1}}}{{f}_{{i0}}}\mathop {R_{{i + 1}}^{{}}}\limits^\centerdot $ – доплеровская поправка частоты. Следовательно, с учетом (1) получаем
(2)
$\vec {r}_{i}^{T}{{\vec {v}}_{i}} + V_{i}^{2}{{\Delta }_{{i + 1}}} = cf_{{i0}}^{{ - 1}}{{F}_{{i + 1}}}{{R}_{{i + 1}}}.$По аналогии с (2), для момента времени ${{t}_{i}}$ имеем
где учтено, что ${{\Delta }_{i}} = {{t}_{i}} - {{t}_{i}} = 0.$ На основании (2) и (3) получаем
(4)
$V_{i}^{2}{{c}^{{ - 1}}}{{f}_{{i0}}} = {{\left( {\Delta {}_{{i + 1}}} \right)}^{{ - 1}}}\left( {{{F}_{{i + 1}}}{{R}_{{i + 1}}} - {{F}_{i}}{{R}_{i}}} \right).$Представим приращение дальности на интервале $\Delta {}_{{i + 1}}$ в виде
(5)
${{R}_{{i + 1}}} - {{R}_{i}} = c{{\delta }_{{i + 1}}} = c\left( {\Delta {}_{{i + 1}} - {{m}_{{i + 1}}}{{T}_{i}}} \right),$при этом если Н удаляется, то ${{R}_{{i + 1}}} > {{R}_{i}}$ и ${{\delta }_{{i + 1}}} > 0$, если Н приближается, то ${{R}_{{i + 1}}} < {{R}_{i}}$ и ${{\delta }_{{i + 1}}} < 0$, а если Н неподвижен, то ${{R}_{{i + 1}}} = {{R}_{i}}$ и ${{\delta }_{{i + 1}}} = 0$. Смена знака для ${{\delta }_{{i + 1}}}$ возможна только в точке траверза.
Выражая из (5) величину ${{R}_{{i + 1}}}$ и подставляя ее в (4), получаем
(6)
$V_{i}^{2}{{c}^{{ - 1}}}{{f}_{{i0}}} = {{\left( {\Delta {}_{{i + 1}}} \right)}^{{ - 1}}}\left[ {\Delta _{{i + 1}}^{F}{{R}_{i}} + c{{F}_{{i + 1}}}\left( {\Delta {}_{{i + 1}} - {{m}_{{i + 1}}}{{T}_{i}}} \right)} \right],$где $\Delta _{{i + 1}}^{F} = {{F}_{{i + 1}}} - {{F}_{i}}$ – приращение доплеровского смещения частоты радиосигнала за время $\Delta {}_{{i + 1}}$. По аналогии с (6) для моментов времени ${{t}_{i}}$ и ${{t}_{{i + 2}}}$ имеем
(7)
$V_{i}^{2}{{c}^{{ - 1}}}{{f}_{{i0}}} = {{\left( {\Delta {}_{{i + 2}}} \right)}^{{ - 1}}}\left[ {\Delta _{{i + 2}}^{F}{{R}_{i}} + c{{F}_{{i + 2}}}\left( {\Delta {}_{{i + 2}}\,\, - {{m}_{{i + 2}}}{{T}_{i}}} \right)} \right].$Приравнивая (6) и (7), формируем искомое выражение для определения дальности ${{R}_{i}}$ в момент времени ${{t}_{i}}$:
(8)
${{R}_{i}} = c\frac{{{{F}_{{i + 2}}}{{\Delta }_{{i + 1}}}\left( {\Delta {}_{{i + 2}}\,\, - {{m}_{{i + 2}}}{{T}_{i}}} \right) - {{F}_{{i + 1}}}{{\Delta }_{{i + 2}}}\left( {\Delta {}_{{i + 1}}\, - {{m}_{{i + 1}}}{{T}_{i}}} \right)}}{{\Delta _{{i + 1}}^{F}\Delta {}_{{i + 2}}\, - \Delta _{{i + 2}}^{F}\Delta {}_{{i + 1}}}}.$С учетом (5), по аналогии с (8), можно найти ${{R}_{{i + 1}}}$ и ${{R}_{{i + 2}}}$ (используя единую запись ${{R}_{{i + 1(i + 2)}}}$) для моментов времени ${{t}_{{i + 1}}}$ и ${{t}_{{i + 2}}}$ соответственно:
(9)
${{R}_{{i + 1\,\left( {i + 2} \right)}}} = {{R}_{i}} + c\left( {{{\Delta }_{{i + 1\,\left( {i + 2} \right)}}} - {{m}_{{i + 1\,\left( {i + 2} \right)}}}{{T}_{i}}} \right).$Подставляя (8) в (6), после несложных преобразований находим формулу для определения скорости движения Н:
(10)
${{V}_{i}} = {{\left| {c{{{\left( {{{f}_{{i0}}}{{\Delta }_{{i + 1}}}} \right)}}^{{ - 1}}}\left( {{{R}_{i}}\Delta _{{i + 1}}^{F} + c{{F}_{{i + 1}}}\left( {{{\Delta }_{{i + 1}}} - {{m}_{{i + 1}}}{{T}_{i}}} \right)} \right)} \right|}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$С учетом того, что $\mathop {{{R}_{k}}}\limits^\centerdot = \pm {{V}_{k}}\cos {{\theta }_{k}} = cf_{{i0}}^{{ - 1}}{{F}_{k}}$, для нахождения курсовых углов можно воспользоваться формулой
(11)
${{\theta }_{k}} = \arccos \left( {cV_{i}^{{ - 1}}f_{{i0}}^{{ - 1}}{{F}_{k}}} \right),\,\,\,\,k \in \left\{ {i,i + 1,i + 2} \right\},$где скорость ${{V}_{i}}$ находится в соответствии с (10).
Выражения (8)–(11) позволяют определять дальность, скорость и курсовой угол Н, по измерениям временных невязок, характеризующих эволюцию периодов излученного радиосигнала в точке наблюдения.
4. РЕШЕНИЕ ЗАДАЧИ ДЛЯ РАДИОСИГНАЛА С НЕИЗВЕСТНЫМ ПЕРИОДОМ
Если период ${{T}_{i}}$ неизвестен, то наряду с ${{t}_{i}}$, ${{t}_{{i + 1}}}$ и ${{t}_{{i + 2}}}$ потребуется четвертый радиоконтакт ${{t}_{{i + 3}}}$. Принимая для простоты, что число накапливаемых периодов между соседними узлами одинаково (т.е. ${{m}_{{i + 2}}} - {{m}_{{i + 1}}} = {{m}_{{i + 3}}} - {{m}_{{i + 2}}}$), запишем следующие выражения (обозначив $\Delta _{{m\,n}}^{'} = {{t}_{n}} - {{t}_{m}}$, ${{G}_{{m\,n\,p}}} = {{F}_{m}}\Delta _{{n\,p}}^{'}$, ${{S}_{{m\,n\,p}}} = \Delta _{{p\,n}}^{'} - 2\Delta _{{n\,m}}^{'}$, ${{Q}_{{m\,n\,p}}} = \Delta _{{n\,p}}^{'} - \Delta _{{n\,m}}^{'}$, $m,\,n,\,p \in $ $ \in \left\{ {i,\,j,k,\,l} \right\}$):
(12)
$\left\{ \begin{gathered} {{R}_{i}} = c\left( {{{L}_{{ijkl}}} + {{M}_{{ijkl}}}} \right){{\left( {{{H}_{{ijkl}}} + {{P}_{{ijkl}}}} \right)}^{{ - 1}}}, \hfill \\ {{R}_{j}} = \left[ {{{R}_{i}}\left( {2{{G}_{{lji}}} - {{G}_{{ili}}} + {{G}_{{iji}}}} \right) - c{{S}_{{ijl}}}{{G}_{{lji}}}} \right]{{\left( {3{{G}_{{lji}}} - {{G}_{{jli}}}} \right)}^{{ - 1}}},\,\,\,j = i + 1, \hfill \\ {{R}_{k}} = c{{Q}_{{ijk}}} + 2{{R}_{j}} - {{R}_{i}},\,\,\,k = i + 2, \hfill \\ {{R}_{l}} = c{{S}_{{ijl}}} + 3{{R}_{j}} - 2{{R}_{i}},\,\,\,l = i + 3, \hfill \\ \end{gathered} \right.$(13)
${{V}_{i}} = {{\left| {c{{{\left( {{{f}_{{i0}}}{{\Delta }_{{i + 1}}}} \right)}}^{{ - 1}}}\left( {{{F}_{j}}{{R}_{j}} - {{F}_{i}}{{R}_{i}}} \right)} \right|}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$(14)
${{\theta }_{{i\left( {j,k} \right)}}} = \arccos \left( {cV_{i}^{{ - 1}}f_{{i0}}^{{ - 1}}{{F}_{{i(j,k)}}}} \right),$где
(15)
$\left\{ \begin{gathered} {{L}_{{ijkl}}} = {{S}_{{ijl}}}{{G}_{{lji}}}\left( {3{{G}_{{lki}}} - 2{{G}_{{kli}}}} \right), \hfill \\ {{M}_{{ijkl}}} = \left( {{{S}_{{ijl}}}{{G}_{{lki}}} - {{Q}_{{ijk}}}{{G}_{{kli}}}} \right)\left( {{{G}_{{jli}}} - 3{{G}_{{lji}}}} \right), \hfill \\ {{H}_{{ijkl}}} = \left( {3{{G}_{{lki}}} - 2{{G}_{{kli}}}} \right)\left( {2{{G}_{{lji}}} - {{G}_{{ili}}} + {{G}_{{iji}}}} \right), \hfill \\ {{P}_{{ijkl}}} = \left( {{{G}_{{jli}}} - 3{{G}_{{lji}}}} \right)\left( {2{{G}_{{lki}}} - {{G}_{{ili}}} + {{G}_{{iki}}} - {{G}_{{kli}}}} \right). \hfill \\ \end{gathered} \right.$Таким образом, выражения (12)–(15) позволяют решать задачу определения параметров движения Н не только при неизвестной скорости, но и для случая, когда период радиосигнала априорно не задан.
5. АНАЛИЗ ЧАСТНЫХ СЛУЧАЕВ
Случай 1: движение Н по линии визирования. В этом случае дальность ${{R}_{i}}\left( t \right)$ есть линейная функция времени, а ее производная $\mathop {{{R}_{i}}}\limits^\centerdot \left( t \right) \equiv \operatorname{const} $, ${{F}_{i}}\left( t \right) = {{F}_{i}} = {{F}_{{i + 1}}} = {{F}_{{i + 2}}}$ и $\Delta _{{i + 1}}^{F} = 0$, $\Delta _{{i + 2}}^{F} = 0$, следовательно, знаменатель в формуле (8) равен нулю и нахождение дальности по формулам (8), (9) и (12) становится невозможным (нарушается условие наблюдаемости метода). Так как
то для скорости Н справедливо
а для курсового угла –
где $k \in \left\{ {i,i + 1,i + 2} \right\}$.
Случай 2: узел ${{t}_{{i + 1}}}$ соответствует точке траверза, при этом выполнено условие ${{R}_{i}} = {{R}_{{i + 2}}}$, ${{\Delta }_{{i + 2}}} = 2\Delta {}_{{i + 1}}$ и ${{F}_{{i + 1}}} = 0$ (утверждение 4). Тогда в (8) знаменатель имеет вид
Следовательно, выражения (8)–(11) для случая 2 некорректны (нарушается условие наблюдаемости метода).
Для случаев, связанных с движением Н в направлении на ИИ, можно воспользоваться энергетическим методом [13–15], принимая в нем курсовой угол равным нулю. Доказано, что данный метод, оперирующий с относительными амплитудами и мощностями принимаемого радиосигнала для различных моментов времени, обеспечивает в направлении на ИИ наивысшую точность. Следовательно, комбинируя развиваемый и энергетический методы, можно выровнять рабочую зону комплексного метода и достичь приемлемых точностных характеристик для всех значений курсовых углов. Для более эффективного применения энергетических методов следует использовать процедуры кластеризации и мажоритарной обработки для редукции и отсева ненадежных измерений.
6. АНАЛИЗ ВЛИЯНИЯ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
Для оценки влияния случайных ошибок измерений ${{\xi }_{{ij}}}$ на точностные характеристики развиваемого метода (в рамках формул (8)–(11), (12)–(15)) зададим вектор оцениваемых параметров в виде ${{{\mathbf{\eta }}}_{i}} = {{\left[ {{{\eta }_{{i\,q}}},q = \overline {1,Q} } \right]}^{T}}$, где размерность $Q$ определяется в зависимости от решаемой практической задачи, а ${{\eta }_{{i\,q}}} \in \left\{ {{{R}_{i}},{{R}_{{i + 1}}},{{R}_{{i + 2}}},{{V}_{i}},{{\theta }_{i}},{{\theta }_{{i + 1}}},{{\theta }_{{i + 2}}}} \right\}$. Для вектора ${{{\mathbf{\eta }}}_{i}}$ можно воспользоваться представлением ${{{\mathbf{\eta }}}_{i}} = {\mathbf{\varphi }}\left( {{{{\mathbf{\delta }}}_{i}}} \right)$ (${{{\mathbf{\delta }}}_{i}} = {{\left[ {{{\delta }_{{ij}}},j = \overline {1,{{J}_{i}} - 1} } \right]}^{T}}$ – единый вектор измеряемых параметров для участка $\left[ {{{t}_{i}},{{t}_{{i + 2}}}} \right]$), которое формируется с учетом ранее полученных аналитических выражений для дальности, скорости и курсового угла. Поскольку вид функции ${\mathbf{\varphi }}\left( {{{{\mathbf{\delta }}}_{i}}} \right)$ нам известен, то можно построить матрицу частных производных ${{{\mathbf{G}}}_{i}} = \partial {{{\mathbf{\varphi }}}_{i}}{{\left( {{{{\mathbf{\delta }}}_{i}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\mathbf{\delta }}}_{i}}} \right)} {\partial {{{\mathbf{\delta }}}_{i}}}}} \right. \kern-0em} {\partial {{{\mathbf{\delta }}}_{i}}}}$, элементы которой вычисляются на математических ожиданиях величин ${{h}_{{ij}}}$, т.е. на ${{\delta }_{{ij}}}$. Далее, применяя традиционную методику оценивания потенциальных возможностей тех или иных методов оценивания (в первом приближении [25]), находим искомую корреляционную матрицу ошибок оценивания координат вектора ${{{\mathbf{\eta }}}_{i}}$:
(16)
${{{\mathbf{K}}}_{{\eta \,i}}} = {{{\mathbf{G}}}_{i}}{{{\mathbf{K}}}_{{i,{{J}_{i}} - 1}}}{\mathbf{G}}_{i}^{T}.$Соотношение (16) позволяет исследовать (в среднем) влияние случайных погрешностей измерений для различной геометрии и возможных условий радиоконтакта пары ИИ–Н, а также обоснованно подходить к выбору основных параметров развитого метода.
7. ЧИСЛЕННЫЙ ПРИМЕР
Рассмотрим прямолинейно и равномерно движущегося Н (с постоянной скоростью $V$) на всем интервале наблюдения. В качестве такого наблюдателя могут быть воздушные объекты, движущиеся со скоростями 500…800 м/с (например, авиационные истребители), или космические объекты, скорости движения которых составляют 7…11 км/с (например, межконтинентальные баллистические ракеты на внеатмосферном участке полета). Наземный ИИ излучает периодический радиосигнал
Здесь и далее время и погрешности измерений временных интервалов задаются в секундах, координаты и дальность Н – в метрах, скорость – в метр на секунду, углы – в градусах и частота – в герцах. Рассматривались два случая:
случай 1 – $V = 7 \times {{10}^{2}}$, ${{x}_{0}} = 3 \times {{10}^{4}}$, ${{y}_{0}} = 15 \times {{10}^{3}}$, $\theta \left( 0 \right) = 33.54$;
случай 2 – $V = 7 \times {{10}^{3}}$, ${{x}_{0}} = {{y}_{0}} = 5 \times {{10}^{5}}$, $\theta \left( 0 \right) = 51.52$.
Для вычисления частоты Доплера формировалась мелкая сетка $\left\{ {{{t}_{{ij}}}} \right\}$ с одинаковым числом накапливаемых периодов для любых двух соседних узлов: $\Delta {{m}_{{i,j + 1}}} = {{m}_{{i,j + 1}}} - {{m}_{{i,j}}} = {{10}^{2}}$ (в этом случае ${{J}_{i}} = 351$) и $\Delta {{m}_{{i,j + 1}}} = {{m}_{{i,j + 1}}} - {{m}_{{i,j}}} = 2 \times {{10}^{2}}$ (в этом случае ${{J}_{i}} = 176$). Для сглаживания в процедуре формирования оценок $F_{i}^{ * }$, $F_{{i + 1}}^{ * }$ и $F_{{i + 2}}^{ * }$ был использован степенной полином (шестой степени).
Для двух вариантов значений ${{m}_{{i + 2}}} = 2{{m}_{{i + 1}}} = $ $ = 8 \times {{10}^{3}}$ и ${{m}_{{i + 2}}} = 2\;{{m}_{{i + 1}}} = 14 \times {{10}^{3}}$ формировалось множество непересекающихся последовательных временных троек $\{ ({{t}_{i}},{{t}_{{i + 1}}},{{t}_{{i + 2}}}),$ $({{t}_{{i + 3}}},{{t}_{{i + 4}}},{{t}_{{i + 5}}}), \ldots ,$ $({{t}_{{I - 2}}},{{t}_{{I - 1}}},{{t}_{I}})\} $ (с целью формирования некоррелированных оценок), для каждой из которых по результатам измерений находились единичные оценки дальности, скорости и курсового угла. Для реализации сглаживающего эффекта все единичные оценки дальности возводились в квадрат (поскольку для модели прямолинейного равномерного движения Н именно квадрат дальности строго описывается полиномом второй степени) и сглаживались полиномом второй степени (утверждение 1). Окончательные значения оценок дальности находили путем извлечения квадратного корня из значений этого полинома в узлах крупной сетки $\left\{ {{{t}_{i}},\;{{t}_{{i + 1}}},...,{{t}_{I}}} \right\}$. Ошибки измерений полагались некоррелированными и формировались по нормальному закону распределения с тремя вариантами среднеквадратического отклонения ${{\sigma }_{{ij}}} = \sigma \in $ $ \in \left\{ {{{{10}}^{{ - 9}}},5 \times {{{10}}^{{ - 9}}},{{{10}}^{{ - 8}}}} \right\}$. Оценки усреднялись по тысяче реализаций.
Для случая 1 модуль частоты Доплера изменялcя от $0.64 \times {{10}^{4}}$ до $2.92 \times {{10}^{4}}$, а для случая 2 – от $1.27 \times {{10}^{5}}$ до $2.19 \times {{10}^{5}}$. При этом для обоих случаев и варианта $\sigma = 5 \times {{10}^{{ - 9}}}$ погрешность вычисления частоты Доплера в узлах крупной сетки не превысила 374.73. В случае 2 для обоих вариантов, $\Delta {{m}_{{i,j + 1}}} = {{10}^{2}}$ и $\Delta {{m}_{{i,j + 1}}} = 2 \times {{10}^{2}}$, получили $\left| {{{\delta }_{{i,j + 1}}} - {{\delta }_{{i,j}}}} \right| \in $ $ \in \left[ {0.78...1.46} \right] \times {{10}^{{ - 6}}}$ и $\left| {{{\delta }_{{i,j + 1}}}\, - \,{{\delta }_{{i,j}}}} \right|\, \in \,\left[ {1.55...2.92} \right] \times {{10}^{{ - 6}}}$ соответственно, а для ${{m}_{{i + 2}}} = 2{{m}_{{i + 1}}}$ $ = 8 \times {{10}^{3}}$ и ${{m}_{{i + 2}}} = 2{{m}_{{i + 1}}}$ $ = 14 \times {{10}^{3}}$ получили $\left| {{{\delta }_{{i + 1}}}} \right|,$ $\left| {{{\delta }_{{i + 2}}} - {{\delta }_{{i + 1}}}} \right| \in $ $ \in \left[ {3.59...5.73} \right] \times {{10}^{{ - 5}}}$ и $\left| {{{\delta }_{{i + 1}}}} \right|,$ $\left| {{{\delta }_{{i + 2}}} - {{\delta }_{{i + 1}}}} \right| \in $ $ \in \left[ {6.02...9.86} \right] \times {{10}^{{ - 5}}}$ соответственно.
На рис. 1–3 представлены зависимости относительных погрешностей оценивания дальности, скорости и курсового угла от времени наблюдения для случаев 1 и 2 при различных значениях исходных данных.
Рис. 1.
Зависимости относительных погрешностей оценивания дальности (а), скорости (б) и курсового угла (в) от времени наблюдения для случая 1 при следующих параметрах: $\Delta {{m}_{{i,j + 1}}} = {{10}^{2}}$, ${{m}_{{i + 2}}} = 2\;{{m}_{{i + 1}}} = 8 \times {{10}^{3}}$, $\sigma = {{10}^{{ - 9}}}$.
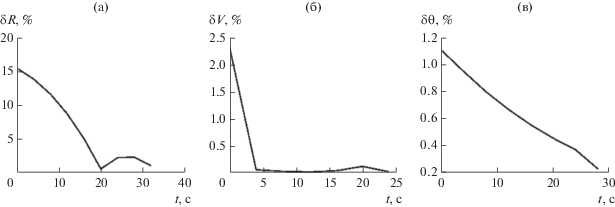
Рис. 2.
Зависимости относительных погрешностей оценивания дальности (а), скорости (б) и курсового угла (в) от времени наблюдения для случая 1 при следующих параметрах: $\Delta {{m}_{{i,j + 1}}} = 2 \times {{10}^{2}}$, ${{m}_{{i + 2}}} = 2\;{{m}_{{i + 1}}} = 14 \times {{10}^{3}}$, $\sigma = 5 \times {{10}^{{ - 9}}}$.
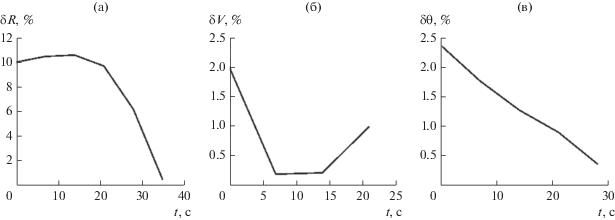
Рис. 3.
Зависимости относительных погрешностей оценивания дальности (а), скорости (б) и курсового угла (в) от времени наблюдения для случая 2 при следующих параметрах: $\Delta {{m}_{{i,j + 1}}} = 2 \times {{10}^{2}}$, ${{m}_{{i + 2}}} = 2\;{{m}_{{i + 1}}} = 14 \times {{10}^{3}}$, $\sigma = {{10}^{{ - 8}}}$.
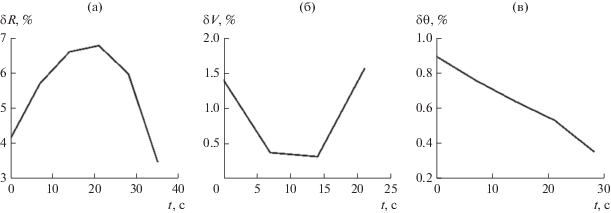
Полученные результаты позволяют сделать следующие выводы: чем больше шаг мелкой сетки, тем выше методическая ошибка вычисления частоты Доплера, однако случайные погрешности измерений оказывают при этом меньшее влияние на результирующую точность оценивания этой частоты; для повышения точности оценивания параметров движения при фиксированной скорости Н следует увеличивать шаг крупной сетки, поскольку именно этот параметр влияет на величину “синтезируемой базы”; шаг крупной сетки должен быть согласован с возможной динамикой Н, а именно: чем меньше скорость движения Н, тем больше должен быть шаг этой сетки; выбор не пересекающихся измерительных троек крупной сетки, обеспечивает некоррелированность формируемых единичных оценок; для более эффективного использования метода следует решать оптимизационную задачу относительно выбора шага крупной и мелкой временных сеток, а также их согласования с учетом динамики Н и погрешностей измерений.
ЗАКЛЮЧЕНИЕ
В отличие от известных результатов разработанный метод характеризуется следующими элементами новизны: для решения задачи определения параметров движения на базе однопозиционной пассивной системы знание скорости Н не требуется; за счет оптимального оценивания производной от функции невязки между периодами излученного и принятого радиосигналов можно строить качественные оценки частот Доплера и, соответственно, параметров движения Н. При выборе параметров развитого метода необходимо достигать баланса между оперативностью и точностью оценивания дальности, скорости и курсового угла Н, с учетом технических возможностей применяемой однопозиционной системы пассивной локации или навигации.
Метод можно реализовать в различных вариантах: по фиксированной выборке измерений, по выборке измерений нарастающего объема, в виде алгоритма динамической фильтрации (линейной, квазилинейной или нелинейной) и др. [7‒10, 18–20, 24].
Следует полагать, что эффективная практическая реализация предложенного метода возможна для различных значений параметров, если имеются соответствующие приемо-регистрирующие устройства для измерения (с требуемой точностью) величины относительного приращения периода принимаемого колебания. При этом все диапазоны указанных в постановке задачи типовых значений параметров радиосигналов в численном примере не проверялись.
Список литературы
Основы маневрирования кораблей / Под ред. М. Скворцова. М.: Воениздат, 1966.
Шебшаевич В.С. Введение в теорию космической навигации. М.: Сов. радио, 1971.
Громов Г.Н. Дифференциально-геометрический метод навигации. М.: Радио и связь, 1986.
Хвощ В.А. Тактика подводных лодок. М.: Воениздат, 1989.
Соловьев Ю.А. Спутниковая навигация и ее приложения. М.: Экотрендз, 2003.
Мельников Ю.П., Попов С.В. Радиотехническая разведка. М.: Радиотехника, 2008.
Ярлыков М.С. Статистическая теория радионавигации. М.: Радио и связь, 1985.
Сосулин Ю.Г., Костров В.В., Паршин Ю.Н. Оценочно-корреляционная обработка сигналов и компенсация помех. М.: Радиотехника, 2014.
Булычев Ю.Г., Манин А.П. Математические аспекты определения движения летательных аппаратов. М.: Машиностроение, 2000.
Булычев Ю.Г., Васильев В.В., Джуган Р.В. и др. Информационно-измерительное обеспечение натурных испытаний сложных технических комплексов. М.: Машиностроение–Полет, 2016.
Гельцер А.А. Однопозиционный метод определения местоположения источника радиоизлучения с использованием отражений сигналов от множества элементов рельефа и местных предметов // Автореф. дис. канд. техн. наук. Томск: Гос. ун-т систем управления и радиоэлектроники, 2012. 22 c.
Сиренко И.Л., Донец И.В., Рейзенкинд Я.А. и др. // Радиотехника. 2019. № 10. С. 28.
Булычев Ю.Г., Ивакина С.С., Насенков И.Г. // Радиотехника. 2015. № 6. С. 107.
Булычев Ю.Г., Мозоль А.А. // Успехи совр. радиоэлектроники. 2017. № 4. С. 58.
Булычев Ю.Г., Мозоль А.А., Насенков И.Г. // РЭ. 2018. Т.63. № 6. С. 563.
Булычев Ю.Г., Булычев В.Ю., Ивакина С.С. и др. // РЭ. 2016. Т. 61. № 4. С. 344.
Дятлов А.П., Дятлов П.А. // Спец. техника. 2010. № 5. С. 16.
Aidala V.J., Nardone S.C. // IEEE Trans. 1982. V. AES-18. № 4. P. 432.
Amelin K.S., Miller A.B. // J. Commun. Technol. Electron. 2014. V. 59. № 6. 2014. P. 622.
Miller A.B. // Automation and Remote Control. 2015. V. 76. № 6. P. 1018.
Кондратьев В.С., Котов А.Ф., Марков Л.Н. Многопозиционные радиотехнические системы. М.: Радио и связь, 1986.
Черняк В.С. Многопозиционная радиолокация. М.: Радио и связь, 1993.
Булычев Ю.Г., Елисеев А.В. // Журн. вычислит. математики и матем. физики. 2008. Т. 48. № 4. С. 580.
Жданюк Б.Ф. Основы статистической обработки траекторных измерений. М.: Сов. радио, 1978.
Вентцель Е.С. Теория вероятностей. М.: Высш. школа, 1999.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


