Радиотехника и электроника, 2021, T. 66, № 5, стр. 419-424

ВВЕДЕНИЕ

Композиционные материалы на основе диполей в виде отрезков проводящих волокон перспективны в качестве радиопоглощающих в технике сверхвысоких частот. Такие материалы имеют релаксационный характер дисперсии эффективной диэлектрической проницаемости (ЭДП), которую можно варьировать в широких пределах изменением концентрации диполей, их проводимости и размеров [1–3]. Проектирование таких композитов основывается на расчете частотной зависимости ЭДП. В случае упорядоченного расположения диполей расчет ЭДП может быть проведен с высокой точностью на основе решения задачи дифракции на периодической структуре с резистивными элементами [4–7]. Однако в реальных композитах имеет место хаотическое распределение ориентации диполей. ЭДП таких композитов вычисляется по приближенным формулам смешения Максвелла Гарнетта, Бруггемана, Оделевского или синтеза этих теорий [8–10]. Характеристикой цилиндрического диполя является его поляризуемость, которая вычисляется путем сопоставления линейному диполю равного ему по объему эллипсоида по статической формуле [3, 11]. Предполагается, что при условии малости длины диполя по сравнению с длиной волны такая замена не приводит к существенной погрешности вычисления поляризуемости, что, однако, не является очевидным. Прямой метод расчета поляризуемости линейного резистивного диполя в квазистатическом поле, предложенный в [12], не учитывает временного запаздывания электромагнитного взаимодействия зарядов на диполе, которое может быть существенным, если длина диполя сравнима с длиной волны. При этом система линейных уравнений, к которой сводится в [12] расчет поляризуемости, имеет медленную сходимость.

Цель данной работы – расчет поляризуемости линейного резистивного диполя в квазистатическом приближении с учетом запаздывания времени взаимодействия зарядов на диполе, улучшение сходимости вычислительного алгоритма и сравнение результатов расчета с моделью эллипсоида, а также оценка применимости этих расчетов к вычислению ЭДП композиционных материалов.

1. РАСЧЕТ ПОЛЯРИЗУЕМОСТИ ДИПОЛЯ В КВАЗИСТАТИЧЕСКОМ ПРИБЛИЖЕНИИ

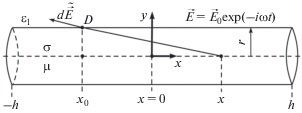
На рис. 1 изображен тонкий цилиндрический диполь радиусом $r$ и длиной $2h$, находящийся во внешнем однородном электрическом поле с амплитудой ${{\vec {E}}_{0}}$, параллельном оси $x$ и зависящем от времени по закону $\exp {\kern 1pt} {\kern 1pt} ( - i{\kern 1pt} {\kern 1pt} {{\omega }}{\kern 1pt} {\kern 1pt} t)$, где $i$ – мнимая единица. Проводимость материала диполя ${{\sigma }}$, его абсолютная магнитная проницаемость ${{\mu }}$. Абсолютная диэлектрическая проницаемость среды, окружающей диполь, равна ${{{{\varepsilon }}}_{{{\kern 1pt} 1}}}$. Ввиду предполагаемой тонкости диполя, ${r \mathord{\left/ {\vphantom {r {(2h)}}} \right. \kern-0em} {(2h)}} \ll 1$, поле текущего по диполю тока на его поверхности можно считать равным полю линейного тока на оси [13, 14].

Рис. 1.

Резистивный диполь в переменном электрическом поле.

Введем линейную плотность заряда ${{\rho }}{\kern 1pt} {\kern 1pt} (x)$ на оси $x$, тогда для $x$-компоненты поля $d{{\tilde {E}}_{x}}$, создаваемого малым элементом $d{\kern 1pt} x$ с координатой $x$ в точке $D$ на поверхности диполя, имеющей координату ${{x}_{0}}$, получим

где $\Delta \,t$ – время запаздывания “сигнала” от точки $x$ до точки ${{x}_{0}}$,

${{{{\varepsilon }}}_{0}}$ – диэлектрическая проницаемость вакуума, $c$ – скорость света в вакууме. В (2) учтено, что скорость распространения поля в окружающей диполь среде равна ${c \mathord{\left/ {\vphantom {c {\sqrt {{{{\varepsilon }} \mathord{\left/ {\vphantom {{{\varepsilon }} {{{{{\varepsilon }}}_{0}}}}} \right. \kern-0em} {{{{{\varepsilon }}}_{0}}}}} }}} \right. \kern-0em} {\sqrt {{{{\varepsilon }} \mathord{\left/ {\vphantom {{{\varepsilon }} {{{{{\varepsilon }}}_{0}}}}} \right. \kern-0em} {{{{{\varepsilon }}}_{0}}}}} }}$. Плотность заряда связана с величиной $I(x)$ линейного тока соотношением [12]

Подставляя (3) в (1), применяя формулу интегрирования по частям и полагая ток на краях диполя $I\left( { \pm h} \right)$ равным нулю, получим для $x$-компоненты собственного поля диполя в точке $D$:

В (4) обозначено

Пренебрегая краевым эффектом, что допустимо ввиду предполагаемой тонкости диполя, имеем

где $Z$ – комплексное погонное сопротивление диполя, выражаемое по известной формуле через функции Бесселя от аргумента ${{(i{\kern 1pt} {{\omega }}\,{{\sigma }}\,{{\mu }})}^{{{\kern 1pt} 1/2}}}$ [13, 15].

С учетом (4) равенство (6) представляет собой интегральное уравнение относительно функции $I(x)$. Поделив отрезок $x \in ( - h,\;h)$ узловыми точками

где $\tilde {N}$ – число элементарных отрезков шириной ${{\delta }}$, получим систему линейных алгебраических уравнений относительно токов $\left\{ {{{I}_{n}}} \right\}$ в узлах:

Матричные элементы вычислены с учетом того, что они выражаются через интегралы от дифференциала функции $F$. Ввиду четности функции $I(x)$ токи на элементах диполя, расположенных симметрично относительно середины диполя, равны, что позволяет при четном $\tilde {N}$ сократить число уравнений и неизвестных системы (8), (9) до значения $N = {{\tilde {N}} \mathord{\left/ {\vphantom {{\tilde {N}} 2}} \right. \kern-0em} 2}$.

Отметим, что по сравнению с [11] в данной работе не только учтено временное запаздывание взаимодействия между элементами диполя, но и получена система уравнений для вычисления токов на элементах, имеющая, как показали численные расчеты, лучшую сходимость.

Поляризуемость диполя определяется из отношения дипольного момента к напряженности внешнего поля:

Подставляя (3) в (10), учитывая, что $I(h) = 0$, и применяя интегрирование по частям, получим

где суммирование ведется по номерам элементов диполя, принадлежащих отрезку $(0,\;h)$ оси $x$.

2. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ ПОЛЯРИЗУЕМОСТИ ДИПОЛЕЙ И ЭЛЛИПСОИДОВ

Расчет поляризуемости ${{\alpha }}$ немагнитных цилиндрических диполей проводился по формуле (11). В целях сравнения проводился также расчет поляризуемости ${{{{\alpha }}}_{x}}$ вытянутого эллипсоида вращения по статической формуле [11]:

где ${{n}_{{{\kern 1pt} x}}}$ – коэффициент деполяризации (КД), ${v} = \frac{4}{3}{{\pi }}{{b}^{2}}a$ – объем эллипсоида, $a$, $b < a$ – полуоси, причем длинная полуось $a$ направлена вдоль оси $x$, параллельной внешнему полю. Диэлектрическая проницаемость ${{{{\varepsilon }}}_{2}}$ эллипсоида вычислялась по формуле [16]

Если отношение ${b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a}$ малой и большой полуосей эллипсоида много меньше единицы, то КД можно вычислять по приближенной формуле [17]:

Полагая объем ${v}$ эллипсоида равным объему диполя, а большую полуось равной полудлине диполя $h$, получим

Из (14), (15) находим КД эллипсоида, сопоставляемого диполю.

При численных расчетах поляризуемостей цилиндрического диполя и эллипсоида полагалось $r = 4$ мкм, ${{\sigma }} = 10\,000$ См, ${{{{\varepsilon }}}_{1}} = 1.8\;{{{{\varepsilon }}}_{0}}$. При таких значениях $r$ и ${{\sigma }}$ скин-эффект незначителен и сравнение квазистатической поляризуемости диполя со статической поляризуемостью сопоставляемого ему эллипсоида является корректным. Расчеты проводили для двух значений длины диполя, ${{l}_{{{\kern 1pt} 1}}} = 2{{h}_{{{\kern 1pt} 1}}} = 10$ мм (“длинные диполи”) и ${{l}_{{{\kern 1pt} 2}}} = 2{{h}_{{{\kern 1pt} 2}}} = 1.5$ мм (“короткие диполи”). Число разбиений полудлины диполя на элементы $N = 80$.

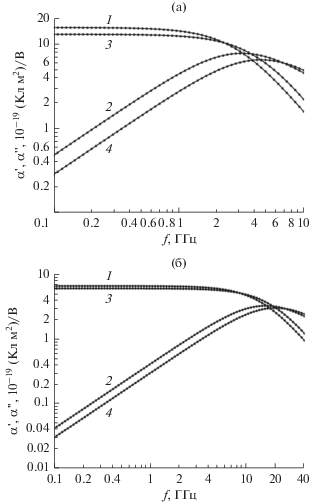
На рис. 2а приведены зависимости от частоты $f$ вещественной и мнимой компонент поляризуемости 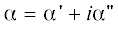диполя длиной ${{l}_{{{\kern 1pt} 1}}} = 10$ мм и компонент поляризуемости 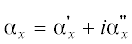аналогичного эллипсоида. На рис. 2б показаны такие же зависимости при ${{l}_{{{\kern 1pt} 2}}} = 1.5$ мм. Из рисунков видно, что замена цилиндрического диполя эллипсоидом в целях вычисления поляризуемости может приводить к значительной количественной ошибке.

Рис. 2.

Зависимость от частоты вещественной (1, 3) и мнимой (2, 4) частей поляризуемости диполей (1, 2) длиной 10 (а) и 1.5 мм (б) и поляризуемости сопоставимых эллипсоидов (3, 4).

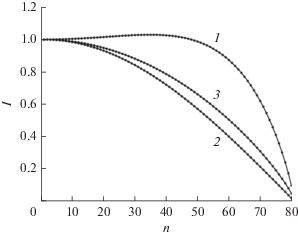
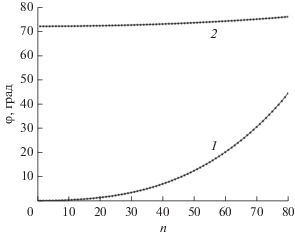
При расчете структур с диполями иногда используется предположение о синусоидальном распределении модуля тока вдоль длины диполя [18], при этом не учитывается изменение фазы тока вдоль диполя. На рис. 3 приведены зависимости распределения нормированного модуля тока на диполе при частоте поля 5 ГГц. По оси абсцисс откладывается номер элемента $n = 1 \ldots 80$, причем $n = 1$ соответствует первому от середины диполя элементу. Для сравнения приведен график синусоидального распределения модуля тока. Из рисунка видно, что распределение модуля тока вдоль диполя существенно отличается от синусоидального, причем для более длинных диполей это отличие значительнее, чем для коротких. На рис. 4 приведено распределение вдоль диполя отставания по фазе тока от внешнего поля, которое является более значительным для короткого диполя.

Рис. 3.

Зависимость распределения вдоль длины диполя нормированного модуля тока: диполь длиной 10 (1) и 1.5 мм (2) и синусоидальное распределение (3).

Рис. 4.

Зависимость распределения вдоль длины диполя отставания по фазе тока от внешнего поля на частоте: диполь длиной 10 (1) и 1.5 мм (2).

3. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ ЭДП КОМПОЗИТОВ НА ОСНОВЕ ДИПОЛЕЙ

Расчет ЭДП композита на основе цилиндрических диполей проводили по формуле Оделевского [8], используемой для анализа композитов с квазиэллипсоидальными включениями. Для случая, когда главная ось включений направлена вдоль среднего электрического поля в композите (ось $x$), формула имеет вид

где ${{{{\varepsilon }}}_{{{\kern 1pt} 1,\;2}}}$ – диэлектрические проницаемости соответственно матрицы и включений, ${{n}_{x}}$ – коэффициент деполяризации включений по оси $x$, p – объемная концентрация включений [8].

Из (12), (16) находим

Для различных вариантов ориентации вытянутых эллипсоидов вращения, поляризацией которых в поперечных по отношению к длинной оси направления можно пренебречь, в (17) следует сделать замену

где $K$ – фактор ориентации, $K = 1$ при ориентации длинных осей эллипсоидов вдоль поля, $K = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$ при хаотической ориентации включений в пространстве и $K = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ при хаотической ориентации в плоскости, параллельной среднему полю в композите [3].

Расчет ЭДП композита на основе хаотически ориентированных в плоскости цилиндрических диполей проводили путем подстановки в (17) на место ${{{{\alpha }}}_{x}}$ поляризуемости ${{\alpha }}$, вычисленной из (11). Полагалось $2h = 10$ мм, $r = 4$ мкм, σ = (10⁶/14) = $ = 71\,429$ См, ${{{{\varepsilon }}}_{1}} = 1.8\,{{{{\varepsilon }}}_{0}}$, $p = 0.05$%. Такие значения параметров соответствуют композиту на основе углеродных волокон, экспериментально исследованному в [3]. В целях сравнения был также проведен расчет ЭДП композита на основе эллипсоидов с длиной, объемом и проводимостью такими же, как у диполей. При расчетах ЭДП как композита с диполями, так и композита с эллипсоидами полагалось $\nu = {{\pi }}\,{{r}^{2}}(2h)$, а величину ${{n}_{z}}$ вычисляли по формулам (14), (15).

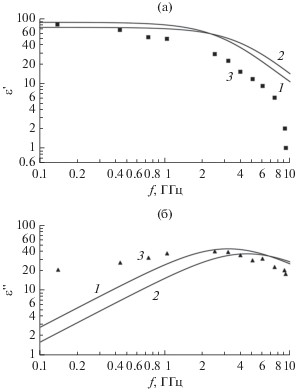
На рис. 5а, 5б изображены расчетные и экспериментальные частотные зависимости вещественной ${{\varepsilon }}{\kern 1pt} {\text{'}}$ и мнимой 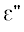компонент относительной эффективной диэлектрической проницаемости композитов с диполями и эллипсоидами. Из рисунков видно, что в целом значения ЭДП, вычисленные для композита с диполями, лучше соответствуют эксперименту. Существенно, что частота, на которой мнимая часть ЭДП максимальна, а также расчетные значения компонент ЭДП на этой частоте для композита с диполями более близки к экспериментальным значениям, чем расчетные значения ЭДП для композита с эллипсоидами.

Рис. 5.

Зависимость от частоты расчетных значений вещественной (а) и мнимой (б) компонент ЭДП композитов на основе диполей длиной 10 мм (1), сопоставимых эллипсоидов (2) и литературные экспериментальные данные (3).

Аналогичные расчеты, проведенные для композита с короткими диполями длиной ${{l}_{{{\kern 1pt} 2}}} = 1.5$ мм, $r = 4$ мкм, ${{\sigma }} = 10\,000$ См, ${{{{\varepsilon }}}_{1}} = 1.8\,{{{{\varepsilon }}}_{0}}$, $p = 0.0001$, показали близость значений компонент комплексной ЭДП при цилиндрических и эллипсоидальных включенияx, однако обе эти компоненты оказались более чем в два раза отличающимися в меньшую сторону от экспериментальных значений, приведенных в [3].

Отметим, что применение к расчету ЭДП теории эффективной среды Бруггемана [10] привело как для композита с диполями, так и для композита с эллипсоидами к значениям ЭДП, намного завышенным по сравнению с приведенными в [3] экспериментальными данными для диполей длиной 10 мм и мало отличающимися от расчетов по Оделевскому для диполей длиной 1.5 мм.

Полученное относительное соответствие эксперименту расчетов ЭДП по дипольной модели композита в случае длинных диполей и неудовлетворительное соответствие в случае коротких диполей можно объяснить следующим. Приближение усредненного поля, в котором находится каждый диполь, основано на предположении относительной изолированности диполей друг от друга и на отсутствии “цепочек” диполей, находящихся в контакте друг с другом. Однако по мере увеличения числа включений в единице объема в композите возникают кластеры, которые становятся аналогом более длинных диполей. Расчеты показывают, что даже небольшое увеличение длины диполей при неизменной объемной концентрации приводит к росту ЭДП, особенно мнимой компоненты. Очевидно, что при образовании в композите кластеров становится неадекватной сама модель композита как совокупности коротких диполей. Введение полуэмпирических поправок к формулам смешения не универсально в том отношении, что не для всех дипольных композитов позволяет получить сопоставимые с экспериментом результаты расчетов ЭДП [9, 19, 20]. Если все же идти по пути введения эмпирических параметров, то, по мнению авторов, таким подгоночным параметром могла бы стать эффективная длина диполей. Другой подход, более перспективный в плане достижения приемлемой точности моделирования – приведенный в [4–7] дифракционный расчет ЭДП ансамбля ориентированных и расположенных в композите по методу случайных чисел диполей. Такой композит можно рассматривать как квазипериодическую структуру с достаточно большим числом диполей разной ориентации и положения на периоде. В настоящее время непринципиальным, но существенным техническим препятствием для реализации дифракционного подхода является большое компьютерное время, требуемое для расчета ЭДП на одной частоте.

ЗАКЛЮЧЕНИЕ

Решена задача о поляризуемости тонкого цилиндрического резистивного диполя в квазистатическом электрическом поле при произвольной глубине проникновения поля в диполь и с учетом запаздывания времени зарядов на диполе. Для случая слабого скин-эффекта проведено сравнение поляризуемости диполя со статической поляризуемостью эллипсоида такой же длины, объема и проводимости. Показано, что поляризуемость эллипсоида значительно отличается от поляризуемости цилиндрического диполя. Показано, что распределение тока на диполе существенно отличается от синусоидального. Проведен расчет эффективной диэлектрической проницаемости композитов с диполями, хаотически ориентированными в плоскости, параллельной среднему электрическому полю в композите. Приведено сравнение результатов расчетов с литературными экспериментальными данными. Получено приближенное соответствие расчетных значений ЭДП экспериментальным данным для более длинных диполей и неудовлетворительное соответствие в случае коротких диполей. Проанализированы возможные причины такого несоответствия. Обсуждена возможность применения дифракционного подхода к расчету ЭДП композитов с хаотическим расположением и ориентацией диполей.