Радиотехника и электроника, 2021, T. 66, № 5, стр. 443-456
Класс оптимальных полиномиальных весовых функций для спектрального анализа сигналов
Г. В. Зайцев a, *, А. Д. Хзмалян a, **
a Научно-производственное объединение “Алмаз”
125190 Москва, Ленинградский просп., 80, корп. 16, Российская Федерация
* E-mail: gennady-zaytsev@yandex.ru
** E-mail: alkhzmalyan@gmail.com
Поступила в редакцию 30.09.2020
После доработки 26.12.2020
Принята к публикации 10.01.2021
Аннотация
Решена задача синтеза полиномиальных весовых функций малого порядка с произвольно заданной скоростью спада лепестков спектра, оптимальных по критерию минимума максимального бокового лепестка на заданном отрезке частотной оси. Разработан метод синтеза оптимальных функций с верификацией найденного решения. Синтезированы весовые функции порядков 1…12 со скоростью спада лепестков 6, 12, 18, 24 и 30 дБ/окт и представлены таблицы их параметров. Проанализированы характеристики полученных функций и проведено их сравнение с известными. Получен простой алгоритм вычисления синтезированных функций.
ВВЕДЕНИЕ
Цифровой спектральный анализ сигналов является одним из наиболее часто используемых методов обработки сигналов. При цифровой обработке спектр сигнала определяется как его дискретное преобразование Фурье (ДПФ) и вычисляется с помощью алгоритмов быстрого преобразования Фурье. Перед вычислением спектра анализируемый сигнал, как правило, умножается на действительную функцию, называемую весовой, или просто окном. Весовая функция служит для уменьшения влияния эффекта размывания спектральных линий и для снижения уровня паразитных боковых лепестков спектра, обусловленных конечностью интервала наблюдения сигнала. Обзор классических весовых функций можно найти в [1].
Требования к весовой функции зависят от решаемой задачи. В различных приложениях могут доминировать требования обеспечения малого среднеквадратичного уровня боковых лепестков спектра, высокой скорости спада лепестков, максимально плоской вершины главного лепестка и другие.
Требования, рассматриваемые в данной работе, вытекают из следующего радиолокационного приложения. Одним из классических классов радиолокационных зондирующих сигналов является квазинепрерывный сигнал, или пачка когерентных импульсов. Обработка сигналов этого типа фактически сводится к спектральному анализу принимаемого сигнала. Далее амплитуды компонент спектра сравниваются с порогом. Каждая компонента, превзошедшая порог, (например, боковой лепесток значительного уровня) может являться отметкой полезного сигнала от некоторого отражающего объекта и требует подробного анализа. Для того, чтобы не вызывать ложных тревог, боковые лепестки мощных мешающих отражений от подстилающей поверхности и гидрометеоров не должны превосходить уровня минимального сигнала. В типичных радиолокационных задачах это условие приводит к необходимости снижения амплитуды боковых лепестков до уровня минус 100…140 дБ относительно главного лепестка. Поэтому естественным требованием к весовым функциям для данного приложения является сведение к минимуму уровня максимального бокового лепестка. Для еще большего снижения уровня дальних боковых лепестков оказывается полезным обеспечить высокую скорость спада лепестков.
Второе требование обусловлено все более широким использованием адаптивных технологий в современных многофункциональных радиолокаторах. При адаптивном использовании квазинепрерывных сигналов их параметры (длительность зондирования, скважность, частота повторения и т.д.) устанавливаются индивидуально для каждого зондирования в соответствии с быстроменяющейся обстановкой. В этом случае число излучаемых и обрабатываемых импульсов заранее не известно и может принимать значения от нескольких десятков до нескольких тысяч. Количество отсчетов в используемой весовой функции также должно меняться в широких пределах. Кроме того, для каждого числа отсчетов желательно иметь несколько весовых функций с различными уровнями боковых лепестков.
Очевидно, имеется два пути обеспечения работы с большим количеством весовых функций: либо хранить отсчеты многочисленных весовых функций в памяти устройства обработки сигналов, либо использовать весовые функции с простым алгоритмом вычисления для обеспечения работы в реальном масштабе времени. Первый вариант неэффективен, так как требует весьма значительных объемов памяти. Для второго варианта необходимо иметь весовые функции, обеспечивающие простое вычисление.
Таким образом, для радиолокационных задач необходимо синтезировать весовые функции, обеспечивающие минимум максимального лепестка и имеющие простой способ вычисления. Указанные требования являются классическими и используются также во многих других приложениях, причем в измерительных системах необходимый уровень боковых лепестков может быть значительно ниже указанного.
Известные по литературе функции, удовлетворяющие этим требованиям имеют вид начального отрезка ряда Фурье с небольшим количеством членов, что обеспечивает простоту вычислений. Малое количество членов ряда позволяет, тем не менее, получить высокие характеристики, поэтому такие функции наиболее востребованы в приложениях. Возможные значения асимптотической (с ростом частоты) скорости спада лепестков для таких функций ограничены набором чисел 6(2k + 1), k = 0, 1, …. Таковыми функциями являются функции Хемминга [1] (одна функция), Блекмана–Хэрриса [1] (одна функция), Наттелла [2] (три функции). В работах Албрехта [3] и независимо Зайцева [4, 5] разработаны методы синтеза континуального семейства оптимальных по минимаксному критерию функций указанного вида с различным уровнем подавления боковых лепестков и табулированы их параметры.
Наиболее широкое семейство оптимальных функций, удовлетворяющих сформулированным выше требованиям, получено в работах авторов [6–10], где описан метод синтеза и приведены таблицы параметров большого количества оптимальных весовых функций, представимых в виде линейной комбинации малого числа членов, каждый из которых является степенью одной и той же косинусоидальной функции. Разработанный метод позволяет синтезировать оптимальную функцию по следующему набору параметров: число членов ряда, ширина главного лепестка спектра и асимптотическая скорость спада его лепестков V ≥ 6 дБ/окт. Заметим, что в литературе, кроме указанных работ, авторам не известно описания функций со скоростью спада, некратной 6 дБ/окт.
Простейший способ вычисления имеют, очевидно, функции в виде полинома, однако в литературе подобные функции с перечисленными свойствами не описаны. Получено лишь незначительное количество функций [11, 12] с узким диапазоном параметров, не перекрывающим указанный выше динамический диапазон. Кроме того, эти функции не являются оптимальными по описанному выше критерию.
В настоящей работе предложено семейство полиномиальных весовых функций, имеющих минимальный уровень максимального бокового лепестка и произвольную асимптотическую скорость спада V ≥ 6 дБ/окт. Функции имеют вид линейной комбинации степеней одного и того же полинома второго порядка, характеризуются малой вычислительной сложностью и конструируются путем численного решения минимаксной задачи оптимизации. Приведены параметры репрезентативного множества синтезированных функций.
1. ПРЕДСТАВЛЕНИЕ ОКНА И БАЗИСНЫЕ ФУНКЦИИ
Весовая функция w(t), используемая при гармоническом анализе непрерывного сигнала на интервале наблюдения –T/2≤ t ≤ T/2 длительностью T, является финитной четной положительной непрерывной функцией времени (кроме, возможно, краев интервала): w(t) = 0 при |t| > T/2.
Спектр Wc(f) весовой функции w(t) определяется интегральным преобразованием Фурье:
(1)
${{W}_{{\text{c}}}}(f) = \int\limits_{{{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2}}^{{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2}} {w(t)\exp ( - j2\pi tf)\,} dt,\,\,\,\, - \infty < f < \infty .$При цифровой обработке сигналов окно представлено N временными отсчетами, взятыми с шагом δ на интервале наблюдения сигнала T = Nδ. Расположим начало координат в центре между крайними отсчетами. Тогда моменты выборок равны tq = – 0.5 (T – δ) + qδ, q = 0, 1, …, N – 1. Дискретную весовую функцию w(tq) будем рассматривать как отсчеты непрерывной функции w(t) в точках tq. Спектр дискретного окна определяется формулой дискретного по времени преобразования Фурье [13]
(2)
$W(f) = \sum\limits_{q = 0}^{N - 1} {w({{t}_{q}})} \exp ( - j2\pi {{t}_{q}}f),\,\,\,f \in [{{ - 1} \mathord{\left/ {\vphantom {{ - 1} {2\delta }}} \right. \kern-0em} {2\delta }},{1 \mathord{\left/ {\vphantom {1 {2\delta }}} \right. \kern-0em} {2\delta }}].$Спектр (2) периодичен по частоте f с периодом 1/δ, и его достаточно анализировать на периоде f ∈[–0.5/δ, 0.5/δ]. При выборе достаточно малого шага δ спектры (1) и (2) различаются незначительно [13].
Ниже решается задача синтеза весовых функций и приводятся таблицы их параметров для случая цифровой обработки. Один из этих параметров, а именно, асимптотическая (при f → ∞) скорость V спада боковых лепестков спектра, относится, строго говоря, к соответствующей непрерывной функции w(t), определяется как величина снижения огибающей модуля спектра Wc ( f ) при увеличении частоты вдвое и измеряется в децибелах на октаву. Тем не менее, этот параметр оказывается полезен для описания и дискретной весовой функции, когда число выборок N велико, а частота не приближается к половине периода 1/2δ. Для краткости слово “асимптотическая” в дальнейшем опускается.
Рассматриваемые в данной работе весовые функции имеют вид линейной комбинации небольшого числа m + 1 базисных функций ψ(pk, t):
(3)
$w(t) = \sum\limits_{k = 0}^m {{{b}_{k}}} \psi ({{p}_{k}},t),\,\,\,\,{{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2} \leqslant t \leqslant {T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2},$где b0, b1, …, bm – коэффициенты, а pk – параметр, определяющий форму k-той базисной функции.
Базисные функции, предлагаемые в настоящей работе, имеют следующий вид:
(4)
$\psi (p,t) = {{[1 - {{({{2t} \mathord{\left/ {\vphantom {{2t} T}} \right. \kern-0em} T})}^{2}}]}^{p}},\,\,\,\,{{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2} \leqslant t \leqslant {T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2},$где p ≥ 0 – неотрицательное действительное число.
Рассмотрим свойства спектра (1) функции (4). Так как функция (4) действительна и четна, то экспоненту в (1) можно заменить косинусом:
(5)
$\begin{gathered} {{\Psi }_{{\text{c}}}}(p,f) = \int\limits_{ - T/2}^{T/2} {{{{[1 - {{{({{2t} \mathord{\left/ {\vphantom {{2t} T}} \right. \kern-0em} T})}}^{2}}]}}^{p}}\cos (2\pi tf)} \,dt, \\ - \infty < f < \infty . \\ \end{gathered} $Спектр (5) симметричен по частоте относительно начала координат, поэтому ниже без ограничения общности полагаем, что частота положительна: f ≥ 0 .
Интеграл (5) согласно [14, п. 3.387.2], при p > –1 равен
(6)
${{\Psi }_{{\text{c}}}}(p,f) = \frac{{\sqrt \pi T}}{2}{{\left( {\frac{2}{{\pi fT}}} \right)}^{{p + 0.5}}}\Gamma (p + 1){{J}_{{p + 0.5}}}(\pi fT),$где Г(∙) – гамма-функция, J(∙) – функция Бесселя.
При больших значениях аргумента функция Бесселя аппроксимируется формулой [14, п. 8.451.1]
(7)
${{J}_{{p + 0.5}}}(x) \approx \sqrt {\frac{{\text{2}}}{{\pi x}}} \cos (x - p\frac{\pi }{2} - \frac{\pi }{2}) + O({{x}^{{ - 1.5}}}).$Поэтому при f → ∞ спектр (6) базисной функции имеет асимптотическое выражение
Отсюда следует, что при f → ∞ спектр (6) имеет асимптотическую оценку O(f–(p+1)). Следовательно, огибающая боковых лепестков спектра базисной функции (4) спадает со скоростью V = 6(p + + 1) дБ/окт. Выбирая степень p в соответствии с соотношением p = V/6 – 1 можно получить произвольно заданное значение скорости спада V ≥ 6 дБ/окт. Насколько известно авторам, весовые функции со скоростью спада лепестков, некратной 6 дБ/окт, в литературе не описаны.
Нули спектра (6) совпадают с нулями функции Бесселя Jp + 0.5 (πfT). При нумерации нулей от 1 асимптотическое положение нуля fzn с большим номером n следует из (7):
(8)
${{f}_{{{\text{z}}n}}} \approx {{(0.5p + n)} \mathord{\left/ {\vphantom {{(0.5p + n)} T}} \right. \kern-0em} T}.$Весовая функция (3) содержит (m + 1) базисных функций вида (4). Для получения низких боковых лепестков в ее спектре лепестки одной базисной функции должны компенсироваться лепестками другой. Для хорошей компенсации целесообразно сделать так, чтобы нули спектров последовательных базисных функций совпадали, а их боковые лепестки были противофазны. Из (8) следует, что асимптотически это достигается, если разности степеней p0, p1, …, pm базисных функций, используемых в (3), равны целым четным числам. Это условие удовлетворяется при выборе степеней в соответствии с соотношением pk = μ + 2k, k = 0, 1, …, m, где μ – неотрицательное действительное число. При этом весовая функция (3) приобретает вид
(9)
$\begin{gathered} w(t) = {{[1 - {{({{2t} \mathord{\left/ {\vphantom {{2t} T}} \right. \kern-0em} T})}^{2}}]}^{{\,\mu }}}\sum\limits_{k = 0}^m {{{b}_{k}}} {{[1 - {{({{2t} \mathord{\left/ {\vphantom {{2t} T}} \right. \kern-0em} T})}^{2}}]}^{{2k}}}, \\ {{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2} \leqslant t \leqslant {T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2}. \\ \end{gathered} $Величину m будем называть порядком весовой функции. Будем также считать, что общий множитель в этой формуле вынесен за знак суммы, т.е. b0 ≠ 0. Тогда скорость спада боковых лепестков спектра функции (9) определяется параметром μ и составляет V = 6(μ + 1) дБ/окт.
Степень μ множителя перед суммой в (9) определяет порядок нуля функции на краях ее области определения и скорость убывания лепестков спектра V = 6(μ + 1) дБ/окт, а коэффициенты суммы подбираются ниже так, чтобы уровень максимального лепестка спектра окна был наименьшим.
Сумму в (9) можно рассматривать как полином с четными степенями относительно переменной x = 1 – (2t/T)2. Вычисление функции вида (9) требует малого объема вычислений, поскольку число членов в сумме (9) мало, выражение в квадратных скобках одинаково для всех членов, а сумма может быть вычислена по схеме Горнера.
Для целых µ выражение (9) можно записать в традиционной форме в виде полинома относительно переменной (2t/T)2. Однако приведенная форма более наглядна и имеет ряд описанных ниже преимуществ.
Рассмотренные свойства спектра непрерывных весовых функций, в основном, сохраняются и для дискретного случая.
2. МИНИМАКСНАЯ ЗАДАЧА
Рассмотрим метод решения задачи синтеза весовых функций для дискретного случая. Для решения необходимо надлежащим образом выбрать неизвестные коэффициенты функции (9). Объединим эти коэффициенты в вектор b = (b0, b1, …, bm) и включим его в явном виде в список аргументов весовой функции (9) и ее дискретного спектра (2): w(b, t) = w(t) и W(b, t) = W(t).
Подставив выражение для весовой функции (9) в формулу (2) для спектра, получаем
(10)
$W({\mathbf{b}},f) = \sum\limits_{k = 0}^m {{{b}_{k}}} \Psi (\mu + 2k,f),\,\,\,f \in [{{ - 1} \mathord{\left/ {\vphantom {{ - 1} {2\delta }}} \right. \kern-0em} {2\delta }},{\text{ }}{1 \mathord{\left/ {\vphantom {1 {2\delta }}} \right. \kern-0em} {2\delta }}],$где Ψ(μ + 2k, f ) – дискретный спектр базисной функции ψ(pk = μ + 2k, t).
Пусть Wmax > 0 – максимальное значение модуля спектра (10). Определим функцию качества φ(b) как максимальное значение нормированного модуля спектра |W (b, f)/Wmax| вне заданной области частот [–β/T, β/T], где β/T в настоящей работе определяет максимально допустимую полуширину главного лепестка по уровню максимального бокового лепестка:
(11)
$\varphi ({\mathbf{b}}) = \mathop {\max }\limits_{\beta /T \leqslant |f| \leqslant N/2T} \left| {{{W({\mathbf{b}},f)} \mathord{\left/ {\vphantom {{W({\mathbf{b}},f)} {{{W}_{{\max }}}}}} \right. \kern-0em} {{{W}_{{\max }}}}}} \right|.$Величина 1/T называется бином [1], при этом полоса β/T составляет β бин.
Построение оптимальной весовой функции заключается в отыскании вектора коэффициентов b, доставляющего минимум ρ целевой функции φ(b):
где правая часть означает аргумент b функции φ(b), при котором достигается минимум.
В работах авторов [6–10] разработан метод решения подобной задачи для случая тригонометрических базисных функций. Этот метод пригоден фактически без изменений и для рассматриваемых в данной работе базисных функций (4). В связи с этим ограничимся здесь только кратким перечислением основных этапов метода. Подробное описание может быть найдено в [8, 10].
1. Преобразование задачи к линейному виду.
Рассмотрим свойства функции вида (9). Во-первых, максимум дискретного спектра (2) достигается при f = 0. Действительно, в выражении (2) для спектра суммируются неотрицательные числа w(b,tp) с весом cos(2πtpf). Очевидно, максимум достигается, если все веса равны единице, что реализуется только при f = 0.
Во-вторых, умножение всех коэффициентов b0, b1, …, bm на фиксированный множитель не изменяет функцию качества (11). Для обеспечения единственности решения зафиксируем максимальное значение спектра Wmax = W(b, 0) =1.
Подстановка в это условие спектра (10) приводит к линейному соотношению между коэффициентами, с помощью которого один из коэффициентов может быть выражен через другие. В результате размерность задачи уменьшается на единицу, знаменатель дроби в функции качества (11) становится равным единице, а нормированный спектр весовой функции приобретает линейную форму относительно коэффициентов. При таком преобразовании задача приводится к виду, стандартному для общей теории линейных чебышевских приближений [15], где, в частности, показано, что решение задачи существует и единственно.
2. Анализ функции качества.
Используемый подход к решению поставленной задачи состоит в непосредственной минимизации функции качества с помощью численных методов. Для построения эффективного численного алгоритма поиска экстремума необходимо прежде всего знать характер поведения оптимизируемой функции.
Нетрудно показать, что функция качества является выпуклой. Однако оптимизируемая функция имеет довольно сложное поведение. Анализ показывает, что, с одной стороны, она имеет регулярные области, в которых превалирует один из лепестков, а функция дифференцируема. С другой стороны, на линиях (областях) соприкосновения этих областей функция является недифференцируемой. В результате рельеф функции качества имеет вид системы оврагов, на пологом дне которых, где и расположен минимум, она недифференцируема.
3. Выбор алгоритма оптимизации.
Сложное поведение функции делает неэффективным непосредственное применение традиционных численных методов минимизации с использованием производных. Алгоритмы, используемые авторами описаны в работах [4, 8]. Возможно использование и других алгоритмов минимизации выпуклых функций [16].
4. Верификация полученного решения.
Так как используемые алгоритмы поиска оптимума являются численными, то необходимо проверить, насколько полученный результат близок к точному решению. Авторами разработан метод такой проверки [8, 10] на основе использования нижней границы минимума, полученной в [15]. Метод дает возможность получить оценку близости полученного решения к оптимальному.
3. КАТАЛОГ СИНТЕЗИРОВАННЫХ ОПТИМАЛЬНЫХ ВЕСОВЫХ ФУНКЦИЙ
Приведем параметры нескольких подклассов весовых функций с различными скоростями спада лепестков, синтезированных по описанной методике. Эти параметры (табл. 1–5) являются наиболее полезными результатами работы, так как для использования весовой функции необходимы только ее коэффициенты. Для сокращения объема таблиц приняты во внимание следующие обстоятельства.
Таблица 1.
Параметры полиномиальных весовых функций со скоростью спада 6 дБ/окт (µ = 0)*
| m | β, бин | P, дБ | b0, b1, …, bm | Пw, дБ | Пs, дБ | Ln, бин | L3, бин | L6, бин |
|---|---|---|---|---|---|---|---|---|
| 2 | 2.0 | –45.7 | 0.095; 1.0; 0.427 | 1.439 | 1.678 | 1.393 | 1.331 | 1.855 |
| 2.25 | –50.4 | 0.0742; 1.0; 0.8973 | 1.701 | 1.495 | 1.479 | 1.410 | 1.970 | |
| 3 | 2.5 | –59.8 | 0.0384; 1.0; 0.9243; 0.2766 | 1.935 | 1.345 | 1.561 | 1.487 | 2.079 |
| 2.75 | –66.4 | 0.01895; 0.69307; 1.0; 0.38542 | 2.148 | 1.223 | 1.640 | 1.560 | 2.183 | |
| 3.0 | –71.7 | 0.01115; 0.52103; 1.0; 0.57788 | 2.326 | 1.130 | 1.708 | 1.623 | 2.273 | |
| 4 | 3.25 | –79.5 | 0.00483; 0.31740; 1.0; 0.56768; 0.11468 | 2.526 | 1.033 | 1.789 | 1.698 | 2.380 |
| 3.5 | –84.7 | 0.00295; 0.22372; 1.0; 0.72433; 0.23953 | 2.698 | 0.956 | 1.861 | 1.765 | 2.477 | |
| 5 | 3.75 | –93.5 | 0.00148; 0.17320; 0.97017; 1.0; 0.29386; 0.04929 | 2.841 | 0.896 | 1.924 | 1.823 | 2.559 |
| 4.0 | –100.6 | 0.000676; 0.103522; 0.750973; 1.0; 0.381826; 0.081473 | 2.982 | 0.841 | 1.987 | 1.882 | 2.643 | |
| 4.25 | –106.6 | 0.000347; 0.064448; 0.576081; 1.0; 0.464813; 0.140552 | 3.114 | 0.793 | 2.048 | 1.939 | 2.725 | |
| 6 | 4.5 | –114.1 | 0.000170; 0.040382; 0.474993; 1.0; 0.664795; 0.159204; 0.027500 | 3.242 | 0.748 | 2.110 | 1.996 | 2.806 |
| 4.75 | –120.7 | 0.000091; 0.026531; 0.383983; 1.0; 0.829658; 0.241908; 0.054658 | 3.359 | 0.710 | 2.167 | 2.050 | 2.883 | |
| 7 | 5.0 | –128.2 | 0.0000469; 0.0173759; 0.3113997; 0.9990288; 1.0; 0.3833289; 0.0785324; 0.0076694 | 3.470 | 0.675 | 2.224 | 2.103 | 2.957 |
| 5.25 | –134.8 | 0.00002207; 0.00981587; 0.21152213; 0.82890561; 1.0; 0.48266727; 0.10740373; 0.01719763 | 3.578 | 0.643 | 2.279 | 2.155 | 3.031 | |
| 5.5 | –140.5 | 0.00001174; 0.00585013; 0.14575848; 0.69175141; 1.0; 0.60627352; 0.14893262; 0.03482239 | 3.683 | 0.613 | 2.335 | 2.207 | 3.105 | |
| 8 | 5.75 | –148.6 | 0.00000513; 0.00328502; 0.10184408; 0.57399594; 1.0; 0.68350736; 0.23987571; 0.03398988; 0.00653009 | 3.776 | 0.588 | 2.386 | 2.254 | 3.172 |
| 6.0 | –155.4 | 0.00000263; 0.00197985; 0.07240244; 0.48439137; 1.0; 0.81527992; 0.33479040; 0.05952100; 0.01224513 | 3.870 | 0.563 | 2.438 | 2.303 | 3.241 | |
| 6.25 | –161.9 | 0.000001415; 0.001238273; 0.052675095; 0.411433597; 1.0; 0.955856095; 0.468068430; 0.094738312; 0.024332087 | 3.959 | 0.541 | 2.488 | 2.350 | 3.308 | |
| 9 | 6.5 | –168.6 | 0.000000678; 0.000680722; 0.033608366; 0.309246799; 0.878212626; 1.0; 0.548201448; 0.157806443; 0.026739586; 0.003527911 | 4.046 | 0.520 | 2.539 | 2.397 | 3.376 |
| 6.75 | –174.7 | 0.00000034; 0.000382524; 0.021434966; 0.227660589; 0.75017776; 1.0; 0.632740839; 0.221205203; 0.038418494; 0.007594668 | 4.130 | 0.501 | 2.588 | 2.443 | 3.441 | |
| 10 | 7.0 | –182.5 | 0.0000001522; 0.0002065851; 0.0137815629; 0.1709118246; 0.6530938516; 1.0; 0.7386957119; 0.2809608439; 0.0716450379; 0.0063648213; 0.0016217902 | 4.208 | 0.483 | 2.635 | 2.487 | 3.504 |
| 7.25 | –189.3 | 0.0000000755; 0.0001168100; 0.0089367294; 0.1281153487; 0.5646583426; 1.0; 0.8464013164; 0.3787999234; 0.1038637653; 0.0141238247; 0.0026397550 | 4.286 | 0.467 | 2.683 | 2.532 | 3.567 | |
| 7.5 | –195.9 | 0.0000000394; 0.0000693885; 0.0060289813; 0.0981684381; 0.4941890295; 1.0; 0.9723317294; 0.4949534635; 0.1590424741; 0.0231381477; 0.0054991227 | 4.360 | 0.451 | 2.729 | 2.575 | 3.628 | |
| 11 | 7.75 | –202.8 | 0.00000001838; 0.00003657936; 0.00362035152; 0.06773013302; 0.39023443821; 0.90564171899; 1.0; 0.59295858025; 0.20233440616; 0.04501869577; 0.00527819499; 0.00086646539 | 4.433 | 0.437 | 2.775 | 2.618 | 3.689 |
| 8.0 | –209.4 | 0.00000000880; 0.00001967995; 0.00219268591; 0.04634047882; 0.30255759657; 0.79728155622; 1.0; 0.67495415356; 0.26065108795; 0.06701446275; 0.00841847547; 0.00173040752 | 4.502 | 0.423 | 2.820 | 2.660 | 3.749 | |
| 12 | 8.25 | –216.7 | 0.000000004034; 0.000010420577; 0.001332987440; 0.032064607499; 0.237130555420; 0.705778708358; 1.0; 0.759173060238; 0.334912856497; 0.092170683972; 0.016657018256; 0.001859326632; 0.000245531471 | 4.568 | 0.410 | 2.863 | 2.700 | 3.806 |
| 8.5 | –223.5 | 0.000000001974; 0.000005749733; 0.000828393854; 0.022426500547; 0.186786703293; 0.626193631544; 1.0; 0.854875107199; 0.426019786774; 0.131070973971; 0.027430958661; 0.003154651581; 0.000542118570 | 4.633 | 0.398 | 2.906 | 2.741 | 3.863 | |
| 8.75 | –229.9 | 0.000000001035; 0.000003334224; 0.000531793439; 0.015985489104; 0.148575591447; 0.557730344514; 1.0; 0.960030621003; 0.539381054683; 0.185204200350; 0.044742831434; 0.005318497322; 0.001164789755 | 4.697 | 0.387 | 2.949 | 2.781 | 3.920 |
* Примечание. В табл. 2–5 приведены следующие общепринятые параметры весовых функций [1]: P – уровень максимального бокового лепестка относительно главного лепестка, Πw – потери в отношении сигнал/шум, вызванные использованием весовой функции, Πs – потери за счет рельефа спектра; Ln – эквивалентная шумовая полоса, L3 и L6 – ширина главного лепестка по уровням –3 и –6 дБ соответственно.
Таблица 2.
Параметры синтезированных весовых функций со скоростью спада 12 дБ/окт (µ = 1)
| m | β, бин | P, дБ | b0, b1, …, bm | Пw, дБ | Пs, дБ | Ln, бин | L3, бин | L6, бин |
|---|---|---|---|---|---|---|---|---|
| 2 | 2.0 | –42.5 | 0.516; 1.0; 0.207 | 1.590 | 1.556 | 1.442 | 1.381 | 1.922 |
| 2.25 | –50.1 | 0.318; 1.0; 0.312 | 1.814 | 1.412 | 1.518 | 1.450 | 2.023 | |
| 2.5 | –56.2 | 0.219; 1.0; 0.545 | 2.030 | 1.284 | 1.596 | 1.521 | 2.125 | |
| 3 | 2.75 | –64.6 | 0.1359; 1.0; 0.5720; 0.1355 | 2.218 | 1.181 | 1.667 | 1.586 | 2.219 |
| 3.0 | –71.7 | 0.0970; 1.0; 0.8329; 0.2614 | 2.397 | 1.091 | 1.737 | 1.651 | 2.312 | |
| 3.25 | –77.4 | 0.0634; 0.8717; 1.0; 0.4407 | 2.563 | 1.014 | 1.804 | 1.713 | 2.401 | |
| 4 | 3.5 | –85.4 | 0.03218; 0.59494; 1.0; 0.45367; 0.06304 | 2.724 | 0.943 | 1.872 | 1.776 | 2.491 |
| 3.75 | –91.5 | 0.01842; 0.42513; 1.0; 0.53917; 0.13524 | 2.875 | 0.882 | 1.939 | 1.838 | 2.579 | |
| 4.0 | –94.8 | 0.01300; 0.32389; 1.0; 0.65109; 0.25163 | 3.008 | 0.831 | 1.999 | 1.894 | 2.659 | |
| 5 | 4.25 | –105.9 | 0.00680; 0.26360; 1.0; 0.95626; 0.27534; 0.05895 | 3.140 | 0.783 | 2.061 | 1.951 | 2.741 |
| 4.5 | –113.0 | 0.003565; 0.174412; 0.831523; 1.0; 0.361866; 0.097155 | 3.263 | 0.741 | 2.120 | 2.006 | 2.819 | |
| 6 | 4.75 | –119.5 | 0.001917; 0.113142; 0.685329; 1.0; 0.506291; 0.114487; 0.014629 | 3.382 | 0.702 | 2.179 | 2.061 | 2.898 |
| 5.0 | –125.7 | 0.0010765; 0.0748166; 0.5590991; 1.0; 0.6426656; 0.1646643; 0.0320827 | 3.496 | 0.667 | 2.236 | 2.115 | 2.974 | |
| 5.25 | 130.5 | 0.0006807; 0.0521163; 0.4619642; 1.0; 0.8054322; 0.2398959; 0.0646287 | 3.603 | 0.636 | 2.293 | 2.167 | 3.049 | |
| 7 | 5.5 | –140.3 | 0.00033195; 0.03497909; 0.38149417; 1.0; 0.91409872; 0.37855700; 0.06789784; 0.01205827 | 3.698 | 0.609 | 2.343 | 2.214 | 3.116 |
| 5.75 | –147.2 | 0.00017816; 0.02241127; 0.29210377; 0.91546726; 1.0; 0.49504887; 0.10617965; 0.02244833 | 3.794 | 0.583 | 2.395 | 2.263 | 3.185 | |
| 6.0 | –151.8 | 0.00010783; 0.01464619; 0.21268202; 0.78135452; 1.0; 0.60839097; 0.14456900; 0.04157587 | 3.884 | 0.560 | 2.446 | 2.310 | 3.252 | |
| 8 | 6.25 | –161.0 | 0.00004617; 0.00805049; 0.14785137; 0.64640001; 1.0; 0.66514345; 0.23596788; 0.03781758; 0.00724027 | 3.975 | 0.537 | 2.497 | 2.358 | 3.320 |
| 6.5 | –167.4 | 0.00002534; 0.00505763; 0.10784897; 0.55087818; 1.0; 0.77809008; 0.32682169; 0.05959198; 0.01410680 | 4.060 | 0.517 | 2.547 | 2.405 | 3.386 | |
| 9 | 6.75 | –175.0 | 0.000013515; 0.003229528; 0.080344403; 0.477427401; 1.0; 0.912234837; 0.424832238; 0.108387663; 0.016651361; 0.002124547 | 4.140 | 0.499 | 2.594 | 2.449 | 3.449 |
| 7.0 | –181.4 | 0.000007359; 0.001991156; 0.056549480; 0.388399592; 0.940639250; 1.0; 0.533303070; 0.164672879; 0.025597772; 0.004849281 | 4.219 | 0.481 | 2.642 | 2.494 | 3.512 | |
| 7.25 | –186.5 | 0.000004163; 0.001208295; 0.037694885; 0.292615103; 0.811239080; 1.0; 0.612482923; 0.225688474; 0.037363887; 0.009391520 | 4.297 | 0.464 | 2.690 | 2.538 | 3.576 | |
| 10 | 7.5 | –195.5 | 0.0000018319; 0.0006607326; 0.0248751826; 0.2249453461; 0.7179349680; 1.0; 0.7108635418; 0.2738804505; 0.0704535510; 0.0077535201; 0.0016720097 | 4.368 | 0.450 | 2.734 | 2.580 | 3.634 |
| 7.75 | –202.4 | 0.0000009485; 0.0003898360; 0.0167387574; 0.1727791654; 0.6290545525; 1.0; 0.8097735147; 0.3571742270; 0.1035240461; 0.0135763947; 0.0031226602 | 4.439 | 0.435 | 2.779 | 2.622 | 3.694 | |
| 8.0 | –207.3 | 0.0000005935; 0.0002607926; 0.0121030442; 0.1371978180; 0.5582094044; 1.0; 0.9227202888; 0.4600840111; 0.1557943532; 0.0217814763; 0.0063006347 | 4.506 | 0.422 | 2.822 | 2.662 | 3.752 | |
| 11 | 8.25 | –215.6 | 0.0000002719; 0.0001400824; 0.0076118832; 0.1005577745; 0.4699912563; 0.9638116049; 1.0; 0.5793340009; 0.2015876399; 0.0458148157; 0.0059085136; 0.0010071402 | 4.576 | 0.409 | 2.868 | 2.705 | 3.812 |
| 8.5 | –221.4 | 0.00000014317; 0.00007941814; 0.00473003302; 0.06976493783; 0.36705331558; 0.85225527319; 1.0; 0.66071218639; 0.25613794733; 0.06953009707; 0.00860778211; 0.00210925750 | 4.643 | 0.397 | 2.913 | 2.747 | 3.872 | |
| 12 | 8.75 | –229.5 | 0.000000065723; 0.000042765860; 0.002944151606; 0.049370127738; 0.292664381262; 0.760804276706; 1.0; 0.732807755910; 0.325093839174; 0.089762721757; 0.018145937839; 0.001726336100; 0.000342711805 | 4.704 | 0.386 | 2.954 | 2.785 | 3.926 |
| 9.0 | –236.4 | 0.000000033348; 0.000024335558; 0.001877499421; 0.035241758194; 0.233775993514; 0.6799252914590001; 1.0; 0.819763650042; 0.407150770024; 0.125581858957; 0.028540385974; 0.002995159902; 0.000677694494 | 4.765 | 0.375 | 2.995 | 2.824 | 3.982 |
Таблица 3.
Параметры синтезированных весовых функций со скоростью спада 18 дБ/окт (µ = 2)
| m | β, бин | P, дБ | b0, b1, …, bm | Пw, дБ | Пs, дБ | Ln, бин | L3, бин | L6, бин |
|---|---|---|---|---|---|---|---|---|
| 1 | 2.25 | –40.5 | 0.577; 1.0 | 2.107 | 1.228 | 1.624 | 1.553 | 2.165 |
| 2 | 2.5 | –51.8 | 0.698; 1.0; 0.312 | 2.190 | 1.189 | 1.656 | 1.579 | 2.205 |
| 2.75 | –59.6 | 0.462; 1.0; 0.431 | 2.354 | 1.107 | 1.720 | 1.638 | 2.289 | |
| 3.0 | –65.0 | 0.3495; 1.0; 0.7042 | 2.518 | 1.031 | 1.786 | 1.698 | 2.377 | |
| 3 | 3.25 | –74.0 | 0.2000; 1.0; 0.6132; 0.1581 | 2.675 | 0.961 | 1.851 | 1.759 | 2.464 |
| 3.5 | –80.3 | 0.1335; 1.0; 0.8109; 0.3127 | 2.834 | 0.895 | 1.920 | 1.823 | 2.556 | |
| 4 | 3.75 | –89.2 | 0.10331; 0.87474; 1.0; 0.35687; 0.04786 | 2.943 | 0.854 | 1.969 | 1.867 | 2.620 |
| 4.0 | –96.2 | 0.06085; 0.65644; 1.0; 0.43268; 0.09070 | 3.072 | 0.806 | 2.029 | 1.922 | 2.699 | |
| 4.25 | –102.0 | 0.03726; 0.48524; 1.0; 0.50830; 0.16488 | 3.199 | 0.761 | 2.089 | 1.978 | 2.779 | |
| 5 | 4.5 | –110.7 | 0.024010; 0.417140; 1.0; 0.743905; 0.169791; 0.036733 | 3.308 | 0.725 | 2.142 | 2.028 | 2.849 |
| 4.75 | –117.7 | 0.015552; 0.333884; 1.0; 0.916084; 0.268759; 0.067568 | 3.420 | 0.690 | 2.198 | 2.080 | 2.923 | |
| 5.0 | –123.2 | 0.009817; 0.243567; 0.878459; 1.0; 0.352951; 0.115389 | 3.524 | 0.658 | 2.251 | 2.129 | 2.994 | |
| 6 | 5.25 | –131.1 | 0.005261; 0.164062; 0.755211; 1.0; 0.512181; 0.119240; 0.019629 | 3.631 | 0.627 | 2.307 | 2.182 | 3.068 |
| 5.5 | –136.7 | 0.003157; 0.112652; 0.629010; 1.0; 0.644449; 0.166207; 0.039884 | 3.732 | 0.599 | 2.362 | 2.232 | 3.141 | |
| 7 | 5.75 | –145.2 | 0.001758; 0.078789; 0.522716; 1.0; 0.727156; 0.266060; 0.039207; 0.007629 | 3.822 | 0.575 | 2.411 | 2.278 | 3.206 |
| 6.0 | –152.1 | 0.0010577; 0.0559231; 0.4409516; 1.0; 0.8675468; 0.3715909; 0.0684953; 0.0143645 | 3.912 | 0.553 | 2.461 | 2.325 | 3.273 | |
| 6.25 | –158.9 | 0.0006489; 0.0400893; 0.3686806; 0.9854598; 1.0; 0.5126111; 0.1063516; 0.0282652 | 3.997 | 0.532 | 2.510 | 2.371 | 3.338 | |
| 8 | 6.5 | –165.7 | 0.00034113; 0.02446856; 0.26524042; 0.82741304; 1.0; 0.57328803; 0.16904509; 0.02999197; 0.00386527 | 4.082 | 0.512 | 2.559 | 2.417 | 3.403 |
| 6.75 | –172.2 | 0.00018771; 0.01537271; 0.19407491; 0.70418309; 1.0; 0.65805987; 0.23913589; 0.04157892; 0.00865322 | 4.163 | 0.493 | 2.608 | 2.462 | 3.468 | |
| 9 | 7.0 | –179.8 | 0.00010211; 0.00989441; 0.14560511; 0.61206848; 1.0; 0.76657167; 0.30710261; 0.07526034; 0.00883909; 0.00153018 | 4.239 | 0.476 | 2.654 | 2.505 | 3.529 |
| 7.25 | –186.8 | 0.000058074; 0.006473982; 0.109779127; 0.531358016; 1.0; 0.881455493; 0.407971081; 0.113618128; 0.016109459; 0.00295259 | 4.314 | 0.461 | 2.700 | 2.548 | 3.590 | |
| 7.5 | –193.3 | 0.000034325; 0.004319143; 0.082808416; 0.457928166; 0.984868474; 1.0; 0.525257996; 0.173248172; 0.025604464; 0.006215767 | 4.386 | 0.446 | 2.746 | 2.591 | 3.650 | |
| 10 | 7.75 | –200.7 | 0.000017365; 0.002524089; 0.055962837; 0.353822359; 0.871140469; 1.0; 0.612020621; 0.211741186; 0.049087775; 0.005396598; 0.001007916 | 4.456 | 0.432 | 2.790 | 2.632 | 3.709 |
| 8.0 | –207.6 | 0.000009188; 0.001517134; 0.038220350; 0.274427667; 0.767424674; 1.0; 0.695606601; 0.272444587; 0.072383247; 0.008744788; 0.001947661 | 4.524 | 0.419 | 2.834 | 2.673 | 3.767 | |
| 8.25 | –213.2 | 0.000005396; 0.00096371; 0.026757276; 0.214736769; 0.677579678; 1.0; 0.791921936; 0.350862028; 0.107797470; 0.014058032; 0.003832804 | 4.591 | 0.406 | 2.878 | 2.714 | 3.826 | |
| 11 | 8.5 | –221.4 | 0.0000027728; 0.0005810183; 0.0185321632; 0.1691004570; 0.6013828130; 1.0; 0.8823986316; 0.4484947411; 0.1421927769; 0.0291887766; 0.0037682987; 0.0005613720 | 4.653 | 0.395 | 2.920 | 2.753 | 3.881 |
| 8.75 | –227.7 | 0.0000016087; 0.0003721596; 0.0131684087; 0.1342067962; 0.5348771736; 1.0; 0.9907732324; 0.5698238953; 0.1998454052; 0.048801166; 0.0059587491; 0.00129658 | 4.716 | 0.384 | 2.962 | 2.793 | 3.937 | |
| 12 | 9.0 | –235.3 | 0.0000007941; 0.0002096189; 0.0084126243; 0.0965164364; 0.4314360660; 0.9014626404; 1.0; 0.6372986259; 0.2566763035; 0.0624948444; 0.0132529662; 0.0007419865; 0.0002610866 | 4.775 | 0.373 | 3.003 | 2.831 | 3.992 |
| 9.25 | –242.1 | 0.00000041264; 0.00012102895; 0.00540932781; 0.06929178811; 0.34590384537; 0.80773028869; 1.0; 0.71365970547; 0.31836083080; 0.08911102980; 0.01933552098; 0.00177370940; 0.00042569212 | 4.835 | 0.364 | 3.044 | 2.870 | 4.046 | |
| 9.5 | –248.9 | 0.00000022009; 0.00007156049; 0.00354602766; 0.05039944164; 0.27955612137; 0.72578702440; 1.0; 0.79366855825; 0.39487445665; 0.12231887229; 0.03000907405; 0.00291207966; 0.00082854176 | 4.892 | 0.354 | 3.085 | 2.908 |
4.100 |
Таблица 4.
Параметры синтезированных весовых функций со скоростью спада 24 дБ/окт (µ = 3)
| m | β, бин | P, дБ | b0, b1, …, bm | Пw, дБ | Пs, дБ | Ln, бин | L3, бин | L6, бин |
|---|---|---|---|---|---|---|---|---|
| 1 | 2.5 | –42.8 | 1.0; 0.843 | 2.449 | 1.051 | 1.757 | 1.678 | 2.341 |
| 2 | 2.75 | –53.8 | 1.0; 0.624; 0.286 | 2.515 | 1.025 | 1.785 | 1.701 | 2.377 |
| 3.0 | –60.9 | 0.826; 1.0; 0.409 | 2.667 | 0.960 | 1.848 | 1.759 | 2.460 | |
| 3.25 | –69.0 | 0.604; 1.0; 0.563 | 2.790 | 0.910 | 1.901 | 1.807 | 2.530 | |
| 3 | 3.5 | –76.1 | 0.3605; 1.0; 0.5242; 0.0975 | 2.931 | 0.855 | 1.964 | 1.865 | 2.613 |
| 3.75 | –82.7 | 0.2392; 1.0; 0.6265; 0.2014 | 3.066 | 0.805 | 2.026 | 1.922 | 2.696 | |
| 4.0 | –86.7 | 0.1590; 1.0; 0.7969; 0.3875 | 3.208 | 0.756 | 2.093 | 1.984 | 2.784 | |
| 4 | 4.25 | –98.9 | 0.1413; 0.8751; 1.0; 0.3478; 0.0713 | 3.276 | 0.734 | 2.126 | 2.014 | 2.828 |
| 4.5 | –106.1 | 0.0889; 0.6797; 1.0; 0.4173; 0.1185 | 3.383 | 0.700 | 2.179 | 2.064 | 2.899 | |
| 5 | 4.75 | –113.6 | 0.05768; 0.57318; 1.0; 0.60224; 0.12511; 0.02353 | 3.488 | 0.668 | 2.232 | 2.113 | 2.969 |
| 5.0 | –120.9 | 0.03856; 0.46669; 1.0; 0.73653; 0.18934; 0.04318 | 3.586 | 0.639 | 2.283 | 2.160 | 3.037 | |
| 5.25 | –127.0 | 0.02662; 0.38369; 1.0; 0.90677; 0.27904; 0.08160 | 3.683 | 0.612 | 2.335 | 2.208 | 3.105 | |
| 6 | 5.5 | –135.4 | 0.017227; 0.301266; 0.955835; 1.0; 0.425306; 0.092704; 0.013052 | 3.773 | 0.588 | 2.384 | 2.254 | 3.170 |
| 5.75 | –142.0 | 0.010205; 0.209844; 0.808238; 1.0; 0.534442; 0.122818; 0.026680 | 3.865 | 0.564 | 2.435 | 2.301 | 3.238 | |
| 6.0 | –146.4 | 0.006604; 0.149873; 0.685938; 1.0; 0.666908; 0.167838; 0.051069 | 3.955 | 0.542 | 2.486 | 2.349 | 3.305 | |
| 7 | 6.25 | –156.6 | 0.0037161; 0.1075303; 0.5730913; 1.0; 0.7122363; 0.2721160; 0.0427845; 0.0092803 | 4.032 | 0.523 | 2.530 | 2.390 | 3.364 |
| 6.5 | –163.7 | 0.0023215; 0.0785726; 0.4896646; 1.0; 0.8327759; 0.3728902; 0.0683126; 0.0174357 | 4.112 | 0.504 | 2.577 | 2.434 | 3.427 | |
| 8 | 6.75 | –170.4 | 0.0014787; 0.0576437; 0.4216545; 1.0; 0.9898137; 0.4904893; 0.1299132; 0.0211133; 0.0026681 | 4.191 | 0.487 | 2.625 | 2.478 | 3.490 |
| 7.0 | –176.9 | 0.00084593; 0.03750587; 0.31639245; 0.86804540; 1.0; 0.56985821; 0.18103717; 0.03063918; 0.00553469 | 4.268 | 0.470 | 2.672 | 2.522 | 3.552 | |
| 7.25 | –182.3 | 0.00049732 ; 0.02434129; 0.23500205; 0.74258394; 1.0; 0.65121985; 0.25227609; 0.04294792; 0.01123664 | 4.344 | 0.454 | 2.719 | 2.566 | 3.615 | |
| 9 | 7.5 | –191.3 | 0.0002769; 0.01636641; 0.18260888; 0.66072028; 1.0; 0.75592558; 0.30361849; 0.08178547; 0.00892918; 0.00207591 | 4.410 | 0.441 | 2.761 | 2.605 | 3.670 |
| 7.75 | –198.3 | 0.00016292; 0.01096411; 0.13989314; 0.57794097; 1.0; 0.86058595; 0.39754824; 0.11940321; 0.01613976; 0.00379593 | 4.479 | 0.427 | 2.805 | 2.646 | 3.729 | |
| 8.0 | –203.9 | 0.00010649; 0.00781806; 0.11011391; 0.51147492; 1.0; 0.98410246; 0.51246316; 0.18116267; 0.02555544; 0.00774006 | 4.545 | 0.415 | 2.848 | 2.687 | 3.786 | |
| 10 | 8.25 | –211.9 | 0.00005424; 0.00462630; 0.07605347; 0.40488360; 0.90681369; 1.0; 0.60949185; 0.21757296; 0.05250725; 0.00633007; 0.00125352 | 4.612 | 0.402 | 2.892 | 2.728 | 3.845 |
| 8.5 | –218.0 | 0.00003063; 0.00287502; 0.05282365; 0.31661976; 0.80202376; 1.0; 0.69267725; 0.27713055; 0.07807592; 0.00963832; 0.00248457 | 4.677 | 0.390 | 2.936 | 2.769 | 3.902 |
Таблица 5.
Параметры синтезированных весовых функций со скоростью спада 30 дБ/окт (µ = 4)
| m | β, бин | P, дБ | b0, b1, …, bm | Пw, дБ | Пs, дБ | Ln, бин | L3, бин | L6, бин |
|---|---|---|---|---|---|---|---|---|
| 1 | 2.75 | –44.7 | 1.0; 0.423 | 2.762 | 0.913 | 1.889 | 1.801 | 2.516 |
| 3.0 | –49.3 | 0.778; 1.0 | 2.941 | 0.844 | 1.968 | 1.874 | 2.621 | |
| 2 | 3.25 | –62.6 | 1.0; 0.642; 0.313 | 2.943 | 0.846 | 1.969 | 1.873 | 2.622 |
| 3.5 | –70.1 | 0.946; 1.0; 0.521 | 3.059 | 0.805 | 2.022 | 1.921 | 2.692 | |
| 3.75 | –77.0 | 0.753; 1.0; 0.742 | 3.160 | 0.771 | 2.070 | 1.964 | 2.754 | |
| 3 | 4.0 | –84.9 | 0.3968; 1.0; 0.5431; 0.1355 | 3.285 | 0.729 | 2.130 | 2.020 | 2.834 |
| 4.25 | –90.5 | 0.2398; 1.0; 0.6123; 0.2634 | 3.415 | 0.688 | 2.195 | 2.080 | 2.920 | |
| 4 | 4.5 | –100.8 | 0.2523; 1.0; 0.9408; 0.2551; 0.0584 | 3.476 | 0.670 | 2.226 | 2.108 | 2.961 |
| 4.75 | –108.6 | 0.17465; 0.86142; 1.0; 0.34228; 0.09394 | 3.568 | 0.643 | 2.274 | 2.153 | 3.025 | |
| 5.0 | –115.3 | 0.11428; 0.67394; 1.0; 0.39635; 0.14868 | 3.662 | 0.617 | 2.324 | 2.199 | 3.091 | |
| 5 | 5.25 | –122.9 | 0.07556; 0.59721; 1.0; 0.61168; 0.14794; 0.02917 | 3.755 | 0.591 | 2.374 | 2.246 | 3.158 |
| 5.5 | –129.6 | 0.051629; 0.494923; 1.0; 0.755101; 0.209437; 0.055677 | 3.844 | 0.568 | 2.423 | 2.291 | 3.223 | |
| 6 | 5.75 | –138.2 | 0.037020; 0.416136; 1.0; 0.859986; 0.326558; 0.061807; 0.009229 | 3.921 | 0.549 | 2.467 | 2.331 | 3.280 |
| 6.0 | –145.5 | 0.026111; 0.345455; 0.988748; 1.0; 0.461241; 0.096363; 0.019540 | 4.002 | 0.530 | 2.513 | 2.375 | 3.341 | |
| 6.25 | –151.9 | 0.016241; 0.247308; 0.848796; 1.0; 0.570567; 0.126370; 0.036018 | 4.084 | 0.510 | 2.561 | 2.419 | 3.405 | |
| 7 | 6.5 | –160.2 | 0.0098677; 0.180925; 0.7092311; 1.0; 0.6074565; 0.2097725; 0.0294861; 0.0063666 | 4.156 | 0.494 | 2.604 | 2.459 | 3.462 |
| 6.75 | –167.4 | 0.0062888; 0.1338891; 0.6101591; 1.0; 0.7068274; 0.2833181; 0.0466282; 0.0115783 | 4.230 | 0.478 | 2.648 | 2.501 | 3.521 | |
| 7.0 | –173.3 | 0.0040240; 0.0986563; 0.5212855; 1.0; 0.8190108; 0.3902201; 0.0709010; 0.0221685 | 4.306 | 0.462 | 2.695 | 2.544 | 3.583 | |
| 8 | 7.25 | –181.3 | 0.0026785; 0.0750361; 0.4599592; 1.0; 0.9676834; 0.4833225; 0.1395149; 0.0216129; 0.0038212 | 4.374 | 0.448 | 2.738 | 2.584 | 3.640 |
| 7.5 | –187.4 | 0.00162224; 0.05099244; 0.35793752; 0.89258634; 1.0; 0.56829734; 0.19603858; 0.03132380; 0.00754829 | 4.445 | 0.434 | 2.783 | 2.626 | 3.699 | |
| 9 | 7.75 | –195.6 | 0.00095857; 0.03503629; 0.27981655; 0.79488915; 1.0; 0.66110605; 0.23514388; 0.06092491; 0.00536292; 0.00147193 | 4.508 | 0.421 | 2.824 | 2.664 | 3.754 |
| 8.0 | –202.6 | 0.00057642; 0.02388884; 0.21672797; 0.69888376; 1.0; 0.74837969; 0.30584449; 0.08691443; 0.01003269; 0.00255014 | 4.573 | 0.409 | 2.866 | 2.704 | 3.810 | |
| 8.25 | –209.6 | 0.00035376; 0.01654085; 0.16944463; 0.61807804; 1.0; 0.84785358; 0.39100151; 0.12663253; 0.01619939; 0.00478304 | 4.635 | 0.398 | 2.908 | 2.743 | 3.865 | |
| 10 | 8.5 | –216.4 | 0.000217733; 0.011420262; 0.132379154; 0.544964150; 1.0; 0.949885577; 0.508345399; 0.170067766; 0.035110399; 0.005050183; 0.000684955 | 4.698 | 0.387 | 2.950 | 2.782 | 3.921 |
| 8.75 | –222.9 | 0.000128188; 0.007468608; 0.097426013; 0.451705648; 0.936829316; 1.0; 0.61009379; 0.222753277; 0.057122453; 0.006930637; 0.001620549 | 4.760 | 0.376 | 2.992 | 2.822 | 3.977 | |
| 11 | 9.0 | –230.5 | 0.000072253; 0.004766460; 0.069757074; 0.361887977; 0.837276871; 1.0; 0.675277470; 0.283404250; 0.072490728; 0.015246861; 0.001050615; 0.000300897 | 4.816 | 0.366 | 3.031 | 2.858 | 4.029 |
| 9.25 | –237.4 | 0.0000415716; 0.0030524748; 0.0499437232; 0.2896641739; 0.7496237470; 1.0; 0.7562313157; 0.3523554669; 0.1028382486; 0.0226930557; 0.0022296549; 0.0005182443 | 4.874 | 0.357 | 3.072 | 2.896 | 4.083 |
Во-первых, характеристики оптимальных весовых функций слабо зависят от числа выборок N. Для различных N разница в уровне максимального лепестка составляет доли, максимум единицы, децибел и тем меньше, чем больше сравниваемые значения N. Для N = 1024 разница с асимптотическим случаем N → ∞, как правило, менее 0.1 дБ. Поэтому в таблицах приводятся характеристики оптимальных функций только для одного значения N = 1024, часто используемого в приложениях. При таком значении N, как коэффициенты, так и характеристики весовых функций, практически совпадают с величинами для непрерывных функций.
Во-вторых, в настоящей работе при минимизации уровня боковых лепестков учитываются все без исключения боковые лепестки. Иными словами, величина параметра β изменяется в пределах главного лепестка и должна быть не больше координаты fz0 первого нуля спектра весовой функции: β ≤ fz0.
Уменьшение уровня максимального бокового лепестка при синтезе достигается за счет увеличения β и порядка функции. Расчеты показывают, что при постоянном β увеличение порядка функции сверх минимально необходимого для обеспечения отсутствия нулей функции на интервале [0, β] приводит к довольно слабому улучшению характеристик функции. Поэтому в табл. 1–5 содержатся параметры функций только для указанного минимального порядка.
В таблицах даны следующие общепринятые параметры весовых функций [1]: уровень P максимального бокового лепестка относительно главного лепестка; потери Πw в отношении сигнал/шум, вызванные использованием весовой функции; потери Πs за счет рельефа спектра (scalloping loss); эквивалентная шумовая полоса Ln, ширины главного лепестка L3 и L6 по уровням минус 3 и минус 6 дБ, соответственно. Так как ширина лепестков спектра обратно пропорциональна T, то все полосы частот и параметр β, как это принято в литературе [1], выражены в относительных единицах (в бинах), т.е. умножены на T.
В табл. 1–5 значения уровня максимального лепестка округлены с точностью до 0.1 дБ, а разрядность коэффициентов выбрана такой, что получающиеся значения P отличаются от оптимальных не более, чем на 0.05 дБ, что гарантировано алгоритмом верификации (этап 4 предыдущего раздела).
Наибольший интерес представляют функции с целым значением параметра μ, так как их вычисление требует наименьшего количества операций. В табл. 1–5 даны параметры синтезированных функций со скоростями спада лепестков 6, 12, 18, 24 и 30 дБ/окт., соответственно. Шаг по параметру β для всех таблиц составляет 0.25 бин. Функции с максимальным лепестком более минус 40 дБ не представляют значительного интереса и поэтому для краткости не приведены.
Функции со скоростью спада лепестков, некратной 6 дБ/окт, не имеют аналогов в литературе, кроме построенных авторами косинус-полиномиальных функций [9, 10]. Изложенный выше метод позволяет синтезировать полиномиальные весовые функции и с этими скоростями спада лепестков, однако в данной работе такие функции не приводятся поскольку при сопоставимых характеристиках они требуют большего объема вычислений, чем функции со скоростями кратными 6 дБ/окт.
4. ХАРАКТЕРИСТИКИ ОПТИМАЛЬНЫХ ВЕСОВЫХ ФУНКЦИЙ
Рассмотрим характеристики построенных полиномиальных функций. Рисунок 1 иллюстрирует зависимость уровня максимального бокового лепестка P от параметра синтеза β при скоростях спада боковых лепестков V = 6, 18 и 30 дБ/окт. Эти значения выбраны таким образом, чтобы не произошло слияния кривых на рисунке.
Рис. 1.
Зависимости уровня P максимального бокового лепестка от параметра β для оптимальных функций со скоростями спада лепестков 6 (1), 18 (2) и 30 (3) дБ/окт.
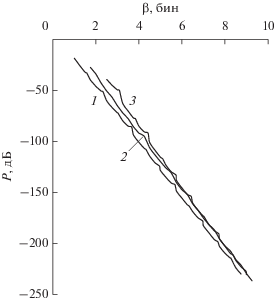
Из рис. 1 видно, что увеличение скорости спада лепестков при постоянном β приводит к некоторому возрастанию уровня максимального бокового лепестка. Для фиксированной скорости спада каждая кривая хорошо аппроксимируется прямой линией, небольшие отклонения от которой имеют случайный вид. Для грубой оценки значения параметра синтеза β, требуемого для получения желаемого уровня P максимального бокового лепестка можно использовать линейное соотношение P ≈ (–27.7β + 19.8) дБ. При увеличении скорости спада лепестков увеличивается крутизна аппроксимирующих прямых с ‒ 27.3 дБ/бин для V = = 6 дБ/окт до ‒ 29.7 дБ/бин для V = 30 дБ/окт. Это приводит к сближению кривых между собой при увеличении β.
Аналогичное сближение кривых при увеличении β наблюдается и для других параметров функций. Поэтому чем больше значение β, тем меньше отличаются характеристики весовых функций при разных скоростях спада лепестков.
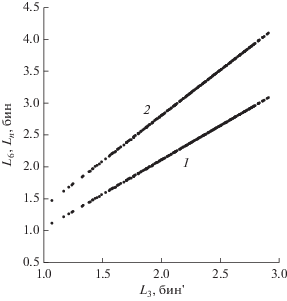
Рисунок 2 иллюстрирует зависимости шумовой полосы Ln и ширины главного лепестка L6 по уровню минус 6 дБ от ширины главного лепестка L3 по уровню половинной мощности. На рисунке приведены указанные параметры более, чем 200 оптимальных функций. Каждая функция отображается одной точкой для каждой из зависимостей.
Параметры оптимальных функций с высокой точностью ложатся на прямолинейные тренды, имеющие уравнения:
С использованием этих уравнений можно довольно точно оценить полосы Ln и L6, по значению полосы L3. Кроме того, полоса Ln определяет потери в отношении сигнал/шум, обусловленные введением весовой функции: Πw = 10 lg Ln. Таким образом, из четырех перечисленных параметров три являются зависимыми.
Малая величина отклонения реальных полос оптимальных весовых функций от прямых линий позволяет использовать эти отклонения в качестве критериев качества весовой функции.
Проведем сравнение весовых функций, полученных в данной работе, с известными. Так как параметры весовых функций зависят от скорости спада лепестков, то это сравнение следует проводить для одной и той же скорости спада лепестков. На рис. 3 такое сравнение дано для скорости спада 6 дБ/окт, где показана взаимозависимость двух основных параметров: ширины главного лепестка по уровню половинной мощности и уровня максимального бокового, для нескольких классов классических весовых функций: Кайзера–Бесселя, Гаусса, Блекмана–Хэрриса [1] наряду с новыми функциями, построенными в данной работе.
Рис. 3.
Зависимости ширины L3 главного лепестка по половинной мощности от уровня P максимального бокового лепестка для функций Гаусса (1), Кайзера–Бесселя (2), Блэкмана–Харриса (3, отдельные кружки ), Дольфа–Чебышева (4) и функций табл. 2 (5).
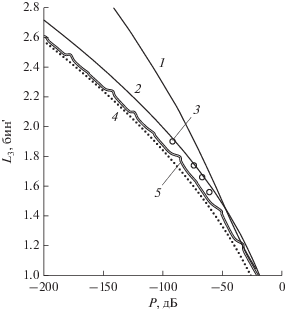
Также представлены функции Дольфа–Чебышева [1], которые имеют нулевую скоростью спада лепестков, обеспечивают минимально возможную ширину главного лепестка при заданном уровне максимального бокового, поэтому соответствующая им линия является границей достижимых параметров. По объему вычислений функции Дольфа–Чебышева не могут конкурировать с функциями малого порядка, так как имеют сложный алгоритм вычисления и максимальный порядок (примерно N/2), что приводит к несоизмеримо большему объему вычислительных операций по сравнению с функциями данной работы, порядок которых не превосходит 12.
Чем ниже расположена кривая на графике рис. 3, тем выше качество соответствующего класса весовых функций с точки зрения решаемой задачи, т.е. наглядно видно преимущество построенного класса функций над известными. Для других скоростей спада лепестков также наблюдается аналогичное преимущество. При фиксированном уровне бокового лепестка P < –40 дБ, ширина главного лепестка по половинной мощности L3 новых функций, несмотря на малый порядок, всего на 2…4% превышает граничное значение.
Кривые для полиномиальных функций на рис. 1 и 3 имеют небольшие выбросы вверх. Соответствующие функции не приведены в таблицах и имеют максимально возможный параметр β для данного порядка функции, при котором отсутствуют нули спектра в области [0, β]. Эти функции имеют также минимально возможный для данного порядка уровень максимального лепестка. Выбросы указывают на небольшое ухудшение качества соответствующих оптимальных функций.
Сравнение описываемых в данной работе функций с косинус-полиномиальными функциями, синтезированными авторами в работах [4‒10], показывает, что их характеристики весьма близки при одинаковых параметрах β и μ. Поэтому на рис. 3 кривая для косинус-полиномиальных функций не приведена во избежание наложения на кривую для полиномиальных функций.
Цена за упрощение вычислений для полиномиальных функций состоит в увеличении порядка по сравнению с косинус-полиномиальными функциями с одинаковыми характеристиками. На рис. 4 показана зависимость порядка оптимальной функции от значения максимального бокового лепестка для полиномиальных (1) и косинус-полиномиальных (2) функций при скорости спада лепестков 6 дБ/окт. При значительных боковых лепестках порядки отличаются незначительно, однако при малых уровнях порядок полиномиальных функций примерно в 1.5 раза больше. Такая ситуация имеет место и для других скоростей спада лепестков.
Рис. 4.
Зависимости порядка оптимальной весовой функции от уровня максимального лепестка для полиномиальных (1) и косинус-полиномиальных (2) функций.
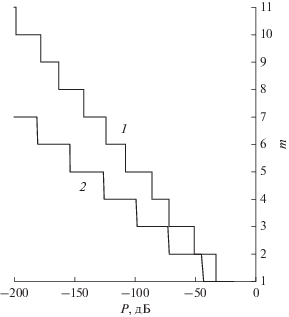
Однако несмотря на различие порядков, по объему вычислений оба класса функций примерно эквивалентны, и преимущество того или другого класса зависит от используемой аппаратной платформы, на которой реализуются вычисления. В сравнении с известными по литературе функциями оба класса существенно лучше. Проведенные оценки показывают, что синтезированные функции дают выигрыш по объему вычислений в 2…3 раза по сравнению с наиболее эффективными известными функциями в виде отрезка ряда Фурье [1–3], что весьма важно для систем реального времени.
Сравнение по объему вычислений с известными полиномиальными функциями [11, 12] показывает преимущество построенных в данной работе функций, так как при сопоставимых максимальных уровнях боковых лепестков известные функции имеют более высокий порядок.
Список литературы
Хэррис Ф.Дж. // ТИИЭР. 1978. Т. 66. № 1. С. 60.
Nuttall A.H. // IEEE Trans. 1981. V. ASSP-29. № 1. P. 84.
Albrecht H.-H. // The Open Signal Processing J. 2010. V. 3. P. 20.
Зайцев Г.В. // Радиотехника. 2011. № 3. С. 21.
Зайцев Г.В. // Радиотехника. 2012. № 1. С. 55.
Хзмалян А.Д. // Вестник ВКО. 2018. № 4(20). С. 90.
Zaytsev G.V., Khzmalyan A.D. // Proc. V Int. Conf. on Eng. and Telecom. (EnT MIPT). Moscow. 15–16 Nov. 2018. N.Y.: IEEE, 2019. P. 103. https://doi.org/10.1109/EnT-MIPT.2018.00030
Зайцев Г.В., Хзмалян А.Д. // РЭ. 2020. Т. 65. № 5. С. 464. https://doi.org/10.1134/S1064226920050137
Zaytsev G.V., Khzmalyan A.D. // Proc. 2019 Int. Conf. on Eng. and Telecom. (EnT). Dolgoprudny. 20–21 Nov. N.Y.: IEEE, 2019. P. 9030552. https://doi.org/10.1109/EnT47717.2019.9030552
Зайцев Г.В., Хзмалян А.Д. // Цифровая обработка сигналов. 2019. № 2. С. 35.
Kulkarni R.G. // Signal Processing. 2003. V. 83. P. 1145.
Okarma K. // Signal Processing. 2007. V. 87. P. 782.
Оппенгейм А.В., Шафер Р.В. Цифровая обработка сигналов. М.: Техносфера, 2006.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Физматгиз, 1963.
Коллатц Л., Крабс В. Теория приближений. Чебышевские приближения и их приложения. М.: Наука, 1978.
Bertsekas D.P. Convex Optimization Algorithms. Belmont. Mass., USA: Athena Scientific, 2015.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника