Радиотехника и электроника, 2021, T. 66, № 5, стр. 500-510
Режим “ионного фонтана” для плоских диодов с ненулевым полем в плоскости отражения ионов
М. А. Завьялов a, Т. М. Сапронова a, П. М. Стальков a, В. А. Сыровой a, *
a ВЭИ – филиал ФГУП “РФЯЦ – ВНИИТФ им. акад. Е.И. Забабахина”
111250 Москва, ул. Красноказарменная, 12, Российская Федерация
* E-mail: red@cplire.ru
Поступила в редакцию 12.03.2020
После доработки 12.03.2020
Принята к публикации 22.12.2020
Аннотация
Исследован эффект усиления электронного тока в плоских униполярном и биполярном диодах при инжекции ионов со стороны проницаемого и разогреваемого ими катода (режим “ионного фонтана”) в общем случае ненулевого электрического поля в плоскости отражения ионов и на аноде. Для эмитируемых катодом электронов рассмотрен весь диапазон возможных ситуаций, простирающийся от нерелятивистских энергий до ультрарелятивистского предела. Изучено влияние инжектируемых ионов на распределение поля в униполярном диоде при эмиссии электронов, ограниченной температурой.
ВВЕДЕНИЕ
Изучению биполярного потока между параллельными плоскостями посвящено значительное число публикаций, начиная с классической работы И. Лэнгмюра [1]. В них рассматривались постановки, различающиеся условиями эмиссии электронов (${{\rho }}$-режим, инжекция с ненулевой скоростью, вторичная эмиссия под действием ионной бомбардировки), эмиссии ионов (${{\rho }}$-режим, Т-режим, инжекция с ненулевой скоростью), положением стартовой поверхности последних (анод, плоскость между катодом и анодом) [1–6]. Одной из важных характеристик биполярных диодов является коэффициент усиления электронного тока ${{K}_{e}}$ (отношение электронных токов в биполярном и униполярном диодах), достигающий у нерелятивистского диода в ${{\rho }}$-режиме максимального значения ${{K}_{e}} = 1.86$ [1].
Для сферического и цилиндрического диодов со сходящимся электронным пучком величина ${{K}_{e}}$ зависит от геометрического фактора – отношения радиусов катода и анода и может существенно превышать характерное для плоской геометрии значение [7]. Случай расходящегося электронного пучка рассмотрен в работе [8].
Публикации [1–8] посвящены исследованию диодов с нерелятивистскими электронами, в работе [9] рассмотрен ультрарелятивистский случай, а в [10] проведено подробное исследование плоского биполярного диода с электронами релятивистских энергий, показавшее, в частности, неадекватность ультрарелятивистского приближения в реальном диапазоне релятивистских скоростей из-за исключительно медленного стремления к ультрарелятивистскому пределу.
Вопросы расчета формирующих электродов для клиновидных и конических нерелятивистских биполярных пучков обсуждались в [11], а в случае ленточного релятивистского пучка – в [12].
В работе [13] во всем диапазоне энергии электронов исследован режим “ионного фонтана” при выполнении условий полного пространственного заряда (нулевое электрическое поле) на катоде, аноде и в плоскости отражения ионов. Подробный сравнительный анализ характеристик плоских диодов при принятых в [13] предположениях выполнен в работе [14].
При энергии инжекции ионов, превышающей энергию электронов на аноде, возможно рассмотрение проблем частичной и полной компенсации по заряду и току биполярного пучка, компоненты которого движутся в одном направлении в заанодном пространстве [15, 16].
Ниже исследованы различные варианты диодных конфигураций с плоской геометрией в режиме “ионного фонтана” в общем случае, когда электрическое поле в плоскости отражения ионов в биполярном диоде и в плоскости анода отлично от нуля. Скорость электронов может быть нерелятивистской, релятивистской (при допустимом для плоского диода потенциале анода) или ультрарелятивистской; последняя определяет границу физически возможных ситуаций при абстрагировании от проблем электрической прочности.
1. УРАВНЕНИЯ ПУЧКА
В релятивистской нормировке, устраняющей из уравнений пучка все физические постоянные используемой системы единиц (потенциал ${{\varphi }}$ при этом нормируется на 511 кВ), биполярный пучок в режиме ионного фонтана описывается уравнениями
(1)
$\begin{gathered} \frac{{{{d}^{2}}{{\varphi }}}}{{d{{z}^{2}}}} = {{J}_{e}}\left[ {\frac{{1 + {{\tilde {\varphi }}}}}{{\sqrt {{{\varphi }}\left( {2 + {{\tilde {\varphi }}}} \right)} }} - \frac{{{\beta }}}{{\sqrt {{\text{2}}\left( {{{{{\varphi }}}_{B}} - {{\varphi }}} \right)} }} - \frac{{{\alpha }}}{{\sqrt {{\text{2}}\left( {{{{{\varphi }}}_{A}} - {{\varphi }}} \right)} }}} \right], \\ 0 \leqslant z \leqslant {{z}_{B}}; \\ \frac{{{{d}^{2}}{{\varphi }}}}{{d{{z}^{2}}}} = {{J}_{e}}\left[ {\frac{{1 + {{\tilde {\varphi }}}}}{{\sqrt {{{\varphi }}\left( {2 + {{\tilde {\varphi }}}} \right)} }} - \frac{{{\alpha }}}{{\sqrt {{\text{2}}\left( {{{{{\varphi }}}_{A}} - {{\varphi }}} \right)} }}} \right],\,\,\,\,{{z}_{B}} \leqslant z \leqslant 1; \\ {{\alpha }} = \frac{{{{J}_{i}}}}{{{{J}_{e}}}}\sqrt {\frac{{{{\eta }_{e}}}}{{{{\eta }_{i}}}}} ,\,\,\,{{\beta }} = \frac{{2{{J}_{{iB}}}}}{{{{J}_{e}}}}\sqrt {\frac{{{{\eta }_{e}}}}{{{{\eta }_{i}}}}} . \\ \end{gathered} $Анод, плоскость отражения ионов и катод обозначены символами А, В, С; ${{J}_{e}}$, ${{J}_{i}}$, ${{J}_{{iB}}}$ – плотности токов электронов и ионов, эмитированных с анода и инжектированных из-за катода соответственно; тильдой отмечены члены, исчезающие в нерелятивистском пределе; $\eta $ – удельный заряд частицы. Слагаемые в правой части первой формулы в (1) описывают пространственный заряд электронов, ионов фонтана и ионов, эмитированных с анода. При малых скоростях электронов потенциал нормируется на потенциал анода ${{{{\varphi }}}_{A}}$.
Первые интегралы уравнений (1) имеют вид
(2)
$\begin{gathered} {{\left( {\frac{{d{{\varphi }}}}{{dz}}} \right)}^{2}} = 2{{J}_{e}}\left[ {\sqrt {{{\varphi }}\left( {2 + {{\tilde {\varphi }}}} \right)} } \right. + {{\beta }}\sqrt 2 \left( {\sqrt {{{{{\varphi }}}_{B}} - {{\varphi }}} - \sqrt {{{{{\varphi }}}_{B}}} } \right) + \\ \left. { + \,\,\,\,{{\alpha }}\sqrt 2 \left( {\sqrt {{{{{\varphi }}}_{A}} - {{\varphi }}} - \sqrt {{{{{\varphi }}}_{A}}} } \right)} \right],\,\,\,\,0 \leqslant z \leqslant {{z}_{B}}; \\ {{\left( {\frac{{d{{\varphi }}}}{{dz}}} \right)}^{2}} = 2{{J}_{e}}\left[ {\sqrt {{{\varphi }}\left( {2 + {{\tilde {\varphi }}}} \right)} } \right. - \\ \left. { - \,\,{{\beta }}\sqrt 2 \sqrt {{{{{\varphi }}}_{B}}} + {{\alpha }}\sqrt 2 \left( {\sqrt {{{{{\varphi }}}_{A}} - {{\varphi }}} - \sqrt {{{{{\varphi }}}_{A}}} } \right)} \right],\,\,\,\,{{z}_{B}} \leqslant z \leqslant 1. \\ \end{gathered} $Выражения (2) удовлетворяют условиям ${{\rho }}$-режима на катоде ($z{\kern 1pt} {\kern 1pt} {\text{ = }}{\kern 1pt} {\kern 1pt} {\text{0}}$, ${{\varphi }} = 0$, ${{E}_{С}} = 0$) и сопряжены в плоскости отражения ионов, где поле принимает значение ${{E}_{B}}$. В сечениях В, А для квадрата поля из (2) имеем
(3)
$\begin{gathered} E_{B}^{2} = 2{{J}_{e}}\left[ {\sqrt {{{{{\varphi }}}_{B}}\left( {2 + {{{{{\tilde {\varphi }}}}}_{B}}} \right)} - {{\beta }}\sqrt {2{{{{\varphi }}}_{B}}} } \right. + \\ \left. { + \,\,{{\alpha }}\sqrt 2 \left( {\sqrt {{{{{\varphi }}}_{A}} - {{{{\varphi }}}_{B}}} - \sqrt {{{{{\varphi }}}_{A}}} } \right)} \right], \\ E_{A}^{2} = 2{{J}_{e}}\left[ {\sqrt {{{{{\varphi }}}_{A}}\left( {2 + {{{{{\tilde {\varphi }}}}}_{A}}} \right)} - {{\beta }}\sqrt {2{{{{\varphi }}}_{B}}} - {{\alpha }}\sqrt {2{{{{\varphi }}}_{A}}} } \right]. \\ \end{gathered} $Интегрирование уравнений (2) приводит к следующему результату:
(4)
$\begin{gathered} z\sqrt {2{{J}_{e}}} = \frac{{{{\varphi }}_{A}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}}}\int\limits_0^{{{\bar {\varphi }}}} {\left[ {\sqrt {t\left( {1 + {{{{{\tilde {\mu }}}}}_{A}}t} \right)} + {{\beta }}\left( {\sqrt {{{{{{\bar {\varphi }}}}}_{B}} - t} - \sqrt {{{{{{\bar {\varphi }}}}}_{B}}} } \right) + } \right.} \\ {{\left. { + \,\,{{\alpha }}\left( {\sqrt {1 - t} - 1} \right)} \right]}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}dt \equiv {{I}_{1}} = \frac{{{{\varphi }}_{A}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}}}{{{\bar {I}}}_{1}}\left( {{{\bar {\varphi }}};{{\alpha }},{{\beta }},{{{{{\bar {\varphi }}}}}_{B}}} \right), \\ 0 \leqslant z \leqslant {{z}_{B}}; \\ \left( {z - {{z}_{B}}} \right)\sqrt {2{{J}_{e}}} = \frac{{{{\varphi }}_{A}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}}}\int\limits_{{{{{{\bar {\varphi }}}}}_{B}}}^{{{\bar {\varphi }}}} {\left[ {\sqrt {t\left( {1 + {{{{{\tilde {\mu }}}}}_{A}}t} \right)} - {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} + } \right.} \\ {{\left. { + \,\,{{\alpha }}\left( {\sqrt {1 - t} - 1} \right)} \right]}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}dt \equiv {{I}_{2}} = \frac{{{{\varphi }}_{A}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}}}{{{\bar {I}}}_{2}}\left( {{{\bar {\varphi }}};{{\alpha }},{{\beta }},{{{{{\bar {\varphi }}}}}_{B}}} \right), \\ {{z}_{B}} \leqslant z \leqslant 1;\,\,\,\,{{{{\mu }}}_{A}} = {{{{{{\varphi }}}_{A}}} \mathord{\left/ {\vphantom {{{{{{\varphi }}}_{A}}} 2}} \right. \kern-0em} 2},\,\,\,\,{{{{\mu }}}_{B}} = {{{{{{\varphi }}}_{B}}} \mathord{\left/ {\vphantom {{{{{{\varphi }}}_{B}}} 2}} \right. \kern-0em} 2};\,\,\,\,{{\bar {\varphi }}} = {{{\varphi }} \mathord{\left/ {\vphantom {{{\varphi }} {{{{{\varphi }}}_{A}}}}} \right. \kern-0em} {{{{{\varphi }}}_{A}}}}. \\ \end{gathered} $В ультрарелятивистском случае интегралы ${{\bar {I}}_{1}}$, ${{\bar {I}}_{2}}$ и формулы (3) принимают вид
(5)
$\begin{gathered} {{{\bar {I}}}_{1}}\, = \,\int\limits_0^{{{\bar {\varphi }}}} {{{{\left[ {t\sqrt {{{{{\mu }}}_{A}}} \, + \,{{\beta }}\left( {\sqrt {{{{{{\bar {\varphi }}}}}_{B}}\, - \,t} \, - \,\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} } \right)\, + \,{{\alpha }}\left( {\sqrt {1\, - \,t} \, - \,1} \right)} \right]}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}} dt, \\ {{{\bar {I}}}_{2}} = \int\limits_{{{{{{\bar {\varphi }}}}}_{B}}}^{{{\bar {\varphi }}}} {{{{\left[ {t\sqrt {{{{{\mu }}}_{A}}} - {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} + {{\alpha }}\left( {\sqrt {1 - t} - 1} \right)} \right]}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}} dt; \\ E_{B}^{2} = 2\sqrt 2 {{J}_{e}}\sqrt {{{{{\varphi }}}_{A}}} \left[ {{{{{{\bar {\varphi }}}}}_{B}}\sqrt {{{{{\mu }}}_{A}}} - {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} + {{\alpha }}\left( {\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} - 1} \right)} \right], \\ E_{A}^{2} = 2\sqrt 2 {{J}_{e}}\sqrt {{{{{\varphi }}}_{A}}} \left[ {\sqrt {{{{{\mu }}}_{A}}} - {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} - {{\alpha }}} \right]. \\ \end{gathered} $Интеграл ${{\bar {I}}_{2}}$ может быть выражен через элементарные функции
(6)
$\begin{gathered} {{{\bar {I}}}_{2}} = \frac{2}{{\sqrt {{{{{\mu }}}_{A}}} }}\left\{ {\sqrt {\sqrt {{{{{\mu }}}_{A}}} {{\bar {\varphi }}} - {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} + {{\alpha }}\left( {\sqrt {1 - {{\bar {\varphi }}}} - 1} \right)} \frac{{^{{^{{}}}}}}{{_{{_{{_{{_{{}}}}}}}}}}} \right. \\ - \,\,\sqrt {\sqrt {{{{{\mu }}}_{A}}} {{{{{\bar {\varphi }}}}}_{B}} - {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} + {{\alpha }}\left( {\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} - 1} \right)} + \\ + \,\,\frac{{{\alpha }}}{{2\sqrt[4]{{{{{{\mu }}}_{A}}}}}}\left[ {\arcsin \frac{{ - 2\sqrt {{{{{\mu }}}_{A}}} \sqrt {1 - {{\bar {\varphi }}}} + {{\alpha }}}}{{\sqrt {{{{\left( {{{\alpha }} - 2\sqrt {{{{{\mu }}}_{A}}} } \right)}}^{2}} - 4{{\beta }}\sqrt {{{{{\mu }}}_{A}}{{{{{\bar {\varphi }}}}}_{B}}} } }} - } \right. \\ - \,\,\left. {\left. {\arcsin \frac{{ - 2\sqrt {{{{{\mu }}}_{A}}} \sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} + {{\alpha }}}}{{\sqrt {{{{\left( {{{\alpha }} - 2\sqrt {{{{{\mu }}}_{A}}} } \right)}}^{2}} - 4{{\beta }}\sqrt {{{{{\mu }}}_{A}}{{{{{\bar {\varphi }}}}}_{B}}} } }}} \right]} \right\}. \\ \end{gathered} $2. ПАРАМЕТРЫ РЕШЕНИЯ И ХАРАКТЕРИСТИКИ ДИОДА
Решение (4) содержит четыре параметра ${{{{\varphi }}}_{A}}$, ${{{{\varphi }}}_{B}}$, ${{\alpha }}$, ${{\beta }}$; зависимость двух последних от ${{E}_{A}}$, ${{E}_{B}}$ следует из формул (3)
(7)
$\begin{gathered} {{\alpha }} = \frac{1}{{\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} }}\left[ {\frac{{E_{B}^{2} - E_{A}^{2}}}{{2\sqrt {2{{{{\varphi }}}_{A}}} {{J}_{e}}}} + \sqrt {1 + {{{{{\tilde {\mu }}}}}_{A}}} - \sqrt {{{{{{\bar {\varphi }}}}}_{B}}\left( {1 + {{{{{\tilde {\mu }}}}}_{B}}} \right)} } \right], \\ {{\beta }} = \left( {\frac{1}{{\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} }} - 1} \right)\frac{{E_{A}^{2}}}{{2\sqrt {2{{{{\varphi }}}_{B}}} {{J}_{e}}}} - \frac{1}{{\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} }}\frac{{E_{B}^{2}}}{{2\sqrt {2{{{{\varphi }}}_{B}}} {{J}_{e}}}} + \\ + \,\,\frac{{\sqrt {1 + {{{{{\tilde {\mu }}}}}_{B}}} }}{{\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} }} - \left( {\frac{1}{{\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} }} - 1} \right)\frac{{\sqrt {1 + {{{{{\tilde {\mu }}}}}_{A}}} }}{{\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} }}. \\ \end{gathered} $При ${{E}_{A}} = {{E}_{B}} = 0$ выражения для ${{\alpha }}$, ${{\beta }}$ в (7) принимают значения ${{{{\alpha }}}_{0}}$, ${{{{\beta }}}_{0}}$, соответствующие ${{\rho }}$-режиму на электродах [13]:
(8)
$\begin{gathered} {{{{\alpha }}}_{0}} = \frac{1}{{\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} }}\left[ {\sqrt {1 + {{{{\mu }}}_{A}}} - \sqrt {{{{{{\bar {\varphi }}}}}_{B}}\left( {1 + {{{{\mu }}}_{B}}} \right)} } \right], \\ {{{{\beta }}}_{0}} = \frac{{\sqrt {1 + {{{{\mu }}}_{B}}} }}{{\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} }} - \frac{{\sqrt {1 + {{{{\mu }}}_{A}}} }}{{\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} }}\left( {\frac{1}{{\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} }} - 1} \right) = \\ = \frac{1}{{\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} }}\left( {\sqrt {1 + {{{{\mu }}}_{A}}} - {{{{\alpha }}}_{0}}} \right). \\ \end{gathered} $В униполярном диоде ${{\alpha }} = 0$; в дальнейшем для интегралов в (4) будем указывать только значение аргумента ${{\bar {\varphi }}}$, опуская набор параметров ${{\alpha }}$, ${{\beta }}$, ${{{{\bar {\varphi }}}}_{B}}$.
Плотность электронного тока, координата плоскости отражения ионов и коэффициент усиления на основании (4) определены выражениями
(9)
$\begin{gathered} \sqrt {2{{J}_{e}}} = {{I}_{1}}\left( {{{{{{\bar {\varphi }}}}}_{B}}} \right) + {{I}_{2}}\left( 1 \right),\,\,\,\,{{z}_{B}} = \frac{{{{I}_{1}}\left( {{{{{{\bar {\varphi }}}}}_{B}}} \right)}}{{{{I}_{1}}\left( {{{{{{\bar {\varphi }}}}}_{B}}} \right) + {{I}_{2}}\left( 1 \right)}}, \\ \sqrt {{{K}_{e}}} = \frac{{\sqrt {2{{J}_{e}}} }}{{\sqrt {2{{J}_{0}}} }}. \\ \end{gathered} $Плотность тока ${{J}_{0}}$ в униполярном релятивистском диоде описывается формулами
(10)
$\sqrt {2{{J}_{0}}} = {{I}_{0}}\left( 1 \right),\,\,\,\,{{I}_{0}}\left( {{{\bar {\varphi }}}} \right) = \frac{{{{\varphi }}_{A}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}}}\int\limits_0^{{{\bar {\varphi }}}} {\frac{{dt}}{{\sqrt[4]{{t\left( {1 + {{{{{\tilde {\mu }}}}}_{A}}t} \right)}}}}{\kern 1pt} {\kern 1pt} } .$В нерелятивистском и ультрарелятивистском пределах из выражений (10) получаем
(11)
$\sqrt {2{{J}_{0}}} = \frac{4}{3}\frac{{{{\varphi }}_{A}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}}},\,\,\,\,\sqrt {2{{J}_{0}}} = 2\sqrt {{{{{\varphi }}}_{A}}} .$В случае ${{E}_{A}},{{E}_{B}} \ne 0$ параметры ${{\alpha }}$, ${{\beta }}$ должны удовлетворять требованиям $E_{A}^{2} > 0$, $E_{B}^{2} > 0$ или в развернутом виде
(12)
$\begin{gathered} {{\alpha }} + {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} < \sqrt {1 + {{{{\mu }}}_{A}}} , \\ {{\alpha }}\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} - \left( {{{\alpha }} + {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} } \right) > \sqrt {{{{{{\bar {\varphi }}}}}_{B}}\left( {1 + {{{{\mu }}}_{B}}} \right)} . \\ \end{gathered} $Для униполярного диода вместо (12) имеем
Условимся обозначать ${{\rho }}$- и Т-режимы в плоскостях А, В соответствующими нижними индексами: ${{A}_{{{\rho }}}}$, ${{B}_{{{\rho }}}}$ и ${{A}_{T}}$, ${{B}_{T}}$.
3. ЧАСТНЫЕ СЛУЧАИ
Униполярный диод с ионным фонтаном, режим ${{B}_{T}}$, нерелятивистские электроны. Интегралы ${{\bar {I}}_{1}}$, ${{\bar {I}}_{2}}$ и поле ${{E}_{B}}$ определены формулами
(14)
$\begin{gathered} {{{\bar {I}}}_{1}} = \int\limits_0^{{{\bar {\varphi }}}} {{{{\left[ {\sqrt t + {{\beta }}\left( {\sqrt {{{{{{\bar {\varphi }}}}}_{B}} - t} - \sqrt {{{{{{\bar {\varphi }}}}}_{B}}} } \right)} \right]}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}dt,\,\,\,\,{{\beta }} < 1;} \hfill \\ {{{\bar {I}}}_{2}} = \int\limits_{{{{{{\bar {\varphi }}}}}_{B}}}^{{{\bar {\varphi }}}} {\frac{{dt}}{{\sqrt {\sqrt t - {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} } }}} = \frac{4}{3}\left( {\sqrt t + 2{{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} } \right) \times \hfill \\ \times \,\,\sqrt {\sqrt t - {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} } \left| {\begin{array}{*{20}{c}} {{{\bar {\varphi }}}} \\ {{{{{{\bar {\varphi }}}}}_{B}}} \end{array}} \right. = \frac{4}{3}\left( {\sqrt {{{\bar {\varphi }}}} + 2{{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} } \right) \times \hfill \\ \times \,\,\sqrt {\sqrt {{{\bar {\varphi }}}} - {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} } - \frac{4}{3}{{\bar {\varphi }}}_{B}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}\left( {1 + 2{{\beta }}} \right)\sqrt {1 - {{\beta }}} ; \hfill \\ E_{B}^{2} = 2\sqrt {2{{{{\varphi }}}_{B}}} {{J}_{e}}\left( {1 - {{\beta }}} \right),\,\,\,\,E_{A}^{2} = 2\sqrt 2 {{J}_{e}}\left( {1 - {{\beta }}\sqrt {{{{{\varphi }}}_{B}}} } \right). \hfill \\ \end{gathered} $Коэффициент усиления ${{K}_{e}}$ описывается выражением
(15)
$\begin{gathered} \sqrt {{{K}_{e}}} = B{{\varphi }}_{B}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}} + \left( {1 + 2{{\beta }}\sqrt {{{{{\varphi }}}_{B}}} } \right)\sqrt {1 - {{\beta }}\sqrt {{{{{\varphi }}}_{B}}} } , \\ B = \frac{3}{4}{{{\bar {I}}}_{1}}\left( {{\beta }} \right) - \left( {1 + 2{{\beta }}} \right)\sqrt {1 - {{\beta }}} , \\ {{{\bar {I}}}_{1}} = \int\limits_0^1 {{{{\left[ {\sqrt t + {{\beta }}\left( {\sqrt {1 - t} - 1} \right)} \right]}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}} dt, \\ \end{gathered} $где ${{\bar {I}}_{1}}\left( {{\beta }} \right)$ – табулированный в [1] интеграл.
Значение ${{{{\varphi }}}_{B}}$, при котором функция $\sqrt {{{K}_{e}}} $ достигает максимума $\sqrt {{{K}_{{em}}}} $, удовлетворяет уравнению
(16)
$B\,{{\varphi }}_{B}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}\sqrt {1 - {{\beta }}\sqrt {{{{{\varphi }}}_{B}}} } + {{\beta }}\left( {1 - 2{{\beta }}\sqrt {{{{{\varphi }}}_{B}}} } \right) = 0.$Корень этого уравнения
(17)
$\sqrt {{{\varphi }}_{B}^{*}} = \frac{1}{{2{{\beta }}}}\left( {1 + \frac{B}{{\sqrt {{{B}^{2}} + 4{{{{\beta }}}^{3}}} }}} \right)$позволяет рассчитать максимальный коэффициент усиления и соответствующие ему параметры диода.
Униполярный диод с ионным фонтаном, режим ${{B}_{T}}$, релятивистские скорости. Интегралы ${{\bar {I}}_{1}}$, ${{\bar {I}}_{2}}$ определены формулами (4) при ${{\alpha }} = 0$, ${{\beta }} < \sqrt {1 + {{{{\mu }}}_{B}}} $; ${{{{\varphi }}}_{A}}$, ${{{{\varphi }}}_{B}}$, ${{\beta }}$ – варьируемые параметры:
(18)
$\begin{gathered} {{{\bar {I}}}_{1}}\, = \,\int\limits_0^{{{\bar {\varphi }}}} {{{{\left[ {\sqrt {t\left( {1\, + \,{{{{{\tilde {\mu }}}}}_{A}}t} \right)} \, + \,l\sqrt {1\, + \,{{{{{\tilde {\mu }}}}}_{A}}{{{{{\bar {\varphi }}}}}_{B}}} \left( {\sqrt {{{{{{\bar {\varphi }}}}}_{B}}\, - \,t} \, - \,\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} } \right)} \right]}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}\,dt} , \\ {{{\bar {I}}}_{2}} = \int\limits_{{{{{{\bar {\varphi }}}}}_{B}}}^{{{\bar {\varphi }}}} {{{{\left[ {\sqrt {t\left( {1 + {{{{{\tilde {\mu }}}}}_{A}}t} \right)} - l\sqrt {1 + {{{{{\tilde {\mu }}}}}_{A}}{{{{{\bar {\varphi }}}}}_{B}}} \sqrt {{{{{{\bar {\varphi }}}}}_{B}}} } \right]}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}dt} ,\,\,\,\,l < 1. \\ \end{gathered} $Униполярный диод с ионным фонтаном, режим ${{B}_{T}}$, ультрарелятивистский предел. Оба интеграла ${{\bar {I}}_{1}}$, ${{\bar {I}}_{2}}$ могут быть выражены через элементарные функции:
(19)
$\begin{gathered} {{I}_{1}} = \int\limits_0^{{\varphi }} {\frac{{dt}}{{\sqrt {t + {{\beta }}\sqrt 2 \left( {\sqrt {{{{{\varphi }}}_{B}} - t} - \sqrt {{{{{\varphi }}}_{B}}} } \right)} }}} = \\ = 2\left[ {\sqrt {{{\varphi + \beta }}\sqrt 2 \left( {\sqrt {{{{{\varphi }}}_{B}} - {{\varphi }}} - \sqrt {{{{{\varphi }}}_{B}}} } \right)} } \right. + \\ \left. { + \,\,\frac{{{{\beta }}\sqrt 2 }}{2}\left( {\arcsin \frac{{ - 2\sqrt {{{{{\varphi }}}_{B}} - {{\varphi }}} + {{\beta }}\sqrt 2 }}{{2\sqrt {{{{{\varphi }}}_{B}}} - {{\beta }}\sqrt 2 }} + \frac{{{\pi }}}{2}} \right)} \right], \\ {{I}_{2}} = \int\limits_{{{{{\varphi }}}_{B}}}^{{\varphi }} {\frac{{dt}}{{\sqrt {t - {{\beta }}\sqrt {{\text{2}}{{{{\varphi }}}_{B}}} } }}} = \\ = 2\left[ {\sqrt {{{\varphi }} - {{\beta }}\sqrt {2{{{{\varphi }}}_{B}}} } - \sqrt {{{{{\varphi }}}_{B}}\left( {1 - {{\beta }}\sqrt 2 } \right)} } \right]; \\ {{\beta }}\sqrt 2 = l\sqrt {{{{{\varphi }}}_{B}}} ,\,\,\,\,l < 1. \\ \end{gathered} $Используя формулы (9), (19), для коэффициента усиления получаем
(20)
${{K}_{e}} = \frac{1}{4}{{\left[ {2\sqrt {1 - l{{{{{\bar {\varphi }}}}}_{B}}} + l\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} \left( {\arcsin \frac{l}{{2 - l}} + \frac{{{\pi }}}{2}} \right)} \right]}^{2}},$причем максимальное значение ${{K}_{{em}}}$ достигается при ${{{{\bar {\varphi }}}}_{B}} = {{\bar {\varphi }}}_{B}^{*}$:
(21)
$\begin{gathered} {{\bar {\varphi }}}_{B}^{*} = \frac{{{{{{\gamma }}}^{2}}}}{{4 + l{{{{\gamma }}}^{2}}}},\,\,\,\,{{\gamma }} = \arcsin \frac{l}{{2 - l}} + \frac{{{\pi }}}{2}, \\ {{K}_{{em}}} = 1 + \frac{1}{4}l{{{{\gamma }}}^{2}}. \\ \end{gathered} $Соответствующие величины ${{z}_{B}}$, ${{\bar {J}}_{{iB}}}$ определены формулами
(22)
$\begin{gathered} {{z}_{B}} = {{\gamma }}\frac{{2\sqrt {1 - l} + l{{\gamma }}}}{{4 + l{{{{\gamma }}}^{2}}}}, \\ {{{\bar {J}}}_{{iB}}} \equiv \frac{{2{{J}_{{iB}}}\sqrt {{{{{\eta }_{e}}} \mathord{\left/ {\vphantom {{{{\eta }_{e}}} {{{\eta }_{i}}}}} \right. \kern-0em} {{{\eta }_{i}}}}} }}{{{{{{\varphi }}}_{A}}\sqrt {2{{{{\varphi }}}_{A}}} }} = \frac{1}{4}l{{\gamma }}\sqrt {4 + l{{{{\gamma }}}^{2}}} . \\ \end{gathered} $Для электронного тока и поля ${{E}_{B}}$ получаем
(23)
$\sqrt {2{{{\bar {J}}}_{e}}} = \sqrt {{{{{\varphi }}}_{A}}} \,\sqrt {4 + l{{{{\gamma }}}^{2}}} ,\,\,\,\,E_{B}^{2} = {{{{\varphi }}}_{A}}{{{{\gamma }}}^{2}}\left( {1 - l} \right).$При $l \to 1$ формулы (20)–(23) переходят в приведенные в работе [13] соотношения для параметров потока.
Биполярный диод без ионного фонтана, режим ${{A}_{T}}$, релятивистские скорости. Этот вариант полностью соответствует рассмотренной выше ситуации с униполярным диодом на интервале $0 \leqslant z \leqslant {{z}_{B}}$ и получается из него при следующих заменах:
(24)
$\begin{gathered} \beta \to \alpha ,\,\,\,\,{{\varphi }_{B}} \to {{\varphi }_{A}},\,\,\,\,{{z}_{B}} \to 1; \\ \alpha = k\sqrt {1 + {{{\tilde {\mu }}}_{A}}} ,\,\,\,\,k < 1. \\ \end{gathered} $Нерелятивистский вариант исследован в работе [1].
Биполярный диод с ионным фонтаном, режим ${{B}_{{{\rho }}}}$, ${{A}_{T}}$, скорости электронов любые. Условие ${{E}_{B}} = 0$ определяет связь между параметрами ${{\alpha }}$, ${{\beta }}$:
(25)
$\begin{gathered} {{\alpha }} = k\frac{{\sqrt {1 + {{{{{\tilde {\mu }}}}}_{A}}} - \sqrt {{{{{{\bar {\varphi }}}}}_{B}}\left( {1 + {{{{{\tilde {\mu }}}}}_{A}}{{{{{\bar {\varphi }}}}}_{B}}} \right)} }}{{\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} }},\,\,\,\,k < 1; \\ {{\beta }} = \frac{1}{{\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} }}\left[ {\sqrt {{{{{{\bar {\varphi }}}}}_{B}}\left( {1 + {{{{{\tilde {\mu }}}}}_{A}}{{{{{\bar {\varphi }}}}}_{B}}} \right)} + {{\alpha }}\left( {\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} - 1} \right)} \right]. \\ \end{gathered} $Электрическое поле на аноде и ионные токи описываются формулами
(26)
$\begin{gathered} {{E}_{A}} = {{\left[ {2\sqrt 2 {{J}_{e}}\sqrt {{{{{\varphi }}}_{A}}} \left( {\sqrt {1 + {{{{{\tilde {\mu }}}}}_{A}}} - {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} - {{\alpha }}} \right)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ {{{\bar {J}}}_{{iB}}} \equiv 2{{J}_{{iB}}}\sqrt {{{{{\eta }_{e}}} \mathord{\left/ {\vphantom {{{{\eta }_{e}}} {{{\eta }_{i}}}}} \right. \kern-0em} {{{\eta }_{i}}}}} = {{\beta }}{{K}_{e}}{{J}_{0}}, \\ {{{\bar {J}}}_{i}} \equiv {{J}_{i}}\sqrt {{{{{\eta }_{e}}} \mathord{\left/ {\vphantom {{{{\eta }_{e}}} {{{\eta }_{i}}}}} \right. \kern-0em} {{{\eta }_{i}}}}} = {{\alpha }}{{K}_{e}}{{J}_{0}},\,\,\,\,{{J}_{e}} = {{K}_{e}}{{J}_{0}}. \\ \end{gathered} $Все интегралы, кроме интеграла ${{\bar {I}}_{2}}$ из (6), поддаются только численной оценке.
Биполярный диод с ионным фонтаном, режим ${{A}_{{{\rho }}}}$, ${{B}_{T}}$, скорости электронов любые. Ситуация аналогична предыдущему случаю: условие ${{E}_{A}} = 0$ задает связь между ${{\alpha }}$ и ${{\beta }}$, интегралы не выражаются через элементарные функции
(27)
$\begin{gathered} {{\beta }} = l\left[ {\frac{{\sqrt {1 + {{{{{\tilde {\mu }}}}}_{A}}{{{{{\bar {\varphi }}}}}_{B}}} }}{{\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} }} - \left( {\frac{1}{{\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} }} - 1} \right)\frac{{\sqrt {1 + {{{{{\tilde {\mu }}}}}_{A}}} }}{{\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} }}} \right],\,\,\,\,l < 1; \\ {{\alpha }} = \sqrt {1 + {{{{{\tilde {\mu }}}}}_{A}}} - {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} . \\ \end{gathered} $Формулы для ${{\bar {J}}_{{iB}}}$, ${{\bar {J}}_{i}}$, ${{J}_{e}}$ из (27) остаются справедливыми, для поля ${{E}_{B}}$ имеем
(28)
$\begin{gathered} E_{B}^{2} = 2\sqrt 2 {{J}_{e}}\sqrt {{{{{\varphi }}}_{A}}} \times \\ \times \,\,\left[ {\sqrt {{{{{{\bar {\varphi }}}}}_{B}}\left( {1 + {{{{{\tilde {\mu }}}}}_{A}}{{{{{\bar {\varphi }}}}}_{B}}} \right)} - {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} + {{\alpha }}\left( {\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} - 1} \right)} \right]. \\ \end{gathered} $4. РЕЗУЛЬТАТЫ РАСЧЕТОВ
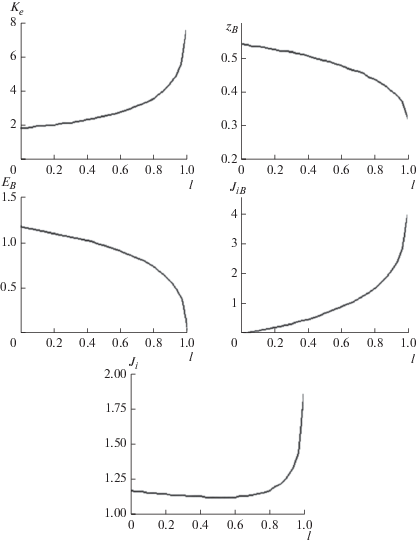
Униполярный диод. На рис. 1 приведены функции ${{{{\varphi }}}_{B}}\left( {{\beta }} \right)$, ${{z}_{B}}\left( {{\beta }} \right)$, ${{E}_{B}}\left( {{\beta }} \right)$, ${{K}_{{em}}}\left( {{\beta }} \right)$, ${{\bar {J}}_{{iB}}}\left( {{\beta }} \right)$ для униполярного нерелятивистского диода с ионным фонтаном, причем последняя из них определяет ток фонтана при максимальном коэффициенте усиления для данного значения ${{\beta }}$. Для ${{\beta }} = 0.2$ поле $E\left( {{\beta }} \right)$ возрастает от нуля на катоде до величины, почти равной значению для плоского конденсатора (0.977) при ${{z}_{B}} = 0.277$, ${{{{\varphi }}}_{B}} = 0.351$, ${{K}_{e}} = 1.134$ и ${{\bar {J}}_{{iB}}}\left( {{\beta }} \right) = 0.143$.
Рис. 1.
Параметры униполярного нерелятивистского диода с ионным фонтаном: (а) функции ${{\varphi }}_{B}^{*}\left( {{\beta }} \right)$ (кривая 1), ${{\bar {z}}_{B}}\left( {{\beta }} \right)$ (кривая 2), ${{E}_{B}}\left( {{\beta }} \right)$ (кривая 3); (б): функции $K_{{em}}^{{}}\left( {{\beta }} \right)$ (кривая 1), $\bar {J}_{{iB}}^{{}}\left( {{\beta }} \right)$ (кривая 2); (в) функции $E_{A}^{{}}\left( {{\beta }} \right)$ (кривая 1), $E_{B}^{{}}\left( {{\beta }} \right)$ (кривая 2).
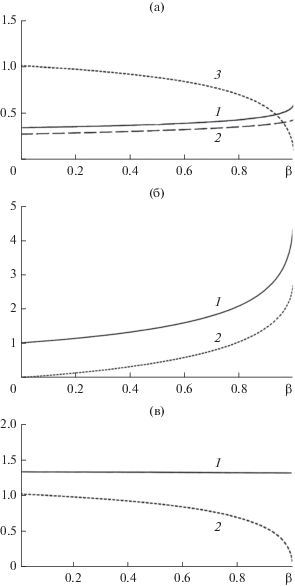
Интересным является тот факт, что поле на аноде ${{E}_{A}}$ не зависит от ${{\beta }}$ и остается равным значению 4/3, характерному для униполярного диода в ${{\rho }}$‑режиме. Часть интервала ${{z}_{B}} \leqslant z \leqslant 1$, занятая униполярным потоком, при вариации ${{\beta }}$ представляет собой диод с зависящими от ${{\beta }}$ расстоянием между электродами, приложенной разностью потенциалов и инжектируемым током. Условие
следующее из равенства ${{E}_{A}} = {4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}$, является нетривиальным тождеством, включающим интеграл ${{\bar {I}}_{1}}$ из (15).
Описываемые зависимостями рис. 1 режимы соответствуют возможным стационарным состояниям, определяемым инжектируемым ионным током фонтана. При ${{\beta }} \to 1$ наступает режим ${{B}_{{{\rho }}}}$ с нулевым полем в плоскости отражения, рассмотренный в работе [13]. Параметры ультрарелятивистского униполярного диода с ионным фонтаном представлены на рис. 2.
Рис. 2.
Параметры ультрарелятивистского униполярного диода с ионным фонтаном: (а) функции ${{\varphi }}_{B}^{{}}\left( {{\beta }} \right)$ (кривая 1) и $z_{B}^{{}}\left( {{\beta }} \right)$ (кривая 2); (б) функции $K_{{em}}^{{}}\left( {{\beta }} \right)$ (кривая 1), $E_{B}^{{}}\left( {{\beta }} \right)$ (кривая 2) и $\bar {J}_{{iB}}^{{}}\left( {{\beta }} \right)$ (кривая 3).
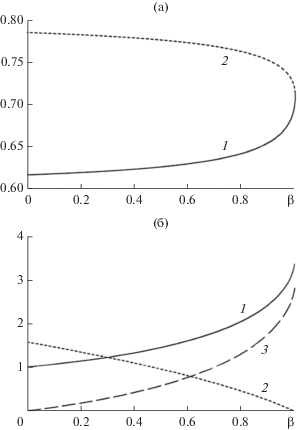
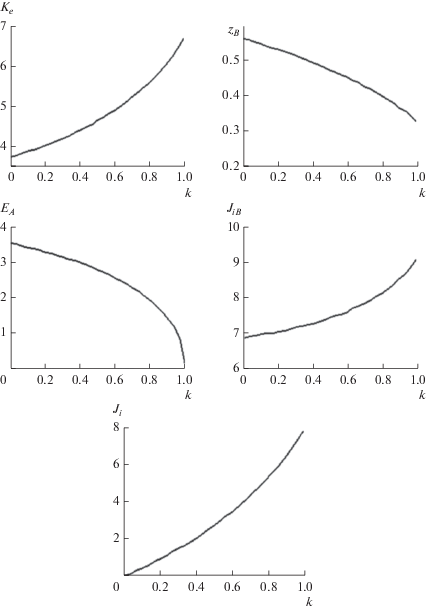
Биполярный диод. В работе [1] рассматривается биполярный диод с отличным от нуля полем на аноде. На рис. 3 представлены параметры набора режимов ${{B}_{{{\rho }}}}$, ${{A}_{{{\kern 1pt} T}}}$ диода с ионным фонтаном. Исходное состояние $k = 0$ соответствует униполярному диоду, при $k = 1$ получаем режим ${{B}_{{{\rho }}}}$, ${{A}_{{{\rho }}}}$ с нулевым полем на аноде. Для энергии ионов фонтана выбрано значение ${{{{\bar {\varphi }}}}_{B}} = 0.55$, приводящее в режиме ${{B}_{{{\rho }}}}$, ${{A}_{{{\rho }}}}$ к максимальному коэффициенту усиления ${{K}_{e}} = 7.827$, ${{z}_{B}} = 0.324$.
Рис. 3.
Параметры нерелятивистского биполярного диода с ионным фонтаном в режиме ${{B}_{{{\rho }}}}$, ${{A}_{{{\kern 1pt} T}}}$.
Переход от униполярного диода к биполярному в режиме ${{A}_{{{\rho }}}}$ в [1] привел к коэффициенту усиления ${{K}_{e}} = 1.86$. Введение ионного фонтана в униполярный диод обеспечило возрастание ${{K}_{e}}$ до 4.58. В биполярном диоде за счет 30%-го увеличения тока фонтана электронный ток вырос в 7.83 раза. В варианте с фонтаном переход от униполярного к биполярному диоду увеличил коэффициент ${{K}_{e}}$ в 7.83/4.58=1.71 раз.
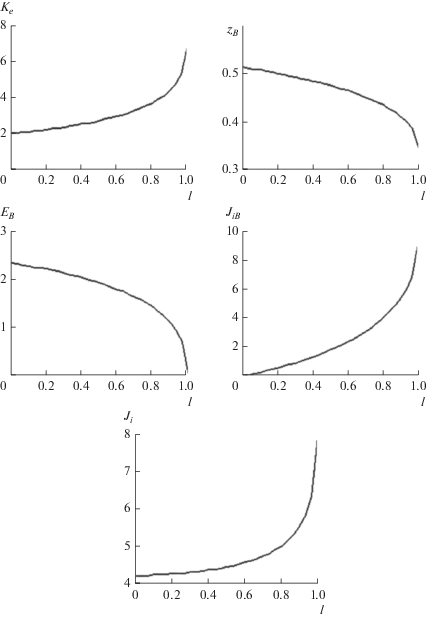
Режимы ${{B}_{T}}$, ${{A}_{{{\kern 1pt} {{\rho }}}}}$ для нерелятивистского случая описывает рис. 4. В исходном состоянии $l = 0$ ионный фонтан отсутствует. Увеличение тока с анода от ${{\bar {J}}_{i}} = 1.2$ в полтора раза при росте тока фонтана от нуля до ${{\bar {J}}_{{iB}}} = 4$ приводит к повышению коэффициента усиления ${{K}_{e}}$ в 4.2 раза. Энергия ионов фонтана соответствует ${{{{\bar {\varphi }}}}_{B}} = 0.55$.
На рис. 5, 6 представлен набор режимов, предшествующих варианту ${{B}_{{{\rho }}}}$, ${{A}_{{{\rho }}}}$ с максимальным коэффициентом усиления ${{K}_{e}} = 6.62$, ${{z}_{B}} = 0.346$, ${{{{\bar {\varphi }}}}_{B}} = 0.49$ для релятивистского диода с анодным потенциалом ${{{{\varphi }}}_{A}} = 2$. Исходным состоянием для рис. 5 является униполярный диод с фонтаном, причем параметр k управляет током ${{\bar {J}}_{i}}$ с анода, при изменении которого пробегается набор режимов ${{B}_{{{\rho }}}}$, ${{A}_{{{\kern 1pt} T}}}$. Для рис. 6 при $l = 0$ имеем биполярный диод без фонтана и набор режимов ${{B}_{T}}$, ${{A}_{{{\kern 1pt} {{\rho }}}}}$ при $l > 0$. Сравнение пар рис. 3, 4 и рис. 5, 6 позволяет судить о промежуточных режимах биполярного диода с ионным фонтаном на концах интервала (0…1 МВ), дающего оценку сверху для возможных значений анодного потенциала φA плоского диода.
5. ЭМИССИЯ С КАТОДА, ОГРАНИЧЕННАЯ ТЕМПЕРАТУРОЙ
В цитированных работах по биполярным пучкам и в разд. 1–4 этой работы предполагалось, что катод находится в ${{\rho }}$-режиме эмиссии, причем главной задачей являлось достижение максимального коэффициента усиления электронного тока.
Представляет интерес исследовать вопрос об электрическом поле в плоском промежутке с инжекцией ионов из-за катода и эмиссией в Т-режиме, когда значение ${{J}_{e}}$ известно. При условии сращивания поля в плоскости отражения ионов имеем
(30)
$\begin{gathered} {{{\bar {E}}}^{2}} = 2{{J}_{e}}\left[ {\sqrt {{{\bar {\varphi }}}\left( {1 + {{{{{\tilde {\mu }}}}}_{A}}{{\bar {\varphi }}}} \right)} + {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}} - {{\bar {\varphi }}}} } \right. + \\ \left. { + \,\,{{\alpha }}\sqrt {1 - {{\bar {\varphi }}}} + C} \right],\,\,\,\,0 \leqslant z \leqslant {{z}_{B}}, \\ {{{\bar {E}}}^{2}} = 2{{J}_{e}}\left[ {\sqrt {{{\bar {\varphi }}}\left( {1 + {{{{{\tilde {\mu }}}}}_{A}}{{\bar {\varphi }}}} \right)} + {{\alpha }}\sqrt {1 - {{\bar {\varphi }}}} + C} \right], \\ {{z}_{B}} \leqslant z \leqslant 1;\,\,\,\,{{{\bar {E}}}^{2}} \equiv {{{{\varphi }}_{A}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}{{E}^{2}}} \mathord{\left/ {\vphantom {{{{\varphi }}_{A}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}{{E}^{2}}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}. \\ \end{gathered} $Значения поля в плоскостях С, В, А определены формулами
(31)
$\begin{gathered} \bar {E}_{C}^{2} = 2{{J}_{e}}\left[ {{{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} + C} \right], \\ \bar {E}_{B}^{2} = 2{{J}_{e}}\left[ {\sqrt {{{{{{\bar {\varphi }}}}}_{B}}\left( {1 + {{{{{\tilde {\mu }}}}}_{A}}{{{{{\bar {\varphi }}}}}_{B}}} \right)} + C} \right], \\ \bar {E}_{A}^{2} = 2{{J}_{e}}\left[ {\sqrt {1 + {{{{{\tilde {\mu }}}}}_{A}}} + C} \right]. \\ \end{gathered} $Неявное решение $z = z\left( {{\varphi }} \right)$, записанное при $z = {{z}_{B}}$ и $z = 1$, приводит к соотношениям
(32)
$\begin{gathered} {{z}_{B}}\sqrt {2{{J}_{e}}\sqrt 2 } = \\ = \int\limits_0^{{{{{{\bar {\varphi }}}}}_{B}}} {{{{\left[ {\sqrt {t\left( {1 + {{{{\mu }}}_{A}}t} \right)} + {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}} - t} + C} \right]}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}dt \equiv {{{\bar {I}}}_{1}},} \\ \left( {1 - {{z}_{B}}} \right)\sqrt {2{{J}_{e}}\sqrt 2 } = \int\limits_{{{{{{\bar {\varphi }}}}}_{B}}}^1 {{{{\left[ {\sqrt {t\left( {1 + {{{{\mu }}}_{A}}t} \right)} + C} \right]}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}dt \equiv {{{\bar {I}}}_{2}}.} \\ \end{gathered} $При заданных значениях Je, φA, φB для вычисления константы С служит уравнение
Плоскость отражения после этого определяется формулой
Ограничимся рассмотрением случая нерелятивистских скоростей в униполярном диоде с ионным фонтаном. Интегралы ${{\bar {I}}_{1}}$, ${{\bar {I}}_{2}}$ из (32) принимают вид
(35)
$\begin{gathered} {{{\bar {I}}}_{1}} = \int\limits_0^{{{{{{\bar {\varphi }}}}}_{B}}} {{{{\left[ {\sqrt t + {{\beta }}\sqrt {{{{{{\bar {\varphi }}}}}_{B}} - t} + C} \right]}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}dt,} \\ {{{\bar {I}}}_{2}} = \int\limits_{{{{{{\bar {\varphi }}}}}_{B}}}^1 {{{{\left( {\sqrt t + C} \right)}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}dt} = \\ = \frac{4}{3}\left[ {\left( {1 - 2C} \right)\sqrt {1 + C} - \left( {\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} - 2C} \right)\sqrt {\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} + C} } \right]. \\ \end{gathered} $Из формул (31) следует связь параметров ${{E}_{C}}$ и ${{E}_{B}}$:
(36)
$\bar {E}_{C}^{2} = 2{{J}_{e}}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} \left( {{{\beta }} - 1} \right) + \bar {E}_{B}^{2}.$При ${{\beta }} \to 1$ (возрастание тока фонтана) напряженности поля сравниваются
Если ${{\beta }} < 1$, то значение ${{E}_{B}}$ не может обращаться в нуль, причем поле
(38)
$\bar {E}_{B}^{2} = 2{{J}_{e}}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} \left( {{\text{1}} - {{\beta }}} \right)$обеспечивает режим ${{C}_{{{\rho }}}}$ на катоде. При $\beta > 1$ невозможна эмиссия, ограниченная пространственным зарядом.
Для демонстрации нескольких численных примеров выберем плотность электронного тока, равную ${1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}{{J}_{0}}$ из (11):
(39)
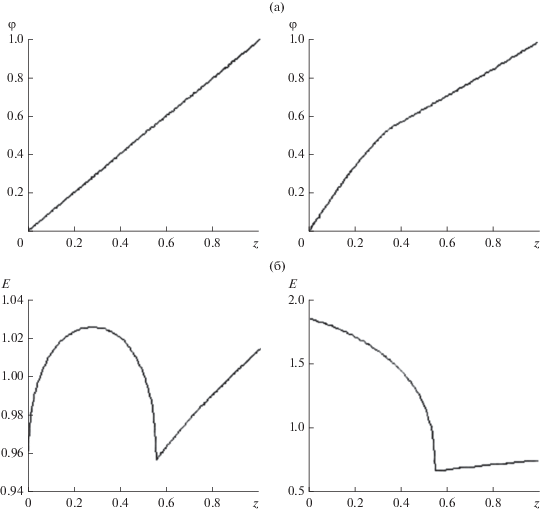
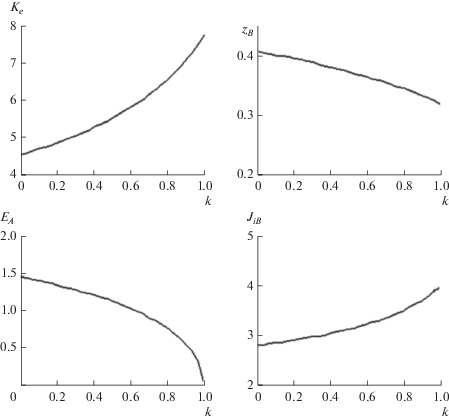
$\sqrt {2{{J}_{0}}} = \frac{{2\sqrt[4]{8}}}{3},\,\,\,\,\sqrt {2{{J}_{e}}} = \frac{{\sqrt[4]{8}}}{3}.$Примем значение ${{{{\bar {\varphi }}}}_{B}} = 0.55$, соответствующее максимальному коэффициенту усиления в варианте ${{C}_{{{\rho }}}}$, ${{B}_{{{\rho }}}}$ (${{K}_{e}} = 7.83$, ${{z}_{B}} = 0.32$). Результаты решения уравнения (33) для нескольких значений параметра ${{\beta }}$ и величѝны напряженности электрического поля на электродах приведены в табл. 1, причем ${{\beta }} = 0$ соответствует униполярному диоду с тем же током ${{J}_{e}}$, но без фонтана. Из данных табл. 1 видно, что возрастание тока фонтана при ${{\beta }} \leqslant $ 1 способствует выравниванию градиентов: в случае ${{\beta }} = 1$ вариация поля составляет 6% с превышением значения Е для плоского конденсатора на 2%: в униполярном диоде (${{\beta }} = 0$) поле изменяется на 22%. При ${{\beta }} > 1$ возрастает поле на катоде, в 1.8 раза для ${{\beta }} = 10$ превышая среднее значение в интервале ${{z}_{B}} \leqslant z \leqslant 1$. Характер изменения потенциала и поля при ${{\beta }} = 1,{\kern 1pt} \,{\kern 1pt} 10$ отражает рис. 7.
Таблица 1.
Параметры униполярного нерелятивистского диода с ионным фонтаном и эмиссией электронов в Т-режиме
| ${{\beta }}$ | C | ${{E}_{C}}$ | ${{E}_{B}}$ | ${{E}_{A}}$ | ${{\bar {z}}_{B}}$ |
|---|---|---|---|---|---|
| 0 | 1.603 | 0.844 | – | 1.076 | – |
| 0.5 | 1.452 | 1.059 | 0.987 | 1.044 | 0.558 |
| 1 | 1.317 | 0.957 | 0.957 | 1.015 | 0.544 |
| 3 | 0.885 | 1.175 | 0.850 | 0.915 | 0.491 |
| 5 | 0.604 | 1.383 | 0.773 | 0.844 | 0.445 |
| 10 | 0.242 | 1.845 | 0.661 | 0.742 | 0.361 |
ЗАКЛЮЧЕНИЕ
При выходе на режим с максимальным коэффициентом усиления электронного тока в униполярном и биполярном диодах с ионным фонтаном, инжектируемым из-за катода, допустимо существование спектра стационарных состояний, характеризуемых меньшими значениями тока фонтана и ненулевым электрическим полем в плоскости отражения. Этот спектр в определенном смысле описывает эволюцию системы при достижении ионным источником максимального тока, или соответствует случаю его недостаточной мощности. Катод и плоскость отражения ионов в униполярном диоде, а также и анод в биполярном варианте работают в режиме ограничения тока пространственным зарядом, в то время как поле в плоскости отражения постепенно достигает нулевого значения.
Для катода, эмиссия с которого ограничена температурой, в униполярном диоде возможны режимы с током фонтана ${{J}_{{iB}}}$, превышающим ток, соответствующий ${{\rho }}$-режиму на упомянутых электродах. При умеренных значениях ${{J}_{{iB}}}$ (${{\beta }} \geqslant 1$) имеет место почти линейное распределение потенциала на бóльшей части промежутка. Дальнейшее увеличение тока ${{J}_{{iB}}}$ (${{\beta }} = 10$) приводит к появлению вблизи катода области с высокими значениями напряженности.
Список литературы
Langmuir I. // Phys. Rev. 1929. V. 33. № 6. P. 954.
Howes W.L. // J. Appl. Phys. 1965. V. 36. № 6. P. 2039.
Вашковский А.В., Завьялов М.А., Сыровой В.А. // РЭ. 1999. Т. 44. № 4. С. 485.
Акимов П.И., Богословская А.Б. // Прикл. физика. 2002. № 4. С. 90.
Астрелин В.Т., Карпов И.В. // Плазменная эмиссионная электроника / Под ред. А.П. Семенова. Улан-Удэ: Изд-во БНЦ СО РАН, 2012. С. 74.
Григорьев С.В., Астрелин В.Т., Кандауров И.В. и др. // Плазменная эмиссионная электроника / Под ред. А.П. Семенова. Улан-Удэ: Изд-во БНЦ СО РАН, 2012. С. 81.
Белкин В.М., Завьялов М.А., Камунин А.А. // РЭ. 1976. Т. 21. № 12. С. 2446.
Завьялов М.А., Сыровой В.А. // РЭ. 2016. Т. 61. № 4. С. 380.
Бобров Ю.К., Быстров В.П., Рухадзе А.А. // Краткие сообщения ФИАН по физике. 2005. № 7. Р. 23.
Белкин В.М., Завьялов М.А., Сыровой В.А. // РЭ. 2011. Т. 56. № 2. С. 212.
Белкин В.М., Камунин А.А. // РЭ. 1979. Т. 24. № 1. С. 142.
Белкин В.М., Завьялов М.А., Сапронова Т.М., Сыровой В.А. // РЭ. 2014. Т. 59. № 6. С. 593.
Завьялов М.А., Стальков П.М., Сыровой В.А. // РЭ. 2017. Т. 62. № 8. С. 799.
Завьялов М.А., Сапронова Т.М., Сыровой В.А. // РЭ. 2018. Т. 63. № 6. С. 597.
Коваль Н.Н., Окс Е.М., Протасов Ю.С., Семашко Н.Н. Эмиссионная электроника. М.: МГТУ им. Н.Э. Баумана, 2009.
Завьялов М.А., Сапронова Т.М., Сыровой В.А. // РЭ. 2018. Т. 63. № 6. С. 590.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника