Радиотехника и электроника, 2021, T. 66, № 6, стр. 559-564

ВВЕДЕНИЕ

Как известно, дифракция электромагнитных волн на наноструктурах из благородных металлов (серебра, золота) в световом диапазоне длин волн $300\,\,{\text{нм}} < \lambda < 900\,\,{\text{нм}}$ сопровождается как образованием поверхностных волн (плазмон-поляритонов), так и существованием их резонансов. При этом интерес к исследованию свойств плазмон-поляритонов связан главным образом с высокой локализацией электромагнитного поля вблизи поверхности наноструктур, которая позволяет использовать их в субволновом и ближнепольном зондировании. В [1] отмечалось, что нанопровода из серебра и золота широко применяются в качестве сенсоров. Отметим, что плазмонные резонансы в цилиндрических наноструктурах (нитях) с постоянной или переменной кривизной, но постоянным знаком кривизны исследовались в целом ряде работ. Так, было показано, что цилиндры с круглым сечением реализуют резонансы плазмонов в ультрафиолетовой части спектра [1]. Используя нанотрубки, можно сместить частоты плазмонных резонансов в видимую область светового диапазона [2, 3]. В работе [4] исследованы плазмонные резонансы в кварцевой нанонити, покрытой слоем золота переменной толщины. При этом предполагалось, что границами оболочки являются круговые цилиндры со смещенными центрами. Различные геометрии оболочек из серебра и кварца, образованные круговыми, эллиптическими цилиндрами или прямоугольными пластинами, рассматривались в работах [5–10].

Цель данной работы – исследовать особенности плазмонных резонансов в 2D-наноструктурах из серебра в случае, когда контур поперечного сечения структуры имеет не только переменную кривизну, но и изменение знака кривизны.

1. ФОРМУЛИРОВКА ЗАДАЧИ

Рассмотрим двумерную задачу дифракции плоской электромагнитной линейно-поляризованной волны на двумерной цилиндрической диэлектрической структуре, контур поперечного сечения которого представляет собой овал Кассини. Как известно, такой контур обладает не только переменной кривизной, но и изменением знака кривизны. Плоская волна распространяется в направлении единичного вектора ($\cos {{\varphi }_{0}},\sin {{\varphi }_{0}},0$) и характеризуется в цилиндрической системе координат $r,\varphi $ следующими компонентами электромагнитного поля:

Зависимость от времени выбрана в виде $\exp (i\omega t)$, где $\omega = kc$ – круговая частота, $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$ – волновое число свободного пространства, $c$ – скорость света в вакууме, $\lambda $ − длина волны, $\eta = 120\pi \,\,Ом$ − волновое сопротивление вакуума.

Контур поперечного сечения ${{r}_{S}}(\varphi )$ структуры в цилиндрической системе координат $r,\varphi $ описывается формулой

Отметим, что, изменяя отношение параметров ${b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a}$ (при фиксированном $b$), можно изменять степень “вогнутости” контура (2) рассеивающей структуры. На рис. 1 изображены контуры поперечного сечения структуры при $\lambda = 400\,\,{\text{нм}}$ и для различных значений параметров $kb = 0.2\pi $, $a = 0.7b,$ $0.9b,$ $0.96b,$ $0.99b,$ $0.999b$. Считается, что среда структуры представляет собой серебро. При этом частотная зависимость относительной диэлектрической проницаемости ${{\varepsilon }_{c}}(\lambda )$ = 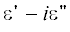$ \equiv $ $\operatorname{Re} ({{\varepsilon }_{c}}) - i\operatorname{Im} ({{\varepsilon }_{c}})$ серебра рассчитывалась на основе интерполяции экспериментальных данных работы [11] кубическими сплайнами.

Рис. 1.

Геометрия задачи и контуров поперечного сечения рассеивателя: $\lambda = 400\,\,{\text{нм}}$, $kb = 0.2\pi $, a = 0.7b (1), 0.9b (2), 0.96b (3), 0.99b (4), 0.999b (5).

Пространственное распределение диэлектрической проницаемости для структур, изображенных на рис. 1, имеет вид

Исследование сформулированной задачи дифракции удобнее проводить, используя $z$-компоненту $U(r,\varphi ) = {{H}_{z}}(r,\varphi )$ магнитного поля, так как краевая задача для функции $U(r,\varphi )$ является скалярной. Полное поле $U(r,\varphi )$, т.е. суперпозиция падающего и рассеянного полей, в кусочно-постоянной среде (3) удовлетворяет уравнению Гельмгольца:

Компоненты электрического поля могут быть выражены через функцию $U(r,\varphi )$

На границах структуры должны быть непрерывны величины $U$ и $\frac{1}{\varepsilon }\frac{{\partial U}}{{\partial N}}$, где $\frac{{\partial U}}{{\partial N}}$ – производная по направлению нормали к границе раздела сред.

Как уже отмечалось, полное поле $U(r,\varphi )$ вне структуры состоит из падающего (${{U}^{0}}$) и рассеянного (${{U}^{s}}$) полей

Падающее поле задано функцией

Рассеянное поле ${{U}^{s}}(r,\varphi )$ в цилиндрической системе координат ($r,\varphi $), где $x = r\cos \varphi $ и $y = r\sin \varphi $, в дальней зоне ($kr \to \infty $) должно удовлетворять условию излучения

где $\Phi (\varphi )$ − диаграмма рассеяния.

Полное сечение рассеяния ${{\sigma }_{S}}$ определяется формулой

2. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Численное решение сформулированной задачи проводили модифицированным методом дискретных источников [12, 13]. При этом точность решения задачи контролировали путем вычисления невязки $\delta $ граничных условий в линейной норме в точках, расположенных в середине между точками, где граничные условия выполняются точно (в таких точках граничные условия выполняются наихудшим образом [12]). Во всех приведенных ниже расчетах максимальная невязка граничных условий не превышает величину $\delta < {{10}^{{ - 3}}}$.

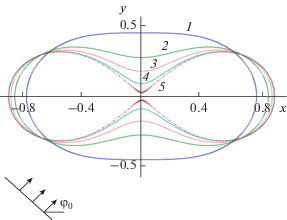
На рис. 2а представлены результаты расчета нормированного поперечника рассеяния $k{{\sigma }_{S}}$ при параметрах овала Кассини $a = 0.7b{\text{,}}\,\,b = 40\,\,{\text{нм}}$ (см. кривую 1 на рис. 1) и различных углах падения плоской волны : ${{\varphi }_{0}} = 0$, π/6, π/4, π/3, π/2. Из результатов, изображенных на рис. 2а, следует, что рассеивающая наноструктура, контур которой не содержит точек изменения знака кривизны и является чисто выпуклым, имеет только один максимум поперечника рассеяния $k{{\sigma }_{S}}$. При этом положение максимума поперечника рассеяния $k{{\sigma }_{S}}$ слабо зависит от угла падения ${{\varphi }_{0}}$ плоской волны и располагается в диапазоне значений длин волн $335\,\,{\text{нм}} < \lambda < 370\,\,{\text{нм}}{\text{.}}$

Рис. 2.

Зависимость нормированного поперечника рассеяния от длины волны для овала Кассини при b = 40 нм и а = = 0.7b (а), 0.96b (б), 0.99b (в), 0.999b (г) и различных углах падения плоской волны: ${{\varphi }_{0}} = 0$ (1), π/6 (2), π/4 (3), π/3 (4), π/2 (5).

Рисунки 2б–2г иллюстрируют аналогичные результаты для параметров овала Кассини $a = 0.96b{\text{,}}$ $b = 40\,\,{\text{нм}}$, $a = 0.99b{\text{,}}$ $b = 40\,\,{\text{нм}}$ и $a = 0.999b{\text{,}}$ $b = 40\,\,{\text{нм}}$ (см. кривые 2–5 на рис. 1) соответственно. При таких значениях параметров $a,b$ контур поперечного сечения структуры имеет точки изменения знака кривизны и имеет разную степень “вогнутости”. Из результатов, представленных на рис. 2б–2г следует, что наличие “вогнутости” контура рассивателя приводит к существованию двух максимумов поперечника рассеяния $k{{\sigma }_{S}}$. Увеличение степени “вогнутости” контура рассивателя сказывается как на значении амплитуд максимумов поперечника рассеивания $k{{\sigma }_{S}}$, так и на их смещении относительно друг друга (увеличении их взаимного расположения). Далее будет показано, что правый максимум поперечника рассеяния $k{{\sigma }_{S}}$ на рис. 2а связан с существованием дипольного резонанса плазмонов. Левый максимум поперечника рассеяния $k{{\sigma }_{S}}$ – наличием квадрупольного резонанса плазмонов. Отметим, что увеличение угла падения ${{\varphi }_{0}}$ приводит к расщеплению максимума поперечника рассеяния $k{{\sigma }_{S}}$, связанного с квадрупольным резонансом. Это свидетельствует о том, что имеет место вырождение квадрупольного резонанса плазмонов. Кроме того, отметим существование нескольких точек пересечения всех кривых поперечника рассеяния $k{{\sigma }_{S}}$.

Для понимания происхождения этих максимумов $k{{\sigma }_{S}}$ на рис. 3 приведены результаты расчета нормированного поперечника рассеяния $k{{\sigma }_{S}}$ при $a = 0.999b,$ $b = 40\,\,{\text{нм}}$, ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ и различных значениях мнимой части относительной диэлектрической проницаемости серебра, которые определяют потери среды. Из этого рисунка, а также расчетов структуры ближнего поля структуры, представленных ниже на рис. 4–6, следует, что при малых значениях потерь среды ($\operatorname{Im} (\varepsilon ) \leqslant \operatorname{Im} ({{\varepsilon }_{c}})$) можно наблюдать как дипольный резонанс, так и расщепленный мультипольный (квадрупольный) резонанс. Кроме того, из рис. 3 видно, что для реальных значений потерь серебра $\operatorname{Im} ({{\varepsilon }_{с}})$ у такой структуры первый (правый) максимум поперечника рассеяния $k{{\sigma }_{S}}$ соответствует дипольному резонансу, а второй (левый) максимум – результат слияния расщепленных мультипольных резонансов.

Рис. 3.

Зависимость нормированного поперечника рассеяния от длины волны при $a = 0.999b,$ $b = 40\,\,{\text{нм}}$, ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ и различных потерях серебра: Im(ε_c) (1), 0.1Im(ε_c) (2) и 0.001 Im(ε_c) (3).

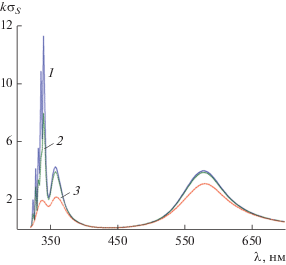
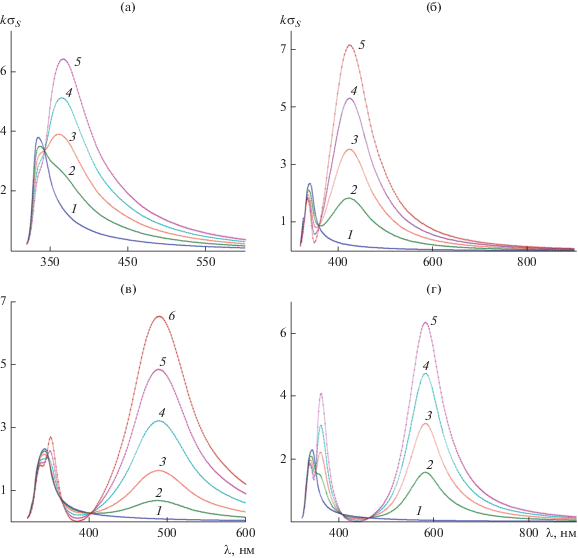
Рис. 4.

Зависимость нормированного поперечника рассеяния от длины волны для овала Кассини при b = = 20 нм и а = 0.96b (а), 0.999b (б) и различных углах падения плоской волны: ${{\varphi }_{0}} = 0$ (1), π/6 (2), π/4 (3), π/3 (4), π/2 (5).

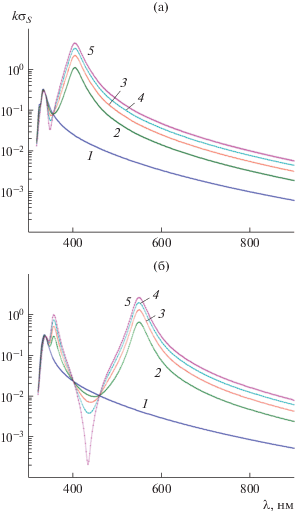
Рис. 5.

Пространственное распределение линий равных амплитуд модуля компоненты ${{H}_{z}}$ поля структуры с параметрами $a = 0.999b{\text{,}}$ $b = 20\,\,{\text{нм}}$, угле падения ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$, при длине волны λ = 581 (а) и 360.43 нм (б).

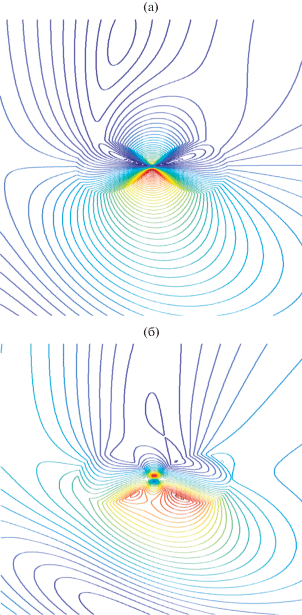
Рис. 6.

Пространственное распределение линий равных амплитуд модуля компоненты ${{H}_{z}}$ поля структуры с параметрами $a = 0.999b{\text{,}}$ $b = 40\,\,{\text{нм}}$, угле падения ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$, при длине волны $\lambda = 340\,\,{\text{нм}}$.

На рис. 4а,4б представлены результаты расчета нормированного поперечника рассеяния $k{{\sigma }_{S}}$ для двух структур с параметрами $a = 0.96b{\text{,}}$ $b = 20\,\,{\text{нм}}$, $a = 0.999b{\text{,}}$ $b = 20\,\,{\text{нм}}$. Отметим, что размеры таких структур в два раза меньше, чем у структур, рассмотренных выше. При этом углы падения плоской волны ${{\varphi }_{0}}$ полагались равными: ${{\varphi }_{0}} = 0$, π/6, π/4, π/3, π/2 соответственно. Из рис. 4а, 4б следует, что и для структур с такими размерами основные тенденции в поведении поперечника рассеяния $k{{\sigma }_{S}}$, отмеченные выше, сохраняются. Однако из кривых, приведенных на этих рисунках, видно, что наличие достаточно сильной “вогнутости” может приводить к уменьшению минимума поперечника рассеяния $k{{\sigma }_{S}}$ приблизительно на четыре порядка.

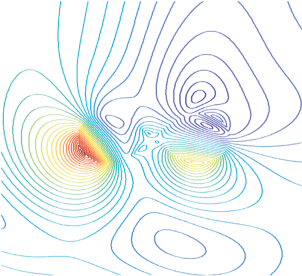
На рис. 5а, 5б, 6 представлены результаты расчета пространственного распределения линий равного уровня для структуры с параметрами $a = 0.999b{\text{,}}$ $b = 40\,\,{\text{нм}}$, ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ и трех длин волн $\lambda = 340\,\,{\text{нм,}}$ ${\text{360}}{\text{.43}}\,\,{\text{нм,}}$ ${\text{581}}\,\,{\text{нм}}$ соответственно. Отметим, что указанным длинам волн отвечают максимумы поперечника рассеяния $k{{\sigma }_{S}}$ (см. кривую 3 на рис. 2г). Данные, приведенные на рис. 5а, 5б, 6 подтверждают наличие у структуры как дипольных, так и квадрупольных резонансов плазмонов, а также эффект их вырождения.

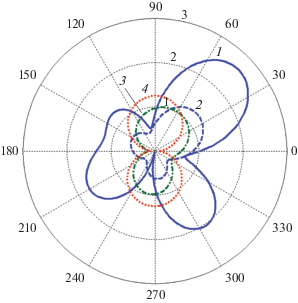
Наконец, обсудим результаты расчета диаграммы рассеяния. На рис. 7 представлены результаты расчетов диаграмм рассеяния для структуры с параметрами $a = 0.999b,$ $b = 40\,\,{\text{нм}}$, при угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ и трех длинах волн – 340, 360.43 и 581 нм. На рисунке представлены следующие случаи: λ = 340 нм в отсутствие (кривая 1) и в присутствии потерь серебра Im(ε) = 0 (кривая 2); λ = 360.43 нм в присутствии потерь серебра (кривая 3); λ = 581 нм в присутствии потерь серебра (кривая 4). Из рисунка видно, что потери сказываются более сильно на мультипольном резонансе, чем на дипольном.

Рис. 7.

Диаграмма рассеяния для структуры с параметрами $a = 0.999b{\text{,}}$ $b = 40\,\,{\text{нм}}$, угле падения ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ и следующих различных параметрах: кривая 1 – $\operatorname{Im} (\varepsilon ) = 0,$ $\lambda = 340$ нм, кривая 2 – $\operatorname{Im} (\varepsilon ),\,\,\lambda = 340\,\,{\text{нм}}$, кривая 3 – $\operatorname{Im} (\varepsilon ),\,\,\lambda = 360.43\,\,{\text{нм}}$, кривая 4 – $\operatorname{Im} (\varepsilon ),\,\,\lambda = 581\,\,{\text{нм}}{\text{.}}$

ЗАКЛЮЧЕНИЕ

Рассмотрена дифракция плоской волны на цилиндрической 2D-структуре, представляющей наноструктуру из серебра, контур которой имеет выпукло-вогнутую границу. Строгими численными методами рассчитаны спектральные и пространственные характеристики рассеянного поля. Показано, что для такой структуры характерно существование нескольких резонансов поперечника рассеяния, связанных с существованием дипольных и квадрупольных резонансов плазмонов. Показано, что изменение угла падения плоской волны на такую структуру приводит к вырождению квадрупольных резонансов. Продемонстрировано влияние геометрических размеров структуры. Обнаружено уменьшение значений минимума поперечника рассеяния до величин порядка ${{10}^{{ - 4}}}$ при реальных потерях серебра.