Радиотехника и электроника, 2021, T. 66, № 6, стр. 552-558

1. ПОСТАНОВКА ЗАДАЧИ

В последнее время в теории периодических сред и структур, таких как фотонные и электромагнитные кристаллы, метаматериалы, фазированные антенные решетки и т.д., активно применяются методы решения граничных задач электродинамики, которые можно объединить под общим названием –метод обобщенной матрицы рассеяния (ОМР) [1]. В рамках этого метода элемент периодической структуры, который в случае периодической среды является искусственной частицей, а в случае антенной решетки элементарным излучателем, описывается при помощи оператора рассеяния, имеющего смысл, близкий к ОМР, известной в теории СВЧ многополюсников [2]. Существенным отличием метода ОМР (МОМР) от теории многополюсников является то, что поле вокруг элемента периодической структуры представляется в виде рядов по пространственным гармоникам. Пространственные гармоники являются собственными волнами свободного пространства. Они разделяются на возбуждающие и рассеянные волны. Оператор рассеяния представляет собой матрицу, связывающую амплитуды волн указанных типов.

В рамках МОМР полагают, что оператор рассеяния полностью описывает электродинамические свойства элемента периодической структуры. Отметим, что известны пространственные гармоники разных видов. В двумерных средах целесообразно использовать представление поля в цилиндрической системе координат и соответствующие цилиндрические волны/гармоники [3]. В трехмерных средах и антенных решетках используются сферические координаты и сферические гармоники [4].

Как отмечено выше, оператор рассеяния описывает изолированную частицу периодической среды. Для полного представления поля внутри периодической среды, являющейся совокупностью частиц, необходимо учесть взаимодействие их полей. В рамках МОМР эта задача решается путем разложения волн, рассеянных некоторой частицей периодической среды по возбуждающим волнам других частиц. Процедура разложения порождает матрицу связей, которая зависит от взаимного положения частиц в среде. Она связывает амплитуды возбуждающих и рассеянных разными частицами волн.

Наличие двух соотношений для волн разных типов позволяет исключить из них, например, амплитуды возбуждающих волн и получить одну систему линейных алгебраических уравнений (СЛАУ) относительно векторов амплитуд волн рассеянных частицами периодической среды. Указанная СЛАУ в отсутствие источников является однородной системой, описывающей распространение собственных волн в периодической среде. Она получила название уравнения распространения.

В работах [3, 5] вводится неоднородное уравнение распространения, учитывающее присутствие в среде сторонних источников, которые называют также компенсирующими источниками [3]. Решение неоднородного уравнения распространения позволяет определить функцию Грина периодической среды. Она является ключевым для анализа неоднородных периодических сред объектом. С ее помощью удается построить эффективные алгоритмы численного решения таких задач [6], имеющих большое практическое значение. К неоднородным периодическим структурам относятся волноводные схемы, которые формируются путем введения в фотонный или электромагнитный кристалл специальных дефектов, образующих волноведущие каналы и другие функциональные элементы, способные решать задачи пространственной и временной обработки и формирования полей и сигналов [7–9]. Схемы данного вида нашли применение как в фотонике, так и в СВЧ-диапазоне.

В исходной форме уравнение распространения неудобно для решения. Основная проблема состоит в том, что элементы матрицы связей медленно убывают при увеличении расстояния между частицами $r$. Такое их поведение следует из зависимости поля пространственной гармоники от указанного расстояния. Например, анализируя цилиндрические волны, которые описываются функциями Ганкеля [10], нетрудно увидеть, что элементы матрицы связей убывают при больших расстояниях весьма медленно, как ${{r}^{{ - 1/2}}}$.

В силу причин, отмеченных выше, непосредственное решение уравнения распространения не используется. В ряде работ [1, 5, 6] был рассмотрен подход, основанный на применении двойного дискретного преобразования Фурье (ДПФ). Собственно ДПФ проблему медленной сходимости не снимает, так как в рамках данного метода возникает необходимость вычисления ДПФ матрицы связей, которое также представляется медленно сходящимся двойным рядом. Однако ДПФ открывает возможность для использования интегральных представлений пространственных гармоник. Их применение позволяет преобразовать двойные ряды в однократные и улучшить их сходимость. Следует отметить, что интегральные представления имеют весьма сложный вид, а улучшение сходимости рядов связано с учетом поведения пространственных гармоник в начале координат, где они имеют особенности высоких порядков. Указанные факторы как существенно усложняют аналитические преобразования, так и снижают эффективность численных алгоритмов, построенных на их основе.

В данной работе предложен новый метод решения задачи, который не требует использования интегральных представлений пространственных гармоник. Он основан на процедуре локализации уравнений распространения, которая, как будет показано ниже, позволяет улучшить сходимость исходных рядов по пространственным гармоникам таким образом, что для их суммирования достаточно учесть лишь весьма ограниченное число членов ряда. Применение локализующего преобразования, таким образом, позволяет создавать эффективные численные алгоритмы решения как однородных, так и неоднородных уравнений распространения. В данной работе мы ограничимся анализом уравнений распространения в двумерных периодических средах.

2. УРАВНЕНИЯ РАСПРОСТРАНЕНИЯ

Рассмотрим уравнение распространения электромагнитных волн в однородной периодической среде, полученное в работе [5]:

Поясним смысл, входящих в уравнение (1) символов. Векторы ${{{\mathbf{A}}}_{{s{\mathbf{\nu }}}}}$ – это векторы амплитуд или амплитудные векторы рассеянных пространственных гармоник. Рассматривается двумерная периодическая среда. Положение ее частиц внутри среды описывается двумя индексами ${{\nu }_{x}},{{\nu }_{y}}$. Они задают положение частицы на плоскости XOY. Координаты ее центра соответственно равны ${{\nu }_{x}}{{P}_{x}},{{\nu }_{y}}{{P}_{y}}$, где ${{P}_{{x,y}}}$ – периоды среды по осям 0х и 0у. Для упрощения записи вместо двух скалярных индексов мы будем использовать один векторный индекс ${\mathbf{\nu }} = ({{\nu }_{x}},{{\nu }_{y}})$, как в уравнении (1).

Суммирование в соотношении (1) ведется по всем частицам, т.е. в бесконечных пределах. Верхний символ $({\mathbf{\nu }})$ означает, что частица с индексом ${\mathbf{\nu }}$ из суммирования исключена. В двумерной среде в качестве пространственных гармоник используются цилиндрические функции

где $H_{N}^{{(2)}}$ – функция Ганкеля второго рода порядка $N$, а ${{J}_{N}}$ – функция Бесселя того же порядка, $k$ – волновое число свободного пространства. Функции Ганкеля описывают рассеянные волны, а функции Бесселя возбуждающие волны. Функции, входящие в выражения (2), записаны в полярной системе координат ${{r}_{{\mathbf{\nu }}}},{{\varphi }_{{\mathbf{\nu }}}}$ с центром, совпадающим с центром ${\mathbf{\nu }}$-й частицы периодической среды.

Матрицы ${{{\mathbf{K}}}_{{{\mathbf{\nu ,\mu }}}}}$ – это упомянутые выше матрицы связей. Каждая из них связывает амплитуды волн, возбуждающих частицу с номером ${\mathbf{\nu }}$ с амплитудами волн, рассеянных ${\mathbf{\mu }}$-й частицей:

здесь ${{{\mathbf{A}}}_{{i{\mathbf{\nu }}}}}$ – вектор амплитуд падающих на ${\mathbf{\nu }}$-ю частицу волн.

Размерность матрицы связей совпадает с размерностью амплитудных векторов. Запишем выражения для ее элементов:

где ${{r}_{{{\mathbf{\nu ,\mu }}}}}$ – расстояние между ${\mathbf{\nu }}$-й и ${\mathbf{\mu }}$-й частицами, ${{\varphi }_{{{\mathbf{\nu ,\mu }}}}}$ – угол, под которым видна ${\mathbf{\mu }}$-я частица в системе координат ${\mathbf{\nu }}$-й частицы.

При наличии сторонних источников ${{{\mathbf{V}}}_{{\mathbf{\nu }}}}$ уравнение распространения (1) становится неоднородным:

Матрица ${\mathbf{L}}$ – это оператор рассеяния, о котором мы говорили выше. Он связывает амплитудные векторы:

В однородной среде все частицы одинаковые с одинаковыми операторами рассеяния. Поэтому в его обозначении отсутствует индекс ${\mathbf{\nu }}$.

Из выражения (4) видно, что элементы матрицы связей действительно весьма медленно убывают при увеличении расстояния между частицами ${{r}_{{{\mathbf{\nu ,\mu }}}}}$. Для такого вывода достаточно воспользоваться асимптотическими выражениями для функций Ганкеля [10]:

Отметим также важное свойство матрицы связей как функции индексов ${\mathbf{\nu }},{\mathbf{\mu }}$. Она зависит только от их разности: ${\mathbf{\nu }} - {\mathbf{\mu }}$. Данное обстоятельство позволяет эффективно использовать для решения уравнений (1), (5) ДПФ. Его применение к данным уравнениям приводит к появлению матрицы ${\mathbf{Q}}(\kappa )$, являющейся ДПФ матрицы связей:

где $\kappa $ – векторный спектральный параметр: $\kappa = ({{\kappa }_{x}},{{\kappa }_{y}})$, ${{{\mathbf{r}}}_{{\mathbf{\nu }}}}$ – радиус-вектор, соединяющий начало координат с центром ${\mathbf{\nu }}$-й частицы. Произведение r_νκ следует понимать как скалярное произведение:

Из соотношения (4) видно, что элементы матрицы связей при ${\mathbf{\nu }} = 0$ не определены. Однако, как следует из формулы (1), элемент с нулевым индексом исключен из суммирования. Он также должен быть исключен из формулы (8). Для того чтобы распространить суммирование на все частицы периодической среды, мы определяем матрицу ${{{\mathbf{K}}}_{0}}$ как нулевую матрицу.

Как видно из выражения (8), вычисление матрицы ${\mathbf{Q}}(\kappa )$ связано с суммированием двойного медленно сходящегося ряда. Его медленная сходимость является следствием слабой локализации уравнения распространения (1), которое описывает взаимодействие частиц в периодической среде. При этом оказывается, что даже сильно удаленные частицы существенно влияют друг на друга.

3. ЛОКАЛИЗУЮЩЕЕ ПРЕОБРАЗОВАНИЕ

Идея локализующего преобразования уравнений распространения может быть понята из анализа явных выражений для элементов матрицы ${\mathbf{Q}}(\kappa )$. Они были получены при помощи интегральных представлений для функций Ганкеля в работах [5, 11]. Рассмотрим выражение для элемента ${\mathbf{Q}}{{(\kappa )}_{{0,0}}}$:

здесь ${{r}_{{n,m}}} = P\sqrt {{{n}^{2}} + {{m}^{2}}} $, ${{P}_{x}} = {{P}_{y}} = P$.

Оно имеет следующий вид:

Постоянная $\xi $ выбирается из условия $\exp ( - \xi P) \ll 1$.

Отметим следующие особенности функции ${\mathbf{Q}}{{({{\kappa }_{x}},{{\kappa }_{y}})}_{{0,0}}}$. Она является периодической по обоим аргументам с периодом ${{2\pi } \mathord{\left/ {\vphantom {{2\pi } P}} \right. \kern-0em} P}$. В пределах главного периода при $\left| {{{\kappa }_{{x,y}}}} \right| < {{2\pi } \mathord{\left/ {\vphantom {{2\pi } P}} \right. \kern-0em} P}$ она имеет простые полюса, положение которых задается решением следующего уравнения:

Нетрудно убедиться, что на плоскости ${{\kappa }_{x}},{{\kappa }_{y}}$ решение уравнения (12) порождает окружность радиусом $k$ с центром в начале координат. Таким образом, функция ${\mathbf{Q}}{{({{\kappa }_{x}},{{\kappa }_{y}})}_{{0,0}}}$ стремится к бесконечности на указанной окружности. Однако в силу периодичности она также ведет себя и на всех окружностях, центры которых периодически смещены из начала координат на величину, кратную ${{2\pi } \mathord{\left/ {\vphantom {{2\pi } P}} \right. \kern-0em} P}$, как показано на рис. 1.

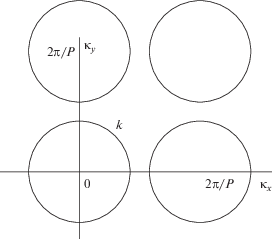
Можно утверждать, что наличие особенностей у анализируемой функции является главной причиной слабой локализации уравнения распространения. Верно также и обратное утверждение, что наличие особенностей в ДПФ является следствием существенной нелокальности уравнения распространения. Действительно, в силу периодичности функции ${\mathbf{Q}}{{({{\kappa }_{x}},{{\kappa }_{y}})}_{{0,0}}}$ ее можно разложить в ряд Фурье. При этом элементы матрицы связей будут коэффициентами Фурье данного разложения. Поскольку ДПФ имеет резкую зависимость от своих аргументов, содержащую разрывы второго рода, то для их описания гладкими функциями экспоненциального вида необходимо взять очень большое число членов разложения, что эквивалентно медленному убыванию матрицы связей при увеличении расстояния между частицами.

Таким образом, мы можем сформулировать основное требование к локализующему преобразованию: оно должно быть таким, чтобы его применение устраняло особенности ДПФ.

Рассмотрим следующее преобразование уравнения (1):

где ${{S}_{{{\mathbf{\nu }} - {\mathbf{\chi }}}}}$ – скалярные величины, являющиеся параметрами локализующего преобразования. Применим к уравнению (13) ДПФ. С учетом теоремы свертки получаем

где

Будем искать неизвестные коэффициенты ${{S}_{{\mathbf{\nu }}}}$ из условия

Отметим, что в силу своего определения (14) скалярная функция $s(\kappa )$ является периодической функцией и, следовательно, удовлетворяя условию (15), мы автоматически обеспечиваем равенство нулю на всех окружностях на плоскости ${{\kappa }_{x}},{{\kappa }_{y}}$.

Важно отметить, что при выполнении равенства (15) элементы матрицы

не имеют особенностей типа полюсов. Они являются непрерывными функциями своих аргументов. Поэтому коэффициенты Фурье обратного ДПФ данной матрицы должны убывать намного быстрее, чем в случае матрицы ${\mathbf{Q}}(\kappa )$, что эквивалентно утверждению о том, что модифицированная матрица связей

имеет существенно большую степень локализации по сравнению с исходной матрицей связей.

Далее нам необходимо найти коэффициенты ${{S}_{{\mathbf{\nu }}}}$, обеспечивающие выполнение условия (15). Возможно, данная задача имеет аналитическое решение. Нам не удалось его найти. Мы можем предложить только численный алгоритм определения искомых параметров локализующего преобразования.

Запишем функцию $s(\kappa )$ в развернутом виде:

Выражение (18) записано для частного случая одинаковых по обеим осям периодов, который будем рассматривать далее. Отметим, что переход к более общему случаю может быть выполнен без труда. В формуле (18) через ${{N}_{m}}$ выражен параметр, определяющий размер зоны локализации. Он был выбран в ходе численных экспериментов из условия заданной точности выполнения условия (15).

Окружность, на которой выполняется равенство (15), задается уравнением

В полярных координатах $\rho ,\alpha $ параметры ${{\kappa }_{{x,y}}}$ на указанной окружности задаются уравнениями

С учетом соотношений (20) формула (18) приобретает вид

где

Поскольку функция $s({{\kappa }_{x}},{{\kappa }_{y}})$ определяется с точностью до произвольного множителя, примем коэффициент ${{S}_{{0,0}}}$ равным единице. Тогда для оставшихся коэффициентов имеем условие

Представим экспоненту, входящую в (22), в виде разложения в ряд Фурье [12]:

Потребуем исходя из условия (22), чтобы все коэффициенты разложения, кроме нулевого, равнялись нулю. Нулевой коэффициент будет равен –1. В результате получаем следующую СЛАУ:

Здесь ${{\delta }_{{q,0}}}$ – символ Кронекера. Размерность СЛАУ (24) определяется параметром ${{N}_{m}}$. Она равна ${{(2{{N}_{m}} + 1)}^{2}} - 1$. Нетрудно увидеть, что точное решение поставленной задачи требует выполнения условий (24) для бесконечного числа гармоник. Численное решение возможно только для конечной СЛАУ.

Рассмотрим результаты численного определения параметров локализующего преобразования. Первое, что необходимо отметить, – это выполнение ряда соотношений между коэффициентами ${{S}_{{n,m}}}$, которые обусловлены пространственной симметрией структуры. Обратим внимание, что квадратная сетка обладает несколькими плоскостями симметрии (рис. 2). Две из них, совпадающие с координатными плоскостями, назовем главными. Еще две плоскости, ориентированные к главным под углом 45°, назовем диагональными плоскостями.

Симметрия относительно главных плоскостей приводит к следующим соотношениям:

Симметрия относительно диагональных плоскостей добавляет еще одно независимое соотношение:

Условия (25) и (26) позволяют существенно уменьшить размерность СЛАУ (24). Например, при ${{N}_{m}} = 2$ размерность СЛАУ (24) равна 24 × 24, а учет связей (25), (26) сокращает ее до 5 × 5.

Для оценки точности численного решения введем параметр $\Delta $:

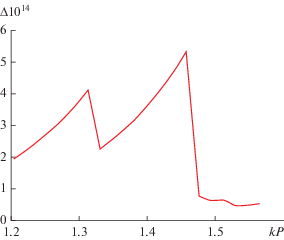
Он равен усредненному значению модуля функции $s({{\kappa }_{x}},{{\kappa }_{y}})$ на окружности (19), а в идеальном случае – равен нулю. На рис. 3 показана зависимость параметра $\Delta $ от электрического периода решетки $kP$. Она получена при ${{N}_{m}} = 2$. Отметим очень высокую точность решения СЛАУ (24). При этом следует также отметить, что зона взаимодействия частиц периодической среды весьма невелика, при ${{N}_{m}} = 2$ она включает частицы, удаленные от выделенной частицы не более чем на два периода.

4. МОДИФИЦИРОВАННАЯ МАТРИЦА СВЯЗЕЙ

Рассмотрим задачу определения модифицированной матрицы связей. Ее ДПФ ${\mathbf{t}}(\kappa )$ описывается выражением (16). Для определения самой модифицированной матрицы связей ${{{\mathbf{T}}}_{{\mathbf{\nu }}}}$ воспользуемся обратным ДПФ:

Входящие в формулу (16) величины можем представить в виде рядов Фурье:

Подставим выражения (29) в формулу (28) и учтем ортогональность экспоненциальных функций:

Суммирование в соотношении (30) ведется по области определения локализующего преобразования (13), которая задается параметром ${{N}_{m}}$. Отметим, что она имеет ограниченные размеры. Модифицированная матрица связей достаточно быстро убывает с ростом индекса ${\mathbf{\nu }}$. Однако область ее локализации необязательно должна совпадать с областью локализации преобразования (13). Выражение (30) дает простой алгоритм вычисления модифицированной матрицы связей. Отметим, что ее ДПФ простым образом связано с ДПФ исходной матрицы связей:

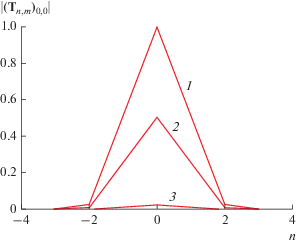
Рассмотрим численный пример. На рис. 4 показана зависимость модуля нормированного элемента матрицы ${{{\mathbf{T}}}_{{\mathbf{\nu }}}}$ с нулевыми индексами $N = M = 0$ от индекса $n$, задающего положение частицы на оси 0х. Кривые 1–3 получены для значений индекса $m = 0,1,2$ соответственно. Период решетки $P$ = = 12 мм, а частота $f$ = 13 ГГц. Нормировка проводилась на значение рассчитываемого параметра при $n = m = 0$.

На рис. 5 представлена зависимость модуля нормированного элемента матрицы ${{{\mathbf{T}}}_{{\mathbf{\nu }}}}$ с индексами $N = 0,M = 1$ от параметра $n$. Кривые 1–3 получены при $m = 0,1,2$ соответственно. Период решетки и частота остались прежними. Нормировка проводилась на значение элемента матрицы при n = 1, $m = 0$.

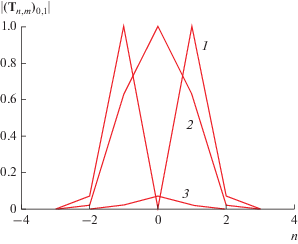
Из рис. 4, 5 видна высокая степень локализации модифицированной матрицы связей. Ее элементы становятся пренебрежимо малыми уже на расстоянии между частицами среды, равном трем периодам.

Для оценки точности предложенного алгоритма было проведено сравнение его результатов с результатами, полученными при помощи интегральных представлений цилиндрических функций. Обоими методами были найдены ДПФ модифицированных матриц связей. Далее определяли относительную разность $\Delta $:

где ${\mathbf{t}}(\kappa )$ и ${{{\mathbf{t}}}_{0}}(\kappa )$ – модифицированные матрица связей, найденные методами локализующего преобразования и интегральных представлений.

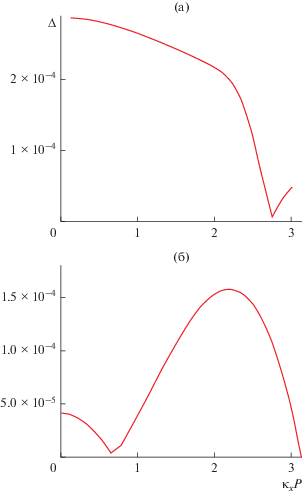
На рис. 6а, 6б показана зависимость параметра $\Delta $ как функции переменной ${{\kappa }_{x}}P$, которая изменяется в пределах от нуля до $\pi $. Кривые на рис. 6а и рис. 6б рассчитаны для $N = M = 0$ и $N = 0,{\text{ }}M = 1$ соответственно при $P$ = 12 мм, $f$ = 13 ГГц и ${{\kappa }_{y}}P = 0$. Если принять результаты по методу интегральных представлений в качестве эталонных, то можно сделать вывод, что относительная погрешность метода локализующего преобразования не превышает $3 \times {{10}^{{ - 4}}}$. При этом нельзя не отметить, что использование метода интегральных представлений в качестве эталона возможно с большой долей условности, так как он сам не является абсолютно точным и для него характерны погрешности, связанные с суммированием бесконечных рядов и выбором параметра $\xi $. Тем не менее хорошее совпадение результатов, полученных двумя независимыми методами, принято считать подтверждением их корректности и высокой точности.

ЗАКЛЮЧЕНИЕ

Предложенный метод вычисления ДПФ матрицы связей, а следовательно, и метод решения однородного и неоднородного уравнений распространения позволяет существенно упростить вычислительный процесс и повысить его эффективность. Немаловажным факторам является также возможность исключить сложные и часто неоднозначные аналитические преобразования, характерные для метода интегральных представлений. Отметим, что весьма высокая точность решения задачи построения локализующего преобразования позволяет предположить существование строгого решения в аналитической форме. Его поиск представляется весьма перспективным направлением научных исследований.