Радиотехника и электроника, 2021, T. 66, № 6, стр. 581-593

ВВЕДЕНИЕ

Общий вариационный подход к задачам синтеза излучающих систем был разработан в работах А.Н. Тихонова, В.И. Дмитриева, А.Г. Свешникова, А.С. Ильинского [1–4], Л.Д. Бахраха, С.Д. Кременецкого [5, 6]. Общий подход к корректным математическим постановкам задач синтеза излучающих систем рассмотрен в работе [7]. Метод математического моделирования антенных решеток, основанный на исследовании интегральных уравнений и применимый к широкому кругу излучателей, рассмотрен в работе [8].

Существует большой класс частных задач по снижению уровня боковых лепестков (УБЛ) диаграммы направленности (ДН) линейной эквидистантной фазированной антенной решетки (ЛЭФАР) [9, 10], основанный на подходе, который был предложен С.А. Щелкуновым [11]. Снижение УБЛ ДН ЛЭФАР осуществляется путем формирования требуемого амплитудно-фазового распределения (АФР) сигналов на входах излучателей ЛЭФАР, при этом происходит управление следующими характеристиками сигналов на входах излучателей ЛЭФАР [12–14]: 1) амплитудами, 2) фазами, 3) и амплитудами, и фазами.

Требуемое АФР сигналов на входах излучателей ЛЭФАР может быть найдено с помощью аналитических (метод Щелкунова [11, 13], метод Фурье преобразования [13, 15], метод парциальных диаграмм Вудворда–Лоусона [16, 17]) и численных методов и алгоритмов (метод наименьших квадратов [18, 19], генетические алгоритмы [20–22], методы роя частиц [23], метод оптимизации Тагучи [24–26], алгоритм опыления цветков [27]).

Аналитические методы поиска амплитудного распределения (АР) сигналов на входах излучателей ЛЭФАР рассмотрены в работах [13, 28, 29], фазового распределения (ФР) – в работе [30], амплитудно-фазового в работах [15, 17].

Численные методы поиска АР сигналов на входах излучателей ЛЭФАР рассмотрены в работах [23, 27, 29, 31, 32], ФР в работах [33–35], амплитудно-фазового в работах [9, 10, 18, 28–30, 36–41].

1. ПОСТАНОВКА ЗАДАЧИ

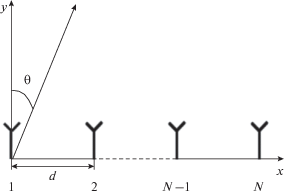
В качестве излучающей системы рассмотрим располагающуюся вдоль оси x и работающую на частоте f ЛЭФАР, апертура которой состоит из N идентичных и одинаково направленных излучателей, с совпадающими функциями распределения тока [14] (рис. 1).

Рис. 1.

Топология линейной эквидистантной фазированной антенной решетки.

Излучатели расположены на расстоянии d, выбранном из критерия отсутствия побочных главных максимумов в области видимых углов [14, 42]. Угол θ задается как угол между нормалью к ЛЭФАР и направлением наблюдения (см. рис. 1).

Рассмотрим ДН такой ЛЭФАР. Согласно теореме перемножения полное электромагнитное поле излучения пропорционально произведению нормированной ДН одиночного излучателя ЛЭФАР на скалярный множитель комбинирования (МК) ЛЭФАР, причем МК полностью учитывает как расположение элементов в пространстве, так и распределение комплексных амплитуд токов на входах излучателей системы [13, 14]:

где $F{\kern 1pt} '(\theta )$ – нормированная ДН одного излучателя ЛЭФАР, ${{f}_{\Sigma }}(\theta )$ – МК ЛЭФАР.

Поскольку нормированная ДН одного излучателя ЛЭФАР $F{\kern 1pt} '(\theta ,\varphi )$ определяется типом излучателя и не зависит от амплитуд и фаз сигналов на входах излучателей, а также количества излучателей N в ЛЭФАР и расстояния между излучателями d, мы не рассматриваем зависимость ДН ЛЭФАР $F\left( \theta \right)$ от множителя $F{\kern 1pt} '(\theta )$ в выражении (1). Рассмотрим способ снижения УБЛ МК ЛЭФАР.

Предлагаемый способ снижения УБЛ МК основан на методе парциальных диаграмм Вудворда–Лоусона [16], где под парциальной диаграммой понимается ДН, соответствующая парциальной функции распределения возбуждения элементов решетки [14]. Отличием способа является:

1) использование в качестве базисных функций не функций, выбранных Вудвордом и Лоусеном, задаваемых выражением [16]:

где Ψ – обобщенный угол [12], а функций следующего вида [13, 14]:

2) применение трех парциальных ДН: i = 1, 2, 3;

3) ориентация главных лепестков парциальных ДН не в направлении формирования нуля, а в направлениях первых нулей первой парциальной ДН.

Такой подход позволяет получить аналитические выражения в явном виде для АФР сигналов на входах излучателей ЛЭФАР для заданного направления снижения УБЛ МК ЛЭФАР, однако при этом существенно используется геометрия выбранной антенной решетки, поэтому он не может быть распространен на решение задачи синтеза дискретных антенн в общем случае.

2. СНИЖЕНИЕ УБЛ МК С ИСПОЛЬЗОВАНИЕМ ВСПОМОГАТЕЛЬНЫХ ПАРЦИАЛЬНЫХ ДН

Рассмотрим выражения (2) и (3). Отличие состоит в том, что выражение (2) справедливо для непрерывного излучателя [14], а (3) – для дискретного излучателя из N элементов [11]. Учтем в выражении (3) для дискретной ЛЭФАР фазовый сдвиг между соседними излучателями ${{\Delta }}{{{{\Phi }}}_{i}}$ [43, 44] и запишем выражения для парциальных ДН в следующем виде:

Обобщенный угол $\Psi \left( {\theta ,\Delta {{\Phi }_{i}}} \right)$ задается следующим выражением [12–14, 16]:

где $k$ – волновое число [12, 14].

Рассмотрим МК ЛЭФАР ${{f}_{{{\Sigma }}}}\left( \theta \right)$, являющийся суммой трех парциальных ДН ЛЭФАР вида (4), отличающихся только сдвигом фаз между соседними излучателями $~\Delta {{\Phi }_{i}}$:

1) ${{f}_{1}}\left( \theta \right)$ – первая парциальная ДН с единичной амплитудой и направлением главного лепестка, совпадающим с направлением нормали к ЛЭФАР, при этом разность фаз между соседними излучателями $\Delta {{\Phi }_{1}}$ составляет 0°;

2) ${{f}_{2}}\left( \theta \right)$ – вторая парциальная ДН, амплитуда которой равняется $\chi $, направление главного лепестка составляет угол $\beta $ с направлением нормали к ЛЭФАР, а разность фаз между соседними излучателями составляет $\Delta {{\Phi }_{2}}$, причем угол $\beta $ соответствует первому нулю первой парциальной ДН;

3) ${{f}_{3}}\left( \theta \right)$ – третья парциальная ДН, амплитуда которой равна $\left( {X - \chi } \right)$, причем направление главного лепестка составляет угол $ - \beta $ с направлением нормали к ЛЭФАР, при этом разность фаз между соседними излучателями составляет $\Delta {{\Phi }_{3}}$.

Введем следующее условие:

тогда сумма амплитудных коэффициентов $\chi $ и $\left( {X - \chi } \right)$ равна амплитуде первой парциальной ДН ЛЭФАР ${{f}_{1}}\left( \theta \right)$.

Определим $\Delta {{\Phi }_{2}}$ и $\Delta {{\Phi }_{3}}$ из условия сдвига главных лепестков парциальных ДН ${{f}_{2}}\left( \theta \right)$ и ${{f}_{3}}\left( \theta \right)$ на первые нули первой парциальной ДН ${{f}_{1}}\left( \theta \right)$, соответствующие углам $\beta $ и $ - \beta $. Для этого рассмотрим выражение (5) из которого следует, что

Учитывая соотношения (4), (5), (7) и (8) получаем следующие выражения для $\Delta {{\Phi }_{2}}$ и $\Delta {{\Phi }_{3}}$:

При таком выборе парциальных ДН ЛЭФАР их нули совпадают, за исключением углов $\beta $ и $ - \beta $.

Для нормировки парциальных ДН $~{{f}_{i}}\left( \theta \right)$ используется следующее выражение [12–14]:

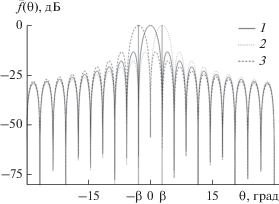
На рис. 2 представлены зависимости нормированных парциальных ДН ${{\bar {f}}_{i}}\left( \theta \right)$ (в дБ) от угла $\theta $ при N = 40 и расстоянии между излучателями, равном половине длине волны в свободном пространстве. Из рис. 2 видно, что при углах $\theta ,~$ больших или равных по модулю углу $2\beta $ ($\left| \theta \right| \geqslant 2\beta $), нулевые значения нормированных парциальных ДН ${{\bar {f}}_{i}}\left( \theta \right)$ совпадают. Выбор именно таких парциальных ДН позволяет сохранить положения нулей МК ЛЭФАР таким же, как и у парциальных ДН ${{\bar {f}}_{i}}\left( \theta \right),~$ за исключением двух ближайших к главному лепестку.

Рис. 2.

Зависимости нормированных парциальных ДН от угла $~\theta $: $\overline {{{f}_{1}}} ~$ (кривая 1), $\overline {{{f}_{2}}} ~$ (кривая 2), $\overline {{{f}_{3}}} ~$ (кривая 3).

Рассмотрим МК ЛЭФАР, задаваемый тремя парциальными ДН ${{f}_{1}}\left( \theta \right)$, ${{f}_{2}}\left( \theta \right)$ и ${{f}_{3}}\left( {{\theta }} \right)$ [46]:

Нормированный МК ЛЭФАР $\overline {{{f}_{{{\Sigma }}}}} \left( {\theta ,\chi ,X} \right)$ (12) запишем в следующем виде [12–14]:

Минимизация УБЛ МК ${{f}_{\Sigma }}\left( {\theta ,\chi ,X} \right)$ для данного случая заключается в подборе амплитудного коэффициента $\chi $ второй парциальной ДН ${{f}_{2}}\left( \theta \right)$ для обращения в нуль МК ЛЭФАР ${{f}_{\Sigma }}\left( {\theta ,\chi ,X} \right)$ в заданном направлении, при амплитуде третьей парциальной ДН ${{f}_{3}}\left( \theta \right)$, равной, с учетом (6), $\left( {1 - \chi } \right)$.

Рассмотрим несколько примеров нормированного МК ЛЭФАР ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,\chi ,X} \right)$, при условии (6) и заданных значениях коэффициента $\chi $.

3. ПРИМЕРЫ НОРМИРОВАННОГО МК ЛЭФАР ПРИ ЗАДАННЫХ ЗНАЧЕНИЯХ КОЭФФИЦИЕНТА $\chi $

В качестве примера рассмотрим случай, для которого значение амплитудного коэффициента второй парциальной ДН $\chi $ составляет значение:

тогда амплитуда первой парциальной ДН ${{f}_{1}}\left( \theta \right)$ с учетом условия (6) будет в два раза превышать амплитуды парциальных ДН ${{f}_{2}}\left( \theta \right)$ и ${{f}_{3}}\left( \theta \right)$.

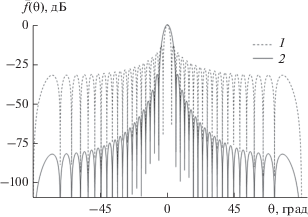
Полученные зависимости нормированной парциальной ДН $\overline {{{f}_{1}}} \left( \theta \right)$, и МК ЛЭФАР ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.5,1} \right)$ от угла $\theta $ при N = 40 представлены на рис. 3. Из расчета следует, что УБЛ нормированного МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.5,1} \right)$ снизился с –13.25 до –31.46 дБ по сравнению с УБЛ нормированной ДН $\overline {{{f}_{1}}} \left( \theta \right)$. При этом ширина МК по уровню половинной мощности увеличилась на 62.53% по сравнению с ДН $\overline {{{f}_{1}}} \left( \theta \right),$ т.е. с 1.27 до 2.06 град.

Рис. 3.

Зависимости нормированных первой парциальной ДН $\overline {{{f}_{1}}} \left( \theta \right)$ (кривая 1) и МК от угла $\theta $: ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.5,1} \right)$ (кривая 2).

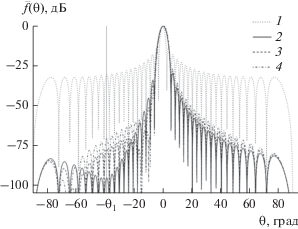
Рассмотрим, как меняется форма нормированного МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,\chi ,X} \right)$ по сравнению с парциальной ДН $\overline {{{f}_{1}}} \left( \theta \right)$ при изменении амплитудного коэффициента $\chi $. На рис. 4 приведены результаты расчета парциальной ДН $\overline {{{f}_{1}}} \left( \theta \right)$, рассчитанной согласно выражению (11), и нормированных МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,\chi ,X} \right)$, рассчитанных согласно (12) и (13), со значениями амплитудного коэффициента $\chi $ равными 0.55, 0.6, 0.65. Из рис. 4 следует, что при изменении амплитуды второго парциального МК $\chi $ форма нормированного МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,\chi ,{\text{{\rm X}}}} \right)$ меняется по сравнению с ДН $\overline {{{f}_{1}}} \left( \theta \right)$. В качестве примера рассмотрим максимум 11-го бокового лепестка ДН $\overline {{{f}_{1}}} \left( \theta \right)$, расположенного слева от направления главного лепестка ДН $\overline {{{f}_{1}}} \left( \theta \right)$ , что соответствует значению угла $ - {{\theta }_{1}} = - 38.66^\circ $. Значение нормированной ДН $\overline {{{f}_{1}}} \left( { - {{\theta }_{1}}} \right) = - 30.44$ дБ, ${{\bar {f}}_{{{\Sigma }}}}\left( { - {{\theta }_{1}},0.55,1} \right) = - 95.1$ дБ, ${{\bar {f}}_{{{\Sigma }}}}\left( { - {{\theta }_{1}},0.6,1} \right)$ = –76.98 дБ, ${{\bar {f}}_{{{\Sigma }}}}\left( { - {{\theta }_{1}},0.65,1} \right)$ = –70.43 дБ.

Рис. 4.

Зависимости нормированных первой парциальной ДН $\overline {{{f}_{1}}} \left( \theta \right)$ (кривая 1) и МК (кривые 2–4) от угла $~\theta $: ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.55,1} \right)$ (кривая 2), ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.60,1} \right)$ (кривая 3), ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.65,1} \right)$ (кривая 4).

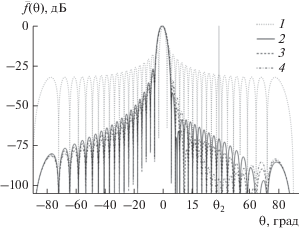
Для снижения УБЛ МК в области углов ${{\theta }}$ от $0$ до $90^\circ $ используем коэффициенты $\chi $, равные 0.35, 0.40, 0.45 (рис. 5). На рис. 5 представлены результаты расчета ДН $\overline {{{f}_{1}}} \left( \theta \right)$ согласно (11) и МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,\chi ,1} \right)$ согласно (12) и (13), при значениях амплитудного коэффициента $\chi $, равных 0.35, 0.4 и 0.45. В области углов ${{\theta }}$ = $0$…$90^\circ $ наблюдается существенное снижение УБЛ по сравнению с парциальной ДН $\overline {{{f}_{1}}} \left( \theta \right)$. Рассмотрим максимум 11-го бокового лепестка ДН $\overline {{{f}_{1}}} \left( \theta \right)$, расположенного справа от направления главного лепестка ДН $\overline {{{f}_{1}}} \left( \theta \right)$, что соответствует значению угла ${{\theta }_{2}} = 38.66^\circ $. Значение нормированной парциальной ДН $\overline {{{f}_{1}}} \left( {{{\theta }_{2}}} \right) = - 30.44$, $\overline {{{f}_{{{\Sigma }}}}} \left( {{{\theta }_{2}},0.35,1} \right) = - 70.43$ дБ, ${{\bar {f}}_{{{\Sigma }}}}\left( {{{\theta }_{2}},0.4,1} \right) = - 76.98$ дБ, ${{\bar {f}}_{{{\Sigma }}}}\left( {{{\theta }_{2}},0.45,1} \right) = - 95.1$ дБ.

Рис. 5.

Зависимости нормированных ДН $\overline {{{f}_{1}}} \left( \theta \right)$ (кривая 1) и МК от угла $\theta $: ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.35,1} \right)$ (кривая 2), ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.40,1} \right)$ (кривая 3), ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.45,1} \right)$ (кривая 4).

На рис. 6 приведены зависимости АР и ФР сигнала на входах излучателей ЛЭФАР для МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,\chi ,1} \right)$. На рис. 6а и 6в представлены АР и ФР на входах излучателей ЛЭФАР для МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,\chi ,1} \right)$ при значениях амплитудного коэффициента $\chi $, равных 0.5, 0.55, 0.6 и 0.65. На рис. 6б и 6г представлены АР и ФР на входах излучателей ЛЭФАР для МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,\chi ,1} \right)$ при значениях амплитудного коэффициента $\chi $ , равных 0.35 , 0.4 и 0.45, 0.5.

Рис. 6.

Амплитуды (а, б) и фазы (в, г) сигналов на входах излучателей ЛЭФАР для различных МК: а, в – ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.5,1} \right)$ (кривая 1), ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.55,1} \right)$ (кривая 2), ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.60,1} \right)$ (кривая 3), ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.65,1} \right){\text{\;}}$(кривая 4); б, г – ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.5,1} \right)$ (кривая 1), ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.35,1} \right)$ (кривая 2), ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.40,1} \right)$ (кривая 3), ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.45,1} \right)$ (кривая 4).

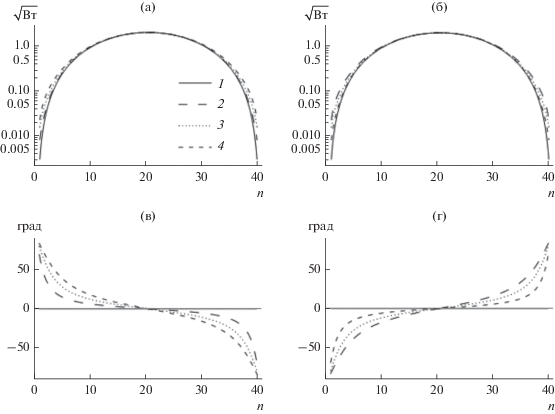
Как видно из рис. 6а и 6б амплитуда сигнала симметрична относительно центральных излучателей и представляет собой четную функцию. Из рис. 6в и 6г следует, что фаза сигнала на каждом излучателе симметрична относительно центральных излучателей и представляет собой нечетную функцию.

Отметим, что АР сигнала на входах излучателей ЛЭФАР для снижения уровня МК в заданном направлении ${{\theta }_{{{\text{min}}}}}$ совпадает с АР для снижения уровня МК ЛЭФАР в направлении $ - {{\theta }_{{{\text{min}}}}}$, а ФР для снижения уровня МК в заданном направлении ${{\theta }_{{{\text{min}}}}}$ совпадает с ФР для снижения уровня МК ЛЭФАР в направлении $ - {{\theta }_{{{\text{min}}}}}$, умноженном на ($ - 1)$. Фазовое распределение для снижения УБЛ МК в области углов $\theta $ = $0 \ldots 90^\circ $ аналогично ФР МК в области углов $\theta $ = $0 \ldots $ $ - 90^\circ $, умноженному на –1.

Полученные результаты показывают, что изменение амплитудного коэффициента второй парциальной ДН $\chi $ с учетом условия (6) позволяет снижать УБЛ МК как при $\theta > 0^\circ $, выбирая значение коэффициента $\chi $ в пределах от 0.5 до 1, так и при $\theta < 0^\circ $, выбирая значение коэффициента $\chi $ в пределах от 0 до 0.5, что дает возможность управлять УБЛ МК ЛЭФАР в заданной области углов.

4. ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ ПАРЦИАЛЬНЫХ МК ИЗ УСЛОВИЯ МИНИМИЗАЦИИ УБЛ В ЗАДАННОМ НАПРАВЛЕНИИ

Рассмотрим возможность минимизации УБЛ в заданном направлении $~{{\theta }_{{{\text{min}}}}}$. Для этого необходимо определить значение амплитудного коэффициента $\chi $, при котором значение МК ЛЭФАР ${{f}_{\Sigma }}\left( {{{{{\theta }}}_{{{\text{min}}}}},{{\chi }},X} \right)$, задаваемого выражением (12), равно нулю для выбранного направления $~{{{{\theta }}}_{{{\text{min}}}}}$ при выполнении условия (6).

Для получения минимума МК ЛЭФАР ${{f}_{\Sigma }}\left( {\theta ,\chi ,X} \right)$ в заданном направлении ${{{{\theta }}}_{{{\text{min}}}}}$ необходимо подобрать такой амплитудный коэффициент $\chi $, который позволит получить нуль при суммировании парциальных ДН ${{\bar {f}}_{i}}\left( \theta \right)$ согласно выражению (12) при выполнении условия (6).

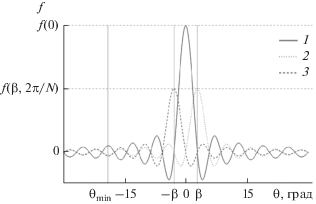
На рис. 7 представлены зависимости парциальных ДН ${{f}_{i}}\left( \theta \right)$ от угла $\theta $. На оси абсцисс отмечено направление ${{{{\theta }}}_{{{\text{min}}}}}$ в направлении, на которое необходимо сформировать минимальное значение МК ЛЭФАР. Необходимо отметить, что при углах $\left| \theta \right| \geqslant 2\beta $ нулевые значения парциальных ДН совпадают по координате $\theta $, при этом амплитудные значения ДН ${{f}_{2}}\left( \theta \right)$ и ${{f}_{3}}\left( \theta \right)$ находятся в противофазе с амплитудными значениями ДН ${{f}_{1}}\left( \theta \right)$.

Рис. 7.

Зависимости парциальных ДН от угла $\theta $: ДН ${{f}_{1}}\left( \theta \right)$ (кривая 1), ДН ${{f}_{2}}\left( \theta \right)$ (кривая 2), ДН ${{f}_{3}}\left( \theta \right)$ (кривая 3).

Учитывая выражение (12), при условии (6) получим аналитическую зависимость, позволяющую определять коэффициент $\chi $ для произвольного угла ${{{{\theta }}}_{{{\text{min}}}}}$:

Подставляя в соотношение (15) выражения для парциальных ДН $~{{f}_{i}}\left( \theta \right)$, задаваемого выражением (4), и обобщенного угла $\Psi \left( {\theta ,\Delta {{\Phi }_{i}}} \right)$, задаваемого выражением (5), а также учитывая выражения для разности фаз (9) (10), получим следующее выражение:

Как видно из выражения (16), амплитудный коэффициент второй парциальной ДН зависит не только от угла ${{{{\theta }}}_{{{\text{min}}}}}$, но и от количества излучателей N в ЛЭФАР, волнового числа k и расстояния между излучателями ЛЭФАР $d$.

Рассмотрим, как меняется форма зависимости коэффициента $\chi $ от угла ${{{{\theta }}}_{{{\text{min}}}}}$ при различном количестве излучателей в ЛЭФАР в наиболее часто встречающемся случае, когда расстояние между излучателями d составляет половину длины волны, т.е.

Тогда коэффициент $\chi $, задаваемый выражением (16), будет определяться только значениям угла минимизации МК ${{{{\theta }}}_{{{\text{min}}}}}$ и количеством излучателей N в ЛЭФАР.

На рис. 8а представлены зависимости амплитудного коэффициента $~\chi $ от угла ${{{{\theta }}}_{{{\text{min}}}}}$, рассчитанные согласно выражению (16), для количества излучателей N, равного 40, 50, 60, 70, 80, 90 и 100 при выполнении условия (6).

Рис. 8.

Зависимость коэффициента $\chi $ от угла ${{{{\theta }}}_{{{\text{min}}}}}$ в масштабе от 0.3 до 0.48 (а) и от 0.42 до 0.48 (б) для АС с различным числом излучателей: N = 40 (1), 50 (2), 60 (3), 70 (4), 80 (5), 90 (6), 100 (7).

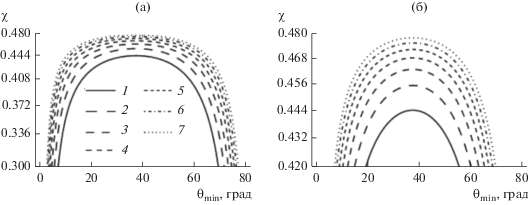
Из рис. 8а следует, что каждому значению коэффициента $\chi $ соответствуют сразу два значения угла ${{{{\theta }}}_{{{\text{min}}}}}$, в направлении, на которые будут сформированы минимальные УБЛ МК. При увеличении числа излучателей ЛЭФАР N происходит расширение формы графика зависимости $\chi \left( {{{{{\theta }}}_{{{\text{min}}}}},N} \right)$. При уменьшении числа излучателей ЛЭФАР наблюдается сужение формы графика зависимости $\chi \left( {{{{{\theta }}}_{{{\text{min}}}}},N} \right)$. Это объясняется тем, что при изменении числа излучателей и сохранении заданного расстояния между соседними излучателями d ЛЭФАР происходит изменение ширины главного лепестка МК и смещение первого бокового лепестка МК. Увеличение количества излучателей приводит к уменьшению значения модуля угла $\beta $, соответствующего первому нулю первой парциальной ДН ${{f}_{1}}\left( \theta \right)$. Уменьшение количества излучателей приводит к увеличению значения модуля угла $\beta $.

На рис. 8б представлена зависимость центральной части графика амплитудного коэффициента $\chi $ от угла ${{{{\theta }}}_{{{\text{min}}}}}$ для различного количества излучателей ЛЭФАР N. В центральной части области определения амплитудного коэффициента $\chi \left( {{{{{\theta }}}_{{{\text{min}}}}},N} \right)$ его значение достигает максимума, при этом максимальному значению $\chi $ соответствует единственный угол ${{{{\theta }}}_{{{\text{min}}}}}$. При подстановке в выражение (6) этот максимум определяет формирование минимума второго порядка МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,\chi ,1} \right)$ на заданном направлении ${{{{\theta }}}_{{{\text{min}}}}}$.

В качестве примера найдем значение $\chi $ для угла

Подставляя значение ${{{{\theta }}}_{{{\text{min}}}}}$ согласно (18) в выражение (16) для нахождения амплитудного коэффициента $\chi $, получаем $\chi = 0.4427$. Как видно из рис. 8б, такому значению амплитудного коэффициента $\chi $ соответствуют два значения угла $\theta $. Первое значение согласно условию (18) и второе значение угла ${{{{\theta }}}_{{{\text{min}}}}}$:

Таким образом, в синтезированном МК будет два минимума: при заданном угле ${{{{\theta }}}_{{{\text{min}}}}}$ (18) и побочный минимум при угле ${{\theta }}_{{{\text{min}}}}^{'}$ (19).

Нормированные первая парциальная ДН $\overline {{{f}_{1}}} \left( \theta \right)$ и МК ЛЭФАР ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.4427,1} \right)$ представлены на рис. 9. Из рисунка видно, что в заданных согласно (18) и (19) направлениях ${{{{\theta }}}_{{{\text{min}}}}}$ сформированы минимальные значения МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.4427,1} \right)$.

Рис. 9.

Нормированные парциальная ДН $\overline {{{f}_{1}}} \left( \theta \right)$ (кривая 1) и МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.4427,1} \right)$ (кривая 2).

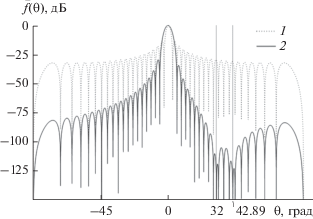
По сравнению с первой нормированной парциальной ДН $\overline {{{f}_{1}}} \left( \theta \right)$ значение МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.4427,1} \right)$ снижается не менее чем на 200 дБ в заданном согласно (18) направлении ${{{{\theta }}}_{{{\text{min}}}}}$. Отметим, что в выбранном частном случае положение нуля МК ЛЭФАР ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,\chi ,1} \right)$ определяется только значением одного параметра $\chi $, что позволяет минимизировать вычисления при синтезе АФР сигнала на входах излучателей ЛЭФАР. Рассмотрим пример синтеза АФР для заданного значения амплитудного коэффициента $\chi $.

5. СИНТЕЗ АФР ДЛЯ ЗАДАННОГО ЗНАЧЕНИЯ АМПЛИТУДНОГО КОЭФФИЦИЕНТА ВТОРОЙ ПАРЦИАЛЬНОЙ ДН $\chi $

Рассмотрим АФР сигнала на входах излучателей ЛЭФАР каждой из трех парциальных ДН ${{f}_{i}}\left( \theta \right)$ в выражении (12) при условии (6).

Первая парциальная ДН ${{f}_{1}}\left( \theta \right)$ с максимальной амплитудой главного лепестка, равной единице, характеризуется равномерным АР и синфазным ФР сигнала на входах излучателей ЛЭФАР:

где ${{B}_{{1n}}}$ – амплитуда сигнала на входе n-го излучателя ЛЭФАР, ${{\varphi }_{{1n}}}$ – фаза сигнала на входе n-го излучателя ЛЭФАР, при $n = 1,~2 \ldots N$ (см. рис. 1).

Вторая парциальная ДН ${{f}_{2}}\left( \theta \right)$ обладает равномерным АР и линейным ФР сигнала, определяемыми соответственно из выражений

где B_2n – амплитуда сигнала на входе n-го излучателя ЛЭФАР, ${{\varphi }_{{2n}}}$ – фаза сигнала на входе n-го излучателя ЛЭФАР, при $n = 1,~2, \ldots ,N$ (см. рис. 1).

Третья парциальная ДН ${{f}_{3}}\left( \theta \right)$ обладает равномерным АР и линейным ФР сигнала, определяемыми соответственно из выражений

где ${{B}_{{3n}}}$ – амплитуда сигнала на входе n-го излучателя ЛЭФАР, ${{\varphi }_{{3n}}}$ – фаза сигнала на входе n-го излучателя ЛЭФАР, при $n = 1,~2, \ldots ,N$ (см. рис. 1).

Амплитудно-фазовое распределение для МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\alpha ,\chi ,1} \right)$, задаваемого суммой трех парциальных ДН в соответствии с выражением (12), в силу линейности системы представляет собой комплексную величину, определяемую суммой АФР трех парциальных ДН ${{f}_{i}}\left( \theta \right)$ [12–14]:

Поскольку АФР МК ${{f}_{\Sigma }}\left( {\theta ,\chi ,{\rm X}} \right)$ имеет комплексный характер, АР сигнала на входах излучателей ЛЭФАР будет определяться выражением [12–14]

Фазовое распределение сигнала на входах излучателей ЛЭФАР будет определяться как [1]:

Используя выражения (27) и (28) для АФР на входах излучателей ЛЭФАР и учитывая полученное соотношение (16) для амплитудного коэффициента $\chi $, получим выражения для амплитудного и фазового распределений сигналов на входах излучателей в явном виде в зависимости от заданного угла, в направлении которого минимизируется УБЛ МК ЛЭФАР.

6. АМПЛИТУДНОЕ И ФАЗОВОЕ РАСПРЕДЕЛЕНИЯ НА ВХОДАХ ИЗЛУЧАТЕЛЕЙ ПРИ ЗАДАННОМ УГЛЕ МИНИМИЗАЦИИ УБЛ МК ЛЭФАР

Амплитудное распределение. Учитывая выражение (16), введем следующие обозначения:

причем $s\left( {N,A} \right)$ не зависит от номера излучателя n.

Подставим в соотношение (27) значения АР парциальных ДН согласно выражениям (20), (22) и (24) и значения ФР парциальных ДН согласно выражениям (21), (23) и (25) на входах излучателей для второй и третьей парциальных ДН, учитывая (29) и (30), а также соотношение (16) для амплитудного коэффициента $\chi $, и тогда получим следующее выражение для расчета АР МК ЛЭФАР:

Как видно из соотношения (31), зависимость амплитуды от номера излучателя определяется значением $\sin \left( {\frac{\pi }{{2N}}\left( {2n - 1} \right)} \right)$, а значение $s\left( {N,A} \right)$ для заданной ЛЭФАР может быть вычислено заранее для минимизации числа операций при синтезе АФР сигнала на входах излучателей ЛЭФАР. Таким образом, получено выражение для вычисления АР сигналов на входах излучателей для заданного направления минимизации УБЛ МК ЛЭФАР.

Фазовое распределение. Получим выражение для фазового распределения сигналов в явном виде в зависимости от заданного угла в направлении которого минимизируется УБЛ МК ЛЭФАР.

Учитывая выражение (16), введем следующее обозначение:

причем $p\left( {N,A} \right),$ так же как и $s\left( {N,A} \right),$ определяемая из выражения (30), не зависит от номера излучателя n.

Подставим в соотношение (28) значения АР парциальных ДН согласно выражениям (20), (22) и (24), и значения ФР парциальных ДН согласно выражениям (21), (23) и (25) на входах излучателей для второй и третьей парциальных ДН, учитывая (29) и (32), а также соотношение (16) для амплитудного коэффициента $\chi $, тогда получим следующее выражение для расчета ФР МК ЛЭФАР:

Как видно из соотношения (33), зависимость фазы от номера излучателя определяется значением ${\text{ctg}}\left( {\frac{\pi }{{2N}}\left( {2n - 1} \right)} \right)$, а значение $p\left( {N,A} \right)$ для заданной ЛЭФАР может быть вычислено заранее для минимизации числа операций при синтезе АФР сигнала на входах излучателей ЛЭФАР. Таким образом, получено выражение для вычисления ФР сигналов на входах излучателей для заданного направления минимизации УБЛ МК ЛЭФАР.

Выражения (30)–(33) позволяют строить эффективные вычислительные процедуры для расчета АФР на входах излучателей ЛЭФАР, поскольку сначала рассчитываются значения $s\left( {N,A} \right)$ и $p\left( {N,A} \right)$, которые одинаковы для всех излучателей заданной ЛЭФАР, а затем АФР в соответствии с выражениями (31) и (33).

7. ПРИМЕР ВЫЧИСЛЕНИЯ АФР ДЛЯ ПОДАВЛЕНИЯ УБЛ МК ЛЭФАР В ЗАДАННОМ НАПРАВЛЕНИИ

Рассмотрим пример вычисления АФР для подавления УБЛ МК ЛЭФАР для угла ${{{{\theta }}}_{{{\text{min}}}}}$, заданного согласно (18). Амплитудное и фазовое рспределения сигнала на входах излучателей ЛЭФАР, рассчитанные в соответствии с выражениями (31) и (33), приведены на рис. 10.

Рис. 10.

Амплитудное ${{A}_{n}}$ (а) и фазовое ${{F}_{n}}$ (б) распределения на входах излучателей апертуры АС для МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,0.4427,1} \right)$.

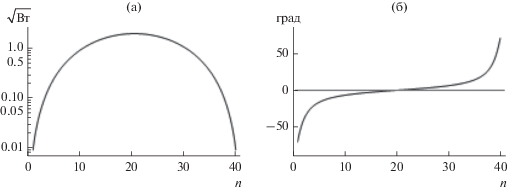
Как видно из рис. 10а, амплитуда сигнала симметрична относительно центральных излучателей и представляет собой четную функцию, а фаза сигнала на каждом излучателе (см. рис. 10б) также симметрична относительно центральных излучателей, но представляет собой нечетную функцию.

8. АНАЛИЗ АФР ДЛЯ СЛУЧАЯ БОЛЬШОГО ЧИСЛА ИЗЛУЧАТЕЛЕЙ ЛЭФАР

Важным является случай, когда число излучателей ЛЭФАР N представляет собой достаточно большую величину [13, 45]:

тогда согласно [45] имеем

Учитывая формулу приведения для синуса [45], соотношение (31) запишем в следующем виде:

Таким образом, получено выражение для АР в случае большого количества излучателей ЛЭФАР N.

Для нахождения ФР в случае большого количества элементов ЛЭФАР также воспользуемся условием (34) и найдем значение выражения (32):

Подставляя (37) в соотношение (33), получим следующие значения для ФР:

Выражения (36) и (38) определяют АР и ФР ЛЭФАР при большом числе излучателей ЛЭФАР N.

Представляет также интерес случай, когда выполняются оба условия, (6) и (14), тогда выражение (31) примет вид (36), а выражение (33) примет вид (38), причем независимо от числа излучателей ЛЭФАР N.

9. ОЦЕНКА ВЛИЯНИЯ ДИСКРЕТИЗАЦИИ АМПЛИТУДЫ И ФАЗЫ СИГНАЛА НА УБЛ МК

В реальных системах невозможно сформировать точные АР и ФР сигнала на входах излучателей ЛЭФАР. Амплитудное распределение обеспечивается за счет различных коэффициентов усиления усилителей мощности (УМ) амплитуды сигнала в каждом канале ЛЭФАР. Фазовое распределение обеспечивается за счет различных фазовых сдвигов в фазовращателях каждого канала ЛЭФАР. Поскольку точность установки коэффициентов усиления и фазовых сдвигов определяется разрядностями УМ и фазовращателей, представляет интерес вопрос, как влияет разрядность УМ и фазовращателей сигнала на уровень МК ЛЭФАР.

МК ЛЭФАР для известного АФР сигнала на входах излучателей определяется из следующего выражения [12, 14]:

где ${{A}_{n}}~$ и ${{F}_{n}}$ – соответственно АР и ФР сигнала на входах излучателей ЛЭФАР.

Для оценки изменений в нормированном МК, вызванных разрядностями УМ, введем дискретизацию по амплитуде, зависимую от разрядности УМ. Тогда МК ЛЭФАР при дискретизации только амплитуды сигнала для угла ${{\theta }}$ можно представить как [12, 14, 46]:

где ${{n}_{A}}$ – разрядность УМ на входе излучателя ЛЭФАР, которая является целым числом: 1, 2 и т.д. Согласно принятым математическим правилам, квадратные скобки в выражении (40) являются оператором округления к целому [47]. Поскольку максимальное значение АР сигнала на входах излучателей равно 2, в степень множителя ${{2}^{{1 - {{n}_{A}}}}}$ включена единица (см. выражение (40)). Выражение $\left[ {\frac{{{{A}_{n}}}}{{{{2}^{{1 - {{n}_{A}}}}}}}} \right]{{2}^{{1 - {{n}_{A}}}}}$ задает дискретизацию АР с учетом разрядности УМ.

Для оценки погрешности, вызванной разрядностью фазовращателей, введем выражение для дискретизации МК ЛЭФАР [34], с учетом того что максимальное значение фазы сигнала на входах излучателей ЛЭФАР равно $2\pi {\kern 1pt} :$

где ${{n}_{F}}$ – разрядность фазовращателя на выходе излучателя ЛЭФАР, которая является целым числом: 1, 2 и т.д. В выражении (41) к фазе добавляется число π, а после округления к целому и умножения на $\pi \times {{2}^{{1 - {{n}_{F}}}}}$ вычитается число π, поскольку значения ФР ${{F}_{n}}$ лежат в диапазоне от $ - \frac{{~\pi }}{2}$ до $\frac{{~\pi }}{2}$ (см. рис. 6б и 10б). Выражение

задает дискретизацию ФР ${{F}_{n}}$ сигнала на входах излучателей ЛЭФАР с учетом разрядности фазовращателей.

Для оценки погрешности, вызванной одновременно разрядностью УМ и фазовращателей ЛЭФАР, воспользуемся следующим выражением для МК, учитывающим дискретизацию как по амплитуде, так и по фазе:

По аналогии с (11) и (13) пронормируем МК ${{f}_{A}}\left( {{{n}_{A}},{{\theta }}} \right)$, ${{f}_{F}}\left( {{{n}_{F}},\theta } \right)$ и ${{f}_{{AF}}}\left( {{{n}_{A}},{{n}_{F}},{{\theta }}} \right)$. На рис. 11 приведены результаты расчета зависимости нормированных МК $\overline {{{f}_{A}}} \left( {{{n}_{A}},{{\theta }}} \right)$, $\overline {{{f}_{F}}} \left( {{{n}_{A}},{{\theta }}} \right)$ и $\overline {{{f}_{{AF}}}} \left( {{{n}_{A}},{{n}_{F}},{{\theta }}} \right)$ от разрядности УМ ${{n}_{A}} = n$ и фазовращателей ${{n}_{F}} = n$ на входах излучателей ЛЭФАР с учетом условия (18). Из рис. 11 следует, что при разрядности фазовращателей $n \leqslant 4$ значения нормированного МК с учетом дискретизации только фазы $\overline {{{f}_{F}}} \left( {n,{{{{\theta }}}_{{{\text{min}}}}}} \right)$ существенно ниже значений МК с учетом дискретизации и амплитуды, и фазы ${{\bar {f}}_{{AF}}}\left( {n,n,{{{{\theta }}}_{{{\text{min}}}}}} \right)$. Существуют углы ${{{{\theta }}}_{{{\text{min}}}}}$, в которых УБЛ нормированного МК с учетом дискретизации и амплитуды, и фазы ${{\bar {f}}_{{AF}}}\left( {n,n,{{{{\theta }}}_{{{\text{min}}}}}} \right)$ ниже УБЛ нормированных МК с учетом дискретизации только амплитуды $\overline {{{f}_{A}}} \left( {n,{{{{\theta }}}_{{{\text{min}}}}}} \right)$ и с учетом дискретизации только фазы $\overline {{{f}_{F}}} \left( {n,{{{{\theta }}}_{{{\text{min}}}}}} \right)$. Это, по-видимому, может быть объяснено тем, что погрешности, вызванные учетом дискретизации, обусловленной конечной разрядностью УМ и фазовращателей, в таких случаях компенсируют друг друга. Как видно из рис. 11, для разрядностей ФР $n \leqslant 13$ не целесообразно использовать только ФР для уменьшения УБЛ МК ЛЭФАР, а целесообразно использовать только АР на входах излучателей.

Рис. 11.

Зависимость нормированных МК ${{\bar {f}}_{A}}\left( {{{n}_{A}},{{{{\theta }}}_{{{\text{min}}}}}} \right)$ (кривая 1), ${{\bar {f}}_{F}}\left( {{{n}_{F}},{{\theta }_{{{\text{min}}}}}} \right)$ (кривая 2) и ${{\bar {f}}_{{AF}}}\left( {{{n}_{A}},{{n}_{F}},{{{{\theta }}}_{{{\text{min}}}}}} \right)$ (кривая 3) от разрядности усилителей мощности ${{n}_{A}}$ фазовращателей ${{n}_{F}}$ при ${{n}_{A}} = n$, ${{n}_{F}} = n$ и заданном ${{{{\theta }}}_{{{\text{min}}}}} = 32^\circ $.

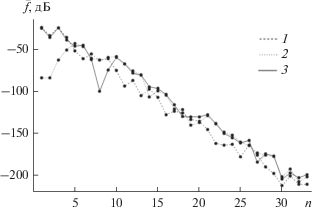
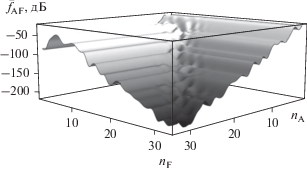
На рис. 12 представлена зависимость нормированного МК с учетом дискретизации и амплитуды, и фазы ${{\bar {f}}_{{AF}}}\left( {{{n}_{A}},{{n}_{F}},{{\theta }_{{\min }}}} \right)$ ЛЭФАР (в дБ) от разрядности УМ ${{n}_{A}}$ и фазовращателей ${{n}_{F}}$ для рассмотренного выше примера (МК ЛЭФАР – см. рис. 9, АФР – см. рис. 10). Как видно из рис. 12, поверхность, образованная значениями ${{\bar {f}}_{{AF}}}\left( {{{n}_{A}},{{n}_{F}},{{{{\theta }}}_{{{\text{min}}}}}} \right){\text{\;}},$ имеет ступенчатый характер и снижается при увеличении значений ${{n}_{A}}$ и ${{n}_{F}}$.

Рис. 12.

Зависимость нормированного МК ${{\bar {f}}_{{AF}}}\left( {{{n}_{A}},{{n}_{F}},{{{{\theta }}}_{{{\text{min}}}}}} \right)$ разрядности усилителей мощности ${{n}_{A}}$ фазовращателей ${{n}_{F}}$ при заданном ${{{{\theta }}}_{{{\text{min}}}}} = 32^\circ $.

На рис. 13 представлена диаграмма уровней для значений нормированного МК ЛЭФАР с учетом дискретизации и амплитуды, и фазы ${{\bar {f}}_{{AF}}}\left( {{{n}_{A}},{{n}_{F}},\theta } \right)$, представленного на рис. 12. На диагонали выражены области, в которых наблюдается как уменьшение УБЛ нормированного МК ${{\bar {f}}_{{AF}}}\left( {{{n}_{A}},{{n}_{F}},\theta } \right)$ ЛЭФАР при увеличении разрядностей ${{n}_{A}}$ и ${{n}_{F}}$, так и повышение УБЛ нормированного МК ${{\bar {f}}_{{AF}}}\left( {{{n}_{A}},{{n}_{F}},\theta } \right)$ ЛЭФАР при уменьшении разрядностей ${{n}_{A}}$ и ${{n}_{F}}$. Как видно из представленных результатов, управление фазой для снижения УБЛ МК при разрядности ${{n}_{F}} \leqslant 12$ не позволяет снизить УБЛ МК ${{\bar {f}}_{{AF}}}\left( {{{n}_{A}},{{n}_{F}},\theta } \right)$ более чем в случае, когда фазовое распределение на излучателях ЛЭФАР задано синфазным.

Рис. 13.

Диаграмма уровня МК ${{\bar {f}}_{{AF}}}\left( {{{n}_{A}},{{n}_{F}},{{{{\theta }}}_{{{\text{min}}}}}} \right)$ от разрядности усилителей мощности ${{n}_{A}}$ фазовращателей ${{n}_{F}}$ при заданном ${{{{\theta }}}_{{{\text{min}}}}} = 32^\circ $.

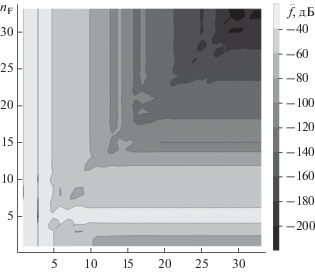
Представляет интерес зависимость МК с учетом дискретизации и амплитуды, и фазы ${{\bar {f}}_{{AF}}}\left( {{{n}_{A}},{{n}_{F}},\theta } \right)$ при заданных разрядностях УМ и фазовращателей ${{n}_{A}}$ и ${{n}_{F}}$ от угла $\theta $. На рис. 14 представлены результаты расчета зависимости нормированного МК ${{\bar {f}}_{{AF}}}\left( {{{n}_{A}},{{n}_{F}},\theta } \right)$ для примера ЛЭФАР при числе излучателей $N = 40$, от угла $\theta $ при разрядности УМ ${{n}_{A}} = n$ и фазовращателей ${{n}_{F}} = n$ для значений разрядности $n$ равных 2 (кривая 1), 4 (кривая 2), 8 (кривая 3), 16 (кривая 4) и 32 (кривая 5). На рис. 14 также представлен нормированный МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,\chi \left( \theta \right),1} \right)~$ (кривая 6), рассчитанный согласно полученному выражению (16), в котором не учитываются погрешности, вносимые УМ и фазовращателями из-за конечной разрядности. Из рис. 14 видно, что при значении разрядности УМ и фазовращателей $n$, равной 2, 4 и 8, значения нормированных МК ${{\bar {f}}_{{AF}}}\left( {n,n,{{\theta }_{{{\text{min}}}}}} \right)$ не опускаются ниже ‒100 дБ. Разность между нормированными МК ${{\bar {f}}_{{AF}}}\left( {32,32,{{\theta }_{{{\text{min}}}}}} \right)$ и ${{\bar {f}}_{{AF}}}\left( {16,16,{{\theta }_{{{\text{min}}}}}} \right)$, ${{\bar {f}}_{{AF}}}\left( {16,16,{{\theta }_{{{\text{min}}}}}} \right)$ и ${{\bar {f}}_{{{\Sigma }}}}\left( {{{\theta }_{{{\text{min}}}}},\chi \left( {{{\theta }_{{{\text{min}}}}}} \right),1} \right)$ составляет –100 дБ.

Рис. 14.

Зависимость нормированного МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,\chi \left( \theta \right),1} \right)$ и МК ${{\bar {f}}_{{AF}}}\left( {{{n}_{A}},{{n}_{F}},\theta } \right)$ от угла $\theta $ при заданных разрядностях усилителей мощности ${{n}_{A}}$ и фазовращателей ${{n}_{F}}$: МК ${{\bar {f}}_{{AF}}}\left( {2,2,\theta } \right)$ (кривая 1), МК ${{\bar {f}}_{{AF}}}\left( {4,4,\theta } \right)$ (кривая 2), МК ${{\bar {f}}_{{AF}}}\left( {8,8,\theta } \right)~$(кривая 3), МК ${{\bar {f}}_{{AF}}}\left( {16,16,\theta } \right)$ (кривая 4), МК ${{\bar {f}}_{{AF}}}\left( {32,32,\theta } \right)$ (кривая 5), МК ${{\bar {f}}_{{{\Sigma }}}}\left( {\theta ,\chi \left( \theta \right),1} \right)$ (кривая 6).

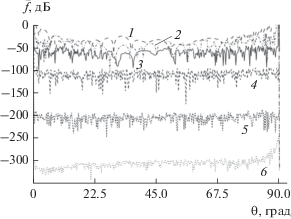
Оценивая приведенные результаты, можно сделать вывод о выборе необходимой разрядности фазовращателей и усилителей мощности для разрабатываемой ЛЭФАР исходя из требуемого УБЛ нормированного МК. Для достижения минимального УБЛ МК на заданной апертуре, разрядность фазовращателей ${{n}_{F}}$ должна превышать разрядность УМ ${{n}_{A}}$ не менее чем на два разряда ${{n}_{F}} \geqslant {{n}_{A}} + 2$ при разрядности ФР ${{n}_{F}} \geqslant 14$.

ЗАКЛЮЧЕНИЕ

Предложен способ снижения УБЛ МК ЛЭФАР в заданном направлении путем использования трех парциальных ДН, который представляет собой вариацию метода Вудворда–Лоусона, что позволяет отнести его к аналитическим способам управления МК. В качестве базисных функций выбраны функции для дискретного излучателя из N элементов ЛЭФАР, используются три парциальные ДН, главные лепестки которых ориентированы не в направлении минимизации УБЛ МК ЛЭФАР, а в направлениях первых нулей первой парциальной ДН. Выбор именно таких парциальных ДН позволяет сохранить положения нулей МК ЛЭФАР таким же, как и у парциальных ДН ${{\bar {f}}_{i}}\left( \theta \right),$ за исключением двух ближайших к главному лепестку.

Найдены коэффициенты парциальных ДН из условия минимизации УБЛ МК в заданном направлении. Приведены примеры МК ЛЭФАР с различными коэффициентами парциальных диаграмм. Получены аналитические зависимости АР и ФР от угла, в направлении на который необходимо сформировать минимум МК ЛЭФАР. Проведена оценка возможности достижения минимального УБЛ МК ЛЭФАР в зависимости от разрядности усилителей мощности и разрядности фазовращателей, обеспечивающих АР и ФР на излучающей апертуре ЛЭФАР (до –200 дБ при разрядности 32).

Получены аналитические зависимости амплитудного коэффициента второй парциальной ДН от угла ${{{{\theta }}}_{{{\text{min}}}}}$, а также АФР от угла ${{{{\theta }}}_{{{\text{min}}}}}$, позволяющие сократить количество операций при адаптивном управлении МК ЛЭФАР.

Необходимо отметить, что в предложенном способе во многом используется геометрия выбранной антенной решетки, поэтому он не может быть распространен на решение задачи синтеза дискретных антенн в общем случае.