Радиотехника и электроника, 2021, T. 66, № 6, стр. 543-551

ВВЕДЕНИЕ

В последнее десятилетие высоколегированный графен стал основной платформой для плазмоники и ее приложений благодаря своим уникальным оптоэлектронным свойствам. В терагерцовом (ТГц) диапазоне графен поддерживает плазмонные колебания – поверхностные плазмон-поляритоны (ППП), которые позволяют значительно увеличить сильно локализованное поле и вызывают относительно долгоживущие, активно перестраиваемые плазмонные ТГц- и ИК-резонансы [1, 2]. Плазмоны в графене могут быть использованы как средство усиления взаимодействия излучения с веществом в ТГц- и ИК-диапазонах в перестраиваемом режиме, особенно путем интеграции графеновых резонансных структур с дополнительными элементами нанофотоники [2].

Графеновая плазмоника находит множество применений в фотонных ТГц-устройствах [3]. Двумерные (2D) технологии на основе плазмонов в графене позволяют разработать сверхбыстродействующие, компактные и недорогие активные фотонные элементы, потому что в отличие от плазмонов в других материалах плазмоны в графене можно перестраивать путем изменения химического потенциала (уровня Ферми) и уровня легирования. Такое управление используется, например, в квантовых каскадных ТГц-лазерах для обратимого изменения их излучения [4].

Комбинированное взаимодействие (синергия) экстремального увеличения сильно локализованного плазмонного поля и большой внутренней оптической нелинейности графена в настоящее время мотивируют интенсивные исследования в области нелинейной графеновой плазмоники [1, 5–7].

Графен представляет собой идеальный материал, особенно для создания нелинейных плазмонных структур (ПС) в ТГц- и ИК-диапазонах. Это связано с тем, что он обладает исключительно сильной нелинейностью третьего порядка [8] в сравнении с широко используемыми диэлектриками и металлами [9], а также сильным плазмонным откликом и гораздо меньшими потерями в ИК- и ТГц-диапазонах [10]. Кроме того, графен имеет однослойную (толщиной в один атом) 2D‑структуру, которая уменьшает объем взаимодействия излучения с веществом до чрезвычайно субволновой области, что впоследствии ослабляет требования к фазовому согласованию различных оптических нелинейных параметрических эффектов. Как линейная, так и нелинейная проводимости графена хорошо управляются с помощью электрического поля или химического легирования. При проектировании графеновых ПС перестройка создает дополнительную степень свободы, обеспечивая управление параметрами без изменения размеров и структуры [10].

Первое экспериментальное исследование нелинейного отклика графеновых плазмонных резонансов и их динамики, релаксации энергии представлено в [11]. При использовании метода ТГц-измерения и накачки лазером на свободных электронах, настроенного на плазмонную частоту 9.4 ТГц, обнаружено сильное насыщение поглощения плазмона в графеновых лентах с размерами меньше длины волны. Установлено, что наблюдаемая нелинейность на два порядка выше, чем у монослоя графена без плазмонного резонанса [11].

Экспериментально обнаружен и теоретически объясняется нелинейный эффект эффективного преобразования частоты ИК-излучения в решетках графеновых нанолент [12], который возникает из-за возбуждения графеновых плазмонов. Нелинейные эффекты как второго, так и третьего порядка наблюдались в экспериментах с пересчитанным коэффициентом нелинейности третьего порядка, достигающим значений 4.5 × 10^–6 esu . Отмечается, что обнаруженный эффект может быть использован в различных приложениях, включая нелинейные модуляторы света, оптические мультиплексоры, оптические цифровые и сенсорные устройства, датчики [12].

Новые механизмы генерации ТГц-излучения электрически возбуждаемыми графеновыми плазмонами исследуются для разработки компактных узкополосных ТГц-источников [2].

Высокое пространственное ограничение и большая частотная перестройка являются двумя ключевыми преимуществами графеновой плазмоники. Тем не менее, диапазон перестройки частоты плазмонных устройств, в которых используется однослойный графен, в итоге ограничен диапазоном перестройки плотности носителей. Как показывает эксперимент [3], диапазон перестройки частоты графеновых плазмонных устройств (резонаторов с управляемым затвором) может быть значительно расширен за счет использования многослойных (двух или трех слоев графена) структур, что является результатом распределения носителей в нескольких слоях и приводит к более высокому общему уровню оптической проводимости.

Цель данной работы – теоретическое исследование нелинейного взаимодействия электромагнитной волны с многослойными ПС на основе двумерно-периодических решеток графеновых нанолент в нижней части ТГц-диапазона.

1. ПОСТАНОВКА ЗАДАЧИ

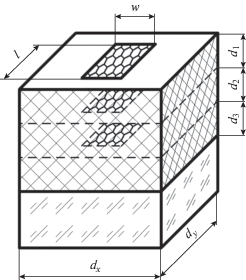
Двумерно-периодическая решетка (рис. 1) образована прямоугольными графеновыми, металлическими и диэлектрическими полосками (пленками). Число полосок в трехмерной элементарной ячейке M – произвольное. Полоски могут лежать как на поверхности, так и в глубине многослойного диэлектрика, у которого произвольное число слоев N. Диэлектрик с номером N – полубесконечная подложка. Диэлектрические слои с потерями, в том числе из плазмонных материалов (Au, Ag, Cu, AZO и др. в оптическом диапазоне). Потери описываются мнимой частью показателя преломления. В разработанных программах создана база данных для частотной зависимости комплексного показателя преломления для более десяти плазмонных материалов. Ось z перпендикулярна границам раздела сред.

Рис. 1.

Элементарная ячейка многослойной двумерно-периодической решетки графеновых микролент.

Полагаем, что из воздуха нормально к ПС падает плоская, линейно-поляризованная электромагнитная волна с частотой ω. В результате взаимодействия внешнего поля и графена в полосках возникает поверхностный ток $\overrightarrow j $. При нелинейном характере взаимодействия, зависящем от амплитуды падающей волны $\overrightarrow E $, в выражении для $\overrightarrow j $ появляются дополнительные слагаемые, ответственные за генерацию гармонических составляющих [8]

где $\vec {n},{{\vec {H}}^{ + }},\,{{\vec {H}}^{ - }}$ – нормаль к полоске, напряженность магнитного поля сверху и снизу полоски.

Кроме того, в разработанной программе может быть два вида полосок: а) тонкие диэлектрические; б) металлические с толщиной меньшей толщины скин слоя. Для них также могут быть записаны приближенные граничные условия вида (1) без нелинейных членов.

Поскольку графен имеет центрально симметричную структуру и у поля падающей волны отсутствует нормальная электрическая составляющая, в разложении (1) четные слагаемые можно не учитывать вследствие малости [13]. Максимальный уровень будет иметь гармоническая составляющая третьего порядка. В этом случае поверхностная проводимость полосок вычисляется по формуле

где σ⁽¹⁾ – линейная часть проводимости [14], σ⁽³⁾ – нелинейная проводимость третьего порядка.

В частотной области существования плазмонных резонансов (низкочастотная часть ТГц-диапазона) нелинейная проводимость третьего порядка определяется только внутризонными переходами, поскольку энергии фотонов недостаточно для осуществления межзонных переходов. Это позволяет нелинейную проводимость σ⁽³⁾ выразить как на основе квазиклассической кинетической теории с распределением Больцмана для носителей [15], так и с помощью квантовой теории вне области резонансных межзонных переходов (ћω $ \ll $ 2µ_с)) [16, 17]. Полагая, что движение носителей заряда является бесстолкновительным, из работы [15] ряд авторов получили [10, 18, 19] следующую формулу:

где e – заряд электрона, µ_c – химический потенциал (уровень Ферми), v_F = 10⁶ м/с – скорость Ферми, ω – частота падающей волны, $\hbar $ – приведенная постоянная Планка.

Однако существуют и другие выражения для нелинейной проводимости, полученные из [14]: σ⁽³⁾ = 3/32π × σ₀ [20], в σ⁽³⁾ = 3/8π × σ₀ [21], σ⁽³⁾ = = 1/8π × σ₀ [16, 17, 22]. Использование выражения (3) при комнатной температуре T = 300 К ограничено значениями химического потенциала: µ_с$ \gg $ k_BT, где k_B – постоянная Больцмана, т.е. µ_с$ \gg $ 0.026 эВ. Анализ приведенных выше формул дает лишь разницу в коэффициентах, при этом зависимости от частоты и химического потенциала одинаковые. Выбор коэффициента в σ⁽³⁾ (3) не принципиален, так как влияет лишь на уровень третьей гармоники.

Полагаем, что полоски тонкие. На них выполняются два граничных условия – непрерывность тангенциальных компонент напряженности электрического поля ${{\vec {E}}_{\tau }}$ и (1).

Для решения задачи нелинейной дифракции используем метод возмущения. Вначале решаем линейную задачу с указанными выше граничными условиями. Это решение назовем ${{\overrightarrow E }_{l}}\left( {x,y,t} \right)$. Находим нелинейный ток:

Зная ${{\overrightarrow j }_{{nl}}}$ и тензорную функцию Грина линейной задачи (см. разд. 2), находим поля на основной гармонике (самовоздействие) и на третьей гармонике.

2. ОСНОВНЫЕ ЭТАПЫ РЕШЕНИЯ ЛИНЕЙНОЙ КРАЕВОЙ ЗАДАЧИ О ДИФРАКЦИИ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ НА МНОГОСЛОЙНОЙ ДВУМЕРНО-ПЕРИОДИЧЕСКОЙ ГРАФЕНОВОЙ СТРУКТУРЕ

А. Вводим внешнее электромагнитное поле ${{\overrightarrow E }^{{{\text{внеш}}}}}$ – поле в многослойной структуре без графеновых и металлических полосок при падении плоской электромагнитной волны. Нахождение ${{\overrightarrow E }^{{{\text{внеш}}}}}$ достаточно простая задача и ее решение здесь не приводится.

Б. Для нахождения поля, рассеянного одной полоской, вводим электрический ${{P}^{E}}$ и магнитный ${{P}^{M}}$ векторы Герца, имеющие только одну $z$-ю компоненту, перпендикулярную поверхности диэлектрических слоев. Для двумерно-периодических планарных структур с периодами d_x и d_y получаем

где ${{\chi }_{{pq}}}\left( {x,y} \right) = {{\alpha }_{p}}x + {{\beta }_{q}}y,$ ${{\alpha }_{p}} = {{2p\pi } \mathord{\left/ {\vphantom {{2p\pi } {{{d}_{x}}}}} \right. \kern-0em} {{{d}_{x}}}} + {{k}_{x}},$ β_q = $ = {{2q\pi } \mathord{\left/ {\vphantom {{2q\pi } {{{d}_{y}}}}} \right. \kern-0em} {{{d}_{y}}}} + {{k}_{y}}$ и ${{k}_{x}},\,\,{{k}_{y}}$ – проекции волнового вектора падающей волны. Функции $\tilde {P}_{{m,pq}}^{{M,E}}\left( z \right)$ представим в виде

где $A_{{m,pq}}^{M}$$A_{{m,pq}}^{E}$ – неизвестные функции, ${{\varepsilon }_{m}},\,{{\mu }_{m}}$ – диэлектрическая и магнитная проницаемости диэлектрического слоя с номером m,

функции $M_{{m,pq}}^{ \pm }\left( z \right),\,\,{\text{E}}_{{m,pq}}^{ \pm }\left( z \right)$ – решения обыкновенных дифференциальных уравнений, которые получаем после подстановки (4) в волновое уравнение для каждого диэлектрического слоя. Они удовлетворяют граничным условиям на границе всех слоев, кроме m-го.

При таком выборе $\tilde {P}_{{m,pq}}^{{M,E}}\left( z \right)$ выполняется условия непрерывности ${{H}_{{x,y}}}$ на границах слоев кроме слоя $z = {{z}_{m}}$ и ${{E}_{{x,y}}}$ для всех границ. Для расчета $M_{{m,pq}}^{ \pm }\left( z \right),\,\,{\text{E}}_{{m,pq}}^{ \pm }\left( z \right)$получена защищенная от переполнения разрядной сетки рекуррентная схема; алгоритм их вывода описан в [23].

В. Следующий этап можно назвать этапом нахождения тензорной функции Грина. Неизвестные коэффициенты в векторах Герца выражаем через компоненты плотности тока на полосках (плотность тока пока неизвестна):

где

Г. Находим компоненты ${{E}_{{x,y}}}$ поля, рассеянного полоской, лежащей на поверхности слоя с координатой ${{z}_{m}}$:

где ${{Z}_{0}} = \sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} $,

В этих формулах

Д. Полное дифрагированное поле – это внешнее ${{\overrightarrow E }^{{{\text{внеш}}}}}$ плюс сумма полей, рассеянных каждой полоской. Удовлетворяем граничным условиям на каждой полоске. В результате получим систему векторных парных сумматорных уравнений относительно плотности токов на полосках. Размерность системы равна числу полосок.

Е. Полученные уравнения решаем методом Галеркина [24]. Токи на m-й полоске запишем в виде

где ${{x}_{m}},\,{{y}_{m}}$ – координаты центра m-й полоски, $2{{l}_{{x,m}}},\,\,2{{l}_{{y,m}}}$ – размеры полоски, ${{X}_{{m,rs}}},\,\,{{Y}_{{m,rs}}}$ – неизвестные коэффициенты, ${{P}_{r}},\,C_{r}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}$ – полиномы Лежандра и Гегенбауэра. В результате получим систему линейных алгебраических уравнений (СЛАУ) относительно неизвестных коэффициентов ${{X}_{{m,rs}}},\,\,{{Y}_{{m,rs}}}$. В матричных элементах СЛАУ все интегралы находятся аналитически.

Для идеально проводящих полосок используется базис, учитывающий условие на ребре:

где ${{T}_{r}},\,{{U}_{r}}$ – полиномы Чебышева.

3. РЕЗУЛЬТАТЫ РАСЧЕТОВ

В случае линейного режима используется только линейная поверхностная проводимость σ⁽¹⁾ (внутризонная проводимость) графена в (1). Результаты расчета частотных зависимостей коэффициентов отражения R, пропускания T и поглощения P падающей ТЕМ-волны в многослойной ПС из графеновых микролент (в линейном режиме) приведены на рис. 2.

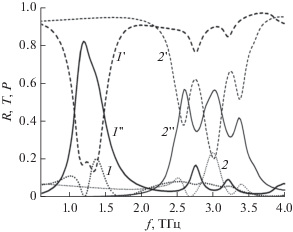
Рис. 2.

Частотные зависимости (в линейном режиме) коэффициентов отражения R (1, 2), прохождения T (1 ', 2 ') и поглощения P (1 '', 2 '') падающей плоской волны многослойной решеткой графеновых микролент (см. рис. 1): w × l = 7 × 20 мкм², при s-поляризации d₁= d₂ = 17 мкм, d₃ = 8 мкм (кривые 1, 1 ' и 1 ''), и p-поляризации d₁= d₂ = 7 мкм, d₃ = 4 мкм (кривые 2, 2 ' и 2 '').

Элементарная ячейка исследуемой многослойной плазмонной структуры представлена на рис. 1а. Она состоит из трех расположенных друг под другом прямоугольных графеновых микролент (ширина w, длина l), разделенных согласующими слоями из диэлектрика SiO₂ с показателем преломления n = 1.45, толщинами d₁ = d₂ и d₃ на полубесконечной подложке Al₂O₃ (n = 1.77). Параметры графена: T = 300 K, τ = 1 пс, μ_с = 0.3 эВ. Элементарные ячейки располагаются с периодами d_x = d_y = 30 мкм по осям x, y.

Графеновые микроленты поддерживают ТГц-резонансы ППП с длиной волны меньше, чем длина электромагнитной волны в вакууме, и ограничением электрического поля на поверхности графена [10]. Поля падающей ТЕМ-волны локально ограничены вдоль поверхности графена (в большей степени, чем внутри разделительных диэлектрических слоев) и резко возрастают на резонансной частоте из-за возбуждения стоячих ППП-волн вдоль микролент графена.

Максимумы коэффициента поглощения P на рис. 2 соответствуют резонансам, определяемым плазмонными модами в графеновых микролентах конечной длины и зависят от поляризации падающей волны. Для s-поляризации первая резонансная частота определяется основной модой ППП (резонанс электрического тока вдоль широкой стороны микролент). Для p-поляризации это резонанс тока вдоль узкой стороны лент, и резонансная частота выше, чем для s-поляризации (см. рис. 2). Наблюдается несколько (три) резонансных частот ближайших высших мод ППП (см. рис. 2).

Во втором случае нелинейного режима общая проводимость включает линейную и нелинейную проводимость третьего порядка σ⁽³⁾ (3) с коэффициентом 3/32. Результаты численного моделирования нелинейного взаимодействия ТГц-волн с многослойной ПС из графеновых микролент, а именно эффекта генерации третьей гармоники – зависимости нормированной мощности волны третьей гармоники, излучаемой в прямом (прохождение T₃) и обратном (отражение R₃) направлении, от частоты падающей ТЕМ-волны с s- и p-поляризацией, представлены на рис. 3. Значения T₃, R₃ рассчитаны нормированием к плотности мощности падающей волны (равной 1 мВт/мм²).

Рис. 3.

Эффект генерации третьей гармоники многослойной решеткой графеновых микролент (параметры см. рис.2): зависимости нормированной мощности волны третьей гармоники, излучаемой в прямом направлении (прохождение T₃, (1, 2)) и обратном направлении (отражение R₃, (1 ', 2 ')), от частоты падающей волны с s- (1, 1 ') и p-поляризацией (2, 2 ').

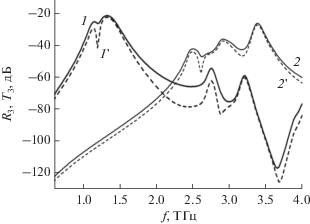
Как видно из графиков на рис. 3, эффективность генерации третьей гармоники может быть увеличена на несколько порядков, когда частота падающей волны близка к резонансной частоте основной моды (и более высоких мод) ППП в многослойной ПС из графеновых микролент. Локализация экстремального поля при ППП-резонансе значительно увеличивает взаимодействие ТГц-волн и графена и приводит к сильному нелинейному отклику.

В дополнение к типичным плазмонным эффектам, таким как увеличение и ограничение поля, локальное поле может быть еще ограничено в многослойных ПС. Эффекты стоячих волн, вызванные отражением от разделительных диэлектрических слоев, подложек, решеток графеновых микролент, вызывают дальнейшее увеличение электрического поля и более острые резонансы ППП-мод на входной частоте, что приводит к значительному усилению нелинейного ТГц-отклика. И наоборот, в нерезонансных условиях эффективность нелинейного взаимодействия ТГц-волн с ПС из графеновых микролент подавляется на многие порядки.

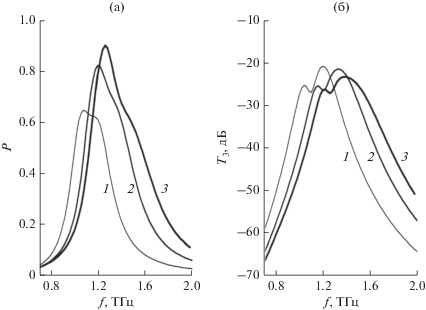
На рис. 4 представлены результаты численного моделирования эффекта генерации третьей гармоники в ПС с различным числом слоев графеновых микролент N. Там же приведены кривые для коэффициента поглощения Р, падающей ТЕМ-волны с s-поляризацией.

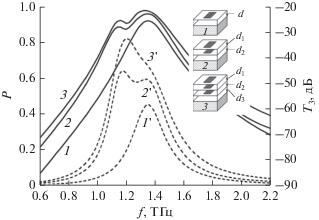
Как следует из результатов, представленных на рис. 4, при увеличении числа слоев решетки эффективность генерации третьей гармоники многослойными графеновыми ПС может быть увеличена на порядок по сравнению с однослойными ПС.

Рис. 4.

Спектр нелинейного прохождения T₃ (1, 2, 3) и линейный спектр поглощения P (1 ', 2 ', 3 ') s-поляризованной волны решетками (приведенными на вставке) с различным числом N слоев графеновых микролент: однослойной, d = 38 мкм (кривые 1, 1 '), двухслойной, d₁ = 30 мкм, d₂ = 14 мкм (кривые 2, 2 ') и трехслойной, d₁ = d₂ = 17 мкм, d₃ = 8 мкм (кривые 3, 3 ').

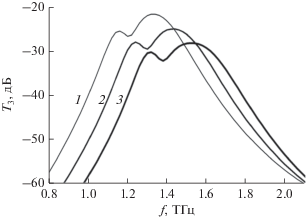
Изменение нелинейного спектра прохождения (третьей гармоники) и для сравнения частотная зависимость коэффициента поглощения P падающей волны (первой гармоники) многослойными ПС с различной периодичностью (плотностью упаковки) решетки графеновых микролент показано на рис. 5.

Рис. 5.

Эффективность генерации третьей гармоники решетками графеновых микролент с различной периодичностью (плотностью упаковки) (см. рис. 1): cпектр нелинейного прохождения T₃ (1, 2) и линейный спектр поглощения P (1 ', 2 ') s-поляризованной волны. Кривые 1, 1 ' – d_x = d_y = 30 мкм, w × l = 7 × 20 мкм², d₁ = d₂ = 17 мкм, d₃ = 8 мкм; кривые 2, 2 ' – d_x = d_y = = 20 мкм, w × l = 4 × 14 мкм², d₁= d₂ = 15 мкм, d₃ = = 8 мкм.

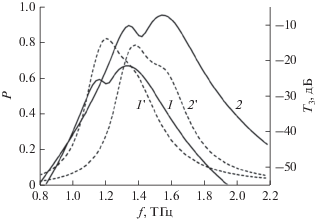
При увеличении ширины графеновых микролент резонансная частота увеличивается в сторону более высоких ТГц-частот (рис. 6). У металлических вибраторов микрополосковых резонаторов, решеток из металлических лент зависимость от ширины противоположная – чем шире, тем больше укорачивающая емкость, тем больше эффективная длина, тем меньше частота. У графеновых решеток появляется дополнительный фактор – в диапазоне частот 0.1…15 ТГц очень сильная дисперсия проводимости графена. При уменьшении резонансной частоты увеличивается нелинейная часть проводимости. При уменьшении периодичности решетки для решеток с высокой плотностью упаковки резонансные частоты перемещаются в сторону более высоких ТГц-частот, и максимумы интенсивности третьей гармоники, излучаемой в прямом направлении (прохождение Т₃), увеличиваются.

Рис. 6.

Резонансные частоты и эффективность генерации третьей гармоники решеткой графеновых микролент (параметры те же, что на рис. 2) при различных значениях ширины графеновых микролент: w = 4 (1), 7 (2) и 10 мкм (3); a – линейный спектр поглощения P, б – спектр нелинейного прохождения T₃s-поляризованной волны.

Таким образом, увеличивая число слоев (см. рис. 4) и плотность упаковки решеток графеновых микролент (см. рис. 5), можно контролировать изменение резонансных частот и эффективность нелинейного взаимодействия ТГц-волн с графеновыми ПС.

На рис. 7 приведен спектр нелинейного прохождения (третья гармоника) волны с s-поляризацией через многослойную графеновую ПС при разных значениях химического потенциала. При уменьшении значения химического потенциала μ_с (0.3…0.4 эВ) частота плазмонного резонанса уменьшается, но амплитуда генерируемой третьей гармоники значительно возрастает (рис. 7).

Рис. 7.

Управляемость генерации третьей гармоники в многослойной решетке графеновых микролент (параметры те же, что на рис. 2) при изменении значения химического потенциала: µ_с = 0.3 (1), 0.35 (2) и 0.4 эВ (3).

Таким образом, поверхностная проводимость графена, а следовательно, и эффективность нелинейного взаимодействия (генерации третьей гармоники) ТГц-волн с графеновыми ПС могут управляться либо химическим легированием, либо электростатическим полем затвора. Показана перестройка резонансной частоты таких реконфигурируемых ТГц-умножителей частоты путем изменения химического потенциала графена без изменения их геометрии и размеров.

Использование многослойных подложек (диэлектрических зеркал (ДЗ)) позволяет контролировать характеристики графеновых ПС. Например, квазипериодическая подложка может подавлять волны первой гармоники, не уменьшая излучаемую мощность третьей гармоники в прямом направлении. Чтобы усилить этот эффект, мы оптимизировали толщину d₁, d₂, d₃ диэлектрических слоев.

Еще одна возможность повышения эффективности нелинейного взаимодействия (уровня генерации третьей гармоники) – использовать многослойную подложку (ДЗ), состоящую из трех пар чередующихся слоев диэлектриков с различными показателями преломления (n₁ = 1.45 и n₂ = = 1.77) толщиной h = λ_рез/4n, где λ_рез – длина волны, соответствующая одной из резонансных частот для пиков поглощения s- (пик 1.18 ТГц) и р‑поляризованной волны (выбран пик 2.92 ТГц) (см. рис. 2). При этом уменьшается линейный коэффициент прохождения T, возрастает коэффициент поглощения P (рис. 8) и увеличивается нормированная мощность T_3norm= T₃/T (рис. 9). Параметры ДЗ для обоих рисунков: для s-поляризации d(n₁) = 44 мкм, d(n₂) = 36 мкм; для р-поляризации d(n₁) = 18 мкм, d(n₂) = 15 мкм.

Рис. 8.

Спектры линейного прохождения T (1_s,p, 2_s,p) и поглощения P ($1_{{s,p}}^{'}$, $2_{{s,p}}^{'}$) s- и р-поляризованной волны для многослойных ПС из графеновых микролент: кривые 1_s,p, $1_{{s,p}}^{'}$ – ПС без ДЗ (см. 2 на вставке рис. 4), кривые 2_s,p, $2_{{s,p}}^{'}$ – ПС с ДЗ из трех пар чередующихся слоев диэлектриков (на вставке).

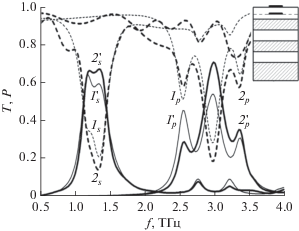
Рис. 9.

Эффективность генерации третьей гармоники ПС из графеновых микролент на ДЗ: спектры нелинейного прохождения T₃ (1_s,p, 2_s,p) и отражения R₃ ($1_{{s,p}}^{'}$, $2_{{s,p}}^{'}$) s- (s-индекс) и р-поляризованной (p-индекс) ТЕМ-волны; кривые 1_s,p, $1_{{s,p}}^{'}$ – ПС без ДЗ (см. 2 на вставке рис. 4), кривые 2_s,p, $2_{{s,p}}^{'}$ – ПС с ДЗ (см. вставку к рис. 8).

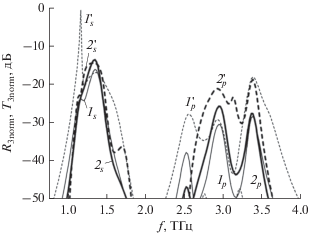
Генерируемая мощность третьей гармоники T_3norm возрастает при увеличении числа слоев ДЗ и мощности падающей волны (рис. 10).

Рис. 10.

Спектры нелинейного прохождения T₃s- (1_s, 2_s) и р-поляризованной (1_p, 2_p) ТЕМ-волны для ПС из графеновых микролент (w × l = 7 × 20 мкм²) на ДЗ разных конфигураций: 1 (1_s, 1_p) и 2 (2_s, 2_p) (сплошные) при двух плотностях мощности падающей волны: 1 (штриховые) и 2 мВт/мм² (сплошные), для s-поляризации d(n₁) = 38 мкм, d(n₂) = 31 мкм; для р-поляризации d(n₁) = 18 мкм, d(n₂) = 15 мкм.

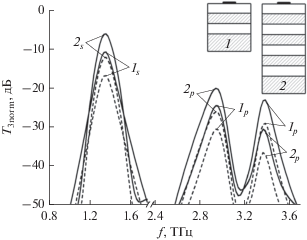
Таким образом, выбор параметров ТГц-умножителей частоты на основе многослойных ПС из микролент графена, в том числе геометрических размеров лент, плотности упаковки решеток, слоистости, толщины диэлектрических слоев и их диэлектрической проницаемости, определяет нелинейный режим работы умножителей.

ЗАКЛЮЧЕНИЕ

С помощью разработанного вычислительного метода проведен анализ эффективности механизма нелинейного взаимодействия, который приводит к увеличению генерации третьей гармоники на порядки в резонансных многослойных графеновых ПС. Показано, что, используя зависимость частоты резонанса локализованных ППП от геометрической конфигурации, можно спроектировать спектральный отклик графеновых ПС. Как результат этот резонансный механизм приводит к увеличению ближнего ТГц-поля и эффективности генерации третьей гармоники. Перестраиваемость графена можно использовать для спектрального сдвига расположения ППП резонансов в большом интервале частот и таким образом значительно упростить проектирование новых конфигураций активных ТГц-устройств на основе нелинейных взаимодействий. Оптимизация взаимодействия ТГц-волн с наноструктурированным графеном путем создания многослойных ПС и метаматериалов, метаповерхностей позволяет дополнительно увеличить нелинейный ТГц-отклик графена, что приводит к еще большей эффективности нелинейного преобразования частоты и, следовательно, к созданию нелинейных устройств на основе графена для сверхбыстрой обработки и манипулирования ТГц-сигналов.

Предложенные многослойные нелинейные графеновые ПС обеспечивают способ реализации эффективных плазмонных умножителей и генераторов ТГц-частоты, устройств четырехволнового смешения для нелинейной ТГц-спектроскопии и неинвазивных ТГц-процессоров. Показано, что управляемая химическим потенциалом (внешним электрическим полем) генерация третьей гармоники может быть достигнута в сверхширокой полосе частот. Это прокладывает путь для реконфигурируемых широкополосных нелинейных ТГц-устройств будущего, таких как перестраиваемые преобразователи частоты, смесители, модуляторы для применений в оптической связи и оптической обработке сигналов.