Радиотехника и электроника, 2021, T. 66, № 6, стр. 602-608

Идентификация геометрической формы локальных отражателей космического аппарата широкополосным поляриметром

В. В. Неёлов^a, *, С. Е. Шалдаев^a, А. А. Самородов^a

^a Военно-космическая академия им. А.Ф. Можайского
197110 Санкт-Петербург, Ждановская ул., 13, Российская Федерация

Поступила в редакцию 14.10.2020
После доработки 12.11.2020
Принята к публикации 05.02.2021

DOI: 10.31857/S003384942106019X

Аннотация

Исследована возможность повышения информативности радиолокационных методов наблюдения космических аппаратов. Предложен способ идентификации геометрической формы локальных отражателей, основанный на совместном применении поляризационных методов и модели рассеяния электромагнитных волн, описываемой геометрической теории дифракции. Рассмотрены основные особенности реализации предложенного способа, а также приведены результаты его апробации в задаче анализа локальных отражателей низкоорбитального космического аппарата. Показано, что предложенный способ позволяет расширить номенклатуру геометрических типов идентифицируемых отражателей и оценить геометрическую форму соответствующих им конструктивных элементов.

ВВЕДЕНИЕ

Вывод космического аппарата (КА) на орбиту и последующий запуск штатного функционирования всех систем является сложной технической задачей, поскольку в ряде случаев возникают отказы в работе оборудования. Анализ информации, посвященной техническим неисправностям КА, выведенных на орбиту, показывает, что в большинстве случаев они обусловлены механическими неполадками [1], такими как отказ приводов солнечных батарей или гравитационной штанги, при этом оперативное получение телеметрических данных от штатных средств самодиагностики не всегда возможно. В связи с этим актуальной является задача удаленного мониторинга конструктивного состояния КА, выведенных на орбиту. Одним из возможных технических решений такой диагностики является восстановление геометрической формы КА по результатам радиолокационного зондирования, что позволяет установить факт наличия элементов конструкции на штатных местах функционирования, определить их положение и ориентацию. Современные широкополосные радиолокационные станции, функционирующие в режиме инверсного синтеза апертуры, обеспечивают высокодетальное наблюдение облика космических аппаратов (КА) в виде совокупности распределённых по координатам продольной и поперечной дальности локальных отражателей (ЛО), соответствующих проявлению различных механизмов рассеяния радиоволн. Пространственная локализация указанных отражателей позволяет оценивать их основные параметры – эффективную площадь рассеяния (ЭПР) и относительное пространственное положение, а также геометрическую форму связанных с ними элементов конструкции.

Анализ тематических источников показывает, что для идентификации геометрической формы радиолокационной цели и ее ЛО в настоящее время используются подходы, основанные на анализе частотных [2–10] или поляризационных [11–20] зависимостей элементов поляризационной матрицы (ПМ) цели. Данные подходы имеют различную методическую базу, описывающую явление рассеяния электромагнитных волн, и являются независимыми. В связи с этим типы идентифицируемых ими геометрических примитивов, а также перечни используемых параметров различны. В табл. 1 приведены геометрические примитивы, идентификация которых возможна с использованием указанных подходов.

Таблица 1.

Состав алфавитов при идентификации геометрической формы ЛО при раздельном использовании ГТД и поляризационных методов

Модель ГТД	Геометрические примитивы	Поляризационные методы
условный идентификатор	Геометрические примитивы	условный идентификатор
A1	Поверхность двойной кривизны (например, зеркальная антенна)	A2
A1	Передняя прямолинейная кромка (например, ребро солнечной батареи)	C2
A1	Длинный тонкий цилиндр (например, телескопическая штанга)	C2
B1	Пластина	A2
B1	Трехгранный уголковый отражатель	A2
B1	Двухгранный уголковый отражатель	B2
С1	Образующая цилиндра	–
D1	Задняя кромка	C2

Поляризационный подход, основанный на декомпозиции матрицы рассеяния Хьюнена, наиболее полно описывает номенклатуру типовых элементов КА и позволяет оценить ориентацию элемента конструкции относительно направления локации. Анализ табл. 1 показывает, что каждый из подходов обладает неоднозначностью относительно оценки геометрической формы ЛО. Так, например, при использовании модели, основанной на геометрической теории дифракции (ГТД) для идентификации геометрической формы элементов конструкции КА, зеркальная антенна и ребро солнечной батареи будут отнесены к одному типу – A1. При использовании поляризационного подхода за зеркальную антенну могут быть приняты элементы конструкции, образующие трехгранный уголковый отражатель. Данная неоднозначность ограничивает практическое применение приведенных методов для решения задачи удаленного мониторинга конструктивного состояния КА.

Следует отметить, что в [10] рассмотрена возможность идентификации геометрической формы ЛО с применением модели ГТД и параметров Хьюнена, однако не в составе единого методологического подхода, а раздельно и без уточнения геометрической формы ЛО. Очевидно, что при разработке и внедрении перспективных широкополосных поляризационных радиолокационных станций в целях повышения качества идентификации ЛО в составе КА рационально объединение обоих указанных подходов.

Цель данного исследования – повысить однозначность идентификации геометрической формы ЛО по результатам измерений частотно-ракурсной характеристики объекта локации широкополосным поляриметром. В качестве показателя достижения цели исследования использован размер алфавита идентифицируемых геометрических примитивов. Для достижения поставленной цели необходимо решить задачу объединения двух различных методических подходов: модели ГТД и феноменологической теории Хьюнена.

1. ИДЕНТИФИКАЦИЯ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ ЛО РАДИОЛОКАЦИОННОЙ ЦЕЛИ ШИРОКОПОЛОСНЫМ ПОЛЯРИМЕТРОМ

Широкополосный поляриметр позволяет оценить зависимость поляризационной матрицы (ПМ) цели от частоты зондирующего сигнала f и ракурса локации $\theta $:

(1)

${\mathbf{\dot {S}}}\left( {f,\theta } \right) = \left[ {\begin{array}{*{20}{c}} {{{{\dot {S}}}^{{{\text{вв}}}}}\left( {f,\theta } \right)}&{{{{\dot {S}}}^{{{\text{вг}}}}}\left( {f,\theta } \right)} \\ {{{{\dot {S}}}^{{{\text{гв}}}}}\left( {f,\theta } \right)}&{{{{\dot {S}}}^{{{\text{гг}}}}}\left( {f,\theta } \right)} \end{array}} \right],$

где $f$ – частота зондирующего сигнала, ${{\dot {S}}_{m}}$ – частотная характеристика m-го локального отражателя, вв, гв, вг, гг – обозначение поляризационных каналов.

Каждый элемент матрицы (1) описывается моделью ГТД [2–9], в соответствии с которой он может быть представлен выражением

(2)

$\begin{gathered} {{{\dot {S}}}^{{pq}}}\left( {f,\theta } \right) = \mathop \sum \limits_{m = 1}^M \dot {S}_{m}^{{pq}}\left( {f,\theta } \right) = \mathop \sum \limits_{m = 1}^M A_{m}^{{pq}}{{\left( {j\frac{f}{{{{f}_{{\text{s}}}}}}} \right)}^{{{{\alpha }_{m}}}}} \times \\ \times \,\,{\text{exp}}\left( {\frac{{ - j4\pi f}}{c}\left( {{{x}_{m}}{\text{cos}}\theta + {{y}_{m}}{\text{sin}}\theta } \right)} \right) + \dot {u}\left( {f,\theta } \right), \\ \end{gathered} $

где $pq = \left\{ {{\text{вв,гв,\;вг,гг}}} \right\}$ – обозначение поляризационного канала, ${{f}_{s}}$ – нижняя частота зондирующего сигнала, $c$ – скорость света, $\dot {S}_{m}^{{pq}}\left( f \right)$ – МР m‑го ЛО, $A_{m}^{{pq}}$ – эффективная длина рассеяния (ЭДР) m-го ЛО, ${{x}_{{m,~}}}~{{y}_{m}}$ – координаты m-го ЛО, ${{\alpha }_{m}}$ – дискретный параметр m-го ЛО, характеризующий закон изменения его ЭДР в зависимости от частоты зондирующего сигнала, $\dot {u}\left( {f,\theta } \right)$ – белый шум.

В модели (2) для идентификации геометрической формы ЛО использована оценка параметра ${{\alpha }_{m}}$, возможные значения которого и соответствующие им геометрические примитивы приведены в табл. 2.

Таблица 2.

Значения параметров идентификации геометрической формы ЛО, соответствующих типовым элементам конструкции КА

Параметры Хьюнена для ракурса локации 0°				Модель ГТД	Геометрическая форма ЛО	Условный идентификатор
ψ	τ	ν	γ	$\alpha $	Геометрическая форма ЛО	Условный идентификатор
$\frac{\pi }{4}$	0	0	$\frac{\pi }{4}$	0	Поверхность двойной кривизны	A3
$\frac{\pi }{4}$	0	0	$\frac{\pi }{4}$	1	Пластина/Трехгранный уголковый отражатель	B3
0	$\frac{\pi }{4}$	$\frac{\pi }{4}$	$\frac{\pi }{4}$	1	Двухгранный уголковый отражатель	C3
0	0	0	$\frac{\pi }{5}$	$\frac{1}{2}$	Образующая цилиндра	D3
0	0	$\frac{\pi }{4}$	$\frac{\pi }{5}$	$\frac{1}{2}$	Длинный тонкий цилиндр	E3
0	0	0	0	$ - \frac{1}{2}$	Задняя кромка	F3
0	0	0	0	0	Передняя прямолинейная кромка	G3

Для оценивания характеристик ЛО в выражении (2) используется модель затухающих экспонент [3]:

(3)

$\dot {S}_{y}^{{pq}}\left( n \right) = {\text{\;}}\mathop \sum \limits_{m = 1}^M \dot {D}_{m}^{{pq}}\dot {p}_{m}^{n},\,\,\,\,\dot {S}_{x}^{{pq}}\left( k \right) = {\text{\;}}\mathop \sum \limits_{m = 1}^M \dot {D}_{m}^{{pq}}\dot {p}_{m}^{k},$

где x и $y$ – обозначение строк и столбцов частотной характеристики, n – номер отсчета частоты зондирующего сигнала, k – номер ракурса локации.

Оценивание числа ЛО может быть произведено методом минимальной длины описания [2–8]. Количественное оценивание полюсов ${{\dot {p}}_{m}}$ производится с использованием алгоритма Root-MUSIC [3], параметра $\dot {D}_{m}^{{pq}}$ – методом наименьших квадратов [4].

Полюсы ${{\dot {p}}_{{m~}}}$ модели (3) содержат информацию об относительной дальности и зависимости частотной характеристики ЛО. Оценки параметров ${{\hat {x}}_{m}},~{{\hat {y}}_{m}}$, ${{\hat {\alpha }}_{m}}$ и $\hat {A}_{m}^{{pq}}$ имеют вид

(4)

${{\hat {x}}_{m}} = c\frac{{{\text{arg}}\left( {{{{\dot {p}}}_{m}}} \right)}}{{ - 4\pi {{f}_{0}}{{\Delta }}\theta }},~\,\,\,\,{{\hat {y}}_{m}} = c\frac{{{\text{arg}}\left( {{{{\dot {p}}}_{m}}} \right)}}{{ - 4\pi {{\Delta }}f}},~\,\,\,\,{{\hat {\alpha }}_{m}} = \frac{{\left( {N - 1} \right){\text{ln}}\left( {\left| {{{{\dot {p}}}_{m}}} \right|} \right)}}{{{\text{ln}}\left( {1 + \left( {N - 1} \right){{{{\Delta }}f} \mathord{\left/ {\vphantom {{{{\Delta }}f} {{{f}_{s}}}}} \right. \kern-0em} {{{f}_{s}}}}} \right)}},$

(5)

$\hat {A}_{m}^{{pq}} = \frac{{\left| {\hat {D}_{m}^{{pq}}} \right|}}{{\left| {{{{\left( {\frac{j}{{{{f}_{s}}}}} \right)}}^{{{{{\hat {\alpha }}}_{m}}}}}} \right|{\text{exp}}\left( {{{{\hat {\alpha }}}_{m}}{\text{ln}}\left( {{{f}_{s}}} \right)} \right){\text{exp}}\left( {\frac{{ - j4\pi {{f}_{s}}\left( {{{x}_{m}}{\text{cos}}\theta + {{y}_{m}}{\text{sin}}\theta } \right)}}{c}} \right)}},$

где N – количество отсчетов частоты зондирующего сигнала, ${{f}_{0}}$ – средняя частота зондирующего сигнала, ${{\Delta }}\theta $ – шаг изменения ракурса локации.

Оценки параметров (4), (5) во всех поляризационных каналах формируют оценку широкополосной ПМ m-го локального отражателя:

(6)

$\begin{gathered} {{{{\mathbf{\hat {S}}}}}_{m}}\left( {f,\theta } \right) = \\ = \left[ {\begin{array}{*{20}{c}} {\hat {A}_{m}^{{{\text{вв}}}}{{{\left( {j\frac{f}{{{{f}_{{\text{s}}}}}}} \right)}}^{{{{{\hat {\alpha }}}_{m}}}}}{\text{exp}}\left( \varepsilon \right)}&{\hat {A}_{m}^{{{\text{вг}}}}{{{\left( {j\frac{f}{{{{f}_{{\text{s}}}}}}} \right)}}^{{{{{\hat {\alpha }}}_{m}}}}}{\text{exp}}\left( \varepsilon \right)} \\ {\hat {A}_{m}^{{{\text{гв}}}}{{{\left( {j\frac{f}{{{{f}_{{\text{s}}}}}}} \right)}}^{{{{{\hat {\alpha }}}_{m}}}}}{\text{exp}}\left( \varepsilon \right)}&{\hat {A}_{m}^{{{\text{гг}}}}{{{\left( {j\frac{f}{{{{f}_{{\text{s}}}}}}} \right)}}^{{{{{\hat {\alpha }}}_{m}}}}}{\text{exp}}\left( \varepsilon \right)} \end{array}} \right], \\ \varepsilon = \frac{{ - j4\pi f}}{c}\left( {{{{\hat {x}}}_{m}}{\text{cos}}\theta + {{{\hat {y}}}_{m}}{\text{sin}}\theta } \right) \\ \end{gathered} $

позволяющую перейти к идентификации его геометрической формы на основе анализа поляризационной информации. В соответствии с феноменологической теорией Хьюнена, ПМ ЛО характеризуется пятью параметрами: эффективной площадью рассеяния A (характеризует волновые размеры ЛО), углом ориентации ЛО ψ (характеризует ориентацию ЛО относительно ортогонального поляризационного базиса), углом эллиптичности τ (является мерой симметрии ЛО относительно ортогонального поляризационного базиса), углом скольжения ν (характеризует множественность переотражений электромагнитной волны от ЛО), углом поляризации объекта γ (характеризует способность ЛО поляризовать падающую на него электромагнитную волну).

Количественные значения параметров Хьюнена для типовых геометрических примитивов приведены в табл. 2. Анализ данных таблицы показывает, что для идентификации геометрической формы ЛО необходима количественная оценка всех четырех углов – ψ, τ, ν, γ.

Для оценки параметров Хьюнена требуется ПМ, приведенная к диагональному виду. Учитывая физическую сущность описываемых процессов, а именно обратное рассеяние электромагнитных волн, обычное разложение на собственные числа для диагонализации ПМ неприменимо, поэтому используется разложение на псевдособственные числа [11–13] в соответствии с выражением:

(7)

${{{\mathbf{\hat {S}}}}_{m}} = {\mathbf{U}}{\text{*}}{\mathbf{\Sigma }}{{{\mathbf{U}}}^{H}}~ \Leftrightarrow ~{\mathbf{\Sigma }} = {{{\mathbf{U}}}^{T}}{{{\mathbf{\hat {S}}}}_{m}}{\mathbf{U}},$

где ${\mathbf{\Sigma }}$ – ПМ m-го ЛО, приведенная к диагональному виду, ${\mathbf{U}}$ – унитарная матрица псевдособственных векторов, * – комплексное сопряжение, $H$ – эрмитово сопряжение. Зависимость ПМ ${{{\mathbf{\hat {S}}}}_{m}}$ и ${\mathbf{\Sigma }}$ от частоты зондирующего сигнала $f$ и ракурса визирования $\theta $ подразумевается здесь и далее, но не приводится.

Тогда применительно к оценке параметров Хьюнена выражение (7) можно переписать в виде

(8)

${\mathbf{\Sigma }}\left( {A,\gamma } \right) = {{{\mathbf{U}}}^{T}}{{{\mathbf{\hat {S}}}}_{m}}{\mathbf{U}} = {\mathbf{U}}_{\nu }^{T}{\mathbf{U}}_{\tau }^{T}{\mathbf{U}}_{\psi }^{T}{{{\mathbf{\hat {S}}}}_{m}}{{{\mathbf{U}}}_{\nu }}{{{\mathbf{U}}}_{\tau }}{{{\mathbf{U}}}_{\psi }},$

где ${{{\mathbf{U}}}_{\nu }},~{{{\mathbf{U}}}_{\tau }}~\,\,{\text{и}}\,\,~{{{\mathbf{U}}}_{\psi }}$ – унитарные матрицы специальной унитарной группы SU(2), зависящие от углов ν, τ, и ψ.

Поляризационная матрица, приведенная к диагональному виду, в соответствии с [11–14] имеет структуру (ξ – фазовая компонента ПМ):

(9)

${\mathbf{\Sigma }} = A\exp \left( {i\xi } \right)\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&{{\text{t}}{{{\text{g}}}^{2}}\gamma } \end{array}} \right].$

Для диагонализации ПМ ${{{\mathbf{\hat {S}}}}_{m}}$ и вычисления матрицы ${\mathbf{\Sigma }}$ использована методика, приведенная в [11]. В соответствии с указанной методикой необходимо трансформировать ПМ ${{{\mathbf{\hat {S}}}}_{m}}$ в матрицу Кеннаха K:

(10)

${\mathbf{K}} = {\mathbf{A}}{\text{*}}\left( {{{{{\mathbf{\hat {S}}}}}_{m}} \otimes {\mathbf{\hat {S}}}_{m}^{{\text{*}}}} \right){{{\mathbf{A}}}^{{ - 1}}},$

где $ \otimes $ – кронекерово умножение, и матрица А имеет следующую структуру:

(11)

${\mathbf{A}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1 \\ 1 \\ {\begin{array}{*{20}{c}} 0 \\ 0 \end{array}} \end{array}}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0 \\ 0 \\ {\begin{array}{*{20}{c}} 1 \\ j \end{array}} \end{array}}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0 \\ 0 \\ {\begin{array}{*{20}{c}} 1 \\ { - j} \end{array}} \end{array}}&{\begin{array}{*{20}{c}} 1 \\ { - 1} \\ {\begin{array}{*{20}{c}} 0 \\ 0 \end{array}} \end{array}} \end{array}} \end{array}} \end{array}} \right].$

После приведения к нулевой собственной поляризации по аналогии с (9), матрица Кеннаха K имеет структуру

(12)

${\mathbf{K}}\left( {A,\gamma } \right) = \frac{{{{A}^{2}}}}{2}\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {1 + {\text{t}}{{{\text{g}}}^{4}}\gamma } \\ {1 - {\text{t}}{{{\text{g}}}^{4}}\gamma } \\ {\begin{array}{*{20}{c}} 0 \\ 0 \end{array}} \end{array}}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {1 - {\text{t}}{{{\text{g}}}^{4}}\gamma } \\ {1 + {\text{t}}{{{\text{g}}}^{4}}\gamma } \\ {\begin{array}{*{20}{c}} 0 \\ 0 \end{array}} \end{array}}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0 \\ 0 \\ {\begin{array}{*{20}{c}} {2{\text{t}}{{{\text{g}}}^{2}}\gamma } \\ 0 \end{array}} \end{array}}&{\begin{array}{*{20}{c}} 0 \\ 0 \\ {\begin{array}{*{20}{c}} 0 \\ { - 2{\text{t}}{{{\text{g}}}^{2}}\gamma } \end{array}} \end{array}} \end{array}} \end{array}} \end{array}} \right].$

Так как матрица (12) не является диагональной, для дальнейших вычислений используется матрица K₃, полученная удалением первой строки и первого столбца матрицы ${\mathbf{K}}$ [11]:

(13)

${{{\mathbf{K}}}_{3}}\left( {A,\gamma } \right) = {\mathbf{\Lambda }}\left( {A,\gamma } \right) = \frac{{{{A}^{2}}}}{2}\left[ {\begin{array}{*{20}{c}} {1 + {\text{t}}{{{\text{g}}}^{4}}\gamma }&0&0 \\ 0&{2{\text{t}}{{{\text{g}}}^{2}}\gamma }&0 \\ 0&0&{ - 2{\text{t}}{{{\text{g}}}^{2}}\gamma } \end{array}} \right].$

Разложение (7) на псевдособственные числа эквивалентно разложению матрицы ${{{\mathbf{K}}}_{3}}$ на собственные числа:

(14)

$\begin{gathered} {\mathbf{\Lambda }}\left( {A,\gamma } \right) = {{{\mathbf{R}}}^{ \top }}{{{\mathbf{K}}}_{3}}{\mathbf{R}} = \\ = {{{\mathbf{R}}}_{\nu }}{{\left( \nu \right)}^{ \top }}{{{\mathbf{R}}}_{\tau }}{{\left( \tau \right)}^{ \top }}{{{\mathbf{R}}}_{\psi }}{{\left( \psi \right)}^{ \top }}{{{\mathbf{K}}}_{3}}{{{\mathbf{R}}}_{\psi }}\left( \psi \right){{{\mathbf{R}}}_{\tau }}\left( \tau \right)~{{{\mathbf{R}}}_{\nu }}\left( \nu \right), \\ \end{gathered} $

где ${{{\mathbf{R}}}_{\psi }}\left( \psi \right),~{{{\mathbf{R}}}_{\tau }}\left( \tau \right)~\,\,{\text{и}}\,\,~{{{\mathbf{R}}}_{\nu }}\left( \nu \right)$ – матрицы вращения специальной ортогональной группы SO(3), зависящие от углов${\text{\;}}\psi $, $\tau $, $\nu $.

Обозначим собственные числа как ${{\lambda }_{k}}$, $k \in \left\{ {1,2,3} \right\}$ и собственные векторы как ${{r}_{k}}$, $k \in \left\{ {1,2,3} \right\}$ матрицы ${{{\mathbf{K}}}_{3}}$:

(15)

${{\lambda }_{1}} = \frac{{{{A}^{2}}}}{2}\left( {1 + {\text{t}}{{{\text{g}}}^{4}}\gamma } \right),~~{{\lambda }_{2}} = {{A}^{2}}{\text{t}}{{{\text{g}}}^{2}}\gamma ,~{{\lambda }_{3}} = - {{A}^{2}}{\text{t}}{{{\text{g}}}^{2}}\gamma ,$

(16)

${\mathbf{R}} = \left[ {{{{\mathbf{r}}}_{1}}~{{{\mathbf{r}}}_{2}}~{{{\mathbf{r}}}_{3}}} \right].$

Из выражения (15) следует, что ${{\lambda }_{2}} = {{\lambda }_{3}}$ при $\gamma = 0$ и ${{\lambda }_{1}} = {{\lambda }_{2}}$ при $\gamma = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$. С учетом принадлежности ${\mathbf{R}}$ специальной ортогональной группе SO(3) можно выделить два особых случая:

(17)

${{{\mathbf{r}}}_{3}} = {{{\mathbf{r}}}_{1}} \times {{{\mathbf{r}}}_{2}}~\,\,\,\,{\text{при}}\,\,\,\,\gamma = 0,$

(18)

${{{\mathbf{r}}}_{1}} = {{{\mathbf{r}}}_{2}} \times {{{\mathbf{r}}}_{3}}~\,\,\,\,{\text{при}}\,\,\,\,\gamma = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}.$

На основе выражения (15) можно определить

(19)

$A = \sqrt {{{\lambda }_{1}} + \sqrt {\lambda _{1}^{2} - \lambda _{2}^{2}} } ,$

(20)

${{\hat {\gamma }}_{m}} = {\text{arctg}}\left( {\frac{{\sqrt {{{\lambda }_{2}}} }}{A}} \right).$

Для оценки параметров $\psi $, $\tau $ и $\nu $ необходимо декомпозировать матрицу ${\mathbf{R}}$. Вектор-столбцы матрицы ${\mathbf{R}}$ имеют вид

(21)

${{{\mathbf{r}}}_{1}} = \left[ {\begin{array}{*{20}{c}} {{\text{cos}}\left( {2\psi } \right){\text{cos}}\left( {2\tau } \right)} \\ {{\text{sin}}\left( {2\psi } \right){\text{cos}}\left( {2\tau } \right)} \\ {{\text{sin}}\left( {2\tau } \right)} \end{array}} \right],$

(22)

$\begin{gathered} {{{\mathbf{r}}}_{2}} = \\ = \left[ {\begin{array}{*{20}{c}} {\cos \left( {2\psi } \right){\text{sin}}\left( {2\tau } \right){\text{sin}}\left( {2\nu } \right) - {\text{sin}}\left( {2\psi } \right){\text{cos}}\left( {2\nu } \right)} \\ {\sin \left( {2\psi } \right){\text{sin}}\left( {2\tau } \right){\text{sin}}\left( {2\nu } \right) + {\text{cos}}\left( {2\psi } \right){\text{cos}}\left( {2\nu } \right)} \\ { - {\text{cos}}\left( {2\tau } \right){\text{cos}}\left( {2\nu } \right)} \end{array}} \right], \\ \end{gathered} $

(23)

$\begin{gathered} {{{\mathbf{r}}}_{3}} = \\ = \left[ {\begin{array}{*{20}{c}} { - \cos \left( {2\psi } \right){\text{sin}}\left( {2\tau } \right){\text{cos}}\left( {2\nu } \right) - {\text{sin}}\left( {2\psi } \right){\text{cos}}\left( {2\nu } \right)} \\ { - \sin \left( {2\psi } \right){\text{sin}}\left( {2\tau } \right){\text{cos}}\left( {2\nu } \right) + {\text{cos}}\left( {2\psi } \right){\text{sin}}\left( {2\nu } \right)} \\ {{\text{cos}}\left( {2\tau } \right){\text{cos}}\left( {2\nu } \right)} \end{array}} \right]. \\ \end{gathered} $

Углы $\psi $, $\tau $, $\nu $ вычисляются с использованием выражений:

(24)

$\begin{gathered} \psi = \frac{1}{2}\operatorname{arc} {\kern 1pt} {\text{tg}}\left( {\frac{{{{r}_{{21}}}}}{{{{r}_{{11}}}}}} \right),~\,\,\,\,\tau = \frac{1}{2}\operatorname{arc} {\kern 1pt} {\text{tg}}\left( {\frac{{{{r}_{{31}}}}}{{\sqrt {r_{{11}}^{2} + r_{{21}}^{2}} }}} \right),~ \\ \nu = - \frac{1}{2}\operatorname{arc} {\kern 1pt} {\text{tg}}\left( {\frac{{{{r}_{{32}}}}}{{{{r}_{{33}}}}}} \right), \\ \end{gathered} $

где ${{r}_{{mn}}},~m,n \in \left\{ {1,2,3} \right\}$ – элементы матрицы ${\mathbf{R}}$. При $\tau = {{ \pm \pi } \mathord{\left/ {\vphantom {{ \pm \pi } 4}} \right. \kern-0em} 4}$ параметры $\psi $ и $\nu $ не определяются, поэтому необходимо выделить два особых случая:

(25)

$\psi = 0\,\,\,\,{\text{и}}\,\,\,\,\nu = \pm \frac{1}{2}{\text{arctg}}\left( {\frac{{{{r}_{{12}}}}}{{{{r}_{{22}}}}}} \right)\,\,\,{\text{при}}\,\,\,\tau = {{ \pm \pi } \mathord{\left/ {\vphantom {{ \pm \pi } 4}} \right. \kern-0em} 4}.$

Важно отметить, что в результате разложения на собственные числа матрицы ${{{\mathbf{K}}}_{3}}$ в (14) собственные векторы могут быть не идентичны векторам (21)–(23) по причине того, что разложение на собственные числа инвариантно к изменению знака собственных векторов:

(26)

${{{\mathbf{K}}}_{3}}\left( { \pm {{r}_{k}}} \right) = {{\lambda }_{k}}\left( { \pm {{r}_{k}}} \right),~\,\,\,\,k \in \left\{ {1,2,3} \right\}.$

Следовательно, матрицу собственных векторов, полученную в результате разложения (14), можно записать в виде

(27)

${\mathbf{\hat {R}}} = \left[ {{{{{\mathbf{\hat {r}}}}}_{1}}~{{{{\mathbf{\hat {r}}}}}_{2}}~{{{{\mathbf{\hat {r}}}}}_{3}}} \right] = \left[ {{{\delta }_{1}}{{{\mathbf{r}}}_{1}}~{{\delta }_{2}}{{{\mathbf{r}}}_{2}}~{{\delta }_{3}}{{{\mathbf{r}}}_{3}}} \right],$

где ${{\delta }_{k}} \in \left\{ { - 1,1} \right\}$, $k \in \left\{ {1,2,3} \right\}$ – произвольный знак собственного вектора. Тогда выражения для вычисления углов $\psi $, $\tau $, $\nu $ будут иметь вид

(28)

$\begin{gathered} {{{\hat {\psi }}}_{m}} = \frac{1}{2}\operatorname{arc} {\kern 1pt} {\text{tg}}\left( {\frac{{{{{\hat {r}}}_{{21}}}}}{{{{{\hat {r}}}_{{11}}}}}} \right),~\,\,\,\,\tau = \frac{{{{\delta }_{1}}}}{2}\operatorname{arc} {\kern 1pt} {\text{tg}}\left( {\frac{{{{{\hat {r}}}_{{31}}}}}{{\sqrt {\hat {r}_{{11}}^{2} + \hat {r}_{{21}}^{2}} }}} \right),~ \\ \nu = - \frac{{{{\delta }_{2}}{{\delta }_{3}}}}{2}\operatorname{arc} {\kern 1pt} {\text{tg}}\left( {\frac{{{{{\hat {r}}}_{{32}}}}}{{{{{\hat {r}}}_{{33}}}}}} \right)~, \\ \end{gathered} $

(29)

${{\hat {\psi }}_{m}} = 0\,\,\,\,{\text{и}}\,\,\,\,\nu = \pm \frac{1}{2}\operatorname{arc} {\kern 1pt} {\text{tg}}\left( {\frac{{{{{\hat {r}}}_{{12}}}}}{{{{{\hat {r}}}_{{22}}}}}} \right)\,\,\,\,{\text{при}}\,\,\,\tau = {{ \pm \pi } \mathord{\left/ {\vphantom {{ \pm \pi } 4}} \right. \kern-0em} 4}.$

Таким образом, угол $\psi $ и два особых случая при $\tau = {{ \pm \pi } \mathord{\left/ {\vphantom {{ \pm \pi } 4}} \right. \kern-0em} 4}$ могут быть определены непосредственно из разложения (14), но углы $~\tau $ и $\nu $ дополнительно зависят от знаков ${{\delta }_{1}}$ и ${{\delta }_{2}}$.

Исходя из того, что $\tau \in \left[ {{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 4}} \right. \kern-0em} 4},~{\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}} \right]$ и $\nu \in \left[ {{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 4}} \right. \kern-0em} 4},~{\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}} \right],$ получаем

(30)

${\text{sign}}{{\hat {r}}_{{11}}} = {{\delta }_{1}}\cos \left( {2\psi } \right)\cos \left( {2\tau } \right) = {{\delta }_{1}},$

(31)

${\text{det}}~{\mathbf{\hat {R}}} = \det {\mathbf{R\Delta }} = \det {\mathbf{R}}\det {\mathbf{\Delta }} = \det {\mathbf{\Delta }} = {{\delta }_{1}}{{\delta }_{2}}{{\delta }_{3}},$

где ${\mathbf{\Delta }}$ – диагональная матрица с ${{\delta }_{k}}$, $k \in \left\{ {1,2,3} \right\}$ в главной диагонали. Выражение (28) позволяют определить $\tau $ и $\nu $ как:

(32)

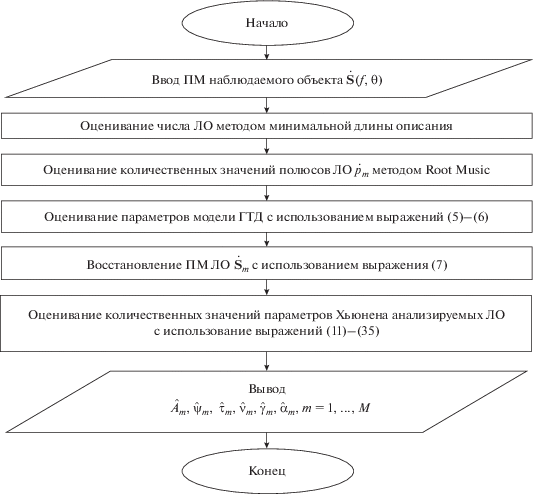
$\begin{gathered} {{{\hat {\tau }}}_{m}} = {\text{sign}}{{{\hat {r}}}_{{11}}}\frac{1}{2}{\text{arctg}}\left( {\frac{{{{{\hat {r}}}_{{31}}}}}{{\sqrt {\hat {r}_{{11}}^{2} + \hat {r}_{{21}}^{2}} }}} \right), \\ {{{\hat {\nu }}}_{m}} = - {\text{det}}~{\mathbf{\hat {R}}}{\text{\;sign}}{{{\hat {r}}}_{{11}}}\frac{1}{2}{\text{arctg}}\left( {\frac{{{{{\hat {r}}}_{{32}}}}}{{{{{\hat {r}}}_{{33}}}}}} \right). \\ \end{gathered} $

Описанный подход к оценке параметров геометрической формы ЛО, основанный на совместном использовании модели ГТД и параметров Хьюнена, реализован при помощи алгоритма, упрощенная блок-схема которого приведена на рис. 1.

Рис. 1.

Блок-схема алгоритма оценивания параметров идентификации геометрической формы ЛО.

Алгоритм состоит из ряда последовательно выполняемых расчетных процедур и позволяет оценивать количественные значения параметров идентификации геометрической формы ЛО по данным измерений частотно-ракурсной характеристики объекта широкополосным поляриметром.

По результатам работы алгоритма формируется вектор параметров ЛО, на основе которого производится идентификация их геометрической формы с использованием опорных данных, приведенных в табл. 2 (представлены количественные значения параметров при ракурсе локации 0°).

При сравнении табл. 1 и 2 видно, что предложенный способ позволил расширить размер алфавита до семи типов идентифицируемых геометрических примитивов.

2. РЕЗУЛЬТАТЫ ИДЕНТИФИКАЦИИ ФОРМЫ ЛОКАЛЬНЫХ ОТРАЖАТЕЛЕЙ В СОСТАВЕ РАДИОЛОКАЦИОННОГО ОБЛИКА МОДЕЛИ КА

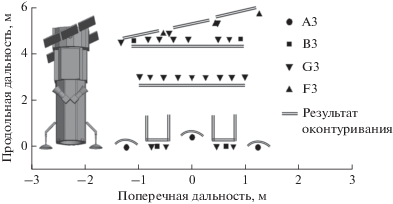
В качестве объекта анализа был выбран КА обзора земной поверхности WorldView-2. Компоновочная схема аппарата включает в свой состав три базовых модуля, а также ряд навесных элементов – антенн, звездных датчиков и панелей солнечных батарей, геометрическое размеры которых существенно превышают длину зондирующего сигнала. Конструктивно модель КА содержит плоские и криволинейные элементы, формирующие ЛО рассмотренных выше типов.

Поле обратного рассеяния КА рассчитано с использованием численных методов электродинамики в полном поляризационном базисе в диапазоне частот 9.5…10.5 ГГц при локации вдоль строительной оси. Внешний вид модели КА и его радиолокационное изображение, полученное методом инверсного синтеза апертуры, представлены на рис. 2.

Рис. 2.

Модель анализируемого космического аппарата и его радиолокационное изображение (поляризация вертикальная согласованная).

Результаты идентификации геометрической формы доминирующих ЛО исследуемого КА приведены на рис. 3. Анализ результатов показывает, что предложенный способ позволяет уверенно идентифицировать в составе радиолокационного облика КА доминирующие ЛО, в частности отражатели двойной кривизны (параболические антенны), пластины (панели солнечных батарей, другие плоские элементы конструкции), кромки (ребра элементов конструкции), что затруднительно при раздельном использовании методов идентификации геометрической формы локальных отражателей.

Рис. 3.

Результаты идентификации геометрической формы доминирующих ЛО в составе РЛ-облика КА.

Дальнейший анализ РЛ-облика КА, связанный с оцениванием геометрических размеров ЛО, может быть выполнен с использованием соотношений, приведенных в [21, 22].

ЗАКЛЮЧЕНИЕ

Предложены способ и алгоритм идентификации геометрической формы ЛО, основанные на совместном использовании параметров Хьюнена и закона изменения ЭДР в зависимости от частоты зондирующего сигнала. Способ ориентирован на обработку полнополяризационных широкополосных данных и позволяет в отличие от известных подходов выполнять идентификацию более широкого перечня ЛО (различные поверхности с кривизной второго порядка, пластина, кромка, двугранный уголковый отражатель), являющихся типовыми элементами конструкций сложных техногенных объектов. Выполненные апробация способа и алгоритма на расчетных данных рассеяния модели КА подтвердила его корректность и информативность.

Способ может быть использован не только для удаленного мониторинга конструктивного состояния КА, но и в ряде других прикладных задач радиолокации, связанных с автоматическим распознаванием целей и идентификацией их состояния. Необходимым условием для применения предложенного способа является квазиоптический характер рассеяния.

Список литературы

Saleh J., Jean-Francois. Spacecraft Reliability and Multi-state Failures: a Statistical Approach. N.-Y.: John Wiley & Sons Limited, 2011.
Zou Y., Gao X., Li X., Liu Y. // Proc. 8th Int. Congress on Image and Signal Processing (CISP). Shenyang, 08–12 Dec. 2015. N.-Y.: IEEE, 2015. P. 1220.
Yan H., Li S., Li H., Yin H. // Proc. IEEE Int. Conf. on Computational Electromagnetics (ICCEM). Chengdu. 26–28 Mar. 2018. N.Y.: IEEE, 2018. P. 12.
Xiao-Yu X., Huo Y., Hong-Cheng C. // Proc. IEEE Int. Conf. on Computational Electromagnetics (ICCEM), Chengdu. 26–28 Mar. 2018. N.Y.: IEEE, 2018. P. 26.
Капылов Е.Л., Неёлов В.В., Самородов А.А. // Вопр. радиоэлектроники. 2019. № 1. С. 13.
Zheng S., Zhang X., Zong B., Li J. // Proc. Photonics & Electromagnetics Research Symp. – Fall (PIERS – Fall). Xiamen. 17–20 Dec. 2019. N.Y.: IEEE, 2019. P. 2282.
Hu P., Xu S., Zou J., Chen Z. // Proc. IEEE SENSORS, Glasgow. 29 Oct.–1 Nov. 2017. N.Y.: IEEE, 2017. P. 18.
Jia S., La D. // Proc. IEEE Advanced Inform. Technol., Electronic and Automation Control Conf. (IAEAC). Chongqing. 18–20 Dec. 2015. N.Y.: IEEE, 2015. P. 636.
Qamar H.H., El-Mashade M.B., Farahat A.E., Hussein K.F. // Proc. 6th Int. Conf. on Advanced Control Circuits and Systems (ACCS) & 5th Intern. Conf. on New Paradigms in Electronics & Inform. Technol. (PEIT). Hurgada, 19–21 Jul. 2019. N.Y.: IEEE, 2019. P. 167.
Jackson J.A., Moses R.L. // Proc. of SPIE. 2006. V. 6237. № 8. P. 205.
Dallmann T., Heberling D. // Electron. Lett. 2009. V. 53. № 13. P. 877.
Li D., Zhang Y. // IEEE Trans. 2016. V. 54. № 2. P. 723.
Li D., Zhang Y. // Proc. IEEE Int. Geoscience and Remote Sensing Symp. (IGARSS). Beijing, 10–15 Jul. 2016. N.Y.: IEEE, 2016. P. 4679.
Li D., Zhang Y. // Proc. 11th European Conf. on Synthetic Aperture Radar. Hamburg, 6–19 Jun. 2016. N.Y.: IEEE, 2016. P. 14.
Liu X., Jiao L., Zhang D., Liu F. // Proc. IEEE Intern. Geoscience and Remote Sensing Symp. Yokohama, 28 Jul.–2 Aug. 2019. N.Y.: IEEE, 2019. P. 3181.
Bi H., Sun J., Xu Z. // Proc. Intern. Workshop on Remote Sensing with Intelligent Proc. (RSIP). Shanghai, 18–21 May. 2017. N.Y.: IEEE, 2017. P. 1.
Zhu F., Zhang Y., Li D. // IET Radar, Sonar & Navigation. 2018. V. 2. № 2. P. 209.
Li D., Zhang Y. // Proc. 10th European Conf. on Synthetic Aperture Radar. Berlin, 6–9 Jun. 2014. N.Y.: IEEE, 2014. P. 68.
Xiang Z., Chen B., Yang M. // IEEE Antennas and Wireless Propagation Lett. 2017. V. 16. № 2. P. 1313.
Xiang Z., Chen B., Yang M. // Proc. Intern. Conf. on Radar. Guangzhou, 10–12 Oct. 2016. N.Y.: IEEE, 2016. P. 126.
Qin X., Hu T., Yu W., Wang P. et al. // Proc. IEEE Intern. Geoscience and Remote Sensing Symp. Valencia, 22–27 Jul. 2018. N.Y.: IEEE, 2018. P. 645.
Knott E., Shaeffer J., Tuley M. Radar Cross Section. 2nd ed. N.Y.: SciTech Publ., 2004.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал