Радиотехника и электроника, 2021, T. 66, № 7, стр. 682-697
Об импедансных условиях в металлических нанопроводах
М. В. Давидович *
Саратовский национальный исследовательский государственный университет им. Н.Г. Чернышевского
410012 Саратов, ул. Астраханская, 83, Российская Федерация
* E-mail: davidovichmv@info.sgu.ru
Поступила в редакцию 11.08.2020
После доработки 22.11.2020
Принята к публикации 29.11.2020
Аннотация
В рамках модели Ландауэра–Датты–Лундстрома получены приближенные формулы для проводимости металлических нанопроволок конечной ширины и толщины, а также пленок конечной толщины, переходящие в известные предельные случаи. Соотношения удобны для определения проводимости наноразмерных структур с учетом обоих поперечных размеров. Для оценки числа мод проводимости квантовых проволок с конечными поперечными размерами предложены приближенные формы распределения потенциала и функционалы для решения соответствующего уравнения Шредингера. Проведена численная оценка числа энергетических уровней. Рассмотрено решение задачи о волне Зоммерфельда–Ценнека в прямоугольном проводе, которая на высоких частотах переходит в поверхностный плазмон. Решение существенно зависит от изменения плазменной частоты, связанной с поперечными размерами.
ВВЕДЕНИЕ
Тонкие металлические, полупроводниковые и другие хорошо проводящие структуры в виде проводов различной формы, включая углеродные нанотрубки (УНТ), ленточные (полосковые) проводники шириной w и толщиной t, широко применяются при создании различных проволочных метаматериалов [1‒12], гиперболических метаматериалов в виде плоскослоистых металлодиэлектрических структур [13‒18], дифракционных решеток, двумерных и трехмерных фотонных кристаллов [9‒12], линий передачи, нанотранзисторов, терагерцевых усилителей [19–21] и т.п. В этих структурах w и t могут иметь размеры от нескольких (или даже одного-двух) нанометров до нескольких десятков или сотен нанометров, а для моделирования необходимо знать их импедансы как функции размеров и частоты. Теория проводимости Друде, которая хорошо работает для вырожденных металлов (${{k}_{{\text{B}}}}T \ll {{E}_{{\text{F}}}}$) и в случае больших по сравнению с длиной свободного пробега (ДСП) размеров проводников становится плохо применимой при уменьшении размеров (включая и длину проводников L) до ДСП ${{\lambda }_{0}}$ и менее [22‒30]. Тем более она не применима к графену, графеновым нанолентам, УНТ, квантовым проволокам и подобным им структурам. Строгий анализ требует решения задач квантовой механики, электродинамики и неравновесной статистической механики, поэтому подобного рода задачи решаются приближенными методами типа формализма Грина–Кубо, модели Ландауэра–Датты–Лундстрома (ЛДЛ) [22‒30], транспортного уравнения Больцмана в приближениях времени релаксации, Бхатнагара–Гросса–Крука [31] и ряда других. В сверхтонких пленках (с толщиной 2…10 нм) существенны поверхностные эффекты, в том числе влияние кластеров обусловленных коагуляцией металла при получении сплошных пленок с металлической проводимостью, отражение носителей заряда от поверхностей. Минимальная достижимая толщина ${{t}_{c}}\sim 1...2$ нм, соответствующая перколяционному барьеру, как раз определяет минимально возможный слой из нескольких атомарных слоев, при котором еще можно говорить о макросвойствах вещества. Влияние поверхностного рассеяния наряду с объемным рассеянием учитывалось в ряде моделей, в частности Фукса–Зондгеймера [32, 33], Майадаса–Шацкеса [34], Телье–Тоссе–Пишара [35], Варкуша [36] и др. Квазибаллистический перенос заряда с размерными эффектами шероховатости количественно описан с помощью соотношений теории Намба [37, 38]. Квантоворазмерные эффекты рассмотрены в ряде работ, в частности [39‒43], а также исследовались и получены экспериментально [44‒51]. В ряде работ получены различные экспериментальные зависимости удельной проводимости металлических пленок $\sigma \left( t \right)$ для толщин от 1 до 100 нм (см. [50, 51]). Обычно проводимость наноструктур определяется на основе числа мод проводимости [25‒30], которое в свою очередь оценивается по числу укладывающихся на структуре волн де-Бройля.
Цель работы – рассмотрение импедансных свойств металлических проволок малых поперечных размеров w, t и тонких металлических пленок в рамках транспортной модели ЛДЛ. При этом акцент сделан на получении простых аналитических соотношений и на точном определении числа мод проводимости.
1. ПОСТАНОВКА ЗАДАЧИ
Удельная проводимость в концепции Друде определяется как $\sigma = qn\bar {\mu } = {{{{q}^{2}}n{{\tau }_{p}}} \mathord{\left/ {\vphantom {{{{q}^{2}}n{{\tau }_{p}}} {{{m}_{e}}}}} \right. \kern-0em} {{{m}_{e}}}}$, где подвижность носителей $\bar {\mu } = {{q{{\tau }_{p}}} \mathord{\left/ {\vphantom {{q{{\tau }_{p}}} {{{m}_{e}}}}} \right. \kern-0em} {{{m}_{e}}}}$, $q$ ‒ заряд, ${{m}_{e}}$ ‒ эффективная масса носителей заряда (например, электронов), ${{\tau }_{p}} = {{{{\lambda }_{0}}} \mathord{\left/ {\vphantom {{{{\lambda }_{0}}} v}} \right. \kern-0em} v}$ ‒ время релаксации импульса, связанное с ДСП ${{\lambda }_{0}}$ в бесконечном образце и со средней скоростью носителей $v$. Дрейфовое в среднем направленное движение, подразумевающее ускорение между двумя наиболее вероятными ближайшими столкновениями, после которых электрон полностью теряет направленный против электрического поля импульс (соответственно, и энергию, передавая ее фононам), для малых длин образцов становится баллистическим. В случае идеальных квантоворазмерных структур имеют место упругие рассеяния носителей относительно границ, что требует, вообще говоря, решения квантовомеханических задач. При $w \ll {{\lambda }_{0}}$ получаем двумерную структуру – двумерный электронный газ (ДЭГ). Для металлов при комнатной температуре соответствующая пленка должна иметь порядок толщин от нескольких нанометров до двух-трех десятков нанометров, поскольку ${{\lambda }_{0}}$ для используемых в наноплазмонике металлов при комнатной температуре имеет порядок от нескольких десятков до сотни нанометров. При снижении температуры ${{\lambda }_{0}}$ растет, поэтому указанные границы сдвигаются в большую сторону. Минимальная толщина обусловлена тем, что в пленке может быть не менее нескольких атомарных слоев. Однако имеются идеальные (атомарно тонкие) структуры ДЭГ типа графена, силицена, борофена.
Получаемые электрофизические параметры следует усреднять по энергиям носителей, используя функцию распределения Ферми–Дирака
где $\mu $ ‒ электрохимический потенциал. Будем также обозначать $f\left( {E,\mu ,T} \right) = f\left( E \right)$. В вырожденном бесконечном проводнике усреднение по энергиям носителей дает формулу Друде [52]. Строгое определение электрофизических параметров требует решения кинетических уравнений при воздействии электромагнитных волн. Имеется ряд приближенных подходов, основанных на методах статистической механики и термодинамики необратимых процессов (транспортном уравнении Больцмана, формализме Кубо, или формулах Грина–Кубо, неравновесных функций Грина–Келдыша). В частности, эти модели позволяют определять проводимости таких структур, как графен [31, 53‒56]. Наиболее простым формализмом является транспортная модель ЛДЛ [23‒30, 57‒60], которой здесь мы и придерживаемся. В ней причиной тока носителей заряда является различие в подготовке равновесных электродов ${{f}_{1}}\left( E \right)$ и ${{f}_{2}}\left( E \right)$, а также наличие в проводящем канале свободных уровней для заполнения носителями с электрода 1 с последующим их переходом на свободные уровни электрода 2. Такой как бы статический подход, тем не менее, позволяет определить проводимость [22‒30], пригодную для достаточно высоких частот, особенно если длина канала мала. Проводники ведут себя по-другому, когда их размеры становятся сравнимы или меньше ДСП ${{\lambda }_{0}}$ в бесконечном материале. Именно, возникает баллистический транспорт, который приводит к тому, что и сама ДСП $\lambda $ изменяется и становится зависимой от размеров. Далее будем рассматривать проводник с размерами w, t, L, считая, что ток течет вдоль длины L. При баллистическом транспорте существенны размерное квантование (размерные квантовые эффекты), т.е. рассмотрение носителей в квантовых ямах (одномерных, двумерных и трехмерных), причем при транспорте носителей имеет значение отражение их от соответствующих стенок. Важно квантово-механическое рассмотрение задачи, определяющее число состояний и число мод проводимости [29, 30], что определяет проводимость структуры. Переход от классического рассмотрения к квантовому изложен в работах [61‒68].
Для численного анализа перечисленных структур желательно иметь выражения в виде простых приближенных формул для проводимости проволоки поперечного размера w, t и длины L, а также погонной проводимости, что и является целью работы. Пусть $d = 1,{\text{ }}2,{\text{ }}3$ означает размерность проводника. Указанные соотношения должны быть, с одной стороны, простыми, а с другой – достаточно точными и переходить в известные формулы в одномерном случае d = 1 (квантовая нить, $w \to 0$, $t \to 0$), двумерном случае d = 2 (квантовая яма $t \to 0$) и трехмерном случае d = 3 неограниченного образца ($w \to \infty $, $t \to \infty $). Случай квантовой точки (искусственного атома) d = 0 для транспорта не интересен, но важен для анализа локализованных плазмонов.
2. АППРОКСИМАЦИИ ДЛЯ ПРОВОДНИКОВ КОНЕЧНЫХ РАЗМЕРОВ
Используя концепцию баллистического сопротивления/проводимости ${{R}_{{\text{B}}}} = {1 \mathord{\left/ {\vphantom {1 {{{G}_{{\text{B}}}}}}} \right. \kern-0em} {{{G}_{{\text{B}}}}}}$, для проводника любой размерности d и длины L можно записать его сопротивление в виде
(1)
$R = {{R}_{{\text{B}}}}{{\left( {L + \lambda } \right)} \mathord{\left/ {\vphantom {{\left( {L + \lambda } \right)} \lambda }} \right. \kern-0em} \lambda } = {{\rho }_{d}}\left( {L + \lambda } \right)\left\{ {1,\frac{1}{w},\frac{1}{{wt}}} \right\}.$Величины в фигурных скобках соответствуют размерностям 1, 2, 3. Это, в частности, означает обычно принятые записи через удельные сопротивления ${{\rho }_{d}}$ и проводимости ${{\sigma }_{d}}$
(2)
${{\rho }_{d}} = \frac{1}{{{{\sigma }_{d}}}} = \frac{1}{{{{G}_{{\text{B}}}}\lambda }}\left\{ {1,w,wt} \right\}.$В (1) и (2) равенства для фигурных скобок определяют соответствующие физические размерности удельных величин для проводников размерностей $d = 1,{\text{ }}2,{\text{ }}3$. При малых размерах соотношения типа (1) нелинейно зависят от размеров (квантуются), однако они весьма удобны для удельных и погонных параметров и поверхностных импедансов при электродинамическом анализе устройств в силу простоты. Естественно размерности ${{\rho }_{d}}$ и ${{\sigma }_{d}}$ в силу (2) разные, при этом обычные удельные величины суть $\rho = {{\sigma }^{{ - 1}}} = {{\rho }_{3}} = \sigma _{3}^{{ - 1}}$. Длина свободного пробега массивного проводника в теории Друде определяется как ${{\lambda }_{0}} = \bar {v}\tau $, где $\bar {v}$ – средняя скорость, $\tau $ ‒ время свободного пробега (релаксации импульса), т.е. ${{\tau }^{{ - 1}}}$ ‒ вероятность рассеяния в единицу времени с полной потерей направления, когда скорость направлена после столкновения случайным образом. Приобретаемая во внешнем поле за время $\tau $ дополнительная энергия полностью релаксирует к равновесному состоянию в точке столкновения, т.е. передается фононам. Очевидно, ДСП зависит от того, как определена средняя скорость. При движении носителей вдоль оси z $\bar {v} = \left\langle {\left| {{{v}_{z}}} \right|} \right\rangle $ при усреднении по энергиям, вводя в рамках теории случайных блужданий коэффициент диффузии $\bar {D} = \left\langle {v_{z}^{2}\tau } \right\rangle $, можно определить проводимость трехмерного проводника как [52]
(3)
$\sigma = {{\sigma }_{3}} = {{q}^{2}}\bar {D}{{d}_{{E{\text{F}}}}} = {{q}^{2}}\bar {D}{{D}_{d}}{{\left( {{{E}_{{\text{F}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{E}_{{\text{F}}}}} \right)} {\left( {Lwt} \right)}}} \right. \kern-0em} {\left( {Lwt} \right)}},$где ${{d}_{{E{\text{F}}}}}$ ‒ плотность состояний на поверхности Ферми, ${{D}_{d}}\left( E \right)dE$ ‒ число энергетических состояний в интервале $dE$ (индекс d означает квантовую размерность (one-dimensional), т.е. 1-d означает структуру, не ограниченную по одной координате). Формула (3) получена усреднением по энергиям в случае вырождения. В общем случае надо усреднять по энергиям с функцией ${{ - \partial {{f}_{0}}} \mathord{\left/ {\vphantom {{ - \partial {{f}_{0}}} {\partial E}}} \right. \kern-0em} {\partial E}}$, где обозначена равновесная функция Ферми–Дирака ${{f}_{0}} = f\left( {E,{{\mu }_{0}},T} \right),$ ${{\mu }_{0}} = {{E}_{{\text{F}}}}$. В случае малой длины L неравновесного проводника, включенного между двумя равновесными проводниками с электрохимическими потенциалами ${{\mu }_{1}}$ и ${{\mu }_{2}}$ следует усреднять с функцией ${{f}_{1}}\left( E \right) - {{f}_{2}}\left( E \right)$. Формула (3) допускает обобщение на любую размерность [30]
(4)
$\begin{gathered} {{\sigma }_{d}} = {{q}^{2}}\bar {D}{{g}_{d}} = \frac{{{{q}^{2}}\bar {D}{{D}_{d}}}}{L}\left\{ {1;\frac{1}{w};\frac{1}{{wt}}} \right\}, \\ {{g}_{d}} = \frac{{{{D}_{d}}}}{L}\left\{ {1;\frac{1}{w};\frac{1}{{wt}}} \right\}. \\ \end{gathered} $Вводя закон дисперсии $E\left( {\vec {p}} \right)$, получаем, вообще говоря, тензорную проводимость. Рассмотрим изотропные зависимости $E\left( p \right)$. Усреднение ${{{v}}_{z}}\left( E \right)$ по углам (направлениям с учетом баллистического движения) дает [29, 30] $\left\langle {\left| {{{v}_{z}}\left( E \right)} \right|} \right\rangle = v\left( E \right)$, $\left\langle {v_{z}^{2}\left( E \right)} \right\rangle = $ $ = {{v}^{2}}\left( E \right)$ для 1-d проводника, $\left\langle {\left| {{{v}_{z}}\left( E \right)} \right|} \right\rangle = {{2v\left( E \right)} \mathord{\left/ {\vphantom {{2v\left( E \right)} \pi }} \right. \kern-0em} \pi }$, $\left\langle {v_{z}^{2}\left( E \right)} \right\rangle = {{{{v}^{2}}\left( E \right)} \mathord{\left/ {\vphantom {{{{v}^{2}}\left( E \right)} 2}} \right. \kern-0em} 2}$ для 2-d проводника, $\left\langle {\left| {{{v}_{z}}\left( E \right)} \right|} \right\rangle = $ $ = {{v\left( E \right)} \mathord{\left/ {\vphantom {{v\left( E \right)} 2}} \right. \kern-0em} 2}$, $\left\langle {v_{z}^{2}\left( E \right)} \right\rangle = {{{{v}^{2}}\left( E \right)} \mathord{\left/ {\vphantom {{{{v}^{2}}\left( E \right)} 3}} \right. \kern-0em} 3}$ для 3-d проводника, что записываем как
(4)
$\left\langle {\left| {{{v}_{z}}} \right|} \right\rangle = \bar {v}\left\{ {1;{{{\text{ }}2} \mathord{\left/ {\vphantom {{{\text{ }}2} \pi }} \right. \kern-0em} \pi };{{{\text{ }}1} \mathord{\left/ {\vphantom {{{\text{ }}1} 2}} \right. \kern-0em} 2}} \right\},$(5)
$\bar {D} = \left\langle {\bar {v}_{z}^{2}\tau } \right\rangle = {{\bar {v}}^{2}}\tau \left\{ {1;{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2};{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right\}.$Используя определение $\lambda = {{2\bar {D}} \mathord{\left/ {\vphantom {{2\bar {D}} {\left\langle {\left| {{{v}_{z}}} \right|} \right\rangle }}} \right. \kern-0em} {\left\langle {\left| {{{v}_{z}}} \right|} \right\rangle }}$, получаем
(6)
$\lambda = \bar {v}\tau \left\{ {2;{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2};{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}} \right\}.$Здесь $\bar {v}$, $\tau $ соответствует бесконечному образцу, а индекс d в (5) и (6) опущен. Обобщим приведенные соотношения на случай проводника прямоугольного сечения так, чтобы имело место совпадение при его вырождении в двумерный и одномерный проводники:
(7)
$\lambda = {{\lambda }_{0}}\left\{ {1 + \frac{1}{2}\left( {\frac{{{{\lambda }_{0}}}}{{{{\lambda }_{0}} + w}} + \frac{{{{\lambda }_{0}}}}{{{{\lambda }_{0}} + t}}} \right)} \right\},$(8)
$\begin{gathered} R = {{R}_{{\text{B}}}}\frac{{L + \lambda }}{\lambda }\left\{ {\frac{1}{2}\left( {\frac{{{{\lambda }_{0}}}}{{{{\lambda }_{0}} + w}} + \frac{{{{\lambda }_{0}}}}{{{{\lambda }_{0}} + t}}} \right)} \right. + \\ \left. {\frac{{}}{{}} + \,\,\left( {2 - \exp \left( { - {w \mathord{\left/ {\vphantom {w {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}} \right) - \exp \left( {{{ - t} \mathord{\left/ {\vphantom {{ - t} {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}} \right)} \right)} \right\}. \\ \end{gathered} $Здесь ${{\lambda }_{0}} = \bar {v}\tau $, ${{R}_{{\text{B}}}} = {{R}_{{{\text{B}}1}}} = {{2L} \mathord{\left/ {\vphantom {{2L} {\left( {{{q}^{2}}D\bar {v}} \right)}}} \right. \kern-0em} {\left( {{{q}^{2}}D\bar {v}} \right)}}$ ‒ баллистическое сопротивление одномерного проводника. Из (7) для ${{\lambda }_{d}}$ следует ${{\lambda }_{1}} = 2{{\lambda }_{0}}$ (если $w = t = 0$), ${{\lambda }_{2}} \approx {{\lambda }_{0}}\left( {1.5 + {{{{\lambda }_{0}}} \mathord{\left/ {\vphantom {{{{\lambda }_{0}}} w}} \right. \kern-0em} w}} \right)$ (если $t = 0$, $w \gg {{\lambda }_{0}}$), что приближенно соответствует ${{\pi {{\lambda }_{0}}} \mathord{\left/ {\vphantom {{\pi {{\lambda }_{0}}} 2}} \right. \kern-0em} 2}$, а также ${{\lambda }_{3}} = {{\lambda }_{0}}$. Соотношение (8) соответствует объемному ограниченному проводнику. Для одномерного проводника получаем $R = {{{{R}_{{\text{B}}}}\left( {L + \lambda } \right)} \mathord{\left/ {\vphantom {{{{R}_{{\text{B}}}}\left( {L + \lambda } \right)} \lambda }} \right. \kern-0em} \lambda }$, для двумерного проводника $R = \left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right){{R}_{{\text{B}}}}{{\left( {L + \lambda } \right)} \mathord{\left/ {\vphantom {{\left( {L + \lambda } \right)} \lambda }} \right. \kern-0em} \lambda }$, для трехмерного $R = 2{{R}_{{\text{B}}}}{{\left( {L + \lambda } \right)} \mathord{\left/ {\vphantom {{\left( {L + \lambda } \right)} \lambda }} \right. \kern-0em} \lambda }$, что хорошо согласуется с определением баллистической проводимости [30]:
(9)
${{G}_{{{\text{B}}d}}} = \frac{{{{q}^{2}}{{D}_{d}}\bar {v}}}{{2L}}\left\{ {1,\frac{2}{\pi },\frac{1}{2}} \right\}.$В случае малых по сравнению с ДСП поперечных размеров для квантовой проволоки имеем
(10)
$\begin{gathered} R = {{R}_{{\text{B}}}}\frac{{L + \lambda }}{\lambda } \times \\ \times \,\left\{ {1 - {{\left( {{w \mathord{\left/ {\vphantom {w {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}} + {t \mathord{\left/ {\vphantom {t {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{w \mathord{\left/ {\vphantom {w {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}} + {t \mathord{\left/ {\vphantom {t {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}} \right)} 2}} \right. \kern-0em} 2} - \left( {{{{\left( {{w \mathord{\left/ {\vphantom {w {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}} \right)}}^{2}} + {{{\left( {{t \mathord{\left/ {\vphantom {t {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}} \right)}}^{2}}} \right)} \right\}. \\ \end{gathered} $Очевидно, при анализе длинных структур из квантовых проволок можно рассматривать их как осевые токи с погонным сопротивлением (импедансом) ${{\rho }_{l}} = {R \mathord{\left/ {\vphantom {R L}} \right. \kern-0em} L} \approx {{R}_{{\text{B}}}}$, при этом формула (10) дает значение погонного сопротивления с учетом конфигурации проволоки. При моделировании структур линейными токами вдоль оси проволоки граничные условия следует накладывать на ее поверхности в виде ${{\vec {J}}_{S}} = {{\sigma }_{S}}{{\vec {E}}_{S}}$, где индексом S обозначена поверхностная плотность тока, поверхностная проводимость и касательное к поверхности электрическое поле. Считая, что ток в баллистической проволоке распределен равномерно (это приближение можно оправдать пропорциональностью числа мод проводимости поперечным размерам и малыми размерами по сравнению с длиной волны), получаем удельное сопротивление $\rho = {{\rho }_{l}}wt$:
(11)
$\begin{gathered} \rho = {{R}_{{\text{B}}}}wt\frac{{L + \lambda }}{{L\lambda }} \times \\ \times \,\,\left\{ {1 - {{\left( {{w \mathord{\left/ {\vphantom {w {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}} + {t \mathord{\left/ {\vphantom {t {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{w \mathord{\left/ {\vphantom {w {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}} + {t \mathord{\left/ {\vphantom {t {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}} \right)} 2}} \right. \kern-0em} 2} - \left( {{{{\left( {{w \mathord{\left/ {\vphantom {w {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}} \right)}}^{2}} + {{{\left( {{t \mathord{\left/ {\vphantom {t {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}} \right)}}^{2}}} \right)} \right\}. \\ \end{gathered} $Определение удельной двумерной (поверхностной) проводимости берется как предел ${{\sigma }_{S}} = {\sigma \mathord{\left/ {\vphantom {\sigma t}} \right. \kern-0em} t}$ при стремлении толщины проводника к нулю. Если ${{\vec {J}}_{S}} = {{\vec {z}}_{0}}{{J}_{S}}$ ‒ поверхностная, а $\vec {J} = {{\vec {z}}_{0}}{{J}_{z}}$ ‒ объемная плотности тока, то осевой ток равен ${{I}_{z}} = 2\left( {w + t} \right){{J}_{S}} = wt{{J}_{z}}$, если считать эти распределения равномерными. Отсюда получаем
(12)
$\begin{gathered} {{\sigma }_{S}} = {{G}_{{\text{B}}}}\frac{\lambda }{{2\left( {1 + {\lambda \mathord{\left/ {\vphantom {\lambda L}} \right. \kern-0em} L}} \right)\left( {w + t} \right)}} \times \\ \times \,\,{{\left\{ {1 - {{\left( {{w \mathord{\left/ {\vphantom {w {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}} + {t \mathord{\left/ {\vphantom {t {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{w \mathord{\left/ {\vphantom {w {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}} + {t \mathord{\left/ {\vphantom {t {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}} \right)} 2}} \right. \kern-0em} 2} - \left( {{{{\left( {{w \mathord{\left/ {\vphantom {w {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}} \right)}}^{2}} + {{{\left( {{t \mathord{\left/ {\vphantom {t {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}} \right)}}^{2}}} \right)} \right\}}^{{ - 1}}}. \\ \end{gathered} $Очевидно, соотношения можно распространить на круглые проволочки с радиусом r, считая что $w = t = r\sqrt \pi $. К сопротивлению (8), которое рассмотрено в условиях постоянного тока, следует, вообще говоря, добавить индуктивную часть, т.е. взять $Z = R + i\omega \left( {{{L}_{G}} + {{L}_{K}}} \right)$, где
(13)
${{L}_{G}} = \frac{{{{\mu }_{0}}L}}{{2\pi }}\ln \left( {\frac{{2L}}{{w + t}} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right),$‒ геометрическая индуктивность,
– кинетическая индуктивность. В (14) добавлен множитель, учитывающий то, что кинетическая индуктивность возникает при баллистическом транспорте. Если период колебаний поля ${{T}_{0}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \omega }} \right. \kern-0em} \omega }$ сравним со временем свободного пробега, то приобретаемая в поле кинетическая энергия начинает резко уменьшаться. Поскольку частоты столкновений ${{\omega }_{с}} = {1 \mathord{\left/ {\vphantom {1 \tau }} \right. \kern-0em} \tau }$ для металлов лежат в инфракрасном диапазоне, то в терагерцевом диапазоне использовать ${{L}_{K}}$ желательно, особенно для коротких проводников. В общем случае можно ввести частотную корректировку:
Естественно, что приведенные формулы приближенные. Более строгие подходы к получению поверхностного или объемного импедансов должны основываться на определении числа мод проводимости из УШ и рассматривать решения уравнений Максвелла с учетом поверхностного эффекта, при этом весьма важно определение параметра $\tau $, который зависит от того, каков характер отражений носителей от границ – зеркальный, смешанный или диффузный. Соответственно важна и структура границ –атомарная или кластерная.
3. ПРОВОДИМОСТЬ, ЧИСЛО ЕЕ МОД И ЭНЕРГЕТИЧЕСКИЕ УРОВНИ
Баллистическая проводимость пропорциональна числу мод ${{M}_{d}}\sim {{{{D}_{d}}} \mathord{\left/ {\vphantom {{{{D}_{d}}} L}} \right. \kern-0em} L}$ [25‒30]:
(15)
${{G}_{{{\text{B}}d}}} = \frac{{{{q}^{2}}{{M}_{d}}}}{h} = \frac{{{{q}^{2}}{{D}_{d}}\bar {v}}}{{2L}}\left\{ {1,\frac{2}{\pi },\frac{1}{2}} \right\},$поэтому число мод определяется плотностью состояний ${{D}_{d}}$. Для широких и толстых проводников естественно считать, что число мод пропорционально wt. Для числа мод с импульсом, меньше некоторого значения p, известно выражение
(16)
${{M}_{d}}\left( p \right) = \left[ {1,\frac{{2t}}{{{h \mathord{\left/ {\vphantom {h p}} \right. \kern-0em} p}}},\frac{{\pi wt}}{{{{{\left( {{h \mathord{\left/ {\vphantom {h p}} \right. \kern-0em} p}} \right)}}^{2}}}}} \right] = \frac{{h{{N}_{d}}\left( p \right)}}{{2Lp}}\left\{ {1,\frac{4}{\pi },\frac{3}{2}} \right\},$где квадратные скобки означают взятие целой части. Здесь
(17)
${{N}_{d}}\left( p \right) = \left[ {\frac{{2L}}{{{h \mathord{\left/ {\vphantom {h p}} \right. \kern-0em} p}}},\pi \frac{{Lt}}{{{{{\left( {{h \mathord{\left/ {\vphantom {h p}} \right. \kern-0em} p}} \right)}}^{2}}}},\frac{{{\text{4}}\pi }}{{\text{3}}}\frac{{Lwt}}{{{{{\left( {{h \mathord{\left/ {\vphantom {h p}} \right. \kern-0em} p}} \right)}}^{3}}}}} \right]$‒ число состояний с импульсом меньше p. Вводя закон дисперсии в виде $E = E\left( p \right)$, для числа состояний и его плотности ${{D}_{d}}$ имеем
(18)
$\begin{gathered} {{N}_{d}}\left( E \right) = \int\limits_{ - \infty }^E {D\left( {E{\kern 1pt} '} \right)dE{\kern 1pt} '} ,\,\,\,{{D}_{d}}\left( E \right) = \frac{{d{{N}_{d}}\left( E \right)}}{{dE}} = \\ = \frac{{d{{N}_{d}}\left( E \right)}}{{dp}}\frac{{dp\left( E \right)}}{{dE}} = \frac{{dp\left( E \right)}}{{dE}}\frac{{{{p}^{{d - 1}}}d}}{{{{h}^{d}}}}\left\{ {2L,\pi Lt,4\pi L{{wt} \mathord{\left/ {\vphantom {{wt} 3}} \right. \kern-0em} 3}} \right\}. \\ \end{gathered} $Для получения формул типа (18) используются простые законы дисперсии типа $E\left( p \right) = {{E}_{с}} + {{{{p}^{2}}} \mathord{\left/ {\vphantom {{{{p}^{2}}} {\left( {2m} \right)}}} \right. \kern-0em} {\left( {2m} \right)}}$. В случаях d = 1, 2, 3 имеем $p = \left| {{{p}_{z}}} \right|$, ${{p}^{2}} = p_{z}^{2} + p_{x}^{2}$, ${{p}^{2}} = p_{x}^{2} + p_{y}^{2} + p_{z}^{2}$. Для графена обычно берут области в зоне Бриллюэна вблизи двух точек Дирака, где дисперсия имеет вид
Отсюда число мод проводимости графеновой ленты ширины w есть $M\left( E \right) = {{2wE} \mathord{\left/ {\vphantom {{2wE} {\left( {\pi \hbar {{v}_{{\text{F}}}}} \right)}}} \right. \kern-0em} {\left( {\pi \hbar {{v}_{{\text{F}}}}} \right)}}$, ${{v}_{{\text{F}}}} \approx {{10}^{6}}$ м/с. Естественно, что приведенные соотношения приближенные, но в силу их простоты они весьма удобны для моделирования. Определяя ток усреднением по энергии [30] –
получаем линейный отклик на разность электрических потенциалов $U$ в виде проводимости [29, 30]
Здесь ${{f}_{1}}\left( E \right) - {{f}_{2}}\left( E \right) = - \left( {\partial {{f}_{0}}{{\left( E \right)} \mathord{\left/ {\vphantom {{\left( E \right)} {\partial E}}} \right. \kern-0em} {\partial E}}} \right)qU$ при определении проводимости $G = {I \mathord{\left/ {\vphantom {I U}} \right. \kern-0em} U}$. Аналогично получаем линейный отклик на изменение температуры, а также и нелинейные отклики [30]. Удельную погонную проводимость можно в первом приближении определить так:
Аналогично получаем эффективную погонную поверхностную проводимость в виде
Указанные проводимости есть функции координаты z, отсчитываемой от истока к стоку. У истока проводимость $G\left( 0 \right) = {{G}_{b}}$ баллистическая и максимальная. Пропорциональность удельных проводимостей длине L не должна смущать, так как линейный отклик пропорционален напряжению U, а компонента электрического поля ${{E}_{z}} = {{ - U} \mathord{\left/ {\vphantom {{ - U} L}} \right. \kern-0em} L}$. Рассматривая указанные величины как статические, в приближении времени релаксации получаем частотные зависимости, например σ(z) = $ = {{{{\sigma }_{0}}\left( z \right)} \mathord{\left/ {\vphantom {{{{\sigma }_{0}}\left( z \right)} {\left( {1 + \omega \tau } \right)}}} \right. \kern-0em} {\left( {1 + \omega \tau } \right)}}$. Приближение справедливо для длин волн, существенно больших L. Поверхностный импеданс бесконечного графенового листа с учетом температурной зависимости приведен в ряде работ, например, [18, 31, 54, 56]. В работах [20, 53, 69, 70] рассмотрен и импеданс графеновой наноленты, который зависит не только от ее ширины, но и структуры, и окружения (подложки), и формы краев, а учет числа мод и плотности состояний проведен в [71].
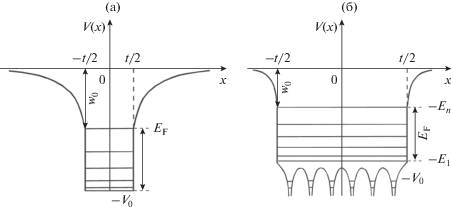
Рассмотрим простые модели для проводимости металлических структур. Для металлической пленки толщиной t имеет место размерное квантование, в результате которого дисперсия принимает вид
Для ленты с размерами w, t имеем E(p) = En + $ + {{p_{z}^{2}} \mathord{\left/ {\vphantom {{p_{z}^{2}} {\left( {2{{m}_{e}}} \right)}}} \right. \kern-0em} {\left( {2{{m}_{e}}} \right)}}$, где ${{E}_{n}}$ ‒ уровни энергии в соответствующей двумерной потенциальной яме, которые можно описать мультииндексом $n = \left( {{{n}_{x}},{{n}_{y}}} \right)$. В бесконечно глубокой двумерной яме имеется бесконечное число состояний ${{E}_{n}}$ = ${{\left( {\pi \hbar } \right)}^{2}} \times $ $ \times \,\,{{\left( {{{{\left( {{{{{n}_{x}}} \mathord{\left/ {\vphantom {{{{n}_{x}}} t}} \right. \kern-0em} t}} \right)}}^{2}} + {{{\left( {{{{{n}_{y}}} \mathord{\left/ {\vphantom {{{{n}_{y}}} w}} \right. \kern-0em} w}} \right)}}^{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\left( {{{{{n}_{x}}} \mathord{\left/ {\vphantom {{{{n}_{x}}} t}} \right. \kern-0em} t}} \right)}}^{2}} + {{{\left( {{{{{n}_{y}}} \mathord{\left/ {\vphantom {{{{n}_{y}}} w}} \right. \kern-0em} w}} \right)}}^{2}}} \right)} {\left( {2{{m}_{e}}} \right)}}} \right. \kern-0em} {\left( {2{{m}_{e}}} \right)}}$, отсчитываемых от дна. Однако для конечной ямы это весьма приближенная модель. На рис. 1 и 2 условно показано распределение энергий электрона в одномерной яме полубесконечного проводника и в яме для пленки проводника толщиной t. В обоих случаях ямы не прямоугольные. Их прямоугольные границы $\left| x \right| \leqslant {t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}$ смещены во вне на некоторое расстояние a по сравнению с областью $\left| x \right| \leqslant {{t{\kern 1pt} '} \mathord{\left/ {\vphantom {{t{\kern 1pt} '} 2}} \right. \kern-0em} 2}$, соответствующей границам центров атомов (см. рис. 1а). Для полубесконечной структуры максимальное значение ${{E}_{n}} = {{E}_{{\text{F}}}}$ определяет уровень Ферми, а число уровней с учетом вырождения по спину – число состояний. Любой реальный образец конечный, но при больших размерах энергия Ферми ${{E}_{{\text{F}}}}$ перестает от них зависеть, число состояний конечно, но велико, а распределение можно считать непрерывным. Отсчитываемая от дна ямы (от энергии внутренних оболочек ядер) энергия ${{E}_{{\text{F}}}}$ вместе с работой выхода ${{W}_{0}}$ образует яму с минимумом потенциала ${{V}_{0}} = - \left( {{{E}_{{\text{F}}}} + {{W}_{0}}} \right)$. На самом деле от $ - {{V}_{0}}$ отсчитываются уровни ${{E}_{n}}$, но в широкой яме ${{E}_{{\text{F}}}} = - \left( {{{E}_{n}} - {{E}_{1}}} \right) \approx - {{E}_{n}}$, где ${{E}_{n}}$ ‒ последний уровень. Нуль потенциала соответствует свободному электрону. Конфигурация ямы зависит от распределения потенциала $V\left( x \right)$, который определяется как работа, необходимая для перемещения электрона из ямы с уровня Ферми во внешнюю точку x (см. рис. 1). Наиболее простая конфигурация – прямоугольная яма $V\left( x \right) = - {{V}_{0}}$ при $\left| x \right| \leqslant {t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}$, $V\left( x \right) = 0$ при $\left| x \right| > {t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}$. Решение уравнения Шредингера (УШ) для нее хорошо известно в виде трансцендентного соотношения [72]
Рис. 1.
Схематическое изображение поверхности массивного (полубесконечного) проводника с плоскостью зеркальных изображений 1 и атомами 2 в решетке (а) и схема энергетических зон и потенциальной ямы (б).
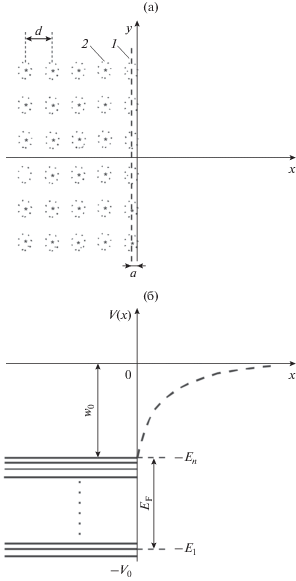
Рис. 2.
Схематический вид энергетических уровней и потенциальной ямы с плоским дном для металлической пленки толщиной t (а) и аналогичной ямы с энергетическими уровнями с учетом квазипериодической структуры атомов (б).
где $k = {{\sqrt {2{{m}_{e}}\left( {E - {{V}_{0}}} \right)} } \mathord{\left/ {\vphantom {{\sqrt {2{{m}_{e}}\left( {E - {{V}_{0}}} \right)} } \hbar }} \right. \kern-0em} \hbar }$, ${{n}_{0}} = 1,2,...$ Из данного соотношения следуют значения толщин ${{t}_{{{{n}_{0}}}}} = {{{{n}_{0}}\pi } \mathord{\left/ {\vphantom {{{{n}_{0}}\pi } {{{k}_{m}}}}} \right. \kern-0em} {{{k}_{m}}}}$, при которых уровни увеличиваются на единицу, где ${{{{k}_{m}} = \sqrt {2{{m}_{e}}\left| {{{V}_{0}}} \right|} } \mathord{\left/ {\vphantom {{{{k}_{m}} = \sqrt {2{{m}_{e}}\left| {{{V}_{0}}} \right|} } \hbar }} \right. \kern-0em} \hbar }$. При ${{n}_{0}} = 1$ происходит дополнение одного уровня к уже имеющемуся при $t < {{t}_{1}}$. Уменьшение $t$ от макроскопических значений к микроскопическим приводит к увеличению расстояний между уровнями и к уменьшению получаемой таким образом работы выхода. Кроме того, уровни расположены неравномерно, сгущаясь ко дну. Рассмотрим приближенную к реальности модель. Считаем, что до энергии Ферми конфигурация ямы прямоугольная, а далее имеется барьер (рис. 2а). Для его расчета необходимо воспользоваться методом теории изображений [73, 74]. Теория достаточно простая, но весьма хорошо описывает форму потенциального барьера. Однако сила изображения $F = {{{{e}^{2}}} \mathord{\left/ {\vphantom {{{{e}^{2}}} {\left( {16\pi {{\varepsilon }_{0}}{{x}^{{'2}}}} \right)}}} \right. \kern-0em} {\left( {16\pi {{\varepsilon }_{0}}{{x}^{{'2}}}} \right)}}$ обращается в бесконечность на границе ямы ($x{\kern 1pt} ' = 0$, см. рис. 1). Эта сила перестает работать на расстояниях порядка атомных, что качественно можно объяснить так. Пусть атом металла отдает один электрон в зону проводимости, при этом a – радиус иона. Такой ион будет притягивать электрон только на расстояниях порядка a и более. Часть электронных оболочек атомов перекрывается, образуя кристалл. Удаление из него электрона проявляется как недостаток электронной плотности в окружении ближайшего атома (атомов), что и определяет зеркальную силу. Величина a примерно равна радиусу атома или иона, который обычно имеет порядок от половины постоянной решетки и менее. В работах [73, 74] на основе метода изображений получены выражения, которые для случая, представленного на рис. 1, позволяют записать потенциал в виде
(19)
$V\left( x \right) = \left\{ {\begin{array}{*{20}{c}} { - {{V}_{0}} = - \left( {{{W}_{0}} + {{E}_{{\text{F}}}}} \right),\,\,\,\,x \leqslant 0;} \\ { - \frac{{{{e}^{2}}}}{{16\pi {{\varepsilon }_{0}}\left( {x + a} \right)}},\,\,\,\,\,\,\,\,\,x > 0.} \end{array}} \right.$Потенциал имеет скачок ${{E}_{{\text{F}}}}$ и согласно (19) W0 = $ = - V\left( 0 \right) = {{{{e}^{2}}} \mathord{\left/ {\vphantom {{{{e}^{2}}} {\left( {16\pi {{\varepsilon }_{0}}a} \right)}}} \right. \kern-0em} {\left( {16\pi {{\varepsilon }_{0}}a} \right)}}$. Экспериментально измеренная работа выхода зависит от кристаллографических направлений, а также от поверхностных таммовских уровней. Следовательно, от них зависит и а. В качестве такой константы можно использовать радиус одиночного атома, радиус иона, ковалентный радиус, что обусловливает некоторый произвол, слабо влияющий на форму потенциального барьера. Желательно определять а через работу выхода, учитывая, что она может зависеть от состояния поверхности, при этом в силу определения работы выхода следует использовать минимальную величину. В качестве примера в табл. 1 приведены постоянные решетки ряда металлов, радиусы атомов, ковалентные радиусы, радиусы ионов решетки +1e, экспериментальные значения работ выхода и соответствующие значения, полученные по приведенной формуле при этих радиусах. Из табл. 1 видно, что наиболее хорошо коррелирует значение a в качестве радиуса иона, хотя есть и исключения, что, по-видимому, связано с количеством отдаваемых электронов в зону проводимости, типом связи атомов в решетке и необходимостью использования радиусов соответствующих ионов. Так, радиус иона серебра +1e составляет 0.126 нм, но если взять радиус иона +2e, равный 0.089 нм, то получаем ${{W}_{0}} = 4.045$ эВ. Нахождение работы выхода строгими квантово-механическими методами было предпринято в ряде ранних работ, например [75], но не увенчалось точными количественными результатами из-за сложности задачи. Современные публикации по применению метода сильной связи позволяют вычислять энергетический спектр и, соответственно, работу выхода для структур конечных размеров весьма точно [71, 76]. По-видимому, достаточно точно работу выхода можно определить методами молекулярной динамики, зная кристаллическую структуру и плотность связанных электронных состояний в кристалле. Поскольку потенциалы ионизации атомов примерно в четыре раза выше, чем работы выхода для соответствующих им материалов, ясно, что используемый простой метод изображений хорошо описывает форму ямы и потенциального барьера. Последний возникает при приложении к проводнику внешнего положительного электрического потенциала [74]. Распределение потенциала для ямы с плоским дном (см. рис. 2а) имеет вид
(20)
$V\left( {x,t} \right) = \left\{ \begin{gathered} - {{V}_{0}} = - \left( {{{W}_{0}} + {{E}_{{\text{F}}}} - {{E}_{1}}} \right),\,\,\,\,x \leqslant {t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}; \hfill \\ - \frac{{{{e}^{2}}}}{{16\pi {{\varepsilon }_{0}}\left( {\left| x \right| - {t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2} + a} \right)}},\,\,\,\,x > {t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}. \hfill \\ \end{gathered} \right.$Таблица 1.
Сравнение экспериментальных и вычисленных по (19) значений работы выхода для радиуса а атома, ковалентного радиуса и радиуса иона +1e
| Материал | Постоянная решетки, нм | а, нм* | W0, эВ | |
|---|---|---|---|---|
| эксперимент | расчет для трех значений a* | |||
| Барий | 0.5020 | 0.222; 0.198; 0.134 | 2.52–2.7 | 1.62; 1.82; 2.68 |
| Золото | 0.4704 | 0.144; 0.134; 0.137 | 5.1–5.47 | 2.5; 2.68; 2.62 |
| Вольфрам | 0.54 | 0.141; 0.170; 0.07 | 4.32–5.22 | 2.55; 2.11; 5.14 |
| Медь | 0.3615 | 0.128; 0.117; 0.077 | 4.36–5.10 | 2.81; 3.07; 4.67 |
| Молибден | 0.315 | 0.139; 0.130; 0.07 | 2.52–2.7 | 2.59; 2.78; 5.14 |
| Серебро | 0.4086 | 0.144; 0.134; 0.126 | 4.52–4.74 | 2.5; 2.69; 2.86 |
Здесь ${{E}_{{\text{F}}}} = {{E}_{n}} - {{E}_{1}} > 0$, ${{E}_{1}}$ ‒ уровень, отсчитываемый от дна ямы $ - {{V}_{0}}$. Аналогичный результат для диэлектрической пластины толщиной t с диэлектрической проницаемостью (ДП) $\varepsilon $ дается бесконечным рядом изображений [73, 74]. При этом потенциал изменяется и внутри пластины, а работа выхода зависит от ее толщины. Измеряя работу выхода относительно центра пластины, можно оценивать ДП тонких пластин. Результат (20) получается заменой коэффициента отражения электрической индукции $k = {{\left( {1 - \tilde {\varepsilon }} \right)} \mathord{\left/ {\vphantom {{\left( {1 - \tilde {\varepsilon }} \right)} {\left( {1 + \tilde {\varepsilon }} \right)}}} \right. \kern-0em} {\left( {1 + \tilde {\varepsilon }} \right)}}$ на $k = - 1$ (что соответствует бесконечной ДП металла $\tilde {\varepsilon }$). Наличие наноразмерной диэлектрической пленки на поверхности металла значительно уменьшает ширину и высоту потенциального барьера [73, 74].
Для определения ${{V}_{0}}$ следует вспомнить, что реально необходимо решать трехмерное многочастичное уравнение Шредингера (УШ) с учетом спина в трехмерном квазипериодическом потенциале (см. рис. 2б). Но поскольку электроны внутренних оболочек атомов сильно связаны и почти не влияют на распределение электронов по энергиям в зоне проводимости, за дно ямы можно принять уровень, соответствующий потенциалу ионизации иона кристаллической решетки (см. рис. 2б) и решать одночастичное УШ. В принципе, решить УШ с таким потенциалом не представляет труда, но проще решать его для потенциальной ямы с плоским дном. Для определения глубины ${{V}_{0}}$ такой ямы следует учесть, что при ее сужении уровни энергии повышаются, а потенциалу ионизации атома ${{W}_{i}} = {{{{e}^{2}}} \mathord{\left/ {\vphantom {{{{e}^{2}}} {4\pi {{\varepsilon }_{0}}a}}} \right. \kern-0em} {4\pi {{\varepsilon }_{0}}a}}$ соответствует радиус иона $a$. Предположим, что кристаллическая решетка кубическая, а в зону проводимости каждый атом отдает один электрон. Объем иона ${{4\pi {{a}^{3}}} \mathord{\left/ {\vphantom {{4\pi {{a}^{3}}} 3}} \right. \kern-0em} 3}$, а объем в плоской яме, приходящийся на один ион есть ${{d}^{3}} - {{4\pi {{a}^{3}}} \mathord{\left/ {\vphantom {{4\pi {{a}^{3}}} 3}} \right. \kern-0em} 3}$. Для получения сдвига $\Delta E = {{W}_{i}} - {{V}_{0}}$ можно связать приходящийся на электрон объем с неопределенностью координат и импульса. Тогда $\Delta E = {{{{{\left( {\pi \hbar } \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {\pi \hbar } \right)}}^{2}}} {\left( {8{{m}_{e}}{{{\left( {{{d}^{3}} - 4\pi {{a}^{3}}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}} \right)}}} \right. \kern-0em} {\left( {8{{m}_{e}}{{{\left( {{{d}^{3}} - 4\pi {{a}^{3}}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}} \right)}}$.
Будем использовать другой способ. В точке ${d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$ на одинаковом расстоянии от ближайших атомов электрические силы на электрон не действуют. Для того чтобы оторвать электрон от иона из точки $r = a$ в точку $r = {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$ (без учета сил от соседних ионов и электронного облака), следует затратить энергию $\Delta E = {{W}_{i}} - {{{{e}^{2}}} \mathord{\left/ {\vphantom {{{{e}^{2}}} {2\pi {{\varepsilon }_{0}}d}}} \right. \kern-0em} {2\pi {{\varepsilon }_{0}}d}}$. Поэтому можно определить дно так: ${{V}_{0}} = {{W}_{i}} - \Delta E$. Реально квазипериодическая структура также влияет на сдвиг, который должен быть немного меньше. Для проволоки потенциал двумерной ямы приближенно записываем в виде $V\left( {x,y,z} \right) = {{\left( {V\left( {x,t} \right)V\left( {y,w} \right)} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$. Для оценки числа мод проводимости в такой проволоке следует решать УШ
(21)
$\left[ { - \frac{{{{\hbar }^{2}}}}{{2{{m}_{e}}}}{{\nabla }^{2}} + V\left( {x,y,z} \right)} \right]\Psi \left( {x,y,z} \right) = {{E}_{n}}.$В одномерном случае решить УШ со сложной конфигурацией потенциала весьма просто. На рис. 3 приведено такое решение для изображенной там же потенциальной ямы. Использованы нормированная энергия $\varepsilon = {{2mE} \mathord{\left/ {\vphantom {{2mE} {{{\hbar }^{2}}}}} \right. \kern-0em} {{{\hbar }^{2}}}}$ и потенциал $v\left( x \right) = {{2mV\left( x \right)} \mathord{\left/ {\vphantom {{2mV\left( x \right)} {{{\hbar }^{2}}}}} \right. \kern-0em} {{{\hbar }^{2}}}}$. В таких обозначениях согласно (21) энергия и потенциал измеряются в обратных квадратах длины. Перевод значений в электронвольты осуществляется множителем 27.61. Для решения УШ был использован метод матриц передачи размерности 2. Матрица связывает значения $\Psi \left( x \right)$ и $\Psi {\kern 1pt} '\left( x \right)$ на левой и правой границах ямы. Поскольку слева $\Psi \left( x \right) = \Psi \left( 0 \right)\exp \left( {i{{k}_{0}}x} \right)$, а справа $\Psi \left( x \right) = \Psi \left( t \right)\exp \left( { - i{{k}_{0}}\left( {x - t} \right)} \right)$, где k0 = $ = {{ - i\sqrt {2m\left( { - E} \right)} } \mathord{\left/ {\vphantom {{ - i\sqrt {2m\left( { - E} \right)} } {{{\hbar }^{2}}}}} \right. \kern-0em} {{{\hbar }^{2}}}}$, при этом в яме k = $ = {{\sqrt {2m\left( {E - V} \right)} } \mathord{\left/ {\vphantom {{\sqrt {2m\left( {E - V} \right)} } {{{\hbar }^{2}}}}} \right. \kern-0em} {{{\hbar }^{2}}}}$, то характеристическое уравнение сводится к нахождению корней определителя системы двух однородных линейных уравнений, что представляет собой весьма простую задачу для ямы произвольной конфигурации. Последнюю можно аппроксимировать ступенчатым потенциалом или же получить интегральное уравнение (ИУ) для параметров рассеяния, если профиль ямы задан в виде аналитической функции.
Рис. 3.
Нормированные энергетические уровни (1–6) и конфигурация потенциала для потенциальной ямы с пятью периодами слева и справа от центральной области с дислокацией 2d при ${{d}_{1}} = {{d}_{2}} = d = 1$ Å, $ - {{v}_{0}} = 1$, $ - {{v}_{1}} = 0.8$, $ - {{{v}}_{2}} = 0.5$.
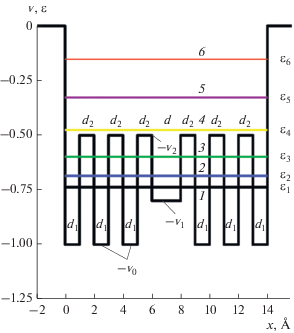
В табл. 2 показано, как влияет вид дислокации на уровни энергии для рис. 3, а на рис. 4 дана зависимость числа уровней от ширины одномерной ямы рис. 2 с барьерами $\tilde {n}$ и резкими стенками ${{n}_{0}}$. Там же приведены результаты оценки числа уровней на основе числа волн де-Бройля. Именно, в яме глубиной ${{V}_{0}}$ максимально возможный импульс есть $p = \sqrt {2{{m}_{e}}{{V}_{0}}} $, поэтому $n = 2t{{\sqrt {2{{m}_{e}}{{V}_{0}}} } \mathord{\left/ {\vphantom {{\sqrt {2{{m}_{e}}{{V}_{0}}} } h}} \right. \kern-0em} h}$. Отметим, что $n$ коррелирует с ${{n}_{0}}$, а именно ${{n}_{0}} = n + 1$. Можно считать их идентичными, если число укладывающихся волн де-Бройля округлять в большую сторону. Конечно, экстремально малые модельные значения толщины не соответствуют реальной яме для металлической пленки, для которой получение толщин порядка 1 нм есть существенная проблема. Немонотонный характер зависимости $\tilde {n}\left( t \right)$ можно объяснить ступенчатой аппроксимацией барьера. Барьер аппроксимировался двенадцатью ступенями, при этом точность аппроксимации составила 7%, а ширина барьера равнялась 12a. Сравнение с расчетом для шести ступеней не привело к существенным изменениям в числе и картине уровней. Дальнейшее увеличение разбиений нецелесообразно в силу ухудшения обусловленности алгоритма. Для ее улучшения элементы матрицы каждой ступени нормировались на максимальный экспоненциальный множитель в матричных элементах.
Таблица 2.
Нормированные уровни энергии для конфигурации рис. 3 (${{d}_{1}} = {{d}_{1}} = d = 1.0$ Å) в зависимости от нормированного потенциала v
| ${{\varepsilon }_{i}}$ | Уровни энергии при разных значениях v | ||
|---|---|---|---|
| –1 | –1.2 | –0.8 | |
| ε6 | –0.1521 | –0.1523 | –0.1518 |
| ε5 | –0.3267 | –0.3433 | –0.3131 |
| ε4 | –0.4763 | –0.4782 | –0.4761 |
| ε3 | –0.5981 | –0.6150 | –0.5810 |
| ε2 | –0.6850 | –0.6857 | –0.6843 |
| ε1 | –0.7375 | –0.7595 | –0.7231 |
Рис. 4.
Числа энергетических уровней $n$, ${{n}_{0}}$ и $\tilde {n}$ в двумерной яме с плоским дном в зависимости от ширины t; кривая 1 – расчет на основе числа волн де-Бройля, 2 – яма с резкими стенками ${{n}_{0}}$, 3 – определение $\tilde {n}$ из решения УШ для ямы с двумя барьерами (см. рис. 2); глубина ямы ${{V}_{0}} = 11.46$ эВ, работа выхода ${{W}_{0}} = 4.36$ эВ.
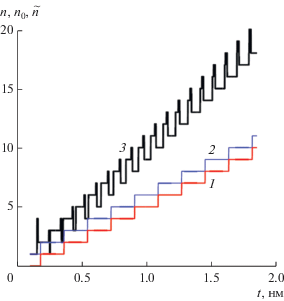
Результаты расчета показывают, что учет барьера приводит к существенному увеличению уровней, часть которых можно трактовать как поверхностные состояния. Рассмотренные модели ямы с плоским дном плохо соответствуют реальности, поскольку сильно поднимаются уровни, а последний уровень плохо соответствует уровню Ферми в реальном металле. Это особенно характерно для широкой ямы с плоским дном, для которой уровень Ферми близок к нулю. Более предпочтительна яма с квазипериодической структурой на дне (см. рис. 3). Определяя ее уровни, т.е. и работу выхода, можно построить конфигурацию барьеров. Расчет с таким потенциалом изменит уровни, что потребует пересчета барьеров. Более точная оценка числа уровней здесь возможна на основе последовательных приближений.
Двумерная яма и трехмерный ящик представляют собой несколько более сложные задачи, по решению которых реальнее оценить число мод проводимости. Выделим в проволоке некую длину L, кратную периоду. Трехмерное решение уравнения (21) будем искать в следующем виде:
(22)
$\begin{gathered} \Psi \left( {x,y,z} \right) = K\left( {x,t} \right)K\left( {y,w} \right) \times \\ \times \,\,\sum\limits_{k = 1}^{{{N}_{x}}} {\sum\limits_{l = 1}^{{{N}_{y}}} {\sum\limits_{m = 0}^{{{N}_{z}}} {{{A}_{{klm}}}\sin \left( {\frac{{k\pi x}}{{t{\kern 1pt} '}} - \frac{1}{2}} \right)} } } \times \\ \times \,\,\sin \left( {\frac{{l\pi y}}{{w{\kern 1pt} '}} - \frac{1}{2}} \right)\exp \left( { - \frac{{2imz}}{L}} \right), \\ \end{gathered} $где $K\left( {x,t} \right) = {{\left( {\sqrt {2\pi } t} \right)}^{{ - 1}}}\exp \left( {{{ - {{x}^{2}}} \mathord{\left/ {\vphantom {{ - {{x}^{2}}} {\left( {2{{t}^{2}}} \right)}}} \right. \kern-0em} {\left( {2{{t}^{2}}} \right)}}} \right)$ ‒ гауссов форм-фактор, а число учтенных функций существенно больше имеющихся уровней. Двумерное решение получается учетом только члена c $m = 0$. Параметры со штрихом означают увеличенные на две ширины барьера размеры ямы. Это приближение означает, что волновая функция обрезается и не выходит за эти пределы. Можно использовать и прямоугольный форм-фактор, но для штрихованных размеров. В этом случае базисные функции ортогональны, однако система не полная, поскольку исключены функции непрерывного спектра. Минимальная отрицательная энергия ищется как минимум квадратичного функционала [72]
(23)
${{E}_{n}} = \frac{{\int\limits_{ - t{\kern 1pt} '}^{t{\kern 1pt} '} {\int\limits_{ - w\,'}^{w\,'} {\int\limits_{ - t{\kern 1pt} '}^{t{\kern 1pt} '} {\int\limits_{ - w\,'}^{w\,'} {\int\limits_{ - {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}}^{{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}} {\int\limits_{ - {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}}^{{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}} {\Psi \left( {x{\kern 1pt} ',y{\kern 1pt} ',z{\kern 1pt} '} \right)\left[ { - \frac{{{{\hbar }^{2}}{{\nabla }^{2}}}}{{2{{m}_{e}}}} + V\left( {x,y,z} \right)} \right]\Psi \left( {x,y,z} \right)dxdydzdx{\kern 1pt} 'dy{\kern 1pt} 'dz{\kern 1pt} '} } } } } } }}{{\int\limits_{ - t{\kern 1pt} '}^{t{\kern 1pt} '} {\int\limits_{ - w{\kern 1pt} '}^{w{\kern 1pt} '} {{{\Psi }^{2}}\left( {x,y,z} \right)} dxdydz} }},$что приводит к нахождению корней равного нулю определителя большой размерности. Усложнение также связано с необходимостью численного интегрирования при вычислении матричных элементов. Отметим, что функционал (23) не требует нормировки волновых функций. Функционал показывает, что число уровней, следовательно, и число мод зависят от глубины ямы ${{V}_{0}}$, и эквивалентен уравнению $\left( {\Psi ,\hat {E}\Psi } \right) = {{E}_{n}}\left( {\Psi ,\Psi } \right)$, в котором скобки означают скалярное произведение согласно (23). Его минимум эквивалентен экстремуму функционала $\left( {\Psi ,\hat {E}\Psi } \right)$, когда ${{E}_{n}}$ выступает в роли множителя Лагранжа условия $\left( {\Psi ,\Psi } \right) = 1$ [72]. Определитель имеет $N = {{N}_{x}}{{N}_{y}}\left( {{{N}_{z}} + 1} \right)$ корней. При их нахождении следует брать только отрицательные значения. Более строгий подход требует ортогонализации, при этом использовать нормировку нецелесообразно из-за возникновения нелинейных уравнений. Если ${{\Psi }_{1}}$ ‒ собственная функция для ${{E}_{1}}$, то ${{E}_{2}}$ ищется с помощью множителя Лагранжа как экстремум функционала $\Lambda = \left( {\Psi ,\hat {E}\Psi } \right) - $ ${{E}_{2}}\left( {\Psi ,\Psi } \right) - {{\lambda }_{1}}\left( {\Psi ,{{\Psi }_{1}}} \right)$, что приводит к системе N + 1 уравнений с множителем Лагранжа ${{\lambda }_{1}}$. Здесь определитель есть полином по ${{E}_{2}}$ степени N. В качестве значения ${{E}_{2}}$ следует использовать минимальный отрицательный корень. Очевидно, ${{\Lambda }_{{ext}}} = 0$. Процесс можно продолжить, найдя все отрицательные значения энергии. Если использовать функцию $\Phi \left( {x,y,z} \right) = $ $\Psi \left( {x,y,z} \right)\exp \left( { - i{{p}_{z}}z} \right)$, то трехмерное УШ сводится к определению дисперсии $E = {{E}_{n}} + {{p_{z}^{2}} \mathord{\left/ {\vphantom {{p_{z}^{2}} {2{{m}_{e}}}}} \right. \kern-0em} {2{{m}_{e}}}}$ для квантовой проволоки с периодическим потенциалом, при этом достаточно взять $L = d$. Поскольку работа выхода и конфигурация барьеров определяются атомной структурой (трехмерными потенциалами атомов) и несущественно отличаются для массивных проводников и тонких пленок, имеющих, по крайней мере, несколько атомарных слоев, то для строгого учета числа уровней и плотности состояний следует рассматривать решения трехмерных УШ (21) и функционал (23) с потенциалами, соответствующими реальным металлам и заменами ${{E}_{n}} \to {{E}_{n}} + {{p_{z}^{2}} \mathord{\left/ {\vphantom {{p_{z}^{2}} {\left( {2{{m}_{e}}} \right)}}} \right. \kern-0em} {\left( {2{{m}_{e}}} \right)}}$, $L \to d$. Такой подход с использованием строгого трехмерного периодического потенциала наиболее точный для определения мод проводимости квантовой проволоки.
4. ЧИСЛО МОД ДЛЯ ПРОВОДНИКОВ КОНЕЧНЫХ РАЗМЕРОВ
Полагая яму прямоугольной и конечной, получаем для отрицательных энергий приближенное условие ($n = \left( {k,l,m} \right)$):
(24)
${{E}_{n}} = \frac{{{{\hbar }^{2}}{{\pi }^{2}}}}{{2{{m}_{e}}}}\left( {{{{\left( {{k \mathord{\left/ {\vphantom {k t}} \right. \kern-0em} t}} \right)}}^{2}} + {{{\left( {{l \mathord{\left/ {\vphantom {l w}} \right. \kern-0em} w}} \right)}}^{2}} + {{{\left( {{{2m} \mathord{\left/ {\vphantom {{2m} L}} \right. \kern-0em} L}} \right)}}^{2}}} \right) \leqslant {{E}_{{\text{F}}}} < {{V}_{0}}.$Рассмотрев потенциальную яму вида $t = w = {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}$, получаем ${{k}^{2}} + {{l}^{2}} + {{m}^{2}} < 2{{m}_{e}}{{E}_{{\text{F}}}}{{{{t}^{2}}} \mathord{\left/ {\vphantom {{{{t}^{2}}} {{{\hbar }^{2}}}}} \right. \kern-0em} {{{\hbar }^{2}}}}{{\pi }^{2}}$. Число решений этого неравенства приближенно дает число уровней. Решений не будет, если V0 < $ < 2{{\hbar }^{2}}{{{{\pi }^{2}}} \mathord{\left/ {\vphantom {{{{\pi }^{2}}} {\left( {2{{m}_{e}}{{t}^{2}}} \right)}}} \right. \kern-0em} {\left( {2{{m}_{e}}{{t}^{2}}} \right)}}$, что указывает на приближенность подхода. Уравнение Шредингера для функционала (23) с конечным потенциалом формально соответствует теории возмущений, а функционал по крайней мере имеет один отрицательный минимум. Переход от бесконечного потенциала к конечному нельзя рассматривать как малое возмущение. Поэтому максимальное значение ${{E}_{n}}$ не следует ассоциировать с $ - {{E}_{{\text{F}}}}$. Однако оценивать нижний уровень как ${{E}_{1}} \approx - {{V}_{0}} + {{{{{\left( {\hbar \pi } \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {\hbar \pi } \right)}}^{2}}} {\left( {2{{m}_{e}}{{t}^{2}}} \right)}}} \right. \kern-0em} {\left( {2{{m}_{e}}{{t}^{2}}} \right)}}$ можно. Теперь следует определить число мод в модели ЛДЛ. Обычно используется простой изотропный закон дисперсии $E\left( {\left| {\vec {p}} \right|} \right)$, например квадратичный или линейный. Энергия Ферми задается плотностью свободных носителей n в бесконечных структурах, а не определяется. Число мод вдоль L вычисляется как число укладывающихся де-бройлевских длин волн ${h \mathord{\left/ {\vphantom {h {{{p}_{z}}}}} \right. \kern-0em} {{{p}_{z}}}}$. Считается, что уровни распределены равномерно с промежутком $\Delta {{p}_{z}} = {h \mathord{\left/ {\vphantom {h L}} \right. \kern-0em} L}$. Поэтому $N\left( {{{p}_{z}}} \right) = {{2L{{p}_{z}}} \mathord{\left/ {\vphantom {{2L{{p}_{z}}} h}} \right. \kern-0em} h}$, что характерно для 1-d проводников. Для 2-d проводников ${{\left| {\vec {p}} \right|}^{2}} = {{p}^{2}} = p_{x}^{2} + p_{z}^{2}$, и число мод получается делением площади круга на площадь одной моды: $N\left( p \right) = {{\pi {{p}^{2}}} \mathord{\left/ {\vphantom {{\pi {{p}^{2}}} {\left( {{L \mathord{\left/ {\vphantom {L h}} \right. \kern-0em} h}} \right)}}} \right. \kern-0em} {\left( {{L \mathord{\left/ {\vphantom {L h}} \right. \kern-0em} h}} \right)}}\left( {{t \mathord{\left/ {\vphantom {t h}} \right. \kern-0em} h}} \right)$. Для 3-d проводника делится объем в импульсном пространстве на объем, приходящийся на одну моду:
(25)
$N\left( p \right) = g\left( {{{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3}} \right){{{{p}^{3}}} \mathord{\left/ {\vphantom {{{{p}^{3}}} {\left( {{L \mathord{\left/ {\vphantom {L h}} \right. \kern-0em} h}} \right)}}} \right. \kern-0em} {\left( {{L \mathord{\left/ {\vphantom {L h}} \right. \kern-0em} h}} \right)}}{{\left( {{t \mathord{\left/ {\vphantom {t h}} \right. \kern-0em} h}} \right)} \mathord{\left/ {\vphantom {{\left( {{t \mathord{\left/ {\vphantom {t h}} \right. \kern-0em} h}} \right)} {\left( {{w \mathord{\left/ {\vphantom {w h}} \right. \kern-0em} h}} \right)}}} \right. \kern-0em} {\left( {{w \mathord{\left/ {\vphantom {w h}} \right. \kern-0em} h}} \right)}}.$Поскольку до этого спин не учитывался, здесь введен фактор вырождения по спину $g = 2$. Формула (25) не учитывает глубину потенциальной ямы и хорошо работает только для достаточно широких и глубоких ям, когда состояний много (точнее говоря, для вырожденного газа невзаимодействующих фермионов). Из нее для максимального импульса ${{p}_{{\text{F}}}}$, как обычно, получаем ${{E}_{{\text{F}}}} = \left( {{{{{\hbar }^{2}}} \mathord{\left/ {\vphantom {{{{\hbar }^{2}}} {2{{m}_{e}}}}} \right. \kern-0em} {2{{m}_{e}}}}} \right){{\left( {3{{\pi }^{2}}n} \right)}^{{2/3}}}.$ Для нанопроводов равномерность распределения уровней нарушается. Нужно решать задачу (23) желательно со сложным потенциалом с неплоским дном. Хотя функция (25) ступенчато зависит от размеров, при малых размерах она может плохо коррелировать с реальным числом уровней (рис. 4). Энергия (24) отсчитывается от дна бесконечно глубокой ямы и плохо определяет уровни вблизи края ямы конечной глубины. Если $ - {{E}_{n}}$ находится из (23), то функцию $N\left( p \right)$ следует определять как число уровней энергии, удовлетворяющих условию ${{E}_{n}} \leqslant {{{{p}^{2}}} \mathord{\left/ {\vphantom {{{{p}^{2}}} {\left( {2{{m}_{e}}} \right)}}} \right. \kern-0em} {\left( {2{{m}_{e}}} \right)}}.$
Рассмотрим медную нанопроволоку с размерами $t = w = 4d$, $L = 20d$, d = 0.3615 нм. Берем ${{W}_{0}} = 4.53$, ${{E}_{{\text{F}}}} = 7.04$ эВ. Потенциал ионизации иона меди ${{W}_{i}} = 20.29$ эВ. Глубину ямы с учетом смещения на ${{{{{\left( {\hbar \pi } \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {\hbar \pi } \right)}}^{2}}} {\left( {2{{m}_{e}}{{t}^{2}}} \right)}}} \right. \kern-0em} {\left( {2{{m}_{e}}{{t}^{2}}} \right)}}$ уровня ${{E}_{1}}$ определяем как ${{V}_{0}} = 11.83$ эВ. Согласно принципу равномерного распределения состояний в фазовом пространстве получаем ${{E}_{1}} = - 11.57$, тогда как минимизация функционала (23) по девяти базисным функциям (три по каждой из координат) дает ${{E}_{1}} = - 11.48$ эВ, а по 25 функциям ${{E}_{1}} = - 11.51$ эВ. Соответственно изменяются уровень Ферми и число мод. Число уровней определяет эффективную плазменную частоту ${{\omega }_{p}}$, которая используется в ДП металла $\tilde {\varepsilon }\left( \omega \right) = {{\varepsilon }_{L}} - {{\omega _{p}^{2}} \mathord{\left/ {\vphantom {{\omega _{p}^{2}} {\left( {{{\omega }^{2}} - i\omega {{\omega }_{c}}} \right)}}} \right. \kern-0em} {\left( {{{\omega }^{2}} - i\omega {{\omega }_{c}}} \right)}}$ для анализа волн в нанопроводах [1‒10] и колебаний локализованных плазмонов. Здесь ${{\varepsilon }_{L}}$ соответствует вкладу в ДП от кристаллической решетки и межзонных переходов. Для квантоворазмерных структур эффективная ${{\omega }_{p}}$ зависит от размеров и может существенно снизится.
Уравнение Шредингера (21) для мод в проводнике конечного поперечного сечения может быть записано по аналогии с уравнением для мод соответствующего диэлектрического волновода (ДВ) в следующем виде:
где ${{k}^{2}} = k_{0}^{2}\varepsilon \left( {x,y} \right) = 2{{m}_{e}}{{\left[ {E - V\left( {x,y} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {E - V\left( {x,y} \right)} \right]} {{{\hbar }^{2}}}}} \right. \kern-0em} {{{\hbar }^{2}}}}$, ${{k}_{0}}\, = \,{p \mathord{\left/ {\vphantom {p \hbar }} \right. \kern-0em} \hbar }\, = $ = ${{\sqrt {2{{m}_{e}}E} } \mathord{\left/ {\vphantom {{\sqrt {2{{m}_{e}}E} } \hbar }} \right. \kern-0em} \hbar }$. В ДВ $\varepsilon \left( {x,y} \right)$ ‒ неоднородная по поперечному сечению ДП, где $\varepsilon \left( {x,y} \right) = 1 - $ $ - \,\,{{V\left( {x,y} \right)} \mathord{\left/ {\vphantom {{V\left( {x,y} \right)} E}} \right. \kern-0em} E}$. Случаю $V \equiv 0$ соответствует свободное движение частицы $\Psi \left( {x,y,z} \right)$ ~ $\sim \exp \left( { - i\left( {{{k}_{x}}x + {{k}_{y}}y + {{k}_{z}}z} \right)} \right)$, $\left| {\vec {k}} \right| = k_{0}^{{}}$. Потенциалу $V > 0$ соответствует потенциальный барьер, причем для энергий, меньших 0 < E < $V\left( {x,y} \right)$, будет $\varepsilon \left( {x,y} \right) < 0$. Если $ - \,V\left( {x,y} \right) < E < 0$, то $0 < \varepsilon \left( {x,y} \right) < 1$. Электродинамический аналог для барьера – туннелирование волн сквозь плазменную структуру с отрицательной ДП. При $V < 0$ получаем потенциальную яму. Для энергий $V\left( {x,y} \right) < E < 0$ будет $\varepsilon \left( {x,y} \right) > 1$. Здесь электродинамический аналог – распространение собственных мод в ДВ. Отличие электродинамической задачи в том, что она векторная, и в том, что она может быть несамосопряженной (для вытекающих мод, а также при наличии диссипации, т.е. для комплексной ДП $\varepsilon $). Соответственно, надо искать решения для ${{E}_{z}}$ и ${{H}_{z}}$ в случае разделения мод, или более сложные задачи с тензорной ФГ для гибридных мод [77, 78]. Решение задачи (26) ищем в виде $\Psi \left( {x,y,z} \right) = \exp \left( { - i{{k}_{z}}z} \right)\Phi \left( {x,y} \right)$, что приводит к УШ
(27)
$\left[ {\nabla _{{x,y}}^{2} + k_{\tau }^{2}} \right]\Phi \left( {x,y} \right) = k_{\tau }^{2}\left( {1 - \varepsilon \left( {x,y} \right)} \right)\Phi \left( {x,y} \right),$где ${{k}_{\tau }} = \sqrt {k_{0}^{2} - k_{z}^{2}} $ ‒ искомое поперечное волновое число. Решение (27) можно записать через функцию Грина (ФГ)
(28)
$\begin{gathered} \Phi \left( {x,y} \right) = \\ = k_{\tau }^{2}\int\limits_S {G\left( {x,\left. y \right|x{\kern 1pt} ',y{\kern 1pt} '} \right)\left( {\varepsilon \left( {x{\kern 1pt} ',y{\kern 1pt} '} \right) - 1} \right)\Phi \left( {x{\kern 1pt} ',y{\kern 1pt} '} \right)dx{\kern 1pt} 'dy{\kern 1pt} '} . \\ \end{gathered} $Здесь ФГ выражается через функцию Ганкеля
а интегрирование ведется по области S поперечного сечения, определяемой из условия V(x, y) < 0. На самом деле это не решение задачи, а ИУ для $\Phi \left( {x,y} \right)$, поскольку волновая функция входит в правую часть под интеграл. Интегральное уравнение (28) удобно тем, что может быть сведено к конечной области, если взять яму конечных размеров. Ему соответствует квадратичный функционал
(29)
$\begin{gathered} \Lambda \left( \Phi \right) = \int\limits_\Omega {{{\Phi }^{2}}\left( {x,y} \right)dxdy} - k_{\tau }^{2}\int\limits_\Omega {\int\limits_\Omega {\Phi \left( {x,y} \right)} G\left( {x,\left. y \right|x{\kern 1pt} ',y{\kern 1pt} '} \right)\left( {\varepsilon \left( {x{\kern 1pt} ',y{\kern 1pt} '} \right) - 1} \right) \times } \\ \times \,\,\Phi \left( {x{\kern 1pt} ',y{\kern 1pt} '} \right)dx{\kern 1pt} 'dy{\kern 1pt} 'dxdy, \\ \end{gathered} $а также и функционал
(30)
$k_{\tau }^{2} = \frac{{\int\limits_\Omega {{{\Phi }^{2}}\left( {x,y} \right)dxdy} }}{{\int\limits_\Omega {\int\limits_\Omega {\Phi \left( {x,y} \right)} G\left( {x,\left. y \right|x{\kern 1pt} ',y{\kern 1pt} '} \right)\left( {\varepsilon \left( {x{\kern 1pt} ',y{\kern 1pt} '} \right) - 1} \right)\Phi \left( {x{\kern 1pt} ',y{\kern 1pt} '} \right)dx{\kern 1pt} 'dy{\kern 1pt} 'dxdy} }}.$Последний позволяет итерационно определять собственную энергию, но совместно с итерационным решением ИУ (28) для собственных функций [77], поскольку параметр ${{k}_{\tau }}$ входит в правую часть (30) нелинейно. При этом можно вводить множители Лагранжа с соответствующими условиями ортогональности собственных функций. Решение задачи о прямоугольном ДВ на основе такого подхода было выполнено в работах [77, 78]. По своей форме ИУ (28) сходно с уравнением метода возмущений. Однако брать волновые функции $\exp \left( { - i{{k}_{x}}x - i{{k}_{y}}y} \right)$ для невозмущенной задачи о свободной частице c $V = 0$ невыгодно. Удобно брать волновые функции типа (22), определенные в конечной области. Тогда метод последовательных приближений для ИУ (28) определяет волновую функцию уже вне ямы, т.е. позволяет определить вероятность обнаружения частицы во всей области, хотя интегрирование проводится только по области $S$ (для трехмерной задачи – в $\Omega $). Такой подход более предпочтителен, чем на основе (23). Для ДВ он позволяет определять комплексные моды [77]. Для определения действительных значений энергии удобнее искать экстремум (29) $\delta \Lambda \left( \Phi \right) = 0$.
5. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ ПРОВОЛОЧНОГО ВОЛНОВОДА
На рис. 5 представлены результаты вычисления дисперсии моды H11 волновода в виде изолированного металлического бруса прямоугольной формы ($w = t$). Впервые возможность распространения волны вдоль одиночного металлического провода рассмотрел А. Зоммерфельд [79, 80]. Это известная втекающая медленная поверхностная волна Зоммерфельда–Ценнека. При очень высоких оптических частотах, когда металл по свойствам становится близок к диэлектрику, она переходит в основную HE11-волну ДВ (см. [77, 80]). Для круглого волновода и проволочного фотонного кристалла волна рассчитана в [10]. Соответствующая волна Ценнека над проводящей полуплоскостью быстрая. Простейший метод расчета в тонком проводнике состоит в возбуждении пространства осевым током с помощью ФГ и наложение импедансных условий на поверхности. Будем придерживаться более строгого метrода объемного ИУ [10, 77], заключающегося в том, что возбуждение происходит за счет тока поляризации
Рис. 5.
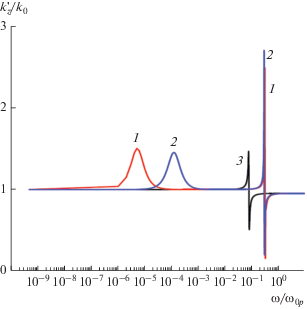
Замедление $n_{z}^{'} = {{k_{z}^{'}} \mathord{\left/ {\vphantom {{k_{z}^{'}} {{{k}_{0}}}}} \right. \kern-0em} {{{k}_{0}}}}$ (штрих означает реальную часть) для квадратного медного провода для $t = 500$ (1), 100 (2) и 5 нм (3).
В нашем случае в силу представления $\vec {E}\left( {\vec {r}} \right) = $ $ = \vec {E}\left( {{{{\vec {r}}}_{\tau }}} \right)\exp \left( { - i{{k}_{z}}z} \right)$ получается двумерное объемное ИУ, т.е. уравнение на поперечном сечении S:
(31)
$\begin{gathered} \vec {E}\left( {{{{\vec {r}}}_{\tau }}} \right) = \left( {\tilde {\varepsilon }\left( \omega \right) - 1} \right)\frac{{\left( {{{\nabla }_{\tau }}{{\nabla }_{\tau }} \cdot + \,\,k_{\tau }^{2}} \right)}}{{4i}} \times \\ \times \,\,\iint\limits_S {H_{0}^{{\left( 2 \right)}}\left( {{{k}_{\tau }}\left| {{{{\vec {r}}}_{\tau }} - \vec {r}_{\tau }^{'}} \right|} \right)}\vec {E}\left( {\vec {r}_{\tau }^{'}} \right)dS{\kern 1pt} '. \\ \end{gathered} $Пусть $N\left( {w,t} \right)$ ‒ число уровней энергии в соответствующей потенциальной яме для двумерного УШ. Оно соответствует случаю, когда длина проводника бесконечно большая, и от соответствующей ей координаты зависимости нет. Определение $N\left( {w,t} \right)$ требует решения задачи квантовой механики, но приближенно можно взять $N\left( {t,t} \right) \approx {{{{E}_{{\text{F}}}}{{m}_{e}}{{t}^{2}}} \mathord{\left/ {\vphantom {{{{E}_{{\text{F}}}}{{m}_{e}}{{t}^{2}}} {\left( {{{\hbar }^{2}}{{\pi }^{2}}} \right)}}} \right. \kern-0em} {\left( {{{\hbar }^{2}}{{\pi }^{2}}} \right)}}$. В яме конечной длины величина ${{N}_{z}} = {{2L{{p}_{z}}} \mathord{\left/ {\vphantom {{2L{{p}_{z}}} h}} \right. \kern-0em} h}$ есть число состояний на длине L в области импульсов $\left( {0,{{p}_{z}}} \right)$. Уровень ${{E}_{k}}$ расщепляется на ${{n}_{k}}$ подуровней в силу зависимости ${{E}_{k}} = {{E}_{{k - 1}}} + {{p_{{z{{n}_{k}}}}^{2}} \mathord{\left/ {\vphantom {{p_{{z{{n}_{k}}}}^{2}} {\left( {2{{m}_{e}}} \right)}}} \right. \kern-0em} {\left( {2{{m}_{e}}} \right)}} \leqslant {{E}_{{\text{F}}}}$. Здесь ${{E}_{0}} = - {{V}_{0}}$. Поэтому ${{n}_{k}} = 2L{{\sqrt {2{{m}_{e}}\left( {{{E}_{k}} - {{E}_{{k - 1}}}} \right)} } \mathord{\left/ {\vphantom {{\sqrt {2{{m}_{e}}\left( {{{E}_{k}} - {{E}_{{k - 1}}}} \right)} } h}} \right. \kern-0em} h}$. В широкой яме уровни близки, и поэтому можно считать ${{E}_{{\text{F}}}} \approx {{E}_{N}}$, поскольку ${{E}_{N}} = {{E}_{{N - 1}}} + {{p_{{z{{n}_{N}}}}^{2}} \mathord{\left/ {\vphantom {{p_{{z{{n}_{N}}}}^{2}} {\left( {2{{m}_{e}}} \right)}}} \right. \kern-0em} {\left( {2{{m}_{e}}} \right)}} \leqslant {{E}_{{\text{F}}}}$. Число электронов проводимости в единице объема проводника есть
(32)
$n = \sum\limits_{k = 1}^N {{{n}_{k}}} = \frac{4}{{twh}}\sum\limits_{k = 1}^N {\sqrt {2{{m}_{e}}\left( {{{E}_{k}} - {{E}_{{k - 1}}}} \right)} } .$Поэтому в $\tilde {\varepsilon }\left( \omega \right)$ следует брать плазменную частоту ${{\omega }_{p}} = \sqrt {{{n{{e}^{2}}} \mathord{\left/ {\vphantom {{n{{e}^{2}}} {\left( {{{\varepsilon }_{0}}{{m}_{e}}} \right)}}} \right. \kern-0em} {\left( {{{\varepsilon }_{0}}{{m}_{e}}} \right)}}} $ со значением n из (32). Для квантовой точки с малым размером L следует рассматривать трехмерную яму с числом уровней $N\left( {t,w,L} \right)$ и определять $n = 2N\left( {t,w,L} \right)$. В случае нескольких атомов в структуре квантовой точки более точный подход может быть основан на более точном определении уровней, например методом сильной связи [71, 76].
Уравнение (31) является гиперсингулярным ИУ. Для его решения образуем билинейный функционал
(33)
$\begin{gathered} \Lambda \left( {\tilde {\vec {E}},\vec {E}} \right) = 4i\iint\limits_S {\tilde {\vec {E}}{\text{*}}\left( {{{{\vec {r}}}_{\tau }}} \right)\vec {E}\left( {{{{\vec {r}}}_{\tau }}} \right)dS} - \left( {\tilde {\varepsilon }\left( \omega \right) - 1} \right) \times \\ \times \,\,\iint\limits_S {\tilde {\vec {E}}{\text{*}}\left( {{{{\vec {r}}}_{\tau }}} \right)}\left( {{{\nabla }_{\tau }}{{\nabla }_{\tau }} \cdot + k_{\tau }^{2}} \right)\iint\limits_S {H_{0}^{{\left( 2 \right)}}\left( {{{k}_{\tau }}\left| {{{{\vec {r}}}_{\tau }} - \vec {r}_{\tau }^{'}} \right|} \right)}\vec {E}\left( {\vec {r}_{\tau }^{'}} \right)dS{\kern 1pt} '. \\ \end{gathered} $Методы понижения порядка сингулярности для ИУ типа (31) получены в ряде работ и приведены в [77]. В качестве $\tilde {\vec {E}}\left( {{{{\vec {r}}}_{\tau }}} \right)$ возьмем разложение по модам прямоугольного волновода, касательные компоненты которых обращаются в нуль на контуре поперечного сечения S. Перенесем действие оператора ${{\nabla }_{\tau }}$ на $\tilde {\vec {E}}$, что уменьшает сингулярность ядра, при этом контурные интегралы не возникают. Поскольку внутри провода $\nabla \cdot \vec {E}\left( {{{{\vec {r}}}_{\tau }}} \right)\exp \left( { - i{{k}_{z}}z} \right)$ = $ = {{\nabla }_{\tau }} \cdot {{\vec {E}}_{\tau }}\left( {{{{\vec {r}}}_{\tau }}} \right) - i{{k}_{z}}{{E}_{z}}\left( {{{{\vec {r}}}_{\tau }}} \right) = 0$ и $\nabla _{\tau }^{2}{{\vec {E}}_{\tau }}\left( {{{{\vec {r}}}_{\tau }}} \right)\, + \,k_{{\tau \tilde {\varepsilon }}}^{2}{{\vec {E}}_{\tau }}\left( {{{{\vec {r}}}_{\tau }}} \right)\, = $ = 0, ${{k}_{{\tau \tilde {\varepsilon }}}} = \sqrt {k_{0}^{2}\tilde {\varepsilon } - k_{z}^{2}} $, где ${{k}_{{\tau \tilde {\varepsilon }}}}$ ‒ поперечное волновое число в металле, то снижается число коэффициентов в представлении поля. Функции, по которым будем разлагать поле, представим так [77]:
где ${{A}_{1}} = {{i{{C}_{1}}{{k}_{z}}\alpha } \mathord{\left/ {\vphantom {{i{{C}_{1}}{{k}_{z}}\alpha } {k_{{\tau \tilde {\varepsilon }}}^{2}}}} \right. \kern-0em} {k_{{\tau \tilde {\varepsilon }}}^{2}}},$ ${{A}_{2}} = {{ - i{{C}_{2}}{{k}_{z}}\alpha } \mathord{\left/ {\vphantom {{ - i{{C}_{2}}{{k}_{z}}\alpha } {k_{{\tau \tilde {\varepsilon }}}^{2}}}} \right. \kern-0em} {k_{{\tau \tilde {\varepsilon }}}^{2}}}$, B1 = $ = {{i{{C}_{1}}{{k}_{z}}\beta } \mathord{\left/ {\vphantom {{i{{C}_{1}}{{k}_{z}}\beta } {k_{{\tau \tilde {\varepsilon }}}^{2}}}} \right. \kern-0em} {k_{{\tau \tilde {\varepsilon }}}^{2}}}$, ${{B}_{2}} = {{ - i{{C}_{2}}{{k}_{z}}\beta } \mathord{\left/ {\vphantom {{ - i{{C}_{2}}{{k}_{z}}\beta } {k_{{\tau \tilde {\varepsilon }}}^{2}}}} \right. \kern-0em} {k_{{\tau \tilde {\varepsilon }}}^{2}}}$, ${{A}_{3}} = {{i{{C}_{3}}{{k}_{z}}\alpha } \mathord{\left/ {\vphantom {{i{{C}_{3}}{{k}_{z}}\alpha } {k_{{\tau \tilde {\varepsilon }}}^{2}}}} \right. \kern-0em} {k_{{\tau \tilde {\varepsilon }}}^{2}}}$, ${{A}_{4}} = {{ - i{{C}_{4}}{{k}_{z}}\alpha } \mathord{\left/ {\vphantom {{ - i{{C}_{4}}{{k}_{z}}\alpha } {\left( {k_{\tau }^{2}\tilde {\varepsilon }} \right)}}} \right. \kern-0em} {\left( {k_{\tau }^{2}\tilde {\varepsilon }} \right)}}$, ${{B}_{3}} = {{ - i{{C}_{3}}{{k}_{z}}\beta } \mathord{\left/ {\vphantom {{ - i{{C}_{3}}{{k}_{z}}\beta } {k_{{\tau \tilde {\varepsilon }}}^{2}}}} \right. \kern-0em} {k_{{\tau \tilde {\varepsilon }}}^{2}}}$, B4 = $ = {{i{{C}_{4}}{{k}_{z}}\beta } \mathord{\left/ {\vphantom {{i{{C}_{4}}{{k}_{z}}\beta } {k_{{\tau \tilde {\varepsilon }}}^{2}}}} \right. \kern-0em} {k_{{\tau \tilde {\varepsilon }}}^{2}}}$, при этом ${{\alpha }^{2}} + {{\beta }^{2}} = k_{{\tau \tilde {\varepsilon }}}^{2} = k_{0}^{2}\tilde {\varepsilon } - k_{z}^{2}$. Для собственных мод ДВ без диссипации $k_{{\tau \tilde {\varepsilon }}}^{2} > 0$ и $k_{\tau }^{2} < 0$. Такая мода медленная: ${{k}_{z}} > {{k}_{0}}$, а величины $\alpha $ и $\beta $ действительные. При понижении частоты мода может стать несобственной быстрой вытекающей. Для металлического провода все поперечные волновые числа, включая $\alpha $ и $\beta $, комплексные. Для квадратного провода $\alpha = \beta = \sqrt {{{\left( {k_{0}^{2}\tilde {\varepsilon } - k_{z}^{2}} \right)} \mathord{\left/ {\vphantom {{\left( {k_{0}^{2}\tilde {\varepsilon } - k_{z}^{2}} \right)} 2}} \right. \kern-0em} 2}} $. На самом деле моды волновода гибридные, т.е. следует учесть электрическое поле, возбуждаемое компонентой ${{H}_{z}}$. Ее запишем в двух видах:
Электрическое поле, соответствующее ${{H}_{z}}$, представляется так:
Здесь ${{Z}_{0}} = 120\pi $ Ом. В силу симметрии все моды удобно классифицировать как четные-нечетные относительно x и y порознь для компонент ${{E}_{z}}$ или Hz [77]. Однако традиционная классификация рассматривает гибридные EH- и HE-моды. Основная мода ДВ без низкочастотной отсечки – это HE11-мода, где индексы соответствуют числу вариаций поля вдоль осей: $\alpha \approx {{{{m}_{x}}\pi } \mathord{\left/ {\vphantom {{{{m}_{x}}\pi } t}} \right. \kern-0em} t}$, $\beta \approx {{{{m}_{y}}\pi } \mathord{\left/ {\vphantom {{{{m}_{y}}\pi } w}} \right. \kern-0em} w}$. В ДВ ${{m}_{x}}$ и ${{m}_{y}}$ не целые и приближаются к таковым значениям только при высоких частотах [77]. В металлическом проводе эти параметры не только не целые, а даже комплексные, поэтому волна экспоненциально затухает к его центру. Это так, если глубина проникновения δ значительно меньше размеров, при этом существенен поверхностный импеданс. Если δ намного больше поперечных размеров, ${\text{то}}$ поле внутри провода почти не изменяется. Этот случай соответствует тому, что имеются только основные волны, различающиеся поляризацией. Пусть $w \gg t$, тогда $\left| \alpha \right| \gg \left| \beta \right|$. Такая HE-мода описывается коэффициентами ${{C}_{3}}$, ${{D}_{3}}$. Для нее $\left| {{{E}_{x}}} \right| \ll \left| {{{E}_{y}}} \right|$ и $\left| {{{В}_{3}}} \right| < \left| {{{D}_{3}}} \right|$, т.е. мода в основном определяется через компоненту Hz(x, y) = $ = {{D}_{3}}\sin \left( {\alpha x} \right)\cos \left( {\beta y} \right)$, а влиянием ${{E}_{z}}$ можно пренебречь. При стремлении частоты к нулю все продольные компоненты стремятся к нулю, и мода становится близка по структуре к плоской волне, идущей со скоростью света. Если $w = t$, имеем четырехкратное поляризационное вырождение. Поперечное волновое число в вакууме удобно определять из функционала совместно с решением ИУ (31):
(34)
$k_{\tau }^{2} = \frac{{4i\iint\limits_S {\tilde {\vec {E}}{\text{*}}\left( {{{{\vec {r}}}_{\tau }}} \right)\vec {E}\left( {{{{\vec {r}}}_{\tau }}} \right)dS - \left( {\tilde {\varepsilon }\left( \omega \right) - 1} \right)\iint\limits_S {\iint\limits_S {{{\nabla }_{\tau }} \cdot \tilde {\vec {E}}{\text{*}}\left( {{{{\vec {r}}}_{\tau }}} \right)\left[ {{{\nabla }_{\tau }}H_{0}^{{\left( 2 \right)}}\left( {{{k}_{\tau }}\left| {{{{\vec {r}}}_{\tau }} - \vec {r}_{\tau }^{'}} \right|} \right) \cdot \vec {E}\left( {\vec {r}_{\tau }^{'}} \right)} \right]dS{\kern 1pt} 'dS}}}}}{{\left( {\tilde {\varepsilon }\left( \omega \right) - 1} \right)\iint\limits_S {\iint\limits_S {\tilde {\vec {E}}{\text{*}}\left( {{{{\vec {r}}}_{\tau }}} \right)H_{0}^{{\left( 2 \right)}}\left( {{{k}_{\tau }}\left| {{{{\vec {r}}}_{\tau }} - \vec {r}_{\tau }^{'}} \right|} \right)}\vec {E}\left( {\vec {r}_{\tau }^{'}} \right)dS{\kern 1pt} '}}}.$Функционал (34) упрощается, если $\tilde {\vec {E}}{\text{*}}\left( {{{{\vec {r}}}_{\tau }}} \right)$ ‒ поперечные функции H-мод полого прямоугольного волновода. В этом случае ${{\nabla }_{\tau }} \cdot \tilde {\vec {E}}{\text{*}}\left( {{{{\vec {r}}}_{\tau }}} \right) = 0$. Тогда для определения моды HE11 достаточно двух мод. Для моды квадратного провода α = β = $ = \sqrt {{{\left( {k_{\tau }^{2} + k_{0}^{2}\left( {\tilde {\varepsilon } - 1} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {k_{\tau }^{2} + k_{0}^{2}\left( {\tilde {\varepsilon } - 1} \right)} \right)} 2}} \right. \kern-0em} 2}} $, поэтому (34) становится дисперсионным уравнением. Его решение приведено на рис. 5. Для толстого провода берем плазменную частоту меди ${{\omega }_{{0p}}} = 2.14 \times {{10}^{{16}}}$. Для медного провода с $w = t = 100$ нм ${{\omega }_{p}} = 2.0 \times $ × 1016 ГГц, что практически совпадает с ${{\omega }_{{0p}}}$. Для провода с $w = t = 5$ нм оценка дает $N\left( {t,t} \right) \approx 250$, n ≈ $ \approx 2{{\left( {N\, + \,\sqrt {{N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0em} 2}} } \right)} \mathord{\left/ {\vphantom {{\left( {N\, + \,\sqrt {{N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0em} 2}} } \right)} {{{t}^{3}}}}} \right. \kern-0em} {{{t}^{3}}}}\, = \,4.2\, \times \,{{10}^{{27}}}\,{{{\text{м}}}^{3}},$ ${{\omega }_{p}}\, = \,5.35 \times {{10}^{{15}}}\,{\text{Гц}}{\text{.}}$ В обоих случаях взято ${{\omega }_{с}} = 7.0 \times {{10}^{{13}}}$, ${{\varepsilon }_{L}} = 10$. На сверхнизких частотах глубина проникновения $\delta $ много больше размеров проволоки, которая является слабо направляющей структурой. Волна идет практически со скоростью света, но чуть медленнее и немного втекает (малая часть энергии идет в проводе, а большая часть энергии распространяется в вакууме). Медленность обусловлена конечностью поперечного сечения. Волна HE11 вырождается в волну H11, для которой приближенно можно написать дисперсионное уравнение $\alpha k_{\tau }^{2} \times $ $ \times \,\,\left( {{{\alpha }^{2}} - {{{\left( {{\pi \mathord{\left/ {\vphantom {\pi t}} \right. \kern-0em} t}} \right)}}^{2}}} \right)\left( {\tilde {\varepsilon }\left( \omega \right) - 1} \right)$$I\left( {{{k}_{\tau }}} \right) = \pi \sin \left( {\alpha t} \right)$, где обозначено
Для провода в низкочастотном пределе EH-волны также трансформируются в E-волны, которые также переходят в плоскую волну. С ростом частоты уменьшается глубина проникновения $\delta $ и замедление растет, достигая максимума при $\delta \sim t$ (если размер не слишком мал). Далее существенен импедансный характер структуры и уменьшение скин-слоя, приводящие к уменьшению втекания и снижению замедления с частотой. Но в области плазмонного резонанса ${{\tilde {\omega }}_{p}} = {{{{\omega }_{p}}} \mathord{\left/ {\vphantom {{{{\omega }_{p}}} {\sqrt {{{\varepsilon }_{L}} + 1} }}} \right. \kern-0em} {\sqrt {{{\varepsilon }_{L}} + 1} }}$ замедление опять растет, возникает медленный поверхностный плазмон, переходящий в области выше плазменной частоты в моду ДВ. Отсутствие низкочастотных отсечек по сравнению с идеальным ДВ связано с комплексной ДП металла.
ЗАКЛЮЧЕНИЕ
В рамках модели ЛДЛ получены простые соотношения для баллистического транспорта в проводниках малых, но конечных размеров, позволяющие использовать импедансный подход на относительно низких частотах с учетом поперечных размеров. Для высокочастотного электродинамического моделирования наноразмерных проволочных и пленочных металлических структур следует учитывать зависимость числа мод проводимости, плотности состояний и плазменной частоты от размеров, при этом поверхностная проводимость становится зависимой от размеров структуры.
Изменение плазменной частоты может существенно повлиять на анализ плазмонов в наноструктурах. Физически объяснить изменение плазменной частоты и проводимости можно путем усиления влияния связанных состояний на поверхности и изменением условий связи в атомах в структуре малых размеров. Строгая оценка указанных эффектов должна быть основана на строгом решении задач квантовой механики. При размерах $t = w > 18$ нм проводимость медного нанопровода выше, чем многослойной структуры аналогичной толщины из графеновых нанолент или углеродных нанотрубок [53], поэтому использование металлических структур весьма перспективно.
Предложены простые виды конфигурации потенциалов в проводниках и соответствующие функционалы для УШ, позволяющие приближенно и точно оценивать число энергетических уровней и мод проводимости. Для квантоворазмерных наноструктур простые приближенные оценки могут существенно расходится с точными значениями.
Список литературы
Belov P.A., Marques R., Maslovski S.I. et al. // Phys. Rev. B. 2003. V. 63. № 11. P. 113103.
Nefedov I.S., Viitanen A.J., Tretyakov S.A. // Phys. Rev. E. 2005. V. 71. № 4. P. 046612.
Nefedov I.S., Viitanen A.J. // Metamaterials Handbook: Theory and Phenomena of Metamaterials / Ed. F. Gapolino. Boca Raton; CRC Press, 2009. P. 1.
Nefedov I.S. // Phys. Rev. B. 2010. V. 82. № 15. P. 155423.
Nefedov I., Tretyakov S. // Phys. Rev. B. 2011. V. 84. P. 113410.
Nefedov I.S., Simovski C.R. // Phys. Rev. B. 2011. V. 84. P. 195459.
Nefedov I.S., Tretyakov S.A. // Photonics and Nanostructures – Fundamentals and Applications. 2011. V. 9. P. 374.
Liberal I., Nefedov I.S., Ederra I. et al. // J. Appl. Phys. 2011. V. 110. P. 104902.
Silveirinha M.G., Fernandes C.A. // IEEE Trans. 2005. V. MTT-53. V. 4. P. 1418.
Давидович М.В., Нефедов И.С. // ЖЭТФ. 2014. V. 145. № 5. P. 771.
Давидович М.В., Стефюк Ю.В., Шиловский П.А. // ЖТФ. 2012. V. 82. V. 3. P. 7.
Давидович М.В., Шиловский П.А. // ЖТФ. 2012. V. 82. № 12. P. 79.
Guo Y., Newman W., Cortes C.L., Jacob Z. // Adv. Optoelectron. 2012. V. 452502. P. 1.
Shekhar P., Atkinson J., Jacob Z. // Nano Convergence. 2014. V. 1. P. 1.
Vinogradov A.P., Ignatov A.I., Merzlikin A.M. et al. // Opt. Express. 2011. V. 19. № 7. P. 6699.
Zapata-Rodríguez C.J., Miret J.J., Vuković S., Belić M.R. // Opt. Express. 2013. V. 21. № 16. P. 19113.
Nefedov I.S., Valagiannopoulos C.A., Melnikov L. // J. Optics. 2013. V. 15. P. 114003.
Mikhailov S.A., Ziegler K. // Phys. Rev. Lett. 2007. V. 99. № 1. P. 016803.
Lemme M.C., Echtermeyer T.J., Baus M., Kurz H. // IEEE Electron. Devic. Lett. 2007. V. 28. № 4. P. 282.
Chen Z., Lin Yu-M., Rooks M.J., Avouris P. // Physica E: Low-dimensional Systems and Nanostructures. 2007. V. 40. № 2. P. 213.
Свинцов Д.А., Вьюрков В.В., Лукичёв В.Ф. и др. // ФТП. 2013. V. 47. № 2. P. 244.
Landauer R. // IBM J. Research and Development. 1957. V. 1. № 3. P. 223.
Landauer R. // Philos. Mag. 1970. V. 21. P. 863.
Landauer R. // J. Mathem. Phys. 1996. V. 37. № 10. P. 5259.
Datta S. Electronic Transport in Mesoscopic Systems. Cambridge: Cambridge Univ. Press, 2001.
Datta S. Quantum Transport: Atom to Transistor. Cambridge: Cambridge Univ. Press, 2005.
Datta S. Lessons from Nanoelectronics: A New Perspective on Transport. Hackensack: World Sci. Publ. Company, 2012.
Lundstrom M., Jeong C. Near-Equilibrium Transport: Fundamentals and Applications. Hackensack: World Sci. Publ. Company, 2013.
Kruglyak Yu.A. // Nanosystems, Nanomaterials, Nanotechnologies. 2013. V. 11. P. 519.
Kruglyak Yu. // J. Nanosci. 2014. Article ID 725420. P. 1.
Lovat G., Hanson G.W., Araneo R., Burghignoli P. // Phys. Rev. B. 2013. V. 87. № 11. P. 115429.
Fuchs K. // Proc. Cambridge Philos. Soc. 1938. V. 34. P. 100.
Sondheimer E.H. // Adv. Phys. 1952. V. 1. № 1. P. 1.
Mayadas A.F., Shatzkes M. // Phys. Rev. B. 1970. V. 1. № 4. P. 1382.
Tellier C.R., Tosser A.J. Size Effects in Thin Films. Amsterdam: Elsevier Sci. Publ. Com., 1982.
Warkusz F. // Prog. Surf. Sci. 1980. V. 10. № 3. P. 287.
Namba Y. // Jpn. J. Appl. Phys. 1970. V. 9. P. 1326.
Munoz R.C., Finger R., Arenas C. et al. // Phys. Rev. B. 2002. V. 66. № 20. P. 205401.
Feibelman P.J. // Phys. Rev. B. 1983. V. 27. № 4. P. 1991.
Boettger J.C., Trickey S.B. // Phys. Rev. B. 1992. V. 45. № 3. P. 1363.
Kurbatsky V.P., Pogosov V.V. // Vacuum. 2004. V. 74. P. 185.
Caндoмиpcкий B.Б. // PЭ. 1967. T. 12. № 1. C. 158.
Лифшиц И.М., Косевич А.М. // Изв. АН СССР. Сер. физ. 1955. Т. 19. № 4. С. 395.
Огрин Ю.Ф., Луцкий В.Н., Елинсон М.И. // Письма в ЖЭТФ. 1966. Т. 3. № 3. С. 114.
Tanachutiwat S., Wang W. // Third Int. ICST Conf. NanoNet 2008. Boston, 2008. P. 49.
Munoz R., Arenas C., Kremer G., Moraga L. // J. Phys. Condens. Matter. 2003. V. 15. № 3. P. 177.
Hoffman H., Fisher G. // Thin Solid Films. 1976. V. 36. P. 25.
Fisher G., Hoffman H. // Solid State Commun. 1980. V. 35. № 10. P. 793.
Fisher G., Hoffman H. // Z. Phys. B: Condens. Matter. 1980. V. 39. № 4. P. 287.
Stasyuk Z.V. // J. Phys. Studies. 1999. V. 3. № 1. P. 102.
Бигун Р.И., Стасюк З.В., Барабаш М.Ю., Куницкий Ю.А. // Химия, физика и технология поверхности. 2010. Т. 1. № 2. С. 128.
Kruglyak Yu.A. // Sci. J. “ScienceRise”. 2015. V. 2/2. № 7. P. 77.
Ragheb T., Massoud Y. // Proc. IEEE/ACM Int. Conf. on Computer-Aided Design (ICCAD 2008). 2008. P. 593.
Hanson G.W. // J. Appl. Phys. 2008. V. 103. P. 064302.
Slepyan G.Ya., Maksimenko S.A., Lakhtakia L. et al. // Phys. Rev. B. 1999. V. 60. № 24. P. 17136.
Falkovsky L.A., Pershoguba S.S. // Phys. Rev. B. 2007. V. 76. № 15. P. 153410.
Tešanović Z., Jarić M., Maekawa S. // Phys. Rev. Lett. 1986. V. 57. № 21. C. 2760.
Tesanovic Z. // J. Phys. C: Solid State Phys. 1987. V. 20. № 6. P. 829.
Trivedi N., Ashcroft N.W. // Phys. Rev. B. 1988. V. 38. № 17. P. 12298.
Fishman G., Calecki D. // Phys. Rev. Lett. 1989. V. 62. № 11. P. 1302.
Sheng L., Xing D.Y., Wang Z.D. // Phys. Rev. B. 1995. V. 51. № 11. P. 7325.
Munoz R., Vidal G., Kremer G. et al. // J. Phys. Condens. Matter. 1999. V. 11. № 26. P. 299.
Makarov N.M., Moroz A.V., Yampolskii V.A. // Phys. Rev. B. 1995. V. 52. № 8. P. 6087.
Makarov N.M., Tarasov Yu.V. // Phys. Rev. B. 2001. V. 64. № 23. P. 235306.
Izrailev F.M., Makarov N.M., Rendon M. // Phys. Rev. B. 2005. V. 72. № 4. P. 041403.
Meyerovich A.E., Ponamarev I.V. // Phys. Rev. B. 2002. V. 65. P. 155413.
Meyerovich A.E., Stepaniants S. // Phys. Rev. Lett. 1994. V. 73. P. 316.
Meyerovich A.E., Cheng Y. // Phys. Rev. B. 2006. V. 73. № 8. P. 085404.
Renteria J.D., Nika D.L., Balandin A.A. // Appl. Sci. 2014. V. 4. P. 525.
Иванченко Г.С., Невзорова Ю.В. // Вестн. Волгогр. гос. ун-та. Сер. 1. Мат. Физ. 2011. Т. 2. № 15. С. 133.
Nakada K., Fujita M. // Phys. Rev. B. 1996. V. 54. № 24. P. 17954.
Ландау Л.Д., Лифшиц Е.М. Квантовая механика. Нерелятивистская теория. М.: Физматлит, 1963.
Давидович М.В., Яфаров Р.К., Доронин Д.М. // Труды 20-й Междунар. Крымской конф. СВЧ-техника и телекоммуникационные технологии (CriMiKo’2010). Севастополь, 2010. С. 733.
Davidovich M.V., Bushuev N.A., Yafarov R.K. // 2014 Tenth Int. Vacuum Electron Sources Conf. and Second Int. Conf. on Emission Electronics, Saint-Petersburg, 2014. P. 67.
Тамм Е.И., Блохинцев Д.И. // ЖЭТФ. 1993. V. 3. № 2. С. 77.
Tran N.T.T., Lin S.Y., Lin M.F., Glukhova O.E. // J. Phys. Chem. 2015. V. 119. № 19. C. 10623.
Давидович М.В. Итерационные методы решения задач электродинамики. Саратов: Изд-во Сарат. ун-та, 2014.
Davidovich M.V. // Proc. Int. Conf. Transparent Optical Networks. Kielce, 1999. P. 181.
Sommerfeld A. // Annal. Phys. 1899. V. 303. № 2. P. 233.
Давидович М.В. Втекающие и вытекающие несобственные моды ‒ анализ диссипативных дисперсионных уравнений и волна Ценнека. Саратов: Изд-во Сарат. ун-та, 2014.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


