Радиотехника и электроника, 2021, T. 66, № 8, стр. 798-804
Синтез алгоритма оценивания искажений сигнала в приемнике прямого преобразования на основе комбинирования регуляризующей процедуры и метода нелинейной фильтрации
Н. Е. Поборчая *
Московский технический университет связи и информатики
111024 Москва, ул. Авиамоторная, 8а, Российская Федерация
* E-mail: n.poborchaya@mail.ru
Поступила в редакцию 17.12.2020
После доработки 04.02.2021
Принята к публикации 19.04.2021
Аннотация
Рассмотрен синтез нелинейного алгоритма совместного оценивания параметров сигнала в условиях априорной неопределенности относительно законов распределения шумов с использованием теории регуляризации и метода нелинейной фильтрации в скользящем временном окне постоянной длины. Показано, что помехоустойчивость предложенного алгоритма выше, чем у нелинейной фильтрации, а также что он обладает вычислительной сложностью меньше, чем известная процедура совместного оценивания, и позволяет в некоторых случаях сократить количество арифметических операций по сравнению с регуляризующим алгоритмом.
1. ПОСТАНОВКА ЗАДАЧИ
При синтезе алгоритмов совместного оценивания неизвестных параметров сигнала, как правило, используют методы минимума средней квадратической ошибки (СКО), максимального правдоподобия (МП), максимальной апостериорной плотности распределения вероятности [1–4]. Недостатком такого подхода является необходимость знания законов распределения случайных процессов, входящих в модель наблюдаемого сигнала [5]. При гауссовских шумах хорошо известным результатом является рекуррентная фильтрация Калмана для линейной модели процессов и рекуррентная фильтрация Стратоновича для нелинейной. Большой вклад в развитие теории оценивания и оптимальной рекуррентной фильтрации внес В.И. Тихонов [6–11]. Если же законы распределения неизвестны, то используют метод наименьших квадратов (МНК) или усреднение по времени. МНК не встречает математических трудностей при выводе алгоритма оценивания неизвестных параметров, если модель процессов линейная [12, 13]. При нелинейной модели встает вопрос о том, каким методом решать систему нелинейных уравнений, чтобы не было расходимости алгоритма. Кроме того, процедуры оценивания при этом обладают высокой вычислительной сложностью [14]. Усреднение по времени при нахождении оценок параметров сигнала требует большого объема выборки наблюдаемого процесса. Существует много работ, посвященных процедурам раздельного оценивания параметров, но они уступают по точности алгоритмам совместной оценки, также часто оценивается только часть неизвестных параметров, остальные не учитываются в модели сигнала или считаются известными [1, 2, 15–21]. В работе [3] приведен алгоритм совместной оценки искажений сигнала в тракте приемника прямого преобразования, который обладает высокой точностью оценивания и полностью решает задачу определения значений амплитудно-фазового дисбаланса, сдвига частоты и постоянных составляющих для систем с одной передающей и приемной антенной (SISO), с несколькими передающими и приемными антеннами (MIMO), а также для систем со многими несущими с ортогональным частотным разделением (OFDM). Но предложенная процедура требует большого количества арифметических операций. Для оценки частоты записан только критерий, в который она входит нелинейно и в неявном виде. Поэтому остается открытым вопрос по ее поиску. Для остальных искажений получены замкнутые выражения для оценок, зависящие от полученной ранее оценки сдвига частоты. В работе [4] рассматривается совместная оценка приведенных выше искажений, полученная по критерию максимального правдоподобия при гауссовских шумах. Данный критерий приводит к системе сложных нелинейных уравнений, которые были решены итерационно, без описания метода. Эти обстоятельства обусловливают необходимость разработки вычислительно эффективных методов определения значений амплитудно-фазового дисбаланса, сдвига частоты и постоянных составляющих для систем SISO, MIMO и OFDM.
Рассмотрим квадратуры сигнала ${{{\mathbf{y}}}_{i}} = {{({{y}_{{ci}}},{{y}_{{si}}})}^{Т}}$ на фоне аддитивного шума ${{{\mathbf{\mu }}}_{i}} = {{({{\mu }_{{ci}}},{{\mu }_{{si}}})}^{Т}}$в тракте приемника прямого преобразования на примере сигнала M позиционной квадратурной амплитудной модуляции (М-QAM) в системе SISO:
Здесь ${{{\mathbf{z}}}_{i}} = {{({{z}_{{ci}}},{{z}_{{si}}})}^{T}} = {{{\mathbf{S}}}_{i}}({{{\mathbf{\Theta }}}_{i}})$, $i = \overline {1,m} $ – дискретное время, $m = {{{{T}_{0}}} \mathord{\left/ {\vphantom {{{{T}_{0}}} {\Delta t}}} \right. \kern-0em} {\Delta t}}$, ${{T}_{0}}$ – время наблюдения, $\Delta t$ – интервал дискретизации, ${{{\mathbf{S}}}_{i}}(\centerdot )$ – нелинейная вектор-функция, описывающая квадратурные компоненты сигнала ${{z}_{{is}}},{{z}_{{ic}}}$:Квадратуры ${{z}_{{ci}}},{{z}_{{si}}}$ сигнала можно переписать в следующей форме:
Вектор Θi оцениваемых параметров в этом случае имеет вид
Задача оценивания неизвестных параметров решалась по тестовой последовательности вида информационного сигнала при следующих условиях:
1. процесс ${{{\mathbf{\mu }}}_{i}}$ – стационарный, $E{{{\mathbf{\mu }}}_{i}} = {{{\mathbf{\bar {0}}}}_{{2 \times 1}}},$ ${\text{ }}E{{{\mathbf{\mu }}}_{i}}{\mathbf{\mu }}_{i}^{T} = \sigma _{\mu }^{2}{{{\mathbf{{\rm I}}}}_{{2 \times 2}}}$ – ковариационная матрица шумов наблюдения, $E{{{\mathbf{\mu }}}_{i}}{\mathbf{\mu }}_{j}^{T} = {{{\mathbf{0}}}_{{2 \times 2}}}$ при $i \ne j$, $E$ – оператор математического ожидания, ${{{\mathbf{{\rm I}}}}_{{2 \times 2}}}$ – единичная матрица размером $2 \times 2$,
2. ${{\varphi }_{i}} = {{\varphi }_{0}} + {{\alpha }_{i}},{{\alpha }_{i}} = {{b}_{0}}{{\zeta }_{{i\varphi }}} + {{b}_{1}}{{\zeta }_{{i - 1\varphi }}} + {{b}_{2}}{{\zeta }_{{i - 2\varphi }}}$ – фазовый шум, $E{{\zeta }_{{i\varphi }}} = 0,$ ${\text{ }}E\zeta _{{i\varphi }}^{2} = \sigma _{{\zeta \varphi }}^{2}$, $E{{\zeta }_{{i\varphi }}}{{\zeta }_{{j\varphi }}} = 0$ при $i \ne j$,
3. $\Delta {{f}_{i}} \ne 0 = {\text{const}}$,
4.${{b}_{{ci}}} = {\text{const}},\,\,{{b}_{{si}}} = {\text{const}}$,
5. $\Delta {{\varphi }_{i}} = {\text{const}},\,\,{{\gamma }_{i}} = {\text{const}}$,
6. амплитуда сигнала и импульсная характеристика канала неизвестны,
7. амплитуды ${{a}_{{1i}}}, \ldots ,{{a}_{{pi}}}$ за время наблюдения не зависят от времени, ${{a}_{{ki}}} = {{a}_{k}},k = 1,...,p$,
8. шаг дискретизации $\Delta t = T$, т.е. взят один отсчет на тестовый символ, $m = n$.
Требуется по выборке ${{{\mathbf{y}}}_{i}}$ найти оценку ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } }}$ вектора ${\mathbf{\Theta }}$.
2. СИНТЕЗ АЛГОРИТМА ОЦЕНИВАНИЯ НА ОСНОВЕ КОМБИНИРОВАНИЯ РЕГУЛЯРИЗУЮЩЕГО АЛГОРИТМА И НЕЛИНЕЙНОЙ ФИЛЬТРАЦИИ
Поставленная задача была решена с помощью регуляризующего алгоритма и процедуры нелинейной фильтрации с тейлоровской аппроксимацией до первого приближения нелинейной вектор-функции ${{{\mathbf{S}}}_{i}}(\centerdot )$ наблюдений, которые описаны в [22–28]. Регуляризующий алгоритм итерационно обрабатывает целиком всю выборку, нелинейная фильтрация – отсчеты квадратур сигнала в каждый момент времени. Начальная тактовая синхронизация осуществлена, как показано в [23].
Регуляризующий алгоритм применялся также в системах с MIMO и OFDM, нелинейная фильтрация использовалась для уточнения некоторых параметров OFDM-сигнала [26–28].
Была произведена приближенная оценка вычислительной сложности для рассматриваемых процедур: количество арифметических операций у регуляризующего алгоритма пропорционально $m{{M}_{0}}$, где ${{M}_{0}}$ – количество итераций, причем, как правило, ${{M}_{0}} < m$; у нелинейной фильтрации – пропорционально $m$, а у алгоритма из [3] – пропорционально ${{m}^{3}}$.
Для возможности уменьшения количества вычислительных операций в данной работе предлагается совместить регуляризующий алгоритм с процедурой фильтрации [6–8] в скользящем временном окне, длина которого ${{m}_{0}} < m$.
С использованием (1) сформируем вектор наблюдений
(2)
${{{\mathbf{Y}}}_{i}} = {{{\mathbf{\bar {S}}}}_{i}}({{{\mathbf{\Theta }}}_{i}}) + {{{\mathbf{\bar {\mu }}}}_{i}},$Так как оцениваемый вектор параметров медленно изменяется со временем, то его можно представить в виде авторегрессии первого порядка:
Здесь ${{{\mathbf{\xi }}}_{i}}$ – вектор белого шума с нулевым средним значением и ковариационной матрицей $E{{{\mathbf{\xi }}}_{i}}{\mathbf{\xi }}_{i}^{T} = \sigma _{\xi }^{2}{\mathbf{{\rm I}}}$, где ${\mathbf{{\rm I}}}$ – единичная матрица размером $(p + 6) \times (p + 6)$. Разложим нелинейную вектор-функцию уравнения (2) в ряд Тейлора до первого приближения в точке ${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } }}}_{{i - 1}}}$, тогда (2) можно переписать в следующей форме:(4)
${{{\mathbf{Y}}}_{i}} \cong {{{\mathbf{\bar {D}}}}_{{i - 1}}}{\mathbf{F}}({{{\mathbf{\Theta }}}_{i}}) + {{{\mathbf{\bar {\mu }}}}_{i}},$Далее возьмем от левой и правой части выражения (3) функцию ${\mathbf{F}}(\centerdot )$ и разложим правую часть получившегося равенства в ряд Тейлора до первого приближения в точке ${{{\mathbf{\Theta }}}_{{i - 1}}}$, в результате получим
(5)
${\mathbf{F}}({{{\mathbf{\Theta }}}_{i}}) = {\mathbf{F}}({{{\mathbf{\Theta }}}_{{i - 1}}}) + {\mathbf{W}}{{{\mathbf{\xi }}}_{i}},$Учитывая (4) и (5), запишем модифицированный метод наименьших квадратов в виде функционала Тихонова относительно переменной ${{{\mathbf{f}}}_{i}} = {\mathbf{F}}({{{\mathbf{\Theta }}}_{i}})$ (причем ${{{\mathbf{\Theta }}}_{i}} = {\mathbf{L}}{{{\mathbf{f}}}_{i}}$, ${\mathbf{L}} = {{{\mathbf{W}}}^{T}}$) :
(6)
$\begin{gathered} \Phi ({{{\mathbf{f}}}_{i}}) = \left\| {{{{\mathbf{Y}}}_{i}} - {{{{\mathbf{\bar {D}}}}}_{{i - 1}}}{{{\mathbf{f}}}_{i}}} \right\|_{{{{{\mathbf{Q}}}^{{ - 1}}}}}^{2} + {{\lambda }_{i}}\left\| {{{{\mathbf{f}}}_{i}} - {{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }}}}_{{i - 1}}}} \right\|_{{{\mathbf{P}}_{i}^{{ - 1}}}}^{2}, \\ i = {{m}_{0}},\,\,\,\,{{m}_{0}} + 1,... \\ \end{gathered} $В результате получаем следующие выражения:
(7)
${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } }}}_{i}} = {{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } }}}_{{i - 1}}} + {\mathbf{L}}{{{\mathbf{K}}}_{i}}{\mathbf{(}}{{{\mathbf{Y}}}_{i}} - {{{\mathbf{\bar {S}}}}_{i}}{\mathbf{(}}{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } }}}_{{i - 1}}}{\mathbf{))}},\,\,\,i = {{m}_{0}},\,\,\,\,{{m}_{0}} + 1,....$(8)
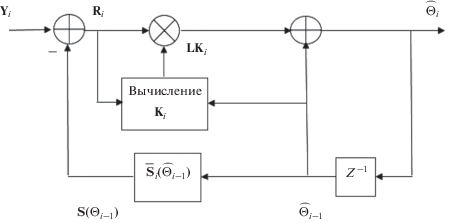
${{\lambda }_{i}} \approx \frac{{\sqrt {2{{m}_{0}}} {\text{ }}{{\sigma }_{\mu }}\left( {\frac{{\left\| {{{{\mathbf{Y}}}_{i}} - {{{{\mathbf{\bar {S}}}}}_{i}}{\mathbf{(}}{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } }}}}_{{i - 1}}}{\mathbf{)}}} \right\|}}{{\sqrt {2({{m}_{0}} - 1)} }} - {{\sigma }_{\mu }}} \right)}}{{\left\| {{\text{diag}}({{{{\mathbf{\bar {D}}}}}_{{i - 1}}}{{{\mathbf{P}}}_{i}}{\mathbf{\bar {D}}}_{{i - 1}}^{T})} \right\|}}.$На рис. 1 представлена структурная схема алгоритма оценивания (7), на рис. 2 – структура формирования матрицы Ki с учетом определения регуляризующего множителя Лагранжа (8), на рис. 3 – структура формирования ковариационной матрицы ошибок фильтрации Гi.
Рис. 2.
Структурная схема формирования матрицы ${{{\mathbf{K}}}_{i}}$ из алгоритма (7) и регуляризующего множителя Лагранжа (8); НП – нелинейный преобразователь.
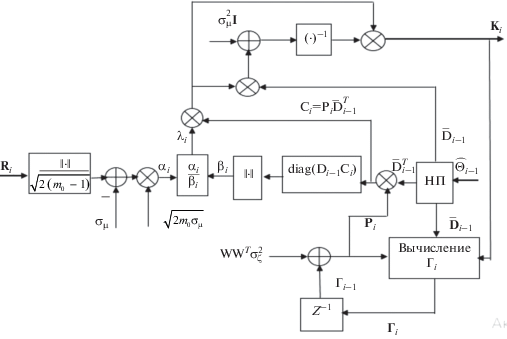
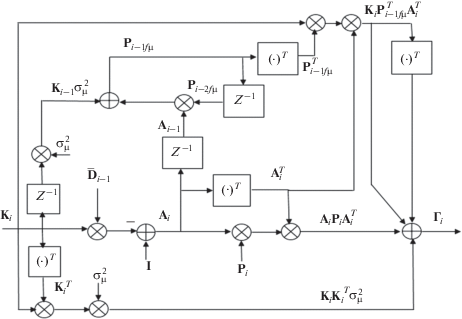
Рис. 3.
Структурная схема формирования ковариационной матрицы ошибок фильтрации ${{{\mathbf{\Gamma }}}_{i}}$ .
Получены приближенные выражения для вычислительной сложности соответственно регуляризующего алгоритма и процедуры (7), (8):
Различие между данными процедурами состоит в том, что регуляризующий алгоритм обрабатывает итерационно всю выбору длиной $m$ целиком, а (7), (8) – выборку длиной ${{m}_{0}}$ в скользящем временном окне, причем при количестве итераций ${{M}_{0}} = m - {{m}_{0}}$ он в результате для оценивания использует тот же объем сигнала $m$, что и регуляризующий алгоритм. При одинаковых количестве итераций у обоих процедур и длине скользящего окна для (7), (8) ${{m}_{0}} = m - {{M}_{0}}$ можно достичь некоторого сокращения вычислительной сложности относительно регуляризующего алгоритма, рассчитанного по формуле
3. ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
Проведено сравнение помехоустойчивости приема сигнала 64-QAM на фоне аддитивного белого гауссовского шума при использовании для оценки неизвестных параметров сигнала регуляризующего алгоритма, процедуры нелинейной фильтрации и известного совместного алгоритма оценивания [3] (рис. 4). Оценка частоты в известном алгоритме [3] производилась методом перебора ${{Q}_{0}}$ значений частоты из априори выбранного интервала и подстановкой их в критерий оптимальности. На рис. 5 представлены зависимости помехоустойчивости приема сигнала 64-QAM при использовании для оценивания его параметров алгоритмов, представленных на рис. 4, и комбинированной процедуры (7), (8). Предложенный алгоритм (7), (8) делал $m - {{m}_{0}}$ итераций. Моделирование проводили при следующих условиях: $p = 1$, $\gamma = 0.5$, $\Delta f = 180.7$ Гц, $T = 0.25$ мкс, ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi {12}}} \right. \kern-0em} {12}}$, $\Delta \varphi = {\pi \mathord{\left/ {\vphantom {\pi {18}}} \right. \kern-0em} {18}},$ ${{b}_{c}} = 1.3,\,\,{{b}_{s}} = 2$, СКО фазового шума – один градус, объем анализируемой выборки тестового сигнала $m = 500$, длина информационной последовательности – 2000 символов. Длина оцениваемого вектора у всех трех алгоритмов одинаковая и равна 7.
Рис. 4.
Зависимости экспериментальной вероятности ошибки на символ P приема сигнала 64-QAM от отношения сигнал/шум q, полученные при использовании регуляризующего алгоритма [24] (кривая 1), нелинейной фильтрации [24] (кривая 2) и алгоритма совместного оценивания из [3] при ${{Q}_{0}} = 25$ (3), 50 (4) и 100 (5).
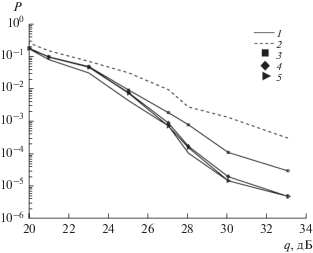
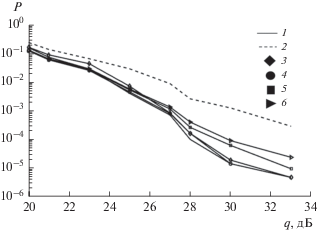
Рис. 5.
Зависимости экспериментальной вероятности ошибки на символ P приема сигнала 64-QAM от отношения сигнал/шум q, полученные при использовании разных алгоритмов оценивания параметров сигнала: регуляризующий алгоритм (кривая 1), нелинейная фильтрация (кривая 2), алгоритм совместного оценивания из [3] при ${{Q}_{0}} = 50$(3), алгоритм (7), (8) при ${{m}_{0}} = 480$ (4), 450 (5) и 400 (6).
Из рис. 4 видно, что регуляризующий алгоритм имеет выигрыш в помехоустойчивости перед процедурой нелинейной фильтрации от 1 до 5.5 дБ и сравним с известным алгоритмом при ${{Q}_{0}} = 50;100$. Если же ${{Q}_{0}} = 25$, то он выигрывает у известной совместной процедуры оценивания до 4 дБ. Исходя из рис. 4 можно сделать вывод, что самым предпочтительным является регуляризующий алгоритм.
Уменьшение длины скользящего окна приводит к потере в энергетической эффективности (см. рис. 5, кривые 4–6), поэтому необходимо искать компромисс между длиной временного окна ${{m}_{0}}$, помехоустойчивостью и вычислительной сложностью.
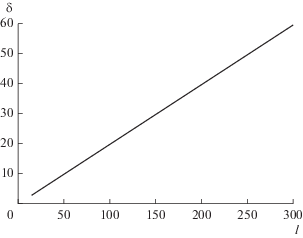
На рис. 6 показана количественная оценка сокращения вычислительной сложности у (7), (8) относительно регуляризующего алгоритма при $p = 1,\,\,p + 6 = 7$, $m = 500$, рассчитанная по формуле (9).
Так, при объеме анализируемой выборки сигнала 500, количестве оцениваемых параметров, равном 7, и числе итераций 50 упрощение составляет около 10%.
4. ОБСУЖДЕНИЕ И АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
Предложенный алгоритм (7), (8) совместного оценивания неизвестных параметров случайного процесса, прошедшего тракт приемника прямого преобразования, позволяет при правильно подобранных длине скользящего окна и объеме выборки тестовой последовательности сократить вычислительную сложность при приемлемой потере в энергетической эффективности относительно известных алгоритмов совместного оценивания искажений сигнала. Например, при длине выборки в 500 тестовых символов, количестве итераций ${{M}_{0}} = 20$ и длине скользящего окна ${{m}_{0}} = 480$ упрощение составляет 4% без потери в энергетической эффективности, а при ${{M}_{0}} = 50$, ${{m}_{0}} = 450$ сложность падает на 10%, практически без потерь в помехоустойчивости при отношении сигнал/шум 23…27 дБ. При более высоких значениях отношения сигнал/шум (28…33 дБ) потери в энергетической эффективности составят от 0.5 до 2 дБ.
Список литературы
Gappmair W., Koudelka O. // Proc. 2012 8th Int. Symp. Commun. Systems, Networks and Digital Signal Processing (CSNDSP). Poznan, 18–20 Jul. N.Y.: IEEE, 2012. P. 6292650.
Gappmair W. // Adv. Electronics and Telecommun. 2013. V. 3. № 5. P. 32.
Hsu Ch.-J., Cheng R., Sheen W.-H. // IEEE Trans. 2009. V. VT-58. № 5. P. 2201.
Weikert O. // Proc. 14th Workshop on Signal Processing Advances in Wireless Commun. (SPAWC). Darmstadt, 16–19 Jun. N.Y.: IEEE, 2013. P. 520.
Aziz M., Ghannouchi F.M., Helaoui M. // Sensors. 2017. V. 17. № 12. P. 2948.
Тихонов В.И., Кульман. Н.К. Нелинейная фильтрация и квазикогерентный прием сигналов. М.: Сов. радио, 1975.
Тихонов В.И., Миронов М.А. Марковские процессы. М.: Сов. радио, 1977.
Тихонов В.И., Харисов В.Н., Смирнов В.А. // РЭ. 1978. Т. 23. № 7. С. 1441.
Тихонов В.И. Статистическая радиотехника. М.: Радио и связь, 1982.
Тихонов В.И. Оптимальный прием сигналов. М.: Радио и связь, 1983.
Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. М.: Радио и связь, 1991.
Вержбицкий В.М. Основы численных методов. М: Высш. школа, 2005.
Голуб Дж., Ван Лоун Ч. Матричные вычисления. М: Мир, 1999.
Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М: Высш. школа, 1994.
Yoshida T., Nojima D., Nagao Y. et al. // Proc. Int. Conf. on Advanced Technologies for Communications (ATC 2011). Da Nang, 2–4 Aug. N.Y.: IEEE, 2011. P. 327.
Пестряков А.В., Хасьянова Е.Р. // Системы синхронизации, формирования и обработки сигналов. 2015. Т. 6. № 3. С. 115.
Хасьянова Е.Р. Исследование и разработка методов компенсации погрешностей квадратурного преобразования в цифровых радиоприемниках с нулевой промежуточной частотой. Дис. … канд. техн. наук. М: МТУСИ, 2019. 112 с.
Chen Y., Li Y., Gao X., Xia X.-G. // IEEE Access. 2020. V. 8. P. 1542.
Khanum K.N., Reddy G.R. // Proc. Int. Conf. on Emerging Trends in Inform. Technology and Engineering (ic-ETITE 2020). Vellore, 24–25 Feb. N.Y.: IEEE, 2020. P. 1.
Sahoo M., Sahoo H.K. // 5th Intern. Conf. for Convergence in Technology (I2CT). Bombay, 29–31 Mar. N.Y.: IEEE, 2019. P. 9033748.
Wang X., Hua H., Xu Y. // IEEE Access. 2020. V. 8. P. 44936.
Поборчая Н.Е. // Электросвязь. 2010. № 3. С. 24.
Поборчая Н.Е. // Электросвязь. 2012. № 5. С. 17.
Поборчая Н.Е. // Электросвязь. 2013. № 5. С. 24.
Поборчая Н.Е. // Электросвязь. 2016. № 12. С. 64.
Поборчая Н.Е., Пестряков А.В. // T-Comm. 2019. Т. 13. № 10. С. 13.
Поборчая Н.Е. // Электросвязь. 2020. № 6. С. 74.
Poborchaya N.E. // Systems of Signal Synchronization, Generating and Processing in Telecommunications (SYNCHROINFO), Svetlogorsk, 1–3 Jul. N.Y.: IEEE, 2020. P. 9166068.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника