Радиотехника и электроника, 2021, T. 66, № 8, стр. 815-824

ВВЕДЕНИЕ

Возбуждение ультразвуковых колебаний сверхвысоких частот с помощью магнитострикционных преобразователей издавна привлекает внимание исследователей [1–4]. Особый интерес представляет возбуждение колебаний намагниченности в нелинейном режиме, что позволяет повысить мощность генерируемого ультразвука на порядок и более [5, 6]. Геометрия преобразователя в этом случае представляет собой нормально намагниченную ферритовую пластину, что обеспечивает возможность возбуждения намагниченности с большими углами прецессии (до 20°…40°) [7–9], недостижимыми при других видах геометрии из-за параметрического возбуждения обменных спиновых волн [10–14]. Высокоамплитудная прецессия намагниченности сопровождается нестационарными колебаниями, в том числе автомодуляционного характера, некоторые из которых описаны в обобщающей работе [15].

В стационарном режиме возможно возбуждение особо высокочастотного гиперзвука (до десятков гигагерц) путем умножения частоты возбуждения [16]. При этом эффективность возбуждения возрастает тем более, чем выше амплитуда возбуждающего сигнала. Однако такое возбуждение при достаточной амплитуде сопровождается нестационарными явлениями, одним из которых является значительное скачкообразное запаздывание развития колебаний относительно момента включения возбуждающего сигнала. Некоторые особенности такого запаздывания отмечены в работе [17]. Однако проведенное там рассмотрение является неполным и отражает лишь качественную описательную сторону явления. Некоторые характерные особенности отмечены в работах [18‒20], однако предложенное там описание является разрозненным, не представляющим цельной картины явления.

Данная работа является развитием проведенных ранее исследований, с целью более последовательного их обобщения и создания единой модели нелинейного запаздывания магнитоупругих колебаний, возбуждаемых в режиме умножения частоты.

1. ГЕОМЕТРИЯ ЗАДАЧИ И ОСНОВНЫЕ УРАВНЕНИЯ

Геометрия задачи, совпадающая с принятой в работах [5, 21–28], показана на рис. 1. В ее основе лежит плоскопараллельная пластина толщины $d$, обладающая магнитными, упругими и магнитоупругими свойствами. Материал пластины имеет кубическую кристаллографическую симметрию, плоскость (100) которой совпадает с плоскостью пластины. Внешнее постоянное магнитное поле ${{\vec {H}}_{0}}$ приложено перпендикулярно плоскости пластины, переменное магнитное поле $\vec {h}$ действует в плоскости пластины. Задача решается в декартовой системе координат $Oxyz$, плоскость $Oxy$ которой совпадает с плоскостью пластины, а оси $Ox$, $Oy$ и $Oz$ параллельны ребрам куба кристаллографической ячейки. Центр системы координат $O$ находится в центре пластины, так что ее плоскости соответствуют координатам $z\,\, = \,\, \pm {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$.

Система уравнений движения для нормированных на намагниченность насыщения M₀ компонент намагниченности имеет вид [5, 21, 22]:

а уравнения для ${{m}_{y}}$ и ${{m}_{z}}$ получаются циклической перестановкой $x$, $y$, $z$. Уравнения для компонент упругого смещения ${{u}_{{x,\,y}}}$ имеют вид граничные условия

В этих выражениях ${{m}_{{x,y,z}}}$ – нормированные компоненты вектора намагниченности, ${{u}_{{x,y}}}$ – компоненты упругого смещения, ${{H}_{{x,y,z}}}$ – эффективные поля, определяемые как производные от плотности энергии по компонентам намагниченности, $\gamma $ – гиромагнитная постоянная, $\alpha $ – параметр магнитного затухания по Гильберту, c₄₄ – модуль упругости, $\beta $ – параметр упругого затухания, $\rho $ – плотность материала магнитной пластины, ${{B}_{2}}$ – константа магнитоупругого взаимодействия.

В полном виде система (1)–(3) сводится к решению семи связанных уравнений первого порядка. Однако в работах [23, 24] показано, что с высокой точностью такую систему в квадратичном приближении можно приблизить к более простой, содержащей всего два уравнения второго порядка, описывающих колебания системы из двух осцилляторов – магнитного и упругого:

Здесь x₁ и ${{x}_{2}}$ – нормированные компоненты намагниченности и упругого смещения в плоскости пластины, ${{\beta }_{1}}$ и ${{\beta }_{2}}$ – параметры затухания той и другой компоненты, ${{\omega }_{1}}$ и ${{\omega }_{2}}$ – собственные частоты осцилляторов, ${{\gamma }_{1}}$ и ${{\gamma }_{2}}$ – константы их линейной связи, $\delta $ – параметр кубической нелинейности, $\eta $ – параметр нелинейной связи первого осциллятора со вторым, $A$ и ${{\omega }_{0}}$ – амплитуда и частота переменного поля соответственно.

Замечание. Ввиду сложности исходной системы (1)–(3) обратимся далее к упрощенной системе (4), (5) с целью выявить возможные особенности колебаний на модельном уровне. Будем рассматривать приведенные далее результаты не более чем стимулирующую подсказку для исследования полной системы (1)–(3). В то же время, учитывая весьма нетривиальный собственный характер системы (4), (5), можно полагать, что ее подробное исследование представляет самостоятельный математический интерес, поэтому на подробности ее численного решения также обратим повышенное внимание.

Полагая частоту $\omega $ для ферромагнитного резонанса (ФМР) в поле 3000 Э порядка 10¹¹ с^–1, находим, что порядок величин слагаемых в обоих уравнениях будет около 10²² с^–2. Для удобства работы с небольшими безразмерными числами далее все параметры задачи будем нормировать на квадрат этой частоты. Выражения коэффициентов уравнений (4), (5) через параметры материала и геометрии задачи приведены в работе [24], здесь не повторяются. Для дальнейшего рассмотрения важен коэффициент $\eta $, связанный с исходными параметрами задачи следующим образом:

Видим, что в зависимости от величины поля ${{H}_{0}}$ знак параметра $\eta $ будет меняться. Критическое значение поля равно

т.е. при ${{H}_{0}} > {{H}_{C}}$ параметр $\eta $ отрицателен, а при ${{H}_{0}} < {{H}_{C}}$ положителен.

Оценим величину параметра $\eta $ по формуле (6) для типичной экспериментальной ситуации [12] в случае пленки железо-иттриевого граната толщиной 15 мкм. При этом ${{M}_{0}}$ = 140 Гс, ${{B}_{2}}$ = = $6.96 \times {{10}^{6}}$ эрг см^–3, а также $\gamma $ = $1.76 \times {{10}^{7}}$ Э^–1 с^–1. Критическое значение поля (7) равно ${{H}_{C}}$ = 2052 Э. Так как для реализации запаздывания параметр $\eta $ должен быть отрицательным, положим поле большим критического: ${{H}_{0}}$ = 3000 Э. При этом из (6) получаем $\eta = - 5.8836 \times {{10}^{{25}}}$ с^–2. Численная оценка показывает, что все слагаемые в уравнении (4) по порядку близки друг к другу, так что параметр $\eta $, нормированный на квадрат частоты, имеет величину порядка ${{10}^{2}}$…${{10}^{3}}$ с^–2.

2. РАЗВИТИЕ КОЛЕБАНИЙ ВО ВРЕМЕНИ

Рассмотрим численное решение системы (4), (5) в режиме умножения частоты. С учетом нормировки на ${{10}^{{\,22}}}$с^–2 зададим следующие величины параметров: ${{\omega }_{1}} = \,\,5$, ${{\gamma }_{1}}$ = 10, ${{\gamma }_{2}}$ = 10, $\delta $ = 5, $\eta $ = –200. Будем рассматривать умножение частоты на три, так что ${{\omega }_{2}}$ = 15. Примем, что частота возбуждения равна ${{\omega }_{0}}$ = 5, амплитуда $A$ = 50. Принципиально важным для настоящего рассмотрения является сильное различие параметров затухания осцилляторов, поэтому возьмем два случая: первый – ${{\beta }_{1}}$ = 1.0, ${{\beta }_{2}}$ = 0.1; второй – ${{\beta }_{1}}$ = 0.1, ${{\beta }_{2}}$ = 1.0. Развитие колебаний во времени для обоих осцилляторов показано на рис. 2а, 2б.

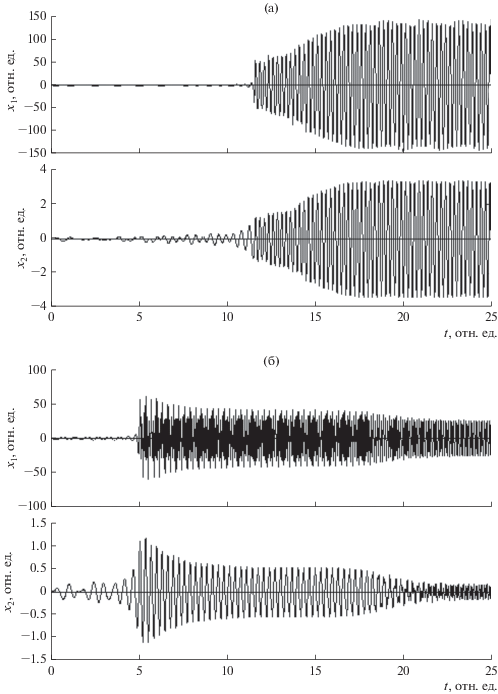
Из рисунка видно, что развитие колебаний того и другого осцилляторов происходит подобным образом, с тем отличием, что амплитуда второго в ~40 раз меньше амплитуды первого. Можно полагать, что такое различие вызвано тем, что именно на первый осциллятор действует возбуждающая сила, тогда как второй раскачивается только за счет возбуждения первого.

Развитие колебаний сначала идет крайне медленно, однако начиная с некоторого момента времени амплитуда колебаний обоих осцилляторов скачком увеличивается сразу на один-два порядка, после чего меняется сравнительно медленно, стремясь к постоянному значению. То есть в обоих случаях наблюдается нестационарное запаздывание развития колебаний. В первом случае (см. рис. 2а) характерное время запаздывания составляет 12 отн. ед., во втором случае (см. рис. 2б) несколько меньшее – около 5 отн. ед.

Значительное отличие параметров затухания осцилляторов друг от друга является для реализации запаздывания принципиально необходимым. При равенстве обоих параметров затухания запаздывание полностью отсутствует. При принятых параметрах затухания время релаксации для осциллятора с $\beta $ = 1.0 составляет 2.2 отн. ед., а для осциллятора с параметром затухания $\beta $ = 0.1 – 22 отн. ед. То есть время запаздывания находится между временами релаксации обоих осцилляторов.

Интересно проследить за характерными периодами процесса колебаний обоих осцилляторов. Так, частоте возбуждения ${{\omega }_{0}}$ = 5 соответствует период 1.2 отн. ед. времени, а утроенной частоте ${{\omega }_{2}}$ = 15 соответствует период 0.4 отн. ед. времени. До скачка амплитуды колебания того и другого осцилляторов происходят именно с этими частотами. После скачка в первом случае период колебаний уменьшается до 0.25 отн. ед., а во втором – до 0.30 отн. ед. Во втором случае при времени около 20 отн. ед. имеет место дополнительный скачок амплитуды – примерно в два раза вниз по величине, причем период колебаний еще более уменьшается, до величины 0.14 отн. ед.¹¹

Из рис. 2 видим, что оба случая, хотя и содержат нестационарную задержку развития колебаний, однако не являются полностью эквивалентными. Можно полагать, что наблюдаемое различие обусловлено тем, что первый осциллятор является сильно нелинейным, тогда как второй – чисто линейным. Ограничимся далее первым случаем: ${{\beta }_{1}}$ = 1.0, ${{\beta }_{2}}$ = 0.1.

3. ПОРОГОВЫЙ ХАРАКТЕР ЗАПАЗДЫВАНИЯ

Запаздывание возбуждения колебаний имеет порог по амплитуде вынуждающей силы. При принятых параметрах критическое значение амплитуды, выше которого запаздывание имеется, а ниже отсутствует, составляет около $A$ = 30 отн. ед. На рис. 3а, 3б показана зависимость времени запаздывания и амплитуды установившихся колебаний от амплитуды возбуждения $A$.

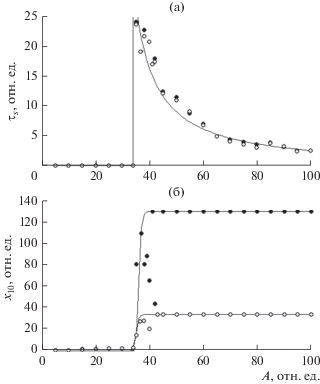
Из рис. 3а видно, что до критического значения амплитуды ${{A}_{S}}$, равного 30.880 отн. ед., запаздывание отсутствует, а при достижении амплитудой этого значения, время запаздывания ${{\tau }_{S}}$ резким скачком возрастает, при $A$ = 30.881 составляет 153 отн. ед. (за пределами рисунка). Максимум времени запаздывания ${{\tau }_{S}}$ = 155 отн. ед. приходится на A = 30.884 отн. ед. При дальнейшем увеличении амплитуды время запаздывания спадает:

и далее по рисунку.

Времена запаздывания для обоих осцилляторов практически совпадают, а при амплитуде возбуждения, больше критической, довольно близко описываются эмпирической зависимостью типа обратной пропорциональности:

Из рис. 2 можно видеть, что после скачкообразного увеличения амплитуды, колебания обоих осцилляторов устанавливаются на стационарном постоянном уровне. Более подробно зависимости амплитуды установившихся колебаний обоих осцилляторов от амплитуды возбуждения показаны на рис. 3б. Характерным свойством обеих зависимостей является резкий скачок амплитуды колебаний при критическом значении амплитуды возбуждения. Зависимости, приведенные на рис. 3б сплошными линиями, построены по эмпирическим формулам типа гиперболического тангенса: ${{x}_{{10}}} = 65\operatorname{th} \left( {A - 36} \right) + 65$; ${{x}_{{20}}} = 17\operatorname{th} \left( {A - 36} \right) + 17.$

4. ДИНАМИЧЕСКИЙ ПОТЕНЦИАЛ

Механизм образования запаздывания можно интерпретировать на основе введения динамического потенциала [18, 19]. Так, из уравнения (4) можно видеть, что потенциал имеет вид

Дифференцирование этого выражения по x₁ дает потенциальную группу слагаемых уравнения (6). При этом переменную ${{х}_{2}}$ следует рассматривать как постоянный параметр.

Рассмотрим зависимость динамического потенциала (8) от амплитуды колебаний первого осциллятора (рис. 4) при различных значениях амплитуды второго осциллятора (индекс 0 при значении амплитуды далее не приводим).

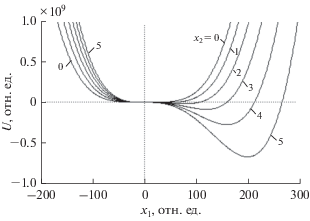
Как видно из рисунка, в отсутствие колебаний второго осциллятора потенциал имеет минимум, приходящийся на ${{x}_{1}} = 0$. При ${{x}_{2}} = 1$ отн. ед. минимум еще остается на прежнем месте (в нуле), но потенциальная кривая несколько расширяется. При ${{x}_{2}} = 2$ отн. ед. проявляется новый минимум, приходящийся на ${{x}_{1}} = 95$ отн. ед. При дальнейшем увеличении ${{x}_{2}}$ минимум потенциала углубляется и смещается в сторону больших значений ${{x}_{1}}$. Так, при ${{x}_{2}} = 5$ отн. ед. минимум приходится уже на ${{x}_{1}} = 205$ отн. ед. При дальнейшем увеличении ${{x}_{2}}$ минимум смещается еще дальше. При критическом значении ${{x}_{2}} = {{x}_{{2C}}}$ около 1.2 отн. ед. минимум при ${{x}_{1}} = 0$ заменяется перегибом и резко смещается в сторону больших значений ${{x}_{1}}$, что проявляется как скачкообразный рост амплитуды колебаний.

Построенный таким образом потенциал (8) является динамическим, т.е. его величина меняется в такт с изменением смещения второго осциллятора ${{x}_{2}}$. То есть если в течение первого полупериода смещения ${{x}_{2}}$ потенциал имеет вид, показанный на рис. 4, то в течение следующего полупериода ${{x}_{2}}$ картина зеркально поворачивается относительно вертикальной оси.

До момента достижения амплитуды второго осциллятора критического значения ${{x}_{{2C}}}$ для первого осциллятора не остается ничего другого, как колебаться в пределах единственного минимума в ближайшей окрестности точки ${{x}_{1}} = 0$. Амплитуда его колебаний остается малой. При превышении амплитуды второго осциллятора критического значения ${{x}_{{2C}}}$, благодаря динамичности потенциала, для первого осциллятора открывается возможность колебаться в пределах, определяемых двумя минимумами кривой потенциала, расположенными симметрично по обе стороны от точки ${{x}_{1}} = 0$, значительно от нее удаленными. Такой “выход на свободу” для первого осциллятора проявляется как резкое увеличение его амплитуды. При этом благодаря обратной связи между осцилляторами амплитуда колебаний второго осциллятора также возрастает, что приводит к еще большему увеличению амплитуды первого осциллятора. Развивается лавинообразно нарастающий процесс, что и проявляется как резкий скачкообразный рост амплитуды колебаний обоих осцилляторов.

Можно полагать, что динамический характер потенциала требует определенного синхронизма между колебаниями обоих осцилляторов, однако при равенстве частот запаздывание отсутствует при любых значениях параметров. Тем не менее синхронизм может проявляться и при кратном соотношении частот осцилляторов между собой. Видимо, требование синхронизма и является причиной, почему запаздывание проявляется только в режиме умножения частоты. Проверка показывает, что кратность умножения должна быть обязательно нечетной. Лучше всего запаздывание проявляется при умножении частоты на три, несколько хуже на пять, еще хуже на семь, а далее уже не реализуется. Если полагать, что условием синхронизма является совпадение периода частоты первого осциллятора с несколькими периодами второго, то можно видеть, что “интеграл перекрытия” периодов обоих осцилляторов отличен то нуля только при нечетном их соотношении, причем величина его будет тем более значительной, чем кратность периодов меньше.

5. ПАРАМЕТР КУБИЧЕСКОЙ НЕЛИНЕЙНОСТИ

Из постоянных параметров системы уравнений (3), (4) весьма важным является параметр кубической нелинейности $\delta $. Из выражения для потенциала (8) видно, что некоторые слагаемые являются нечетными относительно ${{x}_{1}}$. Это означает, что при достаточной величине ${{x}_{1}}$ потенциал может уйти на бесконечность, что противоречит физическому смыслу. Однако потенциал содержит параметр кубической нелинейности $\delta $, который, будучи наиболее высоким по показателю степени ${{x}_{1}}$, при достаточной величине препятствует уходу на бесконечность при любом соотношении других параметров.

На рис. 5 приведена зависимость динамического потенциала от амплитуды колебаний первого осциллятора при различных значениях параметра $\delta $. Амплитуда колебаний второго осциллятора задана равной ${{x}_{2}}$ = 5 отн. ед., так что кривая 1 здесь совпадает с кривой на рис. 4, где ${{x}_{2}}$ также равен 5 отн. ед. Остальные параметры совпадают с принятыми на рис. 4.

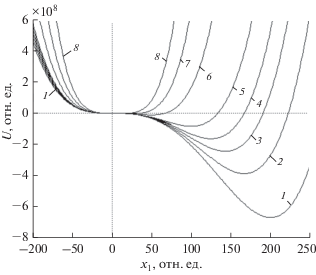
Из рис. 5 видно, что по мере увеличения параметра кубической нелинейности динамический минимум потенциала смещается к меньшим значениям ${{x}_{1}}$ и его глубина убывает. То есть по мере увеличения кубической нелинейности амплитуда колебаний убывает. На кривой 7 минимум становится незначительным, а на кривой 8 переходит в нулевую точку по оси ${{x}_{1}}$, так что амплитуда колебаний первого осциллятора стремится к нулю, т.е. при этих условиях запаздывание полностью подавляется.

На рис. 6 представлена зависимость времени запаздывания от параметра кубической нелинейности. Как видно из рисунка, устойчивые колебания большой амплитуды существуют только в области изменения параметра $\delta $ между 5 и 53 отн. ед. При $\delta \,\, < \,\,5$ отн. ед. колебания большой амплитуды возникают, но продолжаются сравнительно небольшой промежуток времени, после чего система уходит на бесконечность. При $\delta \,\, > \,\,5$ отн. ед. величина этого параметра уже достаточна, чтобы предотвратить уход на бесконечность. При $\delta \,\, > \,\,53$ отн. ед. колебания большой амплитуды отсутствуют, т.е. происходит подавление запаздывания.

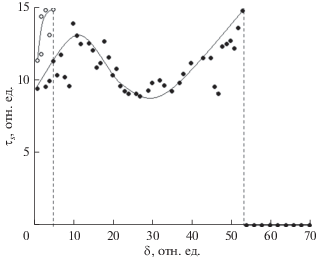
Как видим, скачкообразное увеличение амплитуды колебаний имеет большой разброс по вертикали (темные точки). При изменении параметра нелинейности всего на 3…5 отн. ед. время запаздывания меняется на величину, доходящую до 20…30%. Можно полагать, что функциональная зависимость здесь является сложной и носит стохастический характер, поэтому сплошные линии проведены эмпирически через области, соответствующие максимальному сгущению точек.

Вообще говоря, такой весьма нерегулярный характер расположения точек, колеблющихся в окрестности величины ${{\tau }_{S}} = \left( {12 \pm 2} \right)$ ед., дает повод полагать, что во всем интервале изменения параметра нелинейности $\delta $, от нуля до его критического значения, время запаздывания от этого параметра практически не зависит.

6. АМПЛИТУДА КОЛЕБАНИЙ ПОСЛЕ ЗАПАЗДЫВАНИЯ

Рассмотрим теперь, какое влияние оказывает параметр кубической нелинейности на характер колебаний после запаздывания. На рис. 7 представлена зависимость амплитуды колебаний в установившемся режиме от величины этого параметра. Из рисунка видно, что установившаяся амплитуда при увеличении параметра кубической нелинейности более или менее монотонно спадает. Особенно резкий спад наблюдается при малых значениях параметра $\delta $ (до 10…15 отн. ед., а также на вставке), после чего спад постепенно замедляется. Начиная со значения $\delta $ порядка 53 отн. ед. амплитуда резко уменьшается, что соответствует подавлению запаздывания при достижении параметром $\delta $ критического значения ${{\delta }_{C}}$ (показано стрелкой).

Наблюдаемый характер спада зависимости ${{{\text{x}}}_{{10}}}$ от $\delta $ позволяет приблизить ее эмпирическими кривыми, соответствующими закону обратной пропорциональности на основном рисунке и на вставке соответственно:

7. ИНТЕРПРЕТАЦИЯ СПАДА АМПЛИТУДЫ НА ОСНОВЕ МОДЕЛИ ПОТЕНЦИАЛА

Рассмотрим отмеченный спад амплитуды на основе механизма потенциала при кубической нелинейности. Так, из выражения (8) можно видеть, что кубическая нелинейность соответствует слагаемому, имеющему вид

Потенциал ${{U}_{\delta }}$ представляет собой симметричную яму, сужающуюся по мере увеличения параметра $\delta $. Края ямы при заданном значении потенциала определяют интервал допустимых значений смещения первого осциллятора. То есть чем выше потенциал, тем может быть больше размах колебаний. Проверка показывает, что зависимость допустимой амплитуды колебаний первого осциллятора от величины параметра кубической нелинейности может быть приближена эмпирической формулой, имеющей структуру обратной пропорциональности:

Возвращаясь к формуле (9), отметим, что обе ветви потенциала вследствие его четности стремятся к плюс бесконечности, так что колебания по амплитуде всегда остаются ограниченными. Поскольку степень потенциала (8) по первой переменной ${{x}_{1}}$ равна четырем, а все остальные его слагаемые при постоянной величине ${{x}_{2}}$ имеют по переменной ${{x}_{1}}$ степень не выше третьей, то этот потенциал при достаточной величине своего параметра $\delta $ перевешивает остальные слагаемые и колебания всегда остаются конечными.

Наблюдаемый в некоторых случаях уход системы на бесконечность (см. рис. 6, светлые точки) наблюдается только при довольно малых значениях параметра $\delta $ (менее 5 отн. ед.). Следовательно, может иметь место преобладающая роль слагаемого со смешанной нелинейностью с параметром η, где первая переменная, хотя и имеет всего третью степень, но в динамике к ней добавляется еще вторая переменная, т.е. результирующая степень становится четвертой. Возникающая при этом конкуренция двух четвертых степеней $x_{1}^{4}$ и $x_{1}^{3}{{x}_{2}}$ при малом значении параметра $\delta $, но достаточно большой величине $\eta $, приводит к уходу системы на бесконечность.

8. ВЛИЯНИЕ ДРУГИХ ПАРАМЕТРОВ ПОТЕНЦИАЛА

Как отмечено выше, главными параметрами, определяющими характер нестационарного запаздывания, являются параметры затухания ${{\beta }_{1}}$, ${{\beta }_{2}}$, а также параметр кубической нелинейности $\delta $. Однако потенциал (8) содержит также параметр линейной связи ${{\gamma }_{1}}$ и параметр нелинейной связи $\eta $. Отметим роль этих параметров в формировании эффекта запаздывания.

Параметры линейной связи ${{\gamma }_{1}}$ и ${{\gamma }_{2}}$, по-видимому, должны быть равными друг другу, как это следует из единства потенциала для обоих осцилляторов [28]. Их величина довольно критична, но резкого порога не имеет и сильно зависит от соотношения других параметров. В общем случае можно полагать, что при слишком слабой связи для достижения запаздывания надо значительно повышать другие параметры, в первую очередь амплитуду возбуждения, а при слишком сильной связи время запаздывания падает и стремится к времени релаксации того осциллятора, для которого это время меньше. В данной работе параметры линейной связи полагались равными 10 отн. ед., что позволило не слишком увеличивать остальные параметры, а также получить время запаздывания примерно посередине между временами релаксации обоих осцилляторов.

Параметр нелинейной связи $\eta $ обязательно должен быть отрицательным, так как при положительном параметре запаздывание отсутствует при любом наборе других параметров. Далее, его величина также имеет некоторое среднее значение, ниже которого запаздывание отсутствует, а выше наблюдаются другие нестационарные режимы, такие как многоступенчатое запаздывание и автомодуляционные процессы, в том числе стохастического характера. В данной работе параметр нелинейной связи полагался равным –200 отн. ед., что позволило реализовать запаздывание в его простейшем варианте. Некоторые особенности влияния параметров линейной и нелинейной связи отмечены в работах [19, 20]. Более подробному их рассмотрению авторы предполагают посвятить отдельную работу.

ЗАКЛЮЧЕНИЕ

Рассмотрена задача о возбуждении нелинейных вынужденных колебаний намагниченности и упругого смещения в нормально намагниченной ферритовой пластине. Рассмотрение проведено на основе упрощенной модели системы из двух связанных осцилляторов, один из которых обладает гиромагнитными свойствами.

Для типичных параметров задачи о возбуждении гиперзвука СВЧ-диапазона в пленке железоиттриевого граната выполнена численная оценка коэффициента нелинейного слагаемого, содержащего произведение квадрата амплитуды колебаний магнитного осциллятора на первую степень амплитуды колебаний упругого осциллятора. Выявлено критическое значение постоянного поля, при котором знак коэффициента нелинейной связи меняется на противоположный.

Выполнено исследование развития вынужденных колебаний во времени. Показано, что в условиях умножения частоты второго осциллятора относительно частоты первого возбуждение колебаний происходит с нестационарным запаздыванием во времени. По окончании запаздывания происходит скачкообразный рост амплитуды колебаний на один-два порядка и более, после чего амплитуда развившихся колебаний стремится к стационарному значению.

Выявлены необходимые условия реализации нестационарного запаздывания. Показано, что важнейшим условием является значительное (не менее чем в несколько раз) различие времен релаксации осцилляторов, причем время запаздывания приходится на интервал между временами релаксации обоих осцилляторов.

Отмечен пороговый характер реализации запаздывания по отношению к амплитуде возбуждения и критический характер по параметру кубической нелинейности первого осциллятора.

Для интерпретации эффекта запаздывания предложена гипотеза о наличии наряду с основным дополнительного минимума потенциала системы, отделенного от основного потенциальным барьером. На основании предложенной гипотезы построена модель динамического потенциала, отражающая характер колебаний первого осциллятора при условии использования амплитуды второго осциллятора в качестве параметра.

В рамках предложенной модели подробно исследован характер запаздывания в широком интервале изменения амплитуды возбуждения. Выявлено критическое значение амплитуды, превышение которого является необходимым условием реализации запаздывания.

Подробно исследована зависимость запаздывания и характера возбуждаемых колебаний от параметра кубической нелинейности первого осциллятора. Выявлена решающая роль кубической нелинейности в ограничении амплитуды возбуждаемых колебаний. Отмечен нижний критический уровень параметра кубической нелинейности, необходимый для реализации такого ограничения. Показано, что при значении параметра, ниже критического, запаздывание имеет место, но через некоторое время возбуждаемые колебания теряют устойчивость и система уходит на бесконечность. Обнаружен верхний критический уровень параметра кубической нелинейности, выше которого запаздывание пропадает, т.е. происходит как бы его подавление. Наблюдаемые нижний и верхний критические уровни параметра кубической нелинейности интерпретированы на основе модели динамического потенциала с учетом четной (четвертой) степени потенциала кубической нелинейности.

Работа выполнена в рамках государственного задания.