Радиотехника и электроника, 2021, T. 66, № 8, стр. 772-781
Оценка параметров импульсных сигналов неизвестной формы на фоне аддитивной смеси белого гауссовского шума и линейной составляющей с неизвестными параметрами
А. Г. Вострецов a, b, *, С. Г. Филатова a
a Новосибирский государственный технический университет
630073 Новосибирск, просп. К. Маркса, 20, Российская Федерация
b Институт горного дела им. Н.А. Чинакала Сибирского отделения РАН
630091 Новосибирск, Красный просп., 54, Российская Федерация
* E-mail: vostreczov@corp.nstu.ru
Поступила в редакцию 18.12.2020
После доработки 08.02.2021
Принята к публикации 19.03.2021
Аннотация
Предложен алгоритм оценки параметров импульсных сигналов неизвестной формы, наблюдаемых на фоне аддитивной смеси белого гауссовского шума и линейной составляющей с неизвестными параметрами. Показано, что предлагаемый подход, основанный на использовании метода контраста, метода моментов и свойств полных достаточных статистик, обеспечивает эффективность оценок и не требует априорной информации о форме, временном положении, длительности и амплитуде импульсного сигнала, а также о параметрах фоновой составляющей. Проведено сравнение с алгоритмами, рассчитанными на известную форму сигнала.
ВВЕДЕНИЕ
Проблема оценки параметров импульсных сигналов, наблюдаемых на фоне аддитивных помех, является важной задачей, вызывающей большой интерес специалистов по обработке сигналов, включая радио- и гидролокацию, мобильную связь, беспроводные сенсорные сети и др. К ключевым задачам, связанным с современными цифровыми информационными системами, относятся обеспечение высокой эффективности обработки оцифрованных сигналов, повышение скорости обработки и обеспечение возможности автоматической адаптации к условиям эксперимента. Задача оценки параметров импульсных сигналов заданной формы, наблюдаемых на фоне аддитивного белого гауссовского шума, стала классической и имеет множество применений, таких как радиотехнические системы, включая радиолокацию и радионавигацию [1–3], связь [4], медицина [5], оценка местоположения источника сигнала (например, излучающего радио-, акустические или оптические сигналы) и т.п. [6].
Существует множество практических приложений, требующих оценки параметров импульсного сигнала неизвестной формы и длительности, регистрируемого на фоне шума с неизвестными характеристиками. Такие задачи рассматривались, например, в работах [7, 8], посвященных исследованию источников помех в прецизионных, в том числе криогенных, измерительных системах. Работа [9] посвящена измерению времени прихода импульса артериального давления при оценке кардиоваскулярного риска. В работах [10, 11] предложены алгоритмы оценки параметров импульсных сейсмических сигналов в распределенных системах охраны протяженных периметров. При оценке параметров сигналов в рассмотренных работах авторы, как правило, используют модель аддитивного белого гауссовского шума, аппроксимацию сигнала известной функцией и стандартные методы оценки (байесовский, максимального правдоподобия и т.п.). Здесь качество оценки во многом определяется точностью аппроксимации сигнала и адекватностью применяемой модели аддитивного белого шума.
Существуют задачи обнаружения и оценки сигналов, форма которых априори полностью не известна (обнаружение несанкционированных источников излучения, сейсмолокация и др.). Кроме того, при прецизионных низкочастотных измерениях существенное влияние на качество оценок оказывают фликкер-шум и низкочастотные электромагнитные наводки, параметры которых трудно предсказать на каждом конкретном интервале измерений. При достаточно коротких интервалах наблюдения временная реализация фликкер-шума или низкочастотной наводки хорошо аппроксимируется линейной функцией. Все это делает рассматриваемую в данной работе задачу разработки алгоритмов оценки параметров импульсных сигналов неизвестной формы, наблюдаемых на фоне аддитивной смеси белого гауссовского шума и линейной составляющей с неизвестными параметрами, актуальной.
Целью данной работы является синтез алгоритмов оценки параметров фоновой составляющей, энергетического параметра, временного положения и длительности импульсных сигналов неизвестной формы, наблюдаемых на фоне аддитивной смеси белого гауссовского шума и линейной составляющей с неизвестными параметрами, а также исследование характеристик алгоритмов методами имитационного моделирования.
1. МОДЕЛЬ НАБЛЮДАЕМОГО ПРОЦЕССА
В качестве модели наблюдаемого на временном интервале Tx процесса x(t) примем аддитивную смесь полезного сигнала s(t) и фоновой составляющей η(t): $x(t) = s(t) + \eta (t)$, при этом сигнал s(t) имеет конечную длительность τ0 и полностью находится в пределах интервала наблюдения Tx, т.е. ${{\tau }_{0}} \leqslant {{T}_{x}}$.
Характер фона во многом зависит от конкретного приложения. Например, в прецизионных системах низкочастотных измерений существенную роль играет фликкер-шум и электромагнитные наводки. В том случае, когда интервал наблюдения много меньше времени корреляции фликкер-шума или периода электромагнитной наводки, текущую реализацию фона можно представить в виде суммы квазидетерминированной линейной составляющей $g(t) = {{a}_{0}} + {{a}_{1}}t$ с неизвестными параметрами a0, a1 и белого гауссовского шума $\xi (t)$ с нулевым средним и неизвестной спектральной плотностью: $\eta (t) = {{a}_{0}} + {{a}_{1}}t + \xi (t)$.
Таким образом, наблюдаемый процесс в общем случае будет иметь вид
Сигнал s(t), наблюдаемый на интервале Tx, характеризуется энергией, временным положением и длительностью. Введем понятие текущей энергии сигнала $E(t)$, накопленной в интервале наблюдения Tx к текущему моменту времени t:
Тогда полная энергия полезного сигнала на интервале Tx определится как
а распределение накопленной на интервале Tx энергии сигнала будет определяться функциями нормированных текущей энергииРассмотрим теперь понятия временного положения и длительности сигнала. В литературе имеются различные подходы к их определению. Одним из них является “энергетический” подход, при котором временное положение сигнала $\bar {t}$ определяется как координата центра тяжести текущей энергии сигнала на интервале наблюдения Tx:
Аналогично при энергетическом подходе за длительность сигнала принимают эффективную длительность – среднеквадратическое отклонение от координаты центра тяжести:
Альтернативным способом оценки временных параметров сигнала является подход, предложенный авторами в работе [12], также основанный на энергетических свойствах сигнала. За положение T0 сигнала на оси времени принимается медиана распределения накопленной энергии на интервале Tx, т.е. решение уравнения $e({{T}_{0}}) = {{L}_{0}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$, а длительность сигнала определяется длительностью интервала $\tau = {{T}_{2}} - {{T}_{1}}$, в течение которого энергия сигнала возрастет от ${{E}_{{{{T}_{1}}}}} = {{L}_{1}}{{E}_{s}}$ до ${{E}_{{{{T}_{2}}}}} = {{L}_{2}}{{E}_{s}}$, где L1, L2 – относительные пороговые уровни текущей энергии, T1, T2 – моменты времени, в которые происходит пересечение соответствующего порогового уровня. Эти определения временного положения и длительности сигнала используются в данной работе.
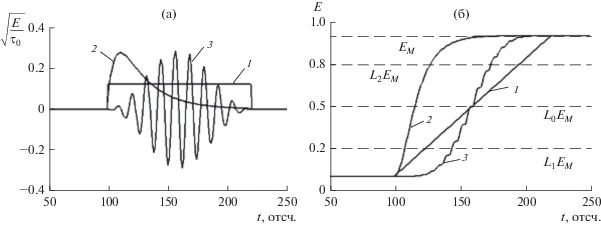
На рис. 1а приведены три импульсных сигнала: прямоугольный, двойной экспоненциальный и косинус-квадрат с гармоническим заполнением. Все импульсы имеют одинаковые энергии ${{E}_{s}} = 1$ и длительность по основанию τ0. На рис. 1б приведены графики зависимости текущей энергии от времени для этих же импульсов (сплошные линии) и пороговые значения энергии (пунктир). Относительные пороговые значения энергии приняты равными ${{L}_{0}} = 0.5$, ${{L}_{1}} = 0.2$ и ${{L}_{2}} = 0.8$.
2. СИНТЕЗ АЛГОРИТМОВ ОЦЕНКИ ПАРАМЕТРОВ СИГНАЛA И ФОНОВОЙ СОСТАВЛЯЮЩЕЙ
В качестве исходных данных для синтеза алгоритмов оценки параметров фоновой составляющей, энергетического параметра и параметров временного положения и длительности импульсных сигналов примем M-мерный выборочный вектор $\vec {x} = {{\left\{ {{{x}_{1}},{{x}_{2}},...,{{x}_{M}}} \right\}}^{T}}$, составленный из статистически независимых отсчетов наблюдаемого процесса (1), взятых в моменты времени kΔt, $k = 1,...,M$, где Δt – шаг дискретизации, MΔt = Tx, ${{\left\{ \cdot \right\}}^{T}}$ означает транспонирование. Вектор $\vec {x}$ в общем случае представляет собой сумму векторов полезного сигнала $\vec {s} = {{\left\{ {{{s}_{1}},{{s}_{2}},...,{{s}_{M}}} \right\}}^{T}}$, линейной составляющей фона
Компоненты вектора $\vec {s}$, параметры a0 и a1 вектора $\vec {g}$ являются априорно неопределенными детерминированными величинами, а компоненты вектора $\vec {\xi }$ – статистически независимыми гауссовскими величинами с нулевым средним значением и неизвестной дисперсией σ2.
Поскольку исходными данными для синтеза алгоритма является дискретная выборка из наблюдаемого процесса, то вместо выражения (2) будем пользоваться его дискретным аналогом:
Очевидно, что полная энергия сигнала на интервале наблюдения Tx, подлежащая оценке, равна EM.
Плотность распределения вероятностей вектора $\vec {x}$ имеет следующий вид:
(5)
$\begin{gathered} w(\vec {x}) = {{\left( {\frac{1}{{\sqrt {2\pi } \sigma }}} \right)}^{M}} \times \\ \times \,\,\exp \left\{ { - \frac{1}{{2{{\sigma }^{2}}}}\sum\limits_{k = 1}^M {{{{\left( {{{x}_{k}} - {{a}_{0}} - {{a}_{1}}k\Delta t - {{s}_{k}}} \right)}}^{2}}} } \right\}. \\ \end{gathered} $Если дисперсия шумовой составляющей фона σ2, параметры a0, a1 и форма сигнала неизвестны, то число неизвестных параметров распределения (5) на 3 больше числа отсчетов M наблюдаемого процесса к моменту времени M, поэтому необходима дополнительная информация о характеристиках наблюдаемого процесса. Поскольку форма сигнала по условию является неизвестной, то единственной возможностью получения дополнительной информации является расширение интервала наблюдения за счет включения в него участка Ty, заведомо содержащего только фоновый процесс. Воспользуемся методом контраста, известным из теории обнаружения сигналов [13]. Указанный метод состоит в том, что на интервале времени ${{T}_{y}} = N\Delta t$, в котором заведомо отсутствует полезный сигнал, формируется “фоновый” выборочный вектор $\vec {y} = {{\left\{ {{{y}_{1}},{{y}_{2}},...,{{y}_{N}}} \right\}}^{T}}$, а затем на интервале Tx – выборочный вектор $\vec {x}$, содержащий отсчеты полезного сигнала и фоновой составляющей. Будем полагать, что интервалы Ty и Tx следуют непосредственно друг за другом.
Совместное распределение вероятностей выборочных векторов $\vec {x}$ и $\vec {y}$ имеет следующий вид:
(6)
$\begin{gathered} w(\vec {x},\vec {y}) = {{\left( {\frac{1}{{\sqrt {2\pi } \sigma }}} \right)}^{{N + M}}} \times \\ \times \,\,\exp \left\{ { - \frac{1}{{2{{\sigma }^{2}}}}\left[ {\sum\limits_{n = 1}^N {{{{\left( {{{y}_{n}} - {{a}_{0}} - {{a}_{1}}n\Delta t} \right)}}^{2}}} + } \right.} \right. \\ \left. {\left. { + \,\,\sum\limits_{k = 1}^M {{{{\left[ {{{x}_{k}} - {{a}_{0}} - {{a}_{1}}(N + k)\Delta t - {{s}_{k}}} \right]}}^{2}}} } \right]} \right\}. \\ \end{gathered} $Для удобства синтеза алгоритма оценки параметров сигнала и фона представим выражение (6) в следующем виде:
(7)
$\begin{gathered} w(\vec {y},\vec {x}) = C\left( {\vec {s},{{a}_{0}},{{a}_{1}},{{\sigma }^{2}}} \right) \times \\ \times \,\,\exp \left\{ { - \frac{1}{{2{{\sigma }^{2}}}}\left( {\sum\limits_{n = 1}^N {y_{n}^{2}} + \sum\limits_{k = 1}^M {x_{k}^{2}} } \right) + } \right. \\ + \,\,\frac{{{{a}_{0}}}}{{{{\sigma }^{2}}}}\left( {\sum\limits_{n = 1}^N {{{y}_{n}}} + \sum\limits_{k = 1}^M {{{x}_{k}}} } \right) + \\ \left. { + \,\,\frac{{{{a}_{1}}\Delta t}}{{{{\sigma }^{2}}}}\left[ {\sum\limits_{n = 1}^N {n{{y}_{n}}} + \sum\limits_{k = 1}^M {(N + k){{x}_{k}}} } \right] + \sum\limits_{k = 1}^M {\frac{{{{s}_{k}}}}{{{{\sigma }^{2}}}}{{x}_{k}}} } \right\}, \\ \end{gathered} $Полученное распределение принадлежит экспоненциальному семейству, характеризуется (M + 3) параметрами с достаточными статистиками:
для параметра ${{ - 1} \mathord{\left/ {\vphantom {{ - 1} {(2{{\sigma }^{2}})}}} \right. \kern-0em} {(2{{\sigma }^{2}})}}$ –
для параметра a0/σ2 – для параметра ${{{{a}_{1}}\Delta t} \mathord{\left/ {\vphantom {{{{a}_{1}}\Delta t} {{{\sigma }^{2}}}}} \right. \kern-0em} {{{\sigma }^{2}}}}$ – и Zk = xk для параметров sk/σ2, k = 1, …, M. При неизвестных σ2, a0, a1, s1, …, sM вектор параметровДля оценки дисперсии шума σ2, параметров линейной составляющей a0, a1 и текущей энергии сигнального импульса Em воспользуемся методом, аналогичным методу моментов. Классический метод моментов предполагает выражение моментов распределения вероятностей наблюдаемых данных нескольких порядков через искомые параметры и отыскание последних решением полученной системы уравнений. Затем истинные моменты заменяются выборочными, и при больших объемах выборки полученная оценка стремится к истинному значению. В нашем случае для составления системы уравнений будем использовать выражения для начальных моментов первого и второго порядка полных достаточных статистик. В полученном решении истинные моменты заменим значениями полных достаточных статистик в соответствующей степени. Полученные таким образом оценки будут зависеть от исходной выборки только через полные достаточные статистики. Особенность оценок, зависящих от полных достаточных статистик, состоит в том, что если искомый параметр представляет собой линейную комбинацию моментов полных достаточных статистик произвольного порядка, то полученная оценка будет эффективной (несмещенной и с минимальным значением квадратичной функции потерь) [13], причем эта оценка будет существенно единственной [16]. Если же зависимость оценки от полных достаточных статистик нелинейная, то полученная оценка может иметь смещение, однако и в этом случае она будет минимизировать квадратичную функцию потерь в классе Kb оценок, имеющих смещение b, и будет существенно единственной [17].
Получим выражения для следующих начальных моментов полных достаточных статистик:
(8)
$\begin{gathered} {\mathbf{M}}\left\{ {{{Z}_{0}}} \right\}\,\,{\text{ = }}\,\,{{\sigma }^{2}}(M + N) + a_{0}^{2}(M + N) + \\ + \,\,a_{1}^{2}\Delta {{t}^{2}}\frac{{(2M + 2N + 1)(M + N + 1)(M + N)}}{6} + \\ + \,\,{{a}_{0}}{{a}_{1}}\Delta t(M + N)(M + N + 1) + 2{{a}_{0}}\sum\limits_{k = 1}^M {{{s}_{k}}} + \,2{{a}_{1}}\Delta t\sum\limits_{k = 1}^M {\left[ {(N + k){{s}_{k}}} \right]} + \sum\limits_{k = 1}^M {s_{k}^{2};} \\ \end{gathered} $(9)
${\mathbf{M}}\left\{ {{{Y}_{0}}} \right\}\,\,{\text{ = }}\,\,a_{0}^{{}}(M + N) + \,\,a_{1}^{{}}\Delta t\frac{{(M + N)(M + N + 1)}}{2} + \sum\limits_{k = 1}^M {{{s}_{k}}} ;$(10)
$\begin{gathered} {\mathbf{M}}\left\{ {{{Y}_{1}}} \right\}{\text{ = }}\,\,a_{0}^{{}}\frac{{(M + N)(M + N + 1)}}{2} + \\ + \,\,a_{1}^{{}}\Delta t\frac{{(M + N)(M + N + 1)(2M + 2N + 1)}}{6} + \,\,\sum\limits_{k = 1}^M {\left[ {(N + k){{s}_{k}}} \right]} ; \\ \end{gathered} $(11)
${\mathbf{M}}\left\{ {{{Z}_{k}}} \right\} = {{a}_{0}} + {{a}_{1}}\Delta t(N + k) + {{s}_{k}},\,\,\,k = 1,...,M;$(12)
$\begin{gathered} {\mathbf{M}}\left\{ {Z_{k}^{2}} \right\} = {{\sigma }^{2}} + a_{0}^{2} + s_{k}^{2} + a_{1}^{2}\Delta {{t}^{2}}{{(N + k)}^{2}} + \,\,2{{a}_{0}}{{a}_{1}}\Delta t(N + k) + 2{{a}_{1}}\Delta t{{s}_{k}}(N + k) + 2{{a}_{0}}{{s}_{k}}, \\ k = 1,...,M. \\ \end{gathered} $В выражениях (8)–(12) ${\mathbf{M}}\left\{ \cdot \right\}$ означает вычисление математического ожидания.
Решая систему уравнений (8)–(12) относительно σ2, a0, a1, $\sum\nolimits_{k = 1}^M {s_{k}^{2}} $, получим
(13)
${{a}_{0}} = \frac{{2(2N + 1){\mathbf{M}}\left\{ {{{Y}_{0}}} \right\} - 6{\mathbf{M}}\left\{ {{{Y}_{1}}} \right\} + 2\sum\limits_{k = 1}^M {\left[ {(N + 3k - 1){\mathbf{M}}\left\{ {{{Z}_{k}}} \right\}} \right]} }}{{N(N - 1)}};$(14)
${{a}_{1}} = \frac{{12{\mathbf{M}}\left\{ {{{Y}_{1}}} \right\} - 6(N + 1){\mathbf{M}}\left\{ {{{Y}_{0}}} \right\} - 6\sum\limits_{k = 1}^M {\left[ {(N + 2k - 1){\mathbf{M}}\left\{ {{{Z}_{k}}} \right\}} \right]} }}{{N({{N}^{2}} - 1)\Delta t}};$(15)
$\begin{gathered} {{\sigma }^{2}} = \frac{1}{{6N}}\left[ {6{\mathbf{M}}\left\{ {{{Z}_{0}}} \right\} - 6Na_{0}^{2} - a_{1}^{2}\Delta {{t}^{2}}N(2{{N}^{2}} + 3N + 1) - } \right. \\ \left. { - \,\,6N{{a}_{0}}{{a}_{1}}\Delta t(N + 1) - 6\sum\limits_{k = 1}^M {{\mathbf{M}}\left\{ {Z_{k}^{2}} \right\}} } \right]; \\ \end{gathered} $(16)
$\begin{gathered} \sum\limits_{k = 1}^M {s_{k}^{2}} = \left[ {\sum\limits_{k = 1}^M {{\mathbf{M}}\left\{ {Z_{k}^{2}} \right\}} + a_{0}^{2}(2N + M) - } \right. \\ - \,\,M{{\sigma }^{2}} - 2{{a}_{0}}{\mathbf{M}}\left\{ {{{Y}_{0}}} \right\} + {{a}_{0}}{{a}_{1}}\Delta t \times \\ \times \,\,\left[ {{{M}^{2}} + 2MN + M + 2{{N}^{2}} + 2N} \right] - \\ - \,\,2{{a}_{1}}\Delta t{\mathbf{M}}\left\{ {{{Y}_{1}}} \right\} + a_{1}^{2}\Delta {{t}^{2}} \times \\ \left. { \times \,\,\frac{{(M + 2N + 1)(2{{M}^{2}} + 2MN + M + 2{{N}^{2}} + 2N)}}{6}} \right]. \\ \end{gathered} $Заменяя в выражениях (13)–(16) моменты ${\mathbf{M}}\left\{ \cdot \right\}$ полными достаточными статистиками, получим выражения для оценок интересующих параметров:
(17)
${{\hat {a}}_{0}} = \frac{{2(2N + 1){{Y}_{0}} - 6{{Y}_{1}} + 2\sum\limits_{k = 1}^M {\left[ {(N + 3k - 1){{Z}_{k}}} \right]} }}{{N(N - 1)}};$(18)
${{\hat {a}}_{1}} = \frac{{12{{Y}_{1}} - 6(N + 1){{Y}_{0}} - 6\sum\limits_{k = 1}^M {\left[ {(N + 2k - 1){{Z}_{k}}} \right]} }}{{N({{N}^{2}} - 1)\Delta t}};$(19)
$\begin{gathered} \widehat {{{\sigma }^{2}}} = \frac{1}{{6N}}\left[ {6{{Z}_{0}} - 6N\hat {a}_{0}^{2} - \hat {a}_{1}^{2}\Delta {{t}^{2}}N(2{{N}^{2}} + 3N + 1) - } \right. \\ \left. { - \,\,6N{{{\hat {a}}}_{0}}{{{\hat {a}}}_{1}}\Delta t(N + 1) - 6\sum\limits_{k = 1}^M {Z_{k}^{2}} } \right]; \\ \end{gathered} $(20)
$\begin{gathered} {{{\hat {E}}}_{M}} = \left( {\sum\limits_{k = 1}^M {s_{k}^{2}} } \right)\Delta t = \\ = \left[ {\sum\limits_{k = 1}^M {Z_{k}^{2}} + \hat {a}_{0}^{2}(2N + M) - M{{\sigma }^{2}} - 2{{{\hat {a}}}_{0}}{{Y}_{0}} + } \right. \\ \,\, + {{{\hat {a}}}_{0}}{{{\hat {a}}}_{1}}\Delta t\left[ {{{M}^{2}} + 2MN + M + 2{{N}^{2}} + 2N} \right] - \\ - \,\,2{{{\hat {a}}}_{1}}\Delta t{{Y}_{1}} + \hat {a}_{1}^{2}\Delta {{t}^{2}} \times \\ \left. { \times \,\,\frac{{(M + 2N + 1)(2{{M}^{2}} + 2MN + M + 2{{N}^{2}} + 2N)}}{6}} \right]\Delta t. \\ \end{gathered} $Для получения оценки текущей энергии ${{\hat {E}}_{m}}$ в выражении (20) следует заменить M на m. В принципе, в выражении (20) в силу случайного характера компонентов выборочных векторов может получиться отрицательное значение энергии, особенно при малых объемах выборки, как это имеет место на начальном этапе оценивания текущей энергии ${{\hat {E}}_{m}}$. В этом случае следует принять ${{\hat {E}}_{m}} = 0$.
Окончательные выражения полученных оценок нетрудно получить, заменив ${{Y}_{0}},{{Y}_{1}},{{Z}_{0}},{{Z}_{1}},...,{{Z}_{M}}$ их значениями. Приведем окончательные выражения для оценок параметров фоновой составляющей:
(21)
${{\hat {a}}_{0}} = \frac{{2\sum\limits_{n = 1}^N {\left( {2N + 1 - 3n} \right){{y}_{n}}} }}{{N(N - 1)}};$(22)
${{\hat {a}}_{1}} = \frac{{6\sum\limits_{n = 1}^N {\left( {2n - N - 1} \right){{y}_{n}}} }}{{N(N - 1)(N + 1)\Delta t}};$(23)
$\widehat {{{\sigma }^{2}}} = \frac{{\left\{ {N(N - 1)(N + 1)\sum\limits_{n = 1}^N {y_{n}^{2}} + 12(N + 1)\left[ {\sum\limits_{n = 1}^N {\left( {n{{y}_{n}}} \right)} } \right]\left( {\sum\limits_{n = 1}^N {{{y}_{n}}} } \right) - 2(2{{N}^{2}} + 3N + 1){{{\left( {\sum\limits_{n = 1}^N {{{y}_{n}}} } \right)}}^{2}} - 12{{{\left[ {\sum\limits_{n = 1}^N {\left( {n{{y}_{i}}} \right)} } \right]}}^{2}}} \right\}}}{{{{N}^{2}}(N - 1)(N + 1)}}.$Из выражений (21)–(23) видно, что параметры фона оцениваются только по фоновой выборке на интервале Ty. На интервале Tx выделить фоновую составляющую не представляется возможным, так как ни уровень, ни форма сигнала, ни его длительность и положение на временной оси неизвестны.
Оценки ${{\hat {a}}_{0}}$ и ${{\hat {a}}_{1}}$ – несмещенные и эффективные, так как они являются линейными комбинациями полных достаточных статистик. Оценки $\widehat {{{\sigma }^{2}}}$ и ${{\hat {E}}_{m}}$ представляют собой нелинейные функции полных достаточных статистик, поэтому требуют отдельного исследования на несмещенность.
Для оценки временного положения T0 и длительности τ сигнала выберем моменты времени, когда оценка текущей энергии ${{\hat {E}}_{m}}$ достигает значений ${{E}_{{{{T}_{0}}}}} = {{L}_{0}}{{\hat {E}}_{M}}$, ${{E}_{{{{T}_{1}}}}} = {{L}_{1}}{{\hat {E}}_{M}}$ и ${{E}_{{{{T}_{2}}}}} = {{L}_{2}}{{\hat {E}}_{M}}$. Соответствующие моменты времени ${{\hat {T}}_{0}}$, ${{\hat {T}}_{1}}$ и ${{\hat {T}}_{2}}$ будут оценками временного положения, начала и окончания сигнала, а величина $\hat {\tau } = {{\hat {T}}_{2}} - {{\hat {T}}_{1}}$ – оценкой его длительности.
3. ОЦЕНКА ЭФФЕКТИВНОСТИ АЛГОРИТМОВ
Как уже отмечалось, оценки ${{\hat {a}}_{0}}$ и ${{\hat {a}}_{1}}$ являются несмещенными, их дисперсии $\sigma _{{{{{\hat {a}}}_{0}}}}^{2}$ и $\sigma _{{{{{\hat {a}}}_{1}}}}^{2}$ легко вычисляются аналитически:
(24)
${\mathbf{D}}({{\hat {a}}_{0}}) = \sigma _{{{{{\hat {a}}}_{0}}}}^{2} = \frac{{2\left( {2N + 1} \right)}}{{N\left( {N - 1} \right)}}{{\sigma }^{2}};$(25)
${\mathbf{D}}({{\hat {a}}_{1}}) = \sigma _{{{{{\hat {a}}}_{1}}}}^{2} = \frac{{12}}{{N\left( {N + 1} \right)\left( {N - 1} \right){{{\left( {\Delta t} \right)}}^{2}}}}{{\sigma }^{2}},$Анализ эффективности оценок оставшихся параметров выполнялся методом статистических испытаний на ЭВМ по 10 000 экспериментов. Для этого на интервалах Ty и Tx в соответствии с формулой (3) моделировались выборочные векторы $\vec {y}$ и $\vec {x}$ размерностью соответственно N и M при следующих значениях параметров: ${{\sigma }^{2}} = 1$, ${{a}_{0}} = - 2\sigma $, ${{a}_{1}} = {{{{{10}}^{{ - 3}}}\sigma } \mathord{\left/ {\vphantom {{{{{10}}^{{ - 3}}}\sigma } {\Delta t}}} \right. \kern-0em} {\Delta t}}$, $\Delta t = 1$. В качестве сигналов использовались рассмотренные ранее прямоугольный, двойной экспоненциальный и косинус-квадрат с гармоническим заполнением импульсы (см. рис. 1) одинаковой длительности по основанию ${{\tau }_{0}} = 120$ отсчетов. Энергия сигналов принималась одинаковой, и ее значение зависело от задаваемого отношения сигнал/шум (ОСШ) ${{q}^{2}} = {{{{E}_{M}}} \mathord{\left/ {\vphantom {{{{E}_{M}}} {({{\tau }_{0}}{{\sigma }^{2}})}}} \right. \kern-0em} {({{\tau }_{0}}{{\sigma }^{2}})}}$.
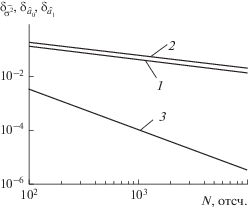
На рис. 2 показаны полученные в результате моделирования зависимости относительного среднеквадратического отклонения (СКО) оценки $\widehat {{{\sigma }^{2}}}$ дисперсии гауссовского шума (${{\delta }_{{\widehat {{{\sigma }^{2}}}}}}$, кривая 1), оценок коэффициентов линейной составляющей фона ${{\hat {a}}_{0}}$ (${{\delta }_{{{{{\hat {a}}}_{0}}}}}$, кривая 2) и ${{\hat {a}}_{1}}$ (${{\delta }_{{{{{\hat {a}}}_{1}}}}}$, кривая 3) от объема шумовой выборки. Нормировка производилась для оценки $\widehat {{{\sigma }^{2}}}$ – к дисперсии гауссовского шума σ2, для оценки ${{\hat {a}}_{0}}$ – к среднеквадратическому значению σ, для ${{\hat {a}}_{1}}$ – к параметру σ/Δt.
Рис. 2.
Зависимость относительных СКО оценок дисперсии ${{\delta }_{{\widehat {{{\sigma }^{2}}}}}}$ (1) гауссовского шума и оценок коэффициентов линейной составляющей фона ${{\delta }_{{{{{\hat {a}}}_{0}}}}}$ (2) и ${{\delta }_{{{{{\hat {a}}}_{1}}}}}$ (3) от объема шумовой выборки N.
Как уже отмечалось, оценки ${{\hat {a}}_{0}}$ и ${{\hat {a}}_{1}}$ являются несмещенными. Их характеристики, полученные в результате моделирования, хорошо совпали с результатами аналитических расчетов. Оценка $\widehat {{{\sigma }^{2}}}$ также является практически несмещенной, величина смещения по результатам моделирования оказалась более чем на порядок меньше СКО оценки.
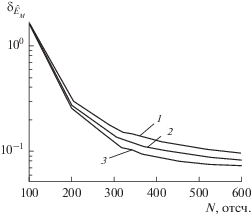
На рис. 3 приведены зависимости относительного СКО ${{\delta }_{{{{{\hat {E}}}_{M}}}}}$ оценки энергии сигналов трех типов от объема шумовой выборки N при фиксированном ОСШ, равном 10 дБ, объеме сигнальной выборки M = 600 и длительности сигнала τ0 = = 120 отсчетов. Нормировка производилась к истинной энергии импульса EM. При объеме шумовой выборки N < 200 относительное СКО оценки энергии становится больше 0.3, практически не зависит от формы сигнала и определяется в основном только объемом выборки. При больших объемах шумовой выборки различие в относительных СКО оценки энергии для рассматриваемых сигналов не превышало 0.01.
Рис. 3.
Зависимость относительного СКО оценки энергии ${{\delta }_{{{{{\hat {E}}}_{M}}}}}$ от объема шумовой выборки (а) и ОСШ (б): 1 – прямоугольный импульс, 2 – двойной экспоненциальный импульс, 3 – косинус-квадрат импульс с гармоническим заполнением.
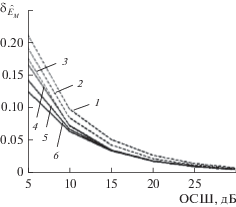
На рис. 4 представлены зависимости относительного СКО ${{\delta }_{{{{{\hat {E}}}_{M}}}}}$ оценки энергии сигналов трех типов от ОСШ при фиксированных длительности сигнала τ0 = 120 отсчетов и объемах шумовой выборки N = 600 и 5000. Объем сигнальной выборки M = 1000, 600 и 300. Видно, что при малых ОСШ СКО оценки зависит от формы импульса, соотношения длительности импульса и длины временного интервала, на котором формировалась сигнальная выборка, а также от объема шумовой выборки. Чем меньше доля импульса в сигнальном интервале и чем меньше шумовая выборка, тем менее точными получаются оценки. При больших отношениях сигнал/шум и рассматриваемых объемах выборки эта разница для рассматриваемых трех сигналов становится незначительной.
Рис. 4.
Зависимость относительного СКО оценки энергии ${{\delta }_{{{{{\hat {E}}}_{M}}}}}$ от ОСШ при τ0 = 120: N = 600 (1–3), 5000 (4–6), M = 1000 (1, 4), 600 (2, 5) и 300 (3, 6).
На рис. 5а–5в приведены зависимости относительных СКО ${{\delta }_{{\hat {T}}}}$ оценок временного положения точек пересечения текущей энергией сигнала соответствующих пороговых уровней от величины этих порогов для трех типов сигналов: прямоугольный импульс, двойной экспоненциальный импульс и косинус-квадрат импульс с гармоническим заполнением. Значения СКО получены при ОСШ = 5, 10 и 15 дБ. Длительность сигнала τ0 = 120 отсчетов и объем шумовой выборки N = 5000 оставались неизменными, объемы сигнальных выборок принимались равными M = 300, 600 и 1000. Нормировка осуществлялась к длительности импульса.
Рис. 5.
Зависимость относительного СКО оценки ${{\delta }_{{\hat {T}}}}$ временного положения точки пересечения порогового уровня от величины порога: а – прямоугольный импульс, б – двойной экспоненциальный импульс, в – косинус-квадрат импульс с гармоническим заполнением; ОСШ = 5 (1), 10 (2), 15 (3), M = 1000 (сплошные кривые), 600 (штриховые) и 300 (пунктирные).
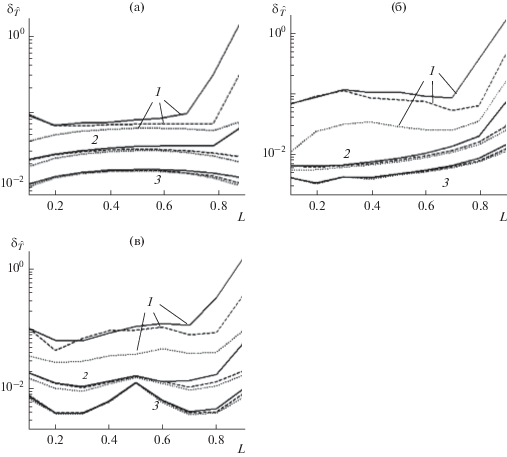
Из рисунка видно, что оценка временного положения существенно зависит от формы импульсов, при этом наименьшая ошибка оценки времени пересечения порога наблюдается на участках сигнала, имеющих наибольшую крутизну. Поэтому, если это возможно, значения порогов L1, L2, используемых при оценке длительности сигнала, следует выбирать таким образом, чтобы крутизна кривой текущей энергии в окрестности уровней ${{E}_{{{{T}_{1}}}}} = {{L}_{1}}{{E}_{M}}$ и ${{E}_{{{{T}_{2}}}}} = {{L}_{2}}{{E}_{M}}$ была максимальной. При ОСШ более 10 дБ для прямоугольного импульса эти значения находятся в диапазоне 0.1…0.3 и 0.7…0.9, а для косинус-квадрат импульса с гармоническим заполнением оптимальными являются пороги в диапазоне 0.2…0.4 и 0.6…0.8. При малых ОСШ (5 дБ) при пороговых уровнях больше 0.7EM алгоритм становится неработоспособным, ошибки превышают 0.2 и только в случае, когда сигнал занимает не менее 40% от длительности сигнального интервала, относительное СКО не превышает 0.1.
Влияние объема шумовой выборки на точность оценки временного положения точки пересечения порогового уровня показано в табл. 1.
Таблица 1.
Относительные СКО ${{\delta }_{{\hat {T}}}}$ оценок временных положений точек пересечения текущей энергией импульса пороговых уровней от величины порога (%)
| N, отсч. | Пороговый уровень L | ОСШ, дБ | |||
|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | ||
| Прямоугольный импульс | |||||
| 600 | 0.7 | 12.8 | 3.7 | 1.7 | 0.9 |
| 0.8 | 31.6 | 3.7 | 1.6 | 0.8 | |
| 0.9 | 95.0 | 11.1 | 1.4 | 0.7 | |
| 5000 | 0.7 | 6.9 | 3.1 | 1.6 | 0.9 |
| 0.8 | 7.1 | 2.9 | 1.4 | 0.8 | |
| 0.9 | 31.7 | 2.6 | 1.2 | 0.6 | |
| Двойной экспоненциальный импульс | |||||
| 600 | 0.7 | 9.5 | 1.5 | 0.7 | 0.4 |
| 0.8 | 39.5 | 2.3 | 1 | 0.5 | |
| 0.9 | 117.4 | 15.3 | 1.7 | 0.8 | |
| 5000 | 0.7 | 2.5 | 1.1 | 0.6 | 0.4 |
| 0.8 | 3.6 | 1.4 | 0.7 | 0.4 | |
| 0.9 | 16.5 | 2.5 | 1.1 | 0.6 | |
| Косинус-квадрат импульс с гармоническим заполнением | |||||
| 600 | 0.7 | 6.7 | 1.5 | 0.4 | 0.2 |
| 0.8 | 29 | 2 | 0.5 | 0.2 | |
| 0.9 | 101 | 10.2 | 1.3 | 0.4 | |
| 5000 | 0.7 | 8.3 | 1.1 | 0.4 | 0.2 |
| 0.8 | 9.1 | 1.4 | 0.4 | 0.2 | |
| 0.9 | 37.3 | 2.1 | 0.9 | 0.4 | |
Видно, что размер шумовой выборки существенно влияет на точность оценки при малых ОСШ, а также при больших пороговых уровнях, что имеет особое значение при оценке длительности импульса. При ОСШ = 5 дБ относительные СКО различаются при пороге 0.9 на 70…100%, при пороге 0.8 – на 20…40%, при пороге меньше 0.7 – меньше чем на 10%. Но уже при ОСШ 10 дБ объем шумовой выборки существенен только для порога 0.9. Таким образом, если при построении алгоритма оценки временного положения не представляется возможным использовать достаточно объемную шумовую выборку для оценки параметров шума, то следует выбрать пороги, не превышающие 0.7.
Для сравнения приведем характеристики алгоритмов, предложенных в работе [18] для оценки временного положения прямоугольного импульса с известной длительностью и полностью известным статистическим описанием наблюдаемых данных и в работе [19] – для импульса известной формы, наблюдаемого на фоне гауссовского шума с неизвестными параметрами. По данным работы [18], при ОСШ = 10 дБ относительное СКО оценки временного положения прямоугольного импульса составляет величину 0.425%. Это значительно меньше значения, полученного предложенным методом (1.4%), однако требует полной информации о форме сигнала и шуме. При неизвестных параметрах шума, но известной форме сигнала [19] СКО оценок временного положения имеют тот же порядок (2…8%), что и приведенные в табл. 1. Существенным преимуществом предлагаемого метода является то, что он допускает присутствие линейно изменяющейся помехи в фоновой составляющей наблюдаемого процесса и не требует априорной информации ни о параметрах фона, ни о параметрах и форме импульсного сигнала.
ЗАКЛЮЧЕНИЕ
Рассмотрена проблема оценки параметров импульсных сигналов неизвестной формы и временного положения, наблюдаемых на фоне аддитивной смеси белого гауссовского шума и линейной составляющей с неизвестными параметрами. Данная проблема особенно актуальна для пассивной локации источников неизвестных сигналов. С использованием метода контраста и свойств полных достаточных статистик получены оценки энергии сигнала и параметров фоновой составляющей. Использование метода контраста обеспечивает автоматическую подстройку алгоритма под параметры фоновой составляющей, а использование полных достаточных статистик гарантирует минимизацию квадратичной функции потерь для полученных оценок. Для оценки временного положения и длительности импульса предложено использовать статистики времен пересечения оценкой текущей энергии импульса пороговых значений.
Результаты расчетов и моделирования показали, что полученные оценки параметров линейной составляющей фона строго несмещенные, оценки дисперсии шума, энергии сигнала и его временных параметров имеют смещение почти на порядок меньше значений СКО. Предложенный алгоритм оценивания обеспечивает достаточную для большого числа практических приложений точность, соизмеримую с точностью известных, разработанных для оценки параметров сигналов заданной формы на фоне гауссовского шума с неизвестными параметрами.
Список литературы
Woodward P.M. Probability and Information Theory with Applications to Radar. N.Y.: McGraw-Hill, 1953.
Тихонов В.И. Статистическая радиотехника. 2-е изд. М.: Радио и связь, 1982.
Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. М.: Радио и связь, 1991.
Van Trees H.L. Detection, Estimation, and Modulation Theory. Pt. I. N.Y.: Wiley, 1968.
Sijber J., den Dekker A.J. // Magnetic Resonance in Medicine. 2004. V. 51. № 3. P. 586.
Xinya Li, Zhiqun D.D., Rauchenstein L., Carlson TJ. // Rev. Sci. Instrum. 2016. V. 87. № 4. P. 041502.
Rachpon K., Laucht A., Dehollain J.P. et al. // Rev. Sci. Instrum. 2016. V. 87. № 7. P. 073905.
Иванов Б.И., Грайцар М., Новиков И.Л. и др. // Письма в ЖТФ. 2016. Т. 42. № 7. С. 90.
Sol`a J., Vetter R., Renevey Ph. et al. // Physiol. Meas. 2009. V. 30. P. 603.
Succi G.P., Clapp D., Gampert R., Prado G. // Proc. SPIE. 2001. V. 4393. P. 22.
Филатова С.Г., Спектор А.А. // Автометрия. 2008. № 4. С. 68.
Курленя М.В., Вострецов А.Г., Кулаков Г.И., Яковицкая Г.Е. // Физико-технические проблемы разработки полезных ископаемых. 1999. № 4. С. 61.
Акимов П.С., Бакут П.А., Богданович В.А. и др. / Под ред. П.А. Бакута. Теория обнаружения сигналов. М.: Радио и связь, 1984.
Lehman E.L. Testing Statistical Hypotheses. N.Y.: Wiley, 1959.
Bocтpeцoв A.Г. // PЭ. 1999. T. 44. № 5. C. 551.
Zacks S. The Theory of Statistical Inference. N.Y.: Wiley, 1971.
Боровков А.А. Математическая статистика. М.: Наука, 1984.
Zehavi E. // IEEE Trans. 1984. V. AES-20. № 6. P.742.
Jingjing Pan, Meng Sun, Yide Wang et al. // Signal Processing. 2020. V. 176. P. 107654.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника