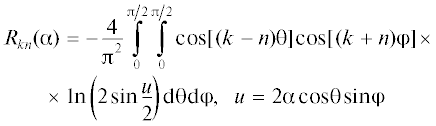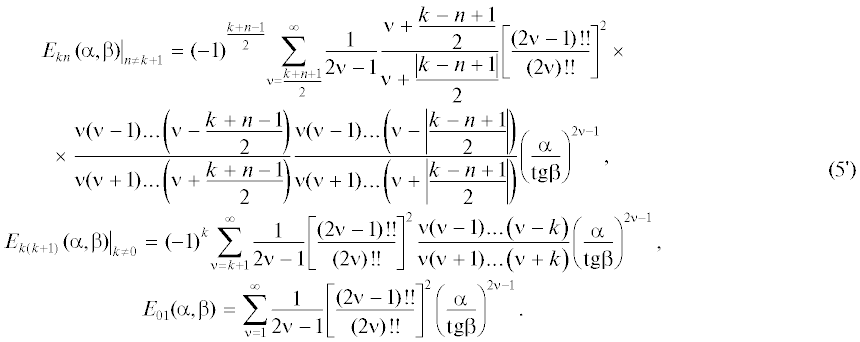Радиотехника и электроника, 2021, T. 66, № 9, стр. 837-844
Повышение эффективности проекционных моделей полосковых линий
А. Н. Коваленко a, А. Д. Ярлыков a, *
a МИРЭА – Российский технологический университет
119454 Москва, просп. Вернадского, 78, Российская Федерация
* E-mail: yarlykov@mirea.ru
Поступила в редакцию 16.09.2020
После доработки 16.09.2020
Принята к публикации 04.02.2021
Аннотация
Представлены матричные коэффициенты проекционных моделей полосковых линий, полученных с использованием чебышевского базиса, в виде суммы бесконечных медленно и быстро сходящихся рядов. Медленно сходящиеся ряды просуммированы и преобразованы в быстро сходящиеся степенные ряды. Установлен диагональный характер матрицы коэффициентов, позволяющий получить асимптотическое решение бесконечной системы линейных алгебраических уравнений. Приведены численные результаты, подтверждающие эффективность использования полученных представлений для медленно сходящихся рядов при построении проекционных моделей полосковых линий.
ВВЕДЕНИЕ
При построении проекционных моделей полосковых линий различного типа (микрополосковой, компланарной, щелевой и др.) граничная задача электродинамики сводится к системе интегральных уравнений относительно плотности тока на полосковых проводниках, или напряженности электрического поля в щелях. Решая ее проекционным методом, получаем бесконечную систему линейных алгебраических уравнений (СЛАУ) относительно коэффициентов разложения плотности тока, или поля по выбранной системе базисных функций. Эта система решается методом редукции и называется проекционной моделью исходной электродинамической задачи. Таким образом, процедура получения СЛАУ носит формальный характер. Сходимость проекционных разложений к точному решению задачи требует специального исследования и доказательства. Если строгое доказательство провести не удается, то проводится численное исследование сходимости от порядка СЛАУ. Точность решения и скорость сходимости существенно зависят от выбора системы базисных функций и их числа – K, а также от точности вычисления матричных коэффициентов. В работе [1] при построении проекционной модели экранированной микрополосковой линии впервые в качестве базисных функций использованы полиномы Чебышева с весовыми функциями, учитывающими в явном виде краевые особенности решения. В [2] получено асимптотическое решение бесконечной СЛАУ для микрополосковой линии в многослойной диэлектрической среде, что позволило теоретически установить быструю сходимость разложений плотности тока по чебышевскому базису и возможность решения бесконечной СЛАУ методом редукции. Для одиночной полосковой линии порядок редуцированной СЛАУ – K не превышает пяти в широком диапазоне изменения параметров. Но для достижения высокой точности решения необходимо также обеспечить высокую точность вычисления матричных коэффициентов СЛАУ, представленных в виде медленно сходящихся рядов. При непосредственном их вычислении нужно учитывать до 10 тысяч членов для одиночной линии, а для близко расположенных связанных линий трудно получить численные результаты с погрешностью менее 1% даже при учете до 50 тысяч членов. Эффективность проекционных моделей полосковых линий можно существенно повысить путем улучшения сходимости рядов для матричных коэффициентов. В [1] изложена методика улучшения сходимости этих рядов и получены выражения для матричных коэффициентов в виде быстро сходящихся рядов для экранированной микрополосковой линии с симметричным расположением полоскового проводника относительно боковых стенок экрана. В настоящей статье получены интегральные представления для медленно сходящихся рядов, через которые определяются асимптотические выражения матричных коэффициентов полосковых линий различного типа. Эти представления позволяют преобразовать выражения для матричных коэффициентов в быстро сходящиеся ряды и существенно повысить эффективность проекционных моделей полосковых линий, построенных с использованием чебышевского базиса.
1. ОБЩИЕ ВЫРАЖЕНИЯ ДЛЯ МАТРИЧНЫХ КОЭФФИЦИЕНТОВ ПРОЕКЦИОННЫХ МОДЕЛЕЙ ПОЛОСКОВЫХ ЛИНИЙ
При построении проекционных моделей полосковых линий с использованием чебышевского базиса матричные коэффициенты имеют вид
Представим выражение для матричных коэффициентов в виде
(1)
$\begin{gathered} {{A}_{{kn}}}({{\alpha }}) = \sum\limits_{m = 1}^\infty {({{A}_{m}} - A_{m}^{\infty }){{J}_{k}}(m{{\alpha }}){{J}_{n}}(m{{\alpha }}){{f}_{m}}({{\beta }})} + \\ + \,\,\sum\limits_{m = 1}^\infty {A_{m}^{\infty }{{J}_{k}}(m{{\alpha }}){{J}_{n}}(m{{\alpha }}){{f}_{m}}({{\beta }})} , \\ \end{gathered} $Таким образом, выражения для матричных коэффициентов проекционных моделей полосковых линий различного типа, полученных с использованием чебышевского базиса, можно представить в виде суммы двух бесконечных рядов, один из которых быстро сходится (коэффициенты в круглых скобках убывают как ${1 \mathord{\left/ {\vphantom {1 {{{m}^{3}}}}} \right. \kern-0em} {{{m}^{3}}}}$ при $m \to \infty $), а второй, медленно сходящийся, определяется через функции ${{R}_{{kn}}}({{\alpha }})$, ${{F}_{{kn}}}({{\alpha }},{{\beta }})$ и ${{E}_{{kn}}}({{\alpha }},{{\beta }})$:
(2)
$\begin{gathered} {{R}_{{kn}}}({{\alpha }}) = \sum\limits_{m = 1}^\infty {\frac{1}{m}{{J}_{k}}(m{{\alpha }}){{J}_{n}}(m{{\alpha }})} , \\ k + n - {\text{четные числа}} \\ {{F}_{{kn}}}({{\alpha }},{{\beta }}) = \sum\limits_{m = 1}^\infty {\frac{{\cos (2m{{\beta }})}}{m}{{J}_{k}}(m{{\alpha }}){{J}_{n}}(m{{\alpha }})} , \\ k + n--{\text{ четные числа}} \\ {{E}_{{kn}}}({{\alpha }},{{\beta }}) = \sum\limits_{m = 1}^\infty {\frac{{\sin (2m{{\beta }})}}{m}{{J}_{k}}(m{{\alpha }}){{J}_{n}}(m{{\alpha }})} , \\ k + n--{\text{ нечетные числа}}{\kern 1pt} . \\ \end{gathered} $В [1] получено интегральное представление для функции ${{R}_{{kn}}}({{\alpha }})$:
Используя интегральные представления для функций Бесселя и их произведений, можно получить следующие интегральные представления для функций ${{F}_{{kn}}}({{\alpha ,\beta }})$ и ${{E}_{{kn}}}({{\alpha ,\beta }})$ (см. Приложение):
(4)
$\begin{gathered} {{F}_{{kn}}}(\alpha ,\beta ) = {{R}_{{kn}}}(2\alpha ) - {{R}_{{kn}}}(\alpha ) - \\ - \,\,\frac{4}{{{{\pi }^{2}}}}\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\cos [(k - n)\theta ]\cos [(k + n)\varphi ]} } \times \\ \times \,\,\left[ {\ln (\sin \beta ) + \frac{1}{2}\ln \left( {{{1 - {\text{t}}{{{\text{g}}}^{2}}\frac{u}{2}} \mathord{\left/ {\vphantom {{1 - {\text{t}}{{{\text{g}}}^{2}}\frac{u}{2}} {{\text{t}}{{{\text{g}}}^{2}}\beta }}} \right. \kern-0em} {{\text{t}}{{{\text{g}}}^{2}}\beta }}} \right)} \right]{\text{d}}\theta {\text{d}}\varphi . \\ \end{gathered} $(5)
$\begin{gathered} {{E}_{{kn}}}(\alpha ,\beta ) = \frac{2}{{{{\pi }^{2}}}}\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\cos [(k - n)\theta ]\sin [(k + n)\varphi ]} } \times \\ \times \,\,\ln \left[ {\frac{{1 + {{{\text{tg(}}{u \mathord{\left/ {\vphantom {u 2}} \right. \kern-0em} 2})} \mathord{\left/ {\vphantom {{{\text{tg(}}{u \mathord{\left/ {\vphantom {u 2}} \right. \kern-0em} 2})} {{\text{tg}}\beta }}} \right. \kern-0em} {{\text{tg}}\beta }}}}{{1 - {{{\text{tg(}}{u \mathord{\left/ {\vphantom {u 2}} \right. \kern-0em} 2})} \mathord{\left/ {\vphantom {{{\text{tg(}}{u \mathord{\left/ {\vphantom {u 2}} \right. \kern-0em} 2})} {{\text{tg}}\beta }}} \right. \kern-0em} {{\text{tg}}\beta }}}}} \right]{\text{d}}\theta {\text{d}}\varphi . \\ \end{gathered} $Разлагая в (3) синус в степенной ряд и вычисляя интеграл, получим разложение функции
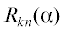 в быстро сходящийся степенной ряд [1], который можно представить в виде
в быстро сходящийся степенной ряд [1], который можно представить в виде
Из полученных выражений видно, что ряд быстро сходится и при расчете функции ${{R}_{{kn}}}({{\alpha }})$ в нем достаточно учесть несколько первых членов. При больших размерах экрана (α $ \ll $ 1) этот ряд близок к нулю, и в этом случае при моделировании неэкранированных полосковых структур можно положить
Выражение (3') можно получить из выражения (3), полагая в нем ${\text{sin}}({u \mathord{\left/ {\vphantom {u 2}} \right. \kern-0em} 2}) \approx {u \mathord{\left/ {\vphantom {u 2}} \right. \kern-0em} 2}$. Полагая в выражениях (4), (5) ${\text{tg}}({u \mathord{\left/ {\vphantom {u 2}} \right. \kern-0em} 2}) \approx {u \mathord{\left/ {\vphantom {u 2}} \right. \kern-0em} 2}$ и разлагая логарифмы в степенные ряды, после интегрирования получим следующие выражения для функций ${{F}_{{kn}}}({{\alpha }},{{\beta }})$ и ${{E}_{{kn}}}({{\alpha }},{{\beta }})$при α $ \ll $ 1:
2. ОПРЕДЕЛЕНИЕ МАТРИЧНЫХ КОЭФФИЦИЕНТОВ ПРОЕКЦИОННОЙ МОДЕЛИ КОМПЛАНАРНОЙ ПОЛОСКОВОЙ ЛИНИИ
Для компланарной полосковой линии, проекционная модель которой построена в [3], медленно сходящиеся ряды для матричных коэффициентов определяются через функции Rkn(α), Fkn(α, β) и Ekn(α, β) по формулам
(6)
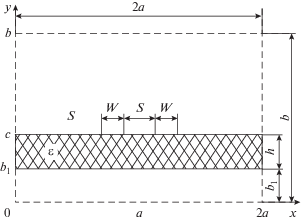
$\begin{gathered} {{S}_{{ql}}}(\alpha ,\beta ) = \frac{1}{2}\left( {{{R}_{{(2q)(2l)}}}(\alpha ) - {{F}_{{(2q)(2l)}}}(\alpha ,\beta )} \right), \\ {{P}_{{ql}}}(\alpha ,\beta ) = \frac{1}{2}\left( {{{R}_{{(2q - 1)(2l - 1)}}}(\alpha ) + {{F}_{{(2q - 1)(2l - 1)}}}(\alpha ,\beta )} \right), \\ {{Q}_{{ql}}}(\alpha ,\beta ) = \frac{1}{2}{{E}_{{(2q)(2l - 1)}}}(\alpha ,\beta ),\,\,\,\,\alpha = \frac{{\pi W}}{{2a}}, \\ \beta = \alpha (1 + {S \mathord{\left/ {\vphantom {S W}} \right. \kern-0em} W}). \\ \end{gathered} $Поперечное сечение компланарной полосковой линии показано на рис. 1.
Рис. 1.
Поперечное сечение компланарной полосковой линии: W – ширина полосковых проводников, S – расстояние между ними, h – толщина подложки, ε – относительная диэлектрическая проницаемость подложки, b1 – расстояние от подложки до нижнего экрана, 2a, b – размеры экрана; $a \ll W + S$, $a \gg h$, $b \gg h$, ${{b}_{1}} \gg h$.
Используя (3')–(5'), получим выражения для функций ${{S}_{{ql}}}({{\alpha ,\beta }})$, ${{P}_{{ql}}}({{\alpha ,\beta }})$, ${{Q}_{{ql}}}({{\alpha ,\beta }})$ в виде быстро сходящихся рядов:
(7)
$\begin{gathered} {{\left. {{{S}_{{ql}}}(\alpha ,\beta )} \right|}_{{q \ne l}}} = - \frac{1}{2}{{F}_{{(2q)(2l)}}}(\alpha ,\beta ), \\ {{\left. {{{S}_{{qq}}}(\alpha ,\beta )} \right|}_{{q \ne 0}}} = \frac{1}{2}\left( {\frac{1}{{4q}} - {{F}_{{(2q)(2l)}}}(\alpha ,\beta )} \right), \\ {{S}_{{00}}}(\alpha ,\beta ) = \frac{1}{2}\ln \left( {\frac{{4\sin \beta }}{\alpha }} \right) - \\ - \,\,\frac{1}{4}\sum\limits_{\nu = 1}^\infty {\frac{1}{\nu }} {{\left[ {\frac{{(2\nu - 1)!!}}{{(2\nu )!!}}} \right]}^{2}}{{\left( {\frac{\alpha }{{{\text{tg}}\,\beta }}} \right)}^{{2\nu }}}, \\ {{\left. {{{P}_{{ql}}}(\alpha ,\beta )} \right|}_{{q \ne l}}} = \frac{1}{2}{{F}_{{(2q - 1)(2l - 1)}}}(\alpha ,\beta ), \\ {{P}_{{qq}}}(\alpha ,\beta ) = \frac{1}{2}\left( {\frac{1}{{2(2q - 1)}} + {{F}_{{(2q - 1)(2q - 1)}}}(\alpha ,\beta )} \right), \\ {{Q}_{{ql}}}(\alpha ,\beta ) = 0.5{{E}_{{(2q)(2l - 1)}}}(\alpha ,\beta ). \\ \end{gathered} $При больших значениях q + l = L бесконечные ряды (4'), (5') близки к нулю и эти функции представляются в виде
Отметим, что при больших значениях L быстро сходящиеся ряды в выражениях (1) для матричных коэффициентов близки к нулю, так как функции Бесселя быстро убывают с ростом индекса, когда индекс больше аргумента. Поэтому при $m\alpha < L$ ($\alpha \ll 1$) близки к нулю функции Бесселя, а при $m\alpha > L$ близки к нулю коэффициенты в круглых скобках (они убывают, как ${1 \mathord{\left/ {\vphantom {1 {{{m}^{3}}}}} \right. \kern-0em} {{{m}^{3}}}}$). Следовательно, при больших значениях L матричные коэффициенты СЛАУ определяются медленно сходящимися рядами, для которых получены представления в виде быстро сходящихся степенных рядов (7).
Из (7') следует вывод о диагональном характере матрицы коэффициентов СЛАУ. В [2] получено асимптотическое решение этой системы для экранированной микрополосковой
линии. Таким же способом можно получить асимптотическое решение СЛАУ для компланарной
и других типов полосковых линий, из которого следует быстрая сходимость разложений
плотности тока на полосковых проводниках по взвешенным полиномам Чебышева и возможность
решения бесконечной системы уравнений методом редукции. Порядок редуцированной системы
$K = 4L + 1$ $(L = 0,1,2,...)$, где $2L$ – число членов (четных и нечетных) в разложении поперечной составляющей плотности
тока и 2L + 1 – продольной. Значение числа L устанавливается путем анализа численных результатов при его изменении. В результате
расчетов основных электродинамических параметров линий – коэффициента замедления и
волнового сопротивления, выполненных на персональном компьютере, установлено, что
число L зависит в основном от отношения ${S \mathord{\left/ {\vphantom {S W}} \right. \kern-0em} W}$ и при ${S \mathord{\left/ {\vphantom {S W}} \right. \kern-0em} W} \geqslant 1$ не превышает 2 в широком диапазоне изменения параметров. При ${S \mathord{\left/ {\vphantom {S W}} \right. \kern-0em} W} = 1$ погрешность расчета волнового сопротивления линии не превышает 0.1%. С уменьшением
отношения ${S \mathord{\left/ {\vphantom {S W}} \right. \kern-0em} W}$ число L увеличивается, и при ${S \mathord{\left/ {\vphantom {S W}} \right. \kern-0em} W}$ = 0.01 такая точность достигается при L = 4. В результате проведенного исследования установлено, что значение числа L, обеспечивающего достаточно точное решение СЛАУ, определяется из условия совпадения
результатов расчета функций ${{S}_{{ql}}}({{\alpha ,\beta }})$, ${{P}_{{ql}}}({{\alpha ,\beta }})$, ${{Q}_{{ql}}}({{\alpha ,\beta }})$ по формулам (7) и (7'). Это значение, как следует из формул (4'), (5'), зависит от отношения 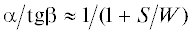 . При уменьшении отношения ${S \mathord{\left/ {\vphantom {S W}} \right. \kern-0em} W}$ сходимость степенных рядов ухудшается и значение числа L увеличивается.
. При уменьшении отношения ${S \mathord{\left/ {\vphantom {S W}} \right. \kern-0em} W}$ сходимость степенных рядов ухудшается и значение числа L увеличивается.
В табл. 1, 2 представлены результаты расчета функций ${{S}_{{ql}}}({{\alpha ,\beta }})$, 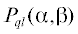 , ${{Q}_{{ql}}}({{\alpha ,\beta }})$ по формулам (6) с использованием формулы (2) при различных значениях числа членов – М, учитываемых в медленно сходящихся рядах. В последних столбцах представлены результаты
расчета этих функций по формулам (7). Приведенные результаты подтверждают быструю сходимость разложений для плотности
тока по взвешенным полиномам Чебышева и медленную сходимость рядов (2). Анализ этих
результатов позволяет выбрать значение числа L, при котором обеспечивается достаточно высокая точность ее решения. Из рассмотрения
полученных данных следует, что при ${S \mathord{\left/ {\vphantom {S W}} \right. \kern-0em} W} \geqslant 1$ значение числа L не превышает 2. Представленные результаты позволяют определить точность расчета матричных
коэффициентов СЛАУ, используя при их расчете медленно сходящиеся ряды (2), и определить
число M, обеспечивающее требуемую точность. Это число зависит в основном от отношения ${a \mathord{\left/ {\vphantom {a W}} \right. \kern-0em} W}$ и для обеспечения погрешности 1…2% должно быть не менее ${{10a} \mathord{\left/ {\vphantom {{10a} W}} \right. \kern-0em} W}$. Из приведенных результатов следует, что для достижения малой погрешности (порядка
0.1%) нужно учитывать более 10 000 членов при ${a \mathord{\left/ {\vphantom {a W}} \right. \kern-0em} W} \geqslant 100$. Сходимость рядов зависит также от необходимого числа L, которое увеличивается с уменьшением расстояния S между проводниками и трудно получить высокую точность для узких близко расположенных
полосковых проводников даже при учете в рядах до 50 тысяч членов. Сказанное подтверждается
результатами расчета волнового сопротивления компланарной полосковой линии, определяемого
через мощность и ток, которые представлены в табл. 3, 4. Параметры линии: a/h = 100, b/h = 50, b1/h = 25, ε = 9.6, f [ГГц] × × h [мм] = 10. Расчеты проводили при различных значениях L. Установлено, что время счета при больших значениях числа членов – M, учитываемых в медленно сходящихся рядах для матричных коэффициентов, пропорционально
M. При расчете девяти точек частотных зависимостей коэффициента замедления и волнового
сопротивления оно составляет 10 с при М = 10 000, L = 4 и 14 с при М = 10 000, L = 5. При использовании формул (7) оно не превышает 0.1 с.
, ${{Q}_{{ql}}}({{\alpha ,\beta }})$ по формулам (6) с использованием формулы (2) при различных значениях числа членов – М, учитываемых в медленно сходящихся рядах. В последних столбцах представлены результаты
расчета этих функций по формулам (7). Приведенные результаты подтверждают быструю сходимость разложений для плотности
тока по взвешенным полиномам Чебышева и медленную сходимость рядов (2). Анализ этих
результатов позволяет выбрать значение числа L, при котором обеспечивается достаточно высокая точность ее решения. Из рассмотрения
полученных данных следует, что при ${S \mathord{\left/ {\vphantom {S W}} \right. \kern-0em} W} \geqslant 1$ значение числа L не превышает 2. Представленные результаты позволяют определить точность расчета матричных
коэффициентов СЛАУ, используя при их расчете медленно сходящиеся ряды (2), и определить
число M, обеспечивающее требуемую точность. Это число зависит в основном от отношения ${a \mathord{\left/ {\vphantom {a W}} \right. \kern-0em} W}$ и для обеспечения погрешности 1…2% должно быть не менее ${{10a} \mathord{\left/ {\vphantom {{10a} W}} \right. \kern-0em} W}$. Из приведенных результатов следует, что для достижения малой погрешности (порядка
0.1%) нужно учитывать более 10 000 членов при ${a \mathord{\left/ {\vphantom {a W}} \right. \kern-0em} W} \geqslant 100$. Сходимость рядов зависит также от необходимого числа L, которое увеличивается с уменьшением расстояния S между проводниками и трудно получить высокую точность для узких близко расположенных
полосковых проводников даже при учете в рядах до 50 тысяч членов. Сказанное подтверждается
результатами расчета волнового сопротивления компланарной полосковой линии, определяемого
через мощность и ток, которые представлены в табл. 3, 4. Параметры линии: a/h = 100, b/h = 50, b1/h = 25, ε = 9.6, f [ГГц] × × h [мм] = 10. Расчеты проводили при различных значениях L. Установлено, что время счета при больших значениях числа членов – M, учитываемых в медленно сходящихся рядах для матричных коэффициентов, пропорционально
M. При расчете девяти точек частотных зависимостей коэффициента замедления и волнового
сопротивления оно составляет 10 с при М = 10 000, L = 4 и 14 с при М = 10 000, L = 5. При использовании формул (7) оно не превышает 0.1 с.
Таблица 1.
Результаты расчета функций ${{S}_{{ql}}}({{\alpha ,\beta ,}}M)$, ${{P}_{{ql}}}({{\alpha ,\beta ,}}M)$, ${{Q}_{{ql}}}({{\alpha ,\beta ,}}M)$ при ${S \mathord{\left/ {\vphantom {S h}} \right. \kern-0em} h} = {W \mathord{\left/ {\vphantom {W h}} \right. \kern-0em} h} = 0.1$, ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-0em} h} = 100$
| М | 1000 | 2000 | 5000 | 10 000 | 20 000 | 50 000 | $\infty $ |
|---|---|---|---|---|---|---|---|
| ${{S}_{{00}}}$ | 0.95529 | 0.96372 | 1.00431 | 1.01229 | 1.01765 | 1.02054 | 1.02285 |
| ${{S}_{{01}}}$ | 0.05769 | 0.06243 | 0.02077 | 0.01502 | 0.00965 | 0.00652 | 0.00448 |
| ${{S}_{{02}}}$ | 0.00097 | 0.00081 | –0.01616 | –0.1017 | –0.00517 | –0.00209 | –0.00005 |
| ${{S}_{{11}}}$ | 0.00688 | 0.06464 | 0.10593 | 0.11420 | 0.11959 | 0.12272 | 0.12477 |
| ${{S}_{{12}}}$ | 0.00016 | 0.00894 | 0.01805 | 0.01032 | 0.00515 | 0.00205 | 0.00001 |
| ${{S}_{{22}}}$ | 0.00000 | 0.00145 | 0.04062 | 0.05201 | 0.05732 | 0.06045 | 0.06250 |
| ${{P}_{{11}}}$ | 0.10345 | 0.19542 | 0.22012 | 0.23142 | 0.23633 | 0.23932 | 0.24134 |
| ${{P}_{{12}}}$ | 0.00715 | 0.03407 | 0.02077 | 0.01000 | 0.00516 | 0.00218 | 0.00016 |
| ${{P}_{{13}}}$ | 0.00018 | 0.00260 | 0.01357 | –0.00907 | –0.00491 | –0.00202 | 0.00000 |
| ${{P}_{{22}}}$ | 0.00065 | 0.01446 | 0.06179 | 0.07334 | 0.07830 | 0.08130 | 0.08332 |
| ${{P}_{{23}}}$ | 0.00002 | 0.00166 | 0.01713 | 0.00967 | 0.00498 | 0.00202 | 0.00000 |
| ${{P}_{{33}}}$ | 0.00000 | 0.00021 | 0.02964 | 0.03971 | 0.04495 | 0.04797 | 0.05000 |
| ${{Q}_{{01}}}$ | 0.04559 | 0.0706 | 0.06490 | 0.06599 | 0.06584 | 0.06579 | 0.06578 |
| ${{Q}_{{02}}}$ | –0.00353 | 0.00401 | 0.00064 | –0.00058 | –0.00047 | –0.00043 | –0.00042 |
| ${{Q}_{{11}}}$ | –0.01330 | –0.00653 | –0.00049 | –0.00139 | –0.00122 | –0.00117 | –0.00116 |
| ${{Q}_{{12}}}$ | –0.00108 | –0.00685 | –0.00073 | 0.00021 | 0.00009 | 0.00005 | 0.00004 |
Таблица 2.
Результаты расчета функций ${{S}_{{ql}}}({{\alpha ,\beta ,}}M)$, ${{P}_{{ql}}}({{\alpha ,\beta ,}}M)$, ${{Q}_{{ql}}}({{\alpha ,\beta ,}}M)$ при ${S \mathord{\left/ {\vphantom {S h}} \right. \kern-0em} h} = {W \mathord{\left/ {\vphantom {W h}} \right. \kern-0em} h} = 1$, ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-0em} h} = 100$
| М | 1000 | 2000 | 5000 | 10 000 | 20 000 | 50 000 | $\infty $ |
|---|---|---|---|---|---|---|---|
| ${{S}_{{00}}}$ | 1.01221 | 1.01759 | 1.0271 | 1.02170 | 1.02215 | 1.02225 | 1.02277 |
| ${{S}_{{01}}}$ | 0.01502 | 0.00965 | 0.00652 | 0.00550 | 0.00499 | 0.00468 | 0.00448 |
| ${{S}_{{02}}}$ | –0.01018 | –0.00517 | –0.00209 | –0.00106 | –0.00055 | –0.00025 | –0.00005 |
| ${{S}_{{11}}}$ | 0.11420 | 0.11959 | 0.12273 | 0.12375 | 0.12426 | 0.12455 | 0.12477 |
| ${{S}_{{12}}}$ | 0.1032 | 0.00515 | 0.00205 | 0.00102 | 0.00051 | 0.00021 | 0.00001 |
| ${{S}_{{22}}}$ | 0.05201 | 0.05733 | 0.06046 | 0.06148 | 0.06199 | 0.06229 | 0.06250 |
| ${{P}_{{11}}}$ | 0.23142 | 0.23633 | 0.23932 | 0.24032 | 0.24083 | 0.24112 | 0.24134 |
| ${{P}_{{12}}}$ | 0.00999 | 0.00516 | 0.00217 | 0.00117 | 0.00066 | 0.00036 | 0.00016 |
| ${{P}_{{13}}}$ | –0.00907 | –0.00491 | –0.00202 | –0.00101 | –0.00051 | –0.00021 | 0.00000 |
| ${{P}_{{22}}}$ | 0.07334 | 0.07831 | 0.08131 | 0.8231 | 0.08282 | 0.08311 | 0.08332 |
| ${{P}_{{23}}}$ | 0.00967 | 0.00498 | 0.00202 | 0.00101 | 0.00051 | 0.00021 | 0.00000 |
| ${{P}_{{33}}}$ | 0.03971 | 0.04495 | 0.04797 | 0.04898 | 0.04948 | 0.04979 | 0.05000 |
| ${{Q}_{{01}}}$ | 0.06597 | 0.06582 | 0.06577 | 0.06576 | 0.06576 | 0.06576 | 0.06576 |
| ${{Q}_{{02}}}$ | –0.00058 | –0.00047 | –0.00043 | –0.00042 | –0.00042 | –0.0042 | –0.0042 |
| ${{Q}_{{11}}}$ | –0.00139 | –0.00122 | –0.00117 | –0.00116 | –0.00116 | –0.00116 | –0.00116 |
| ${{Q}_{{12}}}$ | 0.00021 | 0.00009 | 0.00005 | 0.00004 | 0.00004 | –0.00004 | 0.00004 |
Таблица 3.
Волновое сопротивление компланарной полосковой линии при ${W \mathord{\left/ {\vphantom {W h}} \right. \kern-0em} h} = 0.1$
| М | 1000 | 2000 | 5000 | 10 000 | 20 000 | 50 000 | $\infty $ |
|---|---|---|---|---|---|---|---|
| ${S \mathord{\left/ {\vphantom {S h}} \right. \kern-0em} h} = 1$ | 44.701 | 774.839 | 93.383 | 96.656 | 97.256 | 97.480 | 97.610 |
| ${S \mathord{\left/ {\vphantom {S h}} \right. \kern-0em} h} = 0.1$ | 26.077 | 0.119 | 46.791 | 51.213 | 51.918 | 52.178 | 52.332 |
| ${S \mathord{\left/ {\vphantom {S h}} \right. \kern-0em} h} = 0.01$ | 724.708 | 67.891 | 0.340 | 27.049 | 27.976 | 28.733 | 29.022 |
Таблица 4.
Волновое сопротивление компланарной полосковой линии при ${W \mathord{\left/ {\vphantom {W h}} \right. \kern-0em} h} = 1$
| М | L | 1000 | 2000 | 5000 | 10 000 | 20 000 | 50 000 | $\infty $ |
|---|---|---|---|---|---|---|---|---|
| ${S \mathord{\left/ {\vphantom {S h}} \right. \kern-0em} h} = 1$ | – | 50.488 | 51.169 | 51.430 | 51.497 | 51.525 | 51.533 | 51.560 |
| ${S \mathord{\left/ {\vphantom {S h}} \right. \kern-0em} h} = 0.1$ | – | 26.864 | 27.775 | 28.526 | 28.660 | 28.735 | 28.770 | 28.813 |
| ${S \mathord{\left/ {\vphantom {S h}} \right. \kern-0em} h} = 0.01$ | 3 | 5.623 | 13.684 | 17.940 | 18.863 | 18.955 | 19.113 | 19.219 |
| ${S \mathord{\left/ {\vphantom {S h}} \right. \kern-0em} h} = 0.01$ | 4 | 0.912 | 10.295 | 17.718 | 18.812 | 18.905 | 19.064 | 19.161 |
| ${S \mathord{\left/ {\vphantom {S h}} \right. \kern-0em} h} = 0.01$ | 5 | 0.776 | 9.419 | 17.159 | 17.830 | 17.874 | 17.958 | 19.142 |
ЗАКЛЮЧЕНИЕ
Полученные в данной статье представления (3')–(5') для функций, определяемых через медленно сходящиеся ряды (2), позволяют преобразовать выражения для матричных коэффициентов в быстро сходящиеся ряды, что существенно сокращает время численной реализации алгоритмов расчета собственных волн полосковых линий при высокой точности численных результатов. Использование этих представлений позволяет существенно повысить эффективность проекционных моделей полосковых линий различного типа в многослойной диэлектрической среде с использованием чебышевского базиса.
Список литературы
Коваленко А.Н. // Изв. вузов. Радиофизика. 1978. Т. 21. № 2. С. 188.
Koвaлeнкo A.H. // PЭ. 2019. T. 64. № 2. C. 108.
Коваленко А.Н., Жуков А.Н. // Росс. технол. журн. 2018. Т. 6. № 3. С. 54.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Физматгиз, 1963.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника