1. На главную
  2. Электронные версии
  3. Радиотехника и электроника
  4. T. 66, № 9, 2021

Радиотехника и электроника, 2021, T. 66, № 9, стр. 901-906

Расширенные форматы однополосной модуляции интенсивности света

А. А. Задерновский a, *, В. В. Щербаков b, **, А. Ф. Солодков b

a МИРЭА – Российский технологический университет
119454 Москва, просп. Вернадского, 78, Российская Федерация

b Центр волоконно-оптических систем передачи информации
117342 Москва, ул. Введенского, 3, Российская Федерация

* E-mail: zadernovsky@mirea.ru
** E-mail: vospi@bk.ru

Поступила в редакцию 16.09.2020
После доработки 28.02.2021
Принята к публикации 10.03.2021

Полный текст (PDF)

Аннотация

Выполнен теоретический анализ различных форматов однополосной модуляции, используемых в волоконно-оптических линиях связи с внешним электрооптическим двухэлектродным модулятором Маха–Цендера для генерирования оптических сигналов, устойчивых к дисперсионной деградации мощности. Представлено семейство новых форматов однополосной модуляции, рассмотрены особенности их использования, достоинства и недостатки. Предположено уменьшение нелинейных искажений сигналов при их транспортировке по дисперсионному оптоволокну.

ВВЕДЕНИЕ

Однополосные сигналы модуляции интенсивности света устойчивы к дисперсионной деградации мощности при их распространении в оптоволокне. Стандартным способом [1] генерирования таких сигналов является использование двухэлектродного модулятора Маха–Цендера с квадратурным смещением и управляющими напряжениями, сдвинутыми по фазе на 90°. Однако, это не единственная возможность получить такие сигналы. В данной статье представлено семейство расширенных форматов модуляции двухэлектродного модулятора Маха–Цендера, обеспечивающих генерирование однополосных оптических сигналов. Производится сравнение этих форматов с хорошо известными однополосными форматами модуляции. Обсуждаются особенности их применения, достоинства и недостатки.

1. МОДУЛЯТОР МАХА–ЦЕНДЕРА С ДВУМЯ УПРАВЛЯЮЩИМИ ЭЛЕКТРОДАМИ

Принципиальная схема двухэлектродного модулятора Маха–Цендера показана на рис. 1. Модулятор включает в себя подложку из монокристалла ниобата лития и сформированную на ней путем термодиффузии титана систему канальных оптических волноводов с одним входом и одним выходом (рис. 2). Входной оптический канал расщепляется на два независимых волновода, создавая пространственное разделение входного лазерного излучения на два пучка света, которые затем сводятся вместе в выходном оптическом канале. На подложке устанавливаются управляющие электроды. Электрическое напряжение, подаваемое на электроды, создает электрическое поле, проникающие в сечение каждого волновода. Это поле изменяет оптическую длину пути волноводов. Управляющие напряжения U1 и U2 определяют фазовые сдвиги ${{\varphi }_{1}}$ и ${{\varphi }_{2}}$ приобретаемые световыми волнами при прохождении своего собственного канального волновода.

Рис. 1.

Принципиальная схема модулятора Маха–Цендера с двумя управляющими электродами: ${{U}_{1}}\,,\,{{U}_{2}}$ – модулирующие напряжения; +Ub, − Ub – напряжения смещения противоположной полярности.

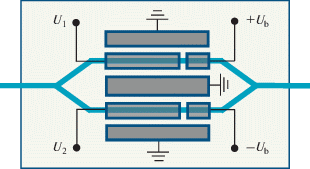
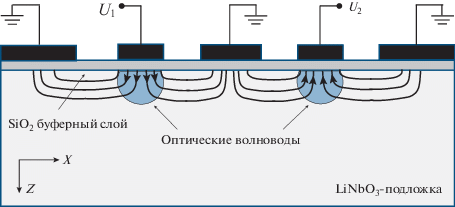
Рис. 2.

Поперечное сечение модулятора Маха–Цендера с двумя управляющими электродами: ${{U}_{1}}\,,\,{{U}_{2}}$ – модулирующие напряжения.

Принцип работы двухэлектродного модулятора Маха–Цендера неоднократно обсуждался в литературе (см., например, [2]). Здесь мы лишь коротко повторим основные моменты необходимые для дальнейшего обсуждения. Если на сигнальные электроды подаются модулирующие напряжения ${{U}_{1}} = {{U}_{0}}\cos ({{\omega }_{m}}{\kern 1pt} t + {{\varphi }_{{m{\text{1}}}}})$ и ${{U}_{2}} = {{U}_{0}}\cos ({{\omega }_{m}}{\kern 1pt} t + {{\varphi }_{{m{\text{2}}}}})$ с одинаковыми частотами ${{\omega }_{m}}$, одинаковыми амплитудами ${{U}_{0}}$, но с разными начальными фазами ${{\varphi }_{{m{\text{1}}}}}$ и ${{\varphi }_{{m{\text{2}}}}}$, то электромагнитная световая волна на выходе из модулятора может быть записана в виде

(1)
$\begin{gathered} E = {{E}_{0}}\exp [i({{\omega }_{0}}t + {{\varphi }_{0}})] \times \\ \times \,\,\cos \frac{\pi }{2}\left( {\frac{{{{U}_{b}}}}{{{{U}_{\pi }}}} + \frac{{{{U}_{1}} - {{U}_{2}}}}{{2{{U}_{\pi }}}}} \right)\exp \frac{{i\pi }}{4}\frac{{{{U}_{1}} + {{U}_{2}}}}{{{{U}_{\pi }}}}, \\ \end{gathered} $
где Ub – напряжение смещения, Uπ – полуволновое (запирающее) напряжение. Спектральное представление такой волны может быть представлено в виде суммы
(2)
$\begin{gathered} E = {{E}_{0}}\exp [i({{\omega }_{0}}t + {{\varphi }_{0}})] \times \\ \times \,\,\sum\limits_{n = - \infty }^{ + \infty } {{{C}_{n}}} \exp \left[ {in\left( {{{\omega }_{m}}t + \frac{{{{\varphi }_{{m1}}} + {{\varphi }_{{m2}}}}}{2}} \right)} \right] \\ \end{gathered} $
с коэффициентами
(3)
${{C}_{n}} = {{i}^{n}}{{J}_{n}}({{\pi {{u}_{0}}} \mathord{\left/ {\vphantom {{\pi {{u}_{0}}} 2}} \right. \kern-0em} 2})\cos \left( {\frac{{\pi {{u}_{b}}}}{2} + n\frac{{{{\varphi }_{{m1}}} - {{\varphi }_{{m2}}}}}{2}} \right),$
где ${{u}_{b}} = {{{{{{U}_{b}}} \mathord{\left/ {\vphantom {{{{U}_{b}}} U}} \right. \kern-0em} U}}_{\pi }}$ и ${{u}_{0}} = {{{{{{U}_{{\text{0}}}}} \mathord{\left/ {\vphantom {{{{U}_{{\text{0}}}}} U}} \right. \kern-0em} U}}_{\pi }}$ – нормированные переменные, ${{J}_{n}}$ – функция Бесселя первого рода порядка n. Соответственно, спектральное представление сигнала модуляции интенсивности света на выходе из модулятора имеет вид

(4)
$\begin{gathered} {{P}_{{{\text{вых}}}}} = \frac{{{{P}_{0}}}}{2}\left\{ {1 + \sum\limits_{n = - \infty }^{ + \infty } {{{i}^{n}}{{J}_{n}}\left( {\pi {{u}_{0}}\sin \frac{{{{\varphi }_{{m1}}} - {{\varphi }_{{m2}}}}}{2}} \right)} } \right. \times \\ \left. { \times \,\,\cos \left( {\pi {{u}_{{\text{b}}}} + n\frac{\pi }{2}} \right)\exp \left[ {in\left( {{{\omega }_{m}}t + \frac{{{{\varphi }_{{m{\text{1}}}}} + {{\varphi }_{{m{\text{2}}}}}}}{2}} \right)} \right]} \right\}. \\ \end{gathered} $

2. ФОРМАТЫ ОДНОПОЛОСНОЙ МОДУЛЯЦИИ ДВУХЭЛЕКТРОДНОГО МОДУЛЯТОРА

Из (3) легко видеть, что условие того, что в спектре электромагнитной волны пропадает одна из гармоник первого или минус первого порядка выглядит как

(5)
$\left| {{{u}_{b}} \pm \frac{{{{\varphi }_{{m1}}} - {{\varphi }_{{m2}}}}}{\pi }} \right| = 1,$
причем знак плюс относится к гармонике с n = = +1, а знак минус к n = −1.

В табл. 1 представлены примеры однополосных форматов модуляции, полученные с помощью выражения (5). Некоторые из них хорошо известны. Так, формат с ub = ±1/2, (φm1 − φm2)/π = ±1/2 исторически был первым предложенным однополосным оптическим форматом модуляции [1]. Он примечателен тем, что выбор квадратурной рабочей точки с нормированным напряжением смещения ${{u}_{b}} = \pm {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ приводит, как это видно из (4), к подавлению всех четных гармоник сигнала модуляции интенсивности. Тем самым, нелинейные искажения сигнала на выходе из модулятора оказываются минимальными.

Таблица 1.

Примеры форматов однополосной модуляции

Нормированное напряжение смещения
${{u}_{{\text{b}}}} = {{{{{{U}_{{\text{b}}}}} \mathord{\left/ {\vphantom {{{{U}_{{\text{b}}}}} U}} \right. \kern-0em} U}}_{\pi }}$		 Нормированная разница фаз модулирующих напряжений
${{({{\varphi }_{{m1}}} - {{\varphi }_{{m2}}})} \mathord{\left/ {\vphantom {{({{\varphi }_{{m1}}} - {{\varphi }_{{m2}}})} \pi }} \right. \kern-0em} \pi }$
n = −1
${{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} 2}} \right. \kern-0em} 2}$ ${{ \mp 1} \mathord{\left/ {\vphantom {{ \mp 1} 2}} \right. \kern-0em} 2}$
${{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} 3}} \right. \kern-0em} 3}$ ${{ \mp 2} \mathord{\left/ {\vphantom {{ \mp 2} 3}} \right. \kern-0em} 3}$
${{ \pm 2} \mathord{\left/ {\vphantom {{ \pm 2} 3}} \right. \kern-0em} 3}$ ${{ \mp 1} \mathord{\left/ {\vphantom {{ \mp 1} 3}} \right. \kern-0em} 3}$
${{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} 4}} \right. \kern-0em} 4}$ ${{ \mp 3} \mathord{\left/ {\vphantom {{ \mp 3} 4}} \right. \kern-0em} 4}$
${{ \pm 3} \mathord{\left/ {\vphantom {{ \pm 3} 4}} \right. \kern-0em} 4}$ ${{ \mp 1} \mathord{\left/ {\vphantom {{ \mp 1} 4}} \right. \kern-0em} 4}$
n = +1
${{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} 2}} \right. \kern-0em} 2}$ ${{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} 2}} \right. \kern-0em} 2}$
${{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} 3}} \right. \kern-0em} 3}$ ${{ \pm 2} \mathord{\left/ {\vphantom {{ \pm 2} 3}} \right. \kern-0em} 3}$
${{ \pm 2} \mathord{\left/ {\vphantom {{ \pm 2} 3}} \right. \kern-0em} 3}$ ${{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} 3}} \right. \kern-0em} 3}$
${{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} 4}} \right. \kern-0em} 4}$ ${{ \pm 3} \mathord{\left/ {\vphantom {{ \pm 3} 4}} \right. \kern-0em} 4}$
${{ \pm 3} \mathord{\left/ {\vphantom {{ \pm 3} 4}} \right. \kern-0em} 4}$ ${{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} 4}} \right. \kern-0em} 4}$

Примечание: n − номер гармоники с амплитудой, равной нулю.

Другой формат с ub= ± 1/3, (φm1 − φm2)/π = = ±2/3 был предложен сравнительно недавно [3]. Он интересен тем, что при выборе ${{u}_{b}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}$, ${{({{\varphi }_{{m1}}} - {{\varphi }_{{m2}}})} \mathord{\left/ {\vphantom {{({{\varphi }_{{m1}}} - {{\varphi }_{{m2}}})} \pi }} \right. \kern-0em} \pi } = + {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}$ или ${{u}_{b}} = {{ + 1} \mathord{\left/ {\vphantom {{ + 1} 3}} \right. \kern-0em} 3}$, ${{({{\varphi }_{{m1}}} - {{\varphi }_{{m2}}})} \mathord{\left/ {\vphantom {{({{\varphi }_{{m1}}} - {{\varphi }_{{m2}}})} \pi }} \right. \kern-0em} \pi }$ = $ = - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}$ в электромагнитной волне пропадает не только полоса $n = - 1$, но и $n = + 2$. А при выборе режима с ${{u}_{b}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}$, ${{({{\varphi }_{{m1}}} - {{\varphi }_{{m2}}})} \mathord{\left/ {\vphantom {{({{\varphi }_{{m1}}} - {{\varphi }_{{m2}}})} \pi }} \right. \kern-0em} \pi } = - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}$ или ub = $ = {{ + 1} \mathord{\left/ {\vphantom {{ + 1} 3}} \right. \kern-0em} 3}$, ${{({{\varphi }_{{m1}}} - {{\varphi }_{{m2}}})} \mathord{\left/ {\vphantom {{({{\varphi }_{{m1}}} - {{\varphi }_{{m2}}})} \pi }} \right. \kern-0em} \pi } = + {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}$ пропадают одновременно полосы $n = + 1$ и $n = - 2$. Таким образом, в этом случае модуляция становится “однополосной” не только по основной, но и по второй гармонике. В результате следует ожидать уменьшения нелинейных искажений оптического сигнала модуляции интенсивности.

Кроме перечисленных, соотношение (5) дает целое семейство новых однополосных форматов модуляции (см. табл. 1). Обсуждение этих форматов обнаружить в литературе не удалось. Это связано, по-видимому, с тем, что применение таких форматов предполагает использование фазовращателей для управления фазой сигнальных напряжений двухэлектродного модулятора Маха–Цендера и формирования СВЧ-сигналов с произвольно заданной разностью фаз. Разработка таких фазовращателей является давней и не простой проблемой СВЧ-электроники. Обсуждение возможных подходов появилось в литературе лишь недавно и вызвало большой интерес [4–8].

3. ОПТИЧЕСКИЙ СИГНАЛ НА ВЫХОДЕ ИЗ ОПТОВОЛОКНА

Из-за дисперсии каждая спектральная компонента электромагнитной волны (2) приобретает на выходе из оптоволокна длиной L свой набег фазы $ - \beta L$. Так, для компоненты с частотой ${{\omega }_{0}} + n{{\omega }_{m}}$ он составляет

$ - \beta L = - {{\beta }_{0}}L - {{\beta }_{1}}n{{\omega }_{m}}L - {{(1} \mathord{\left/ {\vphantom {{(1} 2}} \right. \kern-0em} 2}){{\beta }_{2}}{{n}^{2}}\omega _{m}^{2}L - ...,$
где ${{\beta }_{0}}$ – постоянная распространения на частоте ${{\omega }_{0}} = {{2\pi c} \mathord{\left/ {\vphantom {{2\pi c} {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}$ несущей волны, коэффициент ${{\beta }_{1}} = {1 \mathord{\left/ {\vphantom {1 u}} \right. \kern-0em} u}$ равен обратной величине групповой скорости сигнала и коэффициент ${{\beta }_{2}}$ определяется через коэффициент дисперсии оптоволокна D как ${{\beta }_{2}} = - {{\lambda _{0}^{2}D} \mathord{\left/ {\vphantom {{\lambda _{0}^{2}D} {2\pi c}}} \right. \kern-0em} {2\pi c}}$ [9]. В итоге на выходе из оптоволокна имеем электромагнитную волну в виде
(6)
$\begin{gathered} E = {{E}_{0}}\exp [i({{\omega }_{0}}t - {{\beta }_{0}}L + {{\varphi }_{0}})] \times \\ \times \,\,\sum\limits_{n = - \infty }^{ + \infty } {{{C}_{n}}\exp (i{{n}^{2}}\theta )} \exp \left\{ {in[{{\omega }_{m}}(t - {L \mathord{\left/ {\vphantom {L u}} \right. \kern-0em} u}) + \frac{{{{\varphi }_{{m{\text{1}}}}} + {{\varphi }_{{m{\text{2}}}}}}}{2}]} \right\}, \\ \end{gathered} $
где
(7)
$\theta = \pi c{{\left( {{{{{\omega }_{m}}} \mathord{\left/ {\vphantom {{{{\omega }_{m}}} {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}} \right)}^{2}}DL$
– параметр транспортировки оптического сигнала по волокну.

Интенсивность света на выходе из оптоволокна ${{P}_{{\text{s}}}}$ (а следовательно, и фототок детектора излучения) будет пропорциональна квадрату модуля напряженности электрического поля $E(t)$ (6). Запишем ее в виде

(8)
${{P}_{{\text{s}}}} = \sum\limits_{n = - \infty }^{ + \infty } {{{P}_{n}}\exp \left\{ {in[{{\omega }_{{\text{m}}}}(t - {L \mathord{\left/ {\vphantom {L u}} \right. \kern-0em} u}) + \frac{{{{\varphi }_{{{\text{m1}}}}} + {{\varphi }_{{{\text{m2}}}}}}}{2}]} \right\}} ,$
где
(9)
$\begin{gathered} {{P}_{n}} = {{P}_{0}}\sum\limits_{k = - \infty }^{ + \infty } {{{C}_{{n + k}}}\exp [i{{{(n + k)}}^{2}}\theta ]C_{k}^{*}\exp ( - i{{k}^{2}}\theta ) = } \\ = {{P}_{0}}\sum\limits_{k = - \infty }^{ + \infty } {{{C}_{{n + k}}}\exp [i(n + k)n\theta ]C_{k}^{*}\exp (ikn\theta )} \\ \end{gathered} $
– комплексная амплитуда гармоники с частотой $n{{\omega }_{{\text{m}}}}$. При вычислении (9) воспользуемся теоремой Графа о суммировании бесселевых функций, которую для цели нашего анализа перепишем в виде (см. Приложение)
(10)
$\begin{gathered} {{J}_{n}}({{z}_{3}})\exp (in\gamma ) = \\ = \sum\limits_{k = - \infty }^{ + \infty } {{{J}_{{n + k}}}({{z}_{1}})\exp [i(n + k)\alpha ]{{J}_{k}}({{z}_{2}})} \exp (ik\beta ), \\ \end{gathered} $
где комплексное число z3exp(iγ) есть сумма двух других комплексных чисел ${{z}_{1}}\exp (i\alpha )$ и $ - {{z}_{2}}\exp ( - i\beta )$. В результате получим выражение

(11)
$\begin{gathered} {{P}_{n}} = {{( - 1)}^{n}}\frac{{{{P}_{0}}}}{2}\left\{ {{{J}_{n}}(\pi {{u}_{0}}\sin n\theta )\cos \frac{{n({{\varphi }_{{m1}}} - {{\varphi }_{{m2}}})}}{2}} \right. + \\ + \,\,\frac{1}{2}\exp (i\pi {{u}_{b}}){{J}_{n}}\left[ {\pi {{u}_{0}}\sin \left( {n\theta + \frac{{({{\varphi }_{{m1}}} - {{\varphi }_{{m2}}})}}{2}} \right)} \right] + \\ + \,\,\left. {\frac{1}{2}\exp ( - i\pi {{u}_{b}}){{J}_{n}}\left[ {\pi {{u}_{0}}\sin \left( {n\theta - \frac{{({{\varphi }_{{m1}}} - {{\varphi }_{{m2}}})}}{2}} \right)} \right]} \right\}. \\ \end{gathered} $

Аналогичная, но более громоздкая версия выражения (11) с разделением на четные и нечетные спектральные компоненты была получена также в [10].

В качестве примера, иллюстрирующего устойчивость указанных сигналов к дисперсионной деградации мощности, рассмотрим формат модуляции ${{\varphi }_{{m1}}} = {{\varphi }_{m}}$, ${{\varphi }_{{m2}}} = {{\varphi }_{m}}{{ + 2\pi } \mathord{\left/ {\vphantom {{ + 2\pi } 3}} \right. \kern-0em} 3}$, ${{u}_{b}} = {{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} 3}} \right. \kern-0em} 3}$. Сигнал модуляции интенсивности (4) на выходе из модулятора (на входе в оптоволокно) принимает вид

(12)
${{P}_{{{\text{вых}}}}} = \frac{{3{{P}_{0}}}}{4}\left[ {1 \mp \frac{{\pi {{u}_{0}}}}{2}\cos \left( {{{\omega }_{m}}t + {{\varphi }_{m}} - \frac{\pi }{6}} \right)} \right],$
а на выходе из волокна

(13)
${{P}_{{\text{s}}}} = \frac{{3{{P}_{0}}}}{4}\left\{ {1 \mp \frac{{\pi {{u}_{0}}}}{2}\cos [{{\omega }_{m}}(t - {L \mathord{\left/ {\vphantom {L u}} \right. \kern-0em} u}) + {{\varphi }_{m}} - \frac{\pi }{6} \pm \theta ]} \right\}.$

Из сравнения (12) и (13) видно, что соответствующие сигналы на входе и на выходе из оптоволокна отличаются только фазой, а амплитуды этих сигналов одинаковы по величине (без учета затухания в волокне).

ЗАКЛЮЧЕНИЕ

Выполнен теоретический анализ различных форматов однополосной модуляции, используемых в волоконно-оптических линиях связи с внешним электрооптическим двухэлектродным модулятором Маха–Цендера для генерирования оптических сигналов, устойчивых к дисперсионной деградации мощности. Представлено расширенное семейство новых форматов однополосной модуляции. Среди них форматы, обеспечивающие “однополосный” режим не только по основной, но и по второй гармонике. В результате следует ожидать уменьшения нелинейных искажений оптического сигнала модуляции интенсивности.

К основным трудностям использования указанных форматов модуляции следует отнести необходимость применения фазовращателей для управления фазой сигнальных напряжений двухэлектродного модулятора Маха–Цендера и формирования СВЧ-сигналов с заданной разностью фаз. Разработка таких фазовращателей является давней проблемой СВЧ-электроники. Потребность в таких устройствах диктуется необходимостью их использования для фазовой СВЧ-модуляции, компенсации фазовых искажений СВЧ-сигнала, выравнивания электрической длины линий передачи, в системах управления фазированными антенными решетками и др. Среди экспериментальных достижений можно отметить работу [11], в которой сообщается об экспериментальной демонстрации СВЧ-фазовращателя с непрерывным набором возможных фазовых сдвигов от 0° до 360° в полосе пропускания 10…40 ГГц. В работе [12] обсуждается концепция СВЧ-фазовращателя для осуществления непрерывных от 0 до 360° фазовых сдвигов в широком диапазоне частот до 100 ГГц.

Применение фазовращателей позволит полноценно использовать предложенные в статье расширенные форматы модуляции интенсивности света для формирования однополосных оптических сигналов. Полученные явные выражения наглядно демонстрируют передачу таких сигналов по оптоволокну без дисперсионной деградации мощности. При этом можно ожидать уменьшения нелинейных искажений рассмотренных сигналов при их транспортировке по дисперсионному оптоволокну.

Список литературы

  1. Smith G.H., Novak D., Ahmed Z. // Electron. Lett. 1997. V. 33. № 1. P. 74.

  2. Hui R. Introduction to Fiber-Optic Communications. N.Y.: Acad. Press, 2020. P. 299.

  3. Xue M, Pan Sh., Zhao Y. // J. Lightwave Technology. 2014. V. 32. № 19. P. 3317

  4. Yin Y., Lin T., Zhao S. et al. // Int. J. Physical and Mathematical Sci. 2018. V. 12. № 10. P. 202.

  5. Chew S.X., Huang D., Li L. et al. // Optics Express. 2019. V. 27. № 10. P. 14798.

  6. Guo Zh., Ma J., Huang Sh., Gao X. // Fiber and Integrated Optics. 2019. V. 38. № 4. P. 208.

  7. Yasir M., Savi P. // Micromachines. 2020. V. 11(6). P. 600.

  8. Zhang J., Tianyi Li T., Kokkoniemi R. et al. // AIP Advances. 2020. V. 10. № 6. P. 065128.

  9. Agrawal G.P. Nonlinear Fiber Optics. N. Y.: Acad. Press, 2013.

  10. Щербаков В.В., Солодков А.Ф., Задерновский А.А. // Радиоэлектроника. Наносистемы. Информ. технологии (РЭНСИТ). 2016. Т. 8. № 1. С. 9.

  11. Liu W., Yao J. // Optics Lett. 2014. V. 39. № 4. P. 922.

  12. Cunha M.S.B., Da Silva R.N., Borges R.M., Arismar Cerqueira S.A. // Proc. Conf. SBMO/IEEE MTT-S Int. Microwave and Optoelectronics Conf. (IMOC). Águas de Lindoia. 27–30 Aug. 2017. N.Y.: IEEE, 2017. P. 8121054.

  13. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Т. 2. Функции Бесселя, функции параболического цилиндра, ортогональные многочлены. М.: Наука, 1966.

  14. Справочник по специальным функциям с формулами, графиками и математическими таблицами / Под ред. М. Абрамовица и И. Стиган. М.: Наука, 1979.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал