1. На главную
  2. Электронные версии
  3. Радиотехника и электроника
  4. T. 67, № 1, 2022

Радиотехника и электроника, 2022, T. 67, № 1, стр. 20-29

Спектральная методика расчета щелевых антенн со слоистым диэлектриком

Г. Ф. Заргано a, *, А. М. Лерер a, А. О. Пелевин b

a Южный федеральный университет
344090 Ростов-на-Дону, ул. Зорге, 5, Российская Федерация

b Главный радиочастотный центр
344002 Ростов-на-Дону, просп. Буденновский, 50, Российская Федерация

* E-mail: zargano@yandex.ru

Поступила в редакцию 15.04.2021
После доработки 07.06.2021
Принята к публикации 23.07.2021

Полный текст (PDF)

Аннотация

Представлено решение задачи о возбуждении щелевой антенной решетки (АР) со слоистым диэлектрическим заполнением прямоугольного волновода. Изложен спектральный метод анализа, обладающий существенными преимуществами при численной реализации разработанного алгоритма. Эффективность предложенной методики подтверждена результатами расчетов АР на прямоугольном волноводе с тонким диэлектрическим слоем, примыкающим к щелевым излучателям. Установлено, что введение такого диэлектрического слоя позволяет сместить рабочий диапазон АР вниз по частоте по сравнению с ее аналогом на прямоугольном волноводе с воздушным заполнением без увеличения поперечного сечения волновода.

ВВЕДЕНИЕ

Перспективные технологии, использующие волноводно-щелевые антенные решетки (АР), такие как радары слежения за дорожной обстановкой [1, 2], антенные системы сотовой связи [3], всепогодные радары [4], испытывают острую необходимость в постоянном совершенствовании антенных структур. Практический интерес вызывают расширение рабочей полосы частот, увеличение диапазонных свойств, применение новых материалов для защиты антенн от неблагоприятных погодных условий. Возможными вариантами получения положительного эффекта являются использование слоистого диэлектрического заполнения полости волновода, укрытие апертуры антенны диэлектрическим листом или заполнение щелей диэлектрическим материалом.

Достаточное количество научных работ посвящено исследованию применения диэлектрических материалов в конструкциях волноводно-щелевых антенн. В ряде работ проводится подробный анализ характеристик антенн, апертура которых укрыта диэлектриком. Снижение побочных максимумов диаграммы направленности в результате применения диэлектрического слоя поверх щелей, достигнуто в работах [5, 6]. Расширение рабочей полосы АР и устойчивое поведение луча были получены с помощью диэлектрических пластин [7] и частичного заполнения полости волновода диэлектриком [8]. Щелевая АР с продольными щелями, укрытая диэлектрическим слоем c целью защиты антенны от погодных условий, представлена в работе [9], многослойное укрытие поверх апертуры щелевой антенны – в работе [10], в которой приведены результаты, полученные методом моментов. Использование диэлектрика как укрывного материала для щелевой антенны, а также с целью поддержания давления воздуха в полости волновода для повышения напряжения пробоя показано в работах [11, 12]. Результаты получены также с помощью метода моментов, проведено сравнение его точности с пакетом электромагнитного моделирования. Спектральный метод анализа щелевых антенн на прямоугольных волноводах, укрытых диэлектриком, представлен в работах [13, 14]. Поле на щели было определено с помощью преобразования Фурье, а полученные результаты были сравнены с пакетом электромагнитного моделирования. Теоретический анализ двумерной АР щелевых излучателей, прорезанных в плоском проводящем экране и заполненных магнитодиэлектрическим составом представлен в работе [15].

Диэлектрическое заполнение полости волновода оказывает воздействие на его внутренние характеристики, изменяя среду распространения электромагнитных волн. Критическая частота основной волны снижается, расширяется рабочий диапазон, улучшается согласование антенны.

Цель данной работы – исследовать влияние горизонтального слоистого диэлектрического заполнения прямоугольного волновода на характеристики АР с продольными щелями. В настоящее время в известной литературе недостаточно полно представлены методы анализа волноводно-щелевых АР с диэлектрическим слоем, расположенным вплотную к широкой стенке волновода, в которой расположены прямоугольные щелевые излучатели с диэлектрическим заполнением. Чтобы восполнить этот недостаток, требуется разработать методику анализа такого класса антенн, оценить ее эффективность и получить улучшенные характеристики антенных структур, рассчитанных на основе разработанной методики.

1. ПОСТАНОВКА ЗАДАЧИ

Решение задачи об излучении щелевой АР (рис. 1) может быть сведено к решению интегро-дифференциальных уравнений (ИДУ) или спектральных интегральных уравнений (СИУ) относительно преобразований Фурье тангенциальных компонент напряженности электрического поля на щелях. Тензорное ядро ИДУ имеет бисингулярную особенность, которую при численном решении задачи необходимо выделять и учитывать при аналитических преобразованиях. В СИУ при численном решении бисингулярная особенность проявляется в медленной сходимости рядов и интегралов. Улучшить сходимость оказывается проще, чем аналитически выделить и преобразовать бисингулярную особенность, поэтому для решения данной задачи будем использовать СИУ. Подробно использование спектрального метода представлено в работах [16, 17], а его применение для решения задачи об излучении щелевой АР с воздушным заполнением прямоугольного волновода – в работе [18].

Рис. 1.

Элемент щелевой АР со слоистым диэлектрическим заполнением: I – область внешнего пространства, II – область полости щели, III – внутренняя область волновода.

При расчете щелевых АР со слоистым диэлектрическим заполнением полости волновода для получения СИУ необходимо использовать LM- и LE-волны, которые являются собственными волнами прямоугольных волноводов со слоистым диэлектрическим заполнением, а электромагнитное поле – суперпозицией этих волн. Неизвестные спектральные амплитуды электромагнитных волн выражаются через преобразования Фурье тангенциальных компонент напряженности электрического поля на щелях. Затем находятся и сшиваются тангенциальные компоненты напряженности магнитного поля на щелях. Полученные таким способом СИУ учитывают произвольное количество диэлектрических слоев. Потери в диэлектрике не учитываются. Зависимость от времени берется в виде exp(–iωt).

2. РЕШЕНИЕ ЗАДАЧИ

Рассмотрим излучение щелевой АР, прямоугольный волновод которой заполнен сплошными слоями диэлектрика, расположенными параллельно широкой стенке (рис. 1).

Выражения для электромагнитных полей в области внешнего пространства I и полости щели II, получены в работе [18]. Для определения компонент электромагнитных полей во внутренней области волновода III, а именно в заполненном диэлектриком прямоугольном волноводе, используем аппарат LM- и LE-волн. Для этого запишем векторные потенциалы с одной y-компонентой $\vec {A}(0,{{A}_{y}},0)$ и $\vec {F}(0,{{F}_{y}},0)$ (далее индекс у не приводим). Введение таких потенциалов подробно описано в работе [19].

Определим функции ${{Y}_{{a,f}}}\left( {y,{{\alpha }_{n}},\beta } \right)$, которые являются решениями уравнений (1) и удовлетворяют граничным условиям на стенках волновода и граничным условиям на границах раздела сред в случае многослойного диэлектрика:

(1)
$\left( {\frac{{{{d}^{2}}}}{{d{{y}^{2}}}} + {{k}^{2}}\varepsilon \left( y \right) - \alpha _{n}^{2} - {{\beta }^{2}}} \right){{Y}_{{a,f}}}\left( {y,{{\alpha }_{n}},\beta } \right) = 0,$
где k – волновое число в свободном пространстве, ε(y) – относительная диэлектрическая проницаемость слоя, (αn, β) – волновые числа по х и z соответственно.

Запишем векторный потенциал для LM-волн:

(2)
$\begin{gathered} A\left( {x,y,z} \right) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\sum\limits_{n = 1}^\infty {{{B}_{a}}({{\alpha }_{n}},\beta )\sin \left( {{{\alpha }_{n}}x} \right)} } \times \\ \times \,\,\frac{{{{\varepsilon }_{1}}{{Y}_{a}}\left( {y,{{\alpha }_{n}},\beta } \right)}}{{Y_{a}^{'}\left( {b,{{\alpha }_{n}},\beta } \right)}}\exp (i\beta z)d\beta , \\ \end{gathered} $
где ε1 – относительная диэлектрическая проницаемость слоя, контактирующего со щелями, ${{B}_{{a,f}}}({{\alpha }_{n}},\beta )$ – неизвестные амплитудные коэффициенты, штрих в функции $Y_{{a,f}}^{'}\left( {y,{{\alpha }_{n}},\beta } \right)$ означает производную по y.

Находим тангенциальные компоненты электромагнитных полей для LM-волн:

(3)
$\begin{gathered} {{{\tilde {E}}}_{{x,z}}}\left( {x,y,z} \right) = \eta \left\{ \begin{gathered} {{\alpha }_{n}}\cos \left( {{{\alpha }_{n}}x} \right) \hfill \\ i\beta \sin \left( {{{\alpha }_{n}}x} \right) \hfill \\ \end{gathered} \right\} \times \\ \times \,\,\exp (i\beta z)\frac{{{{\varepsilon }_{1}}Y_{a}^{'}\left( {y,{{\alpha }_{n}},\beta } \right)}}{{\varepsilon \left( y \right)Y_{a}^{'}\left( {b,{{\alpha }_{n}},\beta } \right)}}{{B}_{a}}({{\alpha }_{n}},\beta ), \\ \end{gathered} $
(4)
$\begin{gathered} {{{\tilde {H}}}_{{x,z}}}\left( {x,y,z} \right) = \left\{ \begin{gathered} - i\beta \sin \left( {{{\alpha }_{n}}x} \right) \hfill \\ {{\alpha }_{n}}\cos \left( {{{\alpha }_{n}}x} \right) \hfill \\ \end{gathered} \right\} \times \\ \times \,\,\exp (i\beta z)\frac{{{{\varepsilon }_{1}}{{Y}_{a}}\left( {y,{{\alpha }_{n}},\beta } \right)}}{{Y_{a}^{'}\left( {b,{{\alpha }_{n}},\beta } \right)}}{{B}_{a}}({{\alpha }_{n}},\beta ), \\ \end{gathered} $
где $\eta = {{ - i{{Z}_{0}}} \mathord{\left/ {\vphantom {{ - i{{Z}_{0}}} k}} \right. \kern-0em} k}$, ${{Z}_{0}} = {{\left( {{{{{\mu }_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, $i = \sqrt { - 1} $.

Аналогичным образом запишем векторный потенциал и тангенциальные компоненты электромагнитных полей для LE-волн:

(5)
$\begin{gathered} F\left( {x,y,z} \right) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\sum\limits_{n = 1}^\infty {{{B}_{f}}({{\alpha }_{n}},\beta )\cos \left( {{{\alpha }_{n}}x} \right)} } \times \\ \times \,\,\frac{{{{Y}_{f}}\left( {y,{{\alpha }_{n}},\beta } \right)}}{{Y_{f}^{'}\left( {b,{{\alpha }_{n}},\beta } \right)}}\exp (i\beta z)d\beta , \\ \end{gathered} $
(6)
$\begin{gathered} {{{\tilde {E}}}_{{x,z}}}\left( {x,y,z} \right) = \\ = \left\{ \begin{gathered} i\beta \cos \left( {{{\alpha }_{n}}x} \right) \hfill \\ {{\alpha }_{n}}\sin \left( {{{\alpha }_{n}}x} \right) \hfill \\ \end{gathered} \right\}\exp (i\beta z)\frac{{{{Y}_{f}}\left( {y,{{\alpha }_{n}},\beta } \right)}}{{{{Y}_{f}}\left( {b,{{\alpha }_{n}},\beta } \right)}}{{B}_{f}}({{\alpha }_{n}},\beta ), \\ \end{gathered} $
(7)
$\begin{gathered} {{{\tilde {H}}}_{{x,z}}}\left( {x,y,z} \right) = \hat {\eta }\left\{ \begin{gathered} - {{\alpha }_{n}}\sin \left( {{{\alpha }_{n}}x} \right) \hfill \\ i\beta \cos \left( {{{\alpha }_{n}}x} \right) \hfill \\ \end{gathered} \right\} \times \\ \times \,\,\exp (i\beta z)\frac{{Y_{f}^{'}\left( {y,{{\alpha }_{n}},\beta } \right)}}{{{{Y}_{f}}\left( {b,{{\alpha }_{n}},\beta } \right)}}{{B}_{f}}({{\alpha }_{n}},\beta ), \\ \end{gathered} $
где $\hat {\eta } = {\eta \mathord{\left/ {\vphantom {\eta {Z_{0}^{2}}}} \right. \kern-0em} {Z_{0}^{2}}}$.

Складываем выражения (3) и (6) при y = b. В результате получаем спектральные представления суперпозиции тангенциальных составляющих электрического поля на нижней апертуре щелей для LM- и LE-волн в пространстве волновых чисел αn и β:

(8)
${{\tilde {E}}_{{x,z}}}\left( {x,b,z} \right) = {{\tilde {\tilde {E}}}_{{x,z}}}\left( {{{\alpha }_{n}},\beta } \right)\left\{ \begin{gathered} \cos \left( {{{\alpha }_{n}}x} \right) \hfill \\ \sin \left( {{{\alpha }_{n}}x} \right) \hfill \\ \end{gathered} \right\}\exp (i\beta z),$
где
(9)
${{\tilde {\tilde {E}}}_{{x,z}}}\left( {{{\alpha }_{n}},\beta } \right) = \eta \left\{ \begin{gathered} {{\alpha }_{n}} \hfill \\ i\beta \hfill \\ \end{gathered} \right\}{{B}_{a}}({{\alpha }_{n}},\beta ) + \left\{ \begin{gathered} i\beta \hfill \\ {{\alpha }_{n}} \hfill \\ \end{gathered} \right\}{{B}_{f}}({{\alpha }_{n}},\beta ).$
Неизвестные амплитудные коэффициенты ${{B}_{{a,f}}}({{\alpha }_{n}},\beta )$ определяем через Фурье-образы компонент электрического поля на щелях (9):
(10)
$\begin{gathered} {{B}_{a}}({{\alpha }_{n}},\beta ) = \frac{1}{{\eta {{\rho }^{2}}}}\left( {{{\alpha }_{n}}{{{\tilde {\tilde {E}}}}_{x}}({{\alpha }_{n}},\beta ) - i\beta {{{\tilde {\tilde {E}}}}_{z}}({{\alpha }_{n}},\beta )} \right), \\ {{B}_{f}}({{\alpha }_{n}},\beta ) = \frac{1}{{{{\rho }^{2}}}}\left( { - i\beta {{{\tilde {\tilde {E}}}}_{x}}({{\alpha }_{n}},\beta ) + {{\alpha }_{n}}{{{\tilde {\tilde {E}}}}_{z}}({{\alpha }_{n}},\beta )} \right), \\ {{\rho }^{2}} = \alpha _{n}^{2} + {{\beta }^{2}}. \\ \end{gathered} $
Далее записываем Фурье-образы тангенциальных компонент ${{\tilde {\tilde {H}}}_{{x,z}}}({{\alpha }_{n}},\beta )$ напряженности магнитного поля LM- и LE-волн. Для этого складываем выражения (4) и (7) при y = b:
(11)
${{\tilde {H}}_{{x,z}}}\left( {x,b,z} \right) = {{\tilde {\tilde {H}}}_{{x,z}}}\left( {{{\alpha }_{n}},\beta } \right)\left\{ \begin{gathered} \sin \left( {{{\alpha }_{n}}x} \right) \hfill \\ \cos \left( {{{\alpha }_{n}}x} \right) \hfill \\ \end{gathered} \right\}\exp (i\beta z),$
где
(12)
$\begin{gathered} {{{\tilde {\tilde {H}}}}_{{x,z}}}\left( {\alpha ,\beta } \right) = \left\{ \begin{gathered} - i\beta \hfill \\ \alpha \hfill \\ \end{gathered} \right\}{{\varepsilon }_{1}}\frac{{{{Y}_{a}}\left( {b,{{\alpha }_{n}},\beta } \right)}}{{{{{Y'}}_{a}}\left( {b,{{\alpha }_{n}},\beta } \right)}}{{B}_{a}}({{\alpha }_{n}},\beta ) + \\ + \,\,\hat {\eta }\left\{ \begin{gathered} - \alpha \hfill \\ i\beta \hfill \\ \end{gathered} \right\}\frac{{{{{Y'}}_{f}}\left( {b,{{\alpha }_{n}},\beta } \right)}}{{{{Y}_{f}}\left( {b,{{\alpha }_{n}},\beta } \right)}}{{B}_{f}}({{\alpha }_{n}},\beta ). \\ \end{gathered} $
Подставляя Ba, f (αn, β) из выражения (10) в формулы (12), получаем Фурье-образы тангенциальных компонент ${{\tilde {\tilde {H}}}_{{x,z}}}({{\alpha }_{n}},\beta )$ напряженности магнитного поля:
(13)
${{\tilde {\tilde {H}}}_{x}}\left( {{{\alpha }_{n}},\beta } \right) = \frac{{\hat {\eta }}}{{{{\rho }^{2}}}}\left[ {{{{\tilde {\tilde {E}}}}_{z}}\left( {{{\alpha }_{n}},\beta } \right){{f}^{{11}}} + {{{\tilde {\tilde {E}}}}_{x}}\left( {{{\alpha }_{n}},\beta } \right){{f}^{{12}}}} \right],$
(14)
${{\tilde {\tilde {H}}}_{z}}\left( {{{\alpha }_{n}},\beta } \right) = \frac{{\hat {\eta }}}{{{{\rho }^{2}}}}\left[ {{{{\tilde {\tilde {E}}}}_{z}}\left( {{{\alpha }_{n}},\beta } \right){{f}^{{21}}} + {{{\tilde {\tilde {E}}}}_{x}}\left( {{{\alpha }_{n}},\beta } \right){{f}^{{22}}}} \right],$
в которых введены следующие обозначения:

(15)
$\begin{gathered} {{f}^{{11}}} = {{\beta }^{2}}{{\varphi }_{a}}{{k}^{2}} - {{\alpha }^{2}}{{\varphi }_{f}},\,\,\,{{f}^{{12}}} = {{f}^{{21}}} = i\alpha \beta \left( {{{\varphi }_{a}}{{k}^{2}} + {{\varphi }_{f}}} \right), \\ {{f}^{{22}}} = - {{\alpha }^{2}}{{\varphi }_{a}}{{k}^{2}} + {{\beta }^{2}}{{\varphi }_{f}},\,\,\,\,{{\varphi }_{a}} = {{\varepsilon }_{1}}\frac{{{{Y}_{a}}\left( {b,{{\alpha }_{n}},\beta } \right)}}{{{{{Y'}}_{a}}\left( {b,{{\alpha }_{n}},\beta } \right)}}, \\ {{\varphi }_{f}} = \frac{{{{{Y'}}_{f}}\left( {b,{{\alpha }_{n}},\beta } \right)}}{{{{Y}_{f}}\left( {b,{{\alpha }_{n}},\beta } \right)}}. \\ \end{gathered} $

В результате в компактной форме получены соотношения между тангенциальными компонентами электрического и магнитного полей в пространстве волновых чисел (αn, β). Координатное представление магнитного поля имеет следующий вид:

(16)
$\begin{gathered} {{H}_{{x,z}}}\left( {x,y,z} \right) = \frac{1}{{2\pi }} \times \\ \times \,\,\int\limits_{ - \infty }^\infty {\sum\limits_{n = 1}^\infty {\left\{ \begin{gathered} \sin \left( {{{\alpha }_{n}}x} \right) \hfill \\ \cos \left( {{{\alpha }_{n}}x} \right) \hfill \\ \end{gathered} \right\}{{{\tilde {\tilde {H}}}}_{{x,z}}}\left( {{{\alpha }_{n}},\beta } \right)\exp (i\beta z)d\beta } } . \\ \end{gathered} $

Полученные выражения для напряженности магнитного поля справедливы для любого количества горизонтальных слоев диэлектрика.

Определим теперь собственные функции ${{Y}_{a}}\left( {y,{{\alpha }_{n}},\beta } \right)$, ${{Y}_{f}}\left( {y,{{\alpha }_{n}},\beta } \right)$ для случая заполнения волновода двуслойным диэлектриком. Зададим эти функции в соответствии с условиями на границе слоев для функции ${{Y}_{{a,f}}}\left( y \right)$, имеющей аналитическое представление:

(17)
${{Y}_{{a,f}}}\left( y \right) = \left\{ \begin{gathered} \frac{{{\text{sh}}\left[ {{{\gamma }_{1}}\left( {b - y} \right)} \right] + {{D}_{{a,f}}}{\text{sh}}\left[ {{{\gamma }_{1}}\left( {y - {{h}_{2}}} \right)} \right]}}{{{\text{sh}}({{\gamma }_{1}}{{h}_{1}})}},\,\,\,\,{{h}_{2}} \leqslant y \leqslant b; \hfill \\ \frac{{{\text{ch}}({{\gamma }_{2}}y)}}{{\operatorname{ch} ({{\gamma }_{2}}{{h}_{2}})}},\,\,\,\,0 \leqslant y \leqslant {{h}_{2}}; \hfill \\ \end{gathered} \right.$
(18)
${{Y'}_{{a,f}}}\left( y \right) = \left\{ \begin{gathered} {{\gamma }_{1}}\frac{{ - {\text{ch}}\left[ {{{\gamma }_{1}}\left( {b - y} \right)} \right] + {{D}_{{a,f}}}{\text{ch}}\left[ {{{\gamma }_{1}}\left( {y - {{h}_{2}}} \right)} \right]}}{{{\text{sh}}({{\gamma }_{1}}{{h}_{1}})}},\,\,\,\,{{h}_{2}} \leqslant y \leqslant b; \hfill \\ {{\gamma }_{2}}\frac{{{\text{sh}}({{\gamma }_{2}}y)}}{{{\text{ch}}({{\gamma }_{2}}{{h}_{2}})}},\,\,\,\,0 \leqslant y \leqslant {{h}_{2}}; \hfill \\ \end{gathered} \right.$

В j-м слое постоянная распространения γ j вдоль оси y будет равна:

(19)
$\begin{gathered} {{\gamma }_{j}} = \sqrt { - {{k}^{2}}{{\varepsilon }_{j}} + {{{\left( {{{m\pi } \mathord{\left/ {\vphantom {{m\pi } {{{a}_{n}}}}} \right. \kern-0em} {{{a}_{n}}}}} \right)}}^{2}} + {{\beta }^{2}}} ,\,\,\,\,\,{{{\bar {\gamma }}}_{j}} = {{{{\gamma }_{j}}} \mathord{\left/ {\vphantom {{{{\gamma }_{j}}} {{{\varepsilon }_{j}}}}} \right. \kern-0em} {{{\varepsilon }_{j}}}}, \\ j = 1,2. \\ \end{gathered} $

Неизвестные коэффициенты Da и Df находим из условия непрерывности ${{Y_{a}^{'}\left( y \right)} \mathord{\left/ {\vphantom {{Y_{a}^{'}\left( y \right)} \varepsilon }} \right. \kern-0em} \varepsilon }$ и $Y_{f}^{'}\left( y \right)$ на границе диэлектрических слоев:

(20)
${{D}_{a}} = \left( {{{{\bar {T}}}_{1}} + {{{\bar {C}}}_{2}}} \right)\frac{1}{{{{{\bar {S}}}_{1}}}},\,\,\,\,{{D}_{f}} = \left( {{{T}_{1}} + {{T}_{2}}} \right)\frac{1}{{{{S}_{1}}}},$
где

$\begin{gathered} {{S}_{j}} = \frac{{{{\gamma }_{j}}}}{{\operatorname{sh} ({{\gamma }_{j}}{{h}_{j}})}},\,\,\,{{{\bar {S}}}_{j}} = \frac{{{{{\bar {\gamma }}}_{j}}}}{{\operatorname{sh} ({{\gamma }_{j}}{{h}_{j}})}}, \\ {{T}_{j}} = {{\gamma }_{j}}{\text{cth}}({{\gamma }_{j}}{{h}_{j}}),\,\,\,\,{{{\bar {T}}}_{j}} = {{{\bar {\gamma }}}_{j}}{\text{cth}}({{\gamma }_{j}}{{h}_{j}}), \\ {{{\bar {C}}}_{j}} = {{{\bar {\gamma }}}_{j}}{\text{th}}({{\gamma }_{j}}{{h}_{j}}). \\ \end{gathered} $

Тогда, используя введенные обозначения, получаем

(21)
${{\varphi }_{a}} = \frac{{{{D}_{a}}}}{{ - {{{\bar {S}}}_{1}} + {{D}_{a}}{{{\bar {T}}}_{1}}}},\,\,\,\,{{\varphi }_{f}} = - \frac{{{{S}_{1}}}}{{{{D}_{f}}}} + {{T}_{1}}.$

В итоге компоненты напряженностей магнитного поля на нижней апертуре щели можем определить, подставив функции φa,f (21) в выражения (13) и (14):

(22)
$\begin{gathered} {{H}_{x}}\left( {x,y = b - 0,z} \right) = - \frac{i}{{2\pi k{{Z}_{0}}{{\rho }^{2}}}} \times \\ \times \,\,\sum\limits_{n = 1}^\infty {\sin \left( {{{\alpha }_{n}}x} \right)\sum\limits_{v = 1}^M {\int\limits_{ - \infty }^\infty {d\beta } } } \,\iint\limits_{{{S}_{v}}} {\left[ {{{{\tilde {E}}}_{{vz}}}(x{\kern 1pt} ',z{\kern 1pt} ')\sin ({{\alpha }_{n}}x{\kern 1pt} '){{f}^{{11}}} + } \right.}\left. {{{{\tilde {E}}}_{{vx}}}(x{\kern 1pt} ',z{\kern 1pt} ')\cos ({{\alpha }_{n}}x{\kern 1pt} '){{f}^{{12}}}} \right]\exp ( - i\beta (z{\kern 1pt} '\,\, - z))dx{\kern 1pt} 'dz{\kern 1pt} ', \\ \end{gathered} $
(23)
$\begin{gathered} {{H}_{z}}\left( {x,y = b - 0,z} \right) = - \frac{i}{{2\pi k{{Z}_{0}}{{\rho }^{2}}}} \times \\ \times \,\,\sum\limits_{n = 0}^\infty {\frac{{\cos \left( {{{\alpha }_{n}}x} \right)}}{{1 + {{\delta }_{{0n}}}}}\sum\limits_{v = 1}^M {\int\limits_{ - \infty }^\infty {d\beta } } } \,\iint\limits_{{{S}_{v}}} {\left[ {{{{\tilde {E}}}_{{vz}}}(x{\kern 1pt} ',z{\kern 1pt} ')\sin ({{\alpha }_{n}}x{\kern 1pt} '){{f}^{{21}}}} \right.} + \left. {{{{\tilde {E}}}_{{vx}}}(x{\kern 1pt} ',z{\kern 1pt} ')\cos ({{\alpha }_{n}}x{\kern 1pt} '){{f}^{{22}}}} \right]\exp ( - i\beta (z{\kern 1pt} '\,\, - z))dx{\kern 1pt} 'dz{\kern 1pt} ', \\ \end{gathered} $
где $x,z \in {{S}_{{\nu {\kern 1pt} '}}},\,\,\nu {\kern 1pt} ' = 1,2,...,M,$ М – количество щелей.

Система интегральных уравнений относительно преобразований Фурье тангенциальных компонент напряженности электрического поля на щелях образуется из условий непрерывности тангенциальных компонент магнитного поля на внешней и внутренней апертурах щелей.

Для этого приравниваем соответствующие компоненты магнитных полей на границе области внешнего полупространства I и верхней апертуре щели II, затем на границе области волновода III и нижней апертуры щели II.

Прямоугольный волновод возбуждается основной волной LM10:

(24)
$\begin{gathered} {{H}_{{\nu {\kern 1pt} 'x,z}}}(y = b + t - 0) - {{H}_{{x,z}}}(y = b + t + 0) = 0 \\ {{H}_{{x,z}}}(y = b - 0) - {{H}_{{\nu {\kern 1pt} 'x,z}}}(y = b + 0) = H_{{x,z}}^{{{\text{inc}}}}, \\ \end{gathered} $
где ${{H}_{{x,z}}}(y = b + t + 0)$ – напряженность поля во внешнем полупространстве I, ${{H}_{{\nu {\kern 1pt} 'x,\nu {\kern 1pt} 'z}}}$(y = b + t – 0), ${{H}_{{\nu {\kern 1pt} 'x,\nu {\kern 1pt} 'z}}}(y = b + 0)$ – напряженность поля внутри щели II, ${{H}_{{x,z}}}(y = b - 0)$ – напряженность поля внутри волновода III, $H_{{x,z}}^{{{\text{inc}}}}$ – напряженность поля волны, питающей волновод (LM10), $\nu {\kern 1pt} ' = 1,2,...,M.$

В результате преобразований получаем систему СИУ, которую решаем с помощью метода Галеркина с базисами в виде ортогональных полиномов Чебышева 1-го и 2-го рода, учитывающих особенность поведения электрического поля на ребрах щелей.

Компоненты тангенциального электрического поля на внешних и внутренних апертурах щелей аппроксимируем функциями

(25)
$E_{{\nu ,x}}^{ \pm }(x,z) = \sum\limits_{i = 0}^{{{N}_{x}} - 1} {\sum\limits_{k = 0}^{{{N}_{z}}} {u_{{ik}}^{{ \pm ,\nu x}}} } {{\bar {U}}_{i}}\left( {\frac{{2(x - {{x}_{\nu }})}}{{{{w}_{\nu }}}}} \right){{\bar {T}}_{k}}\left( {\frac{{2(z - {{z}_{\nu }})}}{{{{L}_{\nu }}}}} \right),$
(26)
$E_{{\nu ,z}}^{ \pm }(x,z) = \sum\limits_{i = 0}^{{{N}_{x}}} {\sum\limits_{k = 0}^{{{N}_{z}} - 1} {u_{{ik}}^{{ \pm ,\nu y}}} } {{\bar {T}}_{i}}\left( {\frac{{2(x - {{x}_{\nu }})}}{{{{w}_{\nu }}}}} \right){{\bar {U}}_{k}}\left( {\frac{{2(z - {{z}_{\nu }})}}{{{{L}_{\nu }}}}} \right),$
где ${{\bar {T}}_{i}}(x)\, = \,{{(1 - {{x}^{2}})}^{{ - 1/2}}}\,{{T}_{i}}(x)$, ${{\bar {U}}_{i}}(x) = {{(1 - {{x}^{2}})}^{{1/2}}} \times $ $ \times \,\,{{{{U}_{i}}(x)} \mathord{\left/ {\vphantom {{{{U}_{i}}(x)} {(i + 1)}}} \right. \kern-0em} {(i + 1)}}$ – взвешенные полиномы Чебышева 1-го и 2-го рода, $u_{{ik}}^{{ \pm ,\nu x}}$, $u_{{ik}}^{{ \pm ,\nu y}}$ – неизвестные коэффициенты, ${{x}_{\nu }}\,,\,\,\,{{z}_{\nu }}$ – координаты центра ν-й щели ($\nu = 1,\,\,2,\,\,...,\,M$).

Выбор в качестве базисных функций взвешенных полиномов Чебышева, учитывающих особенность поведения поля на острых ребрах щелей, обеспечивает быструю сходимость решения и позволяет реализовать эффективные алгоритмы вычисления присутствующих интегралов.

В результате представленной методики решения получаем систему линейных алгебраических уравнений. Преобразования Фурье базисных функций определяются через функции Бесселя, поэтому спектральные матричные элементы системы линейных алгебраических уравнений выражаются в явном виде.

Вычисление интеграла Фурье в матричных элементах зависит от расположения точек истока и наблюдения. Если точки расположены на разных щелях, то интеграл вычисляется с помощью теории вычетов. В результате интеграл Фурье заменяется рядом по LM- и LE-волнам. Этот ряд очень быстро (экспоненциально) сходится. Когда точки расположены на одной щели, то применять напрямую теорию вычетов нельзя. Для такого интеграла, содержащего сингулярность на контуре интегрирования, разработана квадратурная формула в работе [20]. Также была разработана процедура улучшения сходимости рядов, представляющая собой двумерный аналог способа Куммера. При нахождении матрицы рассеяния и диаграммы направленности антенны интегралы вычисляются с помощью теории вычетов.

3. ВЕРИФИКАЦИЯ МЕТОДА РЕШЕНИЯ

Перейдем к анализу численной реализации полученного метода расчета щелевых АР с двуслойным диэлектрическим заполнением прямоугольного волновода. Для этого зададим конфигурацию щелевой антенны на прямоугольном волноводе шириной a = 23 мм, высотой b = 10 мм, c толщиной стенки t = 1 мм. В широкой стенке волновода прорезаны 20 прямоугольных продольных щелей длиной Lν = 15 мм, шириной wν = = 1.5 мм (см. рис. 1). Все щели равноудалены от центральной оси волновода на расстояние x = 2.3 мм, период решетки d = 22.5 мм. Горизонтальный слой толщиной h1 = 1.5 мм с диэлектрической проницаемостью ε1 = 2.2 вплотную примыкает к верхней широкой стенке волновода. Второй слой (h2) является воздушным (ε2 = 1). Щелевые излучатели полностью заполнены диэлектрическим материалом с ε3 = 1.58. Волновод работает на основной волне. Анализируются следующие характеристики АР: модули коэффициентов отражения |S11|) и прохождения |S21|, коэффициенты стоячей волны (КСВ), усиления (КУ), полезного действия (КПД) и диаграмма направленности (ДН).

При расчете антенных структур, для которых еще не проведен эксперимент, крайне важен тщательный анализ точности полученного результата. Поэтому был проведен анализ численной сходимости результатов, полученных с помощью данного метода при задании разного количества базисных функций, описывающих поведение электрического поля на щелях. В табл. 1 приведены результаты расчета параметров щелевой АР на частоте f = 8.898 ГГц максимального значения КСВ и на частоте f = = 7.935 ГГц минимального значения |S21| при различном количестве базисных функций, аппроксимирующих поле как вдоль (Nz), так и поперек щели (Nx).

Таблица 1.

Сходимость решения по количеству базисных функций

Nx Nz f = 8.898 ГГц f = 7.935 ГГц
|S11| КСВ |S21| КПД |S11| КСВ |S21| КПД
2 2 0.5785 3.7450 0.4398 0.4719 0.0352 1.0730 0.8477 0.2802
3 0.5741 3.6960 0.4421 0.4750 0.0341 1.0700 0.8487 0.2785
4 0.4801 2.8470 0.7338 0.2310 0.0962 1.2130 0.0728 0.9854
5 0.4826 2.8650 0.7323 0.2309 0.0962 1.2130 0.0729 0.9854
6 0.4799 2.8450 0.7357 0.2284 0.0959 1.2120 0.0696 0.9860
7 0.4800 2.8460 0.7357 0.2284 0.0959 1.2120 0.0696 0.9860
3 3 0.5931 3.9150 0.4013 0.4872 0.0367 1.0760 0.8081 0.3456
4 0.4776 2.8290 0.7380 0.2272 0.0956 1.2110 0.0669 0.9864
5 0.4799 2.8460 0.7366 0.2271 0.0956 1.2110 0.0670 0.9864
6 0.4778 2.8300 0.7393 0.2252 0.0950 1.2100 0.0661 0.9866
7 0.4779 2.8300 0.7392 0.2252 0.0950 1.2100 0.0661 0.9866
4 4 0.4778 2.8300 0.7379 0.2272 0.0956 1.2110 0.0669 0.9864
5 0.4801 2.8470 0.7364 0.2271 0.0956 1.2110 0.0670 0.9864
6 0.4780 2.8320 0.7391 0.2252 0.0950 1.2100 0.0661 0.9866
7 0.4781 2.8320 0.7391 0.2252 0.0950 1.2100 0.0661 0.9866

Погрешность порядка 1.5% получена при трех поперечных базисных функциях Nx = 3 и четырех функциях вдоль щели Nz = 4. Количество членов, учитываемых в матричных элементах итоговой системы линейных алгебраических уравнений, бралось 50 по каждому индексу.

Было проведено сравнение значений внутренних параметров и диаграмм направленностей АР, рассчитанных данным методом, с результатами, полученными с помощью пакетов электромагнитного моделирования. Методом конечного интегрирования, используемым в Dassault Systèmes Simulia Computer simulation software (CST), реализовано решение во временной области. Исходя из этого, скорость расчета нерезонансной щелевой АР будет зависеть от размеров исследуемой структуры и полосы рабочих частот. Точность расчета и его достоверность зависят от величины ячеек, на которые разбивается все пространство структуры. Методом конечных элементов, применяемым в Ansys High Frequency Structural Simulator (HFSS), осуществлены вычисления в частотной области. Скорость решения напрямую зависит от количества частотных точек, а точность расчетов – от количества элементарных тетраэдров, на которые разбивается все исследуемое пространство.

Учитывая все сказанное выше, в работе проведена двойная верификация точности полученного метода с помощью пакетов электромагнитного моделирования CST и HFSS, использующих разные методы решения.

Модуль коэффициента отражения |S11|, рассчитанный с помощью данного метода и пакетов моделирования CST и HFSS, представлен на рис. 2а. Положение максимума модуля коэффициента отражения |S11| одинаково для всех трех методов расчета. Небольшое различие по величине, порядка 1%, наблюдается в значении максимума, однако на работу АР в режиме бегущей волны оно не повлияет. Сравнение результатов расчета модуля коэффициента прохождения |S21| представлено на рис. 2б. В диапазоне его минимальных значений наблюдается почти полное графическое совпадение полученных результатов.

Рис. 2.

Зависимости модулей элементов матрицы рассеяния от частоты, полученные с помощью спектральной методики (1), CST (2) и HFSS (3).

На рис. 3 представлена нормированная ДН АР на частоте 8 ГГц. Главный и боковые лепестки диаграммы направленности хорошо графически совпадают, различия видны лишь на краях диаграммы, что не вносит различий в антенные характеристики, рассчитанные разными методами.

Рис. 3.

Диаграммы направленности АР на частоте 8 ГГц, полученные с помощью спектральной методики (1), CST (2) и HFSS (3).

Анализ результатов, представленных на рис. 2 и 3, свидетельствует о графическом соответствии внутренних (S-параметров) и внешних характеристик (ДН) АР, рассчитанных данным методом и с помощью пакетов электромагнитного моделирования.

Сравнение скорости решения различных методов в диапазоне частот шириной ∆f = 2.4 ГГц (6.5…9.7 ГГц) с шагом 0.05 ГГц представлено в табл. 2 по аналогии с работой [21]. При расчете с помощью пакета CST количество частотных точек Tf на время расчета не влияет. Разработанный в данной работе метод позволил эффективно задействовать все ядра процессора, что ускорило решение. Требования к объему оперативного запоминающего устройства (ОЗУ) оказываются значительно меньшими в пользу данного метода (см. табл. 2) ввиду применения аналитических преобразований, которые позволили значительно снизить количество неизвестных, участвующих в расчетах.

Таблица 2.

Сравнение скорости счета и используемых вычислительных ресурсов

Методы Tf, с T∆f, с ОЗУ, Мбайт Количество ядер
Спектральная методика 4 120 80 4
CST – 1200 350 2
HFSS 120 2400 4005 2

Примечание: Tf – время расчета одной частотной точки, T∆f – время расчета в диапазоне частот.

Таким образом, скорость расчета, быстрая сходимость численных решений и экономичные требования к вычислительным ресурсам являются основными достоинствами разработанного метода.

4. РАСЧЕТ АНТЕННЫХ СТРУКТУР

Перейдем теперь к расчету щелевых АР с различной толщиной и диэлектрической проницаемостью слоя внутри волновода. Рассмотрим характеристики АР исходя из смещения рабочего диапазона вниз по частоте. Смещение рабочего диапазона вниз по частоте на 1.9 ГГц относительно АР с воздушным заполнением (рис. 4, кривая 1) произошло благодаря диэлектрическому слою толщиной h1 = 1.5 мм и ε1 = 1.6 (см. рис. 4, кривая 2). Значение максимального КУ составило 18.3 дБ (табл. 3), что на 0.4 дБ меньше, чем у АР с воздушным заполнением. Однако рабочая полоса частот расширилась до ∆fраб = 1.45 ГГц по уровню –3 дБ от максимального КУ. Необходимо отметить, что максимальное значение КСВ смещено вверх по частоте, относительно рабочего диапазона АР, и не разделяет его на два поддиапазона, как в случае с воздушным заполнением. Таким образом, появилась возможность избавиться от эффекта “ослепления” АР без внесения изменений в металлическую конструкцию антенны.

Рис. 4.

Зависимость КУ и КСВ от частоты для различных ε1 и h1: кривая 1 – h1 = 10 мм и ε1 = 1; кривая 2 – h1 = 1.5 мм и ε1 = 1.6; кривая 3 – h1 = 2.5 мм и ε1 = 1.6; кривая 4 – h1 = 1.5 и ε1 = 2.2; кривая 5 – h1 = 2.5 мм и ε1 = 2.2.

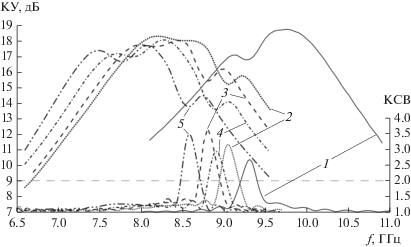
Таблица 3.

Характеристики волноводно-щелевой АР для разных значений ε1 и h1

Сочетание fраб, ГГц ∆fраб, ГГц КУmax, дБ КСВ ϑ(fраб), град ∆ϑ, град
ε1 h1, мм
1.6 1.5 7.5…8.9 1.45 18.3 <1.43 109…92 17
1.6 2.5 7.4…8.65 1.15 18.0 <1.40 108…92 16
2.2 1.5 7.25…8.7 1.45 18.2 <1.20 110…92 18
2.2 2.5 7.05…8.45 1.40 17.8 <1.50 111…92 19

Диэлектрический слой толщиной h1 = 2.5 мм и ε1 = 1.6 сместил рабочий диапазон частот АР на 2 ГГц (см. рис. 4, кривая 3). Значение максимального КУ меньше на 0.8 дБ относительно АР с воздушным заполнением, поскольку диэлектрик заполнил уже четверть волновода. Также максимальное значение КСВ больше, чем у АР с диэлектрическим слоем высотой h1 = 1.5 и ε1 = 1.6, в результате чего наблюдается уменьшение рабочей полосы до 1.15 ГГц (см. табл. 3).

Антенная решетка с диэлектрическим слоем толщиной h1 = 1.5 и ε1 = 2.2 (см. рис. 4, кривая 4) работает в рабочем диапазоне, смещенном на 2.2 ГГц вниз по частоте относительно АР с воздушным заполнением. Ширина рабочего диапазона частот составила 1.45 ГГц. Максимальное значение КУ в полосе составило 18.2 дБ, что на 0.5 дБ меньше, чем для АР с воздушным заполнением. При этом максимум КСВ находится за пределами рабочей полосы частот в отличие от АР с воздушным заполнением.

Увеличение толщины диэлектрического слоя до h1 = 2.5 мм при той же ε1 = 2.2 позволило еще дальше сместить рабочий диапазон АР вниз по частоте (см. рис. 4, кривая 5). Увеличение толщины слоя диэлектрика уменьшило максимальное значение КУ на 1 дБ относительно АР с воздушным заполнением. Ширина рабочей полосы частот данной АР составила 1.4 ГГц (см. табл. 3), значение максимального КСВ находится справа от рабочей полосы.

В табл. 3 приведены предельные углы ϑ(fраб), показывающие положение главного лепестка ДН на крайних частотах рабочего диапазона, а также сектор частотного сканирования ∆ϑ в рабочей полосе частот.

В результате анализа рассмотренных антенных структур установлено, что применение диэлектрического заполнения толщиной более h1 = 2.5 мм и ε1 > 2.2 практически нецелесообразно, что также подтверждается работой [22]. При увеличении толщины диэлектрического слоя рабочий диапазон продолжает смещаться вниз по частоте, при этом снижается максимальное значение КУ и растет максимальное значение КСВ.

ЗАКЛЮЧЕНИЕ

Определено строгое аналитическое представление для электромагнитных полей в прямоугольном волноводе, заполненном произвольным количеством горизонтальных диэлектрических слоев. На основе полученных выражений разработана методика расчета щелевых АР с двуслойным диэлектрическим заполнением полости прямоугольного волновода. Метод обладает быстрой сходимостью решения, высокой скоростью счета одной частотной точки и экономичными требованиями к вычислительным ресурсам.

С помощью данного метода определены антенные характеристики четырех волноводно-щелевых структур с различным диэлектрическим заполнением. Представлено сравнение результатов расчетов внутренних и внешних характеристик АР с пакетами электромагнитного моделирования CST и HFSS.

Рассчитана щелевая АР с диэлектрическим заполнением толщиной h1 = 1.5 мм, ε1 = 2.2, с шириной полосы рабочих частот 1.45 ГГц и смещением рабочего диапазона на 2.2 ГГц вниз по частоте относительно щелевой АР с воздушным заполнением. Благодаря своим параметрам данная АР перспективна для построения фазированных АР на ее основе. Заполнение щелей диэлектрическим материалом с проницаемостью ε3 = 1.56 обеспечивает защиту от неблагоприятных погодных условий без потери качества антенных характеристик.

Список литературы

  1. Menzel W., Moebius A. // Proc. IEEE. 2012. V. 100. № 7. P. 2372.

  2. Qin L., Lu Y., You Q. et al. // IEEE Trans. 2018. V. VT-67. № 11. P. 10574.

  3. Zhou J., Wang H., Cao J. et al. // Proc. 2019 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference (CSQRWC). Taiyuan. 18–21 Jul. N.Y.: IEEE, 2019. P. 8799118.

  4. Hermansyah R.Y., Zulkifli F.Y., Rahardjo E.T. // Proc. 2016 Progress in Electromagnetic Research Symp. Shanghai 8–11 Aug. N.Y.: IEEE, 2016. P. 3988.

  5. Rengarajan S.R., Steinbeck M. // Digest 1991 Antennas and Propagation Soc. Int. Symp. London (Ontario). 24–28 Jun. N.Y.: IEEE, 1991. V. 2. P. 1276.

  6. Joubert J. // IEEE Microwave and Guided Wave Lett. 1995. V. 5. № 2. P. 37.

  7. Shan X., Shen Z. // Proc. 12th Int. Conf. on Antennas and Propagation. Exeter. 31 Mar.–03 Apr. 2003. N.Y.: IEEE, 2003. V. 2. P. 682.

  8. Shan X., Shen Z. // IEEE Trans. 2004. V. AP-52. № 4. P. 1030.

  9. Katehi P.B. // IEEE Trans. 1990. V. AP-38. № 7. P. 1039.

  10. Jin Z., Montisci G., Mazzarella G. et al. // IEEE Antennas Wireless Propag. Lett. 2012. V. 11. P. 1190.

  11. Hwang J.H., Oh Y. // IEEE Antennas Wireless Propag. Lett. 2009. V. 8. P. 1050.

  12. Mazzarella G., Montisci G. // Digest 1998 IEEE Antennas and Propagation Society Int. Symp. Atlanta. 21–26 Jun. N.Y.: IEEE, 1998. V. 4. P. 1910.

  13. Choi S. // Proc. 2001 Asia-Pacific Microwave Conf. (APMC 2001). Taipei. 3–6 Dec. N.Y.: IEEE, 2001. V. 2. P. 441.

  14. Choi S., Lee Y. // Proc. 11th Int. Conf. Microwave and Telecommunication Technology. Sevastopol. 10–14 Sept. 2001. N.Y.: IEEE, 2001. P. 379.

  15. Penkin Y., Katrich V., Nesterenko M., Berdnik S. // Proc. 2020 IEEE Ukrainian Microwave Week (UkrMW). Kharkiv. 21–25 Sept. N.Y.: IEEE, 2020. P. 89.

  16. Cano G., Medina F., Horno M. // IEEE Trans. 1992. V. MTT-40. № 2. P. 217.

  17. Kitazawa T. // IEEE Trans. 1995. V. MTT-43. № 2. P. 445.

  18. Мануилов М.Б., Лерер В.А., Синявский Г.П. // РЭ. 2008. Т. 53. № 12. С. 1466.

  19. Егоров Е.В. Частично заполненные прямоугольные волноводы. М.: Сов. радио, 1967.

  20. Lerer A.M., Schuchinsky A.G // IEEE Trans. 1993. V. MTT-41. № 11. P. 2002.

  21. Vandenbosch G., Vasylchenko A. Microstrip Antennas/ Ed. by N. Nasimudin. Singapore: Inst. for Infocomm Research, 2011. P. 507

  22. Заргано Г.Ф., Лерер А.М., Пелевин А.О. // Физические основы приборостроения. 2020. № 3. С. 28.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал