Радиотехника и электроника, 2022, T. 67, № 2, стр. 185-196
Интеллектуальный анализ характеристик пульсовой волны методами структурной декомпозиции сигналов фотоплетизмографии
Л. В. Лабунец a, b, *, А. Б. Борзов a, Н. Ю. Макарова a
a Московский государственный технический университет им. Н.Э. Баумана
105005 Москва, 2-я Бауманская ул., 5, Российская Федерация
b Российский новый университет
105005 Москва, ул. Радио, 22, Российская Федерация
* E-mail: labunets@bmstu.ru
Поступила в редакцию 22.06.2021
После доработки 22.06.2021
Принята к публикации 25.08.2021
- EDN: YLUZLN
- DOI: 10.31857/S0033849422020097
Аннотация
Предложена методика выделения пульсовой волны методами структурной декомпозиции временных рядов дистанционной фотоплетизмографии (ДФПГ). Структурная декомпозиция сигналов ДФПГ на волновые процессы предусматривает естественный симбиоз методов кратномасштабного, сингулярного и цифрового спектрального анализа нестационарных процессов. С помощью преобразования Гильберта получены адаптивные оценки мгновенных частот сердечных сокращений и их корреляционно-спектральных характеристик. По результатам анализа различных алгоритмов формирования информативных компонент пульсовой волны верифицированы показатели вариационной пульсометрии. Обоснована эффективность структурной декомпозиции временных рядов при исследовании частоты сердечных сокращений методом ДФПГ.
ВВЕДЕНИЕ
Волновые процессы, порождаемые основными системами жизнедеятельности человека, содержат важную информацию о его физиологическом состоянии. В медицинской практике применяют широкий спектр контактных и неконтактных методов диагностики заболеваний пациентов, основанных на различных физических принципах измерения пульсовых, дыхательных, миогенных, нейрогенных и эндотелиальных волн [1]. Эти волновые процессы исследуют с помощью датчиков, функционирующих в различных диапазонах спектра электромагнитных волн [2], методами лазерной доплеровской флоуметрии (ЛДФ) [1], электрокардиографии (ЭКГ) [3], электроэнцефалографии (ЭЭГ) [4], сфигмографии (СФГ) [5]. В этом далеко не полном списке аппаратных методологий исследования биоритмов человека не последнее место занимает дистанционная фотоплетизмография (ДФПГ) [6, 7].
ДФПГ – один из эффективных методов неконтактного мониторинга кровенаполнения сердечно-сосудистой системы человека, например в кардиологии при исследовании вариабельности сердечного ритма (ВСР). Цветное изображение лица испытуемого, регистрируемого RGB-видеокамерой в условиях комнатного или специального освещения в спектральном диапазоне 0.53…0.94 мкм, содержит важную информацию о распространении по телу пульсовой волны. Колебания количества крови в сосудах кожных покровов модулируют поглощение света, проходящего через соответствующий объем ткани испытуемого.
Стандартная методика ДФПГ [6] предусматривает усреднение текущих RGB-видеоизображений по множеству пикселей из так называемой области интереса (Region of Interest – ROI) лица человека. В результате такой предобработки формируют три временных ряда (ВР), соответствующих спектральным диапазонам видеокамеры – “красному” R, “зеленому” G и “синему” B. Динамика этих ВР содержит, как правило, шумы измерений и вычислений, помехи, трендовые и квазициклические компоненты. Помехи в динамике RGB-временных рядов обусловлены условиями освещения и характеристиками отражения – поглощения света кожей испытуемого, а также его движениями или наличием у него физических нагрузок [7]. Соответствующая цифровая постобработка позволяет идентифицировать квазициклы и, в конечном итоге, пульсовую волну.
Современные алгоритмы ДФПГ реализуют сочетание двух подходов к формированию информативных признаков пульсовой волны [8], а именно: фотометрические, индуцированные характеристиками отражения – поглощения света кожными покровами, и априорно известным частотным диапазоном пульсовой волны от 0.667 до 4 Гц, что соответствует 40…240 ударам сердца в минуту. Важно отметить, что границы частотных диапазонов волновых процессов, формируемых системами жизнедеятельности человека, зависят от аппаратных функций этих систем и физических методов измерения волн. В частности, для ЛДФ диагностическим спектральным диапазоном пульсовой волны, порождаемой ритмами сердечно-сосудистой и дыхательной систем, являются частоты от 0.8 до 1.6 Гц [1, с. 16], что соответствует 48…96 ударам сердца в минуту.
Цифровой спектральный анализ сигналов, синхронно измеренных согласно канонам тибетской медицины для шести точек лучевых артерий обеих рук испытуемого [5, 9], убедительно показывает, что 95% энергии пульсовой волны локализованы в частотном диапазоне 0.6…8 Гц. Амплитудно-частотная характеристика фурье-спектра квазипериодического пульсового сигнала, измеренного указанным выше методом, демонстрирует явно выраженную кластерную структуру в виде основной и последующих, как правило, трех локальных мод [9, с. 61]. Частоты мод примерно кратны основной частоте f1 кардиоритма испытуемого. Для условно здорового человека f1 ≈ 1 Гц, а парциальные спектры пульсового сигнала локализованы в диапазонах 0.5…1.5 Гц для основной моды и 1.5…2.5, 2.5…3.5, 3.5…4.5 Гц для последующих мод.
Волновые процессы в системах жизнедеятельности человека демонстрируют нестационарность в широком смысле корреляционно-спектральных характеристик и наличие нелинейных динамических эффектов. Закономерности, скрытые в нестационарности и нелинейности биоритмов человека, обладают несомненной клинической интерпретацией. Фундаментальную методическую основу теоретического анализа такого рода закономерностей, наряду с теорией нелинейных динамических систем [10], составляют методы, модели и алгоритмы структурной декомпозиции сигналов ЛДФ, ЭКГ, ЭЭГ, СФГ.
Частотно-временное исследование локальных особенностей нестационарных ВР биоритмов человека реализуют с помощью непрерывного вейвлет-преобразования [6, 11] или кратномасштабного анализа (КМА) в базисе дискретного вейвлет-преобразования [12, 13], а также на основе различных модификаций эмпирической модовой декомпозиции (Empirical Mode Decomposition – EMD) и преобразования Гильберта–Хуанга (Hilbert–Huang Transformation – HHT) [2, 4, 9, 14, 15]. К этому списку следует добавить метод “Гусеница” сингулярного спектрального анализа (Singular Spectral Analysis – SSA) структуры закономерностей, скрытых в динамике биомедицинских сигналов [16]. Также отметим рациональную тенденцию к комбинированному применению указанных выше методов структурной декомпозиции нестационарных ВР [17].
Цель данной статьи – рассмотреть содержание последовательных этапов интеллектуальной цифровой обработки сигналов ДФПГ, основанных на сочетании дополняющих друг друга методов кратномасштабного, сингулярного и корреляционно-спектрального анализа для формирования робастных оценок информативных характеристик пульсовой волны.
1. ЭКСПЕРИМЕНТАЛЬНОЕ ИЗМЕРЕНИЕ И ПРЕДОБРАБОТКА СИГНАЛОВ ДФПГ
Измерение сигналов ДФПГ выполнялось в экспериментальной лаборатории научно – образовательного медико-технологического центра МГТУ им. Н.Э. Баумана (МТЦ МГТУ). Информационно-измерительный комплекс содержит панель дневного освещения со спектром от 0.53 до 0.94 мкм, RGB-видеокамеру Logitech HD Webcam C270, сопряженную с ноутбуком через высокоскоростное сертифицированное соединение USB 2.0, и стационарное место расположения испытуемого. Камера формирует последовательность видеоизображений с частотой 30 кадров в секунду размером 640 × 480 пикселей с глубиной цвета 24 бита. Текущий i, j-й пиксель представляет собой ri,j(n), gi,j(n), bi,j(n) цветовые компоненты с восьмибитовой точностью.
В наших исследованиях дополнительно анализировались результаты измерений ДФПГ базы данных (БД), записанной добровольцами технологического университета Эйденховен (Нидерланды) [18]. БД содержит набор видеозаписей, а также опорные показатели ВСР, измеренные одновременно с фотоплетизмограммой, что является несомненным преимуществом. Имеются видеозаписи области лица трех испытуемых с различным цветом кожи. Для каждого участника эксперимента имеются записи после физической нагрузки, набор записей в спокойном состоянии, но при различной интенсивности освещения, а также записи с поворотами головы.
Область лица испытуемого (так называемую область интереса) ROI формируют методом Виолы–Джонса. Отсчеты R(n), G(n), B(n) ВР рассчитывают усреднением по i, j-м пикселям, принадлежащим ROI кожного покрова лица в соответствии с методикой, представленной в [6]:
(1)
$\begin{gathered} {{\left[ {R\left( n \right)G\left( n \right)B\left( n \right)} \right]}^{T}} = \\ = \frac{1}{{{\text{ROI}}}}\sum\limits_{i,\,j \in {\text{ROI}}} {{{{\left[ {{{r}_{{i,j}}}\left( n \right){{g}_{{i,j}}}\left( n \right){{b}_{{i,j}}}\left( n \right)} \right]}}^{T}}} . \\ \end{gathered} $Эффективное по критерию вычислительных затрат удаление выбросов и артефактов RGB-сигналов (рис. 1а), измеренных в МТЦ МГТУ, реализует, по нашему мнению, процедура медианной фильтрации median{R(n)}, для R-сигнала (рис. 1б, кривая 5). Апертура фильтра N согласована с интервалом временнóй дискретизации ВР (1) Δt = 1/30 с и нижней границей fмин = 0.15 Гц частотного диапазона дыхательной волны [1, с. 16] в соответствии с формулой
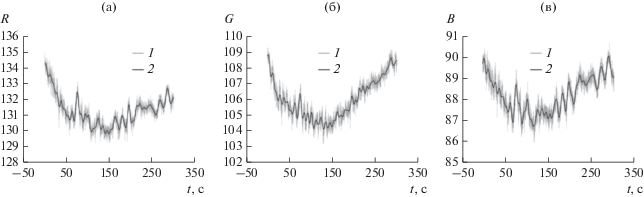
Рис. 1.
Cигналы ДФПГ (а) и компоненты сигнала R (б): кривая 1 – R, 2 – G, 3 – B; 4 – очищенный, 5 – оценка выбросов.

Второй надежный, но более затратный алгоритм, основан на обнаружении классов типичных значений ВР (1) в двумерном пространстве цветового сигнала и его первой разности (рис. 2а) с помощью алгоритма кластеризации DBSCAN) [19], основанного на понятии связности по плотности данных в метрике Евклида. Результаты идентификации аномальных перепадов g(t) текущего уровня R-сигнала представлены на рис. 2б. Параметры DBSCAN представляют собой радиус окружности ближайших соседей e = 0.002 и количество ближайших соседей в этой окрестности minPts = 10.
Рис. 2.
Кластерная структура R-сигнала ДФПГ (а) и его компоненты (б): 1 – выбросы; 2 – типичные значения; 3 – очищенный, 4 – оценка выбросов.
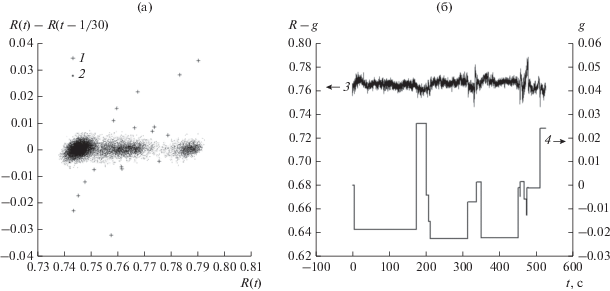
Очищенный сигнал $\tilde {R}(t)$ = R(t) – g(t) формируют в три этапа. На первом шаге DBSCAN маркирует аномальные значения на двумерной диаграмме рассеяния {R(t), R(t) – R(t-Δt)} (см. рис. 2а). На втором шаге из первой разности R(t) – R(t – Δt) исключают маркированные выбросы с последующей их заменой линейно интерполированными оценками. На третьем шаге интегрируют очищенную первую разность. Отметим, что в отличие от медианной фильтрации динамика цветовых сигналов, очищенных от аномальных перепадов указанным выше способом (см. рис. 2б, кривая 3), сохраняет низкочастотные волновые процессы.
Сигналы цветовых каналов ДФПГ, представленные в БД Технологического университета Эйндховена [18], не содержат артефакты в виде перепадов, что свидетельствует о более высоком качестве методики экспериментальных измерений.
Важным этапом последующей предобработки является удаление шумов, обусловленных ошибками измерений и вычислений. Универсальный подход к идентификации шумов очищенных сигналов $\tilde {R}(t)$, $\tilde {G}(t)$, $\tilde {B}(t)$ основан на применении КМА в базисе дискретного вейвлет-преобразования. По определению, шумы – это высокочастотные, практически некоррелированные детализирующие компоненты:
(2)
$\begin{gathered} {{d}_{l}}\left( {n,m} \right) = {{d}_{l}}\left( {n\Delta t,m} \right) = \\ = \sqrt {{{K}_{m}}} \sum\limits_{k = 0}^{{{K}_{{\,m}}} - 1} {{{D}_{l}}\left( {k,m} \right)\psi \left( {{{K}_{m}}n - k} \right)} , \\ {{K}_{m}} = {{2}^{{M - m}}}, \\ \end{gathered} $КМА первого m = 1 или второго m = 2 уровней разложения. Здесь М – количество уровней разложения ВР, согласованное с объемом выборки ≥2M; n – дискретное время, ψ(n) = ψ(nΔt) – вейвлет-функция; l = 1, 2, 3 – номер цветового сигнала, соответствующий последовательности R, G, B. В наших вычислительных экспериментах в качестве базиса применялись вейвлеты Добеши порядка 40 и $M$ = 10, т.е. наименьшее количество отсчетов ВР составляет 210 = 1024, что соответствует длительности записи 1024/30 ≈ 34 c. Такой выбор параметров КМА обеспечил достаточно детальную субполосную фильтрацию и минимизировал эффект перекрытия спектров детализируюших компонент, т.е. обеспечил их приемлемую ортогональность.
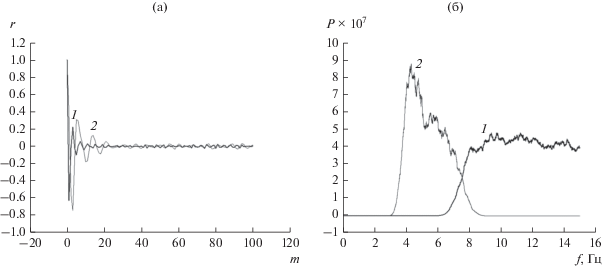
На рис. 3а представлены выборочные оценки автокорреляционных функций (АКФ) ${{r}_{1}}\left( {m\Delta t} \right)$ и ${{r}_{2}}\left( {m\Delta t} \right)$ соответственно первой ${{d}_{1}}\left( {n,1} \right)$ и второй ${{d}_{1}}\left( {n,2} \right)$ детализирующих компонент КМА для сигнала $\tilde {R}(n{\kern 1pt} \Delta t)$. Периодограммы Томсона ${{P}_{1}}\left( f \right)$ и ${{P}_{2}}\left( f \right)$ с параметрами сглаживания 145 и 89 для указанных компонент приведены на рис. 3б. Корреляционно-спектральные оценки получены для всей реализации ВР, содержащего 15 756 отсчетов (≈525 с). Первая компонента ${{d}_{1}}\left( {n,1} \right)$ КМА сигнала $\tilde {R}(n{\kern 1pt} \Delta t)$ демонстрирует достаточно низкий уровень корреляции и относительно равномерное распределение мощности гармоник для частот f ≥ 6.5 Гц. Аналогичный характер поведения корреляционно-спектральных характеристик демонстрируют первые компоненты ${{d}_{2}}\left( {n,1} \right)$ и ${{d}_{3}}\left( {n,1} \right)$ КМА сигналов $\tilde {G}(n{\kern 1pt} \Delta t)$ и $\tilde {B}(n{\kern 1pt} \Delta t)$, измеренных в МТЦ МГТУ, а также ВР из БД [18].
2. ВОЛНОВЫЕ И ТРЕНДОВЫЕ СТРУКТУРНЫЕ КОМПОНЕНТЫ СИГНАЛОВ ДФПГ
Волновые и трендовые, компоненты сигналов цветовых каналов формируют обычно на этапе постобработки [6]. Достаточно большое количество оценок биоритмов нестационарных биомедицинских ВР делят, как правило, на три класса. Первый основан на процедурах синтеза адаптивных цифровых фильтров, таких как, например, HP-фильтр или родственный ему SPA-фильтр. Параметры таких фильтров обеспечивают компромисс между ошибками аппроксимации ВР и критерием простоты модели сглаживания данных. Второй класс оценок, развивающий принцип регуляризации, реализует модели локально взвешенной полиномиальной регрессии Савицкого–Голея, Мешалкина, Клевеланда. Важным достоинством третьего класса оценок, основанных на методологии структурной декомпозиции, является частотно-временной анализ локальных особенностей динамики биоритмов. По этой причине мы отдаем предпочтение методам и моделям структурной декомпозиции.
Цифровой спектральный анализ составляющих КМА обеспечивает идентификацию детализирующих компонент (2), формирующих динамику пульсовой волны. В частности, периодограммы Томсона (рис. 4) третьей ${{d}_{l}}\left( {n,3} \right)$ и четвертой ${{d}_{l}}\left( {n,4} \right)$ (l = 1, 2, 3) компонент сигналов цветовых каналов, полученных в МТЦ МГТУ, всецело принадлежат диапазону частот 0.667…4 Гц пульсовой волны.
Рис. 4.
Периодограммы детализирующих компонент КМА для R-канала: кривая 1 – ${{d}_{1}}\left( {n,2} \right)$, кривая 2 – $d_{1}^{s}\left( {n,2} \right)$; кривая 3 – ${{d}_{1}}\left( {n,3} \right)$; кривая 4 – ${{d}_{1}}\left( {n,4} \right)$; кривая 5 – $d_{1}^{f}\left( {n,5} \right)$; кривая 6 – ${{d}_{{\,1}}}\left( {n,5} \right)$.
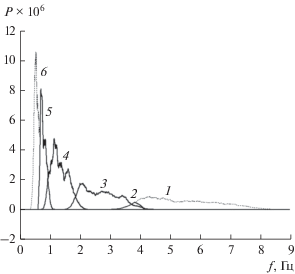
Энергетические спектры P(f) второй ${{d}_{l}}\left( {n,2} \right)$ и пятой ${{d}_{l}}\left( {n,5} \right)$ компонент лишь частично принадлежат указанному выше интервалу частот, а именно “медленная” часть ${{d}_{l}}\left( {n,2} \right)$ и “быстрая” часть ${{d}_{l}}\left( {n,5} \right)$ содержат гармоники с частотами f ≤ 4 Гц и f ≥ 0.667 Гц соответственно. Парциальные части реализаций этих компонент, спектральные плотности мощности (СПМ) которых принадлежат указанному диапазону частот, удобно формировать методом аналитической модовой декомпозиции [20]. В соответствии со свойствами дискретного преобразования Гильберта H:
для компоненты ${{d}_{l}}\left( {n,\,m} \right)$ несложно получить “медленную” часть:
СПМ которой содержит частоты f ≤ fb. Очевидно, что “быстрая” часть ${{d}_{l}}\left( {n,m} \right)$ с частотами СПМ f ≥ fb имеет вид
Ясно, что для второй компоненты разделяющая частота равна fb = 4 Гц, а для пятой компоненты fb = 0.667 Гц.
Применяемый нами в данной работе КМА (2), позволил получить адекватные экспертные модели трендовых составляющих цветовых каналов ДФПГ в виде суммы четырех компонент: восьмой ${{d}_{l}}\left( {n,8} \right)$, девятой ${{d}_{l}}\left( {n,9} \right)$, десятой ${{d}_{l}}\left( {n,10} \right)$ детализирующих и десятой ${{a}_{l}}\left( {n,10} \right)$ аппроксимирующей. Реализации нестационарных ВР цветовых каналов, маркированных именем Р1Н1 в БД [18], а также структурные оценки их трендов представлены на рис. 5 (файл данных Р1Н1 содержит описание условий и результаты измерения сигналов ДФПГ испытуемого после физических упражнений на велоэргометре). Аналогичные оценки трендов получены для сигналов цветовых каналов, измеренных в МТЦ МГТУ.
Предварительные центрированные оценки RGB-пульсовых волн формируют в соответствии с предложенной в [21] процедурой масштабирования волновых процессов на величины трендов ВР цветовых каналов:
Фрагменты реализаций ВР оценок пульсовых волн цветовых каналов для примера Р1Н1 из БД [18] представлены на рис. 6.
3. ИНФОРМАТИВНОЕ ПРОСТРАНСТВО ПУЛЬСОВОЙ ВОЛНЫ
Снижение влияния помеховых факторов, к числу которых относят условия освещения, тон кожного покрова, физические нагрузки, незначительные движения испытуемого в процессе измерения видеоизображений, основано на формировании пространства признаков пульсовой волны и других биоритмов человека в исходном RGB-пространстве ВР цветовых каналов. К настоящему времени предложено и апробировано на практике достаточно большое количество алгоритмов генерации информативных признаков пульсометрии методом ДФПГ [7], а именно: 1) слепое разделение источников (Blind Source Separation – BSS) методами главных и независимых компонент; 2) алгоритмы PVB и CHROM, основанные на модели отражения света кожным покровом; 3) алгоритм POS, формирующий информативный ортонормированный базис в RGB- пространстве на основе ортов тона кожи и импульса объема крови, унаследованных от алгоритма CHROM.
Особое место в этом далеко не полном списке занимает алгоритм 2SR, отслеживающий изменения во времени собственных значений и ориентации собственных векторов взаимной корреляционной матрицы RGB- пикселей видеоизображений. Иными словами, 2SR игнорирует процедуру пространственного усреднения цветовых пикселей в пределах области интереса ROI.
В конечном итоге алгоритмы BSS, PVB, CHROM, POS сводятся к поиску в исходном цветовом пространстве ортонормированного базиса (X, Y, Z), образованного ортом Z и сигнальной плоскостью с ортами (X, Y) (здесь и далее все векторы трактуют как столбцы, если не оговорено иное). Варианты выбора направляющих косинусов ортов (X, Y, Z) для некоторых алгоритмов приведены в табл. 1, где Т – обозначает операцию транспонирования.
Таблица 1.
Алгоритмы оценивания пульсовой волны
| Алгоритм | X | Y | Z | sx | sy |
|---|---|---|---|---|---|
| G | (1, 0, 0)T | (0, 1, 0)T | (0, 0, 1)T | 0 | 1 |
| GRD | (1, 0, 0)T | (0, 1, 0)T | (0, 0, 1)T | –1 | 1 |
| CHROM | (3, –2, 0)T/√13 | (1.5, 1, –1.5)T/√5.5 | (1, 1, 1)T/√3 | 1 | –1 |
| POS | (0, 1, –1)T/√2 | (–2, 1, 1)T/√6 | (1, 1, 1)T/√3 | 1 | 1 |
Проекции отсчетов ВР пульсовых волн цветовых каналов
из RGB-пространства на плоскость (X, Y) формируют оценку центрированной и нормированной пульсовой волны [6, 7]:
Наряду с указанными выше алгоритмами в наших вычислительных экспериментах была исследована эффективность модели ненормированной пульсовой волны w(n) = (112.0, –93.786, –18.214) WC(n)/255.0, основанной на красной цветоразностной компоненте Cr цветового пространства YCbCr видеоизображений.
4. СПЕКТРАЛЬНЫЙ И СИНГУЛЯРНЫЙ АНАЛИЗ СЕГМЕНТОВ ПУЛЬСОВОЙ ВОЛНЫ
Предварительные оценки пульсовой волны pw(n), полученные с помощью указанных выше алгоритмов, демонстрируют явно выраженную нестационарную динамику по критериям основных статистик [22]. Для адекватного исследования изменений спектральных характеристик такого рода ВР в нашей методике применяется скользящий интервал анализа. Реализацию пульсовой волны разбивают на последовательность сегментов, содержащих по 1024 отсчета в каждом. Перекрытие соседних сегментов составляет 98%. Спектральные плотности мощности Pns(f) в пределах каждого сегмента с номером ns оценивают с помощью периодограммы с четырехчленным окном данных Блэкмана–Хэрриса [23] и периодограммы Томсона [24] с параметром сглаживания 3.
Закономерности трансформации периодограмм Томсона по мере увеличения номера сегмента ns пульсовой волны pw(n), полученные для примера Р1Н1 из БД [18] с помощью алгоритма POS и модели Cr, представлены на рис. 7. Графики наглядно демонстрируют тенденцию стабилизации во времени частоты основного тона сердечных сокращений испытуемого после физических упражнений на велоэргометре. Следует также отметить, что альтернативные оценки СПМ по результатам применения алгоритма POS и модели Cr для формирования пульсовой волны практически совпадают.
Рис. 7.
Зависимость периодограмм Томсона от номера сегмента предварительной оценки пульсовой волны согласно алгоритму POS (а) и модели Cr (б).
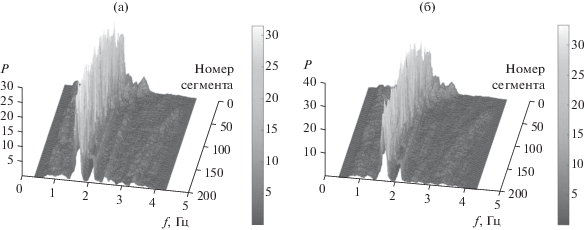
Рациональной предварительной оценкой изменения частоты основного тона сердечных сокращений (hr) испытуемого является, на наш взгляд, зависимость абсолютных максимумов периодограммы от номера сегмента (ns) пульсовой волны
(3)
${{f}_{{{\text{hr}}}}}\left( {{\text{ns}}} \right) = {{\max }_{f}}\left\{ {{{P}_{{{\text{ns}}}}}\left( f \right)} \right\}.$Такие оценки для алгоритма POS и модели Cr пульсовой волны приведены на рис. 8 (кривая 1). Сглаживание подобных оценок с помощью робастной ядерной локально взвешенной квадратичной регрессии Клевеланда (функция rloess в пакете Matlab) с параметром 0.3 дает более адекватное представление о стабилизации частоты сердечных сокращений после окончания физических упражнений (см. рис. 8, кривая 2).
Рис. 8.
Зависимость частоты основного тона сердечных сокращений от номера сегмента пульсовой волны согласно алгоритму POS (а) и модели Cr (б): кривая 1 – абсолютные максимумы периодограмм, кривая 2 – сглаженные оценки.

Результаты скользящего фурье-анализа сегментов предварительной оценки пульсовой волны полученной, например, с помощью алгоритма POS или модели Cr, свидетельствуют о наличии обертонов на частотах 2.1 и 2.5 Гц (см. рис. 7). Плодотворный подход к формированию уточненной оценки основан на декомпозиции каждого сегмента волны на последовательность квазипериодических циклов, не искаженных фантомными обертонами, в частности, методом сингулярного спектрального анализа [16, 25].
Наши вычислительные эксперименты показали, что результаты SSA-декомпозиции критичны к значению параметра вложения текущего сегмента волны в траекторное пространство. Удачным оказался выбор параметра вложения, равный пяти сглаженным периодам сердечных сокращений 5/rloess{fhr (ns), 0.3}. При таком выборе сумма двух первых сингулярных троек формирует для каждого сегмента данных временной профиль основного тона сердечных сокращений (bht), не искаженный фантомными обертонами.
Зависимости периодограмм Томсона суммы двух первых сингулярных троек от номера сегмента ns (рис. 9) иллюстрируют закономерность изменения во времени спектральных характеристик ВР основного тона сердечных сокращений bht (n) для примера Р1Н1 из БД [18]. Полученные оценки СПМ подтверждают правильность выбора первой пары сингулярных троек для удаления фантомных обертонов пульсовой волны. Кроме того, сравнение рис. 8б и 9б наглядно демонстрирует состоятельность оценки (3).
5. МГНОВЕННАЯ ЧАСТОТА И ОГИБАЮЩАЯ ОСНОВНОГО ТОНА ПУЛЬСОВОЙ ВОЛНЫ
Естественной процедурой формирования временного профиля bht (n) является, на наш взгляд, агрегирование ансамбля сегментов данных с учетом их фактических временны́х сдвигов. Зависимость количества перекрывающихся сегментов NS от номера n текущего отсчета времени для выбранной нами степени перекрытия 98% представлена на рис. 10а.
Рис. 10.
Усреднение по ансамблю сегментов уточненной оценки пульсовой волны: зависимость количества сегментов от отсчета времени n (а); результаты усреднения (б): кривая 1 – фрагмент реализации медианной оценки агрегированной пульсовой волны, кривая 2 – мера разброса ансамбля сегментов относительно медианной оценки пульсовой волны.
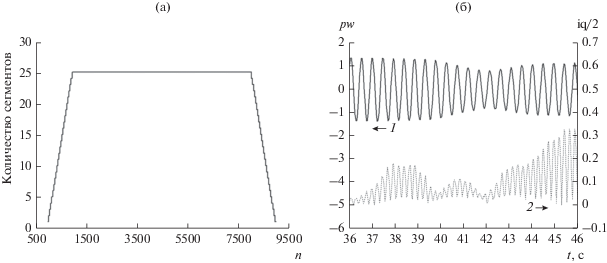
Фрагмент ВР bht(n) уточненной оценки основного тона сердечных сокращений, полученной медианным усреднением по ансамблю сдвинутых сегментов, демонстрирует кривая 1 на рис. 10б. Кривая 2 на этом рисунке иллюстрирует степень разброса ансамбля сегментов относительно медианной скользящей средней. Мерой разброса ансамбля является половина его интерквартильного диапазона iq/2.
Оценка bht(n) представляет собой ВР с достаточно узкой полосой частот (см. рис. 9а). В этом случае состоятельные оценки мгновенной фазы (ip) и мгновенной огибающей (ie) могут быть получены с помощью дискретного преобразования Гильберта
В результате с помощью процедуры развертки мгновенной фазы ipbht(n) во времени (функция unwrap в пакете Matlab) формируют накопленную мгновенную фазу iphbht(n) для основного тона сердечных сокращений. Как правило, этот ВР содержит, к сожалению, разрывную не дифференцируемую составляющую, что приводит к появлению отрицательных величин для мгновенной частоты. Для устранения этих физически не интерпретируемых значений в нашей методике предусмотрено формирование двух структурных компонент накопленной мгновенной фазы. Первая – это непрерывная (continuous – cont), неубывающая составляющая $iph_{{\,bht}}^{{\left( {cont} \right)}}\left( n \right)$. Вторая разрывная (прерывистая) компонента представлена суммой смещенных во времени ступенчатых функций, аналогичных функции включения Хевисайда.
Физически интерпретируемые оценки мгновенной частоты основного тона сердечных сокращений дает первая производная по времени непрерывной, неубывающей компоненты накопленной фазы $iph_{{\,bht}}^{{\left( {cont} \right)}}\left( n \right)$. Численное дифференцирование этого ВР рационально, на наш взгляд, выполнять с помощью сохраняющей форму кусочно-кубической интерполяции полиномами Эрмита [26] (функция pchip в пакете Matlab). Для полинома третьей степени
первая производная в момент времени t = tn = nΔt равна коэффициенту c(n). Иными словами, ВР зашумленной оценки мгновенной частоты (if) основного тона сердечных сокращений имеет вид
Важно отметить, что динамика этого ВР демонстрирует наличие аномальных значений.
6. СТАТИСТИКИ МГНОВЕННЫХ ЧАСТОТ ОСНОВНОГО ТОНА ПУЛЬСОВОЙ ВОЛНЫ
Оценки статистик ВР ifbht(n) рационально формировать с помощью процедуры робастной ядерной локально взвешенной квадратичной регрессии Клевеланда. В частности, тренд afbht(n), СКО sfbht(n) и квазициклическая компонента cfbht(n) представлены следующими моделями сглаживания данных:
Реализации тренда (кривая 1), полос Боллинджера шириной ±3 доли СКО (кривые 2 и 3), а также сумма тренда и квазициклической компоненты, т.е. rloess{ifbht(n), 0.03} (кривая 4) для примера Р1Н1 из БД [18] и модели пульсовой волны Cr представлены на рис. 11а. Шумовую компоненту мгновенных частот сердечных сокращений
Рис. 11.
Статистики мгновенных частот основного тона сердечных сокращений: реализации структурных компонент мгновенных частот (а): кривая 1 – тренд, кривые 2 и 3 – границы полосы Болинджера, кривая 4 – сумма тренда и квазициклической составляющей, кривая 5 – шумовая компонента; плотность распределения вероятностей центрированных и нормированных мгновенных частот (б): кривая 1 – гистограмма сглаженная сдвигом, кривая 2 – гауссовское приближение гистограммы.

иллюстрирует кривая 5.
Оценку плотности распределения вероятностей (Probability Density Function – PDF) центрированного и нормированного ВР (cas) для квазициклической компоненты мгновенных частот основного тона сердечных сокращений
в виде гистограммы, сглаженной сдвигом (Average Shifted Histogram – ASH), [27] иллюстрирует рис. 11б (кривая 1). Для сравнения там же представлено нормальное распределение (кривая 2), соответствующее робастным выборочным оценкам математического ожидания и СКО. В качестве нормированного окна данных ASH-оценки распределения применялось трижды взвешенное ядро Епанечникова. Оптимальное количество разрядных интервалов гистограммы выбиралось по правилу Фридмана–Дьякониса. В конечном итоге модель
описывает зависимость от времени nΔt одномерной плотности распределения вероятностей PDF {cfbht(n)} квазициклической компоненты cfbht(n) мгновенных частот основного тона сердечных сокращений.
ЗАКЛЮЧЕНИЕ
В работе последовательно изложены этапы интеллектуального анализа мгновенных частот основного тона пульсовой волны очищенного от обертонов сердечных сокращений. Результаты обработки экспериментальных данных наглядно демонстрируют эффективность алгоритмов выделения пульсовой волны методами структурной декомпозиции нестационарных временных рядов ДФПГ. В частности, адекватность оценок статистических характеристик биоритмов человека обеспечивает естественный симбиоз современной методологии кратномасштабного, сингулярного и корреляционно-спектрального анализа биомедицинских данных.
Список литературы
Лазерная доплеровская флоуметрия микроциркуляции крови: Руководство для врачей / Под ред. А.И. Крупаткина, В.В. Сидорова. М.: Медицина, 2005.
Al-Naji A., Gibson K., Sang-Heon Lee, Chahl J. // IEEE Access. 2021. V. 5. № 17. P. 15776.
Успенский В.М. Информационная функция сердца. Теория и практика диагностики заболеваний внутренних органов методом информационного анализа электрокардиосигналов. М.: Экономика и информация, 2008.
Bueno-López M., Munoz-Gutierrez P.A., Giraldo E., Molinas M. // IAENG Int. J. Computer Sci. 2019. V. 46. № 2. P. 228. http://www.iaeng.org/IJCS/issues_ v46/issue_2/index.html.
Бороноев В.В. Пульсовая диагностика заболеваний в тибетской медицине: физические и технические аспекты. Улан-Уде: БНЦ СО РАН, 2005.
Unakafov A.M. // Biomedical Physics & Engineering Express. 2018. № 4. P. 045001. https://doi.org/10.1088/2057-1976/aabd09
Wang W., den Brinker A. C., Stuijk S., de Haan G. // IEEE Trans. 2016. V. BE-64. № 7. P. 1479. https://doi.org/10.1109/TBME.2016.2609282
Wang W., den Brinker A.C., Stuijk, S., de Haan G. // Biomedical Optics Express. 2017. V. 8. № 3. P. 1965. https://doi.org/10.1364/BOE.8.001965
Омпоков В.Д. Частотно-временной анализ пульсовых сигналов с помощью преобразования Гильберта–Хуанга // Дис. … канд. физ.-мат. наук. Улан-Уде: Ин-т физ. материаловедения СО РАН, 2019. 106 с.
Флейшман А.Н. Вариабельность ритма сердца и медленные колебания гемодинамики: нелинейные феномены в клинической практике. Новосибирск: Изд-во СО РАН, 2009.
Бороноев В.В., Гармаев Б.З., Омпоков В.Д. // Вест. Бурят. гос. ун-та. 2012. № 3. С. 221.
Martinez J.P., Almeida R., Olmos S. et al. // IEEE Trans. 2004. V. BE-51. № 4. P. 570.
Islam M.R., Ahmad M. // Conf. Dig. 2 nd Int. Conf. Electrical, Computer and Communication Engineering (ECCE). Cox’s Bazar. 7–9 Feb.2019. N.Y.: IEEE, 2019. P. 8679156 https://doi.org/10.1109/ECACE.2019.8679156
Cheng J., Chen X., Xu L., Wang Z.J. // IEEE J. Biomedical Health Informatics. 2017. V. 21. № 5. P. 1422. https://doi.org/10.1109/JBHI.2016.2615472
Xu L., Cheng J., Chen X. // Electron. Lett. 2017. V. 53. № 4. P. 216. https://doi.org/10.1049/el.2016.3611
Sanei Saeid, Hassani Hossein. Singular Spectrum Analysis of Biomedical Signals. Boca Raton: CRC Press/Taylor and Francis Group, 2019.
Tang S.K.D., Goh Y.Y.S., Wong M.L.D., Lew Y.L.E. // 6th Int. Conf. Intelligent and Advanced Systems (ICIAS). Kuala Lumpur, 15–17 Aug. 2016. N.Y.: IEEE, 2016. P. 7824118 https://doi.org/10.1109/ICIAS.2016.7824118
Hoffman W.F.C., Lakens D. Public Benchmark Dataset for Testing rPPG Algorithm Performance. Delft: 4TU.Centre for Research Data, 2019. https://doi.org/10.4121/uuid:2ac74fbd-2276-44ad-aff1-2f68972b7b51
Martin E., Kriegel H.-P., Sander J., Xu Xiaowei // Proc. Second Int. Conf. Knowledge Discovery and Data Mining (KDD-96). Portland. 02–04.08.1996, Palo Alto: AAAI Press, 1996. P. 226.
Zhongzhe Ch., Baqiao L., Xiaogang Y., Hongquan Y. // Energies. 2019. V. 12. № 16. P. 3077. https://doi.org/10.3390/en12163077
de Haan G., Jeanne V. // IEEE Trans. 2013. V. BE-60. № 10. P. 2878.
Borzov A., Kasikin A., Labunets L., Ryakhina M. // Proc. Int. Scientific and Practical Conf. “Information Technologies and Intelligent Decision Making Systems” (ITIDMS 2021) Moscow. 20 Jan. 2021. Aachen: CEUR Workshop Proc., 2021. V. 2843. P. 034. http://ceur-ws.org/Vol-2843.
Harris F.J. // Proc. IEEE. 1978. V. 66. № 1. P. 51.
Thomson D.J. // Proc. IEEE. 1982. V. 70. № 9. P. 1055.
Golyandina N., Nekrutkin V., Zhigljavsky A. Analysis of Time Series Structure: SSA and Related Techniques. Boca Raton: Chapman and Hall/CRC, 2001.
Fritsch F.N., Carlson R.E. // SIAM J. Numerical Analysis. 1989. V. 26. № 1. P. 230.
Scott D.W. Multivariate density estimation: theory, practice, and visualization. N.Y.: John Wiley & Sons Inc., 1992.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника