Радиотехника и электроника, 2022, T. 67, № 3, стр. 275-285
Класс весовых функций для спектрального анализа сигналов с минимизацией уровня боковых лепестков спектра на отрезке частотной оси
Г. В. Зайцев a, *, А. Д. Хзмалян a, **
a Научно-производственное объединение “Алмаз”
125190 Москва, Ленинградский просп., 80, корп. 16, Российская Федерация
* E-mail: gennady-zaytsev@yandex.ru
** E-mail: alkhzmalyan@gmail.com
Поступила в редакцию 30.05.2021
После доработки 01.07.2021
Принята к публикации 15.07.2021
- EDN: UUGGOL
- DOI: 10.31857/S0033849422030196
Аннотация
Решена задача синтеза весовых функций малого порядка с произвольно заданной скоростью спада лепестков спектра, оптимальных по критерию минимума максимального бокового лепестка на заданном отрезке частотной оси и предназначенных для реализации в специализированных системах реального времени. Показано, что уменьшение длины отрезка минимизации позволяет получить значительный выигрыш в основных параметрах весовых функций. Синтезированы весовые функции порядков 1…6 с различными скоростями спада боковых лепестков и проанализированы их характеристики. Приведены параметры синтезированных функций в объеме, имеющем практический интерес и дающем представление о возможностях окон этого класса.
ВВЕДЕНИЕ
Весовые функции, или окна, широко используются при спектральном анализе сигналов для управления шириной главного лепестка, уровнем боковых лепестков и другими параметрами рассчитываемых спектральных составляющих. В зависимости от прикладной задачи, использующей спектральный анализ, требования к весовым функциям различны, поэтому отличаются и критерии оптимальности весовых функций. Классические весовые функции описаны в [1, 2], значительное количество ссылок на сравнительно недавние работы содержится, например, в [3, 4].
В работах авторов [5–7] разработан метод синтеза и приведены параметры многочисленных оптимальных функций, минимизирующих уровень максимального бокового лепестка и имеющих простой способ вычисления. Полученные функции предназначены, в частности, для использования в радиолокационной технике при обнаружения движущихся объектов с помощью квазинепрерывных сигналов. В этой задаче вычисление спектра представляет собой основную операцию обработки принимаемого сигнала, а отличительной чертой является большой динамический диапазон, требующий использования весовых функций с уровнем боковых лепестков значительно ниже –100 дБ относительно главного лепестка. Высокий динамический диапазон обусловлен необходимостью приема слабых отражений от малоразмерных объектов на фоне мощных помех от подстилающей поверхности и гидрометеоров. Вместе с тем доплеровская частота помеховых отражений значительно ниже соответствующего параметра скоростных объектов, что позволяет принимать слабые полезные сигналы при правильном выборе весовой функции.
Простой способ вычисления весовых функций необходим для обеспечения работы в реальном масштабе времени с сигналами, параметры которых определяются во время работы, исходя из текущей окружающей обстановки. В весовых функциях, построенных в работах [5–7] минимизируется уровень максимального лепестка спектра среди полного множества всех боковых лепестков.
Однако минимизация уровня всех лепестков спектра весовой функции требуется не всегда. Например, в радиолокации при сопровождении обнаруженного объекта его скорость известна с хорошей точностью, поэтому боковые лепестки спектра мешающих отражений достаточно подавить в узком частотном диапазоне вокруг доплеровской частоты сопровождаемого объекта. Требования к весовой функции оказываются ослабленными, что создает возможность получения весовой функции со значительно более высокими характеристиками. Принципиальная возможность синтеза таких функций показана в работах [3, 8–11], однако в этих работах не приведено конкретных результатов для случая минимизации боковых лепестков на отрезке.
В данной работе на основе метода, разработанного в [5–7], решена задача синтеза оптимальных функций, имеющих минимальное значение максимального уровня боковых лепестков спектра на отрезке частотной оси, приведены параметры ряда синтезированных функций и проанализированы их характеристики.
1. МЕТОД СИНТЕЗА ОПТИМАЛЬНЫХ МИНИМАКСНЫХ ВЕСОВЫХ ФУНКЦИЙ
В данной работе рассмотрены весовые функции для дискретной обработки сигналов. Однако при теоретическом изложении и практическом применении дискретную весовую функцию удобно считать последовательностью отсчетов соответствующей непрерывной функции. Поэтому сначала рассмотрим непрерывный случай.
Будем считать, как обычно, что весовая функция w(t), используемая при гармоническом анализе непрерывного сигнала на интервале наблюдения –T/2 ≤ t ≤ T/2 длительностью T, является финитной четной положительной непрерывной функцией времени на этом интервале (кроме, возможно, его краев) и равна нулю вне этого интервала: w(t) = 0 при |t| > T/2.
При цифровой обработке из обрабатываемого сигнала и весовой функции на интервале наблюдения берутся выборки с шагом δ, определяемым теоремой Котельникова–Найквиста. Обозначим число выборок символом N. Моменты выборок из весовой функции расположим симметрично относительно начала координат: tq = – 0.5 (T – δ) + qδ, q = 0, 1, …, N – 1. Дискретную весовую функцию w(tq) будем рассматривать как отсчеты w(t) непрерывной функции в точках tq . При такой постановке задачи исходной является непрерывная функция, которая полностью определяет дискретную функцию. Поэтому для упрощения описания дискретных функций в литературе часто используется соответствующая непрерывная функция.
Спектр дискретной весовой функции определяется формулой дискретного по времени преобразования Фурье [12]
(1)
$\begin{gathered} W(f) = \sum\limits_{q = 0}^{N - 1} {w({{t}_{q}})} \exp ( - j2\pi \,{{t}_{q}}f), \\ f \in [{{ - 1} \mathord{\left/ {\vphantom {{ - 1} {2\delta }}} \right. \kern-0em} {2\delta }},{1 \mathord{\left/ {\vphantom {1 {2\delta }}} \right. \kern-0em} {2\delta }}]. \\ \end{gathered} $Спектр (1) периодичен по частоте f с периодом 1/δ, поэтому далее будем анализировать его на периоде f ∈ [–0.5/δ, 0.5/δ]. При выборе достаточно малого шага δ спектр дискретного преобразования (1) незначительно отличается от интегрального преобразования Фурье [12] на рассматриваемом периоде.
Ниже параметры весовых функций приводятся для случая цифровой обработки. Однако один из этих параметров, а именно асимптотическая скорость V спада боковых лепестков спектра (далее слово “асимптотическая” в этом термине опускается), относится, строго говоря, к соответствующей непрерывной функции w(t), определяется как величина снижения огибающей модуля интегрального преобразования Фурье при увеличении частоты f вдвое для f → ∞ и измеряется в децибелах на октаву. Тем не менее этот параметр непрерывной функции оказывается полезен для описания соответствующей дискретной весовой функции, когда число выборок N велико, а частота не приближается к половине периода 1/2δ.
Представление рассматриваемых в данной работе весовых функции предложено в [5, 6] и имеет следующий вид:
(2)
$\begin{gathered} w({\mathbf{a}},t) = \sum\limits_{k = 0}^m {{{a}_{k}}{{{\cos }}^{{2k + \mu }}}\left( {{{\pi t} \mathord{\left/ {\vphantom {{\pi t} T}} \right. \kern-0em} T}} \right)} = \\ = {{\cos }^{\mu }}\left( {{{\pi t} \mathord{\left/ {\vphantom {{\pi t} T}} \right. \kern-0em} T}} \right)\sum\limits_{k = 0}^m {{{a}_{k}}{{{\cos }}^{{2k}}}\left( {{{\pi t} \mathord{\left/ {\vphantom {{\pi t} T}} \right. \kern-0em} T}} \right)} , \\ {{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2} \leqslant t \leqslant {T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2}, \\ \end{gathered} $Функции указанного вида обладают простым способом вычисления, поскольку число членов в сумме (2) малó, аргумент косинуса одинаков для всех членов, а сумма может быть вычислена по схеме Горнера. Нетрудно показать, что количество арифметических операций для расчета таких функций в два-три раза меньше, чем для широко используемых функций в виде отрезка ряда Фурье [1, 2], имеющих среди известных функций наиболее простой способ вычисления.
При надлежащем выборе коэффициентов функции вида (2) позволяют получить произвольную скорость спада боковых лепестков, а их характеристики близки к потенциально достижимым [5, 6]. Это обусловлено следующими обстоятельствами.
Функции (2) имеют вид линейной комбинации небольшого числа m + 1 базисных функций ψ(pk, t):
(3)
$\psi ({{p}_{k}},t) = {{\cos }^{{{{p}_{k}}}}}({{\pi t} \mathord{\left/ {\vphantom {{\pi t} T}} \right. \kern-0em} T}),\,\,\,\,{{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2} \leqslant t \leqslant {T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2},$Далее, нули спектров базисных функций в области вне главных лепестков совпадают, а для любых двух функций (3) с последовательными номерами k боковые лепестки противофазны, что приводит к их хорошей компенсации при суммировании в (2) и обеспечивает высокое качество характеристик весовых функций.
Отметим также, что весовая функция (2) является действительной и четной. Следовательно, такими же свойствами обладает ее дискретный спектр (1) [12]. Поэтому при анализе спектра функции (2) достаточно рассмотреть его при положительных частотах.
В работах [5–7] разработан метод синтеза оптимальных весовых функции вида (2) в интересах цифровой обработки квазинепрерывных радиолокационных сигналов. Математически метод состоит в решении следующей минимаксной задачи. Пусть Wmax > 0 – максимальное значение модуля спектра (1) весовой функции. Определим функцию качества φ(a) как максимальное значение нормированного модуля спектра |W (a, f)/Wmax| на заданном отрезке Ω частотной оси, на котором необходимо получить минимальный уровень боковых лепестков спектра:
(4)
$\varphi ({\mathbf{a}}) = \mathop {\max }\limits_{f \in \Omega } \left| {{{W({\mathbf{a}},f)} \mathord{\left/ {\vphantom {{W({\mathbf{a}},f)} {{{W}_{{\max }}}}}} \right. \kern-0em} {{{W}_{{\max }}}}}} \right|.$Построение оптимальной весовой функции заключается в поиске вектора коэффициентов amin, доставляющего минимум целевой функции φ(a):
(5)
${{{\mathbf{a}}}_{{\min }}} = \arg \left[ {\mathop {\min }\limits_{\mathbf{a}} \varphi ({\mathbf{a}})} \right].$В работах [5, 6] синтезированы и проанализированы весовые функции, оптимальные по критерию (4), (5), обеспечивающие минимум максимального уровня лепестков среди всех боковых лепестков функции. Данные функции используются, в частности, в задаче радиолокационного обзора пространства с помощью квазинепрерывных сигналов, в которой параметры обнаруживаемых объектов неизвестны. В этом случае областью минимизации является отрезок Ω = [β/T, N/2T], его нижняя граница находится в пределах главного лепестка, т.е. β ≤ m + 1, и является полушириной главного лепестка по уровню максимального бокового. Эти функции по постановке задачи аналогичны функциям Дольфа–Чебышева при дополнительном ограничении на порядок m, а параметры многочисленных синтезированных функций приведены в указанных работах.
В данной работе рассмотрен случай минимизации на более узком частотном отрезке. В радиолокационных приложениях этот случай характерен для режима сопровождения обнаруженного объекта, когда скорость объекта известна. При этом боковые лепестки достаточно подавить в сравнительно небольшом частотном диапазоне Ω = [β/T, (β + Δ)/T] вокруг доплеровской частоты сопровождаемого объекта, параметр β может значительно превосходить порядок функции m, а ширина диапазона Δ, как правило, мала: Δ $ \ll $ N.
Напомним, что величина 1/T называется бином, при этом полоса β/T составляет β бин, и далее все полосы выражаются в бинах.
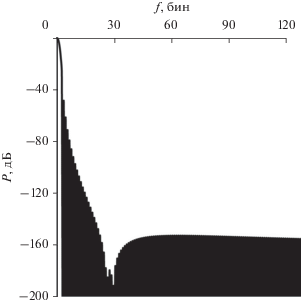
Разработанный в [5–7] метод синтеза оптимальных функций без изменений может быть применен и для этого случая. Рассмотрим результаты его использования для решения поставленной задачи. В качестве примера на рис. 1 приведен спектр оптимальной функции с параметрами N = 1024, m = 2, μ = 0, β = 25 бин, а ширина Δ составляет 6 бин, что является весьма малым значением, равным ширине главного лепестка по нулевому уровню. То есть отрезок минимизации равен [25, 31] бин. На рис. 1 хорошо виден провал в области минимизации, а основная энергия боковых лепестков сосредоточена до этой области. Подавление в области минимизации составляет P = 177.5 дБ.
Рис. 1.
Спектр оптимальной функции с минимизацией на отрезке [25, 31] бин при N = 1024, m = 2, μ = 0.
Для каждого набора из пяти параметров – N, m, μ, β, Δ – указанный метод дает возможность синтезировать функцию, оптимальную по описанному критерию. Поэтому количество возможных функций весьма велико, и общее описание всех функций затруднительно. Случай подавления всех лепестков (параметр β в пределах главного лепестка, параметр Δ максимален) подробно рассмотрен ранее [5, 6].
В данной работе рассмотрен случай, в котором нижняя граница области минимизации находится вне главного лепестка. Расчеты показывают, что характеристики оптимальной функции сильно зависят от значения параметра β и при его варьировании могут изменяться более чем на 100 дБ. В значительно меньшей степени характеристики зависят от ширины Δ области минимизации, причем чем больше β, тем слабее последняя зависимость. Это положение иллюстрирует рис. 2, где показана зависимость уровня максимального лепестка на отрезке [β, (β + Δ)] бин для оптимальной функции от длины отрезка Δ при фиксированной левой границе β и параметрах синтеза, таких же, как на рис. 1.
Рис. 2.
Зависимость уровня максимального лепестка на отрезке [β, (β + Δ)] бин для оптимальных функций от ширины отрезка Δ при N = 1024, m = 2, μ = 0, β = 25 бин.

Как следует из графика, в большей части диапазона изменения параметра Δ максимальный уровень лепестков практически не изменяется. Заметное изменение имеет место при ширине отрезка, сравнимой с шириной главного лепестка по нулевому уровню, представляющей в практических задачах, как правило, минимально возможное значение параметра Δ. И даже с учетом этой области указанное изменение на несколько порядков меньше, чем при изменении параметра β. Поэтому в данной работе рассматриваются весовые функции для случая максимально возможной правой границы отрезка оптимизации β + Δ = 0.5N. В этом случае отрезок оптимизации равен [β, N/2] бин. Одновременно это сокращает количество параметров, задаваемых при синтезе функции, и упрощает описание множества оптимальных функций.
2. АНАЛИЗ ХАРАКТЕРИСТИК ОПТИМАЛЬНЫХ ВЕСОВЫХ ФУНКЦИЙ
С помощью разработанного метода авторами синтезировано значительное количество оптимальных весовых функций. Проведем анализ характеристик оптимальных функций, базируясь на полном множестве синтезированных функций.
Для количественного описания весовых функций будем использовать следующие общепринятые параметры [1, 2]: Р-уровень максимального бокового лепестка относительно главного лепестка на отрезке минимизации; Πw – потери в отношении сигнал/шум, вызванные использованием весовой функции (далее – весовые потери); Πs – максимальные потери за счет рельефа; V – асимптотическая скорость спада боковых лепестков спектра для соответствующей непрерывной функции; Ln – эквивалентная шумовая полоса; L3 и L6 – ширины главного лепестка по уровням –3 и –6 дБ отно сительно максимума главного лепестка, соответственно. Так как полосы спектра L3, L6, Ln обратно пропорциональны N, то далее все частотные параметры, включая β, выражаются, как это принято в литературе, в бинах [1].
Характеристики оптимальных весовых функций слабо зависят от числа выборок N. Поэтому ниже они приведены для значения N = 1024, часто используемого в приложениях. При таком значении N как коэффициенты, так и характеристики весовых функций практически совпадают с величинами для непрерывных функций.
2.1. Выигрыш за счет ограниченной длины отрезка минимизации
Рассмотрим выигрыш, который можно получить, используя подавление не всех боковых лепестков, а только имеющихся на отрезке [β, N/2] бин. На рис. 3 представлены максимальные уровни боковых лепестков на этом отрезке в зависимости от величины β для функций с минимизацией на этом отрезке (сплошные кривые) и для тех функций с минимизацией уровня всех лепестков, которые обеспечивают наименьшие значения лепестков для тех же величин μ и m (пунктирные кривые). Характеристики последних взяты из работ [5, 6]. Разница между кривыми – сплошной и соответствующей ей штриховой – определяет выигрыш в подавлении помехи, который дает применение весовых функций с минимизацией лепестков на отрезке частотной оси.
Рис. 3.
Зависимости уровней максимальных боковых лепестков на отрезке [β, N/2] бин от величины β для функций с минимизацией уровня всех боковых лепестков (пунктирные кривые) и функций с минимизацией на отрезке (сплошные кривые) при m = 1, μ = 0, V = 6 дБ/окт (1, 2) и m = 2, μ = 2, V = 18 дБ/окт (3, 4).
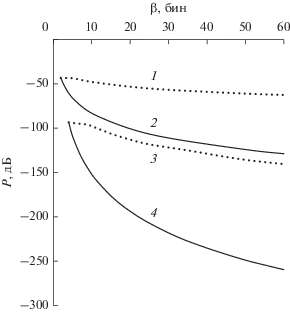
Рисунок 3 наглядно демонстрирует значительное преимущество функций, специально синтезированных для подавления боковых лепестков на отрезке. Например, для кривых 3 и 4 при β = 30 бин преимущество в величине подавления составляет более 100 дБ, в то время как потери весовой функции в отношении сигнал/шум увеличиваются всего на 0.57 дБ.
Используя минимизацию на отрезке, можно значительно улучшить и другие параметры весовых функций. На рис. 4 сравниваются весовые потери для функций со скоростью спада лепестков 6 дБ/окт с минимизацией на отрезке [β, N/2] бин при m = 1, 2, 3 (сплошные кривые) и функций с минимизацией уровня всех боковых лепестков (пунктирная кривая) [5, 6]. При минимизации на отрезке [β, N/2] бин снижение уровня P максимального лепестка достигается за счет увеличения параметра β при фиксированном порядке функции и слабо влияет на весовые потери, а для пунктирной кривой – в основном за счет увеличения порядка функции, что приводит к значительному увеличению потерь. Указанное различие дает возможность выиграть 1…2.5 дБ в отношении сигнал/шум, если имеется возможность выбора подходящей величины параметра β.
Рис. 4.
Зависимости весовых потерь от величины максимального лепестка на отрезке [β, N/2] бин для функций порядков m = 1, 2, 3 с минимизацией на отрезке, а также с минимизацией уровня всех боковых лепестков (пунктир), V = 6 дБ/окт.

Аналогичный выигрыш имеет место и для ширины главного лепестка. Таким образом, в задачах, где не требуется подавление всех боковых лепестков, возможно существенное улучшение основных характеристик весовой функции за счет минимизации уровня лепестков только на отрезке частот, критически значимом для конкретной задачи.
2.2. Основные характеристики оптимальных функций
Рассмотрим теперь поведение основных характеристик весовых функций с минимизацией на отрезке. На рис. 5 представлен уровень максимального лепестка на отрезке минимизации в зависимости от β для оптимальных функций порядков m = 1…6 со скоростью спада лепестков V = 6 дБ/окт. При увеличении β в области β > m + 1 максимальный уровень боковых лепестков быстро снижается. При более высокой скорости спада лепестков V имеют место аналогичные зависимости с еще более быстрым снижением.
Рис. 5.
Зависимость уровня максимального лепестка от параметра β для оптимальных функций порядков m = 1…6 при V = 6 дБ/окт.

Приведенные на рис. 5 кривые хорошо аппроксимируются логарифмическими функциями. (Напомним, что при изменении β в пределах главного лепестка аналогичные зависимости близки к линейным [5, 6].) Рассматриваемые зависимости полезны при решении практических задач, поскольку позволяют оценить необходимые параметры весовой функции m и β при заданной величине P максимального лепестка. Для такой оценки в табл. 1 приведены выражения аппроксимирующих функций в явном виде для трех наиболее используемых скоростей спада лепестков 6, 12 и 18 дБ/окт.
Таблица 1.
Зависимости уровня максимального лепестка P от параметра β для оптимальных функций порядков m = 1…5 при трех значениях V
| m | P(β), дБ | ||
|---|---|---|---|
| при V = 6 дБ/окт | при V = 12 дБ/окт | при V = 18 дБ/окт | |
| 1 | –24.92 lnβ – 26.17 | –34.07 lnβ – 23.89 | –42.85 lnβ – 18.23 |
| 2 | –42.63 lnβ – 25.30 | –52.46 lnβ – 16.33 | –61.09 lnβ – 10.54 |
| 3 | –60.69 lnβ – 16.12 | –70.72 lnβ – 4.22 | –80.41 lnβ + 5.57 |
| 4 | –80.15 lnβ + 1.41 | –89.54 lnβ + 13.60 | –101.80 lnβ + 31.05 |
| 5 | –95.76 lnβ + 15.34 | –121.5 lnβ + 71.18 | –124.21 lnβ + 63.16 |
Высокий уровень подавления боковых лепестков на заданном отрезке при сколько-нибудь значительном параметре β позволяет использовать для повышения качества обработки сигнала функции самых малых порядков m = 1…3, имеющие наименьший уровень энергетических потерь, наименьшую степень расширения главного лепестка и простейший алгоритм вычисления.
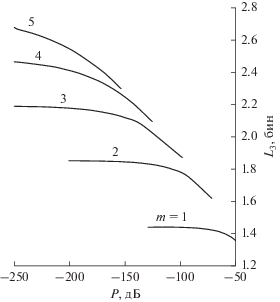
На рис. 6 приведена зависимость ширины главного лепестка L3 от уровня P максимального бокового лепестка на отрезке минимизации [β, N/2] бин для оптимальных функций со скоростью спада лепестков V = 6 дБ/окт, имеющих порядок m = 1…5. Возрастание подавления для каждой кривой достигается за счет увеличения β. Рисунок дает возможность оценить ширину главного лепестка при заданном уровне максимального бокового лепестка.
Рис. 6.
Зависимость ширины главного лепестка L3 от уровня максимального бокового на отрезке минимизации для оптимальных функций порядков m = 1…5 при V = 6 дБ/окт.
На рис. 7 представлено соотношение между шумовой полосой Ln и ширинами главного лепестка L3 и L6 по уровням –3 и –6 дБ, соответственно. Каждая функция отображается одной точкой для каждой из зависимостей. Параметры оптимальных функций с высокой точностью ложатся на прямолинейные тренды, имеющие уравнения
Коэффициенты уравнений с точностью до третьего знака после запятой совпадают с таковыми для функций с подавлением всех боковых лепестков, как косинусоидальных, так и полиномиальных [5–7].
Так как весовые потери Πw связаны с шумовой полосой Ln выражением
то если известен один из параметров L3, L6, Ln, Πw, остальные три можно рассчитать с высокой точностью, используя соотношения (6)–(8).
2.3. Оценка параметров для синтеза оптимальных функций
При решении практических задач, как правило, заданы необходимый уровень максимального лепестка P и граница отрезка β, на котором производится минимизация, и необходимо синтезировать оптимальную весовую функцию. Рис. 8 предназначен для оценки других необходимых параметров для синтеза весовой функции: порядка m и скорости спада боковых лепестков V. На рис. 8а–8в представлены зависимости минимально необходимых значений параметра β от порядка весовой функции m при фиксированном для каждого графика уровне максимального бокового лепестка P = 90, 120, 150 дБ соответственно. На каждом из этих рисунков приведены зависимости для скоростей спада лепестков V = 6, 12, 18, 24 и 30 дБ/окт. Для оценки параметров синтеза необходимо выбрать график, соответствующий заданному параметру P, и провести горизонтальную прямую на уровне заданной величины β. Пересечение этой линии с кривыми графика дает возможные значения порядка функции и скорости спада лепестков. Если величина параметра P находится между имеющимися значениями, то можно провести интерполяцию параметров, полученных для имеющихся значений.
Рис. 8.
Зависимости минимально необходимых значений параметра β от порядка весовой функции m для получения уровня максимального бокового лепестка 90 (а), 120 (б) и 150 дБ (в) при скоростях спада боковых лепестков 6 (1), 12 (2), 18 (3), 24 (4) и 30 дБ/окт (5).
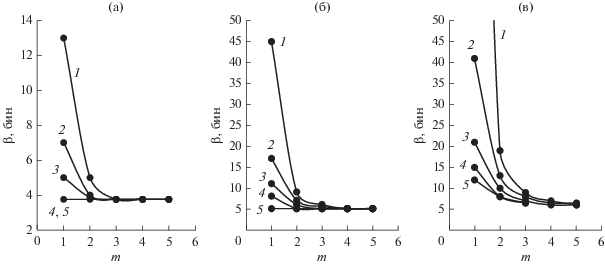
Анализ рис. 8 показывает, что даже сравнительно небольшое увеличение β, в 1.5…2 раза по сравнению с шириной главного лепестка по нулевому уровню, позволяет снизить величину максимального бокового лепестка до –100…–150 дБ с использованием функций весьма малых порядков m = 1…4. При этом ширина главного лепестка и весовые потери существенно ниже, чем для функций с подавлением всех боковых лепестков.
2.4. Параметры оптимальных функций
Полученные в данной работе параметры синтезированных оптимальных функций придены в табл. 2. Для минимизации объема таблицы мы выбрали среди весовых функций вида (2) те, которые представляют наибольший интерес, а именно, функции с целым значением параметра μ, так как их вычисление требует наименьшего количества операций. Кроме того, отметим, что максимальный выигрыш в параметрах весовых функций за счет минимизации на отрезке реализуется в случае, когда параметр β допускает использование функций весьма малого порядка 1…3. Характеристики оптимальных функций с указанными параметрами (μ = 0, 1, 2; m = 1, 2, 3) приведены для скоростей спада 6, 12 и 18 дБ/oкт. Значения уровня максимального лепестка округлены с точностью до 0.1 дБ, а разрядность коэффициентов выбрана такой, что получающиеся значения максимального лепестка P отличаются от оптимальных не более чем на 0.05 дБ.
Таблица 2.
Параметры оптимальных весовых функций порядков m = 1, 2, 3
| m | β, бин | P, дБ | a0, a1, …, am | Пw, дБ | Пs, дБ | Ln, бин | L3, бин | L6, бин |
|---|---|---|---|---|---|---|---|---|
| Скорость спада лепестков V = 6 дБ/окт (µ = 0) | ||||||||
| 1 | 2 | –43.2 | 0.0831; 1.0 | 1.360 | 1.739 | 1.368 | 1.308 | 1.822 |
| 3 | –53.3 | 0.0358; 1.0 | 1.570 | 1.570 | 1.435 | 1.375 | 1.913 | |
| 5 | –65.9 | 0.0132; 1.0 | 1.687 | 1.480 | 1.475 | 1.414 | 1.966 | |
| 10 | –83.1 | 0.00346; 1.0 | 1.741 | 1.439 | 1.493 | 1.433 | 1.991 | |
| 20 | –100.6 | 0.000895; 1.0 | 1.756 | 1.428 | 1.498 | 1.439 | 1.998 | |
| 30 | –111.0 | 0.000403; 1.0 | 1.759 | 1.425 | 1.499 | 1.440 | 1.999 | |
| 50 | –124.1 | 0.000146; 1.0 | 1.760 | 1.424 | 1.500 | 1.440 | 2.000 | |
| 100 | –141.7 | 0.000036; 1.0 | 1.761 | 1.424 | 1.500 | 1.441 | 2.000 | |
| 150 | –151.7 | 0.00001543 1.0 | 1.761 | 1.424 | 1.500 | 1.441 | 2.000 | |
| 2 | 3 | –71.5 | 0.00849; 0.58833; 1.0 | 2.314 | 1.135 | 1.704 | 1.619 | 2.268 |
| 5 | –93.8 | 0.000748; 0.155749; 1.0 | 2.670 | 0.961 | 1.849 | 1.758 | 2.462 | |
| 7 | –108.4 | 0.0001786; 0.0749920; 1.0 | 2.774 | 0.914 | 1.894 | 1.802 | 2.522 | |
| 10 | –123.5 | 0.0000425; 0.0361118; 1.0 | 2.831 | 0.888 | 1.919 | 1.827 | 2.556 | |
| 15 | –140.7 | 0.00000846; 0.01603085; 1.0 | 2.862 | 0.874 | 1.933 | 1.841 | 2.574 | |
| 20 | –153.0 | 0.00000271; 0.00905474; 1.0 | 2.873 | 0.870 | 1.938 | 1.846 | 2.581 | |
| 30 | –170.3 | 0.00000054; 0.00404868; 1.0 | 2.881 | 0.866 | 1.941 | 1.850 | 2.586 | |
| 50 | –192.1 | 0.0000000701; 0.0014626171;1.0 | 2.886 | 0.864 | 1.943 | 1.852 | 2.588 | |
| 3 | 4 | –98.2 | 0.000623; 0.132455; 1.0; 0.585091 | 2.958 | 0.851 | 1.976 | 1.872 | 2.629 |
| 5 | –113.5 | 0.000141; 0.053011; 0.754303; 1.0 | 3.196 | 0.763 | 2.087 | 1.977 | 2.777 | |
| 7 | –135.0 | 0.00001195; 0.00953344; 0.30303469; 1.0 | 3.407 | 0.691 | 2.191 | 2.076 | 2.915 | |
| 10 | –156.3 | 0.000001238; 0.002032527; 0.136103936; 1.0 | 3.520 | 0.654 | 2.249 | 2.132 | 2.993 | |
| 15 | –180.9 | 0.000000100; 0.000375134; 0.057881535; 1.0 | 3.584 | 0.634 | 2.282 | 2.165 | 3.037 | |
| 20 | –198.1 | 0.00000001777; 0.00011797998; 0.03231004646; 1.0 | 3.606 | 0.628 | 2.294 | 2.177 | 3.053 | |
| Скорость спада лепестков V = 12 дБ/окт (µ = 1) | ||||||||
| 1 | 2.5 | –54.3 | 0.2162; 1.0 | 1.977 | 1.315 | 1.577 | 1.503 | 2.099 |
| 4 | –67.6 | 0.0893; 1.0 | 2.190 | 1.190 | 1.656 | 1.579 | 2.205 | |
| 5 | –75.7 | 0.0543; 1.0 | 2.263 | 1.148 | 1.684 | 1.607 | 2.243 | |
| 7 | –87.7 | 0.0265; 1.0 | 2.327 | 1.112 | 1.709 | 1.632 | 2.277 | |
| 10 | –100.2 | 0.0127; 1.0 | 2.360 | 1.093 | 1.722 | 1.645 | 2.295 | |
| 15 | –114.3 | 0.00558; 1.0 | 2.378 | 1.083 | 1.729 | 1.653 | 2.304 | |
| 25 | –132.1 | 0.00200; 1.0 | 2.388 | 1.078 | 1.733 | 1.656 | 2.309 | |
| 40 | –148.5 | 0.00078; 1.0 | 2.391 | 1.076 | 1.734 | 1.658 | 2.311 | |
| 60 | –162.7 | 0.000349; 1.0 | 2.392 | 1.076 | 1.735 | 1.658 | 2.312 | |
| 100 | –180.6 | 0.0001272; 1.0 | 2.392 | 1.075 | 1.735 | 1.658 | 2.312 | |
| 2 | 3.5 | –82.8 | 0.04356; 0.95577; 1.0 | 2.705 | 0.952 | 1.864 | 1.769 | 2.480 |
| 5 | –99.7 | 0.00821; 0.37881; 1.0 | 2.963 | 0.845 | 1.978 | 1.877 | 2.633 | |
| 7 | –118.0 | 0.001688; 0.164614; 1.0 | 3.123 | 0.783 | 2.053 | 1.948 | 2.732 | |
| 9 | –131.7 | 0.000553; 0.093295; 1.0 | 3.191 | 0.758 | 2.085 | 1.980 | 2.775 | |
| 10 | –137.1 | 0.0003576; 0.0745132; 1.0 | 3.210 | 0.751 | 2.094 | 1.989 | 2.787 | |
| 12 | –146.6 | 0.0001680; 0.0507272; 1.0 | 3.235 | 0.742 | 2.106 | 2.001 | 2.804 | |
| 15 | –158.4 | 0.0000666; 0.0318605; 1.0 | 3.256 | 0.734 | 2.117 | 2.011 | 2.817 | |
| 20 | –173.4 | 0.0000208; 0.0177167; 1.0 | 3.272 | 0.728 | 2.124 | 2.019 | 2.828 | |
| 25.0 | –185.1 | 0.000008445; 0.011271458; 1.0 | 3.280 | 0.725 | 2.128 | 2.023 | 2.833 | |
| 30 | –194.5 | 0.00000409; 0.00783179; 1.0 | 3.284 | 0.724 | 2.130 | 2.025 | 2.836 | |
| 40 | 208.0 | 0.000001107; 0.004169168; 1.0 | 3.288 | 0.722 | 2.132 | 2.027 | 2.839 | |
| 3 | 4.5 | –110.3 | 0.00355; 0.22564; 1.0; 0.41389 | 3.247 | 0.746 | 2.112 | 1.999 | 2.809 |
| 5.0 | –116.4 | 0.002255; 0.176383; 1.0; 0.576300 | 3.337 | 0.716 | 2.156 | 2.041 | 2.868 | |
| 6.0 | –131.3 | 0.000706; 0.090215; 0.879184; 1.0 | 3.519 | 0.659 | 2.248 | 2.127 | 2.990 | |
| 7.0 | –142.0 | 0.0002247; 0.0399776; 0.5644248; 1.0 | 3.623 | 0.628 | 2.303 | 2.179 | 3.063 | |
| 8.0 | –151.6 | 0.00008716; 0.02077879; 0.39926295; 1.0 | 3.693 | 0.608 | 2.340 | 2.215 | 3.113 | |
| 9.0 | –159.8 | 0.00003934; 0.01199939; 0.29962240; | 3.742 | 0.594 | 2.367 | 2.241 | 3.149 | |
| 10.0 | –167.2 | 0.00001955; 0.00744624; 0.23415066; 1.0 | 3.777 | 0.584 | 2.386 | 2.259 | 3.174 | |
| 11.0 | –174.0 | 0.00001049; 0.00487894; 0.18848438; 1.0 | 3.804 | 0.576 | 2.401 | 2.273 | 3.194 | |
| 12.0 | –180.1 | 0.000005985; 0.003335414; 0.155207618; 1.0 | 3.824 | 0.571 | 2.412 | 2.284 | 3.209 | |
| 16.0 | –200.6 | 0.0000009575; 0.0009713342; 0.0831016841; 1.0 | 3.872 | 0.558 | 2.439 | 2.310 | 3.245 | |
| Скорость спада лепестков V = 18 дБ/окт (µ = 2) | ||||||||
| 1 | 3 | –64.2 | 0.373; 1.0 | 2.485 | 1.045 | 1.772 | 1.686 | 2.359 |
| 5 | –87.4 | 0.105; 1.0 | 2.737 | 0.930 | 1.878 | 1.787 | 2.501 | |
| 10 | –117.1 | 0.0249; 1.0 | 2.848 | 0.881 | 1.927 | 1.835 | 2.566 | |
| 15 | –134.3 | 0.0111; 1.0 | 2.870 | 0.871 | 1.936 | 1.845 | 2.579 | |
| 20 | –146.6 | 0.0063 1.0 | 2.878 | 0.868 | 1.940 | 1.848 | 2.584 | |
| 30 | –163.9 | 0.00282; 1.0 | 2.883 | 0.865 | 1.942 | 1.851 | 2.587 | |
| 40 | –176.3 | 0.001595; 1.0; | 2.885 | 0.864 | 1.943 | 1.851 | 2.588 | |
| 50 | –185.9 | 0.001025; 1.0; | 2.886 | 0.864 | 1.944 | 1.852 | 2.589 | |
| 60 | –193.7 | 0.000713; 1.0; | 2.887 | 0.864 | 1.944 | 1.852 | 2.589 | |
| 80 | –206.1 | 0.000403; 1.0; | 2.887 | 0.863 | 1.944 | 1.852 | 2.589 | |
| 2 | 4 | –93.3 | 0.0871; 1.0; 0.7348 | 3.056 | 0.812 | 2.021 | 1.915 | 2.689 |
| 5 | –109.1 | 0.02869; 0.61668; 1.0 | 3.262 | 0.739 | 2.119 | 2.008 | 2.820 | |
| 6 | –120.9 | 0.01121; 0.37208; 1.0 | 3.373 | 0.702 | 2.174 | 2.060 | 2.893 | |
| 7 | –130.2 | 0.005532; 0.255345; 1.0 | 3.440 | 0.680 | 2.208 | 2.092 | 2.938 | |
| 9 | –145.4 | 0.001844; 0.144402; 1.0 | 3.515 | 0.656 | 2.247 | 2.130 | 2.989 | |
| 10 | –151.9 | 0.001176; 0.114798; 1.0 | 3.538 | 0.649 | 2.258 | 2.141 | 3.005 | |
| 11 | –157.7 | 0.0007854; 0.0935671; 1.0 | 3.554 | 0.644 | 2.267 | 2.150 | 3.017 | |
| 13 | –167.9 | 0.0003940; 0.0659629; 1.0 | 3.577 | 0.637 | 2.279 | 2.161 | 3.033 | |
| 15 | –176.4 | 0.0002211; 0.0492107; 1.0 | 3.592 | 0.632 | 2.286 | 2.169 | 3.043 | |
| 20 | –193.7 | 0.00006914; 0.02742854; 1.0 | 3.611 | 0.626 | 2.297 | 2.179 | 3.056 | |
| 25 | –207.1 | 0.00002839; 0.01753578; 1.0 | 3.620 | 0.623 | 2.301 | 2.184 | 3.063 | |
| 3 | 5 | –121.5 | 0.010622; 0.332633; 1.0; 0.315655 | 3.516 | 0.661 | 2.247 | 2.125 | 2.988 |
| 6 | –138.3 | 0.003465; 0.182331; 1.0; 0.714361 | 3.718 | 0.603 | 2.354 | 2.225 | 3.130 | |
| 7 | –151.3 | 0.001308; 0.099933; 0.837728; 1.0 | 3.841 | 0.569 | 2.421 | 2.289 | 3.220 | |
| 8 | –162.7 | 0.0004635; 0.0487109; 0.5727040; 1.0 | 3.922 | 0.548 | 2.467 | 2.333 | 3.281 | |
| 9 | –172.3 | 0.0001973; 0.0269628; 0.4203128; 1.0 | 3.978 | 0.534 | 2.499 | 2.364 | 3.324 | |
| 10 | –180.9 | 0.0000946; 0.0163352; 0.3244889; 1.0 | 4.018 | 0.524 | 2.522 | 2.386 | 3.355 | |
| 12 | –194.9 | 0.00002938; 0.00734694; 0.21486149; 1.0 | 4.070 | 0.511 | 2.553 | 2.415 | 3.395 | |
| 14 | –206.9 | 0.00001111; 0.00380480; 0.15359264; 1.0 | 4.102 | 0.503 | 2.572 | 2.433 | 3.420 | |
В табл. 2 приведены весовые функции с уровнем подавления боковых лепестков до минус 200 дБ, а разница параметров P в соседних строках составляет порядка 10…20 дБ. Для каждого порядка m первая строка соответствует функции с максимальным подавлением всех лепестков, при этом параметр β равен положению первого нуля спектра.
ЗАКЛЮЧЕНИЕ
Метод синтеза оптимальных функций, минимизирующих уровень максимального лепестка спектра, разработанный в [5–7], пригоден для решения задачи в случае, когда минимизация проводится на заданном отрезке частотной оси. Анализ полученных оптимальных решений показывает, что сужение области минимизации при фиксированном порядке весовой функции позволяет значительно улучшить основные характеристики: снизить величину максимального лепестка на несколько десятков децибел, выиграть до 2.5 дБ в отношении сигнал/шум, получить меньшую ширину главного лепестка и т.д. Альтернативным методом использования выигрыша является фиксация уровня боковых лепестков и существенное снижение порядка весовой функции, часто вплоть до единицы, что упрощает применение в реальном масштабе времени.
Полученные в работе взаимозависимости основных параметров оптимальных функций позволяют спрогнозировать необходимые параметры для решения практических задач.
Список литературы
Хэррис Ф.Дж. // ТИИЭР. 1978. Т. 66. № 1. С. 60.
Prabhu K.M.M. Window Functions and Their Applications in Signal Processing. Boca Raton: CRC Press, 2013.
Sun Y., Liu Q., Cai J., Long T. // Sensors. 2018. P. 3081. https://doi.org/10.3390/s18093081
Justo J.F., Beccaro W. // IEEE Access. 2020. V. 8. P. 187584. https://doi.org/10.1109/ACCESS.2020.3030903
Зайцев Г.В., Хзмалян А.Д. // РЭ. 2020. Т. 65. № 5. С. 464. https://doi.org/10.1134/S1064226920050137
Зайцев Г.В., Хзмалян А.Д. // Цифровая обработка сигналов. 2019. № 2. С. 35.
Зайцев Г.В., Хзмалян А.Д. // РЭ. 2021. Т. 66. № 5. С. 443. https://doi.org/10.31857/S0033849421050120
Tseng F., Sarkar T., Weiner D. // IEEE Trans. 1981. V. ASSP-29. № 2. P. 177.
Zhong J., Han Z., Lu W. // IEEE Trans. 1992. V. SP-40. P. 1452.
Hanna M.T. // IEEE Trans. 1994. V. SP-42. P. 2037.
Хзмалян А.Д., Кондратьев А.С. // РЭ. 1999. Т. 44. № 1. С. 70.
Оппенгейм А.В., Шафер Р.В. Цифровая обработка сигналов. М.: Техносфера, 2006.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника



