Радиотехника и электроника, 2022, T. 67, № 4, стр. 315-327
Метод расчета рассеяния электромагнитных волн на 2D‑неоднородностях, расположенных на поверхности больших тел
В. В. Лесняк a, *, Д. Ю. Стрелец a
a Московский авиационный институт (национальный исследовательский университет)
125993 Москва, Волоколамское шос., 4, Российская Федерация
* E-mail: maksmai33@gmail.com
Поступила в редакцию 14.04.2021
После доработки 23.09.2021
Принята к публикации 15.10.2021
- EDN: NNYCPZ
- DOI: 10.31857/S0033849422030081
Аннотация
Рассмотрена задача расчета рассеяния на 2D‑неоднородностях с произвольной формой сечения, расположенных на поверхности больших тел. Для решения задачи рассеяния в реальном 3D‑пространстве предлагается модификация метода физической теории дифракции с использованием метода интегральных уравнений. Рассмотрена проблема низкой точности, возникающая при расчете рассеяния на полубесконечных объектах. Предложено решение этой проблемы путем учета неравномерной части тока на полубесконечных гранях контура неоднородности. Приведены экстраполяционные формулы для неравномерной части тока на полубесконечных гранях. Рассмотрен итерационный процесс увеличения точности расчета функций рассеяния Уфимцева.
ВВЕДЕНИЕ
В настоящее время одним из действенных методов расчета эффективной площади рассеяния (ЭПР) является комбинированный метод на основе метода физической оптики (ФО). Для компенсации недостатков метода ФО в комбинированный метод добавляют поправки, расчет которых основывается на аналитических методах, на методах интегральных уравнений или лучевых методах. Частным случаем комбинированного метода, включающего метод ФО и поправки, рассчитанные на двумерных задачах, является метод физической теории дифракции Уфимцева (ФТД) [1, 2]. В данной работе представлен комбинированный метод, который является дальнейшим развитием метода ФТД.
1. ПОСТАНОВКА ЗАДАЧИ
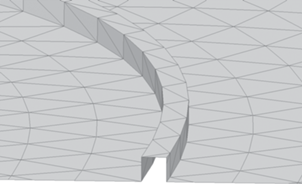
Введем понятие 2D‑неоднородности, название которой связано с тем, что основой предложенного метода является численное решение интегральных уравнений в двумерном пространстве (2-Dimension). Представим большой объект с характерными размерами, включая главные радиусы кривизны поверхности объекта, много больше длины электромагнитной волны облучения. На этот объект накладывается поверхность неоднородности в виде полосы, длина которой много больше ее ширины, а также много больше длины волны облучения. Центральную линию полосы назовем линией расположения 2D‑неоднородности на поверхности большого объекта. Радиус кривизны этой линии также должен быть много больше длины волны. Сечение полосы неоднородности в плоскости, перпендикулярной линии расположения, в классическом методе ФТД Уфимцева имеет форму острого клина, как, например, изломы поверхности у конечного цилиндра, рассмотренного в [2]. В предложенном варианте ФТД форма сечения 2D‑неоднородности является произвольной. Форма сечения является линией, которую будем называть контуром неоднородности. Единственным условием, накладываемым на форму сечения, является непрерывность первой производной контура неоднородности, которая достигается закруглением острых кромок на контуре радиусом порядка 0.01λ, где λ – длина электромагнитной волны облучения. Наряду с линией излома, примером 2D‑неоднородности могут быть канавка на поверхности объекта или, наоборот, выступ (рис. 1). Таким образом, форма 2D-неоднородности определяется двумя независимыми характеристиками: формой сечения и линией расположения неоднородности на поверхности большого объекта.
Предложенный комбинированный метод расчета ЭПР-объектов с 2D-неоднородностями на поверхности, как уже отмечалось, состоит из расчета рассеянного поля методом ФО, к которому добавляется поле поправки, наведенной 2D‑неоднородностями. Формула комбинированного метода может быть записана следующим образом:
где ${{\vec {E}}^{p}}~$ – поле, рассеянное объектом, $~\vec {E}_{{P0}}^{p}$ – нулевое приближение, рассчитывается методом физической оптики$,~\vec {E}_{{2D}}^{p}$ – поправки на 2D-неоднородности.Расчет рассеянного поля методом ФО не представляет сложностей и описан во множестве работ, например, в [3]. Расчет поправок наведенных 2D‑неоднородностями разделяется на несколько этапов.
1. На поверхности объекта задается линия расположения 2D‑неоднородности, которая представляется в виде полилинии с определенным количеством прямых ребер. Длина ребер определяется кривизной линии и длиной волны облучения. Далее задача по расчету поправки в рассеянное поле решается для участка неоднородности на каждом ребре этой линии.
2. Создается контур сечения неоднородности для решения модельной задачи в двумерном пространстве.
3. Из значений углов падения плоской волны на неоднородность на каждом ребре линии вычисляются параметры эквивалентной двумерной задачи. Расчет параметров эквивалентной задачи описан, например в [1, 2], в частности, эквивалентная длина волны ${{\lambda }_{{2D}}} = {{{{\lambda }_{{3D}}}} \mathord{\left/ {\vphantom {{{{\lambda }_{{3D}}}} {{\text{sin}}\left( \gamma \right)}}} \right. \kern-0em} {{\text{sin}}\left( \gamma \right)}}$, где $\gamma $ – угол между направлением ребра линии расположения и направлением плоской волны облучения.
4. Методом интегральных уравнений численно решается двумерная эквивалентная задача по поиску тока на контуре неоднородности. Реально решаются две задачи: для E‑ и H‑поляризаций. Интегрирование найденных токов позволяет вычислить функции рассеяния Уфимцева f1(φ0, φ), g1(φ0, φ).
5. Далее расчет рассеяния переходит в 3D‑пространство, где по найденным функциям f1 и g1 вычисляется эквивалентная нить тока. Этот эквивалентный ток проходит по ребрам полилинии и имеет свои параметры на каждом ребре.
6. Поправка на 2D‑неоднородность в рассеянное поле рассчитывается путем интегрирования в 3D‑пространстве нити эквивалентного тока, проходящего по полилинии.
В предложенном методе расчета поправок, наведенных 2D‑неоднородностями, оригинальным является этап 4. Описание математических выражений, применяемых по остальным этапам, можно найти в [1, 2] и более поздних работах П.Я. Уфимцева.
В данной статье кратко описывается именно этап 4, также приведен полный, пересчитанный в реальное 3D‑пространство результат расчета рассеяния на 2D‑неоднородности.
Рассмотрим задачу, указанную выше в п. 4. Для расчета тока на контуре 2D‑объекта воспользуемся интегральным уравнением магнитного поля (ИУМП) для идеально проводящих поверхностей в двумерном пространстве [4]:
(1)
$\vec {J}\left( {\vec {r}} \right) - 2\left[ {\hat {n}\left( {\vec {r}} \right) \times \vec {M}\left( {\vec {J},\vec {r}} \right)} \right] = 2\left[ {\hat {n}\left( {\vec {r}} \right) \times {{{\vec {H}}}^{i}}\left( {\vec {r}} \right)} \right],$В этих выражениях введены следующие обозначения: $~\vec {r}$ – точка наблюдения, $~{{\vec {r}}_{q}}$ – точка источника, $~\vec {J}\left( {\vec {r}} \right)$ – поверхностный электрический ток, $\hat {n}\left( {\vec {r}} \right)$ – единичная наружная нормаль, $~{{\vec {H}}^{i}}\left( {\vec {r}} \right)$ – напряженность магнитного поля облучающей волны, $G\left( {\vec {r},{{{\vec {r}}}_{q}}} \right) = ~~\frac{1}{{4i}}H_{0}^{2}\left( {kR} \right)$ – функция Грина двумерного пространства, $~R = \left| {\vec {r} - {{{\vec {r}}}_{q}}} \right|$ – расстояние от точки источника до точки наблюдения, $H_{0}^{2}\left( {kR} \right),$ $~H_{1}^{2}\left( {kR} \right)$ – функции Ханкеля 2-го рода нулевого и первого порядка, $~k$ – волновое число.
Задача ставится следующим образом: на контур объекта падает плоская волна (рис. 2) и путем численного решения уравнения (1) требуется найти ток на контуре. Физика процесса рассеяния такова, что векторное уравнение (1) распадается на два независимых скалярных уравнения:
(2)
${{J}_{\tau }}\left( {\vec {r}} \right) + \frac{1}{{2i}}{{M}_{z}}\left( {{{J}_{\tau }},\vec {r}} \right) = - 2H_{z}^{i}\left( {\vec {r}} \right)~,~$(3)
${{J}_{z}}\left( {\vec {r}} \right) + \frac{1}{{2i}}{{M}_{\tau }}\left( {{{J}_{z}},\vec {r}} \right) = 2\left( {{{n}_{x}}H_{y}^{i}\left( {\vec {r}} \right) - {{n}_{y}}H_{x}^{i}\left( {\vec {r}} \right)} \right),~$Уравнение (2) описывает случай H‑поляризации со следующими компонентами облучающего поля:
(4)
$H_{z}^{i}\left( {\vec {r}} \right) = {{H}_{0}}{\text{exp}}\left( {ik\left( {x{\text{cos}}{{\varphi }_{0}} + y{\text{sin}}{{\varphi }_{0}}} \right)} \right)\hat {z}~.$Уравнение (3) описывает случай E‑поляризации, компоненты облучающего поля имеют следующий вид:
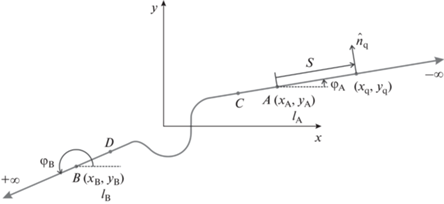
Так как 2D‑неоднородность расположена на поверхности большого объекта, то при построении контура модельной задачи необходимо учесть и этот большой объект. Контур модельной задачи (рис. 3) строится следующим образом. Сначала в контур добавляется сечение 2D‑неоднородности (см. рис. 3 участок CD). Обратим внимание на условие, что объект, на котором расположена 2D‑неоднородность, является большим относительно длины волны, а также имеет главные радиусы кривизны много больше длины волны. В таком случае участки контура, примыкающие к неоднородности и принадлежащие большому объекту, можно аппроксимировать полубесконечными прямыми гранями. Наклон грани11 С определяется касательным вектором к участку в точке С. Аналогично для грани D наклон определяется касательным вектором в точке D. Далее разделим грань С на буферный участок AC и полубесконечную грань A. Также разделим грань D на буферный участок DB и бесконечную грань B. Длину буферных участков разные авторы аналогичных методов выбирают от нескольких длин волн облучения до десяти и более.
Отметим, что контур модельной задачи, так же как и на рис. 2, должен быть замкнут. Поэтому грани A и B соединяются между собой по дуге бесконечного радиуса. Однако, учитывая, что все интегралы, по дуге бесконечного радиуса возникающие при решении задачи, равны нулю, то эта часть контура далее не упоминается.
Грани A и B образуют клин с внешним углом $\alpha = {{\varphi }_{{\mathbf{B}}}} - {{\varphi }_{{\mathbf{A}}}}$, где ${{\varphi }_{{\mathbf{B}}}},{{\varphi }_{{\mathbf{A}}}}$ – углы наклона граней A, B относительно оси x. Таким образом, модельная задача по расчету 2D‑неоднородности в общем случае представляет собой бесконечный клин с произвольной формой кромки. В частности, при угле клина 180° клин раскрывается в плоскость. При этом мы решаем задачу расчета рассеяния на 2D‑неоднородности, расположенной на плоской или слабо искривленной поверхности.
Для решения задачи с полубесконечным модельным контуром (см. рис. 3) также справедливы уравнения (2), (3).
2. РЕШЕНИЕ ЗАДАЧИ
Далее преобразуем приведенные выше общие выражения для решения задачи на модельном полубесконечном контуре. Рассмотрим проблему на примере H‑поляризации. Разделим контур интегрирования на три части по точкам A и B:
(5)
$\begin{gathered} M_{z}^{A}\left( {{{J}_{\tau }},\vec {r}} \right) = \int\limits_{ - \infty }^{k{{l}_{A}}~} {{{J}_{\tau }}\left( {{{{\vec {r}}}_{q}}} \right)} H_{1}^{2}\left( {kR} \right) \times \\ \times \,\,\left[ {n_{y}^{q}\frac{{k{{y}_{q}} - ky}}{{kR}} + n_{x}^{q}\frac{{k{{x}_{q}} - kx}}{{kR}}} \right]d\left( {k{{l}_{q}}} \right)~,~ \\ \end{gathered} $(6)
$\begin{gathered} M_{z}^{B}\left( {{{J}_{\tau }},\vec {r}} \right) = \int\limits_{k{{l}_{B}}}^{\infty ~} {{{J}_{\tau }}\left( {{{{\vec {r}}}_{q}}} \right)} H_{1}^{2}\left( {kR} \right) \times \\ \times \,\,\left[ {n_{y}^{q}\frac{{k{{y}_{q}} - ky}}{{kR}} + n_{x}^{q}\frac{{k{{x}_{q}} - kx}}{{kR}}} \right]d\left( {k{{l}_{q}}} \right)~, \\ \end{gathered} $Интегрирование производится по безразмерному параметру длины контура: $k{{l}_{A}},k{{l}_{B}}$ – значение параметров в точках A и B (см. рис. 3).
Как уже отмечалось, при разбиении контура на участки был опущен интеграл на участке по бесконечному радиусу от +∞ до –∞. Подробное изучение этого интеграла показывает, что его значение стремится к нулю.
Перенесем интегралы по полубесконечным граням в правую часть уравнения (2), тогда получим
(7)
$\begin{gathered} {{J}_{\tau }}\left( {\vec {r}} \right) + \frac{1}{{2i}}M_{z}^{{AB}}\left( {{{J}_{\tau }},\vec {r}} \right) = \\ = - 2H_{z}^{i}\left( {\vec {r}} \right) - \frac{1}{{2i}}M_{z}^{A}\left( {{{J}_{\tau }},\vec {r}} \right) - \frac{1}{{2i}}M_{z}^{B}\left( {{{J}_{\tau }},\vec {r}} \right)~.~ \\ \end{gathered} $Ток на гранях C и D разделим на физоптический и неравномерную часть тока, как предложено в [1, 2]. Неравномерная часть тока определяется возмущением полей от неоднородности, расположенной на части контура LCD:
где $~J_{\tau }^{{{\text{фо}}}}$ – физоптический ток, $~J_{\tau }^{{\text{н}}}$ – неравномерная часть тока.Падающая волна должна распространяться во внешнем пространстве, поэтому очевидно следующее ограничение на угол φ0:
(9)
${{\varphi }_{A}} < \,\,~{{\varphi }_{0}}~\,\, < {{\varphi }_{B}},~\,\,\,\,~\alpha \geqslant \pi .~$Кроме того, поставим условие, что отраженная зеркально волна от одной грани не должна попасть на другую грань. Тогда для угла падения φ0 справедливо дополнительное к условию (9) ограничение:
(10)
${{\varphi }_{A}} - \alpha + \pi < ~{{\varphi }_{0}}~ < {{\varphi }_{B}} + \alpha - \pi ,\,\,\,\,~\alpha < \pi .~$При принятых ограничениях (9), (10) физоптический ток для случая Н‑поляризации полностью определяется магнитной компонентой облучающего поля (4):
(11)
$\begin{gathered} J_{\tau }^{{{\text{фо}}}} = 2\left[ {\hat {n}\left( {\vec {r}} \right) \times H_{z}^{i}\left( {\vec {r}} \right)} \right] = \\ = - 2{{H}_{0}}{\text{exp}}\left( {i\left( {kx{\text{cos}}{{\varphi }_{0}} + ky{\text{sin}}{{\varphi }_{0}}} \right)} \right)~. \\ \end{gathered} $Неравномерная часть тока соответственно определяется магнитной компонентой поля, рассеянного на неоднородности. Степень затухания электромагнитных полей в дальней зоне от источника определяется асимптотикой функции Грина. В свободном 2D‑пространстве асимптотика функции Грина определяется первым членом разложения функции Ханкеля. Тогда для магнитной компоненты можно записать следующую асимптотику:
(12)
$\left| {\vec {H}} \right|\sim \left| {H_{0}^{2}\left( {kR} \right)} \right|~\sim ~\frac{1}{{\sqrt {kR} }}~.$Однако наличие в задаче идеально проводящей грани (рассмотрим каждую грань отдельно) вносит коррективы в степень затухания тангенциальной составляющей магнитного поля при распространении возмущения по грани. В случае H‑поляризации асимптотика остается той же, что и в свободном пространстве (12). Но для случая E‑поляризации степень затухания тангенциальной составляющей магнитного поля увеличивается, это связанно с суммированием реальных и зеркальных (отраженных от грани) источников излучения:
Таким образом, неравномерная часть тока в дальней зоне на грани в случае H‑поляризации будет иметь степень затухания 1/2, как в (12), а в случае E‑поляризации – 3/2.
Далее вернемся к рассмотрению уравнения (6) для случая Н‑поляризации. Учитывая затухание неравномерной части тока на гранях, можно ожидать, что при достаточной ширине буферных зон AC и DB (более нескольких длин волн) амплитуда неравномерной части тока на границах A и B достаточно снизится, чтобы считать ее равной нулю. При этом ток (8) на гранях A и B можно считать равным физоптическому. Таким образом, уравнение (7) преобразовывается в интегральное уравнение с неизвестным током на ограниченной области LAB и известными переменными в правой части. Это обычная процедура, которую применяют многие авторы, например, [5–9]:
(13)
$\begin{gathered} {{J}_{\tau }}\left( {\vec {r}} \right) + \frac{1}{{2i}}M_{z}^{{AB}}\left( {{{J}_{\tau }},\vec {r}} \right) = \\ = - 2H_{z}^{i}\left( {\vec {r}} \right) - \frac{1}{{2i}}M_{z}^{A}\left( {J_{\tau }^{{{\text{фо}}}},\vec {r}} \right) - \frac{1}{{2i}}M_{z}^{B}\left( {J_{\tau }^{{{\text{фо}}}},\vec {r}} \right)~. \\ \end{gathered} $Теперь уравнение (13) для Н‑поляризации можно преобразовать методом моментов (ММ) к системе линейных алгебраических уравнений (СЛАУ), которая без проблем решается численно.
Получим выражения для интегралов в правой части уравнения (13). Сначала для интеграла по грани A. Подставим физоптический ток (11) в выражение (5) и получим
Проведем преобразования данного интеграла. Вектор нормали к грани A связан с углом наклона грани следующими соотношениями:
Введем обозначения:
(14)
$\begin{gathered} k{{l}_{q}} = - s + k{{l}_{A}},\,\,\,\,k{{x}_{q}} = k{{x}_{A}} + s{\text{сos}}{{\varphi }_{A}}, \\ k{{y}_{q}} = k{{y}_{A}} + s{\text{sin}}{{\varphi }_{A}}, \\ k{{\xi }_{A}} = \left( {kx - k{{x}_{A}}} \right){\text{cos}}{{\varphi }_{A}} + \left( {ky - k{{y}_{A}}} \right){\text{sin}}{{\varphi }_{A}},~ \\ k{{\eta }_{A}} = - \left( {kx - k{{x}_{A}}} \right){\text{sin}}{{\varphi }_{A}} + \left( {ky - k{{y}_{A}}} \right){\text{cos}}{{\varphi }_{A}}, \\ kR = \sqrt {{{{\left( {kx - k{{x}_{q}}} \right)}}^{2}} + {{{\left( {ky - k{{y}_{q}}} \right)}}^{2}}} = \\ = \sqrt {{{{\left( {s - k{{\xi }_{A}}} \right)}}^{2}} + {{{\left( {k{{\eta }_{A}}} \right)}}^{2}}} , \\ \end{gathered} $После проведения преобразований получим интеграл следующего вида:
(15)
$\begin{gathered} M_{z}^{A}\left( {J_{\tau }^{{{\text{фо}}}},\vec {r}} \right) = 2{{H}_{0}}k{{\eta }_{A}}{\text{exp}}\left( {i\left( {k{{x}_{A}}{\text{cos}}{{\varphi }_{0}} + k{{y}_{A}}{\text{sin}}{{\varphi }_{0}}} \right)} \right) \times \\ \times \,\,\int\limits_0^{ + \infty ~} {{\text{exp}}\left( {is{\text{cos}}\left( {{{\varphi }_{0}} - {{\varphi }_{A}}} \right)} \right)} \frac{{H_{1}^{2}\left( {kR} \right)}}{{kR}}d\left( s \right).~ \\ \end{gathered} $Аналогично для грани B. Подставим физоптический ток (11) в выражение (6) и получим
Введем обозначения:
(16)
$\begin{gathered} n_{x}^{q} = {\text{sin}}{{\varphi }_{B}},\,\,\,\,~n_{y}^{q} = - {\text{cos}}{{\varphi }_{B}},\,\,\,\,k{{l}_{q}} = s + k{{l}_{B}}, \\ k{{x}_{q}} = k{{x}_{B}} + s{\text{cos}}{{\varphi }_{B}},~~k{{y}_{q}} = k{{y}_{B}} + s{\text{sin}}{{\varphi }_{B}}, \\ k{{\xi }_{B}} = \left( {kx - k{{x}_{B}}} \right){\text{cos}}{{\varphi }_{B}} + \left( {ky - k{{y}_{B}}} \right){\text{sin}}{{\varphi }_{B}},~ \\ k{{\eta }_{B}} = - \left( {kx - k{{x}_{B}}} \right){\text{sin}}{{\varphi }_{B}} + \left( {ky - k{{y}_{B}}} \right){\text{cos}}{{\varphi }_{B}}, \\ kR = \sqrt {{{{\left( {kx - k{{x}_{q}}} \right)}}^{2}} + {{{\left( {ky - k{{y}_{q}}} \right)}}^{2}}} = \\ = \sqrt {{{{\left( {s - k{{\xi }_{B}}} \right)}}^{2}} + {{{\left( {k{{\eta }_{B}}} \right)}}^{2}}} , \\ \end{gathered} $После проведения преобразований получим следующий интеграл:
(17)
$\begin{gathered} M_{z}^{B}\left( {J_{\tau }^{{{\text{фо}}}},\vec {r}} \right) = \\ = - 2{{H}_{0}}k{{\eta }_{B}}{\text{exp}}\left( {i\left( {k{{x}_{B}}{\text{cos}}{{\varphi }_{0}} + k{{y}_{B}}{\text{sin}}{{\varphi }_{0}}} \right)} \right) \times \\ \times \,\,\mathop \smallint \limits_0^{\infty ~} {\text{exp}}\left( {is{\text{cos}}\left( {{{\varphi }_{0}} - {{\varphi }_{B}}} \right)} \right)\frac{{H_{1}^{2}\left( {kR} \right)}}{{kR}}d\left( s \right). \\ \end{gathered} $Для тестирования численных расчетов интегральных уравнений будем сравнивать результаты этих расчетов с аналитическим решением. Так как существует только одно аналитическое асимптотическое решение задачи рассеяния на 2D‑неоднородности в виде острого клина, то воспользуемся решением задачи рассеяния на клине из работ [1, 2], в которых предложены функции рассеяния f 1(φ0, φ), g1(φ0, φ), описывающие поправку к ФО.
Функцию рассеяния g1 для контуров произвольного сечения можно рассчитать с помощью следующего интеграла:
(18)
$\begin{gathered} {{g}^{1}}\left( \varphi \right) = \frac{{ - i}}{2}\int\limits_L {J_{\tau }^{{\text{н}}}} \left( {{{{\vec {r}}}_{q}}} \right)\left( {n_{x}^{q}{\text{cos}}\varphi + n_{y}^{q}{\text{sin}}\varphi } \right) \times \\ \times \,\,{\text{exp}}\left( {i\left( {k{{x}_{q}}{\text{cos}}\varphi + k{{y}_{q}}{\text{sin}}\varphi } \right)} \right)d\left( {k{{l}_{q}}} \right)~. \\ \end{gathered} $Подынтегральное выражение содержит неравномерный ток на контуре, найденный из решения интегральных уравнений в двумерном пространстве. Так как неравномерную часть тока на гранях мы установили равной нулю, то область интегрирования в (18) сократилась до LAB. При этом неравномерная часть тока на области LAB определяется разностью между полным током, найденным при решении уравнения (13), и физоптическим током (11):
Для полноты описания приведем также выражение для расчета функции f 1 для E‑поляризации
(20)
$\begin{gathered} {{f}^{1}}\left( \varphi \right) = \frac{{ - i}}{2}\int\limits_L {J_{z}^{{\text{н}}}\left( {{{{\vec {r}}}_{q}}} \right)} \times \\ \times \,\,{\text{exp}}\left( {i\left( {k{{x}_{q}}{\text{cos}}\varphi + k{{y}_{q}}{\text{sin}}\varphi } \right)} \right)d\left( {k{{l}_{q}}} \right)~. \\ \end{gathered} $Сравним функции рассеяния, рассчитанные через интегралы (18), (20), с функциями, рассчитанными по формулам Уфимцева [1, 2]. Для примера возьмем клин с внешним углом 300°. Для использования клина в интегральных уравнениях закруглим острую кромку радиусом, равным 1% от длины волны, а размер буферной зоны установим равным 5λ, где λ – длина волны облучения. Будем рассчитывать случай обратного рассеяния, при котором угол наблюдения φ равен углу облучения φ0. Результаты расчетов показаны на рис. 4. Отметим, что все численные расчеты выполнены в безразмерном виде, в связи с этим ток нормировался на амплитуду падающего магнитного поля H0 и, соответственно, функции f 1, g1 также получились безразмерными.
Рис. 4.
Функции рассеяния на клине с внешним углом 300º для Н- (1, 2) и Е-поляризации (3, 4), рассчитанные методом интегральных уравнений (1, 3) и с помощью аналитического решения Уфимцева (2, 4).
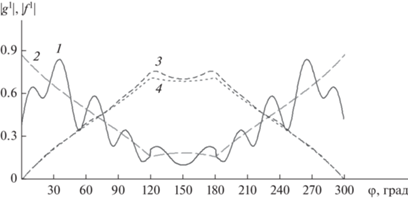
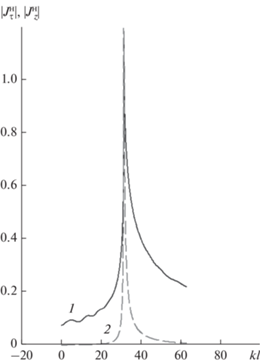
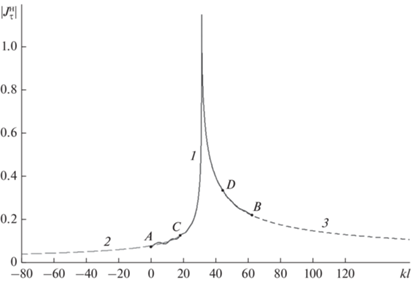
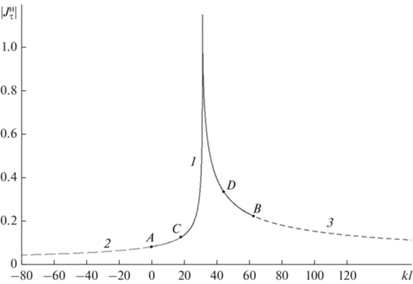
На рис. 4 приведены графики модуля комплексной функции f 1 для E‑поляризации, рассчитанные методом интегральных уравнений и с использованием аналитического решения Уфимцева. Как видно из сравнения, соответствие между графиками достаточно точное. Этим объясняется выбор E‑поляризации для использования в примерах многими авторами. Там же представлен модуль функции g1 для H‑поляризации для численного решения и для аналитического решения Уфимцева. Как видим, численное решение для H‑поляризации имеет большую погрешность. Чтобы проанализировать причины столь большой погрешности, приведем график модуля неравномерной части тока, например, при угле облучении 80°, рассчитанного численно при решении интегральных уравнений. На рис. 5 представлен модуль неравномерного тока на области LAB для H‑ и E‑поляризации. По горизонтальной оси отложен параметр длины контура kl, отчет расстояния начинается от границы A области LAB. Как уже отмечалось, длина контура области LAB, включая буферную зону, составляет примерно 10λ.
Из анализа поведения тока на рис. 5 становится очевидной причина большой погрешности для функции g1, рассчитанной при использовании уравнения (13). Эта причина в недостаточном затухании неравномерного тока на границах области LAB в точках A и B. При преобразовании интегрального уравнения (7) в уравнение (13) мы полагали, что неравномерная часть тока в точках A (kl = 0) и B (kl = 62.8) равна 0, но для H‑поляризации это далеко от действительности. Разрывы тока на границах области LAB образуют фиктивные источники излучения. Эти источники совместно с реальным источником на острие клина создают интерференционную картину, которая определяет колебательный характер функции g1 (см. рис. 4 кривая 1). Попробуем увеличить ширину буферной зоны до 50λ на каждой границе области LAB. Результаты расчетов показаны на рис. 6. Как видно из сравнения с аналитическим расчетом по Уфимцеву, точность расчетов при использовании уравнения (13) улучшилась, однако при углах облучения, близких к скользящим вдоль граней, погрешность все еще недопустимо велика. Из данного примера можно сделать вывод, что проблема точности расчетов не решается путем увеличения ширины буферных зон.
Рис. 6.
Функции рассеяния на клине с внешним углом 300°, ширина буферной зоны 50λ для Н- (1) и Е-поляризации (2).
Как видим для увеличения точности расчетов необходимо учитывать неравномерную часть тока на гранях. В работе [10] предлагается экстраполировать ток следующим выражением:
А для особых случаев падения волны вдоль граней, когда неравномерная часть тока практически не затухает, в той же работе предлагается для соответствующей грани выражение
(22)
$J_{\tau }^{{\text{н}}} = С~{\text{exp}}\left( {ik\xi } \right),~\,\,\,\,~{{\varphi }_{0}} = {{\varphi }_{A}} + \pi ,\,\,\,\,~{{\varphi }_{0}} = {{\varphi }_{B}} - \pi .~$Так как коэффициент С входит в выражение (21) и (22) линейно, то его добавляют в СЛАУ в качестве дополнительного неизвестного. Всего два дополнительных неизвестных по числу граней. Параметр ξ отсчитывается от острой кромки клина. В связи с этим метод невозможно применить к клину с произвольным сечением кромки, так как будет неизвестно положение фазового центра рассеяния, от которого отсчитывается параметр ξ.
В работе [11] приводится вариант решения задачи рассеяния на клине с произвольным сечением кромки, в том числе с диэлектриком на кромке. Здесь предлагается неравномерную часть тока на гранях получать из решения модельной задачи на остром идеально проводящем клине с аналогичным углом раскрыва. Однако проблема несоответствия положения фазовых центров рассеяния в решаемой задаче и модельной задаче до конца не решена.
В данной работе для увеличения точности расчетов рассеяния на полубесконечных структурах предлагается экстраполировать неравномерные токи на гранях следующими выражениями:
(23)
$J_{\tau }^{{\text{н}}} = \frac{{{{A}_{2}}}}{{\sqrt {{{A}_{3}} - kl} }}{\text{exp}}\left( {i\left( {{{A}_{0}} + kl} \right)} \right)~,~$(24)
$J_{\tau }^{{\text{н}}} = \frac{{{{B}_{2}}}}{{\sqrt {{{B}_{3}} + kl} }}{\text{exp}}\left( {i\left( {{{B}_{0}} - kl} \right)} \right)~{\kern 1pt} .$Выражение (23) для неравномерного тока на грани A, а выражение (24) соответственно для грани B. В отличие от выражений (21) и (22) здесь добавлены коэффициенты A0, B0, которые определяют положение фазового центра рассеяния. Кроме того, добавлены коэффициенты A3, B3, которые регулируют степень затухания вблизи неоднородности. Увеличение этих коэффициентов позволяет постепенно, по мере приближения угла облучения к особым случаям, перейти от выражения типа (21) к типу (22). В расчетной программе на коэффициенты A3, B3 искусственно наложено ограничение, поэтому полного перехода к выражению (22) не происходит. Так как величина ограничения достаточно велика, то на точности расчетов это практически не сказывается.
Коэффициенты A0, A3 и B0, B3 входят в выражения (23), (24) нелинейно, поэтому воспользоваться методом их расчета, примененным в [10], не представляется возможным. В данной работе задача расчета рассеяния решается в две итерации (или больше при необходимости). На первой итерации решаем уравнение (13), в котором неравномерные токи на гранях приравнены к нулю. Далее найденный неравномерный ток на граничных участках AC и BD контура LAB используем для вычисления неизвестных коэффициентов A0, A2, A3 и B0, B2, B3. Для этого выделяем участок буферной зоны, примыкающий к границе A, длина этого участка может быть 1…3λ, но можно выбрать буферную зону целиком. И на этом участке при помощи метода наименьших квадратов вычисляем коэффициенты A0, A2, A3 так, чтобы полученная экстраполяция (23) минимально отличалась от неравномерной части тока полученного при численном решении уравнения (13). Аналогично вычисляем коэффициенты B0, B2, B3.
Графики неравномерного тока, рассчитанные по экстраполяциям (23) и (24) для случая, рассмотренного на рис. 5, показаны на рис. 7.
Рис. 7.
Экстраполяция неравномерной части тока на гранях A и B для неравномерного тока на участке LAB (1), экстраполяции (23) на грани A (с заходом на участок AC) (2) и экстраполяции (24) на грани B (3).
Теперь, имея выражения для неравномерного тока на гранях, мы можем рассчитать функцию рассеяния (18) путем интегрирования тока по всему контуру, включая грани. Область интегрирования разделяем на три части:
(25)
${{g}^{1}}\left( \varphi \right) = ~g_{{AB}}^{1}\left( \varphi \right) + g_{A}^{1}\left( \varphi \right) + g_{B}^{1}\left( \varphi \right),$(26)
$\begin{gathered} g_{{AB}}^{1}\left( \varphi \right) = \\ = \frac{{ - i}}{2}\mathop \smallint \limits_{k{{l}_{A}}}^{k{{l}_{B}}~} \left( {{{J}_{\tau }}\left( {{{{\vec {r}}}_{q}}} \right) - J_{\tau }^{{{\text{фо}}}}\left( {{{{\vec {r}}}_{q}}} \right)} \right)\left( {n_{x}^{q}{\text{cos}}\varphi + n_{y}^{q}{\text{sin}}\varphi } \right) \times \\ \times \,\,{\text{exp}}\left( {i\left( {k{{x}_{q}}{\text{cos}}\varphi + k{{y}_{q}}{\text{sin}}\varphi } \right)} \right)d\left( {k{{l}_{q}}} \right), \\ g_{A}^{1}\left( \varphi \right) = \frac{{ - i{{A}_{2}}}}{2} \times \\ \times \,\,\mathop \smallint \limits_{ - \infty }^{k{{l}_{A}}~} \frac{{\left( {n_{x}^{q}{\text{cos}}\varphi + n_{y}^{q}{\text{sin}}\varphi } \right)}}{{\sqrt {{{A}_{3}} - k{{l}_{q}}} }}{\text{exp}}\left( {i\left( {{{A}_{0}} + k{{l}_{q}}} \right)} \right) \times \\ \times \,\,{\text{exp}}\left( {i\left( {k{{x}_{q}}{\text{cos}}\varphi + k{{y}_{q}}{\text{sin}}\varphi } \right)} \right)d\left( {k{{l}_{q}}} \right),~ \\ \end{gathered} $(27)
$\begin{gathered} g_{B}^{1}\left( \varphi \right) = \frac{{ - i{{B}_{2}}}}{2}\mathop \smallint \limits_{k{{l}_{B}}}^{\infty ~} \frac{{\left( {n_{x}^{q}{\text{cos}}\varphi + n_{y}^{q}{\text{sin}}\varphi } \right)}}{{\sqrt {{{B}_{3}} + k{{l}_{q}}} }} \times \\ \times \,\,{\text{exp}}\left( {i\left( {{{B}_{0}} - k{{l}_{q}}} \right)} \right){\text{exp}}\left( {i\left( {k{{x}_{q}}{\text{cos}}\varphi + k{{y}_{q}}{\text{sin}}\varphi } \right)} \right)d\left( {k{{l}_{q}}} \right).~ \\ \end{gathered} $Используя обозначения (14), (16), проведем преобразования интегралов (26) и (27) и получим
(28)
$g_{A}^{1}\left( \varphi \right) = {{P}_{A}}\mathop \smallint \limits_{{{A}_{3}} - k{{l}_{A}}}^{ + \infty ~} \frac{1}{{\sqrt s }}{\text{exp}}\left( { - i\left( {1 - {{\alpha }_{A}}} \right)s} \right)d\left( s \right),~$Аналогично для грани B:
(29)
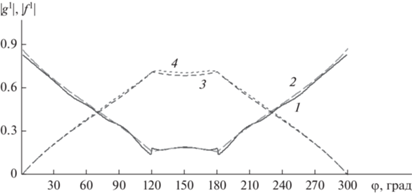
$\begin{gathered} g_{B}^{1}\left( \varphi \right) = {{P}_{B}}\mathop \smallint \limits_{{{B}_{3}} + k{{l}_{B}}}^{\infty ~} \frac{1}{{\sqrt s }}{\text{exp}}\left( { - i\left( {1 - {{\alpha }_{B}}} \right)s} \right)d\left( s \right),~ \\ {{\alpha }_{B}} = {\text{cos}}{{\varphi }_{B}}{\text{cos}}\varphi + {\text{sin}}{{\varphi }_{B}}{\text{sin}}\varphi = {\text{cos}}\left( {\varphi - {{\varphi }_{B}}} \right), \\ {{P}_{B}} = \frac{{i{{B}_{2}}}}{2}{\text{sin}}\left( {\varphi - {{\varphi }_{B}}} \right){\text{exp}}\left( {i\left( {{{B}_{0}} + \left( {1 - {{\alpha }_{B}}} \right){{B}_{3}}} \right.} \right. + \\ \left. {\left. { + \,\,k{{x}_{B}}{\text{cos}}\varphi + k{{y}_{B}}{\text{sin}}\varphi - {{\alpha }_{B}}k{{l}_{B}}} \right)} \right). \\ \end{gathered} $Результаты расчетов функции рассеяния g1 в виде суммы (25) приведены на рис. 8. Отметим, что расчеты проводились для варианта контура с буферной зоной равной 5λ.
Рис. 8.
Функции рассеяния на клине с внешним углом 300º, с учетом неравномерного тока на гранях A и B для Н- (1, 2) и Е-поляризации (3, 4), рассчитанные методом интегральных уравнений (1, 3) и с помощью аналитического решения Уфимцева (2, 4).
Как видим из сравнения графиков функций рассеяния, точность расчета существенно повысилась, однако ее можно еще улучшить. Для этого перепишем уравнение (7) в виде
(30)
${{J}_{\tau }}\left( {\vec {r}} \right) + \frac{1}{{2i}}M_{z}^{{AB}}\left( {{{J}_{\tau }},\vec {r}} \right) = - 2H_{z}^{i}\left( {\vec {r}} \right) - \frac{1}{{2i}}\left( {M_{z}^{A}\left( {J_{\tau }^{{{\text{фо}}}},\vec {r}} \right) + M_{z}^{B}\left( {J_{\tau }^{{{\text{фо}}}},\vec {r}} \right) + M_{z}^{A}\left( {J_{\tau }^{{\text{н}}},\vec {r}} \right) + M_{z}^{B}\left( {J_{\tau }^{{\text{н}}},\vec {r}} \right)} \right)~.~$В этом уравнении учтены неравномерные токи на гранях A и B, которые мы вычислили в виде экстраполяций (23), (24). Подставим выражение для неравномерного тока (23) в интеграл (5) и получим
Учитывая обозначения (14), интеграл можно привести к следующему виду:
(31)
$\begin{gathered} M_{z}^{A}\left( {J_{\tau }^{{\text{н}}},\vec {r}} \right) = - {{A}_{2}}k{{\eta }_{A}}{\text{exp}}\left( {i\left( {{{A}_{{0 + }}}k{{l}_{A}}} \right)} \right) \times \\ \times \,\,\mathop \smallint \limits_0^{\infty ~} \frac{{H_{1}^{2}\left( {kR} \right)}}{{kR\sqrt {{{A}_{3}} - k{{l}_{A}} + s} }}{\text{exp}}\left( { - is} \right)d\left( s \right). \\ \end{gathered} $Аналогично для неравномерного тока на грани B подставим выражение (24) в интеграл (6) и получим
Учитывая обозначения (16), интеграл можно привести к следующему виду:
(32)
$\begin{gathered} M_{z}^{B}\left( {J_{\tau }^{{\text{н}}},\vec {r}} \right) = {{B}_{2}}k{{\eta }_{B}}{\text{exp}}\left( {i\left( {{{B}_{0}} - k{{l}_{B}}} \right)} \right) \times \\ \times \,\,\mathop \smallint \limits_0^{\infty ~} \frac{{H_{1}^{2}\left( {kR} \right)}}{{kR\sqrt {{{B}_{3}} + k{{l}_{B}} + s} }}{\text{exp}}\left( { - is} \right)d\left( s \right). \\ \end{gathered} $Решение уравнения (30) является второй итерацией по поиску тока на контуре 2D‑неоднородности. При этом мы получим более точное значение тока на части контура LAB. Далее можно рассчитать новые коэффициенты для выражений неравномерного тока на гранях (23) и (24). На рис. 9 показаны новые результаты расчета тока на трех участках контура. В отличие от первого расчета (см. рис. 7) во втором расчете отсутствуют колебания амплитуды неравномерной части тока вблизи границ A и B. Кроме того, линии графика рассчитанного тока на пересекающихся участках AC и BD хорошо совпадают с экстраполяционными кривыми.
Рис. 9.
Экстраполяция неравномерной части тока на гранях, вторая итерация для неравномерного тока на участке LAB (1), экстраполяции (23) на грани A (с заходом на участок AC) (2) и экстраполяции (24) на грани B (3).
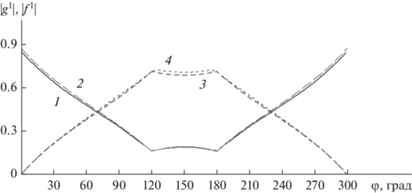
Новый расчет функций рассеяния g1 (21) и f 1 показан на рис. 10. В отличие от графиков на рис. 8 и, тем более, на рис. 4 можно наблюдать полное совпадение численных расчетов с аналитическим решением. Небольшие различия графиков связаны с наличием закругления кромки клина с радиусом 1% от длины волны.
Рис. 10.
Функции рассеяния на клине с внешним углом 300º, с учетом неравномерного тока на гранях, 2-я итерация для Н- (1, 2) и Е-поляризации (3, 4), рассчитанные методом интегральных уравнений (1, 3) и с помощью аналитического решения Уфимцева (2, 4).
При необходимости можно повторить решение уравнения (30), но уже с новыми найденными токами на гранях, и таким образом запустить итерационный процесс улучшения точности расчетов.
Выражения для расчета функций рассеяния для случая E‑поляризации получаются аналогично приведенным здесь выражениям для H‑поляризации. Только следует учесть, что в формулах экстраполяции неравномерного тока степень затухания равна 3/2, а не 1/2, как в выражениях (23), (24).
Полубесконечные интегралы (15), (17), (28), (29), (31), (32) для H‑поляризации и аналогичные для E‑поляризации имеют слабую степень затухания подынтегральных выражений. Для вычисления этих интегралов применяли метод замены контура интегрирования на комплексной плоскости. При этом подынтегральные выражения получали экспоненциальную кривую затухания, что позволило рассчитать интегралы численно.
На основании приведенных здесь сравнений с аналитическим решением можно сделать вывод, что применение итерационного процесса учета неравномерного тока на гранях существенно повышает точность расчета функций рассеяния f 1, g1. Следовательно, полный расчет рассеяния на 2D‑неоднородности в 3D‑пространстве также будет выполнен с высокой точностью.
3. ПРИМЕР: ВЫСТУП НА ИДЕАЛЬНО ПРОВОДЯЩЕЙ ПОВЕРХНОСТИ
Теперь рассмотрим, какое преимущество дает представленный метод расчета поправок к ФО в 3D‑пространстве. В качестве примера выбрана 2D‑неоднородность в виде выступа с квадратным сечением (см. рис. 1). Высота и ширина сечения неоднородности составили 2 мм. Форма линии расположения неоднородности на плоской идеально проводящей поверхности выбрана в виде эллипса (рис. 11). Главные радиусы эллипса составили 200 и 100 мм. Длина волны облучения, на которой проводились расчеты, равна 30 мм. Конкретные размеры плоскости, на которой располагается неоднородность, значения не имеют, так как рассчитываться будет только поправка, связанная с рассеянием на неоднородности, а само рассеяние на плоскости в данном примере нас не интересует. Предполагается выполнение единственного условия, связанного с плоской подложкой под неоднородность: то, что расстояние от любой части неоднородности до края плоскости должны быть много больше длины волны.
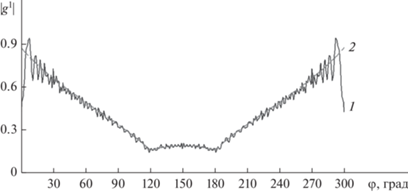
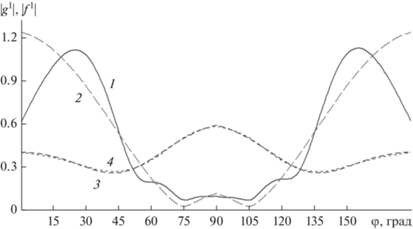
На рис. 12 приведены графики модуля комплексных функций рассеяния g1 и f 1 для неоднородности, показанной на рис. 1. Так как длина волны для эквивалентной задачи зависит от угла между направлением ребра, линии расположения и направлением волны облучения, то и графики функций g1 и f 1 будут зависеть от этого угла. На рис. 12 показаны графики функций g1 и f 1 для случая нормального падения волны на ребро линии неоднородности. Модуль функции g1 рассчитан без учета и с учетом неравномерных токов на гранях. Как видим из сравнения, графики существенно отличаются, особенно при скользящих падениях вдоль граней, углы вблизи 0° и 180°. Функция f 1 также рассчитана без учета и с учетом неравномерных токов на гранях. Как видно из сравнения, для случая E‑поляризации учет неравномерных токов на гранях несуществен. Однако следует заметить, что при пересчете рассеяния в 3D‑пространство обычно участвует комбинация функций g1 и f 1, поэтому учет неравномерных токов на гранях A и B имеет принципиальное значение.
Рис. 12.
Функции рассеяния на выступе для случая нормального падения волны на ребро линии неоднородности (1), модуль функции g1, рассчитанный с учетом неравномерных токов на гранях (2), функция f 1, рассчитанная без учета неравномерных токов на гранях (3) и с учетом этих токов (4).
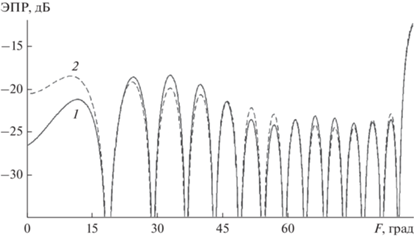
На рис. 13 приведены диаграммы ЭПР неоднородности, пересчитанные в 3D‑пространство, без включения ЭПР поверхности, на которой она расположена. Расчет диаграмм ЭПР проведен в плоскости, перпендикулярной к поверхности, на которой лежит неоднородность, и в то же время перпендикулярной к линии большого диаметра эллипса. Поляризация облучающей волны такова, что вектор магнитной компоненты поля компланарен плоскости, на которой лежит неоднородность. Угол 0° на графике соответствует скользящему облучению вдоль поверхности расположения неоднородности, а угол 90° соответствует нормальному падению на эту поверхность. ЭПР неоднородности рассчитана без учета неравномерных токов на гранях и с учетом неравномерных токов по методу, рассмотренному в данной статье. Значения ЭПР неоднородности вблизи угла облучения 90° не представляют особого интереса, так как в реальности будут теряться на фоне большой ЭПР от поверхности, на которой расположена неоднородность. В этом смысле значения ЭПР при скользящих углах представляют больший интерес. Именно с этих ракурсов проявляется максимальное отличие между ЭПР, рассчитанной без учета и с учетом неравномерных токов. Как видим, различие в случае отсутствия учета неравномерных токов на полубесконечных гранях в данном примере доходит до 6 дБ.
ЗАКЛЮЧЕНИЕ
В работе кратко описан комбинированный метод, являющийся дальнейшим развитием метода физической теории дифракции Уфимцева, позволяющий рассчитывать рассеяние электромагнитных волн на 2D‑неоднородностях с произвольной формой сечения. Приведены уравнения для расчета тока на модельном контуре неоднородности, а также выражения для расчета функций рассеяния Уфимцева f 1(φ0, φ), g1(φ0, φ).
Рассмотрена проблема низкой точности, возникающая при расчете рассеяния на полубесконечных объектах методом интегральных уравнений. Из приведенных выше примеров следует, что даже значительное увеличение ширины буферных зон до 50λ не устраняет эту проблему. Ситуация осложняется тем, что эквивалентная длина волны для задачи в 2D‑пространстве ${{{{\lambda }}}_{{2{\text{D}}}}} = {{{{{{\lambda }}}_{{3{\text{D}}}}}} \mathord{\left/ {\vphantom {{{{{{\lambda }}}_{{3{\text{D}}}}}} {{\text{sin}}\left( {{\gamma }} \right)}}} \right. \kern-0em} {{\text{sin}}\left( {{\gamma }} \right)}}$, что может достигать больших величин при скользящих падениях волны на линию расположения неоднородности в 3D‑пространстве. А это, в свою очередь, требует пропорционального увеличения ширины буферных зон. Кроме того, при расчете рассеяния на 2D‑неоднородности в реальном 3D‑пространстве необходимо решать двумерную эквивалентную задачу на каждом ребре линии неоднородности при каждом угле облучения. При этом для расчета одной диаграммы ЭПР необходимое количество решаемых численно двумерных задач может превышать 10 000 и более. Так как время расчета двумерной задачи зависит от ширины буферных зон, то уменьшение ширины этих зон имеет принципиальное значение.
Предложенный метод расчета рассеяния на 2D‑неоднородностях полностью снимает проблему низкой точности при ограниченной ширине буферных зон и имеет повышенную точность решения даже при ограниченном размере буферных зон, равных 5λ и менее.
Приведен пример расчета ЭПР на неоднородности, расположенной по линии эллипса с сечением в виде выступа. Показано, что различие в диаграммах ЭПР при учете неравномерных токов на бесконечных гранях по разработанному авторами методу и без учета неравномерных токов в данном примере доходит до 6 дБ, что свидетельствует о необходимости такого учета.
Список литературы
Уфимцев П.Я. Метод краевых волн в физической теории дифракции. М.: Сов. радио, 1962.
Ufimtsev P.Ya. Fundamental of the Physical Theory of Diffraction. Hoboken: John Wiley & Sons, Inc., 2007.
Gibson W.C. The Method of Moments in Electromagnetics. Boca Raton: Chapman & Hall/CRC, 2008.
Harrington R.F. Field Computation by Moment Methods. N.Y.: Macmillan Publ. Comp., 1968.
Morita N. // IEEE Trans. 1971. V. AP-19. № 3. P. 358.
Васильев Е.Н., Солодухов В.В. // Радиофизика. 1977. Т. 20. № 2. С. 280.
Васильев Е.Н., Федоренко А.И. // Радиофизика. 1983. Т. 26. № 3. С. 351.
Vasil’ev E.N., Solodukhov V.V. // Electromagnetics. 1991. V. 11. № 2. P. 161.
Jin J.M., Liepa V.V. // Electromagnetics. 1989. V. 9. № 2. P. 201.
Burnside W.D., Yu C.L., Marhefka R.J. // IEEE Trans. 1975. V. AP-23. № 7. P. 551.
Кисель В.Н., Федоренко А.И. // Радиотехника. 1994. № 11. С. 44.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника