Радиотехника и электроника, 2023, T. 68, № 2, стр. 177-187
Влияние спонтанного излучения на автоколебания в волоконных лазерах с микрооптомеханическими резонансными структурами
Ф. А. Егоров a, *, В. В. Никитин b, В. Т. Потапов a
a Фрязинский филиал Института радиотехники и электроники им. В.А. Котельникова РАН
141190 Фрязино, Московской обл., пл. Введенского, 1, Российская Федерация
b Московский государственный университет им. М.В. Ломоносова
119991 Москва, Ленинские горы, 1, стр. 2, Российская Федерация
* E-mail: egorov-fedor@mail.ru
Поступила в редакцию 12.07.2021
После доработки 04.11.2021
Принята к публикации 27.11.2021
- EDN: LCVYWK
- DOI: 10.31857/S0033849423020067
Аннотация
В рамках балансного приближения волоконных лазеров (ВЛ), рассматриваемых как распределенные системы, построена уточненная математическая модель, описывающая низкочастотную динамику ВЛ с зеркалами на основе оптомеханических микроосцилляторов (МО) с учетом влияния спонтанного излучения (СИ), локализованного в оболочечных модах активного световода (АС). Выявлены механизмы влияния СИ на режимы синхронных автоколебаний (СА) в лазерной системе ВЛ–МО: дополнительное снятие инверсии в АС благодаря конечной длине пробега фотонов СИ оболочечных мод в активной среде ВЛ; нарушение условия внутреннего резонанса в лазерной системе; возмущение колебаний МО фотоиндуцированной силой, обусловленной СИ. С помощью численного моделирования СА в эрбий-иттербиевом ВЛ с микроосциллятором и экспериментальных исследований установлена зависимость частоты СА от геометрооптических параметров АС и отражательной способности границы раздела АС–окружающая среда, которые могут быть использованы для повышения стабильности частоты лазерных импульсов в волоконных источниках импульсного излучения и создания нового класса резонансных волоконно-оптических датчиков.
ВВЕДЕНИЕ
Лазерное возбуждение упругих колебаний в микрооптомеханических резонансных структурах (микроосцилляторах) благодаря ряду механизмов (давление света, фототермический эффект, “градиентная” сила и др.) открывает возможности для реализации в лазерах с микроосцилляторами (МО) новых режимов генерации лазерного излучения с уникальными свойствами [1–5], что обусловливает актуальность исследований таких лазерных систем. Особый интерес вызывают режимы генерации в условиях внутренних резонансов – совпадения собственной частоты микроосциллятора $f$ с той или иной характерной частотой в лазере, что приводит к значительному повышению эффективности взаимодействия лазерного излучения с MO. С этой точки зрения большой интерес представляют волоконные лазеры (ВЛ), в которых благодаря возможностям вариации типов и параметров активных волоконных световодов (AС), а также конфигурации лазерного резонатора и характеристик MO могут быть реализованы лазерные системы ВЛ–MO с различными видами внутренних резонансов [6–8]. Отметим, что исследования других типов лазеров с MO в условиях внутренних резонансов были начаты лишь недавно [9–11].
В условиях резонанса вида $f = {{f}_{{{\text{рел\;}}}}}$ $({{f}_{{{\text{рел\;}}}}}$ – частота релаксационных колебаний в лазере) в ВЛ–MO возможны синхронные автоколебания (СА), представляющие собой одновременные колебания интенсивности лазерного излучения и микроосциллятора с единой (общей) частотой $F$, зависящей от собственной частоты MO [6, 7]:
Синхронные автоколебания характеризуются довольно высокой стабильностью частоты, $\left| {{{\Delta F} \mathord{\left/ {\vphantom {{\Delta F} F}} \right. \kern-0em} F}} \right|$ ≈ $ \approx 3 \times {{10}^{{ - 6}}}$ [6], что открывает возможности для создания волоконных источников лазерного излучения со стабильной частотой импульсов (аналог “кварцевой” стабилизации в радиотехнике) и разработки нового класса резонансных волоконно-оптических датчиков (ВОД) с частотным выходом [12, 13].
В работах [14, 15] в приближениях “точечной” и распределенной систем разработаны математические модели эрбий-иттербиевых волоконных лазеров (ЭИВЛ) с микрозеркалами на основе MO. Было показано, что в условиях резонанса $f = {{f}_{{{\text{рел\;}}}}}$ оба подхода приводят к существованию СА, при этом модель распределенной системы обеспечивает более точное описание свойств ЭИВЛ–MO. Следует отметить, что хотя качественную сторону СА эти модели отражают правильно, однако для ряда параметров СА, особенно частоты СА, которую можно измерить с высокой точностью, невозможно получить количественного согласия с экспериментом. Эти расхождения, на наш взгляд, связаны с чрезмерно грубым описанием влияния спонтанного излучения (СИ) – принципиально неустранимого фактора, играющего важную роль в ВЛ [16]. Помимо низкой точности расчетов параметров СА это приводит к искажениям границ зон существования СА, а также зависимостей их характеристик от внешних воздействий и параметров лазерной системы; к неправильным оценкам устойчивости режимов СА, которые имеют определяющее значение при разработке прецизионных устройств на основе ВЛ–MO.
Наряду с “обычным” взаимодействием спонтанного излучения с активной средой [17, 18], влияние СИ на динамику лазерных систем ВЛ–MO имеет ряд особенностей. В них важную роль могут играть такие специфические факторы, как нарушение точного резонанса $\left( {f = {{f}_{{{\text{рел\;}}}}}} \right)$ из-за зависимости ${{f}_{{{\text{рел\;}}}}}$ от интенсивности СИ [17]; влияние фотоиндуцированной силы, обусловленной спонтанным излучением, на характер движения МО, определяющего модуляцию параметров лазерного резонатора.
Кроме того, значительная часть спонтанного излучения в АС может распространяться в виде оболочечных мод (ОМ), характеристики которых зависят от граничных условий на поверхности раздела АС с окружающей средой (ОС). В результате, учитывая взаимодействие спонтанного излучения оболочечных мод СИ(ОМ) с активной сердцевиной, появляются возможности для управления состоянием АС и, как следствие, параметрами СА в ВЛ–MO за счет вариации оптических свойств границы раздела АС–ОС. Исследование указанных особенностей влияния СИ на динамику ВЛ–MO требует существенного усовершенствования имеющихся математических моделей рассматриваемых лазерных систем.
Цель данной работы – изложение базовых положений и подходов, на которых основано построение уточненных математических моделей (ММ), описывающих низкочастотную динамику лазерных систем ВЛ–MO с учетом комплексного влияния спонтанного излучения, включая вклад оболочечных мод АС. В ней получены новые результаты, которые позволяют расширить функциональные возможности и области применений ВЛ–MO.
1. МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА МОДЕЛИ ВЛ–MO, ИСХОДНЫЕ УСЛОВИЯ
Ввиду того, что релаксационные колебания особенно ярко проявляются в лазерах с инерционной активной средой [19] (лазеры класса В), в работе рассмотрены лазерные системы ВЛ–MO на основе активных световодов с редкоземельными элементами (${\text{Er}},{\text{Yb}},{\text{Nd}}$…) [20], в которых времена жизни метастабильного уровня достигают, ${{{{\tau }}}_{{\text{м}}}} = 0.3 \ldots 10\,\,{\text{\;}}{\kern 1pt} {\text{мс}}$. В силу распределенного характера как ВЛ, так и MO математическая модель ВЛ–MO может быть представлена системой дифференциальных уравнений в частных производных, описывающих лазерную подсистему, МО и оптическую связь между ними. В силу инерционности активной среды и сравнительно “низких” частот СА:
($T = {{2L} \mathord{\left/ {\vphantom {{2L} c}} \right. \kern-0em} c}$ – время обхода фотоном резонатора ВЛ с оптической длиной $L;$ $c$ – скорость света в вакууме; ${{\Omega }}$ – межмодовый интервал), лазерная подсистема может быть описана в приближении балансных уравнений [19, 21]. В силу их общего характера ММ для разных типов ВЛ–MO могут быть построены по единой схеме с учетом особенностей рабочих уровней в АС.
Фотоиндуцированные силы (${{\vec {F}}_{{\text{л}}}},{{\vec {F}}_{{{\text{СИ}}}}},{{\vec {F}}_{{\text{н}}}})$, возбуждающие упругие колебания в MO, обусловлены разными спектральными составляющими света, падающего на MO: линией лазерной генерации ${{{{\lambda }}}_{{\text{л}}}}$, спонтанным излучением ${{{{\lambda }}}_{{{\text{СИ}}}}}$, а также излучением накачки ${{{{\lambda }}}_{{\text{н}}}},$ прошедшим через АС (в силу неполного поглощения в АС). Модуляция параметров лазерного резонатора (добротности, собственных частот и др.), связанная с колебаниями MO, определяется из решения волнового уравнения для поля в резонаторе с учетом граничных условий на колеблющейся, деформирующейся отражающей поверхности МО [22].
Уточненную модель рассматриваемых лазерных систем целесообразно построить на примере ЭИВЛ–MO, что объясняется рядом причин (помимо наличия упрощенной модели). Во-первых, основная часть экспериментальных исследований ВЛ–MO выполнена именно с помощью систем данного типа, которые в качестве частных случаев охватывают также иттербиевые и эрбиевые ВЛ. Во-вторых, высокий КПД, большой ресурс работы ЭИВЛ, устойчивость к дестабилизирующим факторам [23], а также совпадение спектральных полос их накачки и генерации с окнами прозрачности типичных кварцевых волоконных световодов позволяют рассматривать в настоящее время именно ЭИВЛ–MO в качестве основы для создания прецизионных ВОД с прогнозируемыми характеристиками и волоконных источников высокостабильных лазерных импульсов. Отметим, что недавние разработки новых типов (${\text{Er}}:{\text{Yb}}$)АС [24] открывают перспективы создания миниатюрных ЭИВЛ–MO с улучшенными характеристиками, позволяющими расширить области их применений.
2. ЛАЗЕРНАЯ СИСТЕМА ЭИВЛ–MO, ОСНОВНЫЕ ДОПУЩЕНИЯ, ОГРАНИЧЕНИЯ
Схема лазерной системы ЭИВЛ–MO показана на рис. 1. В ней оптическая связь активной среды с MO осуществляется с помощью автоколлиматорной схемы на основе селфока – сегмента градиентного волокна с большим диаметром моды. В лазерном резонаторе роль микрозеркала – дефлектора ${{{\text{З}}}_{2}}$ играет колебательный элемент (КЭ) микроосциллятора в виде, например, прямоугольной микробалки (l × b × h) с консольным или двусторонним закреплением. Коллимированное излучение, падающее на КЭ, представляет собой гауссов пучок с малой расходимостью $({{{{\theta }}}_{0}} \ll {{10}^{{ - 2}}}\,~{\text{рад}}$) и диаметром $D \geqslant b \gg {{{{\lambda }}}_{{\text{л}}}}$. Схема АС и структура энергетических уровней в нем показаны на рис. 2. Предполагается, что одномодовая сердцевина АС легирована однородно ${\text{Er}},{\text{Yb}}$ с концентрациями ${{N}_{{{\text{Er}}}}}$,$~{{N}_{{{\text{Yb}}}}}$ (${{N}_{{{\text{Yb}}}}} = 0$ соответствует эрбиевому ВЛ, ${{N}_{{{\text{Er}}}}} = 0$ – иттербиевому), при этом оптическая накачка АС осуществляется либо в активную сердцевину с числовой апертурой и диаметром $\left( {N{{A}_{{\text{c}}}},{{d}_{{\text{c}}}}} \right)$, либо в его оптическую оболочку $\left( {N{{A}_{{\text{о}}}},{{d}_{{\text{о}}}}} \right)$. Длина АС, ${{L}_{{{\text{АС}}}}} \approx {{L}_{{{\text{н,c}}}}}\left( {{{L}_{{{\text{н,о}}}}}} \right),$ где ${{L}_{{{\text{н,c}}}}} = ~\min [{{(\sigma _{{{\text{нп}}}}^{*}{{N}_{{{\text{Yb}}}}})}^{{ - 1}}},{{({{\sigma }_{{{\text{нп}}}}}{{N}_{{{\text{Er}}}}})}^{{ - 1}}})]$ – длина поглощения излучения накачки в сердцевине АС (масштаб неоднородности инверсии [25]), $({{{{\sigma }}}_{{{\text{нп}}}}},~{{\sigma }}_{{{\text{нп}}}}^{*})$ – cечения поглощения $({\text{Er}}$,${\text{Yb}})$; ${{L}_{{{\text{н,о}}}}} = {{L}_{{{\text{н,c}}}}}{{\left( {{{{{d}_{{\text{о}}}}} \mathord{\left/ {\vphantom {{{{d}_{{\text{о}}}}} {{{d}_{{\text{c}}}}}}} \right. \kern-0em} {{{d}_{{\text{c}}}}}}} \right)}^{2}}$. Считаем, что спонтанные излучения (СИ1) и (СИ2), генерируемые в АС иттербием и эрбием, распространяются не только в виде мод сердцевины (1-лучи), но также в оптической оболочке в виде мод оболочки СИ(ОМ) (2-лучи). Резонатор ВЛ полагаем поляризационно изотропным, зеркала ${{{\text{З}}}_{{1,2}}}$ – антиотражающими на линии иттербия, ${{R}_{{1,2}}}({{{{\lambda }}}_{{{\text{Yb}}}}}) = 0$, что исключает лазерную генерацию на этой линии, ${{{{\lambda }}}_{{{\text{Yb}}}}} \approx 1.08\,~{\text{мкм}}$.
Рис. 1.
Схема эрбий-иттербиевого волоконного лазера с микроосциллятором (а): 1 – полупроводниковый лазер накачки $\left( {{{\lambda }_{{\text{н}}}} \approx 980\,\,~{\text{нм}}} \right)$; 2 – волоконно-оптический разветвитель; 3 – пассивный одно(много)модовый волоконный световод с числовой апертурой $N{{A}_{{\text{н}}}} \leqslant N{{A}_{{\text{c}}}}\left( {N{{A}_{{\text{о}}}}} \right)$; 4 – дихроичное зеркало ${{{\text{З}}}_{1}}$ с коэффициентом пропускания ${{\Pi }_{1}}$(${{\lambda }_{{\text{н}}}}$)$~ \approx 1$ и отражения ${{R}_{1}}$$({{\lambda }_{{\text{л}}}}) \approx 1$; 5 – эрбий-иттербиевый активный световод; 6 – селфок (длина 8 мм; диаметр моды $D \approx 300\,~{\text{мкм}});$ 7 – МО с колебательным элементом – микробалкой с размерами $l \times b \times h$; 8 – зеркало ${{{\text{З}}}_{2}}$ – отражающая поверхность микробалки; 9 – оптический фильтр; 10 – фотоприемник; (б) – спектральный состав излучения (качественный) в лазерном резонаторе, $\Delta {{\lambda }_{{\text{л}}}},\Delta {{\lambda }_{{{\text{СИ1}}}}},\Delta {{\lambda }_{{{\text{СИ2}}}}}$ – спектральные ширины лазерного и спонтанного излучений.
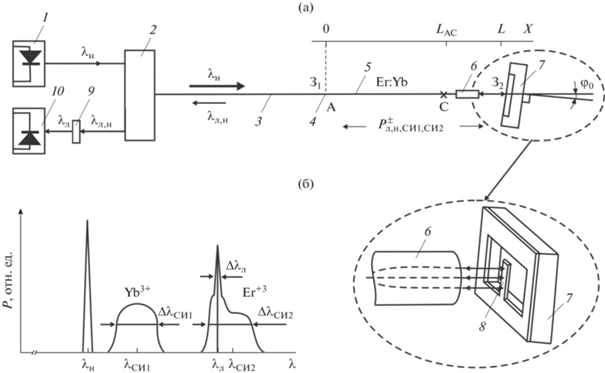
Рис. 2.
Схема фрагмента $AС$ (а): s–s – сечение АС, 1 – световедущая сердцевина; 2 – оптическая оболочка; 3 – окружающая среда (или защитное покрытие АС); ${{\alpha }}$ – угол между траекторией 2-луча и осью АС; угловая зависимость ${{R}_{0}}\left( {{\alpha }} \right)$ с характерными значениями углов: ${{\alpha }_{1}} = \arcsin \left( {{{N{{A}_{{\text{c}}}}} \mathord{\left/ {\vphantom {{N{{A}_{{\text{c}}}}} {{{n}_{{\text{c}}}}}}} \right. \kern-0em} {{{n}_{{\text{c}}}}}}} \right)$; ${{\alpha }_{2}} = \arcsin \left( {{{N{{A}_{{\text{о}}}}} \mathord{\left/ {\vphantom {{N{{A}_{{\text{о}}}}} {{{n}_{{\text{о}}}}}}} \right. \kern-0em} {{{n}_{{\text{о}}}}}}} \right);$ ${{\alpha }_{{\text{н}}}} = \arcsin \left( {{{N{{A}_{{\text{н}}}}} \mathord{\left/ {\vphantom {{N{{A}_{{\text{н}}}}} {{{n}_{{\text{о}}}}}}} \right. \kern-0em} {{{n}_{{\text{о}}}}}}} \right)$ (б); структура энергетических уровней в АС (с).
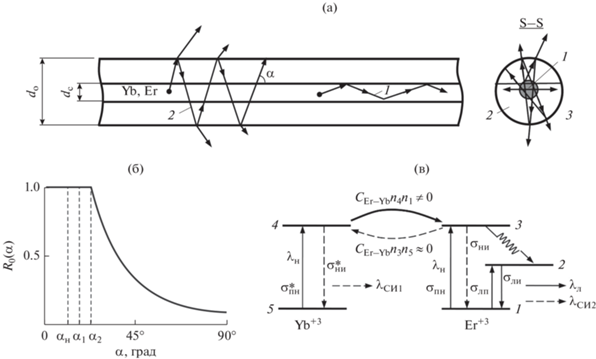
Так как в режимах СА пиковая интенсивность лазерных импульсов ${{I}_{{\text{л}}}}$ в оптоволоконных резонаторах ВЛ–MO значительно ниже порога нелинейности волоконных световодов, ${{\left( {{{I}_{{{\text{л\;}}}}}} \right)}_{{{\text{max}}}}} \ll {{I}_{{{\text{нел}}}}}$ [26], а их длительность равна ${{\tau }} > 10{\text{\;нс}}$ [6–8], то можно пренебречь как оптической нелинейностью, так и хроматической дисперсией в резонаторе. Кроме того, можно пренебречь пространственной решеткой инверсии в АС, которая в лазерах класса B приводит в основном к изменению тонкой структуры спектра релаксационных колебаний [27], что практически не проявляется на суммарной интенсивности генерируемых мод ${{I}_{{\text{л}}}}$.
Упругие колебания (волны) в MO $\vec {u}\left( {\vec {r},t} \right)$ приводят, в частности, к модуляции направления отраженного пучка и эффективного коэффициента отражения ${{{\text{З}}}_{2}}$:
где ${{R}_{2}}\left( {{\theta }} \right) = {{R}_{{20}}}\exp ({{ - {{{{\theta }}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{{\theta }}}^{2}}} {2{{\theta }}_{0}^{2}}}} \right. \kern-0em} {2{{\theta }}_{0}^{2}}})$ – угловая характеристика автоколлиматора в гауссовом приближении; ${{\theta }}\left( {\vec {r},t} \right)$ – угол между осью пучка, падающего на участок поверхности КЭ с координатой $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r} $ и нормалью к этому участку; ${{R}_{{20}}}$ – коэффициент отражения поверхности КЭ (см. рис. 1). Ввиду сложности процессов лазерного возбуждения упругих волн и колебаний в твердых телах [28] ограничимся рассмотрением простых, но при этом широко используемых типов кремниевых MO с КЭ в виде однородных микробалок, для которых характерны значительные интервалы между собственными частотами. Благодаря этому колебания МО могут быть описаны с помощью простых моделей – наборов осцилляторов, соответствующих возбуждаемым модам упругих колебаний [29]. Так, в случае осциллятора, описывающего основную моду поперечных колебаний КЭ $\left( {u\left( {z,t} \right)} \right),$ модуляция угла наклона центра облучаемого участка (с координатой ${{z}_{{\text{ц}}}}$) выражается в виде
где $\Delta {{\theta }}\left( {{{z}_{{\text{ц}}}},t} \right) = u_{z}^{'}\left( {{{z}_{{\text{ц}}}},t} \right) = {{\chi }}u\left( {{{z}_{{\text{ц}}}},t} \right)$ – приращение угла наклона из-за колебаний, ${{{{\varphi }}}_{0}}$ – исходный угол наклона MO. Полагая, что колебания возбуждаются за счет силы давления света и пренебрегая разницей углов падения и отражения света от движущегося КЭ, имеем
где ${{P}_{i}} = {{I}_{i}}{{S}_{i}}$ – поток фотонов с энергией ${{{{\varepsilon }}}_{i}},$ падающих на КЭ; ${{S}_{i}}$ – эффективная площадь основной моды АС, $i = {\text{л,СИ,н}}$.
Колебания MO
приводят к модуляции ряда характеристик нестационарного резонатора ВЛ (длины $\tilde {L}\left( t \right) = L + U\left( t \right);$ потерь $\Pi \left( t \right)$ (добротности); спектра частот и др.), что приводит к сложной структуре поля в нем. При малых и “низкочастотных” колебаниях МО, удовлетворяющих условиям
поле в резонаторе может быть описано с помощью “динамических” мод [22] с падающей на MO и отраженной волнами, имеющими разные частоты, сдвинутые на доплеровскую частоту $\Delta {{\nu }_{D}} = 2{{\nu }_{{\text{л}}}}{v \mathord{\left/ {\vphantom {v c}} \right. \kern-0em} c}$ ($v = {{dU} \mathord{\left/ {\vphantom {{dU} {dt}}} \right. \kern-0em} {dt}}$ – скорость КЭ, ${{{{\nu }}}_{{\text{л}}}} = {{{{{{\omega }}}_{{\text{л}}}}} \mathord{\left/ {\vphantom {{{{{{\omega }}}_{{\text{л}}}}} {2{{\pi }}}}} \right. \kern-0em} {2{{\pi }}}}$ – центральная частота световой волны).
Интерференция указанных волн приводит к колебаниям (биениям) интенсивности лазерного излучения и инверсии в АС на частоте $\Delta {{{{\nu }}}_{D}}$ [30]. При достаточно малых колебаниях $A \ll {{{{{{\lambda }}}_{{\text{л}}}}} \mathord{\left/ {\vphantom {{{{{{\lambda }}}_{{\text{л}}}}} {2{{\pi }}}}} \right. \kern-0em} {2{{\pi }}}}$ (типичных в эксперименте), максимальный сдвиг имеет вид
и, тем самым, в силу $\Delta {{{{\nu }}}_{D}} \ll {{f}_{{{\text{рел}}}}},$ исключается возможность резонансной раскачки биений в АС. Это позволяет пренебречь модуляцией на частоте $\Delta {{{{\nu }}}_{D}}$ как интенсивности излучения, так и инверсии в АС. Таким образом, колебания МО приводят в основном к модуляции ${{R}_{{{\text{2эф}}}}}\left( t \right)$ и потерям в резонаторе
где ${{\beta }}$ – распределенные “серые” потери в АС.
При этом в лазерной системе выполняется ряд соотношений:
где ширина линии генерируемых мод $~\Delta {{{{\nu }}}_{{{\text{л,м}}}}} \propto {{\Pi }^{2}}$ [19]. В этих условиях колебания MO приводят к синфазной модуляции потерь всех генерируемых мод, позволяющей описать лазерное излучение в рамках концепции “излучение как целое” [31]. Многократное отражение СИ от внешней поверхности АС (см. рис. 2), характеризующейся коэффициентом отражения ${{R}_{0}}\left( {{\alpha }} \right),$ приводит к взаимодействию СИ(ОМ) с активной сердцевиной, которое может быть описано в рамках концепции эффективной длины пробега (${{l}_{{{\text{c}}.j}}},j = {\text{Er}},{\text{Yb}})$ фотонов СИ в активной среде [32]. При этом вынужденные переходы активных центров (${\text{E}}{{{\text{r}}}^{{ + 3}}},{\text{Y}}{{{\text{b}}}^{{ + 3}}}$), вызванные СИ(ОМ), приводят к дополнительному “снятию” инверсии в АС, которое в приведенных ниже уравнениях (1)–(3) учтено с помощью членов вида $n\sigma {{l}_{{{\text{c}}.j~}}}$. Они получены в приближении малых длин пробегов фотонов СИ(ОМ) вдоль АС: ${{l}_{{\parallel j}}} \ll {{L}_{{{\text{н,c}}}}}\left( {{{L}_{{{\text{н,о}}}}}} \right),$ которое для типичных АС, как показано ниже, выполняется с достаточным запасом. В результате низкочастотная динамика ЭИВЛ–MO описывается системой дифференциальных уравнений:
(1)
$\begin{gathered} \frac{{\partial {{n}_{1}}}}{{\partial t}} = {{\Gamma }_{{\text{н}}}}\left[ {{{\sigma }_{{{\text{ни}}}}}~{{n}_{3}} - {{\sigma }_{{{\text{нп}}}}}~{{n}_{1}}} \right]\left( {P_{{\text{н}}}^{ + } + P_{{\text{н}}}^{ - }} \right) - \\ - \,\,{{\Gamma }_{{{\text{СИ1}}}}}\left[ {{{\sigma }_{{{\text{СИ1и}}}}}~{{n}_{1}} - {{\sigma }_{{{\text{СИ1п}}}}}~{{n}_{3}}} \right]\left( {P_{{{\text{СИ1}}}}^{ + } + P_{{{\text{СИ1}}}}^{ - }} \right) + \\ + \,\,{{\Gamma }_{{\text{л}}}}\left[ {{{\sigma }_{{{\text{ли}}}}}~{{n}_{2}} - {{\sigma }_{{{\text{лп}}}}}~{{n}_{1}}} \right]\left( {P_{{\text{л}}}^{ + } + P_{{\text{л}}}^{ - }} \right) + \\ + \,\,{{\Gamma }_{{{\text{СИ2}}}}}\left[ {{{\sigma }_{{{\text{СИ2и}}}}}~{{n}_{2}} - ~\,\,{{\sigma }_{{{\text{СИ2п}}}}}{{n}_{1}}} \right]\left( {P_{{{\text{СИ2}}}}^{ + } + P_{{{\text{СИ2}}}}^{ - }} \right) + \\ + \,\,\frac{{{{n}_{2}}}}{{{{\tau }_{{21}}}}}~ + ~{{\Gamma }_{{\text{л}}}}\left( {1 + {{\sigma }_{{{\text{СИ2п}}}}}~{{n}_{2}}~{{l}_{{{\text{c}}{\text{.Er}}}}}} \right) - {{C}_{{{\text{Er}} - {\text{Yb}}}}}{{n}_{1}}{{n}_{4}}, \\ \end{gathered} $(2)
$\begin{gathered} \frac{{\partial {{n}_{2}}}}{{\partial t}} = {{{{\Gamma }}}_{{\text{л}}}}\left[ {{{{{\sigma }}}_{{{\text{лп}}}}}~{{n}_{1}} - {{{{\sigma }}}_{{{\text{ли}}}}}~{{n}_{2}}} \right]\left( {P_{{\text{л}}}^{ + } + P_{{\text{л}}}^{ - }} \right) + \\ + \,\,{{{{\Gamma }}}_{{{\text{СИ2}}}}}\left[ {{{{{\sigma }}}_{{{\text{СИ}}2п}}}~{{n}_{1}} - {{{{\sigma }}}_{{{\text{СИ}}2{\text{и}}}}}~{{n}_{2}}} \right]\left( {P_{{{\text{СИ}}2}}^{ + } + P_{{{\text{СИ}}2}}^{ - }} \right) + \\ + \,\,\frac{{{{n}_{3}}}}{{{{{{\tau }}}_{{23}}}}}\frac{{{{n}_{2}}}}{{{{{{\tau }}}_{{21}}}}}~\left( {1 + ~{{{{\sigma }}}_{{{\text{СИ}}2{\text{и}}}}}{{n}_{2}}~{{l}_{{{\text{c}}.{\text{Er}}}}}} \right) + \frac{{{{n}_{2}}}}{{{{{{\tau }}}_{{32}}}}}, \\ \end{gathered} $(3)
$\begin{gathered} \frac{{\partial {{n}_{5}}}}{{\partial t}} = {{{{\Gamma }}}_{{\text{н}}}}\left[ {{{\sigma }}_{{{\text{ни}}}}^{*}~{{n}_{4}} - {{\sigma }}_{{{\text{нп}}}}^{*}~{{n}_{5}}} \right]\left( {P_{{\text{н}}}^{ + } + P_{{\text{н}}}^{ - }} \right) + \\ {\text{ + }}\,\,{{{{\Gamma }}}_{{{\text{СИ1}}}}}\left[ {{{\sigma }}_{{{\text{СИ1и}}}}^{*}~{{n}_{4}} - {{\sigma }}_{{{\text{СИ1п}}}}^{*}~{{n}_{5}}} \right]\left( {P_{{{\text{СИ}}1}}^{ + } + P_{{{\text{СИ}}1}}^{ - }} \right) + \\ + \,\,{{C}_{{{\text{Er}} - {\text{Yb}}}}}{{n}_{1}}{{n}_{4}} + \frac{{{{n}_{4}}}}{{{{{{\tau }}}_{{45}}}}}~\left( {1 + {{{{\sigma }}}_{{{\text{СИ1и}}}}}~{{n}_{4}}~{{l}_{{{\text{c}}.{\text{Yb}}}}}} \right), \\ \end{gathered} $(4)
${{n}_{1}} + {{n}_{2}} + {{n}_{3}} = {{N}_{{{\text{Er}}}}}\left( х \right);\,\,\,\,{{n}_{4}} + {{n}_{5}} = {{N}_{{{\text{Yb}}}}}\left( х \right),$(5)
$\begin{gathered} \pm ~\frac{{\partial P_{{\text{н}}}^{ \pm }}}{{\partial x}} + \frac{1}{{{{V}_{{\text{н}}}}}}\frac{{\partial P_{{\text{н}}}^{ \pm }}}{{\partial t}} = \\ = {{\Gamma }_{{\text{н}}}}\left[ {{{\sigma }_{{{\text{ни}}}}}~{{n}_{3}} + \sigma _{{{\text{ни}}}}^{*}~{{n}_{4}} - {{\sigma }_{{{\text{нп}}}}}~{{n}_{1}} - \sigma _{{{\text{нп}}}}^{*}~{{n}_{5}}} \right]~P_{{\text{н}}}^{ \pm } - {{\beta }_{{\text{н}}}}~P_{{\text{н}}}^{ \pm } \\ \end{gathered} $(6)
$\begin{gathered} \pm \frac{{\partial P_{{{\text{СИ1}}}}^{ \pm }}}{{\partial x}} + \frac{1}{{{{V}_{{{\text{СИ1}}}}}}}\frac{{\partial P_{{{\text{СИ1}}}}^{ \pm }}}{{\partial t}} = {{{{\Gamma }}}_{{{\text{СИ1}}}}} \times \\ \times \,\,\left[ {{{\sigma }_{{{\text{СИ1и}}}}}~{{n}_{3}} + \sigma _{{{\text{СИ1и}}}}^{*}~{{n}_{4}} - {{\sigma }_{{{\text{СИ1п}}}}}~{{n}_{1}} - \sigma _{{{\text{СИ1п}}}}^{*}~{{n}_{5}}} \right] \times \\ \times \,\,~P_{{{\text{СИ1}}}}^{ \pm } - {{{{\beta }}}_{{{\text{СИ1}}}}}P_{{{\text{СИ1}}}}^{ \pm } + {{{{\gamma }}}_{1}}\frac{{{{n}_{4}}}}{{{{{{\tau }}}_{{45}}}}}{{{{\Gamma }}}_{{{\text{СИ1}}}}}, \\ \end{gathered} $(7)
$\begin{gathered} \pm \frac{{\partial P_{{\text{л}}}^{ \pm }}}{{\partial x}} + \frac{1}{{{{V}_{{\text{л}}}}}}\frac{{\partial P_{{\text{л}}}^{ \pm }}}{{\partial t}} = \\ = {{\Gamma }_{{\text{л}}}}\left[ {{{\sigma }_{{{\text{ли}}}}}~{{n}_{2}} - {{\sigma }_{{{\text{лп}}}}}~{{n}_{1}}} \right]~P_{{\text{л}}}^{ \pm } - {{\beta }_{{\text{л}}}}~P_{{\text{л}}}^{ \pm } + {{\gamma }_{л}}{{\gamma }_{2}}\frac{{{{n}_{2}}}}{{{{\tau }_{{21}}}}}{{\Gamma }_{{\text{л}}}}, \\ \end{gathered} $(8)
$\begin{gathered} \pm \frac{{\partial P_{{{\text{СИ2}}}}^{ \pm }}}{{\partial x}} + \frac{1}{{{{V}_{{{\text{СИ2}}}}}}}\frac{{\partial P_{{{\text{СИ2}}}}^{ \pm }}}{{\partial t}} = \\ = {{\Gamma }_{{{\text{СИ2}}}}}\left[ {{{\sigma }_{{{\text{СИ2и}}}}}~{{n}_{2}} - {{\sigma }_{{{\text{СИ2п}}}}}~{{n}_{1}}} \right]~P_{{{\text{СИ2}}}}^{ \pm } - {{\beta }_{{{\text{СИ2}}}}}~P_{{{\text{СИ2}}}}^{ \pm } + \\ + \,\,\left( {1 - {{\gamma }_{{\text{л}}}}} \right){{\gamma }_{2}}\frac{{{{n}_{2}}}}{{{{\tau }_{{21}}}}}{{\Gamma }_{{{\text{СИ2}}}}}, \\ \end{gathered} $(9)
$\begin{gathered} \frac{{{{d}^{2}}U}}{{d{{t}^{2}}}} + \frac{{{\omega }}}{Q}\frac{{dU}}{{dt}} + {{{{\omega }}}^{2}}U = m_{{{\text{эф}}}}^{{ - 1}}~\mathop \sum \limits_i \left| {{{{\vec {F}}}_{i}}} \right| = \\ = \left[ {{{G}_{{\text{л}}}}} \right.~P_{{\text{л}}}^{ + }\left( {L,t} \right) + {{G}_{{\text{н}}}}~P_{{\text{н}}}^{ + }\left( {L,t} \right) + {{G}_{{{\text{СИ1}}}}}~P_{{{\text{СИ}}1}}^{ + }\left( {L,t} \right) + \\ + \,\,{{G}_{{{\text{СИ2}}}}}\left( {1 - {{{{\gamma }}}_{{\text{л}}}}} \right)~P_{{{\text{СИ}}2}}^{ + }(L,t)] \\ \end{gathered} $с граничными и начальными условиями (предполагая, что ${{L}_{{АС}}} = L)$:
(10)
$\begin{gathered} P_{{\text{н}}}^{ + }\left( {0,t} \right) = {{P}_{{{\text{н0}}}}}\left( t \right) + {{R}_{{{\text{1н}}}}}~P_{{\text{н}}}^{ - }\left( {0,t} \right), \\ P_{{\text{н}}}^{ - }\left( {L,t} \right) = {{R}_{{{\text{2н}}}}}\left( U \right)~P_{{\text{н}}}^{ + }\left( {L,t} \right), \\ \end{gathered} $(11)
$\begin{gathered} P_{{{\text{СИ1}}}}^{ + }\left( {0,t} \right) = {{R}_{{{\text{1СИ1}}}}}P_{{{\text{СИ1}}}}^{ - }\left( {0,t} \right), \\ P_{{{\text{СИ1}}}}^{ - }\left( {L,t} \right) = {{R}_{{{\text{2СИ1}}}}}\left( U \right)~P_{{{\text{СИ1}}}}^{ + }\left( {L,t} \right), \\ \end{gathered} $(12)
$\begin{gathered} P_{{\text{л}}}^{ + }\left( {0,t} \right) = {{R}_{{{\text{1л}}}}}P_{{\text{л}}}^{ - }\left( {0,t} \right), \\ P_{{\text{л}}}^{ - }\left( {L,t} \right) = {{R}_{{{\text{2л}}}}}\left( U \right)~P_{{\text{л}}}^{ + }\left( {L,t} \right), \\ \end{gathered} $(13)
$\begin{gathered} P_{{{\text{СИ2}}}}^{ + }\left( {0,t} \right) = {{R}_{{{\text{1СИ2}}}}}P_{{{\text{СИ2}}}}^{ - }\left( {0,t} \right), \\ P_{{{\text{СИ2}}}}^{ - }\left( {L,t} \right) = {{R}_{{{\text{2л}}}}}\left( U \right)~P_{{{\text{СИ2}}}}^{ + }\left( {L,t} \right), \\ \end{gathered} $где
(14)
$\begin{gathered} {{R}_{{{\text{2,н,л,СИ1}}}}}\left( U \right) = {{R}_{{{\text{20,н,л,СИ1}}}}}~\exp \left[ { - \frac{{{{{\left( {{{\varphi }_{0}} + \chi ~U} \right)}}^{2}}}}{{\theta _{0}^{2}}}} \right], \\ {{n}_{1}}\left( {x,0} \right) = {{N}_{{{\text{Er}}}}};\,\,\,\,{{n}_{2}}\left( {x,0} \right) = {{n}_{3}}\left( {x,0} \right) = \\ = {{n}_{4}}\left( {x,0} \right) = 0;\,\,\,\,{{n}_{5}}\left( {x,0} \right) = {{N}_{{{\text{Yb}}}}}, \\ \end{gathered} $(15)
$\begin{gathered} P_{{\text{н}}}^{ \pm }\left( {x,0} \right) = P_{{\text{л}}}^{ \pm }\left( {x,0} \right) = P_{{{\text{СИ1,2}}}}^{ \pm }\left( {x,0} \right) = 0; \\ U\left( 0 \right) = 0;\,\,\,\,\frac{{dU}}{{dt}}\left( 0 \right) = 0, \\ \end{gathered} $(16)
${{P}_{{н0}}}\left( t \right) = \left\{ \begin{gathered} ~0,~\,\,\,\,t \leqslant 0 \hfill \\ {{P}_{0}}\left( {1 - \exp \left( { - \frac{t}{{{{t}_{0}}}}} \right)} \right),~\,\,\,\,t > 0 \hfill \\ \end{gathered} \right..$Уравнения (1)–(4) описывают кинетику инверсии в АС, (5)–(8) – пространственно-временные распределения лазерного $P_{{\text{л}}}^{ \pm }~$ и спонтанного излучения $P_{{{\text{СИ1,2}}}}^{ \pm }$, а также накачки $P_{{\text{н}}}^{ \pm }$, распространяющихся в положительном (+) и отрицательном (–) направлениях оси 0х; (9) – колебания MO $U$; выражение (16) описывает плавное “включение” мощности накачки до постоянного уровня ${{P}_{0}}$ (${{t}_{0}} \gtrsim {{\tau }_{{\text{м}}}}$). Указанные выше механизмы влияния СИ учтены в уравнениях (1)–(9), в которых ${{\beta }_{i}}$ – распределенные нерезонансные (серые) потери в лазерном резонаторе для разных компонент спектра, $i = {\text{н}},{\text{л}},{\text{СИ}}1,{\text{СИ}}2$; ${{\Gamma }_{i}}$ – фактор перекрытия моды излучения с сердцевиной АС; ${{\gamma }_{1}},{{\gamma }_{2}}$ – факторы спонтанных излучений СИ1, СИ2 в моду сердцевины АС; ${{\gamma }_{{\text{л}}}} = {{\Delta {{\lambda }_{{\text{л}}}}} \mathord{\left/ {\vphantom {{\Delta {{\lambda }_{{\text{л}}}}} {\Delta {{\lambda }_{{{\text{СИ2}}}}}}}} \right. \kern-0em} {\Delta {{\lambda }_{{{\text{СИ2}}}}}}} \ll 1;$ ${{V}_{i}}$ – групповая скорость излучения; ${{R}_{{1,2i}}}$ – коэффициенты отражения зеркал З1,2; ${{G}_{i}}$ – эффективность возбуждения колебаний; ${{\sigma }_{{{\text{нп}}}}},$ ${{\sigma }_{{{\text{лп}}}}},~{{\sigma }_{{{\text{СИ1п}}}}},$ ${{\sigma }_{{{\text{СИ2п}}}}}$ (${{\sigma }_{{{\text{ни}}}}},{{\sigma }_{{{\text{ли}}}}},{{\sigma }_{{{\text{СИ1и}}}}},$ ${{\sigma }_{{{\text{СИ2и}}}}}$) – сечения поглощения (излучения) ионов ${\text{E}}{{{\text{r}}}^{{ + 3}}}$; $\sigma _{{{\text{нп}}}}^{*},~~\sigma _{{{\text{СИ1п}}}}^{*}(\sigma _{{{\text{ни}}}}^{*},~~\sigma _{{{\text{СИ1и}}}}^{*})$ – ${\text{Y}}{{{\text{b}}}^{{ + 3}}}$ [15]; $U\left( t \right)$ – смещение КЭ; ${{m}_{{{\text{эф}}}}},Q$ – эффективная масса и механическая добротность КЭ; $N{{A}_{{\text{c}}}} = {{(n_{{\text{с}}}^{2} - n_{{\text{о}}}^{2})}^{{1/2}}},$ $N{{A}_{{\text{о}}}} = {{\left( {n_{{\text{о}}}^{2} - n_{{{\text{ОС}}}}^{2}} \right)}^{{1/2}}},$ ${{n}_{{\text{c}}}},{{n}_{{\text{о}}}},{{n}_{{{\text{ОС}}}}}$ – показатели преломления сердцевины АС, оптической оболочки и окружающей среды. Полагаем, что
При определенной коррекции уравнения (9) и граничных условий уравнения (1)–(16) могут описывать также ЭИВЛ с внутрирезонаторными оптоволоконными МО [12], которые в лазерном резонаторе играют роль элементов с распределенными потерями, зависящими от упругих колебаний в МО. В случае короткого (по сравнению с длиной резонатора) оптоволоконного МО с отражающим торцом $\left( {{{R}_{{20}}} \approx 1} \right)$ такой элемент может рассматриваться как составное зеркало с эффективным модулированным коэфициентом отражения
где $T\left( {U\left( t \right)} \right)$ – коэффициент пропускания волноводного МО, зависящий от упругих (например, изгибных) колебаний в нем $U\left( t \right)$, возбуждаемых лазерным излучением.
3. ВЛИЯНИЕ СПОНТАННОГО ИЗЛУЧЕНИЯ
Интенсивности спонтанных излучений в сердцевине (${{I}_{{{\text{СИ1,2}}}}})$ существенно зависят от факторов ${{\gamma }_{{1,2}}}$ спонтанных излучений в моду сердцевины $~$– относительных телесных углов канализации АС, при этом в силу слабой дисперсии АС предполагается, что ${{\gamma }_{1}} = {{\gamma }_{2}} = {{N{{A}_{c}}^{2}} \mathord{\left/ {\vphantom {{N{{A}_{c}}^{2}} 2}} \right. \kern-0em} 2}.$ Из уравнений (1)–(3) видно, что влияние СИ(ОМ) можно трактовать как уменьшение эффективного спонтанного времени жизни метастабильного уровня: $\tau _{{\text{м}}}^{*} \approx {{\tau }_{{\text{м}}}}{{(1 + n\sigma {{l}_{{c.j~}}})}^{{ - 1}}}$, ${{\tau }_{{\text{м}}}} = {{\tau }_{{21}}},~{{\tau }_{{45}}}$, которое с учетом зависимости ${{f}_{{{\text{рел}}}}}~(\tau _{{\text{м}}}^{*})$ [17] приводит к нарушению точного резонанса ($f = {{f}_{{{\text{рел}}}}}$) и, тем самым, к зависимости характеристик СА от факторов, определяющих ${{l}_{{{\text{c}}.j~}}}$. При сильном френелевском отражении, ${{R}_{0}}\left( {{\alpha }} \right) \approx 1$, в оболочке АС аккумулируется интенсивное СИ(ОМ), которое в результате многократных отражений от поверхности АС и “фокусировки” в его сердцевину приводит к заметному снятию инверсии, $\tau _{{\text{м}}}^{*} < {{\tau }_{{\text{м}}}}$. При ${{R}_{0}} = 0$, а также сильном поглощении оболочечных мод имеем ${{l}_{{{\text{c}}.{\text{Er}},{\text{Yb}}~}}} = 0$ и, следовательно, $\tau _{{\text{м}}}^{*} = {{\tau }_{{\text{м}}}}$.
4. ОЦЕНКИ ВЛИЯНИЯ ОБОЛОЧЕЧНЫХ МОД
В силу ${{d}_{{\text{о}}}} \gg {{d}_{{\text{c}}}} > {{\lambda }_{{\text{л}}}}$ СИ(ОМ) можно описать в лучевом приближении, полагая, что 2-лучи являются меридиональными (см. рис. 2). Эффективный коэффициент отражения и число отражений 2-лучей с учетом потерь между последовательными отражениями (${{K}_{j}}\left( \alpha \right) \ll 1)$, которые включают потери на отражение на границе сердцевина–оптическая оболочка, составляют:
В предположении изотропного испускания СИ и значительного отражения света на указанной границе $\left( {{{R}_{0}}\left( \alpha \right) \simeq 1} \right)$ средние длины путей, пробегаемых 2-лучами в активной сердцевине и перемещения их вдоль АС, составляют, соответственно
где усреднение по углу производится в пределах: ${{\alpha }_{1}} \leqslant \left| \alpha \right| \leqslant {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2};$ $E\left( {{\text{cos}}\left( {{\alpha }} \right)} \right)$ – эллиптический интеграл второго рода$.$ Для ЭИВЛ–MO со значениями параметров, приведенными в табл. 1, получены оценки: ${{l}_{{\parallel .j}}} \leqslant 0.1\,~{\text{м}},$ ${{L}_{{{\text{н,о}}}}} \approx 0.9~\,{\text{м}},$ которые подтверждают корректность предположения ${{l}_{{\parallel .j}}} \ll {{L}_{{{\text{н,о}}}}}.$ Установлено также, что влияние ${{l}_{{{\text{c}}.{\text{Er}}}}}$ на частоту СА значительно сильнее влияния ${{l}_{{{\text{c}}.{\text{\;Yb}}}}}$, что позволяет пренебречь вкладом последнего и полагать
Таблица 1.
Значения основных параметров ЭИВЛ–МО
| Постоянные величины | Значение | Варьируемые параметры | Значение | Варьируемые параметры | Значение |
|---|---|---|---|---|---|
| σнп, σни , σСИ1п, σСИ1и, м2 | $2 \times {{10}^{{ - 25}}}$ | ${{N}_{{{\text{Er}}}}},{\text{\;}}{{{\text{м}}}^{{ - 3}}}$ | $1 \times {{10}^{{25}}}$ | ${{\beta }_{{\text{л}}}}$ , м–1 | 0.05 |
| $\sigma _{{{\text{нп}}}}^{*},\sigma _{{{\text{ни}}}}^{*},$ м2 | $2 \times {{10}^{{ - 24}}}$ | ${{N}_{{{\text{Yb}}}}},{\text{\;}}{{{\text{м}}}^{{ - 3}}}$ | $1 \times {{10}^{{26}}}$ | ${{\beta }_{{\text{н}}}}$ , м–1 | 0.05 |
| σСИ2п, σлп, м2 | $4 \times {{10}^{{ - 25}}}$ | ${{L}_{{{\text{АС}}}}},{\text{м}}$ | $2$ | $f,~~$ Гц | $2 \times {{10}^{5}}$ |
| σСИ2и, σли, м2 | $6 \times {{10}^{{ - 25}}}$ | ${{\theta }_{0}},~{\text{рад}}$ | $2 \times {{10}^{{ - 3}}}$ | $Q$ | ${{10}^{2}}$ |
| ${{V}_{{\text{л}}}},$ м/с | $2.05 \times {{10}^{8}}$ | ${{\Gamma }_{{\text{н}}}}$ | $6 \times {{10}^{{ - 3}}}$ | ${{R}_{{{\text{1л}}}}}$ | 0.9 |
| ${{\tau }_{{21}}},~\,\,{\text{с}}$ | ${{10}^{{ - 2}}}$ | ${{\Gamma }_{{\text{л}}}}$ | 0.95 | ${{R}_{{{\text{1н}}}}}$ | 0 |
| ${{\tau }_{{32}}},\,{\text{с}}$ | $3 \times {{10}^{{ - 6}}}$ | ${{d}_{{\text{c}}}}$, мкм | 8 | ${{R}_{{{\text{20н}}}}}$ | 0 |
| ${{\tau }_{{45}}},~\,{\text{с}}$ | $1.5 \times {{10}^{{ - 3}}}$ | ${{d}_{{\text{о}}}}$, мкм | 110 | ${{R}_{{{\text{20л}}}}}$ | 0.8 |
| СEr-Yb , м3/с | $7 \times {{10}^{{ - 23}}}$ | N${{A}_{{\text{c}}}}$ | 0.16 | ${{m}_{{{\text{эф}}}}}$, кг | $2 \times {{10}^{{ - 9}}}$ |
| ${{n}_{{\text{c}}}}$ | 1.46 | N${{A}_{{\text{о}}}}$ | 0.36 | $D$, мкм | $3 \times {{10}^{2}}$ |
| ${{\lambda }_{{\text{н}}}};{{\lambda }_{{\text{л}}}},~\,{\text{мкм}}$ | 0.98; 1.55 | $N{{A}_{{{\text{н\;}}}}}$ | $0.14$ | ${{\gamma }_{{\text{л}}}}$ | $4 \times {{10}^{{ - 3}}}$ |
| ${{\varepsilon }_{{{\text{н\;}}}}};{{\varepsilon }_{{{\text{л\;}}}}}{\text{,\;Дж}}$ | $~~2 \times {{10}^{{ - 19}}};$ $1.3 \times {{10}^{{ - 19}}}$ | ${{\varphi }_{0}}$, рад | $ - 2.5 \times {{10}^{{ - 3}}}$ | ${{\chi }}$, рад/м | ${{10}^{3}}$ |
При численном моделировании СА спектральный диапазон СИ $\left( {\Delta {{\lambda }_{{{\text{СИ2}}}}}} \right)$ разделен на две части (в соответствии с подходом, использованным в [33]):
1) узкую область с шириной огибающей генерируемых мод $\left( {\Delta {{\lambda }_{{\text{л}}}}} \right)$,
2) остальную часть с центральной длиной волны ${{\lambda }_{{{\text{СИ2}}}}}$ и шириной $\Delta {{\lambda }_{{{\text{СИ2}}}}} - \Delta {{\lambda }_{{\text{л}}}}$.
На рис. 3 представлены типичные временные зависимости и фурье-спектр сигналов $P_{{\text{л}}}^{ + }\left( {L,t} \right),$ $U\left( t \right)$, полученные путем численного решения системы уравнений (1)–(16) с использованием методов [14] и значений параметров, приведенных в табл. 1.
Рис. 3.
Зависимости от времени мощности лазерного излучения $P_{{\text{л}}}^{ + }\left( {L,t} \right)$ и колебаний микроосциллятора $U\left( t \right)$ на этапе возбуждения СА $~\left( {\Delta {{t}_{{{\text{возб}}}}}} \right)~$ и установившихся автоколебаний ($\Delta {{t}_{{{\text{уст}}}}})$, при значениях ($\gamma ;k) = (5.1 \times {{10}^{{ - 5}}}$; 0.3) (а); фурье-спектр мощности излучения $P_{{{\text{л}},\nu }}^{ + }~\left( {L,t} \right)$ в условиях установившихся СА (б).
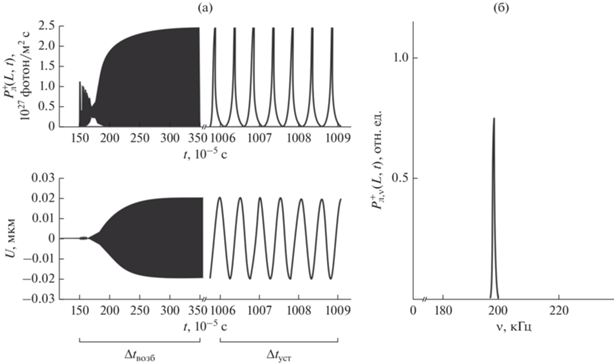
На рис. 4 приведены рассчитанные зависимости частоты СА от параметров $(k;\gamma ) = ({{l}_{{{\text{c}}{\text{.Er}}}}}{{N}_{{{\text{Er}}}}}{{\sigma }_{{{\text{СИ2и}}}}};$ ${{\gamma }_{{\text{л}}}}{{\gamma }_{2}}),$ из которых видно, что влияние СИ(ОМ) приводит к сдвигу частоты $\Delta F\left( {k,\gamma } \right)$, заметно превышающему типичный уровень флуктуаций в эксперименте:
Рис. 4.
Рассчитанные зависимости частоты СА от параметров γ (а) и $k$ (б) в логарифмическом масштабе; размер вертикальных черточек отражает влияние разброса $( \simeq $10%) параметров (${{N}_{{{\text{Er}},{\text{Yb}}}}},~{{{{\tau }}}_{{21}}}),$ связанного с эффектом кластеризации активных частиц в АС.
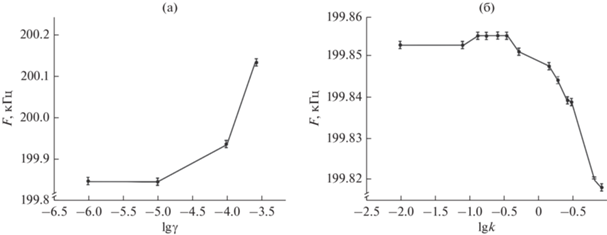
Функции $\Delta F\left( {{{l}_{{{\text{c}}{\text{.Er}}}}}} \right),$ $\Delta F\left( \gamma \right)$ имеют “пороговый” характер – резко возрастают при ${{l}_{{{\text{c}}.{\text{Er}}}}} > {{l}_{п}}$; $\gamma > ~\,{{\gamma }_{{\text{п}}}}$, где “пороговые” значения (${{l}_{{\text{п}}}}$,$~{{\gamma }_{{\text{п}}}}) = \left( {3\,\,~{\text{мм}};\,\,{{{10}}^{{ - 4}}}} \right)$. Эту особенность следует учитывать при разработке высокостабильных ЭИВЛ–MO, так как зависимость величин ${{l}_{{{\text{c}}.{\text{Er}}}}},\gamma $ от ряда параметров $({{R}_{0}},{{d}_{{\text{c}}}},{{d}_{{\text{о}}}},N{{A}_{{\text{л}}}})$ приводит, в силу условий
к дополнительным ограничениям на значения указанных параметров АС. На графиках размер вертикальных черточек отражает влияние разброса $( \simeq $10%) параметров ($\Delta {{N}_{{{\text{Er,Yb}}}}},~\Delta {{\tau }_{{21}}}),$ связанного с эффектом кластеризации активных частиц в АС.
На рис. 5 приведены результаты экспериментальных исследований влияния СИ(ОМ) на частоту СА в эрбиевом ВЛ (ЭВЛ, $~{{N}_{{{\text{Yb}}}}} = 0)$ с микрозеркалом ${{{\text{З}}}_{2}}$ в виде кремниевой микробалки с резонансной частотой $f \approx 68.7{\text{\;кГц}}$ и добротностью $Q \approx 65$. В ЭВЛ использовано специальное эрбиевое кварцевое активное одномодовое волокно $\left( {{\text{Er}}} \right)$АС с оголенной оптической оболочкой (без полимерного покрытия), накачка которого производилась в сердцевину. Оголенный участок расположен в кювете, которая могла заполняться той или иной жидкостью с известными оптическими свойствами, что позволяло варьировать в широких пределах френелевское отражение на границе АС–жидкость. Частоты СА измерены при разных условиях (время усреднения частоты $10\,~{\text{с}}$): 1 – пустая кювета – (${\text{Er}})$АС в воздухе, при этом часть лучей СИ(ОМ) испытывает полное внутреннее отражение; 2 – АС в ртути; 3 – $АС$ в глицерине; 4 – $АС$ в черной туши, сильно рассеивающей и поглощающей свет. Экспериментальные данные четко показывают, что заполнение кюветы ртутью, обеспечивающей высокий коэффициент отражения при всех углах $({{R}_{0}}\left( {{\alpha }} \right) \geqslant 0.85)$, приводит к сдвигу частоты СА (относительно значения на воздухе): ${{({{\Delta F} \mathord{\left/ {\vphantom {{\Delta F} F}} \right. \kern-0em} F})}_{{{\text{рт}}}}} \approx - ~6 \times {{10}^{{ - 5}}}$, который заметно превышает уровень флуктуаций $\left| {{{{\left. {{{\Delta F} \mathord{\left/ {\vphantom {{\Delta F} F}} \right. \kern-0em} F}} \right|}}_{{{\text{фл}}}}}} \right. \approx 3 \times {{10}^{{ - 6}}}$. Погружение $\left( {{\text{Er}}} \right)АС$ в глицерин – иммерсионную жидкость или же в черную тушь, ослабляющих отражение $({{R}_{0}} \approx 0),$ приводят лишь к небольшому росту частоты: $\left| {{{{\left. {{{\Delta F} \mathord{\left/ {\vphantom {{\Delta F} F}} \right. \kern-0em} F}} \right|}}_{{{\text{тушь}}}}} \approx + 1 \times {{{10}}^{{ - 5}}}} \right.$, сравнимому с уровнем флуктуаций.
Рис. 5.
Зависимость частоты СА в лазерной системе ЭВЛ–МО от отражательной способности границы раздела оптическая оболочка $\left( {{\text{Er}}} \right)АС$–окружающая среда (а): 1 – воздух; 2 – ртуть; 3 – глицерин; 4 – тушь (черная); б – схема кюветы (1) с активным световодом $\left( {{\text{Er}}} \right)АС$ (2) и с узлом крепления (3) активного световода.
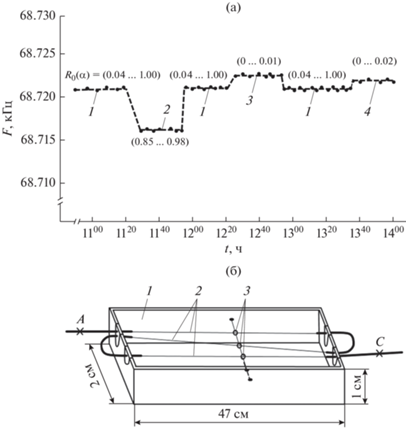
Поскольку ${{l}_{{{\text{c}}.{\text{Er}}}}} \propto {{\left( {1 - {{R}_{0}}} \right)}^{{ - 1}}},$ то можно сделать вывод о сходстве расчетных и экспериментальных зависимостей (см. рис. 4, 5) частоты СА от отражательной способности границы раздела АС–ОС: увеличение отражения приводит к уменьшению частоты СА. Отметим, что возможность и целесообразность сравнения указанных зависимостей, относящихся к разным лазерным системам, основана на том, что в обеих системах ключевым рабочим компонентом АС является один и тот же элемент – эрбий, спонтанное излучение которого в рассматриваемых явлениях играет определяющую роль. Отметим также, что детальное исследование влияния СИ(ОМ) в ВЛ–MO (с количественным сравнением расчетных и экспериментальных данных для одной и той же системы) является достаточно сложной, самостоятельной задачей, которая включает, в частности: определение точных профилей распределений показателя преломления в АС; концентраций активных частиц; степени их “кластеризации”. Важно учитывать также ряд факторов случайного характера: эксцентричность сердцевины и некруглость АС; неоднородность и анизотропию оптической оболочки; наличие на ее поверхности переходных слоев [34], влияющих на отражательную способность и “фокусировку” излучения в сердцевину АС, которая имеет весьма малый размер, ${{d}_{{\text{c}}}} \approx ~$ 4…8 мкм. В исследованных лазерных системах эти параметры и факторы известны с недостаточной точностью. Однако обнаруженный эффект – зависимость частоты СА от оптических свойств границы раздела АС–ОС, указывает на важную роль спонтанного излучения, сосредоточенного в ОМ, что открывает новые возможности для управления параметрами лазерного излучения, генерируемого в ВЛ–MO и разработки новых типов резонансных ВОД параметров окружающей среды, связанных с ее оптическими свойствами.
ЗАКЛЮЧЕНИЕ
Изложены и обоснованы базовые положения, допущения, лежащие в основе предложенной уточненной математической модели, описывающей низкочастотную динамику ВЛ с микроосцилляторами с учетом комплексного влияния спонтанного излучения. Особое внимание уделено спонтанному излучению, сосредоточенному в оболочечных модах активного волокна, влияние которого описано в рамках концепции эффективной длины пробега фотонов СИ(ОМ), рассчитанной в лучевом приближении. Эффект зависимости частоты СА в ВЛ–MO от отражательной способности внешней поверхности АС подтвержден экспериментально. Предложенная модель применима также для описания полностью волоконных ВЛ–MO с внутрирезонаторными волноводными (оптоволоконными) MO, которые весьма технологичны с точки зрения как их изготовления, так и включения в существующие волоконно-оптические схемы, что способствует расширению областей их применения. Отметим важность дальнейшего развития моделей ВЛ–MO с учетом влияния шумов и внешних возмущений, что позволяет исследовать флуктуации в ВЛ–MO и оценить предельно достижимые параметры СА, определяющие, в частности, точностные характеристики ВОД.
Авторы заявляют об отсутствии конфликта интересов.
Список литературы
Aspelmeyer M., Kippenberg T.J., Marquardt F. Cavity Optomechanics, Nano- and Micromechanical Resonators Interacting with Light. Heidelberg: Springer, 2014.
Гуляев Ю.В., Бугаев А.С., Быстров Р.П., Никитов С.А., Черепенин В.А. Микро- и наноэлектроника в системах радиолокации. М.: Радиотехника, 2013.
Bowen W.P., Milburn G.J. Quantum Optomechanics. Boca Raton: CRC Press, 2016.
Yang W., Gerke S.A., Ng K.W. et al. // Sci. Rep. 2015. V. 5. P. 13700. https://doi.org/10.1038/srep13700
Fabert M., Desfarges-Berthelmot A., Kermene V. et al. // Opt. Express. 2012. V. 20. № 20. P. 22895.
Егоров Ф.А., Потапов В.Т. // Квантов. электрон. 2012. Т. 42. № 9. С. 808.
Егоров Ф.А., Потапов В.Т., Мелькумов М.А. и др. // Письма в ЖТФ. 2014. Т. 40. № 8. С. 30.
Егоров Ф.А., Потапов В.Т. // Квантов. электрон. 2020. Т. 42. № 9. С. 808.
Princepe D., Wiederhecker G.S., Favero I. et al. // IEEE Photonics J. 2018. V. 10. № 3. P. 4500610.
Foley J.M., Ganesan A.V., Lawall J.R. et al. // Technical Dig. Conf. “Frontiers in Optics” Washington. 10–16 Oct. 2018. Washington: Opt. Soc. Amer, 2018. paper LW6F.1. https://doi.org/10.1364/LS.2018.LW6F.1
Xiang X., Jingwen M., Xiankai S. // Phys. Rev. A. 2019. V. 99. № 5. P. 053837.
Егоров Ф.А., Потапов В.Т. // Фотон–Экспресс. 2018. № 7. С. 4.
Buks E., Martin I. // Phys. Rev. E 2019. V. 100. № 3. P. 032202. https://doi.org/10.1103/PhysRevE.100.032202
Бурков В.Д., Егоров Ф.А., Потапов В.Т. и др. // РЭ. 2000. Т. 45. № 7. С. 880.
Егоров Ф.А., Неугодников А.П., Никитин В.В. и др. // Вестн. МГУ. Сер. 3. Физика. Астрономия. 2009. № 6. С. 45.
Pavlova S., Tunckol E., Pavlov I. // Opt. Express. 2020. V. 28. № 12. P. 18368.
Stewart G. Vijazaghavan K., Whitenett G. et al. // J. Lightwave Technol. 2007. V. 25. № 7. P. 1786.
Bogdanovich M.V., Grigor’ev A.V., Kabanov V.V. et al. // Lithuanian J. Phys. 2010. V. 50. № 4. P. 413.
Ханин Я.И. Основы динамики лазеров. М.: Наука, 1999.
Ter-Mikirtychev V. V. Fundamentals of Fiber Lasers and Fiber Amplifiers. Cham: Springer, 2019. https://doi.org/10.1007/978-3-319-02338-0-9
Самсон А.М., Котомцева Л.А., Лойко Н.А. Автоколебания в лазерах. Минск: Навука i тэхнiка, 1990.
Красильников В.Н. Параметрические волновые явления в классической электродинамике. СПб.: Изд-во СПбГУ, 1996.
Ladaci A., Girard S., Mescia L. et al. // Proc. SPIE. 2018. V. 10524. P. 1052410. https://doi.org/10.1117/12.2290381
Галаган Б.И., Денкер Б.И., Егорова О.Н. и др. // Квантов. электрон. 2018. Т. 48. № 6. С. 550.
Hyo Y., Cheo P.K., King G.G. // IEEE J. Quantum Electron. 2005. V. 41. № 4. P.573.
Agrawal G.P. Nonlinear Fiber Optics. Waltham: Academic Press, 2012.
Хандохин П.А. Низкочастотная динамика лазеров с инерционной активной средой. Дис. … докт. физ.-мат. наук. Н. Новгород: Институт прикладной физики РАН, 2007. 301 с.
Ахманов С.А., Гусев В.Э. // Успехи физ. наук. 1992. Т. 162. № 3. С. 3.
Бабицкий В.И., Крупенин В.Л. Колебания в сильно нелинейных системах. М.: Наука, 1985.
Дмитриев А.К., Коновалов А.Н., Ульянов В.А. // Квантов. электрон. 2014. Т. 44. № 4. С. 309.
Ратнер А.М. Квантовые генераторы света с большим угловым расхождением. Киев: Наукова думка, 1970.
Раззахи Д., Хаджесмаилбаджи Ф., Рузбехани М. // Квантов. электрон. 2012. Т. 42. № 8. С. 671.
Barmenkov Y.O, Kiryanov A.V., Cruz J.L. et al. // IEEE J. Selected Topics in Quantum Electronics. 2014. V. 20. № 5. P. 1. https://doi.org/10.1109/JSTQE.2014.2304423
Кизель В.А. Отражение света. М.: Наука, 1973.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


