Радиотехника и электроника, 2023, T. 68, № 9, стр. 864-872
Параметрическое семейство фильтров с конечной импульсной характеристикой на основе сплайнов и метод поиска оптимального параметра
К. А. Будунова a, *, В. Ф. Кравченко a, b
a Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая, 11, корп. 7, Российская Федерация
b Научно-технологический центр уникального приборостроения РАН
117342 Москва, ул. Бутлерова, 15, Российская Федерация
* E-mail: 1917schw@mail.ru
Поступила в редакцию 28.04.2023
После доработки 28.04.2023
Принята к публикации 25.05.2023
- EDN: RLGIPL
- DOI: 10.31857/S003384942309005X
Аннотация
Предложено новое параметрическое семейство фильтров с конечной импульсной характеристикой на основе сверток сплайнов с прямоугольным импульсом. Разработан и теоретически обоснован алгоритм поиска параметра, оптимизирующего отклонение амплитудно-частотной характеристики в полосах пропускания и подавления. Проведен численный эксперимент, заключающийся в сравнении новых фильтров с оконными фильтрами и оптимальными фильтрами Чебышева.
ВВЕДЕНИЕ
В работе описывается семейство фильтров с конечной импульсной характеристикой (КИХ), амплитудно-частотная характеристика (АЧХ) которых приближается к финитным сплайнам, аппроксимирующим свертку прямоугольного импульса с атомарной функцией ${{{\text{h}}}_{a}}(x)$ [1, 2]. Отклонение фильтров в полосах пропускания и подавления меняется вместе с изменением параметра, в связи с чем возникает задача разработки метода поиска параметра, оптимизирующего отклонение.
1. ПАРАМЕТРИЧЕСКОЕ СЕМЕЙСТВО КИХ-ФИЛЬТРОВ НА ОСНОВЕ СПЛАЙНОВ
Пусть $f(\omega )$ – четная неотрицательная финитная интегрируемая функция с носителем supp f(ω) = $ = [ - \gamma ,\gamma ]$ и
а ${{B}_{0}}(\omega )$ – прямоугольный импульс:Тогда при ${{\gamma }_{0}} > \gamma $ свертка
(1)
$H(\omega ) = \int\limits_\mathbb{R} {{{B}_{0}}({u \mathord{\left/ {\vphantom {u {(2{{\gamma }_{0}})}}} \right. \kern-0em} {(2{{\gamma }_{0}})}})f(\omega - u)du} $Перечисленные свойства позволяют рассматривать $H(\omega )$ в качестве идеальной АЧХ некоторого фильтра низких частот.
Рассмотрим для фиксированных частот ${{\omega }_{0}}$ и ${{\omega }_{1}}$, $0 < {{\omega }_{0}} < {{\omega }_{1}} < \pi $, семейство фильтров ${{H}_{{a,L}}}(\omega )$, образуемое правой частью (1) в случае, когда ${{\gamma }_{0}} = {{({{\omega }_{1}} + {{\omega }_{0}})} \mathord{\left/ {\vphantom {{({{\omega }_{1}} + {{\omega }_{0}})} 2}} \right. \kern-0em} 2}$ и
Сплайны ${{f}_{{a,L}}}(\omega )$ представляют собой аппроксимации известной атомарной функции ${{{\text{h}}}_{a}}(\omega )$, которая применяется при синтезе дискретных и непрерывных фильтров низких частот с быстро затухающей импульсной характеристикой [3–5].
Функция ${{H}_{{a,L}}}(\omega )$ при $\omega \in \left[ { - \pi ,\pi } \right]$ представляется рядом Фурье
(2)
$\begin{gathered} {{H}_{{a,L}}}(\omega ) = \frac{{{{\omega }_{1}} + {{\omega }_{0}}}}{\pi } \times \\ \times \,\,\left( {\frac{1}{2} + \sum\limits_{k = 1}^\infty {sinc\left( {\frac{{{{\omega }_{1}} + {{\omega }_{0}}}}{2}k} \right){{Y}_{{a,L}}}(k)\cos \left( {k\omega } \right)} } \right), \\ \end{gathered} $(3)
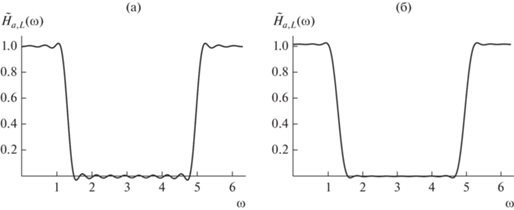
$\begin{gathered} {{{\tilde {H}}}_{{a,L}}}(\omega ) = \frac{{{{\omega }_{1}} + {{\omega }_{0}}}}{\pi } \times \\ \times \,\,\left| {\frac{1}{2} + \sum\limits_{k = 1}^N {sinc\left( {\frac{{{{\omega }_{1}} + {{\omega }_{0}}}}{2}k} \right){{Y}_{{a,L}}}(k)\cos \left( {k\omega } \right)} } \right|. \\ \end{gathered} $Графики АЧХ (3) для некоторых фильтров приведены на рис. 1.
Рис. 1.
Амплитудно-частотные характеристики (3) при ${{\omega }_{0}} = \pi {\text{/}}3$, ${{\omega }_{1}} = \pi {\text{/}}2$, $L = 3$, $N = 15$ для $a = 1.2$ (а) и 5 (б).
Рассмотрим остаток ряда Фурье (2)
(4)
$\begin{gathered} \varepsilon (a,\omega ) = \frac{{{{\omega }_{1}} + {{\omega }_{0}}}}{\pi } \times \\ \times \,\,\sum\limits_{k = N + 1}^\infty {sinc\left( {\frac{{{{\omega }_{1}} + {{\omega }_{0}}}}{2}k} \right){{Y}_{{a,L}}}(k)\cos \left( {k\omega } \right)} . \\ \end{gathered} $Для каждого фиксированного параметра $a$ и заданного набора чисел ${{\omega }_{0}}$, ${{\omega }_{1}}$, $L$, $N$ наибольшее отклонение характеристики (3) в полосах пропускания $0 \leqslant \omega \leqslant \omega {{\,}_{0}}$ и подавления ${{\omega }_{1}} \leqslant \omega \leqslant \pi $ (при условии, что ${{\tilde {H}}_{{a,L}}}(\omega ) \ne 0$ на $\omega \in (0,{{\omega }_{0}})$) задается величиной
где $\Omega = \{ \omega \,\,{\text{:}}\,\,0 \leqslant \omega \leqslant {{\omega }_{0}},\,\,\,\,{{\omega }_{1}} \leqslant \omega \leqslant \pi \} $. Отклонение (5) меняется в зависимости от параметра $a$ и имеет на интервале $a \in [1, + \infty )$ точную нижнюю грань2. ЗАМЕНА НЕПРЕРЫВНОЙ ЗАДАЧИ ОПТИМИЗАЦИИ ОТКЛОНЕНИЯ ДИСКРЕТНОЙ ЗАДАЧЕЙ
Функция (5) в общем случае не является вогнутой, кроме того, точная нижняя грань (6) ищется на неограниченном множестве $a \in [1, + \infty )$, поэтому решение задачи (6) не может быть найдено при помощи стандартных численных методов минимизации.
Для отыскания приближенного решения здесь предлагается ограничить область изменения параметра $a$ и заменить (6) дискретной задачей таким образом, чтобы найденное на сетке решение мало отличалось от (6).
Пусть ${{\varepsilon }_{0}} = \mathop {\inf }\limits_{a \geqslant 1} M(a)$ – решение непрерывной задачи (6). Задавая конечный отрезок $[1,A]$ и сетку ${{A}_{S}} = \{ {{a}_{s}}\} _{{s = 1}}^{S}$ на этом отрезке, $1 = {{a}_{1}} < {{a}_{2}} < $ … < $ < {{a}_{{S - 1}}} < {{a}_{S}} = A,$ рассмотрим также задачу поиска числа ${{\varepsilon }_{1}}$
Определим условия, налагаемые на сетку ${{A}_{S}}$ и число $A$, достаточные для выполнения неравенства
(8)
$\left| {{{\varepsilon }_{1}} - {{\varepsilon }_{0}}} \right| \leqslant \frac{{{{\varepsilon }_{0}}}}{{10}},$Отметим, что для функции $\varepsilon (a,\omega )$ имеет место равномерная на $\Omega $ сходимость $\mathop {\lim }\limits_{a \to + \infty } \varepsilon (a,\omega ) = \tilde {\varepsilon }(\omega )$, где
Обозначим $\tilde {\varepsilon } = \mathop {\max }\limits_{\omega \in \Omega } \left| {\tilde {\varepsilon }(\omega )} \right|$. Предположим, что задано некоторое число $A$, для которого выполняется соотношение
Рассмотрим сначала случай, когда функция $M(a)$ достигает при $a \geqslant 1$ своей нижней грани в точке ${{a}_{0}} \geqslant A$. Тогда для ${{\varepsilon }_{0}}$ справедливо
Полагая ${{\varepsilon }_{1}} = \tilde {\varepsilon }$, получим
Пусть теперь $\mathop {\inf }\limits_{a \geqslant 1} M(a)$ не достигается при конечном $a$ и ${{\varepsilon }_{0}} = \tilde {\varepsilon }$. Тогда ${{\varepsilon }_{1}} > \tilde {\varepsilon }$. В точке $a = A$
Отсюда также следует $\left| {{{\varepsilon }_{0}} - {{\varepsilon }_{1}}} \right| \leqslant \lambda \tilde {\varepsilon }$. Далее, в обоих случаях
Если функция $M(a)$ достигает при $a \geqslant 1$ своей нижней грани в точке ${{a}_{0}} \in [1,A]$, то условие (8) выполняется при правильном выборе сетки на $[1,A]$. Пусть точка ${{a}_{0}}$ принадлежит некоторому отрезку $[\alpha ,\beta ] \subset [1,A]$, на котором задано равномерное разбиение с шагом $\Delta a$, причем
где $\mu $ – некоторое число. Введем функции(9)
${{M}_{1}}(a) = \mathop {\max }\limits_{\omega \,\, \in \,\,\Omega } \varepsilon (a,\omega ),\,\,\,\,{{M}_{2}}(a) = - \mathop {\min }\limits_{\omega \,\, \in \,\,\Omega } \varepsilon (a,\omega ).$Можно показать, что при
справедливоДостаточным условием для выполнения (10), (11) является
где $\tilde {M}$ – оценка сверху модулей производных $M_{1}^{'}(a),{\text{ }}M_{2}^{'}(a)$ на отрезке $[\alpha ,\beta ]$:(13)
$\left| {M_{1}^{'}(a)} \right| \leqslant \tilde {M},\,\,\,\,\left| {M_{2}^{'}(a)} \right| \leqslant \tilde {M}.$3. ФОРМУЛЫ ПРЕДСТАВЛЕНИЯ ПОГРЕШНОСТИ $\varepsilon (a,\omega )$
Далее будем использовать другие представления функции $\varepsilon (a,\omega )$. Обозначим
Справедлива формула
(14)
$\begin{gathered} \sin \left( {n\varphi + \frac{\pi }{2}} \right)\prod\limits_{l = 1}^{L + 1} {\sin (n{{\varphi }_{l}})} \frac{{{{{( - 1)}}^{{L + 1}}}}}{{{{2}^{{L + 1}}}}} = \\ = \,\,\sum\limits_{k = 1}^{{{2}^{{L + 1}}}} {{{{\left( { - 1} \right)}}^{{{{\sigma }_{k}}(L + 1)}}}} \cos \left( {\frac{{\pi (L + 1)}}{2} + n\varphi + \sum\limits_{m = 1}^{L + 1} {{{{( - 1)}}^{{{{s}_{k}}(m)}}}n{{\varphi }_{m}}} } \right). \\ \end{gathered} $Используя (14), погрешность $\varepsilon (a,\omega )$ (4) можно представить в форме выражения, содержащего сумму ${{2}^{{L + 1}}}$ сдвигов функции ${{\Psi }_{L}}$:
(16)
$\begin{gathered} \varepsilon (a,\omega ) = \frac{{{{{( - 1)}}^{L}}}}{\pi }\frac{{{{{(1 + a + ... + {{a}^{{L - 1}}})}}^{L}}}}{{{{a}^{{(L - 1)L{\text{/}}2}}}{{{\left( {{{\omega }_{1}} - {{\omega }_{0}}} \right)}}^{L}}}} \times \\ \times \,\,\sum\limits_{l = 1}^{{{2}^{{L + 1}}}} {{{{( - 1)}}^{{{{\sigma }_{l}}(L + 1) + 1}}}{{\Psi }_{L}}\left( {\omega + \sum\limits_{m = 1}^{L + 1} {{{{( - 1)}}^{{{{s}_{l}}(m)}}}{{\varphi }_{m}}(a)} } \right)} , \\ \end{gathered} $Вводя функцию
(17)
$\begin{gathered} \varepsilon (a,\omega ) = \frac{{{{{( - 1)}}^{L}}}}{\pi }\frac{{{{{(1 + a + ... + {{a}^{{L - 1}}})}}^{L}}}}{{{{a}^{{(L - 1)L{\text{/}}2}}}{{{\left( {{{\omega }_{1}} - {{\omega }_{0}}} \right)}}^{L}}}} \times \\ \times \,\,\sum\limits_{l = 1}^{{{2}^{L}}} {{{{( - 1)}}^{{{{\sigma }_{l}}(L) + 1}}}{{\Phi }_{L}}\left( {\omega + \sum\limits_{m = 1}^L {{{{( - 1)}}^{{{{s}_{l}}(m)}}}{{\varphi }_{m}}(a)} } \right)} . \\ \end{gathered} $Для фиксированной частоты $\omega $ будет использоваться формула
(18)
$\begin{gathered} \varepsilon (a,\omega ) = \frac{{{{{( - 1)}}^{L}}}}{\pi }\frac{{{{{(1 + a + ... + {{a}^{{L - 1}}})}}^{L}}}}{{{{a}^{{(L - 1)L{\text{/}}2}}}{{{\left( {{{\omega }_{1}} - {{\omega }_{0}}} \right)}}^{L}}}} \times \\ \times \,\,\sum\limits_{l = 1}^{{{2}^{{L - 1}}}} {{{{( - 1)}}^{{{{\sigma }_{l}}(L) + 1}}}{{F}_{L}}\left( {\frac{{\sum\limits_{m = 1}^L {{{{( - 1)}}^{{{{s}_{l}}(m)}}}{{a}^{{m - 1}}}} }}{{1 + ... + {{a}^{{L - 1}}}}}} \right)} . \\ \end{gathered} $4. ОПРЕДЕЛЕНИЕ КОНЕЧНОГО ОТРЕЗКА ПОИСКА РЕШЕНИЯ
Используя результаты, полученные в разд. 2, определим метод поиска конечного отрезка $[1,A]$, на котором ищется решение дискретной задачи. На множестве $\omega \in \Omega $ имеет место равномерная сходимость
(19)
$\left| {\varepsilon (a,\omega ) - \tilde {\varepsilon }(\omega )} \right| \leqslant \frac{1}{{11}}\tilde {\varepsilon }$Считая $\omega $ фиксированной частотой, запишем погрешность $\varepsilon (a,\omega )$ (18) виде
гдеПоскольку
производная $\frac{{\partial {{\lambda }_{1}}(a,x)}}{{\partial x}}$ равна(20)
$\Theta (a) = {{\lambda }_{2}}(a,0) - {{\lambda }_{2}}\left( {a,\frac{{ - 2a}}{{1 + ... + {{a}^{{L - 1}}}}}} \right).$Поступая далее аналогичным образом, можно получить формулу
(21)
$\begin{gathered} \Theta (a) = {{( - 1)}^{L}}\frac{{{{{({{\omega }_{1}} - {{\omega }_{0}})}}^{{L - 1}}}{{a}^{{1 + ... + (L - 2)}}}}}{{{{{(1 + ... + {{a}^{{L - 1}}})}}^{{L - 1}}}}} \times \\ \times \,\,{{F}_{1}}\left( {1 + \frac{{ - 2\left( {{{\theta }_{1}} + ... + {{\theta }_{{L - 1}}}{{a}^{{L - 2}}}} \right)}}{{1 + ... + {{a}^{{L - 1}}}}}} \right). \\ \end{gathered} $Обозначим
Для модуля разности
легко вывести оценку
где $d(a)$ – монотонно убывающая функция параметра $a$, равная5. ОЦЕНКИ ДЛЯ ЧАСТНОЙ ПРОИЗВОДНОЙ ПОГРЕШНОСТИ $\varepsilon (a,\omega )$ ПО ПАРАМЕТРУ $a$
В процессе работы алгоритма дискретизации возникают задачи вычисления оценок сверху модуля частной производной
на отрезках вида $[{{a}_{0}},{{a}_{1}}]$. Оценки ищутся для функций $\left| {\delta (a,\tilde {\omega })} \right|$, где $\tilde {\omega }$ – фиксированная частота, и $\left| {\delta (a,\omega )} \right|$, где $\omega $ – переменная, $\omega \in \Omega $.Выражение для частной производной (в формуле ниже частота $\omega $ считается фиксированной) имеет вид
Оценку функции $\left| {\delta (a,\tilde {\omega })} \right|$ для заданной частоты $\tilde {\omega }$ можно найти, используя формулу
(22)
$\begin{gathered} \left| {\delta (a,\tilde {\omega })} \right| \leqslant \left| {\delta ({{a}_{0}},\tilde {\omega })} \right| + \sum\limits_{l = 1}^{{{2}^{{L - 1}}}} {\left( {{{c}_{{l1}}}\left| {{{F}_{{L - 1}}}\left( {{{\nu }_{l}}({{a}_{0}})} \right)} \right| + } \right.} \\ + \,\,\left. {{{c}_{{l0}}}\mathop {\max }\limits_{x \in [{{a}_{0}},{{a}_{1}}]} \left| {{{F}_{{L - 1}}}\left( {{{\nu }_{l}}(x)} \right) - {{F}_{{L - 1}}}({{\nu }_{l}}({{a}_{0}}))} \right|} \right) + \\ + \,\,\left| {\Theta ({{a}_{0}})} \right|\mathop {\max }\limits_{x \in [{{a}_{0}},{{a}_{1}}]} \left| {f(x) - f({{a}_{0}})} \right| + \\ + \,\,\mathop {max}\limits_{x \in [{{a}_{0}},{{a}_{1}}]} \left| {f(x)} \right|\mathop {\max }\limits_{x \in [{{a}_{0}},{{a}_{1}}]} \left| {\Theta (x) - \Theta ({{a}_{0}})} \right|. \\ \end{gathered} $Коэффициенты ${{c}_{{l0}}}$ и ${{c}_{{l1}}}$ в (22) равны
Формула (22) применяется при небольших значениях параметра $a$. Ниже без доказательства приводится другое неравенство, используемое в предлагаемом алгоритме для оценки частной производной при ${{a}_{0}} > 2$:
(23)
$\begin{gathered} \left| {\delta (a,\tilde {\omega })} \right| \leqslant \left| {\delta ({{a}_{0}},\tilde {\omega })} \right| + {{C}_{0}}\mathop {\max }\limits_{w \in [0,y({{a}_{0}})]} \left| {{{F}_{0}}(1 - 2w)} \right| + \\ + \,\,{{C}_{1}}\mathop {\max }\limits_{w \in [0,y({{a}_{0}})]} \left| {{{F}_{1}}(1 - 2w)} \right|. \\ \end{gathered} $В правой части (23) $y(a) = {{({{a}^{{L - 1}}} - 1)} \mathord{\left/ {\vphantom {{({{a}^{{L - 1}}} - 1)} {({{a}^{L}} - 1)}}} \right. \kern-0em} {({{a}^{L}} - 1)}}$, а константы ${{C}_{0}}$ и ${{C}_{1}}$ равны соответственно
Для оценки модуля производной $\left| {\delta (a,\omega )} \right|$ на множестве $[{{a}_{0}},{{a}_{1}}] \times \Omega $ при ${{a}_{0}} \leqslant 2$ используется неравенство
(24)
$\begin{gathered} \left| {\delta (a,\omega )} \right| \leqslant \mathop {\max }\limits_{\omega \in \Omega } \left| {\delta ({{a}_{0}},\omega )} \right| + \sum\limits_{l = 1}^{{{2}^{{L - 1}}}} {{{c}_{{l1}}}{{B}_{l}}} + \\ + \,\,D\mathop {\max }\limits_{x \in [{{a}_{0}},{{a}_{1}}]} \left| {f(x) - f({{a}_{0}})} \right| + \\ + \,\,2\sum\limits_{l = 1}^{{{2}^{{L - 1}}}} {{{c}_{{l2}}}} \left( {\mathop {max}\limits_{x \in [{{a}_{0}},{{a}_{1}}]} \left| {{{f}_{l}}(x)} \right|\mathop {\max }\limits_x \left| {{{\Phi }_{{L - 2}}}\left( x \right)} \right| + } \right. \\ + \,\,\left. {\mathop {max}\limits_{x \in [{{a}_{0}},{{a}_{1}}]} \left| {f(x)} \right|\mathop {\max }\limits_x \left| {{{\Phi }_{{L - 1}}}\left( x \right)} \right|} \right), \\ \end{gathered} $Оценка $\left| {\delta (a,\omega )} \right|$ при ${{a}_{0}} > 2$ задается неравенством
(25)
$\begin{gathered} \left| {\delta (a,\omega )} \right| \leqslant \mathop {\max }\limits_{\omega \in \Omega } \left| {\delta ({{a}_{0}},\omega )} \right| + \\ + \,\,2{{C}_{0}}\mathop {\max }\limits_x \left| {{{\Phi }_{0}}\left( x \right)} \right| + 2{{C}_{1}}\mathop {\max }\limits_x \left| {{{\Phi }_{1}}(x)} \right|. \\ \end{gathered} $6. ОПИСАНИЕ АЛГОРИТМА ДИСКРЕТИЗАЦИИ
Предлагаемый метод дискретизации заключается в разбиении отрезка $[1,A]$ на $S$ подотрезков вида $[{{a}_{s}},{{a}_{{s + 1}}}]$, где ${{a}_{{s + 1}}} = {{a}_{s}} + \Delta a(s)$, $0 \leqslant s \leqslant S - 1$. На каждом $[{{a}_{s}},{{a}_{s}} + \Delta a(s)]$ ищется постоянная оценка снизу функции $M(a)$
Приведем описание алгоритма. Начальное значение параметра $a$ полагается равным ${{a}_{0}} = 1$.
Шаг 1. На множестве $\Omega $ задается некоторый набор частот ${{\omega }_{1}},...,{{\omega }_{Q}}$ и ищется частота ${{\omega }_{{00}}}$ из этого набора, в которой функция $\left| {\varepsilon ({{a}_{s}},\omega )} \right|$ достигает максимального значения
Шаг 2. Если для найденного ранее значения $m$ функции $M(a)$ выполняется неравенство
то с помощью формулы
где ${{M}_{{00}}}$ – полученная с помощью соотношений (22) или (23) оценка сверху модуля производнойПри $m > {{\mu }_{s}}$ выполняется дискретизация $[{{a}_{s}},{{a}_{{s + 1}}}]$ с шагом $\alpha $, определяемым из неравенства
где ${{M}_{{10}}}$ – такое число, что для всех $a \in [{{a}_{s}},{{a}_{{s + 1}}}]$ и $\omega \in \Omega $. Оценка ${{M}_{{10}}}$ вычисляется с помощью неравенств (24), (25). Если минимальное из множества значений $M({{a}_{s}} + \alpha k)$ меньше найденного ранее числа $m$, то полагается7. ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ
С помощью описанного в разд. 6 алгоритма для заданных граничных частот ${{\omega }_{0}},{{\omega }_{1}}$ и различных чисел $N$, $L$ были найдены фильтры с оптимальной относительно величины отклонения АЧХ (3). Из каждого набора найденных для $L = 2,...,10$ оптимальных фильтров с фиксированными ${{\omega }_{0}},{{\omega }_{1}}$, $N$ был выбран наилучший. Полученные погрешности ${{\delta }_{0}}$ и оптимальные параметры $a$, $L$ представлены в табл. 1. Для сравнения там же приведены значения отклонений оптимальных фильтров Чебышева [7], имеющих ту же длину и такие же граничные частоты.
Таблица 1.
Параметры $L,a$ оптимальных фильтров и отклонение ${{\delta }_{0}}$ АЧХ (3) для этих параметров в полосах пропускания и подавления для различных частот ${{\omega }_{0}},{{\omega }_{1}}$ и чисел $N$. Отклонение ${{\delta }_{1}}$ АЧХ оптимальных фильтров Чебышева длиной $2N + 1$ для частот ${{\omega }_{0}},{{\omega }_{1}}$
| ${{\omega }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3},{\text{ }}{{\omega }_{1}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ | ||||
|---|---|---|---|---|
| N | L | $a$ | ${{\delta }_{0}}$ | ${{\delta }_{1}}$ |
| 10 | 2 | 6.465 | 2.67 × 10–2 | 2 × 10–2 |
| 20 | 2 | 1 | 1.99 × 10–3 | 9.5 × 10–4 |
| 30 | 3 | 1 | 2.56 × 10–4 | 5.03 × 10–5 |
| 40 | 4 | 1.114 | 2.14 × 10–5 | 3.21 × 10–6 |
| 50 | 5 | 1.114 | 2.1 × 10–6 | 2.28 × 10–7 |
| ${{\omega }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4},\,\,\,\,{{\omega }_{1}} = {{7\pi } \mathord{\left/ {\vphantom {{7\pi } {12}}} \right. \kern-0em} {12}}$ | ||||
| 10 | 2 | 1 | 1.81 × 10–3 | 1.04 × 10–3 |
| 20 | 4 | 1.116 | 2.21 × 10–5 | 2.81 × 10–6 |
| 30 | 6 | 1.099 | 2.62 × 10–7 | 1.92 × 10–8 |
| 40 | 8 | 1.076 | 4.07 × 10–9 | 6.4 × 10–11 |
| 50 | 10 | 1.044 | 4.8 × 10–11 | 2.43 × 10–13 |
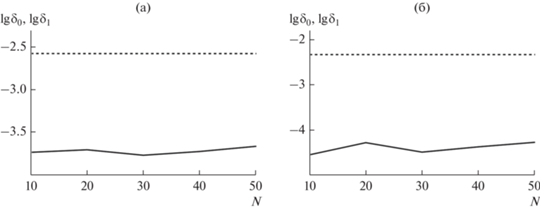
Был проведен также эксперимент, заключавшийся в сравнении новых фильтров с оконными фильтрами на основе весовых функций [7, 8] Блэкмана
Для ${{W}_{1}}(\omega )$ и ${{W}_{2}}(\omega )$ получено соответственно ${{S}_{{{\text{эф}}}}} = 7.3$ и ${{S}_{{{\text{эф}}}}} = 9.3$. Переходная полоса оконных фильтров длиной $2N + 1$ на основе ${{w}_{1}}(x)$ и ${{w}_{2}}(x)$ занимает отрезок
(26)
$[{{\omega }_{c}} - {{{{S}_{{{\text{эф}}}}}} \mathord{\left/ {\vphantom {{{{S}_{{{\text{эф}}}}}} N}} \right. \kern-0em} N},\,\,\,\,{{\omega }_{c}} + {{{{S}_{{{\text{эф}}}}}} \mathord{\left/ {\vphantom {{{{S}_{{{\text{эф}}}}}} N}} \right. \kern-0em} N}],$где ${{\omega }_{c}}$ – частота среза. Для набора чисел $L = 2,...,10$ с помощью предложенного в работе алгоритма были построены оптимальные по параметрам $L$ и $a$ фильтры длиной $2N + 1$ при $N = 10k$, $k = 1,...,5$, с переходной полосой вида (26) при ${{S}_{{{\text{эф}}}}} = 7.3$ и ${{S}_{{{\text{эф}}}}} = 9.3$. Частота ${{\omega }_{c}}$ принята равной ${{5\pi } \mathord{\left/ {\vphantom {{5\pi } {12}}} \right. \kern-0em} {12}}$. Сравнение отклонений АЧХ ${{\delta }_{0}}$ полученных оптимальных фильтров с отклонениями ${{\delta }_{1}}$ оконных фильтров приведено на рис. 2.
ЗАКЛЮЧЕНИЕ
Предложено новое параметрическое семейство КИХ-фильтров с АЧХ, аппроксимирующей свертку прямоугольного импульса с финитным сплайном конечного порядка. Отклонения АЧХ рассмотренных фильтров меняются с изменением параметра $a$, в связи с чем возникает задача поиска оптимального фильтра в семействе. Разработан и теоретически обоснован алгоритм оптимизации, заключающийся в замене непрерывной задачи дискретной. Проведен численный эксперимент, где выполнено сравнение разработанных фильтров с часто используемыми оконными и оптимальными фильтрами. По величине неравномерности в полосах пропускания и подавления новые фильтры оказались лучше оконных. Отличие между отклонениями АЧХ новых фильтров и фильтров Чебышева составило один-два порядка.
Список литературы
Кравченко В.Ф., Кравченко О.В. Конструктивные методы алгебры логики, атомарных функций, вейвлетов, фракталов в задачах физики и техники / Под ред. В.Ф. Кравченко. М.: Техносфера, 2018.
Кравченко В.Ф., Чуриков Д.В. Цифровая обработка сигналов атомарными функциями и вейвлетами. М.: Техносфера, 2019.
Будунова К.А., Кравченко В.Ф., Пустовойт В.И. // РЭ. 2019. Т. 64. № 10. С. 984.
Budunova K.A., Kravchenko V.F. // Proc. 2021 Photonics and Electromagnetics Research Symp. (PIERS). Hangzhou, 21–25 Nov. N.Y.: IEEE, 2021. P. 270.
Будунова К.А., Кравченко В.Ф., Пустовойт В.И. // РЭ. 2021. Т. 66. № 11. С. 1085.
Демьянов В.Ф., Малоземов В.Н. Введение в минимакс. М.: Наука, 1972.
Айфичер Э.С., Джервис Б.У. Цифровая обработка сигналов. М.: ИД “Вильямс”, 2008.
Дворкович В.П., Дворкович А.В. Оконные функции для гармонического анализа сигналов. М.: Техносфера, 2016.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника