1. На главную
  2. Электронные версии
  3. Расплавы
  4. № 1, 2020

Расплавы, 2020, № 1, стр. 37-45

Направленное затвердевание с двухфазной зоной с учетом зависимости плотности жидкой фазы от температуры и концентрации примеси

Д. В. Александров a, *, И. В. Александрова a, А. А. Иванов a, И. О. Стародумов a, Л. В. Торопова a

a Уральский федеральный университет им. Б.Н. Ельцина, кафедра теоретической и математической физики, Лаборатория многомасштабного математического моделирования
Екатеринбург, Россия

* E-mail: dmitri.alexandrov@urfu.ru

Поступила в редакцию 17.05.2019
После доработки 28.05.2019
Принята к публикации 16.06.2019

Полный текст (PDF)

Аннотация

Исследован процесс квазистационарной кристаллизации бинарной системы с двухфазной областью при учете зависимости плотности жидкой фазы от температуры и концентрации примеси. Определены аналитические решения нелинейной системы уравнений тепло- и массопереноса. Найдены распределения концентрации примеси, температуры и доли твердой фазы, скорость процесса затвердевания и положения межфазных границ твердая фаза–двухфазная область и двухфазная область–жидкая фаза.

Ключевые слова: фазовые переходы, направленная кристаллизация, двухфазная область

ВВЕДЕНИЕ

Процессы структурно-фазового превращения из жидкого состояния в твердое лежат в основе многих технологических процессов получения материалов с необходимыми свойствами [1–6]. Часто такие процессы протекают при наличии области (двухфазной зоны), заполненной растущими элементами твердого материала и жидкостью. Особенности процесса кристаллизации в двухфазной зоне определяют формирующиеся свойства твердого материала, получаемого путем затвердевания из жидкого состояния.

Первые математические модели затвердевания с двухфазной зоной были предложены в работах [6–8]. Эти модели описываются нелинейными интегро-дифференциальными уравнениями переноса тепла и примеси при наличии движущихся границ структурно-фазовых превращений, законы движения которых неизвестны и должны быть определены из решения задачи. Отметим, что общих методов решения таких задач не существует и каждый отдельный процесс требует разработки особенных (зачастую уникальных) подходов к решению модели.

Следует специально подчеркнуть разработанный ранее метод перехода к новой независимой переменной (доле твердой фазы в двухфазной зоне) для интегрирования нелинейных уравнений квазиравновесной двухфазной области (когда переохлаждение компенсируется выделяемой теплотой фазового превращения при росте твердой фазы), кристаллизующейся с постоянной скоростью [9–12]. Аналитический метод, основанный на разложении искомых функций в степенные ряды по автомодельной переменной, был разработан в статьях [13, 14] для описания процесса кристаллизации бинарного расплава, когда скорость движения границ двухфазной зоны обратно пропорциональна квадратному корню из времени. Затем этот метод был применен в работах [15, 16] для описания автомодельной кристаллизации трехкомпонентных систем с двумя областями фазового превращения – основной и котектической двухфазными зонами. Аналитические методы описания нестационарной кристаллизации, когда динамика движения межфазных границ квазиравновесной двухфазной области зависит от временных изменений температуры на охлаждаемой поверхности, были предложены в серии работ [17–23]. Отметим также еще методы аналитического решения уравнений неравновесной двухфазной зоны (когда в модели учитывается нуклеация и рост кристаллов), развитые в работах [23–26].

В настоящей работе предложен метод решения нелинейных уравнений квазиравновесной двухфазной области, затвердевающей с постоянной скоростью, когда плотность жидкой фазы определяется линеаризованным уравнением состояния (зависит от температуры и концентрации примеси в области фазового превращения).

МОДЕЛЬ ТЕПЛО- И МАССОПЕРЕНОСА

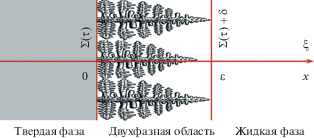
Рассмотрим процесс направленной кристаллизации бинарной системы вдоль пространственной оси $\xi $ (рис. 1). Двухфазная область располагается между чисто твердым материалом $\left( {\xi < {\Sigma }\left( \tau \right)} \right)$ и чисто жидкой фазой $\left( {\xi > {\Sigma }\left( \tau \right) + \delta } \right)$ и имеет протяженность $\delta $. Здесь $\tau $ и ${\Sigma }\left( \tau \right)$ обозначают время и координату межфазной границы твердый материал – двухфазная область. Уравнения теплопроводности и диффузии примеси в области фазового превращения $\left( {{\Sigma }\left( \tau \right) < \xi < {\Sigma }\left( \tau \right) + \delta } \right)$ имеют вид:

(1)
${{\rho }_{m}}{{C}_{m}}\frac{{\partial {{\theta }_{m}}}}{{\partial \tau }} = \frac{\partial }{{\partial \xi }}\left( {{{\lambda }_{m}}\frac{{\partial {{\theta }_{m}}}}{{\partial \xi }}} \right) + {{L}_{V}}\frac{{\partial \varphi }}{{\partial \tau }},$
(2)
$\frac{\partial }{{\partial \tau }}\left[ {\left( {1 - \varphi } \right){{\sigma }_{m}}} \right] = \frac{\partial }{{\partial \xi }}\left( {{{D}_{m}}\frac{{\partial {{\sigma }_{m}}}}{{\partial \xi }}} \right) - k{{\sigma }_{m}}\frac{{\partial \varphi }}{{\partial \tau }},$
где температура ${{\theta }_{m}}$ и концентрация примеси ${{\sigma }_{m}}$ связаны уравнением линии ликвидус
(3)
${{\theta }_{m}} = {{\theta }_{L}}\left( {{{\sigma }_{0}}} \right) + {\Gamma }\left( {{{\sigma }_{m}} - {{\sigma }_{0}}} \right).$
Здесь введены следующие обозначения: ${{\rho }_{m}}$ и ${{C}_{m}}$ – плотность и теплоемкость двухфазной системы, ${{\lambda }_{m}}$ и ${{D}_{m}}$ – коэффициенты теплопроводности и диффузии примеси в двухфазной области, ${{L}_{V}}$ и $k$ – скрытая теплота кристаллизации и коэффициент распределения примеси, $\varphi $ и ${\Gamma }$ – доля твердой фазы в двухфазном регионе и коэффициент наклона линии ликвидус, ${{\sigma }_{0}}$ и ${{\theta }_{L}}$ – характерная концентрация примеси и температура ликвидуса. Коэффициенты переноса в двухфазном слое запишем в соответствии с правилом смесей [27]
(4)
${{\rho }_{m}}{{C}_{m}}\left( \varphi \right) = {{\rho }_{l}}{{C}_{l}}\left( {1 - \varphi } \right) + {{\rho }_{s}}{{C}_{s}}\varphi ,\,\,\,\,~{{\lambda }_{m}}\left( \varphi \right) = {{\lambda }_{l}}\left( {1 - \varphi } \right) + {{\lambda }_{s}}\varphi ,\,\,\,\,{{D}_{m}}\left( \varphi \right) = {{D}_{l}}\left( {1 - \varphi } \right),$
где ${{\rho }_{l}}$ и ${{\rho }_{s}}$ – плотности жидкой и твердой фаз, ${{C}_{l}}$ и ${{C}_{s}}$ – их теплоемкости, а ${{D}_{l}}$ – коэффициент диффузии примеси в расплаве (диффузией примеси в твердой фазе пренебрегаем).

Рис. 1.

Схематическая иллюстрация процесса направленной кристаллизации с двухфазной областью.

Плотность жидкой фазы будем описывать линеаризованным уравнением состояния

(5)
${{\rho }_{l}} = {{\rho }_{0}}\left[ {1 - \alpha {\text{*}}\left( {{{\theta }_{m}} - {{\theta }_{L}}\left( {{{\sigma }_{0}}} \right)} \right) + \beta {\text{*}}\left( {{{\sigma }_{m}} - {{\sigma }_{0}}} \right)} \right],$
где ${{\rho }_{0}}$ – характерная плотность, а $\alpha {\text{*}}$ и $\beta {\text{*}}$ – коэффициенты расширения, соответствующие температуре и концентрации примеси.

Граничные условия на межфазных поверхностях твердая фаза–двухфазная область $\left( {\xi = {\Sigma }\left( \tau \right)} \right)$ и двухфазная область–жидкость $\left( {\xi = {\Sigma }\left( \tau \right) + \delta } \right),$ имеют вид [6–10]

(6)
${{\lambda }_{s}}\frac{{\partial {{\theta }_{s}}}}{{\partial \xi }} - {{\lambda }_{m}}\frac{{\partial {{\theta }_{m}}}}{{\partial \xi }} = {{L}_{V}}\left( {1 - \varphi {\text{*}}} \right)\frac{{d{\Sigma }}}{{d\tau }},\,\,\,\,~\left( {1 - k} \right)\left( {1 - \varphi {\text{*}}} \right){{\sigma }_{m}}\frac{{d{\Sigma }}}{{d\tau }} + {{D}_{m}}\frac{{\partial {{\sigma }_{m}}}}{{\partial \xi }} = 0,\,\,\,\,\xi = {\Sigma }\left( \tau \right),$
(7)
${{\sigma }_{m}} = {{\sigma }_{l}},\,\,\,\,\frac{{\partial {{\sigma }_{m}}}}{{\partial \xi }} = \frac{{\partial {{\sigma }_{l}}}}{{\partial \xi }},\,\,\,\,\frac{{\partial {{\theta }_{m}}}}{{\partial \xi }} = \frac{{\partial {{\theta }_{l}}}}{{\partial \xi }},\,\,\,\,\varphi = 0,\,\,\,\,\xi = {\Sigma }\left( \tau \right) + \delta .$
Здесь ${{\theta }_{s}}$ и ${{\theta }_{l}}$ – температуры в твердой и жидкой фазах, а ${{\sigma }_{l}}$ и ${{\varphi }_{*}}$ – концентрация примеси в расплаве и доля твердой фазы на границе $\xi = {\Sigma }\left( \tau \right).$

Будем рассматривать процесс направленной кристаллизации при фиксированных градиентах температуры в твердой $\left( {{{g}_{s}}} \right)$ и жидкой $\left( {{{g}_{l}}} \right)$ фазах, а распределение концентрации примеси в расплаве – моделировать стандартным уравнением диффузии примеси, т.е.

(8)
$\begin{gathered} \frac{{\partial {{\theta }_{s}}}}{{\partial \xi }} = {{g}_{s}},\,\,\,\,\xi < {\Sigma }\left( \tau \right),\,\,\,\,\frac{{\partial {{\theta }_{l}}}}{{\partial \xi }} = {{g}_{l}},\,\,\,\,~~\xi > {\Sigma }\left( \tau \right),\,\,\,\,\frac{{\partial {{\sigma }_{l}}}}{{\partial \tau }} = {{D}_{l}}\frac{{{{\partial }^{2}}{{\sigma }_{l}}}}{{\partial {{\xi }^{2}}}},\,\,\,\,\xi > {\Sigma }\left( \tau \right) + \delta , \\ {{\sigma }_{l}} \to {{\sigma }_{0}},\,\,\,\,\xi \to \infty . \\ \end{gathered} $
Отметим, что $\delta ,$ ${{g}_{s}}$ и ${{g}_{l}}$ считаются неизменными величинами в установившемся процессе затвердевания с постоянной скоростью ${{d{\Sigma }} \mathord{\left/ {\vphantom {{d{\Sigma }} {d\tau }}} \right. \kern-0em} {d\tau }} = {{u}_{s}}.$ Модель этого процесса кристаллизации (1)–(8) является нелинейной дифференциальной моделью в частных производных с двумя движущимися границами фазового превращения. Общих методов решения таких задач не существует, а рассматриваемый ниже метод является оригинальным подходом, позволяющим получить аналитические решения модели (1)–(8).

МЕТОД РЕШЕНИЯ НЕЛИНЕЙНОЙ МОДЕЛИ С ДВУХФАЗНОЙ ОБЛАСТЬЮ

Для удобства дальнейшего решения введем безразмерные переменные и параметры следующим образом:

(9)
$\begin{gathered} x = \frac{{{{u}_{s}}}}{{{{D}_{l}}}}\left( {\xi - {{u}_{s}}\tau } \right),\,\,\,\,{{c}_{m}} = \frac{{{{\sigma }_{m}}}}{{{{\sigma }_{0}}}},\,\,\,\,{{c}_{l}} = \frac{{{{\sigma }_{l}}}}{{{{\sigma }_{0}}}},\,\,\,\,{{T}_{m}} = \frac{{{{\theta }_{m}}}}{{m{{\sigma }_{0}}}},\,\,\,\,{{{\Lambda }}_{0}}\left( \varphi \right) = \frac{{{{\lambda }_{m}}\left( \varphi \right)}}{{{{\lambda }_{s}}}}, \\ \tilde {\beta } = \left( {\beta {\text{*}} + m\alpha {\text{*}}} \right){{\sigma }_{0}},\,\,\,\,R = \frac{{{{\rho }_{s}}{{C}_{s}}}}{{{{\rho }_{l}}{{C}_{l}}}},\,\,\,\,m = - {\Gamma },\,\,\,\,{{T}_{0}} = \frac{{{{\theta }_{0}}}}{{m{{\sigma }_{0}}}},\,\,\,\,{{\theta }_{0}} = {{\theta }_{L}}\left( {{{\sigma }_{0}}} \right) - {\Gamma }{{\sigma }_{0}}, \\ ~{{a}_{1}} = \frac{{{{\lambda }_{s}}}}{{{{\rho }_{0}}{{C}_{l}}{{D}_{l}}}},\,\,\,\,{{a}_{2}} = \frac{{{{L}_{V}}}}{{{{\rho }_{0}}{{C}_{l}}m{{\sigma }_{0}}}},\,\,\,\,\widetilde {{{L}_{V}}} = \frac{{{{L}_{V}}{{D}_{l}}}}{{{{\lambda }_{s}}m{{\sigma }_{0}}}},\,\,\,\,{{G}_{s}} = \frac{{{{g}_{s}}{{D}_{l}}}}{{{{u}_{s}}m{{\sigma }_{0}}}},\,\,\,\,{{G}_{l}} = \frac{{{{g}_{l}}{{D}_{l}}}}{{{{u}_{s}}m{{\sigma }_{0}}}}, \\ ~\varepsilon = \frac{{{{u}_{s}}\delta }}{{{{D}_{l}}}},\,\,\,\,g\left( {{{c}_{m}},\varphi } \right) = \left[ {1 + \tilde {\beta }\left( {{{c}_{m}} - 1} \right)} \right]\left( {1 - \varphi } \right) + R\varphi . \\ \end{gathered} $

Вышеприведенная модель (1)–(8) при подстановке переменных (9) примет вид

(10)
$g\left( {{{c}_{m}},\varphi } \right)\frac{{d{{c}_{m}}}}{{dx}} + {{a}_{1}}\frac{d}{{dx}}\left[ {{{{\Lambda }}_{0}}\left( \varphi \right)\frac{{d{{c}_{m}}}}{{dx}}} \right] + {{a}_{2}}\frac{{d\varphi }}{{dx}} = 0,\,\,\,\,0 < x < \varepsilon ,$
(11)
${{T}_{m}} = {{T}_{0}} - {{c}_{m}},\,\,\,\,0 < x < \varepsilon ,$
(12)
$\frac{d}{{dx}}\left[ {\left( {1 - \varphi } \right){{c}_{m}}} \right] + \frac{d}{{dx}}\left[ {\left( {1 - \varphi } \right)\frac{{d{{c}_{m}}}}{{dx}}} \right] + k{{c}_{m}}\frac{{d\varphi }}{{dx}} = 0,\,\,\,\,0 < x < \varepsilon ,$
(13)
${{G}_{s}} + {{{\Lambda }}_{0}}\left( {\varphi {\text{*}}} \right)\frac{{d{{c}_{m}}}}{{dx}} = \widetilde {{{L}_{V}}}\left( {1 - \varphi {\text{*}}} \right),\,\,\,\,\varphi = \varphi *,\,\,\,\,~x = 0,$
(14)
$\left( {1 - k} \right){{c}_{m}} + \frac{{d{{c}_{m}}}}{{dx}} = 0,\,\,\,\,x = 0,\,\,\,\,\varphi {\text{*}} \ne 1\,\,\,\,{\text{или}}\,\,\,\,\varphi {\text{*}} = 1,\,\,\,\,x = 0,$
(15)
${{c}_{m}} = {{c}_{l}},\,\,\,\,\frac{{d{{c}_{m}}}}{{dx}} = \frac{{d{{c}_{l}}}}{{dx}} = - {{G}_{l}},\,\,\,\,\varphi = 0,\,\,\,\,x = \varepsilon ,$
(16)
$~\frac{{{{d}^{2}}{{c}_{l}}}}{{d{{x}^{2}}}} + \frac{{d{{c}_{l}}}}{{dx}} = 0,\,\,\,\,x > \varepsilon ,\,\,\,\,{{c}_{l}} \to 1,\,\,\,\,x \to \infty .$

Интегрируя сейчас первое уравнение (16) и учитывая граничные условия (15) и (16) при $x = \varepsilon $ и $x \to \infty ,$ получим безразмерное распределение концентрации примеси в жидкой фазе

(17)
${{c}_{l}}\left( x \right) = 1 + {{G}_{l}}\exp \left( {\varepsilon - x} \right),\,\,\,\,x > \varepsilon .$
Для отыскания концентрационного профиля в двухфазной зоне (при $0 < x < \varepsilon $), найдем производную ${{d{{c}_{m}}} \mathord{\left/ {\vphantom {{d{{c}_{m}}} {dx}}} \right. \kern-0em} {dx}} = {{c}_{{mx}}}$ из уравнений (10) и (12) в виде
(18)
$\frac{{d{{c}_{m}}}}{{dx}} = \frac{{\left[ {{{f}_{1}}\left( \varphi \right) - {{f}_{2}}\left( \varphi \right){{c}_{m}}} \right]{{d{{c}_{m}}} \mathord{\left/ {\vphantom {{d{{c}_{m}}} {d\varphi }}} \right. \kern-0em} {d\varphi }} - {{f}_{3}}\left( \varphi \right) - {{f}_{4}}\left( \varphi \right){{c}_{m}}}}{{{{f}_{5}}\left( \varphi \right)}},$
где
$\begin{gathered} {{f}_{1}}\left( \varphi \right) = \left( {1 - \varphi } \right)\left[ {{{a}_{1}}{{{\Lambda }}_{0}}\left( \varphi \right) + \left( {\tilde {\beta } - 1} \right)\left( {1 - \varphi } \right) - R\varphi } \right],\,\,\,\,{{f}_{2}}\left( \varphi \right) = \tilde {\beta }{{\left( {1 - \varphi } \right)}^{2}}, \\ {{f}_{3}}\left( \varphi \right) = {{a}_{2}}\left( {1 - \varphi } \right),\,\,\,\,{{f}_{4}}\left( \varphi \right) = \left( {1 - k} \right){{a}_{1}}{{{\Lambda }}_{0}}\left( \varphi \right),\,\,\,\,{{f}_{5}}\left( \varphi \right) = {{a}_{1}}\left[ {\left( {1 - \varphi } \right)\frac{{d{{{\Lambda }}_{0}}}}{{d\varphi }} + {{{\Lambda }}_{0}}\left( \varphi \right)} \right]. \\ \end{gathered} $
Подставляя теперь производную ${{d{{c}_{m}}} \mathord{\left/ {\vphantom {{d{{c}_{m}}} {dx}}} \right. \kern-0em} {dx}}$ из формулы (18) в уравнение переноса примеси (12), получаем стандартную задачу Коши для определения концентрации примеси ${{c}_{m}}\left( \varphi \right)$ в области фазового перехода ($c_{m}^{'} = {{d{{c}_{m}}} \mathord{\left/ {\vphantom {{d{{c}_{m}}} {d\varphi }}} \right. \kern-0em} {d\varphi }},$ ${{d{{f}_{5}}} \mathord{\left/ {\vphantom {{d{{f}_{5}}} {d\varphi }}} \right. \kern-0em} {d\varphi }} = 0$)
(19)
$\frac{{{{d}^{2}}{{c}_{m}}}}{{d{{\varphi }^{2}}}} = \frac{{F(c_{m}^{'},{{c}_{m}},\varphi ){{f}_{5}}\left( \varphi \right) - \left( {1 - \varphi } \right){{h}_{{\,1}}}(c_{m}^{'},{{c}_{m}},\varphi )}}{{\left( {1 - \varphi } \right){{h}_{2}}\left( {{{c}_{m}},\varphi } \right)}},$
(20)
${{c}_{m}} = 1 + {{G}_{l}},\,\,\,\,\frac{{d{{c}_{m}}}}{{d\varphi }} = \frac{{{{f}_{3}}\left( 0 \right) + \left( {1 + {{G}_{l}}} \right){{f}_{4}}\left( 0 \right) - {{G}_{l}}{{f}_{5}}\left( 0 \right)}}{{{{f}_{1}}\left( 0 \right) - \left( {1 + {{G}_{l}}} \right){{f}_{2}}\left( 0 \right)}},\,\,\,\,\varphi = 0,$
где введены обозначения
$\begin{gathered} {{h}_{{{\kern 1pt} 1}}}(c_{m}^{'},{{c}_{m}},\varphi ) = \left[ {f_{1}^{'}\left( \varphi \right) - f_{2}^{'}\left( \varphi \right){{c}_{m}} - {{f}_{2}}\left( \varphi \right)c_{m}^{'}} \right]c_{m}^{'} - f_{3}^{'}\left( \varphi \right) - f_{4}^{'}\left( \varphi \right){{c}_{m}} - {{f}_{4}}\left( \varphi \right)c_{m}^{'}, \\ {{h}_{2}}\left( {{{c}_{m}},\varphi } \right) = {{f}_{1}}\left( \varphi \right) - {{f}_{2}}\left( \varphi \right){{c}_{m}},\,\,\,\,F(c_{m}^{'},{{c}_{m}},\varphi ) = \left( {1 - k} \right){{c}_{m}} - \left( {1 - \varphi } \right)c_{m}^{'} + {{c}_{{mx}}}(c_{m}^{'},{{c}_{m}},\varphi ) \\ \end{gathered} $
и использованы выражения (15), (17) и (18).

Отметим, что при рассмотрении случая $\varphi * \ne 1,$ из граничных условий (13) и (14) можно определить пограничное значение концентрации примеси

(21)
${{c}_{m}}\left( {\varphi {\text{*}}} \right) = \frac{{{{G}_{s}} - \widetilde {{{L}_{V}}}\left( {1 - \varphi {\text{*}}} \right)}}{{\left( {1 - k} \right){{{\Lambda }}_{0}}\left( {\varphi {\text{*}}} \right)}}.$
Подставляя в левую часть выражения (21) концентрацию примеси из решения задачи Коши (19), (20), определим значение доли твердой фазы $\varphi {\text{*}}$ на границе твердый материал–двухфазная область.

Далее, из первого выражения (14) следует уравнение

$\left( {1 - k} \right){{c}_{m}}\left( {\varphi {\text{*}}} \right) + {{c}_{{mx}}}\left( {\varphi {\text{*}}} \right) = 0$
для отыскания ${{u}_{s}},$ в котором ${{c}_{{mx}}}\left( {\varphi {\text{*}}} \right)$ определяется формулой (18). Если теперь $\varphi {\text{*}} = 1,$ то скорость кристаллизации ${{u}_{s}}$ находится из условия (13).

Учитывая теперь, что

$\frac{{d{{c}_{m}}}}{{dx}} = \frac{{d{{c}_{m}}}}{{d\varphi }}\frac{{d\varphi }}{{dx}},$
найдем выражения для безразмерной толщины двухфазной области $\varepsilon $ и зависимости $x\left( \varphi \right),$ определяющей распределение доли твердой фазы $\varphi \left( x \right)$ в двухфазном регионе в виде обратной функции
(22)
$\varepsilon = - \int\limits_0^{{\varphi *}} {\frac{{{{d{{c}_{m}}} \mathord{\left/ {\vphantom {{d{{c}_{m}}} {d{{\varphi }_{1}}}}} \right. \kern-0em} {d{{\varphi }_{1}}}}}}{{{{c}_{{mx}}}\left( {{{\varphi }_{1}}} \right)}}d{{\varphi }_{1}}} ,\,\,\,\,x\left( \varphi \right) = \varepsilon + \int\limits_0^{\varphi } {\frac{{{{d{{c}_{m}}} \mathord{\left/ {\vphantom {{d{{c}_{m}}} {d{{\varphi }_{1}}}}} \right. \kern-0em} {d{{\varphi }_{1}}}}}}{{{{c}_{{mx}}}\left( {{{\varphi }_{1}}} \right)}}d{{\varphi }_{1}}} ,~~$
где ${{c}_{{mx}}}\left( {{{\varphi }_{1}}} \right)$ и ${{d{{c}_{m}}} \mathord{\left/ {\vphantom {{d{{c}_{m}}} {d{{\varphi }_{1}}}}} \right. \kern-0em} {d{{\varphi }_{1}}}}$ подставляются из (18)–(20).

Специально отметим, что аналитическое решение (18)–(22) задачи о квазистационарной кристаллизации двухфазной области с учетом непостоянной плотности жидкости, построено в параметрическом виде (параметром является доля твердой фазы в двухфазном регионе).

ЗАКЛЮЧЕНИЕ

В настоящей статье развито теоретическое описание процесса направленной кристаллизации с областью фазового превращения – двухфазной зоной. На рис. 2–4 показано характерное поведение выведенных в работе аналитических решений (18)–(22). Поскольку решение построено в параметрическом виде (параметром является $\varphi $), на рис. 2 и 3 изображены зависимости концентрации примеси и пространственной координаты от этого параметра: с ростом $\varphi $ концентрация ${{c}_{m}}$ возрастает, а $x$ – уменьшается. При исключении параметра $\varphi $ можно построить зависимость концентрации примеси от координаты $x$, которая показана на рис. 4. Здесь, как и ожидалось, вследствие эффекта вытеснения примеси растущей твердой фазой, ${{c}_{m}}$ с ростом $x$ уменьшается. Распределения концентрации примеси в жидкой фазе, показанные на этом же рисунке точечными линиями, получены с помощью явной зависимости ${{c}_{l}}\left( x \right)$ (формула (17)). Отметим, что концентрационные профили в двухфазной зоне ${{c}_{m}}\left( x \right)$ и жидкой фазе ${{c}_{l}}\left( x \right)$ совпадают на межфазной границе двухфазная область – жидкость $(x = \varepsilon ).$ Увеличение исходной концентрации ${{\sigma }_{0}}$ примеси в расплаве приводит к возрастанию протяженности $\varepsilon $ двухфазного региона и доли твердой фазы $\varphi {\text{*}}$ на границе $x = 0~$ твердый материал – двухфазная область. Концентрационное распределение ${{\sigma }_{s}}$ в твердой фазе можно получить из выражения ${{\sigma }_{s}} = k{{\sigma }_{0}}{{c}_{m}},$ вычисленное на границе $x = 0,$ которое возникает вследствие эффекта захвата примеси твердым материалом с коэффициентом распределения $k.$ Отметим, что по известному распределению концентрации примеси в двухфазной области можно легко получить распределение температуры с помощью выражения (11). Распределения же температуры в чисто твердой и жидкой фазах задаются известными температурными градиентами ${{G}_{s}}$ и ${{G}_{l}}.$

Рис. 2.

Концентрация примеси в зависимости от доли твердой фазы в двухфазной области. Вертикальные линии обозначают координату межфазной границы – твердая фаза–двухфазная область, на которой $\varphi = \varphi {\text{*}}.$ Для расчета использовались параметры: ${{{{\lambda }_{l}}} \mathord{\left/ {\vphantom {{{{\lambda }_{l}}} {{{\lambda }_{s}}}}} \right. \kern-0em} {{{\lambda }_{s}}}} = 0.565,$ $\tilde {\beta } = 0.75,$ $\widetilde {{{L}_{V}}} = 0.538,$ $R = 0.623,$ $k = 0.68,$ ${{a}_{1}} = 4958,$ ${{a}_{2}} = 2.669,$ ${{G}_{l}} = 0.057,$ ${{G}_{s}} = 0.57.$

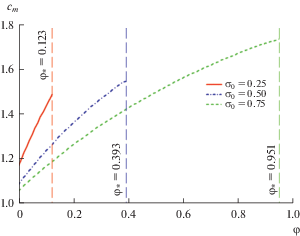
Рис. 3.

Зависимость пространственной переменной от доли твердой фазы в двухфазной области. Вертикальные линии обозначают координату межфазной границы – твердая фаза–двухфазная область, на которой $\varphi = \varphi {\text{*}}$ и $x = 0.$

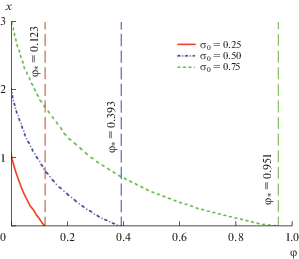
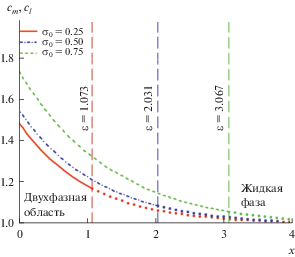
Рис. 4.

Концентрация примеси в двухфазной области и жидкой фазе в зависимости от пространственной координаты. Вертикальные линии обозначают координату межфазной границы – двухфазная область–жидкая фаза. Концентрационные профили в жидкой фазе (точечные линии) лежат справа от вертикальных линий при различных концентрациях примеси ${{\sigma }_{0}}.$

Важно отметить, что развитая теория может быть применена к описанию направленной кристаллизации различных веществ, встречающейся в науках о материалах и природных процессах. Предложенный в настоящей работе метод интегрирования нелинейных уравнений тепло- и массопереноса в двухфазной области может быть обобщен на описание более сложных процессов нестационарного затвердевания или кристаллизации с учетом нуклеации зародышей в метастабильной жидкости в духе ранее развитых теорий [17–19, 24, 25].

Работа выполнена при финансовой поддержке Российского научного фонда (грант 18-19-00008).

Список литературы

  1. Flemings M. Solidification Processing. N.Y.: McGraw Hill. 1974.

  2. Chalmers B. Principles of Solidification. N.Y.: Wiley. 1964.

  3. Alexandrov D.V., Aseev D.L., Nizovtseva I.G., Huang H.-N., Lee D. Nonlinear dynamics of directional solidification with a mushy layer. Analytic solutions of the problem // Int. J. Heat Mass Trans. 2007. 50. P. 3616–3623.

  4. Kurz W., Fisher D.J. Fundamentals of Solidification // Aedermannsdorf: Trans. Tech. Publ. 1989.

  5. Alexandrov D.V., Aseev D.L. Directional solidification with a two-phase zone: thermodiffusion and temperature-dependent diffusivity // Comp. Mater. Sci. 2006. 37. P. 1–6.

  6. Борисов В.Т. Теория двухфазной зоны металлического слитка. М.: Металлургия. 1987.

  7. Hills R.N., Loper D.E., Roberts P.H. A thermodynamically consistent model of a mushy zone // Q. J. Appl. Maths. 1983. 36. P. 505–539.

  8. Fowler A.C. The formation of freckles in binary alloys // IMA J. Appl. Math. 1985. 35. P. 159–174.

  9. Alexandrov D.V., Aseev D.L. One-dimensional solidification of an alloy with a mushy zone: Thermodiffusion and temperature-dependent diffusivity // J. Fluid Mech. 2005. 527. P. 57–66.

  10. Aseev D.L., Alexandrov D.V. Unidirectional solidification with a mushy layer. The influence of weak convection // Acta Mater. 2006. 54. P. 2401–2406.

  11. Alexandrov D.V., Malygin A.P. Coupled convective and morphological instability of the inner core boundary of the Earth // Phys. Earth Planet. Inter. 2011. 189. P. 134–141.

  12. Alexandrov, D.V., Malygin, A.P. The steady-state solidification scenario of ternary systems: Exact analytical solution of nonlinear model // Int. J. Heat Mass Trans. 2012. 55. P. 3755–3762.

  13. Alexandrov D.V., Malygin A.P. Self-similar solidification of an alloy from a cooled boundary // Int. J. Heat Mass Trans. 2006. 49. P. 763–769.

  14. Alexandrov D.V., Ivanov A.A., Malygin A.P. Self-similar solidification of binary alloys // Acta Physica Polonica A. 2009. 115. P. 795–799.

  15. Alexandrov D.V., Ivanov A.A. The Stefan problem of solidification of ternary systems in the presence of moving phase transition regions // J. Exper. Theor. Phys. 2009. 108. P. 821–829.

  16. Alexandrov D.V., Ivanov A.A. Solidification of a ternary melt from a cooled boundary, or nonlinear dynamics of mushy layers // Int. J. Heat Mass Trans. 2009. 52. P. 4807–4811.

  17. Alexandrov D.V., Malygin A.P. Analytical description of seawater crystallization in ice fissures and their influence on heat exchange between the ocean and the atmosphere // Dokl. Earth Sci. 2006. 411. P. 1407–1411.

  18. Alexandrov D.V., Malygin A.P., Alexandrova I.V. Solidification of leads: Approximate solutions of non-linear problem // Ann. Glaciol. 2006. 44. P. 118–122.

  19. Alexandrov D.V., Nizovtseva I.G. Nonlinear dynamics of the false bottom during seawater freezing // Dokl. Earth Sci. 2008. 419. P. 359–362.

  20. Alexandrov D.V., Bashkirtseva I.A., Malygin A.P., Ryashko L.B. Sea ice dynamics induced by external stochastic fluctuations // Pure Appl. Geophys. 2013. 170. P. 2273–2282.

  21. Alexandrov D.V., Netreba A.V., Malygin A.P. Time-dependent crystallization in magma chambers and lava lakes cooled from above: The role of convection and kinetics on nonlinear dynamics of binary systems // Int. J. Heat Mass Trans. 2012. 55. P. 1189–1196.

  22. Alexandrov D.V., Bashkirtseva I.A., Ryashko L.B. Nonlinear dynamics of mushy layers induced by external stochastic fluctuations // Phil. Trans. R. Soc. A. 2018. 376. Art. no. 20170216.

  23. Alexandrov D.V., Ivanov A.A., Alexandrova I.V. Analytical solutions of mushy layer equations describing directional solidification in the presence of nucleation // Phil. Trans. R. Soc. A. 2018. 376. Art. no. 20170217.

  24. Aseev D.L., Alexandrov D.V. Directional solidification of binary melts with a non-equilibrium mushy layer // Int. J. Heat Mass Trans. 2006. 49. P. 4903–4909.

  25. Aseev D.L., Alexandrov D.V. Nonlinear dynamics for the solidification of binary melt with a nonequilibrium two-phase zone // Dokl. Phys. 2006. 51. P. 291–295.

  26. Alexandrov D.V., Malygin A.P. Convective instability of directional crystallization in a forced flow: The role of brine channels in a mushy layer on nonlinear dynamics of binary systems // Int. J. Heat Mass Trans. 2011. 54. P. 1144–1149.

  27. Batchelor G.K. Transport properties of two-phase materials with random structure // J. Fluid Mech. 1974. 6. 227–255.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Расплавы

Архивы выпусков Информация о журнале Отправить рукопись в журнал