Расплавы, 2020, № 1, стр. 46-51

ВВЕДЕНИЕ

При переходе простого (однокомпонентного) вещества из кристаллического состояния в жидкое, локальный порядок может довольно сильно измениться (например, при плавлении германия и кремния), а может и сохраниться, как у многих металлов. В данной работе мы обсуждаем второй случай. Если локальный порядок сохраняется, то плавление можно представить как потерю глобального ориентационного порядка из-за спонтанного увеличения количества топологических дефектов – дислокаций и дисклинаций. Для двумерных кристаллов такой подход является традиционным. Он основан на теории топологических фазовых переходов Березинского–Костерлица–Таулесса [1, 2], которая была применена к двумерному плавлению Нельсоном и Гальпериным [3]. В этой теории плавление представляется как последовательность двух непрерывных фазовых переходов, приводящих к появлению в системе свободных сначала дислокаций, а потом дисклинаций. Между этими переходами может существовать т.н. гексатическая фаза, в которой трансляционные корреляции спадают экспоненциально, а ориентационные – по степенному закону. Для детального изучения можно рекомендовать обзор [4].

Для трехмерных систем такой подход также существует [5, 6], несмотря на то, что в трехмерном веществе топологические дефекты являются не точками, а линиями, что создает математические трудности. В рамках подхода показано, что плавление может быть представлено как появление в системе посредством перехода первого рода равновесной сети топологических дефектов бесконечной длины.

Основным предположением теории как в двумерном, так и в трехмерном случае является то, что плотность дефектов как в упорядоченном состоянии (кристалле), так и в разупорядоченной среде (жидкости) является небольшой – только в этом случае статистически значимые конфигурации системы можно описать в терминах областей с хорошо определенным локальным порядком, и дефектов, где этот порядок нарушен; последние организованы в одномерные (в трехмерных системах) и точечные (в двумерных) дефекты, и обеспечивают когерентное сопряжение между собой упорядоченных кластеров. Вакансии в системе также присутствуют, но они могут быть представлены как пара близких дислокаций (в двумерной системе) или как малая дислокационная петля (в трехмерной). При выполнении этого предположения конфигурации конденсированной системы (как кристаллической, так и жидкой) оказываются параметризованы двумя полями: полем ориентаций локально упорядоченных областей и полем плотности топологических дефектов. Такое возможно отнюдь не для всех веществ, а только для тех, в которых локальный порядок во-первых, не меняется при плавлении, а во-вторых, область, занимаемая локально упорядоченным веществом, является связной как в кристалле, так и в жидкости. Возможность последнего утверждения была проверена в работе [7], где в результате численного моделирования было показано, что не очень большая плотность линейных дефектов приводит к функции радиального распределения, характерной для жидкости, так что для расчетов термодинамических величин можно использовать традиционный [8, 9] формализм.

Поля локальных ориентаций и плотности дефектов не являются независимыми и связаны условием совместности [6], так что можно оставить только одно из них. В [5, 6] рассматривалась статистика дефектов, но было показано, что возможна также формулировка, основанная на статистике ориентаций. В несколько огрубленном виде она представлена в [10]. В настоящей работе мы даем ее усовершенствованный вариант.

ПЛАВЛЕНИЕ В РАМКАХ МОДЕЛИ ПОТТСА

Общий вид теории, основанной на статистике ориентаций, приведен в [10], и выглядит следующим образом. Пусть в каждой точке пространства задана ориентация локального порядка, так что мы имеем поле $U({\mathbf{r}})$ – элементов группы вращений (двумерных или трехмерных, согласно размерности пространства). Для того, чтобы применить статистику Гиббса, нам необходимо записать энергию системы как функционал этого поля (эффективный гамильтониан), а затем вычислить статсумму:

В [11] было показано, как можно получить (1) из микроскопической модели путем суммирования по конфигурациям дефектов, обеспечивающих данное поле ориентаций. Для исследования модели (1) в [10] было использовано простое, но эффективное приближение. Вместо непрерывной группы рассматривалось разбиение группового пространства на $n$ ориентационных ячеек, так что ориентация каждого кластера задавалась грубо – указывался лишь номер ячейки. При этом ядро взаимодействия $\hat {K}$ конструировалось следующим образом. Если в соседствующих кластерах ориентации совпадали (попадали в одну ориентационную ячейку), то выигрыш в энергии составлял $ - J.$ Если ориентации были разными, то энергия приравнивалась к нулю. Величина $J$ представляет собой энергию дефектов, которые нужно создать, чтобы обеспечить разориентацию соседних локальных кластеров. Таким образом, параметры $J,n$ характеризуют глубину и ширину ориентационного взаимодействия. Нетрудно заметить, что получившаяся модель представляет собой модель Поттса с $n$ состояниями. Ее свойства легко исследовать в приближении среднего поля. Очевидно, что основное состояние системы – когда все локальные ориентации одинаковы (попадают в одну ориентационную ячейку). Оно реализуется при нулевой температуре. С ростом температуры появляется вероятность попасть в другую ячейку, но по-прежнему вероятность попасть в выделенную ячейку $\omega \sim 1,$ а остальные – равновероятны, и вероятность попасть в них $\frac{{1 - \omega }}{{n - 1}}.$ Рассматривая некоторый кластер и полагая, что соседние с ним распределены по ориентациям в соответствии с этими вероятностями, получаем, что его энергия равна $ - J\nu \omega ,$ если его ориентация попадает в выделенную ячейку, и $\frac{{J\nu (1 - \omega )}}{{n - 1}}$ в остальных $n - 1$ случаях. Здесь $\nu $ – количество ближайших соседей. Поскольку локальный кластер так же, как и система в целом, подчиняется статистике Гиббса, получаем уравнение Обозначив $x = \frac{{J\nu (n\omega - 1)}}{{T(n - 1)}},$ перепишем это уравнение в удобном для графического решения виде Графическое решение представлено на рис. 1.

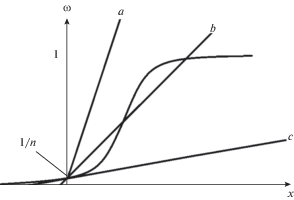
При высокой температуре (кривая a) существует только одно решение $\omega = \frac{1}{n}$ (все ориентации равновероятны, что соответствует жидкости). При температуре ${{T}_{{\text{c}}}} = \frac{{J\nu (n - 2)}}{{2(n - 2)\ln (n - 1)}}$ (кривая b) происходит переход к решению $\omega \sim 1$ (кристалл), которое устойчиво при низких температурах. Несмотря на очевидную грубость, модель качественно неплохо описывает плавление: оно представляется переходом первого рода, причем кристалл можно перегреть лишь на малую величину, в то время как жидкость можно значительно переохладить. Основные недостатки модели – наличие низкотемпературной точки абсолютной неустойчивости жидкости (кривая с на рис. 1), что приводит к невозможности аморфного состояния, а также идентичное описание плавления в двумерном и трехмерном случаях. Ниже мы предлагаем решение модели (1), свободное от этих недостатков. Отметим, что идея такого решения была предложена в [10].

ИНТЕГРИРОВАНИЕ ПО ГРУППЕ И ПРИБЛИЖЕНИЕ СРЕДНЕГО ПОЛЯ

В модели (1) $U({\mathbf{r}})$ – элемент группы вращений в представлении унитарных матриц

где ${\mathbf{e}}_{i}^{'}({\mathbf{r}})$ – векторы базиса, соответствующего ориентации локального порядка в точке ${\mathbf{r}},$ а ${{{\mathbf{e}}}_{j}}$ – векторы глобального базиса. Используем преобразование к сопряженному полю $\Omega {\text{:}}$Теперь необходимо вычислить локальный интеграл по группе вращений с использованием инвариантной меры на группе. Такой интеграл вычислен в [12]: где $d$ – размерность пространства. Поле $\Omega $ является свободным, можно функциональный интеграл по нему вычислить методом перевала, что соответствует приближению среднего поля. Для средней $\Omega $ естественно предположить изотропный вид $\left\langle {{{\Omega }_{{ij}}}} \right\rangle = {{\delta }_{{ij}}},$ тогда средняя матрица поворота тоже изотропна: Обозначив получим удельный термодинамический потенциал среднеполевой теории в виде: Минимизация (10) по $x$ дает уравнение на однородное перевальное значение: Для двумерной системы ${{\Phi }_{2}}(x)$ есть модифицированная функция Бесселя нулевого порядка, и уравнение (11) предсказывает переход второго рода при температуре ${{T}_{{\text{c}}}} = K$ от упорядоченной фазы ($x \ne 0,y\sim 1$) к разупорядоченной ($x = 0,y = 0$). Нетрудно, однако, заметить, что в двумерной системе модель (1) в предположении (8) представляет собой известную $XY$ модель, свойства которой известны (см., например, [2]). Таким образом, (11) дает решение $XY$ модели в приближении среднего поля. При учете флуктуаций ориентационный порядок разрушается также и ниже ${{T}_{{\text{c}}}},$ а переход становится непрерывным.

Для трехмерной системы графическое решение (11) представлено на рис. 2. Оно дает переход первого рода от ориентационно упорядоченной фазы ($x \ne 0,$ $y\sim 1,$ кристалл) к разупорядоченной ($x = 0,$ $y = 0,$ жидкость).

Это решение похоже на решение на рис. 1, но для него жидкость сохраняет метастабильную устойчивость вплоть до нулевой температуры.

ВЫВОДЫ

• Рассмотренная теория справедлива для веществ, в которых локальный порядок сохраняется при плавлении, а область, составленная из локально упорядоченных кластеров, остается связной.

• Вторым допущением является выражение (8), нарушение которого включит в рассмотрение неизотропные жидкости (жидкие кристаллы).

• В теории имеется один явный феноменологический параметр $K$ – он задает температуру плавления. Вторым (скрытым) параметром является количество атомов, участвующих в интеграле (9). Оно определяет молярную теплоту перехода. Это число зависит только от типа локальной симметрии. Таким образом, молярная теплота перехода, измеренная в единицах температуры плавления, должна быть универсальна для веществ с одинаковым локальным порядком.

• Рассмотренная теория дает адекватное описание как в двумерном, так и трехмерном случае. В последнем случае она предсказывает метастабильность жидкости вплоть до нулевой температуры, в отличие от работы [10].

Работа поддержана РФФИ (проекты 18-03-00433, 18-02-00643).