1. На главную
  2. Электронные версии
  3. Расплавы
  4. № 5, 2020

Расплавы, 2020, № 5, стр. 469-479

К теории направленного затвердевания при наличии области фазового превращения

Д. В. Александров a, *, И. Г. Низовцева a, И. В. Александрова a, А. А. Иванов a, И. О. Стародумов a, Л. В. Торопова a, О. В. Гусакова b, В. Г. Шепелевич c

a Уральский федеральный университет им. первого Президента России Б.Н. Ельцина
Екатеринбург, Россия

b УО “Международный государственный экологический институт им. А.Д. Сахарова”
Минск, Беларусь

c Белорусский государственный университет
Минск, Беларусь

* E-mail: dmitri.alexandrov@urfu.ru

Поступила в редакцию 25.07.2018
После доработки 12.10.2018
Принята к публикации 11.01.2019

Полный текст (PDF)

Аннотация

В работе развита модель процесса направленного затвердевания бинарных расплавов с двухфазной зоной, когда доля жидкой фазы описывается пространственно-временнóй скейлинговой зависимостью. Введены автомодельные переменные с законами роста межфазных границ обратно пропорциональными квадратному корню из времени. Математическая модель процесса переформулирована с использованием автомодельных переменных. Определены точные автомодельные решения уравнений тепломассопереноса при наличии двух подвижных границ фазового перехода: твердая фаза–двухфазная зона и двухфазная зона–жидкая фаза. В виде интегральных выражений найдены распределения температуры и концентрации примеси в твердой фазе, двухфазной области и расплаве. Уменьшение безразмерной температуры охлаждаемой границы приводит к увеличению скорости кристаллизации и повышению доли жидкой фазы. Определены скорость кристаллизации, константы параболического роста и доля жидкой фазы на границе твердая фаза–двухфазная зона в зависимости от скейлингового параметра, а также теплофизических констант затвердевающего расплава. Найдены положения границ фазового перехода между твердой фазой и двухфазной областью, а также двухфазной областью и бинарным расплавом. Проанализированы зависимости для скорости затвердевания (обратно пропорциональные квадратному корню из времени). При этом показано, что скейлинговый параметр существенно влияет на скорость процесса затвердевания и на долю жидкой фазы в области фазового превращения. Развитая модель и метод ее решения могут быть обобщены на случай направленного затвердевания многокомпонентных расплавов при наличии нескольких областей фазового превращения (например, основной и котектической двухфазных зон при кристаллизации трехкомпонентных расплавов).

Ключевые слова: фазовые переходы, кристаллизация, двухфазная зона

ВВЕДЕНИЕ

Большое число процессов кристаллизации описывается с помощью классической термодиффузионной модели Стефана с плоской границей раздела фаз между чисто твердым материалом и жидким расплавом [1–5]. Математическая модель процесса включает в себя уравнения теплопроводности и диффузии растворенной примеси, записываемые в твердой и жидкой фазах, начальные условия, а также граничные условия баланса тепла и массы, непрерывности температуры и скачка концентрации на фронте затвердевания. Однако, при росте твердой фазы происходит вытеснение растворенной примеси в окружающий расплав. При этом интенсивность процесса вытеснения примеси зависит от химического состава растворенных примесей (от расплава, претерпевающего фазовое превращение), а также от скорости кристаллизации в случае высокоскоростного затвердевания [6–9]. С течением времени градиент концентрации примеси (умноженный на коэффициент наклона линии ликвидус) на фронте кристаллизации может превысить температурный градиент, что приведет к возникновению концентрационного переохлаждения [3, 10–13]. Появление переохлажденного слоя расплава перед фронтом затвердевания создает благоприятные условия для развития морфологической неустойчивости, роста выступов твердой фазы вглубь расплава, зарождения и роста элементов твердой фазы [15–23]. Другими словами, перед фронтом кристаллизации образуется область двухфазного состояния вещества – двухфазная зона [24–29]. Процессы роста твердой фазы в такой зоне определяют динамические характеристики процесса кристаллизации и свойства затвердевающего материала. В литературе известно большое количество различных реализаций процесса роста твердого вещества в переохлажденной двухфазной области, которые описываются различными математическими моделями (см., например, [30–39]). В настоящей работе рассматривается теория направленной кристаллизации, когда плотность жидкой фазы в двухфазной области описывается с помощью пространственно-временнóй скейлинговой зависимости [40].

УРАВНЕНИЯ ТЕПЛОМАССОПЕРЕНОСА

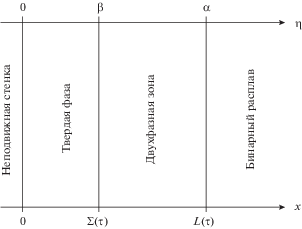
Рассмотрим процесс направленного затвердевания бинарного расплава вдоль пространственной оси x (рис. 1). Область протекания процесса разделена на три региона: твердую фазу, двухфазную зону и расплав. Обозначим через $\Sigma \left( \tau \right)$ и $L\left( \tau \right)$ координаты границ областей твердая фаза–двухфазная зона и двухфазная зона–расплав, соответственно. Эти границы двигаются вдоль оси $x$ вследствие заданного температурного режима, обеспечивающего процесс затвердевания. Диффузия примеси в двухфазной зоне (${\Sigma }\left( \tau \right) < x < L\left( \tau \right)$) описывается уравнением

(1)
$S\frac{\partial }{{\partial \tau }}\int\limits_x^{x + {\Delta }x} {{{c}_{m}}} \left( {\xi ,\tau } \right)\rho \left( {\xi ,\tau } \right)d\xi = - \left[ {{{S}_{l}}\left( {x + {\Delta }x,\tau } \right)j\left( {x + {\Delta }x,\tau } \right) - {{S}_{l}}\left( {x,\tau } \right)j\left( {x,\tau } \right)} \right],~$
где $S$ и ${{S}_{l}}$ – общее поперечное сечение образца и поперечное сечение, занятое жидкой фазой; ${{c}_{m}}$ – концентрация примеси, определенная по жидкой фазе; $\rho $ – объемная доля жидкой фазы в двухфазной области; $\tau $ – время. Диффузионный поток $\vec {j}$ определяется классическим законом Фика: $\vec {j} = - {{D}_{l}}\nabla {{c}_{m}}$, где ${{D}_{l}}$ – коэффициент диффузии примеси. Связь между $S$ и ${{S}_{l}}$ будем описывать с помощью простейшего закона: ${{S}_{l}} = S\rho $. Подставляя эту зависимость в уравнение (1), применяя теорему о среднем для преобразования интегрального слагаемого, умножая уравнение на ${\Delta }{{x}^{{ - 1}}}$ и переходя к пределу ${\Delta }x \to 0$, получим:

(2)
$\frac{\partial }{{\partial \tau }}\left( {{{c}_{m}}{\kern 1pt} {\kern 1pt} \rho } \right) = {{D}_{l}}\frac{\partial }{{\partial x}}\left( {\rho \frac{{\partial {{c}_{m}}}}{{\partial x}}} \right),\,\,\,\,~\Sigma \left( \tau \right) < x < L\left( \tau \right).$
Рис. 1.

Схема процесса направленного затвердевания с двухфазной зоной.

Уравнение диффузии в расплаве запишем в традиционном виде

(3)
$\frac{{\partial {{c}_{l}}}}{{\partial \tau }} = {{D}_{l}}\frac{{{{\partial }^{2}}{{c}_{l}}}}{{\partial {{x}^{2}}}},\,\,\,\,~x > L\left( \tau \right),$
где ${{c}_{l}}$ – концентрация примеси в жидкой фазе. Диффузией примеси в твердой фазе будем пренебрегать.

Уравнение теплопроводности в двухфазной зоне выводится аналогично уравнению (2) и имеет вид

(4)
$\left( {{{C}_{l}}{\kern 1pt} {{\rho }_{l}}{\kern 1pt} \rho + {{C}_{s}}{\kern 1pt} {{\rho }_{s}}\left( {1 - \rho } \right)} \right)\frac{{\partial {{\theta }_{m}}}}{{\partial \tau }} = \frac{\partial }{{\partial x}}\left( {\lambda \left( \rho \right)\frac{{\partial {{\theta }_{m}}}}{{\partial x}}} \right),\,\,\,\,~\Sigma \left( \tau \right) < x < L\left( \tau \right),$
где ${{\theta }_{m}}$ – температура в двухфазной области, $\lambda \left( \rho \right) = {{\lambda }_{s}}\left( {1 - \rho } \right) + {{\lambda }_{l}}{\kern 1pt} \rho $, ${{C}_{l}}$ и ${{C}_{s}}$ – теплоемкости в жидкой и твердой фазах, ${{\rho }_{l}}$ и ${{\rho }_{s}}$ – плотности жидкой и твердой фаз, ${{\lambda }_{l}}$ и ${{\lambda }_{s}}$ коэффициенты теплопроводности в этих фазах.

Уравнения теплопроводности в затвердевшем материале ($0 < x < {\Sigma }\left( \tau \right)$) и расплаве ($x > L\left( \tau \right)$) запишем в виде

(5)
$\frac{{\partial {{\theta }_{s}}}}{{\partial \tau }} = {{a}_{s}}\frac{{{{\partial }^{2}}{{\theta }_{s}}}}{{\partial {{x}^{2}}}},\,\,\,\,~0 < x < {\Sigma }\left( \tau \right),$
(6)
$\frac{{\partial {{\theta }_{l}}}}{{\partial \tau }} = {{a}_{l}}\frac{{{{\partial }^{2}}{{\theta }_{l}}}}{{\partial {{x}^{2}}}},\,\,\,\,~x > L\left( \tau \right),$
где ${{\theta }_{s}}$ и ${{\theta }_{l}}$ – температуры твердой и расплавленной фаз, ${{a}_{s}}$ и ${{a}_{l}}$ – коэффициенты температуропроводности в этих фазах.

В качестве граничного условия на твердой поверхности $x = 0$ возьмем условие фиксированной температуры, т.е.

(7)
${{\theta }_{s}} = {{\theta }_{0}},\,\,\,\,~x = 0.$

На поверхности между твердой фазой и двухфазной зоной, имеем граничные условия непрерывности температуры, баланса тепла и массы

(8)
${{\theta }_{s}} = {{\theta }_{m}} = \theta {\text{*}} - m{{c}_{m}},~\,\,\,\,~\left( {1 - k} \right){{c}_{m}}\frac{{d{\Sigma }}}{{d\tau }} = - {{D}_{l}}\frac{{\partial {{c}_{m}}}}{{\partial x}},\,\,\,\,~x = {\Sigma }\left( \tau \right),$
(9)
${{\lambda }_{s}}\frac{{\partial {{\theta }_{s}}}}{{\partial x}} - \lambda \left( \rho \right)\frac{{\partial {{\theta }_{m}}}}{{\partial x}} = \rho {{L}_{V}}\frac{{d{\Sigma }}}{{d\tau }},\,\,\,\,~x = {\Sigma }\left( \tau \right),$
где $k$ – коэффициент распределения примеси, ${{L}_{V}}$ – скрытая теплота затвердевания, $\theta {\text{*}}$ – температура фазового перехода чистого (без примеси) расплава, $m$ – наклон линии ликвидус.

На границе между двухфазной областью и расплавом выполняются условия непрерывности температуры и концентрации примеси, а также их потоков:

(10)
${{\theta }_{m}} = {{\theta }_{l}},\,\,\,\,~{{c}_{m}} = {{c}_{l}},\,\,\,\,~\frac{{\partial {{\theta }_{m}}}}{{\partial x}} = \frac{{\partial {{\theta }_{l}}}}{{\partial x}},\,\,\,\,~\frac{{\partial {{c}_{m}}}}{{\partial x}} = \frac{{\partial {{c}_{l}}}}{{\partial x}},\,\,\,\,~x = L\left( \tau \right).$
Температура (${{\theta }_{{l\infty }}}$) и концентрация примеси (${{c}_{{l\infty }}}$) вдали от границы $L\left( \tau \right)$ в жидкой фазе считаются заданными, т.е.
(11)
${{\theta }_{l}} \to {{\theta }_{{l\infty }}},\,\,\,\,~{{c}_{l}} \to {{c}_{{l\infty }}},~\,\,\,\,~x \to \infty .$
Представим объемную долю жидкой фазы в двухфазной области с помощью следующей масштабно-временнóй скейлинговой зависимости [40, 41]
(12)
$\rho \left( x \right) = {{\left[ {a\frac{x}{L} + 1 - a} \right]}^{{D - 1}}},$
где $D$ – скейлинговый параметр, $a$ – параметр, аппроксимирующий функцию $\rho \left( x \right).$ Отметим, что функция $\rho \left( x \right)$ может быть определена с помощью модели неравновесной двухфазной зоны [42–44]. Однако такой подход потребует решения очень сложной интегро-дифференциальной модели с движущимися границами.

АВТОМОДЕЛЬНЫЕ РЕШЕНИЯ

Решение модели (2)–(12) будем искать с использованием следующих автомодельных переменных и безразмерных параметров:

(13)
$\begin{gathered} \eta = \frac{x}{{\sqrt {{{D}_{l}}\tau } }},~\,\,\,\,~\alpha = \frac{L}{{\sqrt {{{D}_{l}}\tau } }},\,\,\,\,~\beta = \frac{{\Sigma }}{{\sqrt {{{D}_{l}}\tau } }},\,\,\,\,~{{p}_{s}} = \frac{{{{\theta }_{s}}}}{{m{{c}_{{l\infty }}}}},\,\,\,\,~{{p}_{l}} = \frac{{{{\theta }_{l}}}}{{m{{c}_{{l\infty }}}}},\,\,\,\,~{{p}_{m}} = \frac{{{{\theta }_{m}}}}{{m{{c}_{{l\infty }}}}}, \\ {{q}_{l}} = \frac{{{{c}_{l}}}}{{{{c}_{{l\infty }}}}},\,\,\,\,~{{q}_{m}} = \frac{{{{c}_{m}}}}{{{{c}_{{l\infty }}}}},\,\,\,\,~{{p}_{0}} = \frac{{{{\theta }_{0}}}}{{m{{c}_{{l\infty }}}}},\,\,\,\,~{\Lambda } = \frac{{{{\lambda }_{s}}}}{{{{\lambda }_{l}}}},\,\,\,\,~p{\kern 1pt} * = \frac{{\theta {\kern 1pt} {\text{*}}}}{{m{{c}_{{l\infty }}}}},\,\,\,\,~{{p}_{{l\infty }}} = \frac{{{{\theta }_{{l\infty }}}}}{{m{{c}_{{l\infty }}}}}. \\ \end{gathered} $
Интегрируя уравнения (2)–(6) в переменных (13) и переписывая с их помощью условия (7)–(11), получим
(14)
${{q}_{m}}\left( \eta \right) = {{C}_{1}} + {{C}_{2}}\int\limits_\beta ^\eta {\frac{{\exp ({{ - {{y}^{2}}} \mathord{\left/ {\vphantom {{ - {{y}^{2}}} 4}} \right. \kern-0em} 4})}}{{\rho \left( y \right)}}} dy,\,\,\,\,~\beta < \eta < \alpha ,$
(15)
${{p}_{m}}\left( \eta \right) = {{C}_{5}} + {{C}_{6}}\int\limits_\beta ^\eta {\frac{{J\left( y \right)dy}}{{g\left( y \right)}}} ,~\,\,\,\,\beta < \eta < \alpha ,$
(16)
${{q}_{l}}\left( \eta \right) = {{C}_{3}} + {{C}_{4}}\int\limits_\alpha ^\eta {\exp ({{ - {{y}^{2}}} \mathord{\left/ {\vphantom {{ - {{y}^{2}}} 4}} \right. \kern-0em} 4})dy} ,\,\,\,\,\eta > \alpha ,$
(17)
${{p}_{s}}\left( \eta \right) = {{p}_{0}} + {{C}_{7}}\int\limits_0^\eta {\exp \left( { - \frac{{{{\varepsilon }_{s}}{{y}^{2}}}}{4}} \right)dy} ,~\,\,\,\,0 < \eta < \beta ,$
(18)
${{p}_{l}}\left( \eta \right) = {{C}_{8}} + {{C}_{9}}\int\limits_\alpha ^\eta {\exp \left( { - \frac{{{{\varepsilon }_{l}}{{y}^{2}}}}{4}} \right)dy} ,~\,\,\,\,\eta > \alpha .$
Здесь введены следующие обозначения: ${{\varepsilon }_{s}} = {{{{D}_{l}}} \mathord{\left/ {\vphantom {{{{D}_{l}}} {{{a}_{s}}}}} \right. \kern-0em} {{{a}_{s}}}},$ ${{\varepsilon }_{l}} = {{{{D}_{l}}} \mathord{\left/ {\vphantom {{{{D}_{l}}} {{{a}_{l}}}}} \right. \kern-0em} {{{a}_{l}}}}$,
$\rho \left( y \right) = {{\left[ {a\frac{y}{\alpha } + 1 - a} \right]}^{{D - 1}}},\,\,\,\,~g\left( y \right) = \rho \left( y \right) + {\Lambda }\left[ {1 - \rho \left( y \right)} \right],$
$J\left( y \right) = \exp \left[ { - \frac{{{{D}_{l}}}}{{2{{a}_{l}}}}\int\limits_0^y {\frac{{\left[ {\rho \left( y \right) + {\Lambda }{{a}_{l}}a_{s}^{{ - 1}}\left( {1 - \rho \left( y \right)} \right)} \right]ydy}}{{g\left( y \right)}}} } \right].$
Произвольные постоянные ${{C}_{i}}$ ($i = 1 \ldots 9$) и параметр $\beta $ определяются следующими граничными условиями:
(19)
${{p}_{s}} = {{p}_{m}} = p{\text{*}} - {{q}_{m}},~\,\,\,\,~\frac{{\left( {1 - k} \right)\beta {{q}_{m}}}}{2} = - \frac{{d{{q}_{m}}}}{{d\eta }},\,\,\,\,~\eta = \beta ,$
(20)
${\Lambda }\frac{{d{{p}_{s}}}}{{d\eta }} - \left[ {\rho + {\Lambda }\left( {1 - \rho } \right)} \right]\frac{{d{{p}_{m}}}}{{d\eta }} = G\rho \beta ,\,\,\,\,~G = \frac{{{{L}_{V}}{{D}_{l}}}}{{2{{\lambda }_{l}}m{{c}_{{l\infty }}}}},\,\,\,\,~\eta = \beta ,$
(21)
${{p}_{m}} = {{p}_{l}},\,\,\,\,~{{q}_{m}} = {{q}_{l}},\,\,\,\,~\frac{{d{{p}_{m}}}}{{d\eta }} = \frac{{d{{p}_{l}}}}{{d\eta }},~\,\,\,\,\,~\frac{{d{{q}_{m}}}}{{d\eta }} = \frac{{d{{q}_{l}}}}{{d\eta }},~\,\,\,\,~\eta = \alpha ,$
(22)
${{p}_{l}} \to {{p}_{{l\infty }}},\,\,\,\,~{{q}_{l}} \to 1,~\,\,\,\,~\eta \to \infty .$
Таким образом, распределения концентрации примеси и температуры в двухфазной системе определяются решениями (14)–(18), а девять произвольных постоянных и параметр $\beta $ (который характеризует скорость движения границы между твердой фазой и двухфазной зоной), определяются десятью граничными условиями (19)–(22).

ЗАКЛЮЧЕНИЕ

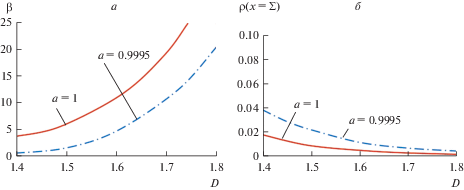
Полученное аналитическое решение показано на рис. 2–4 для сплавов Al–Cu и Fe–Ni. Рисунки 2a–4a демонстрируют, что скорость движения межфазной границы (скорость затвердевания ${{d{\Sigma }} \mathord{\left/ {\vphantom {{d{\Sigma }} {d\tau }}} \right. \kern-0em} {d\tau }} = {\beta \mathord{\left/ {\vphantom {\beta {(2\sqrt {{{D}_{l}}\tau } )}}} \right. \kern-0em} {(2\sqrt {{{D}_{l}}\tau } )}}$) увеличивается с ростом скейлингового параметра $D$. Рисунки 2б–4б иллюстрируют, что с ростом скейлингового коэффициента уменьшается объемная доля жидкой фазы на границе $x = {\Sigma }$ фазового перехода. Это означает, что с ростом $D$ уменьшается свободное пространство между растущими структурами твердого материала. Уменьшение безразмерной температуры ${{p}_{0}}$ охлаждаемой границы приводит к увеличению скорости кристаллизации (рис. 2a, 3a) и повышает долю жидкой фазы $\rho $ (рис. 2б, 3б). На рис. 4 показано влияние изменения параметра $a$ (определяющего плотность затвердевшего вещества в области фазового превращения) на скорость затвердевания и граничную долю жидкости. С увеличением этого параметра скорость ${{d{\Sigma }} \mathord{\left/ {\vphantom {{d{\Sigma }} {d\tau }}} \right. \kern-0em} {d\tau }}$ увеличивается, а доля жидкой фазы $\rho $ уменьшается при фиксированном значении скейлингового параметра $D$.

Рис. 2.

Зависимости константы параболического роста $\beta $ и доли жидкой фазы $\rho $ на границе твердая фаза–двухфазная зона (при $x = {\Sigma }$ или $\eta = \beta $) от скейлингового параметра $D$ для сплава Al–Cu (4 мас. % Cu): $k = 0.17$, ${\Lambda } = 2.32$, $a = 1$, $G = 0.01$, $p* = 66$, ${{\varepsilon }_{l}} = {{\varepsilon }_{s}} = {{10}^{{ - 4}}}$, $\alpha = 7071$, ${{p}_{{l\infty }}} = 100$.

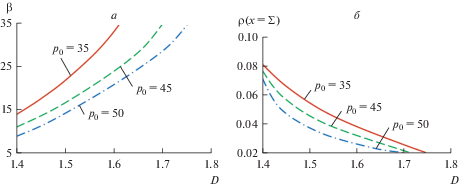
Рис. 3.

Зависимости константы параболического роста $\beta $ и доли жидкой фазы $\rho $ на границе твердая фаза–двухфазная зона (при $x = {\Sigma }$ или $\eta = \beta $) от скейлингового параметра $D$ для сплава Fe–Ni (0.38 мас. % Ni): $k = 0.68$, ${\Lambda } = 1.76$, $a = 1$, $G = 0.2$, $p* = 1529.5$, ${{\varepsilon }_{l}} = {{\varepsilon }_{s}} = {{10}^{{ - 4}}}$, $\alpha = 7071$, ${{p}_{{l\infty }}} = 1700$.

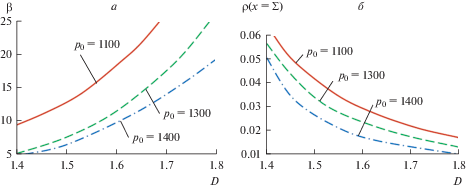
Рис. 4.

Зависимости константы параболического роста $\beta $ и доли жидкой фазы $\rho $ на границе твердая фаза–двухфазная зона (при $x = {\Sigma }$ или $\eta = \beta $) от скейлингового параметра $D$ для сплава Al–Cu (0.4 мас. % Cu): $k = 0.17$, ${\Lambda } = 2.32$, ${{p}_{0}} = 500$, $G = 0.1$, $p* = 660$, ${{\varepsilon }_{l}} = {{\varepsilon }_{s}} = {{10}^{{ - 4}}}$, $\alpha = 7071$, ${{p}_{{l\infty }}} = 800$.

Развиваемая в настоящей работе скейлинговая теория двухфазной зоны, описывающая кристаллизацию двухкомпонентных расплавов, может быть обобщена на затвердевание трехкомпонентных систем с основной и котектической двухфазными регионами на основе экспериментальных данных и теории предшествующих исследований [45–50].

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-58-00034 Бел_а и БРФФИ в рамках научного проекта № Ф18Р-195.

Список литературы

  1. Любов Б.Я. Теория кристаллизации в больших объемах. Москва: Наука. 1975.

  2. Авдонин Н.А. Математическое описание процессов кристаллизации. Рига: Зинатне. 1980.

  3. Buvevich Yu.A., Alexandrov D.V., Mansurov V.V. Macrokinetics of crystallization. New York: Begell House. 2001.

  4. Alexandrov D.V., Galenko P.K. Boundary integral approach for propagating interfaces in a binary non-isothermal mixture // Physica A. 2017. 469. P. 420–428.

  5. Galenko P.K., Alexandrov D.V., Titova E.A. The boundary integral theory for slow and rapid curved solid/liquid interfaces propagating into binary systems // Phil. Trans. R. Soc. A. 2018. 378. P. 20170218.

  6. Kurz W., Fisher D.J. Fundamentals of solidification // Aedermannsdorf: Trans. Tech. Publ. 1989.

  7. Galenko P.K. Rapid advancing of the solid-liquid interface in undercooled alloys // Mater. Sci. Eng. A. 2004. 375–377. P. 493–497.

  8. Galenko P.K., Danilov D.A., Alexandrov D.V. Solute redistribution around crystal shapes growing under hyperbolic mass transport // Int. J. Heat Mass Transfer. 2015. 89. P. 1054–1060.

  9. Alexandrov D.V., Galenko P.K. Selected mode for rapidly growing needle-like dendrite controlled by heat and mass transport // Acta Mater. 2017. 137. P. 64–70.

  10. Иванцов Г.П. “Диффузионное” переохлаждение при кристаллизации бинарного сплава // Доклады АН СССР. 1951. LXXXI. С. 179–182.

  11. Worster M.G. Solidification of an alloy from a cooled boundary // J. Fluid. Mech. 1986. 167. P. 481–501.

  12. Alexandrov D.V., Churbanov A.G., Vabishchevich P.N. Emergence of a mushy region in processes of binary melt solidification // Int. J. Fluid Mech. Research. 1999. 26. P. 248–264.

  13. Alexandrov D.V. On the theory of the formation of the two-phase concentration-supercooling region // Doklady Physics. 2003. 48. P. 481–486.

  14. Mullins W.W., Sekerka R.F. Stability of a planar interface during solidification of a dilute binary alloy // J. Appl. Phys. 1964. 35. P. 444–451.

  15. Sekerka R.F. Morphological stability // J. Cryst. Growth. 1968. 3–4. P. 71–81.

  16. Delves R.T. The theory of the stability of the solid-liquid interface under constitutional supercooling (II) // Phys. Stat. Sol. 1966. 17. P. 119–130.

  17. Alexandrov D.V., Ivanov A.O. Dynamic stability analysis of the solidification of binary melts in the presence of a mushy region: changeover of instability // J. Cryst. Growth. 2000. 210. P. 797–810.

  18. Alexandrov D.V. Self-similar solidification: morphological stability of the regime // Int. J. Heat Mass Transfer. 2004. 47. P. 1383–1389.

  19. Alexandrov D.V., Malygin A.P. Convective instability of directional crystallization in a forced flow: The role of brine channels in a mushy layer on nonlinear dynamics of binary systems // Int. J. Heat Mass Transfer. 2011. 54. P. 1144–1149.

  20. Alexandrov D.V., Malygin A.P. Transient nucleation kinetics of crystal growth at the intermediate stage of bulk phase transitions // J. Phys. A: Math. Theor. 2013. 46. P. 455101.

  21. Alexandrov D.V. Nucleation and crystal growth in binary systems // J. Phys. A: Math. Theor. 2014. 47. P. 125 102.

  22. Alexandrov D.V., Nizovtseva I.G. Nucleation and particle growth with fluctuating rates at the intermediate stage of phase transitions in metastable systems // Proc. R. Soc. A. 2014. 470. P. 20 130 647.

  23. Alexandrov D.V. On the theory of transient nucleation at the intermediate stage of phase transitions // Phys. Lett. A. 2014. 378. P. 1501–1504.

  24. Борисов В.Т. Теория двухфазной зоны металлического слитка // М.: Металлургия. 1987.

  25. Flemings M. Solidification processing // New York: McGraw Hill. 1974.

  26. Chalmers B. Principles of solidification // New York: Wiley. 1964.

  27. Herlach D., Galenko P., Holland-Moritz D. Metastable solids from undercooled melts // Amsterdam: Elsevier. 2007.

  28. Hills R.N., Loper D.E., Roberts P.H. A thermodynamically consistent model of a mushy zone // Q. J. Appl. Math. 1983. 36. P. 505–539.

  29. Fowler A.C. The formation of freckles in binary alloys // IMA J. Appl. Math. 1985. 35. P. 159–174.

  30. Alexandrov D.V., Malygin A.P., Alexandrova I.V. Solidification of leads: approximate solutions of non-linear problem // Ann. Glaciol. 2006. 44. P. 118–122.

  31. Martin S., Kauffman P. The evolution of under-ice melt ponds, or double diffusion at the freezing point // J. Fluid Mech. 1974. 64. P. 507–527.

  32. Worster M.G. Convection in mushy layers // Annu. Rev. Fluid Mech. 1997. 29. P. 91–122.

  33. Schulze T.P., Worster M.G. A time-dependent formulation of the mushy-zone free-boundary problem // J. Fluid Mech. 2005. 541. P. 193–202.

  34. Alexandrov D.V., Malygin A.P. Self-similar solidification of an alloy from a cooled boundary // Int. J. Heat Mass Transfer. 2006. 49. P. 763–769.

  35. Kerr R.C., Woods A.W., Worster M.G., Huppert H.E. Solidification of an alloy cooled from above. Part I. Equilibrium growth // J. Fluid Mech. 1990. 216. P. 323–342.

  36. Alexandrov D.V., Malygin A.P. Coupled convective and morphological instability of the inner core boundary of the Earth // Phys. Earth Planet. Inter. 2011. 189. P. 134–141.

  37. Jones D.W.R., Worster M.G. Fluxes through steady chimneys in a mushy layer during binary alloy solidification // J. Fluid Mech. 2013. 714. P. 127–151.

  38. Alexandrov D.V., Bashkirtseva I.A., Ryashko L.B. Nonlinear dynamics of mushy layers induced by external stochastic fluctuations // Phil. Trans. R. Soc. A. 2018. 376. P. 20170216.

  39. Alexandrov D.V., Ivanov A.A., Alexandrova I.V. Analytical solutions of mushy layer equations describing directional solidification in the presence of nucleation // Phil. Trans. R. Soc. A. 2018. 376. P. 20 170 217.

  40. Alexandrov D.V., Ivanov A.O. Scaling properties of a two-phase zone in directed crystallization // Doklady Physics. 2002. 47. P. 499–503.

  41. Vicsek T. Fractal growth phenomena // Singapore: World Scientific. 1989.

  42. Mansurov V.V. The nonlinear dynamics of solidification of a binary melt with a nonequilibrium mushy region // Math. Comput. Modell. 1990. 14. P. 819–821.

  43. Aseev D.L., Alexandrov D.V. Directional solidification of binary melts with a nonequilibrium mushy layer // Int. J. Heat Mass Transfer. 2006. 49. P. 4903–4909.

  44. Aseev D.L., Alexandrov D.V. Nonlinear dynamics for the solidification of binary melt with a nonequilibrium two-phase zone // Phys. Dokl. 2006. 51. P. 291–295.

  45. Aitta A., Huppert H.E., Worster M.G. Diffusion-controlled solidication of a ternary melt from a cooled boundary // J. Fluid Mech. 2001. 432. P. 201–217.

  46. Anderson D.M. A model for diffusion-controlled solidification of ternary alloys in mushy layers // J. Fluid Mech. 2003. 483. P. 165–197.

  47. Alexandrov D.V., Ivanov A.A. The Stefan problem of solidification of ternary systems in the presence of moving phase transition regions // J. Exper. Theor. Physics. 2009. 108. P. 821–829.

  48. Alexandrov D.V., Ivanov A.A. Solidification of a ternary melt from a cooled boundary, or nonlinear dynamics of mushy layers // Int. J. Heat Mass Transfer. 2009. 52. P. 4807–4811.

  49. Alexandrov D.V. Nonlinear dynamics of solidification in three-component systems // Doklady Physics. 2008. 53. P. 471–475.

  50. Alexandrov D.V., Ivanov A.A. Nonlinear dynamics of directional solidification of ternary solutions with mushy layers // Heat Mass Transfer. 2009. 45. P. 1467–1472.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Расплавы

Архивы выпусков Информация о журнале Отправить рукопись в журнал