1. На главную
  2. Электронные версии
  3. Расплавы
  4. № 5, 2020

Расплавы, 2020, № 5, стр. 521-531

Структурные характеристики малой группы зафиксированных частиц и максимальная плотность случайной упаковки жестких сфер

А. Б. Шубин *

Институт металлургии Уральского отделения РАН
Екатеринбург, Россия

* E-mail: abshubin@gmail.com

Поступила в редакцию 26.05.2020
После доработки 15.06.2020
Принята к публикации 19.06.2020

Полный текст (PDF)

Аннотация

Рассмотрено определение случайных упаковок жестких сфер, не предполагающее каких-либо специфических особенностей ближнего порядка. Полученные результаты позволяют (в частности) определить максимально возможную плотность случайной упаковки, в которой отсутствуют какие-либо виды явного или скрытого дальнего порядка. Представлены новые данные компьютерных экспериментов, описывающие статистико-геометрические свойства случайных упаковок двухмерных (2D) и трехмерных (3D) жестких сферических частиц. Исследованы закономерности поведения малой группы случайно выбранных и зафиксированных сфер при разных плотностях упаковки, различия между свойствами этой группы и основного “большого” ансамбля, которые следуют, в том числе, из полученных теоретических результатов. Найденные экспериментально закономерности согласуются с предложенным теоретическим решением. Пусть ансамбль состоит из N частиц, занимающих общий объем V (при плотности упаковки η = Nu/V, где u – объем одной частицы). Максимально возможная плотность случайной упаковки сферических частиц (ηmax) задается следующим геометрическим условием: средний объем многогранника Вороного в случайной плотной упаковке не может быть меньше, чем среднее значение исключенного объема для всех точек этой упаковки. Для произвольной точки ансамбля, лежащей на расстоянии x от ближайшего к ней центра сферы (единичного радиуса, R = 1), исключенный объем (w) определяется следующими соотношениями. В двухмерном пространстве: w(x) = π(2 – x)2 при 0 ≤ x ≤ 2; w(x) = 0 при x > 2. В трехмерном пространстве: w(x) = (4π/3)(2 – x)3 при 0 ≤ x ≤ 2; w(x) = 0 при x > 2. Усредняя w(x) для всех точек объема ансамбля частиц, можно найти средний исключенный объем 〈w〉 для данной плотности упаковки (η). Можно сформулировать также следующее положение, вытекающее из описанного выше условия: если плотность упаковки η превышает ηmax, то такая упаковка не может быть статистически однородной (гомогенной). Использованный в работе подход позволяет вычислить максимально возможное значение (верхнюю границу) для плотности случайной плотной упаковки. Эта величина составляет ηmax = 0.6813 ± 0.001 (в двухмерном случае ансамбля жестких дисков) и ηmax = 0.6329 ± 0.0005 (для трехмерного ансамбля жестких сфер).

Ключевые слова: случайная плотная упаковка, средний исключенный объем, жесткие сферы, жесткие диски, максимальная плотность, фиксированная частица, малая группа, случайная подрешетка

ВВЕДЕНИЕ

Случайные упаковки (ансамбли) одинаковых сферических частиц в двух- и трехмерном евклидовом пространстве могут служить удобными идеализированными моделями структуры ряда жидких и коллоидных систем, композитов, расплавов и аморфных металлов [1], использоваться при расчете термодинамических и структурных свойств жидкометаллических систем [2]. Эти модели продолжают привлекать внимание исследователей, обнаруживающих новые неочевидные закономерности их строения и свойств [3–9]. Историография работ Бернала и ряда других известных авторов в данной области представлена в обзорной работе Финни [10]. Предельная плотность (η = Nu/V, где N – количество частиц; u – объем одной частицы; V – общий объем всего ансамбля) для трехмерной упаковки жестких сфер (случайная плотная упаковка, СПУ), найденная экспериментально Скоттом [11] и равная 0.637, была подтверждена в дальнейших исследованиях. Принятым значением считается величина, полученная в работе [12] и равная 0.6366. В работе [13] систематизированы и табулированы близкие значения η (СПУ), полученные различными методами – прямым (натурным) экспериментом, в различных вычислительных моделях упаковок, а также путем термодинамических расчетов. Финни и Вудкок [14] полагают, что данная величина имеет глубокий фундаментальный смысл и отвечает известной математической постоянной – константе Буффона (2/π = 0.6366198…).

Одной из основных проблем, касающихся СПУ жестких сфер, является отсутствие общепринятого определения этих объектов. В известной работе [15], с одной стороны, принимается, что это – упаковка, в которой отсутствует статистически значимый дальний порядок. С другой стороны, предложенное определение СПУ [15] основано на предположении об особенностях только ближайшего окружения сфер (размерности 1, 2 или 3).

Вопросу определения случайной плотной упаковки специально посвящена, в частности, широко цитируемая работа Торквато с соавторами [16]. В этом исследовании отмечается, что точное математическое определение СПУ-состояния ансамбля сфер должно относиться (быть применимым) к статистически гомогенной и изотропной системе идентичных сфер в пространстве размерности D. Далее в работе [16] констатируется, что случайная плотная упаковка не имеет строгого определения (ill-defined), что требует введения несколько иного понятия – “случайной максимально сжатой” (maximally random jammed, MRJ) упаковки.

Ранее [17, 18] автором было введено определение случайной плотной упаковки жестких сфер и, далее, одинаковых жестких выпуклых частиц [9] (в трехмерном пространстве), которое позволило найти, в частности, предел плотности СПУ. В работе [19] была рассмотрена система жестких дисков, а впоследствии в [20, 21] – случайные ансамбли жестких сфер в евклидовом пространстве любой размерности. Статьи [20, 21] содержат также доказательство основного положения и следствий из него, приведенных в более ранних работах.

В данном сообщении представлены новые результаты компьютерных экспериментов, описывающие статистико-геометрические свойства случайных упаковок двухмерных (2D) и трехмерных (3D) жестких сферических частиц. В частности, исследованы закономерности поведения малой группы случайно выбранных и зафиксированных сфер при разных плотностях упаковки, различия между свойствами этой группы и основного “большого” ансамбля, которые следуют, в том числе, из полученных ранее теоретических результатов.

СРЕДНИЙ ИСКЛЮЧЕННЫЙ ОБЪЕМ И ГЕОМЕТРИЧЕСКИЙ ПРЕДЕЛ ПЛОТНОСТИ

Основная идея работ автора, касающихся расчетов предельно возможной плотности случайных упаковок, состоит в следующем. В статистически однородной упаковке N одинаковых сфер в объеме V (численные значения N и V могут быть сколь угодно велики), дополнительно размещают группу из K таких же сфер (K $ \ll $ N). Каждая из этих добавочных частиц размещается в объеме V последовательно, случайным образом, и далее имеет фиксированные координаты. При заданной плотности упаковки η, это приводит к увеличению общего объема на Ku/η. Можно потребовать, чтобы алгоритм размещения (сколь угодно сложный) обеспечивал статистическую однородность упаковки. Это означает, что статистико-геометрические свойства произвольной частицы (из числа K) будут неотличимы от таковых для любой другой частицы ансамбля. В то же время, мы помним, что сферы (из числа K) размещены со случайными и фиксированными координатами друг относительно друга, т.е. образуют своего рода случайную “подрешетку”.

Можно показать, что для “большой” случайной упаковки, содержащей малую группу случайно расположенных частиц (из числа K), существует предельная плотность ηmax. При плотности упаковки η > ηmax статистическая гомогенность ансамбля неизбежно нарушается. Максимально возможная плотность случайной упаковки сферических частиц задается геометрическим условием [9, 17–21]: Средний объем многогранника Вороного в случайной плотной упаковке не может быть меньше, чем среднее значение исключенного объема для всех точек этой упаковки.

Это утверждение может быть записано в виде:

(1)
${u \mathord{\left/ {\vphantom {u \eta }} \right. \kern-0em} \eta } \geqslant \left\langle w \right\rangle (\eta ).~$

В данной формуле u/η есть средний объем многогранника Вороного (МВ), а функция 〈w〉(η) представляет собой зависимость среднего исключенного объема по всему ансамблю от плотности упаковки. Она задается следующим образом.

Для произвольной точки ансамбля, лежащей на расстоянии x от ближайшего к ней центра сферы (единичного радиуса, R = 1), исключенный объем определяется соотношениями:

В двухмерном пространстве:

$w(x) = \pi {{(2--x)}^{2}}\,\,{\text{при}}\,\,0 \leqslant x \leqslant 2,\,\,\,\,w(x) = 0\,\,{\text{при}}\,\,x > 2.$

В трехмерном пространстве:

$w(x) = ~({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3}){{(2--x)}^{3}}\,\,{\text{при}}\,\,0 \leqslant x \leqslant 2,\,\,\,\,w(x) = 0\,\,{\text{при}}\,\,x > 2.$

Усредняя w(x) для всех точек объема ансамбля частиц можно найти величину 〈w〉 для данного η.

Можно сформулировать также следствия из условия (1):

Следствие 1. Плотность η случайной упаковки жестких сфер не может превышать u/〈w〉.

Следствие 2. Если плотность упаковки η превышает u/〈w〉, то такая упаковка не может быть статистически однородной (гомогенной).

Таким образом, плотность упаковки, при которой ансамбль становится статистически неоднородным, может различаться для разных алгоритмов уплотнения; однако не существует алгоритма, который позволял бы построить гомогенный ансамбль жестких сфер при плотности η > u/〈w〉.

Зависимость 〈w〉(η) может быть рассчитана аналитически [17, 18] путем использования различных приближений, либо определена путем исследования статистико-геометрических свойств компьютерных моделей СПУ.

Верхний предел ηmax для плотности случайной упаковки жестких сфер (при единичном радиусе) может быть найден из условия:

(2)
${u \mathord{\left/ {\vphantom {u {{{\eta }_{{{\text{max}}}}}}}} \right. \kern-0em} {{{\eta }_{{{\text{max}}}}}}} = \left\langle w \right\rangle ({{\eta }_{{{\text{max}}}}}).$

Следует отметить, что данная величина задает предел плотности в рамках системы определений, предложенной в работах [9, 17–21]. Разумеется, существуют и другие факторы (например, термодинамические – если учитывается энергия частиц), а также различные алгоритмы генерации, которые определяют наибольшую плотность различных модельных “случайных” ансамблей сферических частиц. Указанная плотность может быть меньше или равна ηmax. Однако, существует геометрический предел (соотношение (2)), превышение которого неизбежно приводит к появлению фазовой неоднородности (или дальнего порядка).

КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ

Упаковку жестких сфер первоначально генерировали путем размещения частиц в боксах с линейными размерами 1000 × 1000 для 2D сфер (может быть выбрана любая единица длины) и 100 × 100 × 100 для 3D-сфер. Этот “стартовый” ансамбль, полученный методом случайной последовательной адсорбции (RSA-алгоритм), включал (соответственно) 250–350 тысяч дисков, или 100–115 тысяч 3D-cфер.

Далее производили уплотнение начального ансамбля путем пошагового увеличения радиуса сфер. Одновременно задавали случайное смещение каждой частицы. Таким образом, использованный в работе способ близок к алгоритму, предложенному Берналом и Мэйсоном, наряду с другими методами, описанному в работе [22]. В разумное время нами достигалась плотность упаковки η = Nu/V для ансамбля дисков – 0.820–0.845, а для ансамбля трехмерных сфер – 0.610–0.625 (где N – количество частиц, которое не изменялось в ходе уплотнения, u – объем одной частицы (соответствует площади 2D-сферы), V – объем бокса (соответствует площади для ансамбля дисков)). Таким образом, плотность упаковки увеличивалась от первоначального значения (0.45–0.50 для дисков и 0.30–0.35 для трехмерных сфер) до описанного выше предела для данного алгоритма уплотнения.

Статистико-геометрические свойства ансамбля определяли для выделенной области внутри бокса, достаточно удаленной от его границ, центр которой совпадал с центром бокса. Эта область для случая 2D имела размер 960 × 960, а в 3D – 80 × 80 × 80. Плотность упаковки, средний исключенный объем [9] и функцию радиального распределения (ФРР) находили методом Монте-Карло (МК) по данным о 107 точек, случайно выбранных в описанной “внутренней” области. Интегрируя ФРР до определенного расстояния (заданной максимальной дистанции для ближайших соседей), находили среднее координационное число (КЧ) Z. Эти данные были получены во всем интервале исследованных значений плотности упаковки.

Малая группа частиц, свойства которой исследовали отдельно, представляла собой набор из K сфер (K-группу), случайным образом выбранных из числа частиц первоначального (несжатого) ансамбля и лежащих в заданной выше “внутренней” области упаковки. Количество этих сфер (K $ \ll $ N) лежало в интервале 50–300. Координаты данных частиц фиксировали и не изменяли на протяжении всего процесса уплотнения (jamming). При этом радиус частиц пошагово увеличивали синхронно с радиусом всех остальных сфер ансамбля. Статистико-геометрические характеристики этой группы зафиксированных частиц (ФРР, координационные числа и др.) определяли отдельно и сравнивали их с таковыми для ансамбля в целом; это позволило сделать определенные выводы об особенностях поведения подобных случайных “подрешеток” в процессе генерации плотных упаковок (RCP).

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Полученные в результате компьютерных экспериментов зависимости среднего исключенного объема (приведенного к единичному радиусу сфер), и соответствующие кривые для среднего объема МВ для двух- и трехмерного случая представлены на рис. 1.

Рис. 1.

Зависимости среднего исключенного объема 〈w〉(η) и среднего объема многогранника Вороного u/η для случайного ансамбля жестких дисков (а) и жестких 3D-сфер (б) (рассчитано для сферических частиц единичного радиуса).

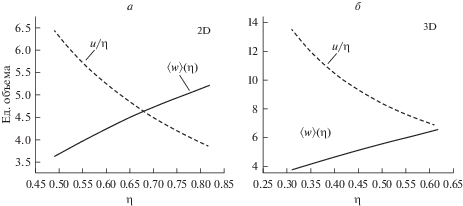
Геометрическому условию для максимально возможной плотности соответствует точка пересечения кривых. Для ансамбля жестких дисков величина ηmax оказалась равной 0.6813 ± 0.001. Для упаковки жестких 3D-сфер: 0.6329 ± 0.0005.

Согласно сформулированным выше положениям, отличие статистико-геометрических свойств (для K-группы случайно выбранных и зафиксированных частиц) от свойств остальных частиц ансамбля возникает при плотности упаковки, меньшей или равной величине ηmax. При плотности η > ηmax такое расхождение обязательно будет иметь место. С целью проверки этого утверждения, для компьютерных моделей 2D и 3D-ансамблей определяли зависимости функций радиального распределения (ФРР) отдельно для указанных групп сфер.

На рис. 2 показаны ФРР для ансамбля жестких дисков и жестких сфер при плотности упаковки, близкой к пределу уплотнения для использованных компьютерных алгоритмов. ФРР для основной группы из ~(1–3) ⋅ 105 частиц показана сплошной линией, а для малой группы – точками. Величина x/D обозначает расстояние до центра сфер x, отнесенное к диаметру сферы D. Функция радиального распределения g(x) = = ρ(x)/ρ0 – отношение числовой плотности при данном (x/D) к средней числовой плотности ρ0 = N/V, определенной методом МК для исследуемой “внутренней” области бокса.

Рис. 2.

Функция радиального распределения для ансамбля жестких дисков (а) и случайной упаковки жестких сфер (б) при высоких плотностях упаковки. Точки – K-группа; кривая – остальные частицы ансамбля.

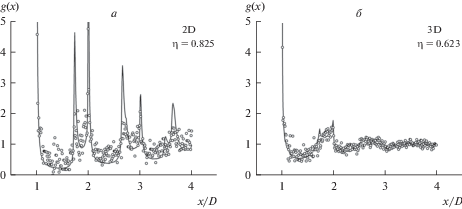
Можно видеть, что при плотности упаковки η = 0.825 для системы жестких дисков (рис. 2а), имеет место появление пиков, отражающих появление дальнего порядка (частичной кристаллизации случайного ансамбля). При этом “невооруженным” глазом можно заметить существенное отклонение ФРР для K-группы частиц (точки), даже несмотря на их значительный статистический разброс. Отметим, что статистический разброс кривой для остальных частиц ансамбля очень мал – поэтому на рисунке показана совершенно несглаженная кривая (сплошная линия), соединяющая экспериментальные точки ФРР для основной группы сфер.

В то же время, для случая 3D-сферических частиц (рис. 2б), зарождение скрытого дальнего порядка (или неоднородности) не столь очевидно при плотности η = 0.623, сравнительно близкой к пределу, заданному соотношением (2). Эта величина соответствует практически наибольшему уплотнению ансамбля с использованием, описанного выше алгоритма.

Для математической оценки различия ФРР K-группы и основного ансамбля первоначально использовали среднеквадратическое отклонение S0 указанных зависимостей друг от друга. Оказалось, что эта величина зависит от плотности упаковки и демонстрирует существенное возрастание, когда величина сжатия стремится к своим предельным значениям (рис. 3). Существенный статистический разброс отдельных значений S0 (особенно для 3D-сфер, рис. 3б) не столь сильно проявляется, если использовать интегральную характеристику – координационное число (Z). Первое координационное число рассчитывали для максимального расстояния 1.07D от центров сферических частиц. Были получены зависимости Z(η) для малой группы зафиксированных частиц (точки) и остальных частиц (сплошные кривые), показанные на рис. 4. Можно видеть, что и в случае жестких дисков (рис. 4а), и в случае жестких 3D-сфер (рис. 4б), имеет место симбатность (или почти совпадение) зависимостей вплоть до определенного значения плотности упаковки. Далее кривые расходятся и это расхождение (как правило) растет с ростом плотности упаковки.

Рис. 3.

Среднеквадратичное отклонение ФРР K-группы и остальных частиц для ансамбля жестких дисков (а) и жестких сфер (б) при различных плотностях упаковки.

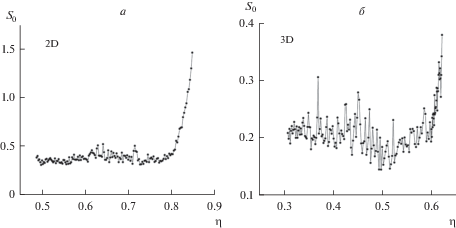
Рис. 4.

Среднее первое координационное число Z для частиц K-группы (точки, 2) и остальных частиц (сплошная кривая, 1) в ансамбле жестких дисков (а) и жестких сфер (б) при различных плотностях упаковки.

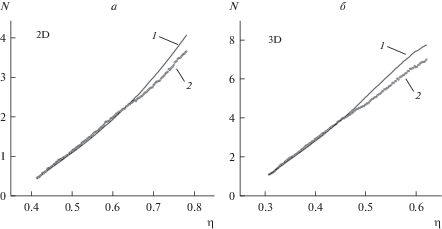
Интервал плотностей η, в которых зависимости Z(η) начинают существенно расходиться, соответствует приблизительно 0.63–0.68 для ансамбля жестких дисков и 0.45–0.50 для упаковки трехмерных сфер. Эти величины согласуются с интервалами плавления–затвердевания ансамблей жестких сфер и дисков [23], а также с более точно вычисленными значениями критических плотностей упаковки для перехода “замерзания” (freezing): 0.697 [24], 0.690 [25] (2D-сферы) и 0.516 [24], 0.494 [25] (3D-сферы).

Можно видеть, что различия в статистико-геометрических свойствах малой группы зафиксированных частиц и всего ансамбля возникают (при данном алгоритме уплотнения) задолго до рассчитанного выше максимально возможного предела плотности случайного ансамбля жестких 3D-сфер. В то же время, для упаковки жестких дисков наблюдаемая плотность упаковки при фазовом переходе “замерзания” [24, 25] близка к полученному нами значению (ηmax = 0.6813 ± 0.001) и интервалу начала “расхождения” статистико-геометрических характеристик на рис. 4б (η ∼ 0.63–0.68).

Напомним, что использованный в работе подход дает лишь максимально возможное значение (верхнюю границу) для плотности СПУ. Реальное значение может быть меньше или равно ηmax = 0.6813 ± 0.001 в двухмерном случае и ηmax = 0.6329 ± 0.0005 для трехмерного ансамбля сферических частиц.

Величина максимальной плотности для случайной упаковки жестких дисков не согласуется с “принятым” литературным значением (0.82–0.84) [26]. Данный интервал плотности для системы твердых дисков отражает максимальное сжатие при использовании многих вычислительных алгоритмов генерации подобных упаковок (в том числе, использованных автором). По-видимому, величина η в интервале (0.82–0.84) может рассматриваться как “состояние максимального сжатия” (maximally random jammed, MRJ [27]) для двухмерной системы жестких сфер, а не как СПУ. Это подтверждается данными исследования [19] и настоящей работы, в которых признаки появления скрытого дальнего порядка (рис. 4а) появляются в случайной упаковке жестких дисков уже при плотностях упаковки, близких к 0.68 и существенно меньших, чем плотность MRJ-состояния. Предсказанная в данной работе максимальная плотность случайной упаковки 2D-сфер хорошо согласуется с известным интервалом плотностей плавления-затвердевания системы жестких дисков: η (fluid-solid) = 0.674–0.710 [28] и значениями критических плотностей [24, 25].

В то же время, найденный в данном исследовании абсолютный максимум плотности для трехмерной случайной упаковки жестких сфер (0.6329) согласуется с “принятым” значением 0.6366, однако, не совпадает с ним. Поэтому, вопрос обоснования близости указанной величины и константы Буффона [8] остается весьма интересным и, вообще говоря, открытым.

ЗАКЛЮЧЕНИЕ

Появление явной или “скрытой” упорядоченности, которая может быть неочевидна и выявляется на различных масштабах, отличает упаковки сфер с плотностью, превышающей плотность СПУ, от полностью случайных упаковок. Это явление было детально исследовано Торквато c соавторами, которыми сравнительно недавно был введен термин “гиперуниформность” (hyperuniformity) [29, 30].

Если вернуться к определению случайной плотной упаковки, предложенному в данной работe, можно сделать следующие выводы. В том случае, когда плотность случайной упаковки жестких сфер превышает строго определенный предел, заданный полученным выше утверждением и его следствиями, в объеме упаковки неизбежно возникает негомогенность. Она может проявляться, например, как возникновение фазовых границ, гиперуниформность, или иные виды явного или скрытого дальнего порядка.

Присутствие в объеме ансамбля сферических частиц малой группы зафиксированных сфер со случайными координатами создает своего рода “случайную подрешетку”. Сравнение статистико-геометрических свойств частиц этой группы и остальных частиц упаковки позволяет при определенных плотностях выявить существенные расхождения между ними, которые служат “индикатором” перехода от случайного ансамбля к “неслучайному” – т.е. демонстрирующему явный или скрытый дальний порядок и статистическую неоднородность.

Работа выполнена по Государственному заданию ИМЕТ УрО РАН.

Список литературы

  1. Полухин В.А., Ватолин Н.А. Моделирование аморфных металлов. М.: Наука, 1985.

  2. Dubinin N.E., Yuryev A.A., Vatolin N. A. Pseudopotential calculation of the structure and thermodynamics of liquid alkali metals with a square-well model as a reference system. // J. of Structural Chemistry. 2012. 53. № 3. P. 468–475.

  3. Torquato S. Perspective: Basic understanding of condensed phases of matter via packing models. // J. Chem. Phys. 2018. 149. P. 020901–1–31.

  4. Klumov B.A., Jin Yuliang, Makse A.H. Structural properties of dense hard sphere packings // J. Phys. Chem. B. 2014. 118. № 36. P. 10761–10766.

  5. Buryachenko V.A., Pagano N.J., Kim R.Y., Spowart J.E. Quantitative description and numerical simulation of random microstructures of composites and their effective elastic moduli. // International Journal of Solids and Structures. 2003. 40. P. 47–72.

  6. Blatov V.A., Serezhkin V.N. Order and topology in systems with many particles // Acta Crystallographica. 1997. A53. P. 144–160.

  7. Anikeenko A.V., Medvedev N.N. Polytetrahedral nature of the dense disordered packings of hard spheres // Phys. Rev. Letters. 2007. 98. P. 235504-1–235504-8.

  8. Berlin A.A., Gendelman O. V., Mazo M.A., Manevitch L. I., Sinelnikov N. N. On solid–liquid transition in plane disc systems // J. Phys.: Condens. Matter. 1999. 11. P. 4583–4596.

  9. Shubin A.B. The geometric condition for density limits in idealized models of liquids. // Russian J. Phys. Chem. A. 1996. 70. № 4. P. 711–712.

  10. Finney J.L. Bernal’s road to random packing and the structure of liquids // Phylosophical Magazine. 2013. 93. № 31–33. P. 3940–3969.

  11. Scott G.D. Packing of spheres: packing of equal spheres. // Nature. 1960. 188. P. 908–909.

  12. Finney J.L. Random packings and the structure of simple liquids. I. The geometry of random close packing // Proc. Roy. Soc. London A. 1970. 319. № 1539. P. 479–493.

  13. Woodcock L.V. Thermodynamic description of liquid-state limits // J. Phys. Chem. B. 2012. 116. P. 3735–3744.

  14. Finney J.L., Woodcock L.V. Renaissance of Bernal’s random close packing and hypercritical line in the theory of liquids // J. Physics. Condensed Matter. 2014. 26. P. 463102–463121.

  15. Berryman J.G. Random close packing of hard spheres and disks // Phys. Rev. A. 1983. 27. № 2. P. 1053–1061.

  16. Torquato S., Truskett T.M., Debenedetti P.G. Is random close packing of spheres well defined? // Phys. Rev. Letters. 2000. 84. № 10. P. 2064–2067.

  17. Шубин А.Б. О максимальной плотности случайной упаковки одинаковых твердых сфер // Расплавы. 1995. № 1. С. 93–97.

  18. Shubin A.B. Concerning the geometric limit of the density of a loose medium modeled by identical spherical particles // J. Engineering Physics and Thermophysics. 1995. 68. № 4. P. 460–463.

  19. Shubin A.B., Yatsenko S.P. Geometric constraints for the density limit in the two-dimensional model of liquid // Russian J. Phys. Chem. A. 1999. 73. № 1. P. 140–141.

  20. Шубин А.Б. Предельная плотность случайной упаковки одинаковых фигур в D-мерном пространстве // Расплавы. 1999. № 3. С. 95–100.

  21. Shubin A.B. Density limit for random close packing of equal figures in D-dimensional Euclidean space // Proceedings of the 8th International Conference on Material Technologies and Modeling MMT-2014. Ariel, Israel. 2014. P. 1-130–1-135.

  22. Speedy R.J. Random jammed packings of hard discs and spheres // J. Phys.: Condensed Matter. 1998. 10. P. 4185–4194.

  23. Hoover W.G., Ree F.H. Melting transition and communal entropy for hard spheres // J. Chem. Physics. 1968. 49. № 8. P. 3609–3617.

  24. Bayer M., Brader J., Ebert F. et al. Dynamic glass transition in two dimensions // Phys. Rev. E. 2007. 76. P. 011508–1–12.

  25. Truscett T.M., Torquato S., Sastry S., Debenedetti P.G., Stillinger F.H. Structural precursor to freezing in the hard-disk and hard-sphere systems // Phys. Rev. E. 1998. 58. № 3. P. 3083–3088.

  26. Meyer S., Song Chaoming, Jin Yuliang, Wang Kun, Hernán A. Makse A.H. Jamming in two-dimensional packings // Physica A. 2010. 389. P. 5137–5144.

  27. Atkinson S., Stillinger F.H., Torquato S. Existence of isostatic, maximally random jammed monodisperse hard-disk packings // PNAS. 2014. 111. № 52. P. 18436.

  28. Huerta A., Henderson D., Trokchymchuk A. Freezing of two-dimensional hard disks // Physical Review E. 2006. 74. P. 061106-1–061106-4.

  29. Torquato S. Hyperuniform states of matter // Physics Reports. 2018. 745. P. 1–95.

  30. Ma Zheng, Torquato S. Hyperuniformity of generalized random organization models // Physical Review E. 2019. 99. P. 022115.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Расплавы

Архивы выпусков Информация о журнале Отправить рукопись в журнал