Записки Российского минералогического общества, 2022, T. 151, № 2, стр. 110-125

ВВЕДЕНИЕ

В настоящее время большинство объектов минералогии продолжают отвечать определению А.Г. Бетехтина: минерал – однородное природное твердое тело, находящееся или бывшее в кристаллическом состоянии. Для обсуждения проблем кристаллогенезиса, остановимся на природном кристалле как единичном объекте, опираясь на это классическое определения минерала. До недавнего времени минералом считалось макроскопическое кристаллическое тело, видимое невооруженным глазом, размеры которого во много раз превышают его элементарную кристаллическую ячейку, поэтому синонимом минерала была термодинамическая фаза, как однородная часть термодинамической системы, отделенная от другой части фазовой границей (Пригожин, Кондепуди, 2002).

Оба определения – минерала и термодинамической фазы объединяют “однородность” и наличие некоторого объема тела (подсистемы) с его поверхностью (границей). Определение термодинамической фазы является более общим, но не противоречит сложному строению реального индивида минерала с его дефектностью, зональностью, секториальностью, мозаичностью.

Известно, что физические переменные несовершенного природного кристалла – его химический состав, плотность, показатели преломления, твердость, магнитная и диэлектрическая восприимчивости, проводимость, теплопроводность, температура плавления, картина дифракции рентгеновских лучей и проч. находятся вблизи некоторых средних значений, характерных для данного минерала. Именно эти средние значения макроскопических интенсивных переменных термодинамической фазы составляют основу физической диагностики минерала. Многие из них описываются тензорными величинами, которые подчеркивают кристаллическое строение тела как особой термодинамической фазы. И наконец – свободная форма кристалла. Это наиболее яркий признак термодинамической фазы, поскольку напрямую свидетельствует о существовании физических закономерностей, реализовавшихся при росте кристалла как динамическом фазовом переходе.

Включение квазикристаллов в арсенал объектов минералогии, или обсуждение случаев сложного изоморфизма и чередования структурных мотивов в теле одного индивида не может служить аргументом для исключения понятия термодинамической фазы для обозначения минерала. При конечном, равновесном взаимодействии с окружающей химически активной средой любой минеральный индивид будет обладать локальным минимумом свободной энергии и по этой, главной причине, некоторые однородность и порядок во внутренней организации вещества будут неизбежно диагностированы. Термодинамика утверждает, что всегда найдутся такие переменные описывающие физические свойства данного тела в окружении равновесной среды, свидетельствующие о его определенной однородности. К примеру, для зерна квазикристалла это будет симметрия 5-го порядка, выявляемая методом рентгеновской дифракции, которая говорит об упорядочении (однородности) структуры при математическом описании данного объекта в модели многомерного пространства.

Если принять понятие фазы, как обязательный атрибут минерала согласно определению А.Г. Бетехтина, то остается один шаг до установления нижнего предела линейного размера минерального индивида. Хорошо известно механико-статистическое решение проблемы измерения физических переменных тела как термодинамической фазы (Ландау, Лифшиц, 1976). Если размеры тела насчитывают количество атомов, равное N, а размеры системы всегда можно оценить в лучшем случае с точностью до одного атома, тогда относительная погрешность измерений любых интенсивных термодинамических переменных, связанных фундаментальным уравнением Гиббса с внутренней энергией равновесной термодинамической системы не может быть меньше ${1 \mathord{\left/ {\vphantom {1 {\sqrt N }}} \right. \kern-0em} {\sqrt N }}$.

Поэтому, например, температуру одного кубического микрометра любого конденсированного вещества при нормальных условиях можно установить с точностью порядка 3 × 10^–6, что обычно вполне достаточно для физических расчетов. Для гексаэдра галита с длиной ребра в 100 нм относительная погрешность определения температуры превышает 10^–4, что уже на границе допустимого. Число атомов на поверхности такого кристалла будет все еще гораздо меньше числа атомов в кристалле и его вещество вполне можно считать термодинамической фазой. Перейдя на уровень масштаба в 10 нм, температуру такого кристалла можно будет определить с относительной погрешностью не лучше 3 × 10^–3. При этом число атомов, условно относимых к поверхности (для определенности возьмем двойной слой атомов), составит около четверти от общего числа атомов такого объекта. В этом случае величины поверхностной энергии и энергии химических связей в объеме такого индивида размываются, а понятие термодинамической фазы уже теряет физический смысл.

Заметим, что термодинамика образования зародыша новой фазы – кристалла, весьма проста и связана с теорией флуктуаций Дж.У. Гиббса. Критический размер зародыша, являющегося термодинамической флуктуацией в данных квазиравновесных условиях, определяется условием экстремума при расчете вкладов поверхностной и внутренней энергий вещества новой фазы в ее свободную энергию. Классическая теория зародышеобразования полностью основана на понятии фазы и предусматривает строгое различие между внутренней и поверхностной энергиями кристалла. Таким образом, зародыш новой фазы должен иметь свое термодинамическое начало в области размеров порядка 10 нм, что не отрицает существование квантовых закономерностей формирования молекулярных комплексов-прекурсоров и переходных состояний молекулярных ансамблей в диапазоне размеров от 0.1 до 10 нм, предшествующих зародышу новой фазы как термодинамической флуктуации.

Сохранность минералов в течение долгого периода времени – до 10¹³ с, несопоставимого со временем жизни биологических структур, ставит на первое место проблему термодинамического равновесия природных кристаллов в масштабе полиминерального геологического тела. Но одновременно кристаллогенезис как фазовый переход вещества, часто из неупорядоченного состояния в кристаллическое, являет собой неравновесный динамический процесс.

На фундаментальном уровне рост кристалла это атомарное явление. Но на макроуровне теория роста кристалла должна быть согласована с термодинамикой, и этот переход сопряжен с проблемами масштабного фактора.

Известно свойство обратимости во времени уравнения квантовой механики, описывающего взаимодействие атома с однородной поверхностью кристалла. Но при этом рост кристалла как наблюдаемый макропроцесс согласно второму началу термодинамики является необратимым процессом. Поэтому фундаментальное время атомарного процесса взаимодействия строительной частицы с поверхностью кристалла, с характерным интервалом порядка 10^–13 с, нельзя считать тождественным феноменологическому времени в теории неравновесного термодинамического процесса роста (секунды, минуты, часы, …). Так же и понятие геологического времени накладывает свой отпечаток на интерпретацию явлений кристаллогенезиса. Геодинамические макропроцессы Земли, обусловленные явлениями гравитации и теплового излучения по характерному времени значительно превышают время минералообразования и занимают годы, тысячи, миллионы лет (10¹³ с). Не смотря на то, что скорости процессов различаются, при описании условий сосуществования минералов в изучаемых парагенетических ассоциациях в рамках определенных геологических структур необходимо максимально корректно обосновывать выбор между неравновесным и равновесным термодинамическими подходами к описанию минеральной системы.

В попытках построения теории роста кристалла особым образом “высвечивается” проблема пространственного перехода от атомарных (10^–10 м) к макроявлениям (10^–3–1 м). В этом диапазоне возможно протекание промежуточных процессов, сопровождающих рост кристалла. Поэтому вновь необходимо строгое физическое обоснование перехода через семь–десять порядков линейного масштаба.

Следующая проблема связана с нелинейностью процессов минералообразования. Известен ряд предельных термодинамических принципов неравновесной термодинамики – Онзагера, Пригожина, Дьярмати, Циглера и др. При этом обобщенный линейный случай – принцип минимума принуждения Дьярмати, описываемый постулатами Онзагера, достаточно понятен, поскольку легко демонстрирует, как открытая система стремится к равновесному состоянию. Но принцип Циглера – максимум плотности производства энтропии, применимый для нелинейных сильно неравновесных систем, таит многие нерешенные загадки в отношении генезиса метастабильных кристаллических фаз.

Одна из проблем кристаллогенезиса в реальной минералообразующей системе связана с принципом суперпозиции симметрий Кюри, как основополагающего теоретического принципа, связывающего общие свойства симметрии физического окружения и системы кристаллизации. Практическая значимость морфологии кристаллов, как раздела кристаллографии, для наук о Земле, как известно во многом связана с применением принципа симметрии. Однако классический принцип Кюри, сформулированный в рамках равновесных представлений и предполагающий знание конечного, строго равновесного состояния системы, не применим непосредственно к открытой динамической системе кристаллизации, в которой состояния объекта непрерывно сменяют друг друга. Обращает на себя внимание и второй недостаток классического принципа суперпозиции симметрий, связанный с невозможностью количественной оценки степени влияния фактора диссимметрии на изучаемое явление.

Отдельно стоит проблема интерпретации известных определений энтропии и, связанная с ней проблема выбора критериев огрубления – отказа от учета ряда факторов, относимых к слабым. Как говорил Р. Декарт – “Уточняйте понятия и мы избавим мир от большинства заблуждений”. Все это создает дополнительные трудности в установлении термодинамических закономерностей кристаллогенезиса.

Перечисленные проблемы на наш взгляд являются ключевыми, но не исчерпывают все сложности на пути построения феноменологической теории кристаллогенезиса, являющейся необходимой переходной стадией перед созданием в перспективе фундаментальной квантовой теории зарождения и роста кристаллов. На этом этапе в пограничных областях разделов физической науки, применяемых для описания роста кристалла, принцип соответствия Бора, требующий согласования всех теоретических подходов к описанию кристаллогенезиса и в первую очередь между двумя разделами термодинамики, служит важнейшим критерием верификации теоретических моделей.

КЛАССИЧЕСКАЯ ДИСЛОКАЦИОННАЯ ТЕОРИЯ РОСТА КРИСТАЛЛА

Дислокационная теория роста кристаллов (Burton et al., 1951; Чернов и др., 1980) сформулирована таким образом, что при переходе от атомарных явлений на незарастающих элементарных ступенях, до макроскопических измерений скорости роста грани, возникают сложности с проверкой принципа соответствия Бора (Rakin, 2022b). Для описания общей картины кристаллизации, в ставших классическими теориях роста причудливо переплетают равновесные и неравновесные представления, сочетая порой несовместимые понятия.

Рассмотрим классическую работу У.К. Бартона, Н. Кабреры и Ф.К. Франка (Burton et al., 1951) более подробно. На первых станицах статьи, с целью описания числа адсорбированных молекул (строительных, но, заметим, не примесных частиц) ${{n}_{{s0}}}$ на единице площади поверхности грани авторы приводят классическое термодинамическое равновесное распределение по энергиям:

Заметим, что равновесное распределение Гиббса (1946), лежащее в основе данного закона, предусматривает безусловное использование понятия фазы. В этом случае числитель и знаменатель под знаком экспоненты следует понимать как энергии, рассчитываемые на молярные количества вещества, для которых применимо понятие фазы. Облегчает ситуацию дробь, которая по замечанию самого Дж.У. Гиббса (1946), допускает преобразование в соответствии с любым масштабным фактором и делает приведенное распределение независимым от используемых единиц. Поэтому, рассуждая о молекулах, строительных частицах, исследователи в XX веке часто переходят к масштабу атомов и не задумываются далее более об этом.

Разделив числитель и знаменатель на число Авогадро, получим отношение (1), где ${{W}_{s}}$ – энергия испарения частицы, находящейся на изломе элементарной ступени, k – постоянная Больцмана, Т – температура. Однако не следует забывать, что данный масштабный переход допустим только при условии наличия как минимум локального термодинамического равновесия. Вместе с тем, величины, находящиеся в данной формуле за пределами экспоненты, не являются собственно термодинамическими переменными. Согласно представлениям Дж.У. Гиббса (1946) термодинамический смысл в выражении (1) может нести только отношение ${{{{n}_{{s0}}}} \mathord{\left/ {\vphantom {{{{n}_{{s0}}}} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$, отражающее статистическую вероятность явления равновесной адсорбции строительных частиц на грани кристалла.

Далее, для оценки длины пробега адсорбированных молекул по поверхности грани авторы обсуждаемой статьи обращаются к известной формуле Эйнштейна для диффузии, описывающей заведомо неравновесный, винеровский случайный процесс. На этом этапе теории вводится характерное время процесса через равновесную частоту тепловых колебаний атомов:

где $W_{s}^{'}$ – энергия испарения молекулы с поверхности кристалла в паровую фазу. Заметим, что характерное время ${{\tau }_{s}}$ составляет порядка 10^–13 с и отражает среднестатистическое время жизни молекулы в состоянии адсорбции на поверхности грани, но не связано непосредственно с процессом фазового перехода. Однако авторы в дальнейшем активно используют равновесное время жизни (2) в тесной связи с пересыщением в уравнениях теории поля, отражающих неравновесный процесс потоков вещества к растущей грани, и получают скорость движения ступени роста.

В итоге, в конечных математических выражениях одновременно присутствуют средние энергии десорбции молекул, характерные для условий локального термодинамического равновесия, равновесный частотный фактор, формально вводящий время в неравновесный процесс и величина, определяющая все динамические процессы в системе – пересыщение.

Подчеркнем, что равновесное термодинамическое или статистическое описание физической задачи адсорбции–десорбции молекулы не может быть использовано согласно теореме Лиувилля (Ландау, Лифшиц, 1976) для введения переменной времени в истинно неравновесном процессе. Неясно, как в такой ситуации можно проверить выполнение принципа соответствия Бора хотя бы в таком простом вопросе, как переход от роста кристалла к термодинамическому равновесию.

Стоит отметить, что авторы обсуждаемой работы и их последователи справедливо замечают, что дислокационная, незарастающая элементарная ступень является главным фактором, облегчающим присоединение строительных частиц к поверхности кристалла и, по существу, правы в главном – рост кристалла, представляет макроскопический феномен, который в первую очередь должен быть описан языком феноменологической теории. Но при этом нужны весомые обоснования для введения переменной времени в теории роста кристалла.

ФЛУКТУАЦИОННАЯ МОДЕЛЬ РОСТА КРИСТАЛЛА

Последовательная цепь физических явлений, охватывающая четыре уровня масштабов изложена в альтернативной флуктуационной модели роста грани кристалла (Rakin, 2016; Ракин, 2021). Особенность модели заключается в том, что характерное время – элементарное время неравновесного процесса (феноменологическое время) вводится не сразу при описании взаимодействия отдельной молекулы (строительной частицы) с гранью кристалла, а на уровне описания термодинамических явлений.

На самом глубоком атомарном и надмолекулярном уровне термодинамические переменные не измеряемы и не несут физического смысла. Диапазон временных событий захватывает интервал от периода тепловых колебаний до характерных времен существования переходных состояний молекулярных кластеров. Однако, некоторые явления химической природы, в классическом пределе обладают набором равновесных, макроскопических, статистических свойств. Особенностью обсуждаемой модели является использование на этом уровне теории адсорбции Ленгмюра (Карнаухов, 1999). В предельном случае все активные центры адсорбции на поверхности растущего кристалла (некомпенсированные химические связи) практически всегда заняты атомами и молекулами примеси, поэтому рост кристалла в масштабе атомарных процессов (10^–13 с) практически не наблюдается. Заметим, что при макроскопическом взгляде на такую систему, наличие примесей в ней требует выполнения предельного случая адсорбции. Только тогда будет соблюдаться второе начало и достигается минимум свободной энергии, характерный для состояния локального равновесия.

Второй, квазиравновесный, локальный, термодинамический уровень определяется масштабом термодинамических флуктуаций Гиббса. На нем термодинамические переменные, такие как энтропия, температура, свободная и поверхностная энергии, химический потенциал вполне измеряемы. Интервал времени процессов релаксации флуктуаций ограничивается уже термодинамическими соображениями – условиями описания квазизамкнутой, локальной, равновесной системы, когда потоками вещества или тепла за ее пределы можно пренебречь. Поэтому и на данном уровне феноменологическое время роста вводить не рационально.

Последовательность релаксационных процессов на участке поверхности в результате положительной флуктуации свободной энергии включает: десорбцию атомов примеси с активных центров, что приводит к повышению свободной энергии поверхности; присоединение некоторого количества строительных частиц на освободившиеся центры или изломы ступеней роста или отрыв частиц, приводящее к понижению свободной энергии прилегающего к грани многокомпонентной среды; понижение свободной энергии поверхности за счет адсорбции новых частиц примеси. Следует учесть, что в масштабе атомарных случайных явлений оба события – присоединение и отрыв строительной частицы в момент релаксации флуктуации происходят почти с одинаковой скоростью, но ничтожный количественный перевес событий роста или растворения будут обусловлены знаком разности химических потенциалов строительных молекул в кристалле и в окружающей среде. На этом масштабном уровне рост и растворение продолжают оставаться симметричными относительно инверсии фундаментального времени.

Важно, что процесс релаксации флуктуационных изменений не должен приводить к изменению физического состояния грани, а неравновесная плотность поверхностной энергии участка грани не должна меняться в результате флуктуации. Последние ограничения предполагаются в любой теории роста кристаллов (например, Burton et al., 1951).

Заметим также, что согласно равновесной теории флуктуаций Гиббса (1946), описываемой каноническим экспоненциальным распределением подсистем по энергиям, релаксационные явления, связанные с отдельной флуктуацией энтропии (свободной энергии) являются независимыми от феноменологического времени, а флуктуации также независимы между собой.

Следующий микроскопический неравновесный уровень выделяется с единственной целью – для введения элементарного интервала времени неравновесного процесса, как одной из важнейших термодинамических переменных неравновесной кристаллообразующей системы (Rakin, 2016). Этот уровень не связан с каким-либо особым физическим явлением, но необходим по гносеологическим основаниям – для осуществления перехода от равновесной к неравновесной термодинамике.

В теории вероятностей известна теорема переноса (Хинчин, 1938; Гнеденко, Колмогоров, 1949), которую применительно к случаю роста грани кристалла можно сформулировать следующим образом – если случайное число флуктуаций в определенной области на поверхности грани за определенное время τ описывается геометрическим законом распределения с параметром, приближающемся к единице, тогда нарастающее за это время вещество будет описываться показательным законом:

Средняя величина прироста вещества, зависящая от пересыщения – ${1 \mathord{\left/ {\vphantom {1 {{\lambda }}}} \right. \kern-0em} {{\lambda }}}$. Тогда скорость стационарного роста составит $v = {1 \mathord{\left/ {\vphantom {1 {{{\lambda \tau }}}}} \right. \kern-0em} {{{\lambda \tau }}}}$. На этом масштабном уровне важным является не только элементарный интервал феноменологического времени τ, позволяющий перейти к открытой системе, но и минимальный линейный размер участка грани, на котором реализуются эти явления. Островки флуктуации имеют вполне определенные линейные размеры, легко выявляемые в атомно-силовых экспериментах по росту кристаллов. Было установлено, что для кристаллов, растущих при нормальных условиях в водных растворах средний островок флуктуации имеет размер порядка 100 нм, а элементарное время стационарного неравновесного процесса – около 1 мин (Rakin, 2016). Таким образом, начиная с этого пространственно-временного масштаба, рост кристалла может быть описан с помощью аппарата неравновесной термодинамики.

Последний, четвертый, макроскопический уровень, определяется вполне естественным образом – на нем суммируются события, происходящие последовательно на всех интервалах стационарного элементарного времени вплоть до текущего момента наблюдения растущего кристалла. Если общее время роста кристалла $t = n{{\tau }}$ отсчитывать от момента образования данной грани (текущей формы стационарного роста), то с помощью метода характеристических функций (Гнеденко, Колмогоров, 1949) можно показать, что сумма наросших слоев кристаллического вещества, распределенных по показательному закону (3), будет описываться гамма-распределением плотности вероятности нарастания толщины слоя (распределением Эрланга)

где h является кумулятивной толщиной наросшего слоя кристаллического вещества на грани за все время роста.

Статистический закон распределения толщины прироста кристаллического вещества (4), обусловленный случайными флуктуациями имеет важное для морфологии минералов следствие – симметрично-эквивалентные грани кристалла всегда находятся на разных расстояниях от некоторого, единственного согласно предельному принципу, центра стационарной формы. Поэтому форма растущего кристалла часто описывается вместо одного типа многогранника набором комбинаторно различных многогранников, описываемых определенными группами идеальной симметрии и различными вероятностями. Это свойство морфологии свободной формы макрокристалла можно назвать морфологическим спектром динамической формы кристалла (Ракин, 2021). Для изотропного случая вероятности морфотипов многогранников легко рассчитываются по закону (4), а реальные диссимметризованные обстановки – влияние гравитации, движения среды кристаллизации, направленной диффузии или инфильтрации вещества – также можно учесть введением дополнительных условий в вероятностно-теоретическую модель процесса (Ракин, 2021).

ТЕРМОДИНАМИКА НЕРАВНОВЕСНОЙ ФОРМЫ КРИСТАЛЛА

В рамках представлений Л. Онзагера о линейном режиме развития открытой термодинамической системы был выполнен расчет производства энтропии кристаллом в ходе его стационарного роста в растворе (Rakin, 2020в). На основании принципа минимума производства энтропии было показано, что динамическая форма кристалла в предельном случае стационарного роста описывается уравнением:

где ${{h}_{j}}$ и ${{v}_{j}}$ – центральное расстояние до растущей грани и нормальная скорость ее стационарного роста соответственно, ${{r}_{j}}$ – нормированный термодинамический коэффициент, определяющий особенности тепло- и массопереноса у поверхности данной грани, m – число граней кристалла, t – текущее время процесса. Данное уравнение было получено без учета флуктуаций свободной энергии в системе.

При квазистационарном росте кристалла в изотропных условиях и приближении к равновесию, уравнение (5) преобразуется (Rakin, 2022б) в уравнение Вульфа для равновесной формы кристалла:

где ${{{{\gamma }}}_{j}}$ – капиллярная постоянная равновесной грани кристалла, C – константа. Однако этот переход справедлив только при условии слабости гравитационного фактора (Rakin, 2022а).

Центральная предельная теорема теории вероятностей декларирует, что при стационарном росте кристалла и увеличении параметра n > 100 гамма-распределение (4) приближается к нормальному закону. Но и равновесная форма кристалла (6) в приближении теории флуктуаций Гиббса и без учета гравитации будет также описываться нормальным законом. Это легко показать на примере равновесной изохорно-изотермической гетерогенной системы (Rakin, 2022б).

Важно отметить, что при переходе от гамма-распределения к нормальному закону, вероятности комбинаторных разновидностей многогранников, слагающих спектр стационарной формы, перестают зависеть от коэффициента вариации, а морфологический спектр включает только полногранный класс многогранников как и равновесная форма (Rakin, 2020а). С этого момента морфологический спектр стационарной формы не зависит от времени. Это важное обстоятельство связано со свойством марковского процесса динамической формы кристалла (Ракин, 2021). Таким образом, совпадение морфологических спектров равновесной и стационарных форм иллюстрирует принцип соответствия Бора и обнаруживается гораздо раньше достижения равновесия. Поэтому появляется возможность оценить диапазон значений кинетических параметров процесса роста кристалла на основании термодинамических равновесных параметров системы.

ЭНТРОПИЯ – ФУНКЦИЯ СОСТОЯНИЯ РАВНОВЕСНОЙ СИСТЕМЫ

В равновесной термодинамике еще в XIX веке введено несколько эквивалентных определений энтропии. Главные из них – энтропия по Р. Клаузиусу, сформулированная путем “взгляда извне”, через тепловое взаимодействие с окружением (Пригожин, Кондепуди, 2002), и по Дж.У. Гиббсу, определенная через “взгляд изнутри”, через вероятность посещения термодинамической системой определенной области в фазовом пространстве (Гиббс, 1946). Энтропия, как известно представляет собой функцию состояния равновесной системы, зависящую от объема, количества вещества и внутренней энергии. В неравновесной системе, в рамках представления о локальном равновесии, энтропию можно представить как функцию времени, что, заметим, не было предусмотрено основоположниками равновесной термодинамики. После процедуры деления системы на локальные области, энтропия неравновесной системы согласно второму началу определяет необратимое направление естественных процессов к равновесию – стрелу времени. Сделав следующий шаг и определив дифференциальную характеристику энтропии – плотность производства энтропии в локальной квазиравновесной области неравновесной системы – можно перейти к открытой системе. Скорость изменения энтропии составляет основу предельных принципов неравновесной термодинамики: Онзагера, Пригожина, Дьярмати, Циглера, которые связаны между собой различными уровнями обобщения.

Рассматривая газ как систему молекул, подчиняющуюся законам Ньютона, Л. Больцман искал связь термодинамической энтропии с молекулярно-кинетической теорией, выйдя за рамки термодинамики (Больцман, 1984). Введенное им статистическое понимание энтропии основано на расчете логарифма числа микросостояний, определяющих наблюдаемое макросостояние системы. В его определении ни молекулярно-кинетические, ни термодинамические переменные не принимают участия. Основная задача Н-теоремы Л. Больцмана состояла в том, чтобы обосновать необратимость термодинамических процессов в макросистеме на основе законов обратимой ньютоновской механики, описывающих взаимодействие молекул в газе. Сегодня принято считать, что эта теорема осталась недоказанной и поэтому, в частности, между обратимыми атомарными процессами и макроявлением роста кристалла продолжает существовать непреодоленное препятствие, в частности запрещающее использовать фундаментальное время ньютоновской механики (и квантовой механики в общем случае) для описания кинетики роста макрокристалла. Именно по этой, главной причине во флуктуационной модели (Rakin, 2016) время введено на феноменологическом, термодинамическом уровне.

Важно заметить, что энтропия по Больцману обладает свойством, создающим трудности для ее использования, но и возможности для развития. В частности если система находится под воздействием внешних сил – гравитационных, магнитных или электростатических, то способ сортировки микросостояний (способ огрубления) в рамках наблюдаемого макросостояния системы представляет ответственную задачу. Кроме того, оказалось, что если учесть геометрию системы, то в энтропии по Больцману появляется дополнительное симметрийное слагаемое (Ракин, 2021). Это небольшое по величине число в случае кристалла, помогает наглядно описать особенности реализации принципа суперпозиции симметрий Кюри.

Во всяком случае, между термодинамическими (Клаузиус, Гиббс), механико-статистическим (Больцман), квантово-механическим (фон Нейман) определениями энтропии существует тесная взаимосвязь и определенная эквивалентность, обусловленная предельными переходами ко второму началу термодинамики. С информационной энтропией дело обстоит сложнее.

Энтропия К. Шеннона имеет форму записи, совпадающую с выражением для термодинамической энтропии по Гиббсу, но смысл величин, входящих в формулы принципиально иной. Известен принцип Ландауэра (Landauer, 1961), гласящий, что при стирании одного бита информации в необратимом процессе на физическом устройстве, выделяется фиксированное количество бесполезной тепловой энергии. Имитируя такой процесс на приборе, не имеющем механических частей и не производящем механическую работу, можно вполне надежно установить физический предел этого явления. Поэтому информационная энтропия в узком смысле может служить отображением термодинамической энтропии Р. Клаузиуса для закрытой системы. Однако, если считать информационную энтропию полным аналогом термодинамической энтропии, могут возникнуть трудности в интерпретации результатов. Главная причина заключается в том, что предельные принципы неравновесной термодинамики, описывающие производство энтропии в неравновесной термодинамической системе, базируются на строгом определении термодинамической энтропии по Клаузиусу и Гиббсу в рамках принятого в термодинамике феноменологического подхода. Пока только на их основе можно делать предсказания динамики развития естественного необратимого процесса. Но информационная энтропия базируется на иной системе понятий, и принцип Ландауэра в общем виде не решает проблему.

При расчете энтропии согласно представлениям Гиббса и Клаузиуса должны учитываться все природные факторы, какими бы слабыми они ни казались. Иллюстрацией важности этого обстоятельства может служить расчет влияния гравитации на энтропию, который неожиданно показал, что равновесный размер кристаллов минералов на космических телах должен быть ограничен (Rakin, 2022а). Зерна породообразующих минералов в низах литосферы Земли не должны превышать первых сантиметров. Полученный результат позволяет объяснить верхнюю границу диапазона размеров зерен мантийной горной породы и подвижность конденсированного мантийного вещества. При этом гравитация не ограничивает размер неравновесного растущего кристалла.

РОСТ КРИСТАЛЛОВ ПРИ БОЛЬШИХ ОТКЛОНЕНИЯХ ОТ РАВНОВЕСИЯ

Рассмотрим физико-химическую систему кристаллизации фосфата кальция в диффузионной колонке (Ракин, 2006). Эксперименты по встречной диффузии компонентов – фосфат-аниона (${{{\text{H}}}_{2}}{\text{PO}}_{4}^{ - }$) (при концентрации фосфата калия 0.5 моль/л), однородно растворенного в гелевой колонке, и катиона Ca²⁺, поступающего из контактирующего с гелем раствора хлорида кальция с той же концентрацией, демонстрируют сложную цепь событий. На первом этапе, на границе гель–раствор последовательно в две стадии формируется коллоидная фаза дикальцийфосфата по составу близкая к монетиту CaHPO₄. Через 20–25 мин коллоидная фаза, служащая источником вещества для одновременной кристаллизации монетита, брушита, октакальцийфосфата и гидроксиапатита, начинает формировать пространственную структуру Лизеганга (рис. 1).

Экспериментально установлено, что последовательность кристаллообразования политипов фосфата кальция не соответствует закономерностям существования равновесных фаз при той или иной кислотности среды кристаллизации (Корбридж, 1982; Чайкина, Никольская, 1973). Оказалось, что монетит успешно кристаллизуется в широком диапазоне от кислых до нейтральных сред, но устойчив в кислых средах (рН < 4), а октакальцийфосфат и гидроксиапатит образуются в слегка подкисленных растворах (рН < 6), хотя устойчивы в нейтральных средах рН > 6.

Была построена математическая модель химической системы в рамках теории динамических систем, адаптированная по порядкам и константам реакции, а также коэффициентам диффузии к динамике физико-химических экспериментов. Модель позволяет рассчитать плотность производства энтропии как функцию времени и глубины гелевой колонки (рис. 2). В результате моделирования было установлено, что главный вклад в производство энтропии дает нелинейная автокаталитическая реакция образования конечного продукта – аморфного дикальцийфосфата. Расчеты свидетельствуют (рис. 2), что на фронте диффузии плотность производства энтропии не превышает 10^–2 Дж/(К м³ с), но на краях полос Лизеганга, в краткие моменты их активного формирования, плотность производства энтропии взрывообразно возрастает в десятки раз. В эти интервалы времени, длящиеся считанные минуты, на краях полос зарождаются и растут сферокристаллы октакальцийфосфата (рис. 1), содержащие небольшое количество дендритоподобных кристаллов гидроксиапатита. В дальнейшем плотность производства энтропии в этих узких областях геля падает, но не ниже 0.5 × 10^–3 и сохраняется на этом уровне до полного исчерпания исходных компонентов. Анализ места расположения, момента зарождения, длительности роста, и состава кристаллических фаз позволил установить основную закономерность кристаллизации политипов фосфата кальция в данной нелинейной неравновесной химической системе, связанную со шкалой плотности производства энтропии:

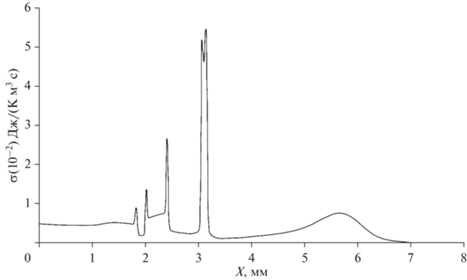
– монетит формируется главным образом на переднем фронте реакции при малых скоростях процессов, описываемых величинами 10^–4–10^–3 Дж/(К м³ с);

– удлиненный пластинчатый брушит формируется практически в любой части гелевой колонки в интервале значений от 10^–3 до 10^–2 Дж/(К м³ с), соответствующих средним величинам плотности производства энтропии в данной физико-химической системе;

– октакальцийфосфат кристаллизуется в интервале 10^–2–0.1 Дж/(К м³ с), главным образом на краях полос Лизеганга и приобретает форму сферокристаллов;

– гидроксиапатит является наиболее редкой фазой и кристаллизуется в краткие моменты превышения значений 0.1 Дж/(К м³ с) и только в присутствии активно растущего октакальцийфосфата, зарождаясь эпитаксиально на его иголках.

Для всех кристаллов фосфата кальция в гелевой среде проявляется зависимость от анизотропии диффузионного питания. Данный фактор является главным препятствием к формированию крупных кристаллов. Все политипы растут практически одновременно и по соседству, но существенно отличаются по скоростям роста. Скорость роста октакальцийфосфата в направлении удлинения более чем на порядок уступает скорости роста пластинчатого брушита, находящегося в той же концентрационной обстановке, а дендритный гидроксиапатит в это же время не поспевает расти даже за октакальцийфосфатом.

Известная равновесная закономерность (Корбридж, 1982; Чайкина, Никольская, 1973), отражающая устойчивость политипов в зависимости от значения рН среды, вступает в свои права только на заключительном этапе процесса, когда скорости диффузии, реакций и кристаллизации значительно уменьшаются до значений, описываемых критическим значением плотности производства энтропии порядка <10^–4 Дж/(К м³ с). На следующий день после выполнения эксперимента, когда водородный показатель среды рН выравнивается и опускается до 4–5, брушит составляет основную массу фосфата кальция в химической системе (до 95 мас. %), а коллоидный дикальцийфосфат полностью растворяется. Октакальцийфосфат и гидроксиапатит в этих условиях подвергаются гидролизу.

Таким образом, рост метастабильных фаз фосфата кальция обусловлен нелинейной химической реакцией, протекающей в среде кристаллизации в непосредственной близости к растущей грани. Эти явления можно объединить в рамках общих феноменологических представлений о нелинейных топохимических реакциях на растущей грани кристалла (Гликин, 2004) и описать в рамках неравновесной термодинамики и теории динамических систем.

ПРИНЦИП СУПЕРПОЗИЦИИ СИММЕТРИЙ КЮРИ

Классический принцип симметрии-диссимметрии Кюри традиционно демонстрируется на примере формы реального макрокристалла (Юшкин и др., 1987). Он позволяет установить максимально общие свойства окружения кристалла – описать характер движения среды кристаллизации и действие внешних физических полей на кристаллогенезис. Использование классического принципа симметрии всегда неявно подразумевает, что процесс естественным образом завершился к этому моменту – кристаллобразующая система пришла к равновесию. Однако любое нарушение кристаллообразующей системы: удаление одной из подсистем – раствора или смену среды кристаллизации, а также извлечение кристалла из природной обстановки, нельзя считать достижением равновесия той физической системы, в которой формировался кристалл. Например, наличие свободных форм кристаллов жильных минералов свидетельствует напрямую о нарушении термодинамической системы с удалением маточного гидротермального раствора.

Но в открытой термодинамической системе, в которой непрерывно протекает неравновесный процесс, влияние окружения на симметрию формы макрокристалла не может быть точно и однозначно установлено в каждый момент времени, поскольку форма кристалла и его симметрия непрерывно испытывают изменения.

На примере кристалла кварца описаны особенности реализации принципа суперпозиции симметрий в свободной форме кристаллов в открытой неравновесной динамической системе (Rakin, 2020b; Ракин, 2021). Показано, что при реализации эффекта полного огранения принцип Кюри в его классической формулировке: “Если определенные причины вызывают соответствующее следствие, то элементы симметрии причин должны проявляться в вызванных ими следствиях. Если в каких-то явлениях обнаруживается определенная диссимметрия, то эта же диссимметрия должна проявляться в причинах их породивших”, будет применим ко всем без исключения полногранным морфотипам многогранников. Но в остальных случаях принцип суперпозиции симметрий соблюдается главным образом для класса морфологических разновидностей многогранников свободной формы кристаллов. Другие, редко встречающиеся морфотипы, входящие во вспомогательные классы, в конкретных условиях кристаллизации играют второстепенную роль и для них принцип Кюри в классической трактовке может нарушаться. Детали этих закономерностей прослежены пока только на природном алмазе и α-кварце (Ракин, 2021).

Доказано, что фактор диссимметрии, обусловленный физическим окружением термодинамической макросистемы, оказывает на физическое явление минимально возможное воздействие, уменьшающее энтропию наблюдаемой подсистемы при равновесии в закрытой системе, и увеличивающее ее производство энтропии в стационарном неравновесном процессе в открытой системе (Rakin, 2021). Данный тезис выражает принцип минимальной диссимметрии, который позволяет устранить второй недостаток классического принципа симметрии Кюри и дает основание для введения количественного показателя диссимметрии формы растущих кристаллов.

Упомянутая выше симметрийная поправка к энтропии Больцмана (Ракин, 2021) обладает важным свойством – она не зависит от того, растет данный кристалл-многогранник, растворяется или находится в состоянии равновесия с окружающей средой. Поправка оказалась весьма эффективной при решении задач морфологии кристаллов, и принцип минимальной диссимметрии закономерно проявляется в изменении симметрийной поправки, рассчитываемой для динамического морфологического спектра кристаллов.

С одной стороны, показатель диссимметрии формы кристалла можно рассчитать по значениям полной энтропии кристалла. Однако энтропийный путь весьма трудоемок и предполагает знание многих неизвестных термодинамических переменных. Другой, симметрийный маршрут проще и понятнее. В диссимметризованной природной системе претерпевает изменения весь морфологический спектр кристалла – число комбинаторных типов многогранников и их вероятности. Располагая теоретическими данными по эталонному морфологическому спектру изотропной открытой системы, а также эмпирическими данными по спектру морфотипов реальных кристаллов легко выполнить расчет показателя диссимметрии формы при предельном минимальном воздействии диссимметризующего фактора. Единственным условием для такого расчета является требование равенства коэффициентов вариации центральных расстояний реальных кристаллов-многогранников и эталонного спектра. Но и это требование существенно смягчается, если исследуемая совокупность реальных кристаллов демонстрирует эффект полного огранения (Rakin, 2020a). В этих обстоятельствах вероятности морфотипов динамической формы не зависят от коэффициента вариации центральных расстояний до граней динамической формы кристалла.

ЗАКЛЮЧЕНИЕ

Таким образом, кристаллогенезис как направление исследований процессов минералообразования сталкивается в первую очередь с проблемами применения различных физических подходов к явлениям фазового перехода в широком интервале пространственно-временных масштабов. Необходимость обращения к физике продиктована логикой развития минералогии, как отрасли естествознания. В данной статье на примере результатов, полученных автором в ходе исследований свободной формы кристаллов (Ракин, 2021), продемонстрирована эффективность применения методов неравновесной термодинамики. Представляется, что одной из главных задач современного этапа исследований зарождения и роста природных кристаллов, является переход на теоретический базис неравновесной физики и в первую очередь – неравновесной термодинамики и смежных с ней разделов физических наук. Длительный рост монокристалла с формированием макроскопического тела чаще всего описывается линейным режимом стационарного неравновесного термодинамического процесса. Теория такого процесса хорошо разработана, и главные теоретические трудности связаны с адаптацией достижений термодинамики для описания явлений кристаллогенезиса.

Развитию этого направления придает особую актуальность активизация поиска новых минералов в природе, обозначенного приоритетным в программе фундаментальных научных исследований в “Науках о Земле”. Часто оказывается, что в неравновесных физико-химических системах нелинейные эффекты оказывают решающее воздействие и приводят к неожиданным явлениям, которые не вписываются в традиционные представления о минералообразовании. Возможно образование широкого спектра неожиданных для минералога метастабильных фаз, не выдерживающих в дальнейшем сосуществования с устойчивыми кристаллическими соединениями при приближении к равновесию. Нелинейность неравновесной термодинамической системы можно оценивать по критерию И.Р. Пригожина – возникновению и функционированию диссипативных структур, реализующихся в открытой системе (Пригожин, Кондепуди, 2002). В живой природе это явление имеет повсеместное распространение, но при абиогенном минералообразовании – явление не столь частое, связанное чаще всего с реакционно-диффузионными процессами в конденсированных средах. Можно согласиться с тем, что проблема стабильности вновь обнаруженной природной термодинамической фазы не оказывает прямого влияния на факт ее признания как нового минерала, но учитывая традиционное понимание минерала, как устойчивого природного соединения, на следующем этапе изучения минералогического объекта неизбежно возникают вопросы сосуществования фаз в многокомпонентной системе. И здесь вновь методы термодинамики безусловно имеют решающее значение.