Сенсорные системы, 2019, T. 33, № 1, стр. 52-59
Сопоставление снимков в радио и видимом диапазонах через независимую привязку к векторной карте
И. А. Кунина 1, *, Е. И. Панфилова 1, А. П. Гладков 1
1 Институт проблем передачи информации им. А.А. Харкевича РАН
127051 Москва, Большой Каретный пер., 19, Россия
* E-mail: kunina@iitp.ru
Поступила в редакцию 05.09.2018
Аннотация
В работе рассматривается способ сопоставления снимков местности, сделанных с большой высоты в радио и видимом диапазонах, через их независимую визуальную локализацию относительно векторной карты дорог. В основе метода лежит представление дорог на изображении и на карте местности в виде совокупностей прямолинейных сегментов, аппроксимирующих дороги этой местности. Поиск таких сегментов на изображении опирается на быстрое преобразование Хафа, а вычисление параметров преобразования, связывающего локальные координаты снимка с координатами карты, осуществляется через сопоставление найденных сегментов с сегментами дорог карты алгоритмом RANSAC с использованием информации о положении и ориентации сегментов. Приведены результаты экспериментов на реальных данных, демонстрирующие преимущество данного подхода по сравнению с сопоставлением снимков без посредства карты.
ВВЕДЕНИЕ
В настоящее время все больше воздушных и космических летательных аппаратов предоставляют большое количество данных дистанционного зондирования Земли (ДЗЗ). Сканирующие земную поверхность подсистемы этих аппаратов различаются свойствами своих сенсоров, а полученные ими изображения по-разному характеризуют один и тот же участок сканируемой местности (рис. 1). Объединение таких изображений в одно более информативное находит свое применение, например, в системах мониторинга: для обнаружения мелких животноводческих районов, потенциально ответственных за загрязнение окружающей среды (Errico et al., 2015), определения уровня влажности почвы (Prakash et al., 2012), детектирования изменений в наблюдаемой городской местности (Lopez et al., 2017) и другое.
Рис. 1.
Сравнение изображений, сделанных в радио и видимом диапазонах для г. Норт-Пол (Аляска) с высоты ≈7 км
а – изображение в видимом диапазоне; б – изображение в радиодиапазоне.

Системы объединения изображений (Socolinsky, Wolff, 2002; Sidorchuk et al. 2018) предполагают, что изображения выровнены друг относительно друга, т.е. задано преобразование между их системами координат (или решена задача сопоставления). Учитывая, что в большинстве своем данные ДЗЗ геопривязаны – это разумное допущение, однако на практике для качественного объединения изображений точности геоданных не всегда хватает, а в некоторых случаях, например, когда изображения получены из неизвестного источника, они и вовсе могут отсутствовать.
В связи с этим возникает необходимость альтернативных способов сопоставления изображений. Классически задача сопоставления изображений решается с применением аппарата особых точек (SIFT, SURF, YAPE и другие). Однако алгоритмы детектирования особых точек разрабатывались для оптических изображений, поэтому их применение к изображениям, полученным с сенсоров разных типов, может привести к непредсказуемым результатам. Поэтому ведутся работы по развитию аппарата ключевых особенностей для случая разнородных изображений. Среди них можно выделить три направления: создание особых точек (Fan et al., 2013; Abulkhanov et al. 2018), особых линий (line features) (Cheng et al., 2004; Sui et al., 2015; Zhang et al., 2017), а также выделение признаков форм (Ye et al., 2017).
В данной работе мы ставим задачу создания прототипа системы сопоставления изображений радио и оптического диапазонов через их независимое сопоставление с векторной картой дорог. При этом, поскольку съемка проводится с большой высоты, мы используем модель плоской поверхности Земли. В этом случае исходное изображение представляет собой ее ортогональную проекцию, а координаты снимка связаны с географическими координатами только неизвестным преобразованием подобия.
Сопоставление разнородных изображений при помощи привязки к векторной карте – подход новый и отличается от классических решений. Его достоинством является то, что он допускает создание специфицированных алгоритмов сопоставления, наилучшим образом подходящих для конкретного типа изображений. Кроме того, в этом случае возможно сопоставить изображения одной территории с сильно отличающимся урбанистическим ландшафтом, сделанные в разное время, за счет сопоставления с векторной картой, соответствующей дате снимка.
В отличие от предшественников мы работаем над созданием метода, который опирается только на структуру линейных объектов векторной карты и целевого изображения. Мы выделяем на полученных снимках дороги в виде прямолинейных сегментов, используя быстрое преобразование Хафа (БПХ) (Brady, 1998; Nikolaev et al. 2008). Затем полученные сегменты сопоставляются с сегментами дорог векторной карты, используя алгоритм RANSAC, с опорой только на информацию о положении и ориентации прямолинейных сегментов, но не на их длину (это позволяет скомпенсировать ошибки разметки векторной карты и ошибки детектора дорог). Данный подход сопоставления сегментов является развитием предложенного нами ранее подхода (Kunina et al., 2017) для случая работы с большим количеством пар сегментов.
Статья состоит из трех глав. В первой главе описан поиск дорог для радио и оптических изображений, во второй – сопоставление найденных дорог на изображениях с векторной картой соответствующей местности, в третьей – представлены результаты применения данного метода на реальных данных.
ПОИСК ДОРОГ НА ИЗОБРАЖЕНИИ
Подавление фона. На изображениях в видимом диапазоне, снятых с большой высоты, дороги представлены, главным образом, как слабо текстурированные однородные вытянутые области. Характерная особенность данных областей – это большое значение градиента в направлении, перпендикулярном изображению дороги, и малое – в параллельном. Поэтому для их выделения мы анализируем форму структурного тензора (Jähne, 1993) в окрестности каждой точки: если эксцентриситет эллипса, описываемого структурным тензором, высок, то точка, вероятно, принадлежит изображению дороги. Для оценки эксцентриситета в пикселе с координатами $(x,y)$ мы вычисляли следующую функцию от собственных чисел тензора инерции:
где ${{\lambda }_{1}},\;{{\lambda }_{2}}$ – собственные значения 2D – матрицы структурного тензора для пикселя с координатами $(x,y)$, γ – настраиваемый параметр.В результате выделение дорог на оптическом изображении осуществляется следующим образом: при необходимости выполняется деколоризация входного изображения, затем для каждого пикселя вычисляется маска дорог по формуле (1) и, наконец, формируется выходное изображение как попиксельное перемножение входного деколорированного и полученной маски. Пример выделения дорог на оптических изображениях приведен на рис. 2, б для входного изображения, представленного на a.
Рис. 2.
а – входное изображение в видимом диапазоне; б – результат фильтрации (а) с использованием структурного тензора; в – входное изображение в радиодиапазоне; г – результат фильтрации (в) с использованием пороговой фильтрации.

Для выделения дорог на радиоизображениях в большинстве примеров оказалось приемлемым использование пороговой фильтрации, чего, как будет показано далее, достаточно для проверки концепции. Пример выделения дорог на радиоизображениях приведен на г для входного изображения, представленного на в.
Поиск дорог. Предложенный алгоритм поиска дорог опирается на предположение, что дороги, как правило, содержат многочисленные прямолинейные участки. Алгоритм принимает на вход изображение с подавленным фоном и возвращает набор ломаных линий, заданных упорядоченным набором точек. Алгоритм состоит из трех последовательных этапов.
На первом этапе полученное изображение разбивается на участки одинакового размера с фиксированной площадью перекрытия соседних участков. В каждом участке ищется один доминирующий отрезок (задаваемый границами рассматриваемого участка) с использованием БПХ (Bradly, 1998; Nikolaev et al., 2008). Если сумма значений пикселей вдоль прямой, содержащей отрезок, превышает сумму значений пикселей по любой параллельной ей прямой, в некоторой заданной ее окрестности, то найденный сегмент считается принадлежащим некоторому участку дороги (рис. 3, а).
Рис. 3.
Поиск дорог.
а – поиск сегментов; б – группировка сегментов; в – объединение сегментов в ломаные и их упрощение.

На втором этапе найденные сегменты группируются в неупорядоченные множества, соответствующие линиям дорог, если пространственное и угловое расстояния между ними находятся в заданном диапазоне (б). Пространственное расстояние между двумя сегментами считается как размер минимального отрезка, соединяющего точки сегментов. Угловое расстояние оценивается как угол между точкой пересечения сегментов (или серединой отрезка, соединяющего ближайшие точки сегментов, если они не пересекаются) и лучами, идущими в направлении дальних концов первого и второго сегментов соответственно.
На третьем этапе в каждом множестве определяется порядок обхода, используя информацию о взаимном расположении сегментов, а сами сегменты аппроксимируются последовательностью точек. Полученные ломаные фильтруются по длине (отбрасываются слишком короткие) и обрабатываются с использованием алгоритма упрощения полилинии (Psimpl. generic n-dimensional poyline simplification, 2017) для уменьшения количества звеньев в ломаных (в). Такая фильтрация важна для сопоставления, поскольку длинные прямолинейные сегменты являются более устойчивыми признаками сопоставления, нежели короткие, так как для них точнее вычисляется угол наклона.
СОПОСТАВЛЕНИЕ ДОРОГ
После детекции прямолинейных сегментов дорог на изображениях следует этап их сопоставления с векторной картой. В данной работе мы это делаем при помощи RANSAC-подобного алгоритма сопоставления, ключевыми составляющими которого являются: способ вычисления преобразования между координатами карты и снимка на основе корреспонденций сегментов, а также способ оценки качества этого преобразования.
Вычисление геометрического преобразования
Геометрическое преобразование плоскости. Поскольку мы считаем, что съемка проводится с достаточно большой высоты и ориентация камеры относительно плоскости Земли либо неизменна, либо скомпенсирована с использованием данных инерциальных датчиков, то преобразование Ψ координат точки изображения $r = (x,y)$ описывается уравнением
Расстояние между сегментами. С одной стороны, в силу описанной специфики работы выбранного детектора дорог, концы полученных сегментов дорог часто определяются с большой погрешностью, следовательно попарное расстояние между ними не подходит для измерения близости сегментов. С другой – угол наклона сегмента, как правило, оценивается с высокой точностью, поэтому следует его использовать для вычисления преобразования. Однако для оценки близости одного только угла явно недостаточно, поэтому мы будем дополнительно использовать координаты центров сегментов, учитывая, что точность определения координаты поперек сегмента гораздо выше, чем вдоль.
Обозначим системы координат изображения и карты через E и M соответственно. Здесь Ψ – это преобразование из E в M. Рассмотрим пару сегментов ${{t}^{E}} \in E$ и ${{t}^{M}} \in M$. Преобразование сегмента ${{t}^{E}}$ в систему M записывается следующим образом: ${{t}^{{E'}}} = (\Psi [\overline {r_{0}^{E}} ],\Psi [\overline {r_{1}^{E}} ])$, где $r_{0}^{E},\;r_{1}^{E}$ – координаты концов сегмента ${{t}^{E}}$.
Будем определять сегмент t координатами центра ${{\bar {r}}_{c}} = ({{x}_{c}},{{y}_{c}})$ и углом наклона ${{\alpha }_{t}}$ относительно положительного направления оси X. С учетом сделанных обозначений расстояние между двумя сегментами будем определять в системе M вектором
(2)
${{Q}^{\Psi }}({{t}^{E}},{{t}^{M}}) = \left[ {\begin{array}{*{20}{c}} {Q_{\alpha }^{\Psi }({{t}^{E}},{{t}^{M}})} \\ {Q_{y}^{\Psi }({{t}^{E}},{{t}^{M}})} \\ {Q_{x}^{\Psi }({{t}^{E}},{{t}^{M}})} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\left| {\alpha _{t}^{{E'}} - \alpha _{t}^{M}} \right|} \\ {\left| {y_{c}^{{E'}} - y_{c}^{M}} \right|} \\ {\left| {x_{c}^{{E'}} - x_{c}^{M}} \right|} \end{array}} \right],$Регрессия параметров преобразования. Пусть даны два набора сегментов из E и M соответственно: ${{T}^{E}} = t_{1}^{E},t_{2}^{E},\;...,\;t_{K}^{E}$ и ${{T}^{M}} = t_{1}^{M},t_{2}^{M},\;...,\;t_{K}^{M}$, причем $t_{i}^{E}$ и $t_{i}^{M}$ – один и тот же сегмент на изображении и на карте. Тогда, как было показано в работе (Kunina et al., 2017), каждая i-я пара сегментов порождает следующие ограничения на параметры преобразования:
(3)
$\left\{ \begin{gathered} \Psi [\overline {r_{{{{c}_{i}}}}^{E}} ] = \overline {r_{{{{c}_{i}}}}^{M}} \hfill \\ \Psi [\overline {n_{i}^{E}} ] \cdot \overline {n_{i}^{M}} {\text{/}}s = 1 \hfill \\ \end{gathered} \right.,$Однако в системе (3) для K пар сегментов требуется учесть вышеописанную специфику точности детекции параметров сегментов. Для этого каждая пара сегментов поворачивается так, чтобы $t_{i}^{M}$ совпал с осью абсцисс, и уже в этой системе координат выполняется нормировка расстояния между компонентами центров. В результате получаем систему для i-й пары:
(4)
$\left\{ \begin{gathered} {{R}_{{{{\alpha }_{i}}}}}\Psi [\overline {r_{{{{c}_{i}}}}^{E}} ] \circ \overline {{{W}_{i}}} = {{R}_{{{{\alpha }_{i}}}}}\overline {r_{{{{c}_{i}}}}^{M}} \circ \overline {{{W}_{i}}} \hfill \\ \Psi [\overline {n_{i}^{E}} ] \cdot \overline {n_{i}^{M}} {\text{/}}s = 1 \hfill \\ \end{gathered} \right.,$Оценка качества преобразования
После того, как преобразование найдено, требуется оценить его качество. Для этого в свою очередь требуется установить корреспонденции между сегментами (поскольку изначально мы не приписывали сегментам никаких дескрипторов), а потом оценить качество совмещения сегментов изображения E и карты M. Считаем, что сегменту ${{t}^{M}}$ может соответствовать любой сегмент ${{t}^{E}}$. В дальнейшем мы планируем разработку дескриптора сегмента по локальной структуре его окружения, что позволит значительно ускорить процедуру оценки преобразования.
Установление соответствия между сегментами. Будем считать, что сегменту ${{t}^{E}}$ соответствует ${{t}^{M}}$, если выполнены следующие условия:
– $Q_{\alpha }^{\Psi }({{t}^{E}},{{t}^{M}}) < {{\varepsilon }_{\alpha }},$
– $Q_{y}^{\Psi }({{t}^{E}},{{t}^{M}}) < {{\varepsilon }_{y}}$ в системе координат, повернутой на угол $\alpha _{t}^{M}$,
– $Q_{x}^{\Psi }({{t}^{E}},{{t}^{M}}) < {{\varepsilon }_{x}} + 0.5\left| {{{t}^{M}}} \right|$ в системе координат, повернутой на угол $\alpha _{t}^{M}$.
Порядок условий в этом списке определяет их приоритет. Если этим условиям удовлетворяет несколько ${{t}^{M}}$, требуется сопоставить ${{t}^{E}}$ с каждым ${{t}^{M}}$ и выбрать тот ${{t}^{M}}$, который даст наилучшее сопоставление, при этом процедура сравнения сопоставления должна учитывать приоритет изложенных выше условий. Данная процедура будет описана нами далее.
Важно, что предложенные условия проверки согласуются с метрикой близости в системе (4), поскольку в идеальном случае (точной детекции и правильной векторной карты) для корректно вычисленного преобразования будет установлено правильное соответствие между сегментами.
Сравнение двух сопоставлений
Вышеописанный поиск соответствия между сегментами является основой для процедуры сравнения двух сопоставлений, выраженных в векторной форме (2). Формально ее можно записать следующим образом:
(5)
$MIN(\Upsilon ,\Omega ) = \left\{ \begin{gathered} \Upsilon ,{{\Upsilon }_{x}} < {{\Omega }_{x}} \wedge \left| {{{\Upsilon }_{\alpha }} - {{\Omega }_{\alpha }}} \right| < \varepsilon \cdot {{\varepsilon }_{\alpha }} \wedge \left| {{{\Upsilon }_{y}} - {{\Omega }_{y}}} \right| < \varepsilon \cdot {{\varepsilon }_{y}} \hfill \\ \Upsilon ,{{\Upsilon }_{y}} < {{\Omega }_{y}} \wedge \left| {{{\Upsilon }_{\alpha }} - {{\Omega }_{\alpha }}} \right| < \varepsilon \cdot {{\varepsilon }_{\alpha }} \wedge \left| {{{\Upsilon }_{y}} - {{\Omega }_{y}}} \right| \geqslant \varepsilon \cdot {{\varepsilon }_{y}} \hfill \\ \Upsilon ,{{\Upsilon }_{\alpha }} < {{\Omega }_{\alpha }} \wedge \left| {{{\Upsilon }_{\alpha }} - {{\Omega }_{\alpha }}} \right| \geqslant \varepsilon \cdot {{\varepsilon }_{\alpha }} \hfill \\ \Omega ,\;in\;other\;cases \hfill \\ \end{gathered} \right.,$Покомпонентный способ сравнения сопоставлений позволяет в явном виде задавать приоритизацию сравниваемых параметров сегментов и, как следствие, избежать вопроса установления эквивалентности между величиной погрешности по углу и по координате.
Оценка и выбор лучшего преобразования. Пусть даны два набора сегментов ${{T}^{E}} = t_{1}^{E},t_{2}^{E},\;...,\;t_{K}^{E},$ $t_{i}^{E} \in E$ и ${{T}^{M}} = t_{1}^{M},t_{2}^{M},\;...,\;t_{K}^{M},$ $t_{i}^{M} \in M$, таких, что каждому $t_{i}^{M}$ поставлен в соответствие единственный $t_{i}^{E}$ при помощи алгоритма, изложенного в пункте “Установление соответствия между сегментами”. Тогда, согласно (2), каждой паре сегментов поставлен в соответствие вектор ${{Q}^{\Psi }}(t_{i}^{E},t_{i}^{M})$. Будем оценивать качество преобразования как сумму этих векторов:
(6)
${{Q}^{\Psi }}({{T}^{E}},{{T}^{M}}) = \sum\limits_{i = 1}^K {{Q}^{\Psi }}(t_{i}^{{E{\text{'}}}},t_{i}^{M}).$В результате для каждой гипотезы о преобразовании мы построили способ оценки ее качества, а для сравнения гипотез между собой мы повторно используем (5):
(7)
$\begin{gathered} Q({{\Psi }_{1}},{{\Psi }_{2}},{{T}^{E}},{{T}^{M}}) = \\ = \;MIN({{Q}^{{{{\Psi }_{1}}}}}({{T}^{E}},{{T}^{M}})),{{Q}^{{{{\Psi }_{2}}}}}({{T}^{E}},{{T}^{M}})), \\ \end{gathered} $Алгоритм
В данном пункте сжато по шагам описан алгоритм сопоставления сегментов, найденных на изображении, и сегментов векторной карты. На вход алгоритму подаются два множества сегментов ${{T}^{E}} = t_{1}^{E},t_{2}^{E},\;...,\;t_{K}^{E},$ $t_{i}^{E} \in E$ и ${{T}^{M}} = t_{1}^{M},t_{2}^{M},\;...,\;t_{S}^{M},$ $t_{i}^{M} \in M$, причем S может быть не равно K. Далее выполняются следующие действия:
1. Повторить N раз:
а. Найти две пары случайных сегментов $t_{i}^{E},\;t_{j}^{M}$ и $t_{h}^{E},\;t_{g}^{M}$;
б. На их основе вычислить и сохранить преобразование $\hat {\Psi }$ согласно (4).
2. Для каждого сохраненного $\hat {\Psi }$:
а. Установить соответствие между наборами ${{T}^{E}}$ и ${{T}^{M}}$ согласно пункту “Установление соответствия между сегментами”;
б. По всем найденным соответствиям выполнить уточнение преобразования $\hat {\Psi }'$ согласно (4);
в. Если $Q(\hat {\Psi },\hat {\Psi }',{{T}^{E}},{{T}^{M}}) = \hat {\Psi }'$, то $\hat {\Psi } = \hat {\Psi }'$ и перейти к шагу 2а, иначе к следующему $\hat {\Psi }$.
3. Выбрать лучший $\hat {\Psi }'$ согласно пункту “Оценка и выбор лучшего преобразования”.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
Входные данные
Для проверки предложенного алгоритма мы использовали карты и фотографии городов Аляски: Ном, Гленналлен, Норт-Пол, Фэрбанкс, Колледж. Выбор городов именно этого региона продиктован наличием для них радиоизображений, которые были получены на портале IFSAR ORI Alaska, а соответствующие оптические изображения были получены после при помощи ресурса Google Earth.
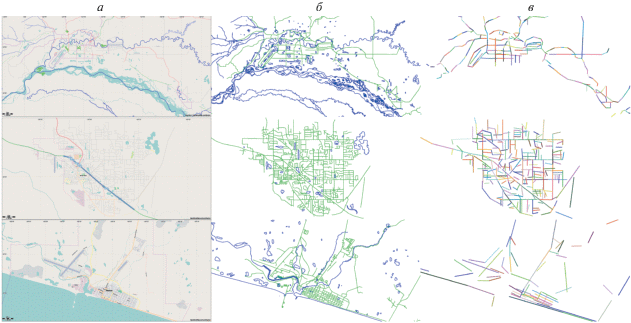
Векторные карты указанных городов были получены с использованием ресурса Open Street Map. Далее, при помощи пользовательской визуализации карт (рис. 4, а) программой Maperitive, из карт извлекались только главные дороги и контуры водных регионов (б), затем дороги проходили стадию упрощения, используя (Psimpl. generic n-dimensional poyline simplification, 2017) (в).
Рис. 4.
а – пользовательская визуализация карт с ресурса OSM; б – карты с отображением только дорог и контуров водных регионов; в – карты, содержащие только упрощенные прямолинейные сегменты дорог.
Сформированный набор данных доступен здесь (SAR and Optical Kunina Dataset, 2018).
Результаты тестирования предложенного подхода
Для каждого исходного изображения нами были подобраны истинные параметры преобразования Ψ. Чтобы сравнить найденное алгоритмом преобразование $\hat {\Psi }'$ с соответствующим идеальным Ψ, вычислялось максимальное евклидово расстояние между положением соответствующих угловых точек изображения после применения Ψ и $\hat {\Psi }'$. Полученное расстояние нормировалось на размер изображения после применения Ψ.
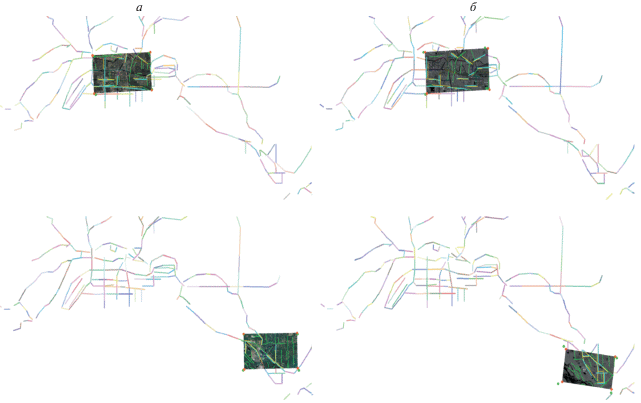
Было проведено восемь экспериментов по сопоставлению различных изображений с картой. Каждый эксперимент включал пару изображений в радио и видимом диапазонах соответственно. На рис. 5, а продемонстрированы примеры сопоставления изображений в видимом диапазоне с векторной картой, на б – изображений в радиодиапазоне. Зеленым отмечены угловые точки изображения после применения к нему истинного преобразования, красным – после найденного. Средняя ошибка сопоставления изображений в видимом диапазоне c картой составила 2.54%, для изображений в радиодиапазоне – 4.62%, что дало среднюю ошибку сопоставления изображений друг с другом – 6.62%. При этом прямое сопоставление дало среднюю ошибку сопоставления – 52.24%.
ЗАКЛЮЧЕНИЕ
В данной работе предложен RANSAC-подобный алгоритм сопоставления снимков в радио и видимом диапазонах через независимую визуальную локализацию относительно векторной карты дорог. Предложенный алгоритм связывает координаты каждого снимка с координатами карты, выделяя на снимке линейные сегменты дорог и осуществляя поиск такого геометрического преобразования, который наилучшим образом сопоставит полученный набор линейных сегментов с линейными сегментами дорог векторной карты. Для реализации данного алгоритма в работе предложен способ сравнения двух различных преобразований, адаптированный для сравнения качества сопоставления сегментов, характеристики которых не сравнимы по Парето. Относительная средняя евклидова ошибка сопоставления угловых точек изображения составила 0.06 для снимков, полученных с высоты 6–7 км, что в 8 раз меньше прямого сопоставления изображений без посредства карты. Полученные численные результаты в работе свидетельствуют о перспективности данного подхода для дальнейшего развития.
Исследование выполнено за счет гранта Российского научного фонда 14-50-00150.
Список литературы отсутствует.
Дополнительные материалы отсутствуют.
Инструменты
Сенсорные системы