Сенсорные системы, 2019, T. 33, № 2, стр. 166-172
Алгебраическая реконструкция в условиях недостатка памяти графического процессора в задаче компьютерной томографии
М. В. Чукалина 1, *, А. И. Ингачева 2, А. В. Бузмаков 1, А. П. Терехин 2, Ю. Шикина 3
1 Институт кристаллографии им. А.В. Шубникова ФНИЦ “Кристаллография и фотоника” РАН
119333 Москва, Ленинский проспект, дом 59, Россия
2 Институт проблем передачи информации им. А.А. Харкевича РАН
127051 Москва, Большой Каретный переулок, д. 19, Россия
3 Университет "Пари-Саклэ"
91191 Жив сюр Ивет, Франция
* E-mail: chukalinamarina@gmail.com
Поступила в редакцию 23.10.2018
Аннотация
В работе рассмотрена задача томографической реконструкции с применением алгебраического подхода в условиях недостатка памяти графического процессора для одновременной работы с полным набором собранных томографических проекций. Такая ситуация возникает, например, при конусной схеме регистрации проекций. В работе сформулирована оптимизационная задача для случая разбиения реконструируемого объема на субобъемы, описана схема разбиения и показана связь методов решения возникающей оптимизационной задачи с требованиями по оперативной памяти. Сравниваются результаты реконструкции при наличии и в отсутствие разбиения реконструируемого объема на субобъемы.
ВВЕДЕНИЕ
Метод компьютерной томографии позволяет восстанавливать внутреннюю структуру объекта без его физического разрушения, т.е. описывать локальную способность объекта ослаблять рентгеновское излучение. Если зондирующее рентгеновское излучение монохроматично, то решением задачи компьютерной томографии является пространственное распределение линейного коэффициента ослабления рентгеновского излучения для используемой длины волны. При полихроматическом зондировании, если не применяются специализированные методы реконструкции (Zhao et al., 2018), то восстанавливается распределение “усредненного по спектру линейного коэффициента”. В медицинских томографах применяется полихроматическое зондирование, что в некоторых случаях затрудняет интерпретацию получаемых результатов (Birnbacher et al., 2018).
Задача томографической реконструкции в методе рентгеновской томографии формулируется следующим образом: по зарегистрированным 2D-изображениям восстановить пространственное (3D) распределение коэффициента ослабления, описывающего способность объекта ослаблять рентгеновское излучение. Зарегистрированные позиционно-чувствительным оборудованием пиксельные изображения называют томографическими проекциями. Значение в пикселе – это число рентгеновских квантов, зарегистрированных ячейкой детектора, установленного за объектом. Излучение, сформированное рентгеновским источником, распространяясь прямолинейно, проходит через объект, на своем пути ослабляется материалом объекта, и ослабленное излучение регистрируется позиционно-чувствительным детектором, т.е. матрицей регистрирующих элементов. Каждый из элементов будем описывать пикселем изображения. Говоря о размере элемента матрицы (она же ячейка детектора), мы опустим из рассмотрения функцию размытия точки. Будем считать, что размер ячейки определяет пространственное разрешение метода. Тогда для повышения пространственного разрешения метода томографии следует увеличивать число ячеек регистрирующего оборудования, уменьшая их геометрические размеры. Сегодня в лабораторных приборах используются детекторы с числом пикселей порядка четырех тысяч в одном направлении, т.е. число регистрируемых данных на одну проекцию – 1.6 × 107, а число вокселов восстанавливаемого объема – 6.4 × 1010. Это и есть число неизвестных в задаче реконструкции. Чтобы уменьшить ошибку при решении обратной некорректно поставленной задачи, потребуем, чтобы число неизвестных в задаче было приблизительно равно числу наблюдаемых значений, т.е. число проекционных углов приблизительно равно числу ячеек детектора в одном из направлений.
Разнотипные подходы применяются для решения задачи томографической реконструкции. Рассмотрим подробнее два подхода – интегральный и алгебраический (Наттерер, 1990). Их принципиальное различие заключается в том, что в интегральных методах реконструкции, использующих аналитическое обращение, задача дискретизуется только на последнем шаге при вычислении интегралов. Аналитическое решение построено в предположении, что функции пространства Радона (пространства проекций) и функция пространства объекта (восстанавливаемое распределение) – непрерывны. Алгебраические подходы к решению задачи реконструкции используют сразу дискретные данные. Измерения – это дискретные изображения. Восстанавливаемый объем покрывается сеткой вокселей, на которой восстанавливается кусочно-постоянная функция. Каждый из этих типов реконструкции обладает своим набором достоинств и недостатков. Интегральные методы выполняются за приемлемое время, сравнимое со временем проведения измерений, и не налагают строгих требований к ресурсам памяти, алгебраические – являются сильно ресурсно-затратными. Однако именно алгебраические методы сегодня привлекают внимание многих групп исследователей. Это обусловлено стремлением снизить дозовые нагрузки при проведении измерений. Есть два способа это сделать – уменьшить число проекционных углов или уменьшить экспозицию. Первый ведет к потере пространственного разрешения, второй ухудшает отношение сигнал-шум. Сильная сторона алгебраических подходов в том, что основанные на них методы реконструкции с регуляризацией решения устойчивы к шуму входных данных (томографических проекций). Поскольку эти методы реконструкции итеративные, то время вычислений значительно больше по сравнению с интегральными методами. Создаются оптимальные версии итерационных алгоритмов (Прун и др., 2013), но существенно ускорить томографическую реконструкцию позволяет использование графических ускорителей (GPU). Их применение позволяет параллельно обрабатывать тысячи пикселей и вокселей (Xu, Mueller, 2007; Buzmakov et al., 2011). Появляются программные пакеты с открытым исходным кодом для выполнения операций прямого и обратного проецирования (основные операции в алгоритмах реконструкции) на GPU, эффективно реализованные и поддерживающиеся сообществом ученых, работающих в области решения задач реконструкции (Van Aarle, 2016). Однако, если все измеренные томографические данные не помещаются в память GPU, то необходимо изменять реализацию существующих алгоритмов реконструкции (Andersson et al., 2016).
В работе рассмотрена задача томографической реконструкции в условиях недостатка ресурсов памяти графического процессора для реализации итерации алгебраического метода с регуляризацией решения. Задача возникает в тех случаях, когда последовательная послойная реконструкция сечений невозможна ввиду конусной схемы измерения. Для такого случая сформулирована оптимизационная задача с регуляризирующим оператором для реконструкции полного объема. Описана схема разбиения полного объема на субобъемы. Переформулирована оптимизационная задача для субобъема. Показана связь методов решения возникающей оптимизационной задачи и требований по памяти. Обсуждаются результаты работы алгоритма реконструкции, реализующего разбиение на субобъемы. Модельные данные были использованы для расчетов.
ОПТИМИЗАЦИОННАЯ ЗАДАЧА ДЛЯ РЕКОНСТРУКЦИИ ПОЛНОГО ОБЪЕМА
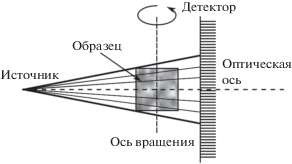
Принципиальная схема формирования томографической проекции для случая конусной схемы зондирования представлена на рис. 1. Здесь объект вращается вокруг некоторой оси, проходящей через него. Однако объект в некоторых реализациях томографической конусной процедуры может оставаться неподвижным, а система источник-детектор вращается вокруг объекта по окружности.
Математическая модель формирования проекции при монохроматическом зондировании, применяемая для решения обратной задачи, одинакова для обеих, описанных выше, схем сбора томографических проекций и включает следующие предположения. Источник рентгеновского излучения является точечным. Каждой ячейкой детектора регистрируется ровно один бесконечно тонкий луч. Запишем выражение, которое связывает величину сигнала I(r, φ), регистрируемого ячейкой позиционно-чувствительного детектора, с восстанавливаемым распределением величины коэффициента линейного ослабления m(x, y, z) при монохроматическом зондировании:
(1)
$I\left( {r,\varphi } \right) = {{I}_{0}}\exp \left( { - \mathop \smallint \limits_0^{{{L}_{{r,\varphi }}}} \mu \left( l \right)dl} \right).$Здесь r – радиус-вектор, определяющий положение наблюдаемой ячейки детектора или пикселя на изображении 2D-томографической проекции, φ – проекционный угол, под которым зондируется объект, ${{I}_{0}}$ – начальная интенсивность бесконечно тонкого зонда, ${{L}_{{r,\varphi }}}$ – траектория луча, формирующего сигнал в ячейке детектора, и $\mu \left( l \right)$ – коэффициент линейного ослабления текущей точки объема, через которую проходит траектория. Интегрирование ведется вдоль направления распространения луча. Мы ввели декартову систему координат, связанную с неподвижным объектом, описав объект функцией $\mu \left( {x,y,z} \right)\quad$, и описали процедуру получения набора проекций движением системы источник-детектор по круговой траектории. После нормирования зарегистрированного сигнала на начальную интенсивность и взятия отрицательного логарифма приходим к выражению, известному в непрерывном случае, как преобразование Радона:
(2)
$\ln \left( {\frac{{{{I}_{0}}}}{{I\left( {r,\varphi } \right)}}} \right) = \mathop \smallint \limits_0^{{{L}_{{r,\varphi }}}} \mu \left( l \right)dl.$Важнейшим свойством этого преобразования является его обратимость при выполнении некоторых условий. Это свойство использовано в интегральных методах реконструкции, о преимуществах и недостатках которых говорилось выше. Чтобы перейти к рассмотрению алгебраического подхода, вспомним, что томографические проекции представляют собой изображения с пикселями конечных размеров. Введем вектор измерений P размера ${{N}^{{dx}}} \times {{N}^{{dz}}} \times {{N}^{\varphi }}$, координатами которого являются левые части выражения (2) для всех пикселей детектора и всех проекционных углов. Здесь ${{N}^{{dx}}}$ – число пикселей в линейке детектора, ${{N}^{{dz}}}$ – число строк детектора и ${{N}^{\varphi }}$ – число проекционных углов. Будем использовать воксельное представление реконструируемого объекта. Покроем куб сеткой вокселов. Физический размер воксела свяжем геометрическим соотношением с размером пикселя изображения, формируемого детектором
где SO – расстояние источник – ось вращения, SD – расстояние источник–плоскость окна детектора. Количество вокселов в восстанавливаемом объеме ${{N}^{x}} \times {{N}^{y}} \times {{N}^{z}}$, где ${{N}^{x}} = {{N}^{y}} = {{N}^{{dx}}}$, а ${{N}^{z}} = {{N}^{{dz}}}$. Введем вектор решения $\vec {x}$ размерности ${{N}^{x}} \times {{N}^{y}} \times {{N}^{z}}$, координаты которого есть значения восстанавливаемой кусочно-постоянной функции. Перепишем выражение (2) где – проекционная матрица. Каждая строка матрицы содержит ${{N}^{x}} \times {{N}^{y}} \times {{N}^{z}}$ элементов. Число элементов строки равно числу вокселов восстанавливаемого объема. Число строк равно полному числу измерений ${{N}^{{dx}}} \times {{N}^{{dz}}} \times {{N}^{\varphi }}$. В самом простом случае элементами этой матрицы являются 0 и 1. Если луч, формирующий сигнал в текущей ячейке детектора, пересекает воксел, то элемент матрицы – “1”, в противном случае – “0”. Модели отрезков и весовых фракций также используются при составлении проекционных матриц (Kak, Slaney,1988). Размер системы линейных алгебраических уравнений (СЛАУ) (3) при рассматриваемых нами размерах детекторов составляет порядка нескольких миллиардов уравнений, поэтому прямые методы не используются для их решения. Переформулируем задачу поиска решения СЛАУ как задачу оптимизации. Будем искать такой вектор $\vec {x}$, который минимизирует функционал(5)
${\Phi }\left( x \right) = \left( {1 - \alpha } \right){{\left\| {P - Ax} \right\|}^{2}} + \alpha R\left( x \right).$Здесь α – параметр, определяющий вклад каждого из слагаемых в оптимизируемое выражение, $R\left( x \right)\quad$ – линейная комбинация регуляризирующих операторов, областью определения которых является векторное пространство решений. Поскольку искажения восстанавливаемого изображения могут иметь разную природу (Nikolaev et al., 2016), параметр α введен таким образом, чтобы регулировать вклад каждого из слагаемых в решаемую оптимизационную задачу.
Будем решать задачу алгебраическими методами на графическом процессоре. Для метода наискорейшего спуска решение на i-м итерационном шаге будет иметь вид
(6)
$x_{i}^{j} = x_{{i - 1}}^{j} + 2\beta \left( {1 - \alpha } \right){{A}^{T}}\left( {P - A{{x}_{i}}} \right) + \alpha \nabla R\left( {{{x}_{i}}} \right).{\;}$Здесь β – шаг в направлении наискорейшего спуска. Чтобы реализовать итерацию алгоритма на GPU потребуется память под несколько областей размера вектора измерений и несколько областей размера вектора решений. Точное количество областей зависит от метода, используемого для решения оптимизационной задачи. Таблица 1 позволяет провести сравнение требуемого количества памяти для метода градиентного спуска с постоянным шагом, метода наискорейшего спуска и метода сопряженных градиентов. Для эффективных расчетов на GPU для хранения каждой переменной использовалось четыре байта (т.е. переменные хранились в формате FLOAT). Объем памяти, доступный графическому процессору, на сегодняшний день не превышает нескольких гигабайт, т.е. позволяет одновременно загрузить приблизительно миллиард переменных. Как упоминалось выше, количество уравнений в системе имеет примерно такой же порядок (размер вектора измерений), плюс такое же количество неизвестных (размер вектора решений). С учетом значений, указанных в таблице, приходим к выводу о необходимости разбивать итерируемый объем на субобъемы и работать с каждым из них по отдельности.
Таблица 1
| № | Название метода | Векторы решений S | Векторы измерений M |
|---|---|---|---|
| 1 | Метод градиентного спуска | 3 | 3 |
| 2 | Метод градиентного спуска с регуляризацией | 3 | 3 |
| 3 | Метод наискорейшего спуска | 3 | 5 |
| 4 | Метод наискорейшего спуска с регуляризацией | 3 | 5 |
| 5 | Метод сопряженных градиентов | 4 | 5 |
| 6 | Метод сопряженных градиентов с регуляризацией | 4 | 5 |
ПРОЦЕДУРА ВЫДЕЛЕНИЯ СУБОБЪЕМА
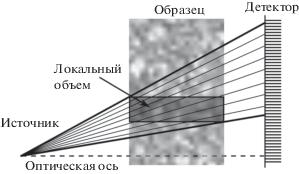
На рис. 2 проиллюстрирован предложенный нами ранее метод разбиения объема на субобъемы. Чтобы рассчитать количество слоев субобъема, запишем выражение, которое связывает его $N_{S}^{z}$ и требуемый для вычислений объем памяти ${\Pi }$ в байтах
где S и M – величины из таблицы. Если зафиксировать количество слоев субобъема, то в зависимости от их удаленности от оптической оси, количество соответствующих им строк детектора будет разным. Однако соответствие легко рассчитать из геометрии. В нашей программной реализации использована верхняя граница для этой величины, т.е. взята оценка для самого верхнего или нижнего субобъема. Половину памяти ассоциируем с данными объема, вторую половину – с данными измерений. Если данных второго типа оказывается больше, чем выделенный объем, то берутся не все проекционные углы одновременно. Мы разбиваем набор проекционных углов на соответствующее число поднаборов и выполняем расчеты последовательно для каждого поднабора.ОПТИМИЗАЦИОННАЯ ЗАДАЧА ДЛЯ СУБОБЪЕМА
После того, как объем разбит на субобъемы, необходимо переформулировать оптимизационную задачу. Запишем невязку с использованием значений вектора решений на предыдущем шаге итерационной процедуры
Поскольку на GPU доступны только данные субобъема, рассчитаем для них лучевые суммы
и будем решать следующую систему уравнений:Тогда оптимизационная задача для субобъема формулируется так
(11)
$\begin{gathered} \left( {1 - \alpha } \right){{\left\| {{{A}^{{local}}}x - \left( {{\Delta } + SUM_{{i - 1}}^{{local}}} \right)} \right\|}^{2}} + \\ + \;\alpha R\left( x \right)\mathop \to \limits^x \min . \\ \end{gathered} $В следующем разделе представлены результаты реконструкции, полученные описанным способом, с использованием томографических проекций, рассчитанных методом имитационного моделирования.
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
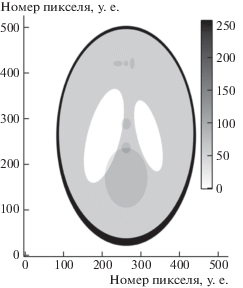
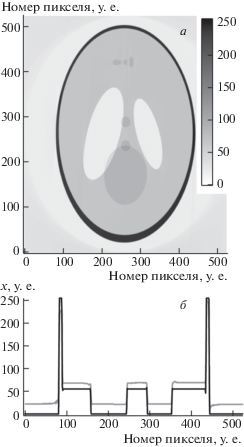
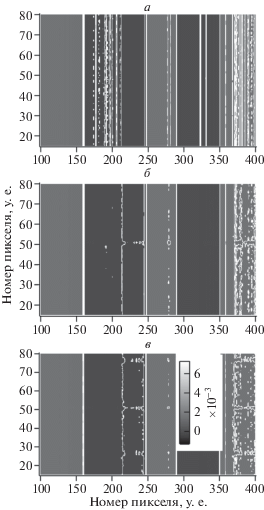
Для расчета модельных томографических проекций в качестве фантома был использован цилиндр, все поперечные сечения которого одинаковы и представляют собой фантом Шеппа-Логана (рис. 3). Для расчета модельных проекций использовались следующие параметры: число строк детектора – 100, в каждой строке 525 ячеек; физический размер ячейки детектора – 11 мкм; расстояние источник-объект – 55 мм; расстояние источник-детектор – 225 мм; схема измерения – конусная. Проекционные данные рассчитаны для интервала углов 0–180°, величина проекционного угла – 0.2°. Чтобы протестировать места сшивки субобъемов на результате восстановления, мы провели три эксперимента. Восстановили объем целиком, провели реконструкцию, разделив объем на два и четыре субобъема. Расчеты проведены для десяти итераций. Следов сшивки субобъемов на идеальных данных визуально обнаружить не удалось. Чтобы визуально оценить качество реконструкции, мы представляем центральное горизонтальное сечение объекта, восстановленного с использованием четырех субобъемов (рис. 4, а) и двух профилей (б), соответствующих 250 линиям этого сечения (серая линия) и центральному сечению фантома. Чтобы продемонстрировать наличие слабого эффекта сшивки, мы приводим участки вертикальных центральных сечений трех восстановленных объемов, наложив на изображения белые линии равного уровня (рис. 5). На а представлен участок сечения восстановленного целиком объема, на б – результат восстановления с использованием двух субобъемов, место сшивки в районе 50-го слоя. На в представлен результат восстановления с использованием четырех субобъемов, места сшивки в районе 25-, 50- и 75-го слоев. Полученные результаты подтверждают приемлемое качество реконструкции при разбиении описанным методом восстанавливаемого объема на субобъемы.
ЗАКЛЮЧЕНИЕ
Компьютерный томограф является аппаратно-программным комплексом. В настоящее время активно ведутся исследования, связанные с оптимизацией аппаратных частей томографа. Все более чувствительное оборудование с высоким пространственным разрешением регистрирует излучение, но требования к уменьшению дозовых нагрузок на объект не позволяют сильно улучшить отношение сигнал-шум. В связи с этим активно создаются новые методы реконструкции, способные работать в условиях наличия высокого шума. Однако эти методы серьезно проигрывают по скорости классическим. На помощь приходит использование графических ускорителей. Параллельно с этим увеличение пространственного разрешения метода (при сохранении физического размера поля вида) ведет к увеличению количества данных, регистрируемых в ходе томографического измерения. В данной работе рассмотрена задача реконструкции в условиях недостатка ресурсов памяти графического процессора для реализации итерации алгебраического метода при конусной схеме сбора проекций, описана схема разбиения полного объема на субобъемы, сформулирована оптимизационная задача для субобъема. Показана связь методов решения возникающей оптимизационной задачи и требований по памяти. Результаты реконструкции, полученные без использования процедуры разбиения на субобъемы, сравниваются с результатами реконструкции при наличии разбиения. Для идеальных модельных проекций визуально места сшивки обнаружить не удается. Мы планируем продолжить исследования с целью определения пределов применимости предлагаемого подхода, варьируя источники возникающих при томографической реконструкции искажений.
В заключение хотелось бы отметить, что в июле 2018 г. CERN поместил на своей странице новость о создании регистрирующего устройства нового поколения для использования при решении задач компьютерной томографии в медицинских приложениях (Greenwood, 2018). Новый прибор позволяет регистрировать в каждом пикселе детектора рентгеновский спектр. Это означает, что число измерений, с которыми придется работать при решении задачи томографической реконструкции, увеличится в число раз, равное числу регистрируемых спектральных линий. В связи с этим мы уверены, что создаваемые для работы с субобъемами данных алгоритмы в дальнейшем найдут свое применение при решении задач спектральной компьютерной томографии.
Исследования, связанные с анализом требуемых вычислительных ресурсов для решения задачи томографии, проводились при поддержке Министерства науки и высшего образования в рамках выполнения работ по Государственному заданию ФНИЦ “Кристаллография и фотоника” РАН. Работы по оптимизации необходимых расчетов выполнялись при частичной финансовой поддержке РФФИ (проекты № 17-29-03492 и № 18-52-7819).
Список литературы
Наттерер Ф. Математические аспекты компьютерной томографии. М. Мир, 1990. 288 с.
Прун В.Е., Бузмаков А.В., Николаев Д.П., Чукалина М.В., Асадчиков В.Е. Вычислительно эффективный вариант алгебраического метода компьютерной томографии. Автоматика и телемеханика. 2013. № 10. С. 86–97.
Andersson F., Carlsson M., Nikitin V.V. Fast algorithms and efficient GPU implementations for the Radon transform and the back-projection operator represented as convolution operators. SIAM Journal on Imaging Sciences. 2016. V. 9 (2). P. 637–664.
Birnbacher L., Willner M., Marschner M., Pfeiffer D., Pfeiffr F., Herzen J. Accurate effective atomic number determination with polychromatic grating-based phase-contrast computed tomography. Optics express. 2018. V. 26. № 12. P. 15153–15166.
Buzmakov A., Nikolaev D., Chukalina M., Schaefer G. Efficient and Effective Regularised ART for Computed Tomography. 33rd Annual International Conference of the IEEE EMBS. Boston. Massachusetts USA. 2011. P. 6200–6203.
Greenwood M. CERN Technology Powers World’s First 3-D Color X-Ray of a Human. 2018. https://www.engineering.com/Hardware/ArticleID/17302/CERN.
Kak A.C., Slaney M. Principles of Computerized Tomographic Imaging. New York, IEEE Press. 1988. 329 p.
Nikolaev D., Buzmakov A., Chukalina M., Yakimchuk I., Gladkov A., Ingacheva A. CT Image Quality Assessment based on Morphometric Analysis of Artifacts. Proc. SPIE 10253. 2016. V. 10253-06. P. 102530B. https://doi.org/10.1117/12.2266268
Van Aarle W., Palenstijn W. J., Cant J., Janssens E., Bleichrodt F., Dabravolski A., De Beenhouwer J., Batenburg K. J., Sijbers J. Fast and Flexible X-ray Tomography Using the ASTRA Toolbox. Optics Express, 2016. V. 24 (22). P. 25129–25147.
Xu F., Mueller K. Real-time 3D computed tomographic reconstruction using commodity graphics hardware. Physics in Medicine and Biology. 2007. № 52. P. 3405–3419.
Zhao W., Vernekohl D., Han F., Han B., Peng H., Yang Y., Xing L., Min J.K. A unified material decomposition framework for quantitative dual- and triple-energy CT imaging. Med. Phys. 2018. V. 45. № 7. P. 2964–2977.
Дополнительные материалы отсутствуют.
Инструменты
Сенсорные системы