Сенсорные системы, 2019, T. 33, № 2, стр. 124-134
Участие спектрального и временного механизмов в анализе сложных звуковых сигналов
О. Н. Милехина 1, Д. И. Нечаев 1, А. Я. Супин 1, *
1 Институт проблем экологии и эволюции им. А.Н. Cеверцова РАН
119071 Москва, Ленинский проспект, 33, Россия
* E-mail: alex_supin@mail.ru
Поступила в редакцию 01.08.2018
Аннотация
Измеряли частотную разрешающую способность (ЧРС) слуха здоровых испытуемых, определяемую как максимальная разрешаемая плотность (цикл/окт) гребней в гребенчатом спектре тест-сигнала. Тест-сигнал характеризовался периодически (каждые 400 мс) реверсиями фазы гребней спектра. Измерения основывались на сравнении тест-сигнала с референтным сигналом, в качестве которого использовали либо сигнал с гребенчатым спектром, в котором, в отличие от тест-сигнала, фаза гребней была постоянной, либо сигнал с “плоским” (без гребенчатой структуры) спектром. При измерениях каждая проба включала один тест-сигнал и два референтных сигнала, чередующихся в случайном порядке. Испытуемый идентифицировал тест-сигнал как отличающийся от двух других (референтных). При использовании референтного сигнала с гребенчатым спектром оценка ЧРС составила 8.9 ± 0.6 цикл/окт; при использовании референтного сигнала с плоским спектром оценка ЧРС составила 26.1 ± 8.8 цикл/окт. Это различие может быть обусловлено участием спектрального и временного механизмов частотного анализа: различение двух гребенчатых спектров происходит преимущественно на основе спектрального механизма, тогда как различение гребенчатого и плоского спектров происходит преимущественно на основе временного механизма.
ВВЕДЕНИЕ
В анализе спектрально-временной структуры звуковых сигналов принимают участие два основных механизма, представленных в слуховой системе: спектральный и временной. Эти термины условны, поскольку любой сигнал и любое преобразование сигнала равнозначно могут быть описаны как во временном, так и в частотном представлении. Тем не менее эти термины закрепились, и под ними подразумеваются конкретные физиологические процессы в слуховой системе.
Под спектральным механизмом подразумевается способ анализа, основанный на частотно-избирательных свойствах слуховой улитки. Разные участки базилярной мембраны улитки максимально чувствительны к разным звуковым частотам (проксимальный конец мембраны – к высоким частотам, дистальный – к низким). В зависимости от частоты воздействующего звука, колебания базилярной мембраны достигают максимума в том участке мембраны, который избирателен к данной частоте. При этом информация о частоте воздействующего звука кодируется тем участком улитки, от которого поступает поток нервных импульсов, т.е. кодирование частоты звука происходит по принципу места.
Под временным механизмом подразумевается способ анализа, основанный на структуре потока нервных импульсов, поступающих от слуховой улитки в слуховые нервные центры. В пределах некоторого диапазона частот импульсы в волокнах слухового нерва привязаны к определенной фазе звукового колебания. В результате поток нервных импульсов модулирован частотой воздействующих звуковых колебаний и таким образом передает в нервные центры слуховой системы информацию о частоте колебаний.
При различении звуковых сигналов по их спектрально-временным рисункам могут действовать оба механизма. Однако степень вовлеченности одного или другого механизма зависит от характера сигналов. Наиболее полно эти процессы исследованы для чистых звуковых тонов.
Временной анализ (т.е. определение частоты сигнала по структуре потока нервных импульсов) действует в диапазоне частот до 4–5 кГц (Moore, 1973; Sek, Moore, 1995). При более высоких звуковых частотах временной анализ неэффективен: поскольку частотный спектр нервного импульса не превышает нескольких кГц, никакая комбинация нервных импульсов не может нести информацию о более высоких частотах. В пределах доступного диапазона частот временной анализ может действовать не только при действии чистых тонов, но и при действии более сложных сигналов. При этом структура потока нервных импульсов несет информацию о временной структуре сигнала.
Спектральный анализ (т.е. определение частоты сигнала по месту возбуждения в улитке) эффективен во всем частотном диапазоне воспринимаемых звуков. Модель спектрального анализа подразумевает, что в улитке возникает некоторый “профиль возбуждения”, или “внутренний спектр” как результат прохождения спектра сигнала через гребенку частотно-избирательных слуховых фильтров (Zwicker, 1970).
Можно ожидать, что при различении натуральных звуков со сложными спектрально-временными рисунками действуют оба механизма. Каково их соотношение в зависимости от характера сигнала – принципиальный вопрос, важный как для понимания фундаментальных механизмов слухового анализа, так и в практическом аспекте, при установлении причин нарушений слуха, поскольку спектральный и временной анализ выполняются на разных уровнях слуховой системы.
Для исследования роли спектрального и временного механизмов в анализе звуковых сигналов продуктивно применение модельных сигналов, которые по степени сложности приближаются к натуральным, однако могут строго контролироваться по ограниченному числу параметров. К таким сигналам относятся, в частности, шумы с гребенчатыми спектрами. Они характеризуются спектральным рисунком, в котором периодически чередуются максимумы и минимумы спектральной амплитуды – гребни и провалы. Помимо обычных параметров, которыми характеризуются звуковые сигналы (спектральная полоса и интенсивность), гребенчатые шумы характеризуются плотностью и глубиной спектральных гребней.
Имеются данные, согласно которым в различении сигналов с гребенчатым спектром могут участвовать как спектральный, так и временной механизмы анализа. Возможность участия временного механизма требует специального пояснения, поскольку гребенчатые сигналы физически являются шумами, т.е. не имеют четкой временной структуры, характерной для периодических сигналов. Однако они имеют скрытую временную структуру, которая проявляется в их автокорреляционной функции (АКФ): рисунок гребенчатого шума повторяется через интервалы времени, которые являются обратной величиной от частотного интервала между гребнями. Эта структура наиболее выражена в варианте гребенчатого шума с широкой спектральной полосой и одинаковыми частотными интервалами между соседними гребнями. Такие сигналы создают ощущение некоторой тональности звука, соответствующей высоте тона с частотой, равной частотному интервалу между спектральными гребнями шума – “тональность повторений” (repetition pitch) (Bilsen, Ritsma, 1969; Yost, Hill, 1978; Yost, 1996; Yost et al., 1978, 1996). В появлении тональности повторений ведущая роль приписывалась временному анализу. Предполагалось, что в слуховой системе существуют процессы, которые соответствуют вычислению автокорреляционной функции звукового сигнала (Yost, 1996; Yost et al., 1996; Patterson et al., 1996; Krumbholz et al., 2001). Тональность повторений наиболее сильно ощущается на частотах около 500 Гц и практически не ощущается на частотах ниже 50 и выше 2000 Гц, т.е. возникает именно в том диапазоне частот, в котором эффективно работает механизм временного анализа.
Помимо сигналов с постоянными частотными интервалами между гребнями спектра, во многих работах применяются сигналы с частотно-пропорциональными интервалами (Попов, Супин, 1984, 1987; Green, 1986; Supin et al., 1994, 1998, 1999). Такой гребенчатый спектр лучше соответствует зависимости добротности слуховых каналов-фильтров от частоты. У сигналов с частотно-пропорциональным гребенчатым спектром АКФ не столь явно отражает скрытую временную структуру сигнала как у сигналов с постоянными частотными интервалами между гребнями. Поэтому в ряде работ приводились аргументы в пользу спектрального, но не временного механизма анализа таких сигналов (Супин и др., 2002, 2006; Supin et al., 1998, 2003; Nechaev, Supin, 2013).
Степень участия спектрального и временного механизмов в различении гребенчатых спектров может зависеть не только от типа сигнала, но и от задачи, для решения которой требуется различение сигналов. Наиболее распространенная задача, для решения которой используются сигналы с гребенчатыми спектрами, – определение максимальной разрешаемой плотности гребней – частотная разрешающая способность (ЧРС). Измерение ЧРС при помощи гребенчатых спектров – эффективная диагностическая процедура, применяемая, в частности, для определения эффективности кохлеарных имплантов. Такой способ тестирования в последние годы приобретает все большее распространение (Litvak et al., 2007; Saoji et al., 2009; Anderson et al., 2012; Aronoff, Landsberger, 2013; Narne et al., 2016). Если не рассматривать эксперименты, в которых оценивалось субъективное качество сигналов (тональность повторений), то все варианты измерения ЧРС сводятся к выбору между тест-сигналом, каковым является гребенчатый шум, и некоторым сигналом сравнения (референтным сигналом). При этом предполагается, что различение между тест- и референтным сигналами возможно только тогда, когда гребенчатая структура тест-сигнала разрешаема слуховой системой. Однако нет единого представления о том, каким должен быть референтный сигнал для измерения ЧРС. Применялись две основных схемы эксперимента.
При первой схеме тестовый и референтный сигналы имеют гребенчатые спектры и одинаковы по интенсивности, ширине спектральной полосы и плотности гребней спектра, различаясь только по фазе гребенчатой структуры. В тестовом сигнале фаза гребней несколько раз меняется на противоположную, т.е. положение пиков и провалов спектральной амплитуды на частотной шкале взаимно заменяется (Supin et al., 1994, 1997, 1998, 1999), либо фаза гребней сдвигается на некоторую величину (Nechaev, Supin, 2013). В референтном сигнале гребенчатый рисунок остается постоянным. Вариант этой схемы – фазы гребней в тестовом и референтном сигналах постоянны, но противоположны друг другу (Henry et al., 2005; Won et al., 2007, 2014; Anderson et al., 2011; Jeon et al., 2015; Milekhina et al., 2018).
Альтернативная схема эксперимента состоит в том, что тестовый сигнал имеет гребенчатый спектр, а референтный – не имеет (“плоский” спектр). Термин “плоский” в данном контексте означает не постоянство амплитуды спектральных компонентов в полосе спектра, а лишь отсутствие гребенчатого рисунка. По остальным параметрам (интенсивность, спектральная полоса) тест- и референтный сигналы одинаковы (Van Zanten, Senten, 1983; Chi et al., 1999; Nechaev et al., 2018). Вариант данной схемы – использование референтного сигнала не с плоским, а с гребенчатым спектром, но с плотностью гребней, заведомо превышающей предел разрешения. Предполагалось, что такой сигнал, в котором гребенчатая структура спектра неразличима, воспринимается как плоский (Aronoff, Landsberger, 2013; Narne et al., 2016). В данной схеме также возможны варианты, при которых фаза гребней в спектре тест-сигнала или постоянна, или периодически меняется на противоположную, или градуально сдвигается.
Выбор референтного сигнала для измерений ЧРС может быть принципиально важен для диагностики нарушений слуха и определения эффективности слуховых аппаратов или кохлеарных имплантов. Поскольку измерения основаны на способности различать тестовый и референтный сигналы, выбор референтного сигнала может влиять на результат измерения. В большинстве случаев для измерений ЧРС в практических целях использовался референтный сигнал с плоским спектром, который противопоставлялся тест-сигналу с гребенчатым спектром. Однако это не единственно возможная схема эксперимента, следовательно, возникает вопрос о корректности получаемых оценок ЧРС. Важно знать, совпадают ли оценки при применении разных схем измерения, а если не совпадают, то какую схему следует считать правильной. Решить вопрос о корректности той или иной схемы измерения ЧРС можно сравнением результатов, полученных на одном и том же контингенте испытуемых при применении разных схем.
Сравнение оценок ЧРС, полученных при различных схемах эксперимента, важно не только для решения прикладных задач. Такие данные имеют значение для фундаментальной физиологии слуха, поскольку могут прояснить роль частотного и временного механизмов в анализе сложных звуковых сигналов. Для обоснования этого предположения рассмотрим предсказания спектральной и временной моделей при измерении ЧРС в различных схемах эксперимента: при использовании референтных сигналов с гребенчатым и плоским спектром.
На рис. 1 представлены результаты расчета прохождения нескольких форм сигналов – с низкой плотностью гребней (а), с высокой плотностью гребней (б) и без гребенчатой структуры (в) через гребенку частотно-избирательных слуховых фильтров с шириной 0.16 окт в соответствии с моделью спектрального анализа. В качестве фильтра принята функция скругленной экспоненты (rounded exponent, roex) c эквивалентной прямоугольной шириной 12% от центральной частоты фильтра, что следует из формулы, приведенной в работе (Glasberg, Moore, 1990), и составляет приблизительно 0.16 окт. После прохождения через такие фильтры внутренние спектры (профили возбуждения) имеют вид, представленный на г–е. При низкой плотности гребней (а) профиль возбуждения (г) также имеет гребенчатую структуру, мало отличающуюся от спектра сигнала. Профили с противоположными фазами гребней (г, 1 и 2) и плоский профиль (д) существенно различаются. По таким профилям возможно как различение друг от друга гребенчатых сигналов с противоположными фазами гребней, так и различение между гребенчатым и плоским сигналами. При повышении плотности гребней их глубина в профиле возбуждения уменьшается вследствие интегрирования в пределах полосы пропускания фильтров. При некоторой достаточно высокой плотности гребней их глубина в профиле возбуждения уменьшается настолько, что гребенчатый профиль вырождается в плоский. При этом гребенчатые и плоские сигналы воспринимаются одинаково и не могут отличаться слуховой системой один от другого. Этим определятся разрешаемая плотность гребней, т.е. ЧРС.
Рис. 1.
Преобразования сигналов в соответствии с моделью спектрального анализа.
а–в – спектры сигналов, применяемых для измерений; г–е: “внутренние спектры” (профили возбуждения), получаемые при прохождении этих сигналов через гребенку полосовых фильтров с эквивалентной прямоугольной шириной 0.16 окт. Спектры представлены в логарифмической шкале частот, адекватной для частотно-пропорциональной ширины фильтров. а и г – гребенчатый спектр с плотностью гребней 2 цикл/окт; 1 и 2 –спектры с противоположными фазами гребней, замещающие друг друга в тест-сигнале; б и д – то же при плотности гребней 8 цикл/окт; в и е – то же для плоского спектра.
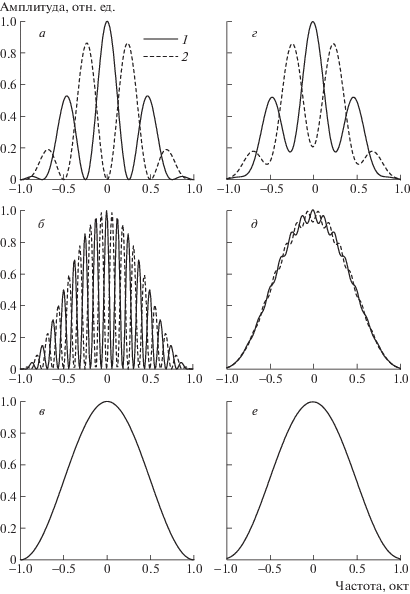
Таким образом, модель предсказывает одинаковую эффективность спектрального механизма различения как при гребенчатом, так и при плоском референтном сигнале и соответственно должна давать одинаковые оценки ЧРС при обеих схемах эксперимента.
Результаты вычислений в соответствии с моделью временного анализа на основе автокорреляционной функции (АКФ) сигнала представлены на рис. 2. Сигналы с гребенчатым спектром (а, б) имеют АКФ, которая характеризуется наличием двух сегментов: основного (незадержанного) и задержанного (г, д). Задержка равна величине, обратной частотному интервалу между гребнями: она короче при низкой плотности гребней (г) и длиннее при высокой плотности (д). Оба сегмента содержат колебания с частотой, которая лежит в пределах частотной полосы сигнала. При изменении фазы гребней в спектре сигнала меняется фаза колебаний в задержанном сегменте. Таким образом, возможность обнаружить различие в фазе гребней зависит от разрешения колебаний внутри задержанного сегмента АКФ, следовательно, зависит не от задержки сегмента АКФ (т.е. не от плотности гребней), а от частоты колебаний в задержанном сегменте (т.е. от частотной полосы сигнала). Поэтому сравнение сигналов с разными фазами гребенчатых спектров на основе их АКФ не выявляет разрешаемую плотность гребней, т.е. ЧРС.
Рис. 2.
Преобразование сигналов в соответствии с моделью временного анализа.
а–в – спектры сигналов, применяемых для измерений; г–е – соответствующие АКФ. Спектры представлены в линейной шкале частот, адекватной для расчета АКФ. а и г – гребенчатый спектр с плотностью гребней 2 цикл/окт; 1 и 2 –спектры с противоположными фазами гребней, замещающие друг друга в тест-сигнале; б и д – то же при плотности гребней 8 цикл/окт; в и е – то же для плоского спектра.
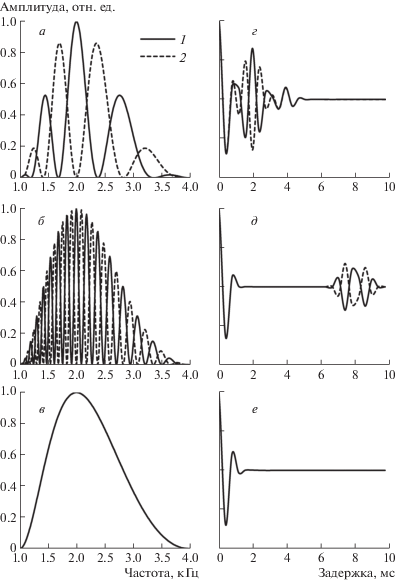
Иная ситуация создается при сравнении сигналов с гребенчатым и с плоским спектрами. Плоский спектр (рис. 2, в) характеризуется АКФ без задержанного сегмента (е). Поэтому временной анализ на основе АКФ позволяет различить гребенчатый и плоский сигналы. Различение возможно при таких плотностях гребней, при которых задержанный сегмент АКФ не выходит за пределы “окна” вычисления АКФ. При высоких плотностях гребней задержанный сегмент АКФ оказывается за пределами окна анализа, т.е. АКФ гребенчатого сигнала становится такой же, как АКФ плоского. Гребенчатый и плоский сигналы становятся неразличимыми. Этим ограничением определяется различимая плотность гребней, т.е. ЧРС.
Таким образом, согласно представленным моделям, спектральный и временной механизмы по-разному проявляют себя в зависимости от задачи, для которой применяются тест-сигналы с гребенчатым спектром. Ожидается, что спектральный механизм одинаково действует как при различении гребенчатых спектров с разными фазами гребней, так и при различении гребенчатого и плоского спектров, причем в обоих случаях должен давать одинаковые оценки ЧРС. Временной механизм должен быть неэффективен при различении гребенчатых спектров с разными фазами гребней, но эффективен для различения гребенчатого и плоского спектров.
Экспериментальная проверка этих предсказаний возможна путем сравнения оценок ЧРС при разных схемах эксперимента, а именно, при референтном сигнале с гребенчатым или с плоским спектром. Сравнение позволит оценить реальную степень участия спектрального и временного механизмов анализа в различении некоторых характерных спектрально-временных рисунков.
Такая проверка была целью настоящей работы. Для достижения этой цели выполняли измерения ЧРС на одной и той же группе испытуемых при одинаковых тест-сигналах (шум с гребенчатым спектром варьирующей плотности), но при разных референтных сигналах. В качестве референтного сигнала использован либо шум с гребенчатым спектром, либо шум с плоским спектром.
МЕТОДИКА
Испытуемые и условия эксперимента. В исследовании принимали участие шесть испытуемых в возрасте от 23 до 49 лет: четверо мужчин и две женщины. Для всех испытуемых имелись стандартные аудиограммы, которые показали слух в пределах нормы (пороги не выше 15 дБ) в диапазоне от 1 до 4 кГц, в котором проводили измерения.
Во время эксперимента испытуемый находился в звукозаглушающей кабине MINI 350 (IAC, Германия).
Сигналы. Применявшиеся в исследовании звуковые сигналы были двух типов, которые условно обозначались как тестовые и референтные. Тест-сигналы всегда имели гребенчатую структуру спектра. Гребенчатый рисунок спектра был частотно-пропорциональным: во всей спектральной полосе сигнала интервал между соседними гребнями составлял одну и ту же пропорцию от частоты, т.е. отношение δf/f (где δf – частотный интервал и f – центральная частота гребня) было постоянным. В таком варианте гребенчатого спектра плотность гребней характеризуется количеством гребней на октавный интервал частоты (цикл/окт). В процессе измерений плотность гребней меняли, чтобы определить максимальную разрешаемую плотность гребней, что принимали за оценку ЧРС. Референтные сигналы имели либо гребенчатый спектр с такой же плотностью гребней, как у тест-сигнала, но отличающийся по фазе гребней, либо плоский (не гребенчатый) спектр.
Все сигналы представляли собой полосовой шум со спектральной полосой, центрированной на частоте 2 кГц. Огибающей спектральной полосы был один цикл косинусоидальной функции от логарифма частоты; период функции составлял 2 окт, т.е. полоса охватывала диапазон частот от 1 до 4 кГц.
В тестовом сигнале каждые 400 мс происходила реверсия фазы гребней спектра, т.е. один из спектров, представленных на рис. 1, а, заменялся другим, еще через 400 мс происходила обратная замена – всего три полных цикла замены фазы гребней на противоположную, и обратно. Таким образом, длительность сигнала составляла 2400 мс.
Референтный сигнал мог быть одного из двух типов: с гребенчатым или с плоским спектром. В обоих случаях огибающая спектра сигнала была такой же, как у тест-сигнала, и длительность сигнала также составляла 2400 мс.
Референтный сигнал с гребенчатым спектром имел такую же плотность гребней, как тест-сигнал, но фаза гребней оставалась постоянной в течение всего времени действия сигнала, т.е. 2400 мс. Референтный сигнал с плоским спектром также оставался неизменным в течение 2400 мс.
Все сигналы генерировали цифровым способом с частотой стробирования 32 кГц. Программа синтеза включала фильтрацию белого шума (случайная последовательность чисел). Выбранным фильтром определялся характер сигнала: гребенчатый тестовый, гребенчатый референтный или плоский референтный.
Для генерации тестового сигнала использовали два фильтра с гребенчатыми характеристиками и с противоположными фазами гребней. Каждые 400 мс белый шум перенаправляли со входа одного фильтра на вход другого, и обратно; выходы фильтров суммировали. В результате получали сигнал с гребенчатым спектром, в котором фаза гребней менялась на противоположную каждые 400 мс.
Для генерации референтного сигнала с гребенчатым спектром использовали один фильтр с гребенчатой частотной характеристикой. Для генерации референтного сигнала с плоским спектром использовали фильтр с плоской (без гребенчатой структуры) частотной характеристикой.
Программа генерации сигналов была создана в форме “виртуального прибора” (virtual instrument) на базе программной оболочки LabVIEW (National Instruments, США) и реализована на стандартном персональном компьютере. Синтезированные сигналы переводили из цифровой формы в аналоговую при помощи цифроаналогового преобразователя, входящего в состав платы сбора данных NI USB-6251 (National Instruments). Сигналы воспроизводили через головные телефоны HD580 (Sennheiser, Германия). Неравномерность частотной характеристики телефонов была в пределах 1.5 дБ в диапазоне частот применявшихся сигналов, т.е. от 1 до 4 кГц.
Процедура измерений. Измерения состояли в определении предельной различаемой плотности гребней тест-сигнала, т.е. ЧРС. Для этого использована трехальтернативная процедура с принудительным выбором. В каждой пробе предъявляли три сигнала: один тестовый и два референтных. Сигналы длительностью 2400 мс каждый следовали один за другим с паузами 400 мс между ними (рис. 3). Порядок следования сигналов меняли от пробы к пробе в случайном порядке, т.е. в последовательности из трех сигналов тестовый сигнал мог оказаться первым, вторым или третьим. От испытуемого требовали определить, какой из трех сигналов отличается по звучанию от двух других – по этому признаку идентифицировался тестовый сигнал. Поскольку инструкция подразумевала выбор одного из трех одинаково возможных вариантов, процедура была трехальтернативной. Требование выбрать один из сигналов относило процедуру к категории принудительного выбора. Инструкция испытуемому не включала указания на какой-либо признак сигнала, которые требовалось бы выделить, т.е. при принятии решения испытуемый мог использовать любой признак, отличающий тестовый сигнал от референтных.
Рис. 3.
Временные диаграммы предъявления сигналов при измерениях в различных схемах эксперимента. а – при использовании референтного сигнала с гребенчатым спектром; б – при использовании референтного сигнала с плоским спектром. 1 и 2 – сигналы со спектрами, представленными на рис. 1, а и 2, а (соответственно спектры 1 и 2). В приведенных примерах тест-сигнал был первым из трех, но его положение могло меняться в случайном порядке.
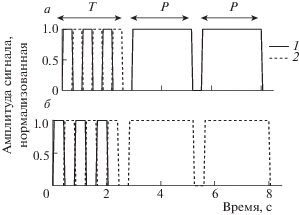
Для измерения ЧРС плотность гребней в спектре тест-сигнала (соответственно также и в спектре референтного сигнала, если в качестве такового применяли сигнал с гребенчатым спектром) меняли от пробы к пробе по адаптивной процедуре в варианте “два – вверх, один – вниз”. Согласно такой процедуре, после двух последовательных правильных ответов (правильное определение тест-сигнала из трех предъявленных) плотность гребней повышали на один шаг; после каждой ошибки плотность гребней снижали на один шаг. Такая процедура приводит изменяемый параметр сигнала (в нашем случае – плотность гребней) к значению, которое обеспечивает вероятность обнаружения тест-сигнала, равную 0.51/2 = 0.71. Эту вероятность принимали за порог обнаружения, поскольку она близка к среднему значению (0.67) между 100% правильных ответов при уверенном обнаружении сигналов и 33% правильных ответов при невозможности обнаружить сигнал и случайном выборе ответа. Ступенчатая шкала изменений плотности гребней включала следующие значения: 2, 3, 5, 7, 10, 15, 20, 30, 50, 70, 100 цикл/окт. Адаптивное варьирование плотности гребней продолжали до получения десяти точек перегиба – перехода от повышения плотности гребней к понижению и обратно. Среднее значение плотности гребней в этих десяти точках перегиба принимали за оценку ЧРС в данном эксперименте. Измерения повторяли 3 раза, и полученные оценки ЧРС усредняли, таким образом получая оценку ЧРС для данного испытуемого. Окончательную оценку ЧРС получали усреднением данных по всем испытуемым.
РЕЗУЛЬТАТЫ
Таблицы 1 и 2 и рис. 4 суммируют результаты всех выполненных измерений при одинаковой форме тест-сигнала, но разных формах референтного сигнала: с гребенчатым (табл. 1) и с плоским (табл. 2) спектрами.
Таблица 1.
Индивидуальные и усредненные оценки ЧРС (цикл/окт) при использовании референтного сигнала с гребенчатым спектром
| Испытуемый | № измерения | Среднее | Стандартное отклонение | ||
|---|---|---|---|---|---|
| 1 | 2 | 3 | |||
| А | 8.5 | 7.6 | 8.5 | 8.2 | 0.5 |
| Н | 9.5 | 8.5 | 8.5 | 8.8 | 0.6 |
| К | 8.5 | 8.5 | 9.5 | 8.8 | 0.6 |
| Ф | 8.5 | 8.5 | 8.5 | 8.5 | 0 |
| М | 8.5 | 10 | 8.5 | 9 | 0.9 |
| С | 11.3 | 9.8 | 8.8 | 10.0 | 1.3 |
| Среднее | – | 8.9 | – | ||
| Стандартное отклонение | – | 0.6 | – | ||
Таблица 2.
Индивидуальные и усредненные оценки ЧРС (цикл/окт) при использовании референтного сигнала с плоским спектром
| Испытуемый | № измерения | Среднее | Стандартное отклонение | ||
|---|---|---|---|---|---|
| 1 | 2 | 3 | |||
| А | 16 | 30.7 | 18.6 | 21.8 | 7.8 |
| Н | 22 | 44 | 33.5 | 33.2 | 11.0 |
| К | 22.9 | 10.2 | 13.9 | 15.7 | 6.5 |
| Ф | 30 | 28.2 | 57 | 38.4 | 16.1 |
| М | 24.5 | 32.7 | 29.2 | 28.8 | 4.1 |
| С | 22.5 | 23.5 | 10.1 | 18.7 | 7.5 |
| Среднее | – | 26.1 | – | ||
| Стандартное отклонение | – | 8.8 | – | ||
Рис. 4.
Оценки ЧРС при различных схемах эксперимента.
1 – референтный сигнал с гребенчатым спектром, 2 – референтный сигнал с плоским спектром. Планки погрешностей – стандартные отклонения по всему массиву измерений.
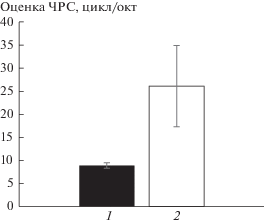
При референтном сигнале с гребенчатым спектром полученные значения ЧРС варьировали от 7.6 (испытуемый А, измерение 2) до 11.3 (испытуемый С, измерение 1) цикл/окт. Разброс результатов между несколькими измерениями для каждого испытуемого был относительно невелик: стандартные отклонения (СО) от 0 (испытуемый Ф) до 1.3 (испытуемый С) цикл/окт. Среднее значение и стандартное отклонение ЧРС по всем измерениям на всех испытуемых: 8.9 ± ± 0.6 цикл/окт.
При референтном сигнале с плоским спектром были получены существенно более высокие значения ЧРС. В отдельных экспериментах они варьировали от 15.7 (испытуемый К) до 38.4 (испытуемый Ф) цил/окт. При этом имел место значительный разброс данных от измерения к измерению для каждого испытуемого: от 4.1 (испытуемый М) до 16.1 (испытуемый Ф) цикл/окт. Среднее значение и стандартное отклонение ЧРС по всем измерениям на всех испытуемых: 26.1 ± ± 8.8 цикл/окт (рис. 4).
Таким образом, использование референтного сигнала с плоским спектром позволяло испытуемым правильно идентифицировать тест-сигнал при плотности гребней в среднем в 2.9 раза выше, чем при использовании референтного сигнала с гребенчатым спектром.
ОБСУЖДЕНИЕ
Приведенные экспериментальные данные показывают, что оценки ЧРС, получаемые с применением тест-сигналов с гребенчатыми спектрами, могут существенно различаться в зависимости от поставленной испытуемому задачи различения. Если ЧРС оценивается по способности отличить гребенчатый сигнал от сигнала с другим рисунком гребенчатого спектра (в нашем случае – отличающегося по фазе гребней), то допустима плотность гребней почти втрое ниже, чем если требуется различить гребенчатый и плоский спектры.
Возможный вопрос, вытекающий из этих результатов: если два метода дают столь сильно различающиеся оценки одной и той же переменной, то какой из методов тестирования дает “правильную” оценку ЧРС? Однако такая постановка вопроса представляется нецелесообразной, если рассмотреть возможную роль механизмов, участвующих в анализе сигналов в одном и в другом случае.
Как следует из рассмотрения основных моделей анализа, приведенного во введении, при референтном сигнале с гребенчатым спектром временной анализ мало эффективен ввиду значительного сходства АКФ тестового и референтного сигналов, тогда как спектральный анализ более эффективен. Следовательно, измерения с применением гребенчатого референтного сигнала преимущественно дают сведения о разрешающей способности, обусловленной возможностями спектрального анализа.
Модель спектрального анализа предсказывает одинаковые результаты при применении референтных сигналов с гребенчатым и с плоским спектрами. Как показали результаты, при применении референтного сигнала с плоским спектром оценки ЧРС в несколько раз выше. Очевидно, эти высокие оценки ЧРС обусловлены подключением другого механизма анализа в дополнение к спектральному. Таким механизмом может быть временной анализ, который в этом случае эффективен ввиду значительного различия АКФ тестового и референтного сигналов.
Таким образом, различие между двумя схемами эксперимента (с гребенчатым и плоским спектром референтного сигнала) состоит не в том, что одна из них дает “правильную”, а другая – “неправильную” оценку ЧРС. Различие в том, что эти две схемы дают сведения о возможностях двух взаимодополняющих механизмов частотного анализа – спектрального и временного. Эта особенность схем эксперимента может быть использована в тех случаях, когда требуется дифференцированно оценить работоспособность разных уровней слуховой системы.
Работа поддержана РФФИ (грант № 17-04-00096).
Список литературы
Попов В.В., Супин А.Я. Количественное измерение разрешающей способности слуха человека. Докл. АН СССР. 1984. Т. 278. С. 1012–1016.
Попов В.В., Супин А.Я. Частотная разрешающая способность слуха человека. Физиол. человека. 1987. Т. 13. С. 28–34.
Супин А.Я., Попов В.В., Милехина О.Н., Тараканов М.Б. Частотная разрешающая способность слуха человека: зависимость от интенсивности сигнала и помех. Сенсорные системы. 2002. Т. 16. С. 309–329.
Супин А.Я., Попов В.В., Милехина О.Н., Тараканов М.Б. Частотная разрешающая способность слуха человека при различных соотношениях помеха/сигнал. Сенсорные системы. 2006. Т. 20. С. 141–148.
Anderson E.S., Nelson D.A., Kreft H., Nelson P.B., Oxenham A.J. Comparing spatial tuning curves, spectral ripple resolution, and speech perception in cochlear implant users. J. Acoust. Soc. Am. 2011. V. 130. P. 364–375.
Anderson E.S., Oxenham A.J., Nelson P.B., Nelson D.A. Assessing the role of spectral and intensity cues in spectral ripple detection and discrimination on cochlear-implant users. J. Acoust. Soc. Am. 2012. V. 132. P. 3925–3934.
Aronoff J.M., Landsberger D.M. The development of a modified spectral ripple test. J. Acoust. Soc. Am. 2013. V. 134. P. EL217-222.
Bilsen F.A., Ritsma R.J. Repetition pitch and its implication for hearing theory // Acustica. 1969. V. 22. P. 63–68.
Chi T., Gao Y., Guyton M.G., Ru P., Shamma S. Spectro-temporal modulation transfer function and speech intelligibility. J. Acoust. Soc. Am. 1999. V. 106. P. 2719–2732.
Glasberg B.R., Moore B.C.J. Derivation of auditory filter shapes from notched-noise data. Hearing Res. 1990. V. 47. P. 103–138.
Green D. Frequency and the detection of spectral shape change. Auditory Frequency Selectivity. Ed. B.C.J. Moore, R.D. Patterson. Plenum, New York. 1986. P. 351–358.
Henry B. A., Turner C. W., Behrens A. Spectral peak resolution and speech recognition in quiet: Normal hearing, hearing impaired, and cochlear implant listenersю J. Acoust. Soc. Am. 2005. V. 118. P. 1111–1121.
Jeon E.K., Turner C.W., Karsten S.A., Henry B.A., Gantz B.J. Cochlear implant users’ spectral ripple resolution. J. Acoust. Soc. Am. 2015. V. 138. P. 2350–2358.
Krumbholz K., Patterson R.D., Nobbe A. Asymmetry of masking between noise and iterated rippled noise: Evidence for time-interval processing in the auditory system. J. Acoust. Soc. Am. 2001. V. 110. P. 2096–2107.
Litvak L.M., Spah, A.J., Saoji A.A., Fridman, G.Y. Relationship between perception of spectral ripple and speech recognition in cochlear implant and vocoder listeners,” J. Acoust. Soc. Am. 2007. V. 122. P. 982–991.
Milekina O.N., Nechaev D.I., Supin A.Ya. Estimates of frequency resolving power of humans by different methods: the role of sensory and cognitive factors. Human Phisiol. 2018. V. 44. P. 357–363.
Moore B.C.J. Frequency difference limens for short-duration tones. J. Acoust. Soc. Am. 1973. V. 54. P. 610–619.
Narne V.K., Van Dun B., Bansal S., Prabhu L., Moore B.C.J. Effects of spectral smearing on performance of the spectral ripple and spectro-temporal ripple tests. J. Acoust. Soc. Am. 2016. V. 140. P. 4298–4306.
Nechaev D.I., Milekhina O.N., Supin A.Ya. Hearing sensitivity to gliding rippled spectrum patterns. J. Acoust. Soc. Am. 2018. V. 143. P. 2387–2393.
Nechaev D.I., Supin A.Ya. Hearing sensitivity to shifts of rippled-spectrum patterns. J. Acoust. Soc. Am. 2013. V. 134. P. 2913–2922.
Patterson R.D., Handel S., Yost W.A., Datta A.J. The relative strength of the tone and noise components in iterated rippled noise. J. Acoust. Soc. Am. 1996. V. 100. P. 3286–3294.
Saoji A.A., Litvak L., Spahr A.J., Eddins, D.A. Spectral modulation detection and vowel and consonant identification in cochlear implant listeners. J. Acoust. Soc. Am. 2009. V. 126. P. 955–958.
Sek A., Moore B.C.J. Frequency discrimination as a function of frequency, measured in several ways. J. Acoust. Soc. Am. 1995. V. 97. P. 2479–2486.
Supin A.Ya., Popov V.V., Milekhina O.N., Tarakanov M.B. Frequency resolving power measured by rippled noise. Hearing Res. 1994. V. 78. P. 31–40.
Supin A.Ya., Popov V.V., Milekhina O.N., Tarakanov M.B. Frequency-temporal resolution of hearing measured by rippled noise. Hearing Res. 1997. V. 108. P. 17–27.
Supin A.Ya., Popov V.V., Milekhina O.N., Tarakanov M.B. Ripple density resolution for various rippled-noise patterns. J. Acoust. Soc. Am. 1998. V. 103. P. 2042–2050.
Supin A.Ya., Popov V.V., Milekhina O.N., Tarakanov M.B. Ripple depth and density resolution in rippled noise. J. Acoust. Soc. Am. 1999. V. 106. P. 2800–2804.
Supin A.Ya., Popov V.V., Milekhina O.N., Tarakanov M.B. Rippled-spectrum resolution dependence on level. Hearing Res. 2003. V. 185. P. 1–12.
van Zanten G.A., Senten C.J.J. Spectro-Temporal Modulation Transfer Function (STMTF) for various types of temporal modulation and a peak distance of 200 Hz. J. Acoust. Soc. Am. 1983. V. 74. P. 52–62.
Won J.H., Drennan W.R., Rubinstein J.T. Spectral-ripple resolution correlates with speech reception in noise in cochlear implant users. J. Assoc. Res. Otolaryngol. 2007. V. 8. P. 384–392.
Won J.H, Humphrey E.L., Yeager K.R., Martinez A.A., Robinson C.H., Mills K.E., Johnstone P.M., Moon I.J., Woo J. Relationship among the physiologic channel interactions, spectral-ripple discrimination, and vowel identification in cochlear implant users. J. Acoust. Soc. Am. 2014. V. 136. P. 2714–2725.
Yost W.A. Pitch strength of iterated rippled noise. J. Acoust. Soc. Am. 1996. V. 100. P. 3329–3335.
Yost W.A., Hill, R. Strength of the pitches associated with ripple noise. J. Acoust. Soc. Am. 1978. V. 64. P. 485–492.
Yost W.A., Hill R., Perez-Falcon T. Pitch and pitch discrimination of broadband signals with rippled power spectra. J. Acoust. Soc. Am. 1978. V. 63. P. 1166–1173.
Yost W.A., Patterson R.D., Sheft S. A time domain description for the pitch strength of iterated rippled noise. J. Acoust. Soc. Am. 1996. V. 99. P. 1066–1078.
Zwicker E. Masking and psychophysical excitation as consequences of the ear’s frequency analysis. Frequency Analysis and Periodicity Detection in Hearing. Ed. R. Plomp, G.F. Smoorenburg (Sijthoff, Leiden), 1970. P. 376–394.
Дополнительные материалы отсутствуют.
Инструменты
Сенсорные системы


