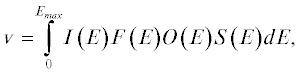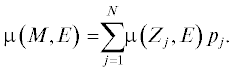Сенсорные системы, 2019, T. 33, № 3, стр. 212-221
Спектральная модель сигнала одноканальных рентгеновских измерительных приборов, использующих полихроматическое зондирующее излучение
А. С. Ингачева *
Институт проблем передачи информации РАН
127051 Москва, Большой Каретный переулок 19, Россия
* E-mail: ingacheva@gmail.com
Поступила в редакцию 12.02.2019
После доработки 18.03.2019
Принята к публикации 16.04.2019
Аннотация
В работе рассматривается спектральная модель оптического тракта приборов, измеряющих коэффициент пропускания в рентгеновском диапазоне. Это могут быть трансмиссионные томографы, рентгеновские микроскопы и другие рентгеновские аппараты. В задаче компьютерной томографии рассмотренная модель описывает эффект “ужесточения пучка” при использовании полихроматического рентгеновского излучения. В работе вводится понятие функции интегрального ослабления полихроматического сигнала и указывается ее связь с так называемыми формулами коррекции полихроматических лучевых сумм. Модель реализована в виде программного пакета XRayUtil с открытым исходным кодом на языке Python. XRayUtil позволяет моделировать спектральную плотность интенсивности излучения рентгеновских трубок с анодами из хрома, меди, молибдена, серебра и вольфрама. Пакет позволяет моделировать введение в тракт прибора рентгеновских фильтров определенной толщины и состава, задаваемого в виде химической формулы. Эта функциональность реализована при помощи сторонней библиотеки XRAYLIB. Также пакет позволяет моделировать ослабление рентгеновского излучения исследуемым однородным образцом, толщина и состав которого задаются аналогично фильтрам. Модель включает одноканальные детекторы рентгеновского излучения со сцинтилляторами, которые описываются функциями спектральной эффективности сцинтиллятора и спектральной чувствительности сенсора. Рассматриваемая математическая модель учитывает ослабление только за счет поглощения; рассеяние и нелинейно-оптические эффекты не учитываются. Для оценки адекватности модели были использованы данные, полученные на лабораторном микротомографе, сконструированном и функционирующем во ФНИЦ “Кристаллография и фотоника” РАН. В работе приведены оценки отклонения предсказаний модели от экспериментальных данных.
ВВЕДЕНИЕ
Рентгеновские методы исследования – распространенный способ изучения внутренней структуры или состава образца без его физического разрушения. Большинство рентгеновских приборов основаны на свойстве химических элементов в разной степени ослаблять рентгеновское излучение. К этой группе приборов относятся рентгеновские микроскопы, трансмиссионные томографы и другие рентгеновские аппараты. Все они в широком диапазоне своих рабочих режимов легко позволяют визуализировать общую структуру исследуемого образца. При этом количественно описать локальный состав мешают два обстоятельства. Во-первых, измеренная величина характеризует оптические свойства образца, а не искомые массовую плотность и/или химический состав. Во-вторых, измеренная величина может оказаться зависящей от внешних факторов. Это происходит, например, при наличии неучтенного рассеяния или при томографической реконструкции в полихроматической моде (Ingacheva, Chukalina, 2019). В последнем случае говорят об эффекте “ужесточения пучка”, когда от окружения исследуемой области зависит спектральный состав излучения, который ее достигнет. Поэтому для правильной интерпретации данных, полученных при помощи таких приборов, используют дополнительные калибровочные измерения. В работе (Nikolaev et al., 2015) авторы решали задачу классификации алмазов по рентгенографии алмазосодержащей руды, опираясь на калибровочную информацию о контрасте между пустой рудой и алмазами. В работе (Bam et al., 2019) дополнительные измерения использовались для оценки эффекта “ужесточения пучка”. Авторами была предложена методика, позволяющая количественно оценить влияние эффекта “ужесточения пучка” на точность восстановления параметров образца. Эта методика использовалась авторами для определения минимальных параметров питания рентгеновского источника, при которых возможно получить достоверную информацию о составе проб железной руды при заданном максимальном размере пробы. Дополнительные калибровочные измерения в работе (Dewulf et al., 2012; Kachelrieß et al., 2006) использовались для уменьшения искажений реконструированных изображений, возникающих из-за несоответствия измеряемых величин модели данных, заложенной в используемый алгоритм реконструкции. Предложенный авторами метод подавления этих искажений заключается в применении некоторой функции, называемой ими формулой коррекции полихроматических лучевых сумм, к каждому измеренному значению перед применением алгоритма реконструкции. Параметры этой функции и определялись по калибровочным измерениям.
В случаях, когда дополнительная лучевая нагрузка на образец нежелательна, а использование имитатора технически затруднено, предпочтительным способом определения недостающих параметров является численное моделирование оптического тракта рентгеновского прибора. Для моделирования оптического тракта рентгеновских приборов в синхротронных центрах было разработано программное обеспечение (ПО) syris с открытым исходным кодом (Farago et al., 2017). Авторы провели расчеты волнового поля, описывающего распространение излучения через произвольное количество объектов до достижения детектора. Разработанное ПО позволяет моделировать динамические эксперименты, например, четырехмерную томографию и ламинографию. Для оценки адекватности разработанного ПО результаты моделирования были сопоставлены с экспериментальными данными, полученными в европейском синхротронном центре в Гренобле (ESRF). К сожалению, данная программа не подходит для моделирования оптического тракта рентгеновских лабораторных приборов, так как спектральные плотности интенсивности излучения рентгеновской трубки и синхротронного источника существенно отличаются.
При этом рентгеновские трубки распространены повсеместно. Например, они используются в рентгеновских инспекционно-досмотровых комплексах. Для определения их геометрических параметров была разработана система компьютерного моделирования (Трофимчук, 2017), в которой реализовано моделирование объектов контроля в виде трехмерных поверхностей, построенных в системах автоматизированного проектирования (CAD). При моделировании томографических изображений объектов контроля система позволяет изменять положения источника и детектора рентгеновского излучения, а также скорость движения ленты, но физические характеристики рентгеновской трубки и детектора в данной системе фиксированы. В работе (Duvauchelle et al., 2000) описана система для расчета рентгенографических, радиоскопических или томографических оптических изображений с учетом спектральной плотности яркости рентгеновской трубки. Модель взаимодействия рентгеновского излучения с образцом в этой системе опирается на закон Бугера-Ламберта-Бера. Рентгеновские фильтры и детекторы при этом не рассматриваются. Еще одна программа, позволяющая моделировать часть оптического тракта рентгеновского прибора, – Spektr (Siewerdsen et al., 2004). В первой версии программы Spektr было реализовано моделирование спектра излучения рентгеновской трубки методом Монте-Карло, а также ослабление рентгеновского излучения веществом согласно закону Бугера-Ламберта-Бера. Во второй версии программы (Punnoose et al., 2016) добавлена возможность введения в оптический тракт бериллиевых, водных и алюминиевых фильтров. Программа предназначена для расчета спектральных характеристик рентгеновского излучения в методе рентгеноспектрального анализа, а также для расчета характеристик рентгеновских детекторов. Расчет спектра рентгеновской трубки реализован только для анодов из вольфрама.
Таким образом, существующие программы не предназначены и не подходят для решения нашей задачи, а именно для моделирования выходного сигнала прибора, включающего всю последовательность узлов: источник, фильтр или система фильтров, образец, регистрирующее оборудование. Далее в статье будет рассмотрена модель оптического тракта лабораторного рентгеновского прибора, состоящего из всех перечисленных выше узлов, описан программный пакет XRayUtil, реализующий эту модель, а также приведены экспериментальные данные, подтверждающие адекватность модели.
МОДЕЛЬ ОПТИЧЕСКОГО ТРАКТА ОДНОКАНАЛЬНОГО РЕНТГЕНОВСКОГО ПРИБОРА
Пусть ${{E}_{{max}}}$ – максимальная энергия, ограничивающая спектр излучения рентгеновской трубки. Тогда отклик $v$ одноканального рентгеновского прибора в некоторой точке детектора в некоторый момент времени в приближении далекого точечного источника можно описать следующим выражением:
где E – энергия кванта рентгеновского излучения, I(E) – спектральная плотность облученности (энергетической освещенности), создаваемой источником в рассматриваемой точке детектора в отсутствие фильтра и объекта, F(E) – спектральный коэффициент пропускания фильтра (системы фильтров), O(E) – спектральный коэффициент пропускания зондируемого образца на прямой, соединяющей источник и рассматриваемую точку детектора, а S(E) – спектральная чувствительность детектора.Выражение (1) позволяет рассчитывать отклик одноканального рентгеновского прибора. В многоканальном случае от канала к каналу обычно различаются функции чувствительности каналов детектора. Реже встречается ситуация, когда различаются спектры излучения (Nikolaev et al., 2015).
Ниже каждый элемент модели будет рассмотрен отдельно.
СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ СИЛЫ ИЗЛУЧЕНИЯ РЕНТГЕНОВСКОЙ ТРУБКИ
Рентгеновское излучение в рентгеновских трубках возникает как результат двух независимых процессов: резкого торможения при ударе об анод электронов, испускаемых катодом (так называемое тормозное излучение, будем обозначать его силу ${{I}_{b}}\left( E \right)$), и высокоэнергетических переходов в электронных оболочках атомов, вызванных взаимодействием электронов с материалом анода (так называемое характеристическое излучение, будем обозначать его силу ${{I}_{h}}\left( E \right)$). Таким образом, облученность незатененного детектора можно выразить через эти две величины:
(2)
$I\left( E \right) = \frac{{\cos \theta }}{{{{r}^{2}}}}\left( {{{I}_{b}}\left( E \right) + {{I}_{h}}\left( E \right)} \right),$Сила тормозного излучения определяет плотность непрерывного потока рентгеновского излучения в энергетическом диапазоне от 0 до ${{E}_{{max}}}.$ Максимальное значение энергии ${{E}_{{max}}}\quad$определяется величиной подаваемого напряжения на трубку и рассчитывается как ${{E}_{{max}}} = eU$, где e – элементарный заряд электрона, U – ускоряющее напряжение, подаваемое на трубку. Приближенная эмпирическая формула для расчета силы тормозного излучения была найдена Крамерсом (Павлинский, 2007) и представлена в виде
где ${{C}_{1}}$ – эмпирический коэффициент, определяемый для каждого вида рентгеновских трубок, i – ток трубки, Z – атомный номер элемента, из которого сделан материал анода.Спектральное распределение силы характеристического излучения – линейчатое, положение и форма каждого его пика (так называемая характеристическая линия) зависит от материала анода. В состав ${{I}_{h}}$ входят все характеристические линии, потенциал которых не превышает ускоряющего напряжения на трубке. Форма отдельной линии представляет из себя пик, ширина которого в наибольшей степени определяется эффектом Доплера. Длина волны характеристической линии определяется законом Мозли и включена, например, в химический справочник (Thompson et al., 2009). Представим силу характеристического излучения в виде суммы дисперсионных контуров характеристических линий
(4)
${{I}_{h}}\left( E \right) = \mathop \sum \limits_{j = 1}^n {{I}_{j}}\left( Z \right)\frac{{{{{\left( {\frac{{{\Delta }{{\lambda }_{j}}}}{2}} \right)}}^{2}}}}{{{{{\left( {\frac{{12.398}}{E} - {{\lambda }_{j}}} \right)}}^{2}} + {{{\left( {\frac{{{\Delta }{{\lambda }_{j}}}}{2}} \right)}}^{2}}}},$Сила j-й линии определяется формулой
(5)
${{I}_{j}}\left( Z \right) = C_{2}^{j}i{{\left( {U - {{U}_{j}}\left( Z \right)} \right)}^{{1.5}}},$Таким образом, для моделирования спектральной плотности энергетической светимости $I\left( E \right)$ рентгеновской трубки, необходимо задать материал анода ${{M}_{a}}$, величину тока i и ускоряющего напряжения U, подаваемые на трубку
МОДЕЛЬ РЕНТГЕНОВСКОГО ФИЛЬТРА И ОБРАЗЦА ИССЛЕДОВАНИЯ
Для описания взаимодействия рентгеновского излучения с веществом будем использовать
математическую модель, учитывающую ослабление рентгеновского излучения только за счет
поглощения. Эффектами упругого и неупругого рассеяния и другими нелинейно-оптическими
эффектами в данной модели пренебрежем, как эффектами второго порядка. Линейный коэффициент
поглощения 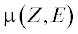 химического элемента зависит от его атомного номера Z и энергии кванта зондирующего рентгеновского излучения E и включен в различные рентгеновские базы данных, например в библиотеку XRAYLIB (Schoonjans
et al., 2011). Если вещество M состоит из N химических элементов $j = 1 \ldots N$, то суммарный линейный коэффициент поглощения $\mu \left( {M,E} \right)$ рассчитывается как взвешенная сумма линейных коэффициентов поглощения $\mu \left( {{{Z}_{j}},E} \right)$ химических элементов, входящих в состав вещества, умноженных на их фракцию ${{p}_{j}}$ в веществе
химического элемента зависит от его атомного номера Z и энергии кванта зондирующего рентгеновского излучения E и включен в различные рентгеновские базы данных, например в библиотеку XRAYLIB (Schoonjans
et al., 2011). Если вещество M состоит из N химических элементов $j = 1 \ldots N$, то суммарный линейный коэффициент поглощения $\mu \left( {M,E} \right)$ рассчитывается как взвешенная сумма линейных коэффициентов поглощения $\mu \left( {{{Z}_{j}},E} \right)$ химических элементов, входящих в состав вещества, умноженных на их фракцию ${{p}_{j}}$ в веществе
Спектральный коэффициент пропускания рентгеновского излучения однородным веществом M с коэффициентом линейного поглощения $\mu \left( {M,E} \right)$, согласно закону Бугера-Ламберта-Бера, описывается формулой
где ${{I}_{o}}\left( E \right)$ – спектральная плотность облученности при наличии слоя однородного образца из вещества M толщины t, $I\left( E \right)$ – спектральная плотность облученности в отсутствие образца (Фелдман, 1989). Фильтр и исследуемый образец рассмотрены в предлагаемом подходе как однородный слой вещества определенной толщины, т.е. для проведения расчетов согласно выражению (8), необходимо задать химическую формулу вещества и толщину. Для расчета спектрального коэффициента пропускания фильтром $F\left( E \right)$ рентгеновского излучения энергии E на прямой, соединяющей источник и рассматриваемую точку детектора, будем использовать выражение(9)
$F\left( E \right) = F\left( {E,{{M}_{f}},{{l}_{f}}} \right) = \quad{{e}^{{ - \mu \left( {\quad{{M}_{f}},E} \right){{l}_{f}}}}},$Аналогично описывается спектральный коэффициент пропускания зондируемого образца $O\left( E \right)$:
(10)
$O\left( E \right) = O\left( {E,{{M}_{o}},{{l}_{o}}} \right) = \quad{{e}^{{ - \mu \left( {\quad{{M}_{o}},E} \right){{l}_{o}}}}},$МОДЕЛЬ ОДНОКАНАЛЬНОГО СЦИНТИЛЛЯЦИОННОГО ДЕТЕКТОРА
Рассмотрим одноканальные детекторы ионизирующего излучения, состоящие из сцинтиллятора, оптоволокна и сенсора (Byun, 2017).
Сформированное рентгеновской трубкой и прошедшее через образец излучение достигает детектора и поглощается сцинтиллятором. Эффективность процесса поглощения, зависящая от состава и толщины сцинтиллятора, описывается функцией спектральной эффективности поглощения (Crystals, 2016)
(11)
$A\left( {E,{{M}_{s}},{{l}_{s}}} \right) = 1 - {{e}^{{ - \mu \left( {{{M}_{s}},E} \right){{l}_{s}}}}},$Спектральное распределение энергетической светимости $L\left( \lambda \right)$ сцинтиллятора зависит от материала сцинтиллятора и его можно найти, например в работе (Seferis et al., 2014). Свет распространяется изотропно, поэтому для определения положения упавшего кванта рентгеновского излучения часто используют оптоволокно. Так как диаметр каналов намного меньше площади пикселя позиционно-чувствительного детектора, то эффектом попадания светового фотона между пикселями можно пренебречь. Световые кванты достигают сенсора (фотодетектора) и преобразуются в ток. Пусть относительная спектральная чувствительность сенсора $R\left( \lambda \right)$, тогда общее число зарегистрированных квантов света $v$ рассчитывается согласно выражению
(12)
$v = \mathop \smallint \limits_0^{{{E}_{{max}}}} I\left( E \right)A\left( {E,{{M}_{s}},{{l}_{s}}} \right)dE\mathop \smallint \limits_{{{\lambda }_{{min}}}}^{{{\lambda }_{{max}}}} L\left( \lambda \right)R\left( \lambda \right)d\lambda \quad,$Величина $q = \int_{{{\lambda }_{{min}}}}^{{{\lambda }_{{max}}}} {L\left( \lambda \right)R\left( \lambda \right)d\lambda } $, называемая квантовой эффективностью сенсора, может быть вычислена заранее для используемой модели детектора. Тогда функция спектральной чувствительности детектора может быть переписана как
РАЗРАБОТАННЫЙ ПАКЕТ XRayUtil
Для программной реализации предложенной модели был выбран язык программирования Python. Пакет подключается вызовом команды “import XRayUtil”. Подключенный пакет дает возможность работать с новыми сущностями: спектр рентгеновского излучения и детектор. Для генерации спектральной плотности энергетической светимости рентгеновской трубки необходимо задать ток, напряжение, материал анода и тип излучения: тормозное (название в пакете – ‘BRELUNG’, характеристическое (‘CHARLINES’) или оба сразу (‘XRAYTUBE’) и дискретизацию. Ниже представлен код, создающий спектр рентгеновской трубки с параметрами: напряжение – 60 В, ток – 20 мА, материал анода – Молибден (Mo), число точек при разбиении энергии на интервалы – 10 000.
import XRayUtil
I = 20 # ток в (мА)
U = 60 # напряжение в (кВ)
M_a = 'Mo' # название вещества анода
SP = 10000 # число точек
spec = XRayUtil.GenerateSpectrum(I, U, M_a, SP, 'XRAYTUBE')
В пакете имплементирована работа с анодами из нескольких материалов: хром (название – ‘Cr’), медь (‘Cu’), молибден (‘Mo’), серебро (‘Ag’) или вольфрам (‘W’).
Кроме этого, изменение спектрального состава возможно путем добавления фильтра или образца, задаваемого толщиной и материалом. Так как они одинаковы в реализации, то объединены в одну функцию AddMatter в сущности спектр рентгеновского излучения. Код для добавления образца из хлорида натрия (NaCl) толщиной 0.3 см и плотностью 2.17 г/см3:
matter = 'NaCl' # химическое название вещества
density = 2.17 # плотность вещества в г/см3
thickness = 0.3 # толщина вещества в см
spec.AddMatter(matter, density, thickness)
Для создания детектора нужно задать его модель, которую можно выбрать из следующего списка: Hamamatsu C12849-101U (название в пакете 'HAMTSU_101U'), Hamamatsu C12849-102U ('HAMTSU_102U'), XIMEA xiRay 11 MPix ('XIMEA_11'), Varian 2520Dx ('VARIAN_2520DX'). Величину отклика рентгеновского прибора можно получить с помощью вызова функции пакета GetRegisteredValue, которой необходимо передать в качестве входных параметров заранее созданные спектр рентгеновского излучения и детектор. Код для создания детектора XIMEA xiRay 11 MPix и получение отклика рентгеновского прибора от созданного ранее спектра spec и детектора det:
name = 'XIMEA_11' # Название модели детектора
det = XRayUtil.CreateDetector(name)
value = GetRegisteredValue(spec, det)
Данные о взаимодействии рентгеновского излучения с веществом были взяты из библиотеки XRAYLIB (Schoonjans et al., 2011). Она предоставляет доступ к физическим базам данных в виде удобных для пользователя функций. Библиотека использовалась для вычисления таких характеристик, как потенциал возбуждения K-й линии вещества анода, коэффициента линейного поглощения веществ, фильтров и материала сцинтиллятора детектора.
Разработанный программный пакет XrayUtil доступен по ссылке https://github.com/ingacheva/XRayUtil.git.
ОЦЕНКА АДЕКВАТНОСТИ ПРЕДЛОЖЕННОЙ МОДЕЛИ
Оценка адекватности модели оптического тракта рентгеновского прибора проводилась путем сравнения данных, полученных с использованием разработанного пакета, и результатов измерений, проведенных на микротомографе, собранном и функционирующем во ФНИЦ “Кристаллография и фотоника” РАН (Buzmakov et al., 2015, Бузмаков и др., 2018). Экспериментальные параметры установки: рентгеновская трубка с молибденовым (Mo) анодом, напряжение – 60 кВ, ток – 20 мА, детектор – XiRay 11 MPix, время экспозиции 1 с, рентгеновский фильтр не использовался. В качестве исследуемого образца брался однородный алюминиевый клин, вид которого приведен на рис. 1. Линейные размеры образца: длина 12.3 см, высота треугольников 3.3 см, 4.2 см, толщина 1 см.
Рис. 1.
Алюминиевый образец, использованный в эксперименте. Белым цветом выделена область, для которой рассчитывались экспериментальные значения.

Прямоугольником отмечена область, выбранная для получения экспериментальных значений. Образец закреплялся вертикально, острым концом треугольника вниз, узкая часть объекта параллельна плоскости детектора. На томографе было зарегистрировано 10 кадров темнового тока, 50 кадров образца. Темновой ток регистрируется при выключенной рентгеновской трубке и отсутствии образца. Он используется для оценки шума и фильтрации кадров. Полученные при наличии объекта кадры были усреднены между собой, затем из результата вычиталось усредненное значение темнового тока. На рис. 2 показано усредненное отфильтрованное изображение кадров объекта. Под образцом на изображении можно видеть столик-держатель.
Рис. 2.
Изображение алюминиевого образца, сформированного детектором XiRay 11 MPix. Белыми линиями показаны области, использованные для оценки уровня сигнала при определенной толщине образца.

На полученном изображении было выбрано 50 равномерно распределенных по всей длине образца точек. Каждая точка обрамлялась прямоугольником 7 на 100 пикселей, в котором вычислялось среднее значение. Выбранные прямоугольники показаны на рис. 2. Толщина клина, равная 1 см, занимает 1100 пикселей в строке матрицы детектора. По этому соотношению и подобию треугольников была вычислена толщина образца на выбранной высоте. Таким образом, вычисленные средние значения помещались на график в виде точек (рис. 3).
Рис. 3.
Сравнение точности моделирования отклика рентгеновского лабораторного микротомографа при зондировании алюминиевого образца в предложенной и монохроматической моделях.
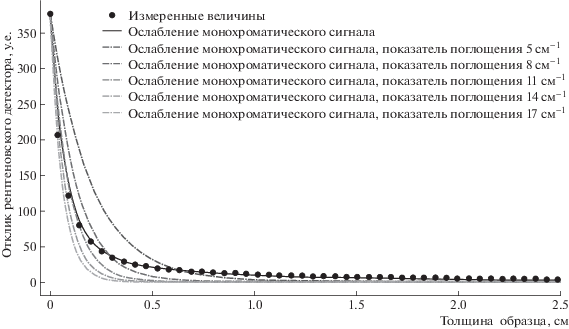
Зависимость отклика одноканального рентгеновского прибора в некоторой точке детектора от толщины образца будем называть функцией интегрального ослабления полихроматического сигнала. Сплошной линией на рис. 3 показана функция интегрального ослабления полихроматического сигнала для алюминиевого образца, полученного при помощи разработанного пакета XRayUtil. Пунктирными линиями показаны функции ослабления монохроматического зондирующего излучения по закону Бугера-Ламберта-Бера с коэффициентами поглощения от 5 до 17 см–1 с шагом 3 см–1.
Для численной оценки предложенной модели было вычислено среднеквадратическое отклонение экспериментальных значений от данных, полученных с применением разработанного пакета. Оно составило 7.07 усл. ед. Такие же величины были вычислены для функций ослабления монохроматического сигнала, они приведены в таблице 1. Минимальное значение среднеквадратического отклонения для монохроматического сигнала составило 9.88 усл. ед., коэффициент поглощения при этом равен 13.5 и 14.0 см–1. Из построенного графика и посчитанного среднеквадратического отклонения видно, что разработанная модель хорошо описывает отклик одноканального рентгеновского прибора и не может быть адекватно приближена никакой монохроматической моделью поглощения.
Таблица 1.
Среднеквадратическое отклонение экспериментальных данных от закона ослабления монохроматического излучения для различных показателей поглощения
| Показатель поглощения, см–1 | Среднеквадратическое отклонение, усл. ед. |
|---|---|
| 4.0 | 40.09 |
| 4.5 | 35.97 |
| 5.0 | 32.38 |
| 5.5 | 29.22 |
| 6.0 | 26.43 |
| 6.5 | 23.96 |
| 7.0 | 21.77 |
| 7.5 | 19.82 |
| 8.0 | 18.09 |
| 8.5 | 16.56 |
| 9.0 | 15.22 |
| 9.5 | 14.04 |
| 10.0 | 13.03 |
| 10.5 | 12.18 |
| 11.0 | 11.47 |
| 11.5 | 10.91 |
| 12.0 | 10.47 |
| 12.5 | 10.17 |
| 13.0 | 9.97 |
| 13.5 | 9.88 |
| 14.0 | 9.88 |
| 14.5 | 9.96 |
| 15.0 | 10.10 |
| 15.5 | 10.29 |
| 16.0 | 10.52 |
| 16.5 | 10.79 |
| 17.0 | 11.08 |
| 17.5 | 11.39 |
| 18.0 | 11.71 |
| 18.5 | 12.05 |
ЗАКЛЮЧЕНИЕ
В данной работе построена и описана спектральная модель оптического тракта рентгеновских приборов, таких как трансмиссионный томограф, рентгеновский микроскоп, дефектоскопический рентгеновский аппарат или рентгеновский досмотровый сканер. В предложенной модели рентгеновский прибор включает следующие узлы: источник рентгеновского излучения, фильтр или система фильтров, образец, регистрирующее устройство. В качестве источника рентгеновского излучения рассмотрена рентгеновская трубка, в качестве регистрирующего устройства – одноканальный рентгеновский детектор со сцинтиллятором. На основе предложенной модели реализован программный пакет XRayUtil с открытым исходным кодом на языке Python. Разработанный пакет предназначается для расчета величины отклика рентгеновского прибора при известных параметрах рентгеновской трубки (ток, напряжение, материал анода), толщины и состава фильтра и образца, а также известной модели детектора. Несмотря на то что в использованной модели рассматривались только эффекты поглощения, результаты моделирования показали лишь незначительные отклонения от экспериментальных данных. При этом модель ослабления монохроматического излучения показала существенно меньшую точность аппроксимации.
Реализованный программный пакет XRayUtil позволяет проводить сравнение откликов одноканальных рентгеновских приборов при использовании детекторов и трубок с различными характеристиками. Также результаты моделирования могут быть использованы для выбора оптимальных параметров эксперимента, например, с целью уменьшения времени эксперимента и лучевой нагрузки на образец.
Работа выполнена при частичной финансовой поддержке РФФИ (проекты № 18-29-26022 и № 18-29-26037).
Список литературы
Бузмаков А.В., Асадчиков В.Е., Золотов Д.А., Чукалина М.В., Ингачева А.С., Кривоносов Ю.С. Лабораторные рентгеновские микротомографы: методы предобработки экспериментальных данных. Известия РАН. Серия Физическая. 2018. Т. 83. № 2. С. 194–197.
Трофимчук А.М. Компьютерное моделирование рентгеновских изображений, полученных с помощью инспекционно-досмотровых комплексов. Инженерный вестник Дона. 2017. Т. 44. № 1. URL: https://cyberleninka.ru/article/n/kompyuternoe-modelirovanie-rentgenovskih-izobrazheniy-poluchennyh-s-pomoschyu-inspektsionno-dosmotrovyh-kompleksov (дата обращения: 09.04.2019).
Фелдман Л., Джеймс М. Основы анализа поверхности и тонких пленок. М.: Мир, 1989. 344 с.
Павлинский Г. Основы физики рентгеновского излучения. М.: ФИЗМАТЛИТ, 2007. 240 с. ISBN 978-5-9221-0783-9.
Bam Lunga Cleartone, Jodie Ann Miller, Megan Becker, Ian James Basson. X-ray computed tomography: Practical evaluation of beam hardening in iron ore samples. Minerals Engineering. 2019. V.131. P. 206–215. https://doi.org/10.1016/j.mineng.2018.11.010
Beckhoff B., Kanngießer B., Langhoff N., Wedell R. and Wolff H. Handbook of practical X-ray fluorescence analysis. Springer Science & Business Media. 2007. P. 878.
Buzmakov A., Chukalina M., Nikolaev D., Gulimova V., Saveliev S., Tereschenko E., Seregin A., Senin R., Zolotov D., Prun V., Shaefer G. Monochromatic computed microtomography using laboratory and synchrotron sources and X-ray fluorescence analysis for comprehensive analysis of structural changes in bones. Journal of applied crystallography. 2015. V. 48. № 3. P. 693–701. https://doi.org/10.1107/S1600576715006214
Byun S.H. Radioisotopes and Radiation Methodology I, II. Lecture Notes. Radiation Sciences Graduate Program. McMaster University Hamilton, Ontario Canada. 2017. P. 4–10.
Crystals S.G. Efficiency calculations for selected scintillators. Saint-Gobain Ceramics & Plastics. 2016. P. 12.
Dewulf Wim, Ye Tan, Kim Kiekens. Sense and non-sense of beam hardening correction in CT metrology. CIRP Annals-Manufacturing Technology. 2012. V. 61. № 1. P. 495–498. https://doi.org/10.1016/j.cirp.2012.03.013
Duvauchelle P., Freud N., Kaftandjian V., Babot D. A computer code to simulate X-ray imaging techniques. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms. 2000. V. 170 (1–2). P. 245–258. https://doi.org/10.1016/S0168-583X(00)00185-3
Farago Tomáš, Petr Mikulík, Alexey Ershov, Matthias Vogelgesang, Daniel Hänschke, Tilo Baumbach. Syris: a flexible and efficient framework for X-ray imaging experiments simulation. Journal of synchrotron radiation. 2017. V. 24 (6). P. 1283–1295. https://doi.org/10.1107/S1600577517012255
Gokhale B.G. Contribution à l'étude de la largeur des raies dans les spectres de rayons X. In Annales de Physique. 1952. V. 12. № 7. P. 852–902. https://doi.org/10.1051/anphys/195212070852
Ingacheva A.S., Chukalina M.V. Polychromatic CT Data Improvement with One-Parameter Power Correction. Mathematical Problems in Engineering. 2019. ID 1405365. P. 12. https://doi.org/10.1155/2019/1405365
Kachelrieß M, Sourbelle K, Kalender W.A. Empirical cupping correction: A first-order raw data precorrection for cone-beam computed tomography. Medical physics. 2006. V. 33 (5). P. 1269–74. https://doi.org/10.1118/1.2188076
Nikolaev D.P., Gladkov A., Chernov T., Bulatov K. Diamond recognition algorithm using two-channel x-ray radiographic separator. In Seventh International Conference on Machine Vision (ICMV 2014). 2015. V. 9445. P. 944507. https://doi.org/10.1117/12.2181204
Punnoose J., Xu J., Sisniega A., Zbijewski W., Siewerdsen J.H. spektr 3.0 – A computational tool for x-ray spectrum modeling and analysis. Medical physics. 2016. V. 43. № 8 Part 1. P. 4711–7. https://doi.org/10.1118/1.4955438
Salem S.I., Lee P.L. Experimental widths of K and L x-ray lines. Atomic Data and Nuclear Data Tables. 1976. V. 18. № 3. P. 233–241.
Schoonjans T., Brunetti A., Golosio B., del Rio M.S., Solé V.A., Ferrero C., Vincze L. The xraylib library for X-ray–matter interactions. Recent developments. Spectrochimica Acta Part B: Atomic Spectroscopy. 2011. V. 6. № 11–12. P. 776–784. https://doi.org/10.1016/j.sab.2011.09.011
Seferis I., Michail C., Valais I., Zeler J., Liaparinos P., Fountos G., Kalyvas N. Light emission efficiency and imaging performance of Lu2O3: Eu nanophosphor under X-ray radiography conditions: comparison with Gd2O2S: Eu. Journal of Luminescence. 2014. V. 151. P. 229–234. https://doi.org/10.1118/1.3451113
Siewerdsen J.H., Waese A.M., Moseley D.J., Richard S., Jaffray D.A. Spektr: A computational tool for x-ray spectral analysis and imaging system optimization. Medical physics. 2004. V. 31. № 11. P. 3057–67. https://doi.org/10.1118/1.1758350
Sorum H. The Kα1, 2 x-ray spectra of the 3d transition metals Cr, Fe, Co, Ni and Cu. Journal of Physics F: Metal Physics. 1987. V. 1. № 2. P. 417. https://doi.org/10.1088/0305-4608/17/2/011
Thompson A., Attwood D., Gullikson E., Howells M., Kortright J., Robinson A. X-ray data booklet (2009). URL: http://xdb. lbl. gov. 2009. https://doi.org/10.1016/0092-640X(76)90026-7
Дополнительные материалы отсутствуют.
Инструменты
Сенсорные системы