Сенсорные системы, 2019, T. 33, № 3, стр. 181-196
Алгоритм имитации зрения дихроматов и его применение для выявления аномалий цветовосприятия
П. В. Максимов 1, *, Е. М. Максимова 1, М. А. Грачева 1, А. А. Казакова 1, 2, А. С. Кулагин 3
1 Институт проблем передачи информации им А.А. Харкевича РАН
127051 Москва, Б. Каретный пер., 19, стр. 1, Россия
2 Российский национальный исследовательский медицинский университет им. Н.И. Пирогова Минздрава России
117997 Москва, ул. Островитянова, д. 1, Россия
3 ГБОУ Школа № 1501
Москва, Тихвинский пер., д. 3, Россия
* E-mail: pmaximov@iitp.ru
Поступила в редакцию 20.02.2019
После доработки 11.03.2019
Принята к публикации 16.04.2019
Аннотация
В основе нормального цветового зрения человека лежит наличие в сетчатке трех типов приемников – (колбочек) с различной спектральной чувствительностью – длинноволновых (L), средневолновых (M) и коротковолновых (S). Среди основных патологий цветового зрения различают дихромазию – отсутствие одного из типов приемников, и аномальную трихромазию – отклонение максимума спектральной чувствительности одного из типов приемников от его нормального положения на оси длин волн. Дихромазия в свою очередь подразделяется на протанопию (отсутствие длинноволнового приемника), дейтеранопию (отсутствие средневолнового приемника) и очень редко встречающуюся тританопию (отсутствие коротковолнового приемника). Разработана программа-симулятор цветового зрения дихроматов, позволяющая наблюдателю с нормальным цветовым зрением оценить, какие цвета в изображении различимы, а какие неразличимы для протанопов и дейтеранопов. Симулятор осуществляет прямые и обратные преобразования между пикселями в изображении (R, G, B) и рассчитанными относительными возбуждениями колбочек (L, M, S). При моделировании цветового зрения дихроматов значения возбуждений колбочек преобразуются так, что размерность пространства (L, M, S) снижается с трех (у нормального трихромата) до двух (у дихромата). На основе разработанной программы-симулятора создана другая программа, предназначенная для тестирования цветового зрения человека. Испытуемому последовательно предъявляются тройки изображений: “трихроматическое” и два других, моделирующих цветовое восприятие протанопов и дейтеранопов. Задача испытуемого – выбрать из предложенной тройки изображений то, которое наиболее сильно отличается от двух других по цвету. Испытуемые с нормальным цветовым зрением выбирают “трихроматическое” изображение, протанопы выбирают изображение, моделирующее цветовое восприятие дейтеранопов, а дейтеранопы выбирают изображение, моделирующее цветовое восприятие протанопов. Приведены данные предварительной апробации программы на 83 испытуемых, показывающие эффективность программы.
ВВЕДЕНИЕ
Цветовым зрением называется способность различать излучения по спектральному составу, независимо от интенсивности. Эта способность обеспечивается наличием в сетчатке нескольких приемников с различающейся спектральной чувствительностью и нервным аппаратом, сравнивающим сигналы этих приемников. Животное с двумя приемниками называется дихроматом, с тремя – трихроматом.
В сетчатке человека три типа колбочек, различающихся по наличию в их наружных сегментах одного из трех зрительных пигментов. Максимумы чувствительности пигментов – 430 нм у коротковолновых колбочек (S-приемника), 540 и 570 нм у средне- и длинноволновых колбочек соответственно (у M- и L-приемников). Гены, кодирующие эти пигменты, находятся в седьмой аутосоме (S) и в половой Х-хромосоме (L, M) (Nathans et al., 1986; Mollon et al., 1993; Nathans, 1999). Известно, что около 8% мужчин и 0.4% женщин среди европейцев страдают наследственными нарушениями цветового зрения (Birch, 2012). К таким нарушениям относятся дихромазия – отсутствие в сетчатке одного из типов колбочек, и аномальная трихромазия – сдвиг положения максимума кривой спектральной чувствительности у одного из типов колбочек по оси длин волн. Наиболее часто встречаются нарушения в длинноволновых (протанопия или протоаномалия) и средневолновых (дейтранопия или дейтроаномалия) колбочках. Случаи тританопии – отсутствия коротковолновых колбочек, S-приемника – очень редки (0.002%) (Simunovic, 2010; Wright, 1952; Baraas et al., 2007). Причина протанопии и дейтеранопии – расположение генов пигментов L- и M-приемников друг за другом в q-плече Х-хромосомы. При кроссинговере могут получиться варианты с отсутствием или изменением одного из генов (Sharpe et al., 2000; Nathans et al., 1986; Nathans, 1999).
При помощи адаптивной оптики (благодаря которой можно наблюдать сетчатку человека in vivo) было обнаружено, что у протанопов нормальная плотность колбочек, и все колбочки (за исключением коротковолновых) содержат средневолновый пигмент. У дейтеранопов все колбочки (за исключением коротковолновых) содержат длинноволновый пигмент, а мозаика колбочек неполная – отсутствует примерно треть колбочек. Генетический анализ подтвердил, что у протанопов отсутствует ген длинноволнового пигмента, а у дейтеранопов ген средневолнового пигмента не способен произвести жизнеспособный пигмент (Sharpe et al., 2000; Nathans, 1999; Carroll et al., 2004).
Часто можно слышать утверждения, что человек-дихромат (в просторечии – дальтоник) вообще не различает цветов, или, что он различает всего два цвета. Конечно, это неверно, просто любое попадающее на сетчатку излучение дихромат описывает не тремя параметрами, а двумя. Для нормального трихромата этими параметрами могут быть как первичные данные – возбуждения трех типов колбочек, так и результат их “осмысления” – например, цветовой тон, светлота и насыщенность. Дихромат не может охарактеризовать излучение тремя величинами возбуждений колбочек, поскольку в его сетчатке имеется только два типа колбочек. Точно так же дихромат не способен раздельно воспринимать цветовой тон, светлоту и насыщенность. Например, для нормального трихромата серый (предельно ненасыщенный) цвет не соответствует никакому спектральному (монохроматическому) излучению. Для дихромата серый выстраивается среди цветов радуги, так как среди монохроматических излучений найдется такое, которое вызовет то же соотношение возбуждений двух имеющихся у дихромата типов колбочек, какое вызывает серый цвет.
Люди с цветоаномалиями часто не знают о своем недостатке: они знают, что трава и листья деревьев зеленые, а у светофора верхний фонарь – красный, а нижний – зеленый. Только в таких задачах, как сбор спелых ягод или выбор клубков шерсти (когда нет подсказки) дихроматы терпят неудачу. (Не все так внимательны к своим ощущениям, как великий химик Джон Дальтон, заметивший, что они с братом не так называют окраску цветков герани, как окружающие (Dalton, 1798)). Однако многие профессии (врачи, химики, дизайнеры, машинисты, летчики) требуют тонкого цветоразличения. Существует много тестов для оценки цветового зрения, из которых самыми употребимыми в практике до сих пор являются полихроматические таблицы Рабкина и Ишихара (Кравков, 1932).
Работа с полихроматическими таблицами требует не только способности цветоразличения, но и способности категоризации “скрытого” изображения (геометрических фигур, цифр), что, как показала практика, вызывает трудности у некоторых испытуемых. Качество полиграфии тоже вносит “свои поправки”. Таблицы, наконец, можно выучить, как и поступали многие в случае крайней необходимости. Другие тесты (Farnsworth-Munsell и его модификации) требуют много времени и не годятся для массовых обследований.
Для того, чтобы оценить, какие цвета дихромат может различать, а какие для него неразличимы, разрабатываются специальные программы-симуляторы цветового зрения дихроматов. Изображение, наблюдаемое нормальным трихроматом, которое мы будем называть исходным, симулятор преобразует в другое изображение, неотличимое от исходного для дихромата. Это изображение мы будем называть преобразованным для протанопа или дейтеранопа. Чтобы получить такое изображение, необходимо сделать так, чтобы во всех его точках рассчитанные возбуждения двух типов колбочек, имеющихся у дихромата, были такими же, как возбуждения колбочек тех же типов при наблюдении исходного изображения. Рассчитанные для нормального трихромата по преобразованному изображению возбуждения колбочек третьего типа могут быть любыми, поскольку колбочки этого типа у дихромата отсутствуют. Таким образом, каждому исходному изображению, наблюдаемому нормальным трихроматом, соответствует бесконечно много изображений, неотличимых от исходного для дихромата. Поэтому предсказать ощущения дихромата при наблюдении какого-нибудь изображения, т.е. ответить на вопрос, каким данный дихромат видит тот или иной цвет, вообще говоря, невозможно. Тем не менее попытка ответить на этот вопрос была сделана (Brettel et al., 1997; Viénot et al., 1995). Для описания цветовых ощущений дихроматов авторы использовали литературные данные о цветовых ощущениях унилатеральных дихроматов – людей, у которых дихромазия наблюдается только в одном глазу (Judd,1948; Ruddock, 1991; Alpern et al., 1983). В качестве цветов, которые должны сохраняться при переходе от исходного изображения к преобразованным для дихроматов, авторы выбрали те цвета, которые у унилатеральных дихроматов вызывают одинаковые ощущения в обоих глазах. Это во всех случаях – нейтральный белый, а также излучения с доминантными длинами волн 575 нм (желтый) и 475 нм (синий) у унилатеральных протанопов и дейтеранопов и излучения с доминантными длинами волн 660 нм (красный) и 485 нм (синий) у испытуемых с приобретенной унилатеральной тританопией. Однако сами авторы статьи обращают внимание на то, что случаи унилатеральной дихромазии – особенные случаи нарушений цветового зрения, и обобщать восприятие цветов унилатеральными дихроматами на обычные случаи билатеральной дихромазии, возможно, некорректно. На наш же взгляд, размышления о том, каким представляется в сознании билатерального дихромата тот или иной цвет из множества неразличимых им цветов, вовсе лишены смысла.
Моделирование цветового восприятия протанопов и дейтеранопов позволяет нормальному трихромату обнаружить на изображениях те важные детали, которые неразличимы для дихроматов или их различение представляет большие трудности. Учет особенностей восприятия зрительной информации людьми с нарушениями цветового зрения может потребоваться, например, при верстке web-сайтов, которые посещают широкий круг людей, где могут быть лица с нарушениями цветового зрения.
Протанопию, дейтеранопию и тританопию можно рассматривать, как крайние случаи нарушения цветового зрения. При помощи небольшого изменения алгоритма работы симулятора можно моделировать и цветовое восприятие аномальных трихроматов (Lucassen et al., 2006).
В настоящей работе оценивалась возможность применения программы, моделирующей цветовое восприятие дихроматов, для диагностики нарушений цветового зрения. Поскольку случаи тританопии (отсутствия в сетчатке коротковолновых колбочек) встречаются крайне редко, мы не включили в программу моделирование цветового зрения тританопов.
В первой части статьи рассмотрена структура программы-симулятора; во второй части статьи – особенности построенной на основе этого симулятора программы для проверки цветового зрения и предварительные результаты ее апробации.
РАБОТА СИМУЛЯТОРА ЦВЕТОВОГО ЗРЕНИЯ ДИХРОМАТОВ
Преобразования координат
В основе работы симулятора лежит прямое и обратное попиксельные преобразования из мониторных значений (R, G, B) в значения физиологических цветовых координат (L, M, S). Значения L, M, S – это некоторые числа, пропорциональные интенсивностям излучений, попадающих в глаз и поглощаемых длинноволновыми, средневолновыми и коротковолновыми колбочками, соответственно. Будем также называть эти значения “относительными возбуждениями колбочек” в ответ на некоторое излучение, а также “сигналами колбочек”, хотя физиологически измеряемые величины (такие, как потенциал колбочки или концентрация медиатора в синаптической щели) мы рассматривать не будем.
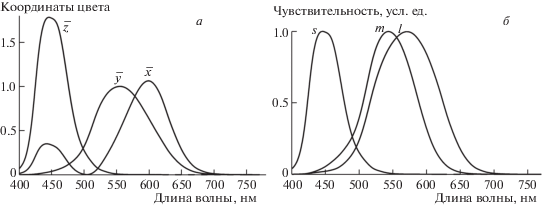
В качестве промежуточной системы цветовых координат в симуляторе используется колориметрическая система координат XYZ для стандартного наблюдателя (стандарт МКО 1931 г.). Матрицы перехода из системы физиологических координат в систему XYZ и обратно могут быть построены при помощи набора трех характерных точек в пространстве цветности xyz (copunctal points, intersection points): протанопической (xp = = 0.75; yp = 0.25; zp = 0.0), дейтеранопической (xd = 1.7; yd = –0.7; zd = 0.0) и тританопической (xt = 0.17; yt = 0.0; zt = 0.83) (Нюберг, Юстова, 1956; Юстова, 2000). Эти точки задают ориентации трех векторов в цветовом пространстве, изменения цвета вдоль которых незаметны протанопам, дейтеранопам и тританопам соответственно. Используя полученные на основе этих векторов формулы преобразования координат, Н.Д. Нюберг и Е.Н. Юстова получили из известных спектральных кривых x(λ), y(λ) и z(λ) усредненные психофизические кривые спектральной чувствительности колбочек человека (рис. 1). Рассматриваемый подход позволяет получить матрицу перехода, основываясь только на психофизических экспериментальных данных, полученных на дихроматах. Хотя сейчас известны спектральные кривые поглощения колбочек, полученные методами электрофизиологии и микроспектрофотометрии (Schnapf et al., 1987; Bowmaker et al., 1991), используемый подход позволяет избежать возможных дополнительных неточностей, которые могли бы возникнуть при аппроксимации спектральных кривых поглощения колбочек и учете спектра поглощения передних сред глаза.
Рис. 1.
Кривые сложения цветов стандартного колориметрического наблюдателя МКО 1931 (а) и кривые спектральной чувствительности колбочек человека, нормированные по максимумам (б).
Очевидно, что векторы (xp, yp, zp), (xd, yd, zd) и (xt, yt, zt) задают ориентации (но не направления) физиологических осей L, M и S в пространстве XYZ, т.е. те прямые, вдоль которых перемещается точка в пространстве XYZ при изменении возбуждения каждого из типов колбочек. Таким образом, уравнения изменения координат X, Y и Z в зависимости от возбуждений колбочек L, M и S запишутся в следующем виде:
или в матричной форме:(1)
$\begin{gathered} \left( {\begin{array}{*{20}{c}} X \\ Y \\ Z \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{x}_{p}}}&{{{x}_{d}}}&{{{x}_{t}}} \\ {{{y}_{p}}}&{{{y}_{d}}}&{{{y}_{t}}} \\ {{{z}_{p}}}&{{{z}_{d}}}&{{{z}_{t}}} \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {{{w}_{L}} \cdot L} \\ {{{w}_{M}} \cdot M} \\ {{{w}_{S}} \cdot S} \end{array}} \right) = \\ \, = \left( {\begin{array}{*{20}{c}} {{{w}_{L}} \cdot {{x}_{p}}}&{{{w}_{M}} \cdot {{x}_{d}}}&{{{w}_{S}} \cdot {{x}_{t}}} \\ {{{w}_{L}} \cdot {{y}_{p}}}&{{{w}_{M}} \cdot {{y}_{d}}}&{{{w}_{S}} \cdot {{y}_{t}}} \\ {{{w}_{L}} \cdot {{z}_{p}}}&{{{w}_{M}} \cdot {{z}_{d}}}&{{{w}_{S}} \cdot {{z}_{t}}} \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} L \\ M \\ S \end{array}} \right). \\ \end{gathered} $Весовые коэффициенты wL, wM и wS отражают то, что реальные значения поглощенных колбочками энергий излучений нам неизвестны, а знаки этих коэффициентов определяют положительные направления физиологических осей L, M и S по отношению к направлениям векторов, задающих ориентации осей. Удобно выбрать эти коэффициенты такими, чтобы единичные значения физиологических координат (L = 1, M = 1, S = 1) соответствовали восприятию яркого белого цвета, предъявляемого на мониторе (R = 255, G = 255, B = 255). Способ расчета этих весовых коэффициентов будет описан чуть позже. Из (1) нетрудно получить и формулу для обратного преобразования координат XYZ→LMS.
Таким образом, зная координаты цвета излучения в системе XYZ, можно рассчитать относительные возбуждения колбочек, вызванные этим излучением, и наоборот, по заданным соотношениям возбуждений колбочек вычислить цветовые координаты в системе XYZ. Остается связать колориметрические координаты XYZ со значениями R, G и B, задающими цвет точки на экране.
Для того, чтобы получить грубое представление о том, какие цвета на изображении дихромат уверенно различает, а какие путает, необязательно точно знать параметры монитора. Цифровые изображения “подстроены” под их демонстрацию на стандартном мониторе, и их преобразование по описанному здесь алгоритму также можно подстроить под тот же стандарт. Если же моделирование цветового восприятия дихроматов используется для проверки цветового зрения, то параметры видеосистемы компьютера желательно знать как можно точнее. Гольц и МакЛеод показали, что даже в том случае, когда измерительная аппаратура недоступна, применение мониторов на электронно-лучевой трубке (ЭЛТ) обеспечивает достаточно большую точность воспроизведения цветов на экране для того, чтобы наблюдать индивидуальные различия свойств цветового зрения нормальных трихроматов (Golz, MacLeod, 2003). Это связано с использованием в различных ЭЛТ близких по составу люминофоров. Про распространенные сейчас жидкокристаллические (ЖК) дисплеи нам о подобных исследованиях неизвестно, и в настоящей работе мы сделали лишь предварительную оценку возможности использования ЖК монитора для скрининговой проверки цветового зрения.
Переход от мониторных значений (R, G, B) в систему колориметрических координат XYZ – хорошо известная процедура, описанная в литературе (Домасёв, Гнатюк, 2007), но здесь мы повторим ее описание, чтобы читателю было понятно, на какие особенности этого преобразования стоит обратить внимание для того, чтобы корректно моделировать цветовое восприятие дихроматов.
Основным стандартом представления цветов на экране монитора является стандарт sRGB. Стандарт определяет цветовой охват (область воспроизводимых монитором цветов в пространстве цветности xy), координаты цветности белого цвета и вид кривой гамма-коррекции.
Цветовой охват определяется координатами цветности чистых мониторных цветов: красного, зеленого и синего. В стандарте sRGB приняты следующие значения этих цветностей:
Красный: xR = 0.64; yR = 0.33.
Зеленый: xG = 0.30; yG = 0.60.
Синий: xB = 0.15; yB = 0.06.
Наша работа над программой-симулятором начиналась еще до того, как стандарт sRGB получил широкое распространение. В качестве координат цветности чистых цветов мы использовали цветности, измеренные при помощи колориметра на одном из ЭЛТ мониторов:
Красный: xR = 0.625; yR = 0.342.
Зеленый: xG = 0.307; yG = 0.587.
Синий: xB = 0.156; yB = 0.069.
Эти цветности очень близки к приведенным в упоминавшейся работе Гольца и МакЛеода данным, усредненным по пятнадцати ЭЛТ мониторам (Golz, MacLeod, 2003).
Белый цвет в стандарте sRGB принят соответствующим стандартному источнику света D65, имеющему коррелированную цветовую температуру 6500 K. Мы в расчетах предполагали, что координаты цветности белого на мониторе равны xW = 0.3127, yW = 0.3291.
Система мониторных значений (R, G, B) не является колориметрической системой координат, поскольку интенсивности излучений красного, зеленого и синего каналов монитора зависят от задаваемых значений R, G и B нелинейно. В связи с этим, для того, чтобы иметь возможность работать с цветом свечения точки на экране, как с вектором, необходимо перейти к линеаризованным координатам Rlin, Glin и Blin, пропорциональным интенсивностям излучений. В разных стандартных цветовых пространствах приняты различные зависимости интенсивности света от значений R, G и B (кривые гамма-коррекции). Например, в пространстве Adobe RGB принята степенная зависимость со степенью 2.2, а в пространстве sRGB кривая гамма-коррекции представляется не только степенной функцией, а содержит линейный и степенной участки. В реальных, по крайней мере, непрофессиональных системах видеоадаптер-монитор такая зависимость соблюдается с невысокой точностью, изменяется в зависимости от настроек яркости и контрастности монитора, может быть различной для разных каналов, а показатель степени степенной функции, аппроксимирующей эту зависимость, может принимать значения 2–2.5. В нашем симуляторе для простоты расчетов мы использовали степенную функцию с показателем 2 (γ = 2). Влияние неточности учета нелинейности видеосистемы на правильность моделирования цветового зрения дихроматов нами пока детально не исследовалось.
Таким образом, первым шагом перехода от мониторных значений цвета точки к каким-либо колориметрическим цветовым координатам должен быть переход к линеаризованным значениям интенсивностей. Удобно определить эти значения в диапазоне [0, 1]:
Матрица перехода из системы линеаризованных мониторных координат Rlin, Glin, Blin в систему координат XYZ строится следующим образом:
(2)
$\begin{gathered} \left( {\begin{gathered} X \\ Y \\ Z \\ \end{gathered} } \right) = \left( {\begin{array}{*{20}{c}} {{{x}_{R}}}&{{{x}_{G}}}&{{{x}_{B}}} \\ {{{y}_{R}}}&{{{y}_{G}}}&{{{y}_{B}}} \\ {{{z}_{R}}}&{{{z}_{G}}}&{{{z}_{B}}} \end{array}} \right) \cdot \left( {\begin{gathered} {{a}_{R}} \cdot {{R}_{{lin}}} \\ {{a}_{G}} \cdot {{G}_{{lin}}} \\ {{a}_{B}} \cdot {{B}_{{lin}}} \\ \end{gathered} } \right) = \\ \; = \left( {\begin{array}{*{20}{c}} {{{a}_{R}} \cdot {{x}_{R}}}&{{{a}_{G}} \cdot {{x}_{G}}}&{{{a}_{B}} \cdot {{x}_{B}}} \\ {{{a}_{R}} \cdot {{y}_{R}}}&{{{a}_{G}} \cdot {{y}_{G}}}&{{{a}_{B}} \cdot {{y}_{B}}} \\ {{{a}_{R}} \cdot {{z}_{R}}}&{{{a}_{G}} \cdot {{z}_{G}}}&{{{a}_{B}} \cdot {{z}_{B}}} \end{array}} \right) \cdot \left( {\begin{gathered} {{R}_{{lin}}} \\ {{G}_{{lin}}} \\ {{B}_{{lin}}} \\ \end{gathered} } \right) \\ \end{gathered} .$Здесь x, y и z с индексами R, G и B – координаты цветности соответствующих каналов монитора – непосредственно измеренные или взятые из стандарта. Координаты цветности обычно задаются парой значений (x, y), значение координаты z определяется исходя из условия x + y + z = 1. Весовые коэффициенты aR, aG и aB в формуле (2) задают баланс белого – соотношение интенсивностей мониторных лучей, обеспечивающее заданную цветность белого. Для определения этих коэффициентов потребуем, чтобы максимально яркий белый цвет, предъявляемый на мониторе (Rlin = 1, Glin = 1, Blin = 1), имел заданную цветность в системе цветности xy (x = xW, y = yW), а также максимальную (единичную) яркость (YW = 1) в системе цветовых координат XYZ. Тогда цветовые координаты этого белого цвета будут следующими:
Подставив эти значения в уравнение (2), получим:
В этом уравнении все величины, кроме коэффициентов aR, aG и aB – уже известные:
Решая это уравнение, получаем значения коэффициентов и, подставив их в уравнение (2), приходим к окончательному виду матрицы преобразования (Rlin, Glin, Blin) → (X, Y, Z):
Теперь вернемся к преобразованию из системы физиологических координат LMS в систему координат XYZ стандартного наблюдателя и определим недостающие весовые коэффициенты wL, wM и wS в формуле (1). Как уже указывалось, удобно выбрать их такими, чтобы яркому белому цвету, предъявляемому на мониторе (Rlin = 1, Glin = 1, Blin = 1), соответствовали единичные значения физиологических координат (L = 1, M = 1, S = 1) . Подставив эти значения, а также координаты максимально яркого белого цвета монитора в системе XYZ, в формулу (1), получим систему уравнений, решив которую, получим искомые значения весовых коэффициентов:
Подставив найденные значения коэффициентов в (1), получим окончательную матрицу преобразования (L, M, S) → (X, Y, Z), а обратив эту матрицу, получим возможность и обратного преобразования координат:
В приведенных расчетах система координат XYZ использовалась, как промежуточная для пересчета линеаризованных “мониторных” координат (Rlin, Glin, Blin) в физиологические координаты (L, M, S) и обратно. В программе-симуляторе вычисления удобнее производить в одно действие. Для этого перемножим соответствующие матрицы:
Особенности моделирования цветового зрения дихроматов
Мы рассмотрели, как при помощи простых матричных операций можно вычислять значения физиологических цветовых координат человека с нормальным цветовым зрением по цветам, предъявляемым на экране компьютера. Теперь рассмотрим, как можно моделировать цветовое зрение дихроматов. В данной работе мы ограничимся рассмотрением моделирования цветового зрения протанопов и дейтеранопов – людей, у которых в сетчатке отсутствуют длинноволновые (L) и средневолновые (M) колбочки соответственно.
Задача симулятора – так преобразовать исходное цветное изображение, чтобы в каждой его точке осталась информация, определяемая только двумя типами колбочек: M и S – при моделировании зрения протанопов, L и S – при моделировании зрения дейтеранопов. В результате дейтераноп, глядя на изображение, преобразованное для дейтеранопа, не сможет отличить его от исходного, поскольку у него в сетчатке отсутствуют колбочки M-типа. Точно так же протаноп, глядя на изображение, сгенерированное из исходного для протанопа, не сможет отличить его от исходного, поскольку в сетчатке протанопа отсутствуют колбочки L-типа. Нормальный трихромат в любом из этих случаев увидит разницу – по сигналу третьего типа колбочек на исходном изображении. Рассмотрим алгоритм преобразования изображения при моделировании цветового зрения протанопа и дейтеранопа более подробно (буквы с индексом p здесь означают величины, пересчитанные для моделирования зрения протанопа, с индексом d – дейтеранопа).
1. Исходное изображение загружается в память компьютера и выводится на экран.
2. Для каждой точки исходного изображения производятся следующие действия:
2.1) линеаризация мониторных значений цвета пикселя: (R, G, B) → (Rlin, Glin, Blin);
2.2) переход в систему координат LMS нормального трихромата: (Rlin, Glin, Blin) → (L, M, S);
2.3) присвоение переменным Mp и Sp сигналов, присутствующих у протанопа колбочек: Mp = M, Sp = S;
2.4) замена независимого сигнала колбочек L-типа у нормального трихромата на функцию от сигналов колбочек двух других типов в модели протанопа: Lp = f(M, S);
2.5) присвоение переменным Ld и Sd сигналов, присутствующих у дейтеранопа колбочек: Ld = L, Sd = S;
2.6) замена независимого сигнала колбочек M-типа у нормального трихромата на функцию от сигналов колбочек двух других типов в модели дейтеранопа: Md = f(L, S);
2.7) обратный переход к линеаризованным мониторным координатам: (Lp, Mp, Sp) → (Rplin, Gplin, Bplin), (Ld, Md, Sd) → (Rdlin, Gdlin, Bdlin);
2.8) переход к мониторным значениям цвета: (Rplin, Gplin, Bplin) → (Rp, Gp, Bp), (Rdlin, Gdlin, Bdlin) → → (Rd, Gd, Bd).
3. Преобразованные изображения выводятся на экран.
В приведенном упрощенном алгоритме предполагается, что все преобразованные для дихроматов цвета, рассчитываемые в пункте 2, попадают в область цветового охвата монитора и укладываются в диапазон доступных яркостей. В действительности это, как правило, не так – всё зависит как от выбранных функций для замены сигналов отсутствующих колбочек, так и от набора цветов исходного изображения. Отрицательные рассчитанные значения Rplin, Gplin, Bplin, Rdlin, Gdlin или Bdlin говорят о недостаточном цветовом охвате монитора, а значения этих переменных, превышающие единицу, о недостаточной максимальной яркости данного цветового канала монитора. Таким образом, не для любого изображения можно вывести на экран компьютера два других изображения, неотличимые от исходного для дихроматов. На этот неочевидный факт обращали внимание и Бреттель с соавторами (Brettel et al., 1997). В общем случае, если предполагается работа программы с произвольно выбранными исходными изображениями, алгоритм приходится делать двухпроходным. На первом проходе фиксируются максимальные и минимальные значения координат Rplin, Gplin, Bplin, Rdlin, Gdlin, Bdlin и определяется такое преобразование исходного изображения (уменьшение яркости и насыщенности), при котором выхода значений этих координат за пределы отрезка [0, 1] не будет. На втором проходе исходное изображение изменяется в соответствии с расчетом и происходит преобразование уже измененного изображения, после чего все три изображения (измененное полноцветное и преобразованные для протанопа и дейтеранопа) выводятся на экран.
Если функции подмены сигналов отсутствующих колбочек для моделирования восприятия протанопов и дейтеранопов выбраны линейные, то весь процесс преобразования линеаризованных мониторных значений можно выразить одной матричной формулой. Пусть для моделирования восприятия протанопов эта функция имеет вид: Lp = pp ⋅ M + qp ⋅ S, где pp и qp – весовые коэффициенты. Тогда формула преобразования будет такой
Для моделирования восприятия дейтеранопов зададим функцию подмены сигнала отсутствующих колбочек M-типа в виде: Mp = pd ⋅ L + qd ⋅ S. Тогда
Рассмотрим вопрос выбора сигнала отсутствующего типа колбочек при моделировании цветового восприятия дихроматов. Остановимся на нескольких более или менее очевидных вариантах.
– Поскольку у дихроматов отсутствуют колбочки одного из типов, может показаться естественным при моделировании сделать в преобразованном изображении сигналы этого типа колбочек равными нулю. Однако такие изображения для протанопов и дейтеранопов невозможно изобразить на мониторе. Более того, для моделирования восприятия протанопов такое изображение вообще невозможно создать физически. Связано это с близким расположением кривых спектральной чувствительности колбочек L- и M-типов, в результате чего любое излучение, возбуждающее колбочки M-типа, будет возбуждать и колбочки L-типа.
– Поскольку у дихроматов только два типа колбочек, для построения изображений, моделирующих их цветовое восприятие, можно использовать два (из трех) мониторных канала. Такой подход был нами опробован. Как при построении изображения для протанопов, так и для дейтеранопов, лучше подходит использование зеленого и синего каналов монитора. При использовании красного и синего каналов для преобразования, как правило, требуется значительное уменьшение яркости и насыщенности входного полноцветного изображения. Надо заметить, что при использовании такого способа отображения невозможен баланс белого: белые точки на входном изображении переходят в пурпурные при использовании красного и синего каналов монитора или в бирюзовые при использовании зеленого и синего каналов. Это само по себе не является недостатком симулятора, но вызывает недоумение у нормальных трихроматов. Привычнее было бы видеть, что белый цвет на входном изображении переходит в белый на преобразованном. Тем не менее такой подход имеет право на существование.
Определим, какой должна быть функция Lp = = f(M, S) для того, чтобы преобразовать исходное изображение в изображение, моделирующее цветовое восприятие протанопа, при условии использования зеленого и синего каналов монитора. Пусть для одного из пикселей исходного изображения мы получили вектор-столбец возбуждений колбочек нормального трихромата:
Для нахождения цвета этого пикселя на изображении, моделирующем восприятие протанопа, необходимо найти такое значение координаты Lp, при котором интенсивность красного канала монитора обращается в 0 (Rplin = 0). Запишем формулу для обратного перехода в систему линеаризованных мониторных координат и подставим в нее данное условие:
В этой системе уравнений три неизвестные величины: Lp, Gplin и Bplin. Выразим Lp:
Аналогично нетрудно получить функцию Md = = f(L, S) для моделирования восприятия дейтеранопа:
– Сигнал отсутствующих у протанопа колбочек L-типа можно сделать при моделировании равным сигналу колбочек M-типа: Lp = M, а сигнал отсутствующих у дейтеранопа колбочек M-типа при моделировании можно сделать равным сигналу колбочек L-типа: Md = L. Очевидно, что при такой схеме преобразования белые точки на исходном изображении остаются белыми на преобразованных изображениях. Такой подход использовали Лукассен и Альфердинк в своем симуляторе дихромазии (Lucassen, Alferdinck, 2006). Кроме того, они предложили основанный на этом подходе способ моделирования цветового восприятия аномальных трихроматов, когда в качестве сигнала дефектного типа колбочек берется взвешенная сумма сигналов L- и M-колбочек нормального трихромата.
– Часто изображения, воспринимаемые протанопами и дейтеранопами, представляют в сине-желтой палитре. Здесь осмысленно было бы потребовать, кроме баланса белого, чтобы желтый цвет на исходном изображении оставался желтым на преобразованных. Этот вариант преобразования очень похож на предыдущий, но есть небольшое отличие. Например, при выбранных нами параметрах монитора яркий желтый цвет (Rlin = 1, Glin = 1, Blin = 0) соответствует следующим сигналам колбочек нормального трихромата: L = 0.937, M = 0.888, S = 0.135. Нетрудно видеть, что сигналы L- и M-колбочек нормального трихромата различаются, и это легко объясняется. Белый цвет монитора (Rlin = 1, Glin = 1, Blin = 1) вызывает единичные возбуждения всех колбочек нормального трихромата. Желтый цвет получается при гашении синего канала монитора. Синий канал дает больший вклад в сигнал M-колбочек, чем в сигнал L-колбочек, поэтому при гашении синего сигнал M-колбочек уменьшается (от единицы) сильнее, чем сигнал L-колбочек. Таким образом, как при присвоении Lp = M для моделирования протанопии, так и при присвоении Md = L для моделирования дейтеранопии желтые точки на преобразованном изображении “зеленеют” по сравнению с соответствующими точками исходного изображения. Рассмотрим подробно поиск такой функции Lp = f(M, S), которая обеспечит сохранение цвета желтых точек на преобразованных для протанопа изображениях. Функцию будем искать в виде Lp = pp ⋅ M + qp ⋅ S, где pp и qp – весовые коэффициенты. Для того, чтобы белые точки на входном изображении оставались белыми на преобразованном, сумма pp и qp должна быть равна единице.
Запишем формулу преобразования цвета желтой точки на экране в физиологические координаты нормального трихромата LY, MY, SY:
Раз мы потребовали сохранение цвета желтой точки на преобразованном изображении, то значение Lp для желтого цвета должно совпадать со значением сигнала L-колбочек нормального трихромата LY. Отсюда получим
Это выражение можно упростить, если принять во внимание то, что матрица перехода из системы линеаризованных мониторных координат (Rlin, Glin, Blin) в систему физиологических цветовых координат (L, M, S) строилась так, чтобы яркому белому цвету на экране монитора (Rlin = 1, Glin = 1, Blin = 1) соответствовали единичные возбуждения колбочек (L = 1, M = 1, S = 1). Из этого следует, что сумма значений по строкам этой матрицы равна единице. Отсюда получим
Очевидно, что такие же значения коэффициентов получились бы, если бы мы потребовали, чтобы на преобразованном изображении сохранялся цвет синих точек (Rlin = 0, Glin = 0, Blin = 1). Функция расчета значения канала L в изображении, преобразованном для протанопа, выглядит следующим образом:
Аналогично можно получить выражение для отсутствующего у дейтеранопа приемника M:
ПРИМЕНЕНИЕ ПРОГРАММЫ-СИМУЛЯТОРА ДЛЯ ПРОВЕРКИ ЦВЕТОВОГО ЗРЕНИЯ
Адаптация программы-симулятора
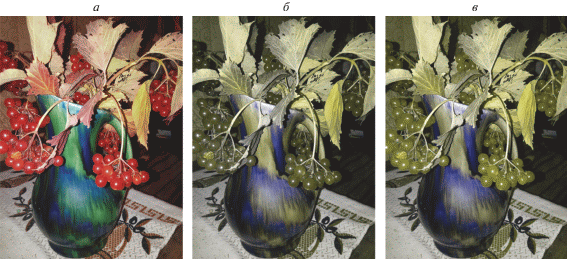
В том случае, когда изображения, моделирующие цветовое восприятие протанопов и дейтеранопов, строятся в соответствии с некоторым общим правилом (например, с сохранением на преобразованных изображениях белого, желтого и синего цветов), для нормального трихромата эти изображения выглядят очень похоже друг на друга, а исходное полноцветное изображение резко от них отличается (рис. 2). В то же время с точки зрения, например, протанопа, изображение, моделирующее цветовое восприятие протанопов, не отличается от исходного, а изображение, моделирующее восприятие дейтеранопов, отличается от остальных двух. Дейтеранопу при наблюдении трех изображений, отличающимся от двух других, будет казаться то, которое моделирует цветовое восприятие протанопов. Это свойство симулятора позволило создать на его основе программу для проверки цветового зрения.
В настройках программы выбираются набор исходных тестовых изображений и число предъявлений изображений для каждого испытуемого. При нажатии на кнопку “Проверка” запускается серия предъявлений изображений. Порядок выбора тестовых изображений из набора – случайный, но каждое из них демонстрируется испытуемому 1 раз. Таким образом, если изображений в списке больше, чем заданное в настройках число предъявлений, разным испытуемым будут показаны разные случайные подмножества изображений из общего списка.
Каждое загружаемое тестовое изображение обрабатывается двухпроходным алгоритмом, на выходе которого генерируются три изображения: измененное полноцветное; преобразованное под восприятие протанопа; преобразованное под восприятие дейтеранопа. Изображения, моделирующие восприятие дихроматов, генерируются в сине-желтой палитре с сохранением баланса белого, т.е. черные, белые, желтые и синие точки на полноцветном изображении сохраняют свои цвета на преобразованных. Все три изображения предъявляются на экране одновременно в горизонтальном ряду, причем порядок их в этом ряду выбирается случайно. Испытуемый должен нажать левую кнопку мыши на том изображении, которое кажется ему сильно отличающимся от двух других. После этого ему предъявляется следующая тройка изображений. Имена предъявляемых файлов, соответствие положения в ряду свойству изображения (полноцветное, для протанопов, для дейтеранопов) и ответы испытуемых записываются в текстовый файл.
Предварительная апробация программы
Целью апробации было сравнение двух существующих изданий полихроматических таблиц Е.Б. Рабкина и нового цветового теста на основе описанного выше симулятора.
Материалы и методы. В работе были использованы следующие тесты для оценки цветовосприятия:
– полихроматические таблицы Е.Б. Рабкина, 9-е издание (1971 г.),
– полихроматические таблицы Е.Б. Рабкина, 10-е издание (1998 г.)
– компьютерный тест П.В. Максимова (ИППИ РАН).
Методика работы. Таблицы предъявлялись на расстоянии чтения (около 40 см); работа с компьютерной программой проводилась с расстояния примерно 50–60 см. Освещенность в помещении составляла 300 люкс. Каждый испытуемый сначала проходил тест на компьютере, а затем – по таблицам Рабкина.
В первой серии опытов (при использовании 10-го издания таблиц Е.Б. Рабкина) предъявлялись таблицы № 3, 4, 6, 10, 13, 14, 17, 20, 23, 26. В этой серии принимали участие учащиеся одиннадцатых классов (53 человека).
Во второй серии опытов (при использовании 9-го издания таблиц Е.Б. Рабкина) предъявлялись все таблицы. В этой серии принимали участие ученики седьмых, четвертых и третьих классов (28 человек), а также учащиеся одиннадцатых классов (15 человек), у которых в ходе первой серии опытов были выявлены проблемы с выполнением тестов по таблице Е.Б. Рабкина.
Оборудование. Для тестирования по программе П.В. Максимова использовался ноутбук ASUS ZenBook UX305 с IPS-экраном с антибликовым покрытием, диагональ 13.3 дюйма. Для тестирования по таблицам Е.Б. Рабкина в первой серии экспериментов использовалось 10-е издание 1998 г.; во второй серии экспериментов использовалось 9-е издание 1971 г., считающееся эталонным.
Испытуемые. В исследовании принимали участие 81 испытуемый школьного возраста (26 юношей, 55 девушек).
К выборке школьников мы добавили двоих взрослых испытуемых, которые знали о своем дихроматическом зрении. Таким образом, всего в эксперименте приняли участие 83 испытуемых: 53 учащихся 11 класса (15 юношей, 38 девушек, 16–17 лет); восемь учащихся 7 класса (один юноша, семь девушек, 12–13 лет); десять учащихся 4 класса (пять мальчиков, пять девочек, 9–10 лет); десять учащихся 3 класса (пять мальчиков, пять девочек, 8–9 лет).
Все испытуемые участвовали в исследовании добровольно, для всех участников были получены информированные согласия законных представителей.
Результаты. В первой серии измерений из 53 испытуемых двое не смогли увидеть ни одной из тестовых таблиц Рабкина. Из этих двоих по компьютерному тесту аномалия (дейтеранопия) была выявлена только у одной испытуемой. По таблицам Рабкина тип аномалии этой испытуемой не определялся.
Из остальных 13 испытуемых не смогли увидеть изображения на части таблиц (по 10-му изданию) и были предварительно отнесены в группу “аномалов”; из этих испытуемых компьютерный тест ни у кого аномалий не выявил. При повторном тестировании у всех испытуемых с подозрением на цветоаномалию с использованием 9-го издания таблиц Рабкина и бóльшего числа изображений в компьютерном тесте было диагностировано нормальное цветовое зрение; один испытуемый сомневался в одной из таблиц, все остальные таблицы видел как трихромат. Судя по данным тестирования, 10-е издание таблиц Е.Б. Рабкина дает очень высокий процент ложноположительных результатов в сравнении с 9-м изданием. Субъективно тестовые таблицы в 10-м и 9-м изданиях сильно отличаются по цвету и контрасту, поэтому по факту являются разными тестами. Очевидно, что таблицы Е.Б. Рабкина показывают очень плохую повторяемость при использовании разных экземпляров таблиц.
По результатам компьютерного теста в первой серии был выявлен один дихромат, указан тип аномалии (таблицы Е.Б. Рабкина не могли выявить тип аномалии ни у одного из наших испытуемых, хотя некоторые таблицы должны по-разному распознаваться аномалами разного типа). Второго выявленного таблицами Е.Б. Рабкина дихромата компьютерный тест определил как нормального трихромата. Первая испытуемая знала о своем нарушении цветовосприятия, у второй испытуемой нарушений прежде диагностировано не было, однако ей было известно, что у ее отца дихроматическое зрение.
Во второй серии были протестированы испытуемые младшего возраста. Из 28 человек дихроматическое зрение по таблицам Рабкина было выявлено у четырех. Компьютерный тест выявил трех из них как дихроматов. Четвертый испытуемый из одиннадцати предъявленных троек изображений дал десять ответов как нормальный трихромат и один ответ – как дейтераноп. На этом основании мы определили его как дейтераномала.
Из двоих взрослых испытуемых-дихроматов по программе П.В. Максимова один был определен как протаноп, а второй – как дихромат с неясным типом дихромазии (один ответ был как у дейтеранопа и два – как у протанопа). По таблицам Е.Б. Рабкина оба испытуемых были определены как дихроматы, но тип аномалии менялся от таблицы к таблице, поэтому однозначного вывода по ним сделать было нельзя.
Одной из задач апробации было оценить, легко ли испытуемые понимают задачу тестирования (“выбрать наиболее отличающееся изображение”). Судя по субъективным комментариям протестированных испытуемых, задача несколько яснее для трихроматов: для них есть сильно выделяющееся изображение (сгенерированное для трихромата, с сохранением красных и зеленых оттенков оригинального изображения). Дихроматы чуть дольше понимали задачу; один из испытуемых прокомментировал, что все картинки довольно похожи, и хотя одна отличается, но различие не слишком сильное. Аналогичное мнение было высказано взрослым протанопом, знающим цель эксперимента. Тем не менее все испытуемые справлялись с задачей, и программа оказалась понятной и удобной для работы даже с детьми младшей возрастной группы (8–9 лет).
Разумеется, для введения компьютерной диагностики в практику требуются подбор подходящих стимульных изображений и учет спектра монитора. Однако очевидно, что протестированная компьютерная программа является перспективной заменой таблицам Е.Б. Рабкина: во-первых, программа не подвержена физическому устареванию, в отличие от выцветающих со временем таблиц; во-вторых, программу труднее обмануть, потому как запомнить правильные ответы на предъявляемые стимулы невозможно. Так как дихроматическое зрение встречается примерно у 8% мужчин, для дальнейшего усовершенствования программы и для более полной оценки ее диагностической мощности требуется проведение апробаций на бóльших выборках.
В наше время широкого употребления компьютеров странно использовать для проверки зрения бумажные таблицы, страдающие от плохой полиграфии, что было обнаружено и в настоящем исследовании. К тому же называние “скрытых” на них фигур, как уже отмечалось выше, требует не только цветового зрения, но и способности категоризации, т.е. узнавания изображения. Возможно и заучивание таблиц заранее. Предлагаемая программа лишена выше описанных недостатков и не вызывает трудностей при постановке вопроса испытуемым разных возрастов и уровней развития.
ОБСУЖДЕНИЕ
Значение цветового зрения
Цветовое зрение способствует существенному увеличению возможности животного в добывании пищи, обнаружении хищников, в социальных отношениях, выборе брачных партнеров, т.е. помогает успешно взаимодействовать с окружающей средой, тем самым способствуя эволюции (Jacobs, 2012). Генетика зрительных пигментов показывает, что предпосылки к существованию цветового зрения были очень давно – 700–500 млн. лет назад. Судя по рецепторному составу ныне живущих примитивных позвоночных – миног, а также рыб, рептилий и птиц, цветовое зрение уже на заре эволюции могло быть тетрахроматическим (Collin, et al., 2009). Млекопитающие, вынужденные и способные в соревновании с динозаврами перейти к сумеречному и скрытному образу жизни, утратили два гена зрительных пигментов (из четырех) и стали дихроматами с двумя генами, кодирующими коротковолновый и средневолновый зрительные пигменты. Почти все ныне живущие млекопитающие – дихроматы (Jacobs, 1993). Только приматы снова стали трихроматами. Дупликация гена средневолнового пигмента и последующие мутации привели к трихромазии, поддерживаемой естественным отбором (Ibbotson et al., 1992; Dulai et al., 1994; 1999). Главным фактором естественного отбора на трихромазию у приматов, как полагают, является тип их питания: фруктоядение и листоядение (Lucas et al., 1998; Sumner, Mollon, 2000). Положение максимумов зрительных пигментов у обезьян стереотипно. У людей отмечается полиморфизм, возникший, вероятно, в результате отсутствия жесткого естественного отбора (Neitz, 1990). По теоретическим расчетам добавление к двум приемникам третьего приводит к тому, что различение примерно 10 000 цветовых оттенков увеличивается до миллиона. На некоторых участках спектра трихромат замечает разницу оттенков в 1 нм.
Дихромазия у людей является досадным ограничением их возможностей. Пока единственным мыслимым способом “лечения”, например, протанопии является введение под сетчатку гена отсутствующего длинноволнового пигмента с помощью аденовируса. Такая операция была проведена на самце-дихромате обезьянки саймири и привела к желаемому результату. Ген встроился в часть средневолновых колбочек, а обезьяна по психофизическим тестам в поведении стала трихроматом (Mancuso et al., 2009).
Встречаются среди млекопитающих и монохроматы, или ахроматы. Это, как правило, ночные животные (Hunt et al., 2009). Киты и ластоногие тоже ахроматы. У них ген коротковолнового пигмента превратился в псевдоген, неспособный производить работающий пигмент (Peichl et al., 2001). Однако это исключения, по-видимому, связанные с жесткими экологическими требованиями. Наличие цветового зрения в различных его формах (ди-, три-, тетрахромазии) в животном царстве, поддерживаемого миллионы лет естественным отбором, говорит о его значимости.
Особенности разработанной программы-симулятора
В отличие от программы-симулятора, предложенного Бреттелем и соавт. (Brettel et al., 1997), где кривые спектральной чувствительности колбочек взяты из работы Стокмана (Stockman, 1993), в нашей работе кривые спектральной чувствительности (а также исходные данные для их построения – протанопическая, дейтеранопическая и тританопическая характерные точки в пространстве цветности) были взяты из работы Нюберга и Юстовой (Нюберг, Юстова, 1955). Другое отличие предложенного нами симулятора – выбор цветов, которые будут сохранены на преобразованных изображениях. Бреттель и соавт. большое внимание уделили соответствию результата работы симулятора наблюдениям унилатеральных дихроматов. В качестве цветов, которые сохраняются на преобразованных изображениях, они выбрали нейтральный белый и излучения с доминантными длинами волн 575 нм (желтый) и 475 нм (синий) – для моделирования цветового зрения протанопов и дейтеранопов и излучения с доминантными длинами волн 660 нм (красный) и 485 нм (синий) – для моделирования цветового зрения тританопов. Мы рассмотрели несколько вариантов “палитр” для преобразованных изображений и остановились на варианте с сохранением белого, синего и желтого мониторных цветов.
Особенности разработанной программы для оценки цветового зрения
Разработанная программа для проверки цветового зрения одновременно предъявляет на экране три изображения: полноцветное, преобразованное для протанопов и преобразованное для дейтеранопов. Испытуемому требуется выбрать из трех изображений одно, сильно отличающееся от двух других. Как нормальные трихроматы, так и люди с наиболее частыми формами дихромазии (протанопы и дейтеранопы) могут это сделать. При этом для нормальных трихроматов, строго говоря, все три изображения выглядят по-разному, но исходное изображение сильно отличается от преобразованных бóльшим набором цветов. В идеальном случае при правильно настроенной видеосистеме и соответствующей подгонке алгоритма преобразования изображений дихромат не будет видеть никаких отличий одного из преобразованных изображений от исходного. Оставшееся изображение, преобразованное под другую форму дихромазии, будет отличаться, но отличие это (по крайней мере, на взгляд нормального трихромата) не очень существенно.
При мониторном предъявлении важно учитывать цветовую температуру, цветовой охват и показатель степенной функции гамма-коррекции видеосистемы. При несоответствии этих параметров значениям, заданным в алгоритме, изображения, моделирующие восприятие дихроматов, будут отличаться от исходного даже с точки зрения дихроматов. Для того, чтобы проверка цветового зрения при помощи программы была возможна, необходимо, чтобы исходное изображение, рассматриваемое протанопом, отличалось (на его взгляд) от преобразованного под зрение протанопа меньше, чем от преобразованного под зрение дейтеранопа. Аналогично и на взгляд дейтеранопа отличие исходного изображения от изображения, преобразованного для дейтеранопа, должно быть меньше, чем от изображения, преобразованного для протанопа. В дальнейшем предстоит выяснить, какие отклонения параметров реального монитора от заданных в программе значений допустимы для того, чтобы программой можно было пользоваться для проверки цветового зрения.
Отдельный вопрос – выбор изображений для проверки цветового зрения. Как было описано выше, симулятор автоматически пересчитывает цвета на исходном изображении так, чтобы было возможно предъявить на экране одновременно и это изображение, и изображения, моделирующие цветовое восприятие дихроматов. Чем больше на изображении насыщенных зеленых и красных цветов, тем легче будет трихроматам (как нормальным, так и аномальным) отличить полноцветное изображение от преобразованных под дихроматическое зрение. Тем самым аномалы не будут выявлены. Чтобы уверенно обнаруживать и аномальных трихроматов, нужны, наоборот, изображения с ненасыщенными цветами, с различением цветов на которых у аномальных трихроматов, по-видимому, возникнут трудности, и аномалы будут обнаружены. Таким образом, в тестовом наборе должны присутствовать как изображения, состоящие из насыщенных крупных цветных пятен, так и изображения, содержащие мелкие и малонасыщенные детали. Мы ожидаем, что с малонасыщенными изображениями и дихроматы, и аномалы будут путаться (давать случайные ответы), а при помощи изображений с насыщенными цветами можно будет выявить дихроматов, хотя это потребует большого числа тестовых изображений.
Список литературы
Домасёв М.В., Гнатюк С. Цвет, управление цветом, цветовые расчеты и измерения. СПб.: “Питер”, 2007. 224 с.
Кравков С.В. Глаз и его работа. М.: Медицина, 1932. 245 с.
Нюберг Н.Д., Юстова Е.Н. Исследование цветного зрения дихроматов. Труды ГОИ. 1955. Т. 24(143). С. 33–93.
Юстова Е.Н. Цветовые измерения (Колориметрия). СПб.: Изд-во СПб ун-та, 2000. 397 с.
Alpern M., Kitahara K., Krantz D.H. Perception of colour in unilateral tritanopia. J. Physiol. (London). 1983. V. 335. P. 683–697.
Baraas R.C., Carroll J., Gunther K.L., Chung M., Williams D.R., Foster D.H., Neitz M. Adaptive optics retinal imaging reveals S-cone dystrophy in tritan color-vision deficiency. J Opt Soc Am A Opt Image Sci Vis. 2007. V. 24(5). P. 1438–1447.
Birch J. Worldwide prevalence of red-green color deficiency. J Opt Soc Am A. 2012. V. 29(3). P. 313–320.
Bowmaker J.K., Astell S., Hunt D.M., Mollon J.D. Photosensitive and photostable pigments in the retinae of Old World monkeys. J Exp Biol. 1991. V. 156. P. 1–19.
Brettel H., Viénot F., Mollon J.D. Computerized simulation of color appearance for dichromats. J. Opt. Soc. Am. A. 1997. V. 14 (10). P. 2647–2655.
Carroll J., Neitz M., Hofer H., Neitz J., Williams D.R. Functional photoreceptor loss revealed with adaptive optics: An alternate cause of color blindness. PNAS. 2004. V. 101m (22). P. 8461–8466.
Collin Sh.P., Davies W.L., Hart N.S., Hunt D.M. The evolution of early vertebrate photoreceptors. Phil. Trans. R. Soc. B. 2009. V. 364. P. 2925–2940. https://doi.org/10.1098/rstb.2009.0099
Dalton J. Extraordinary facts relating to the vision of colours: with 19 observations. Memoirs of the Literary and Philosophical Society of Manchester. 1798. V. 5. P. 28–45.
Dulai K.S., Bowmaker J.K., Mollon J.D., Hunt D.M. Sequence divergence, polymorphism and evolution of middle-wave and long-wave visual pigment genes of great apes and Old World monkeys. Vision Res. 1994. V. 34 (19). P. 2483–2491.
Dulai K.S., von Dornum M., Mollon J. D., Hunt D.M. The evolution of trichromatic color vision by opsin gene duplication in New World and Old World primates. Genome Res. 1999. V. 9 (7). P. 629–638.
Golz J., Macleod D.I.A. Colorimetry for CRT displays. J. Opt. Soc. Am. A. 2003. V. 20(5). P. 769–781.
Hunt D.M., Carvalho L.S., Cowing J.A., Davies W.L. Evolution and spectral tuning of visual pigments in birds and mammals. Phil. Trans. R. Soc. B. 2009. V. 364. P. 2941–2955.
Ibbotson R.E., Hunt D.M., Bowmaker J.K., Mollon J.D. Sequence divergence and copy number of the middle-and long-wave photopigment genes in Old World monkeys. Proc. R. Soc. Lond. B. 1992. V. 247 (1319). P. 145–154.
Jacobs G.H. The evolution of vertebrate color vision. Sensing in Nature. Springer, New York, NY. 2012. P. 156–172.
Jacobs G.H. The distribution and nature of colour vision among the mammals. Biol. Rev. 1993. V. 68. P. 413–471.
Judd D.B. Color perceptions of deuteranopic and protanopic observers. J. Res. Natl. Bur. Stand. 1948. V. 41. P. 247–271.
Lucas P.W., Darvell B.W., Lee P.K.D., Yuen T.D.B., Choong M.F. Colour cues for leaf food selection by long-tailed macaques (Macaca fascicularis) with a new suggestion for the evolution of trichromatic colour vision. Folia Primatol. 1998. V. 69. P. 139–154.
Lucassen M.P., Alferdinck J.W.A.M. Dynamic Simulation of Color Blindness for Studying Color Vision Requirements in Practice. Proc. CGIV. 2006. P. 355–358.
Mancuso K., Hauswirth W.W., Li Q., Connor T.B., Kuchenbecker J.A., Mauck M.C., Neitz J., Neitz M. Gene therapy for red–green colour blindness in adult primates. Nature. 2009. V. 461. P. 784–787.
Maximov P.V. The program simulating dichromacy as a possible tool for detecting colour deficiencies. Perception. V. 48. Suppl., Proc. ECVP. 2019. P. 46.
Mollon J.D., Estevez O., Cavonius C.R. The two subsystems of colour vision. Vision: Coding and efficiency. Cambridge University Press. 1993. P. 117–149.
Nathans J. The Evolution and Physiology of Human Color Vision: Insights from Molecular Genetic Studies of Visual Pigments. Neuron. 1999. V. 24. P. 299–312.
Nathans J., Thomas D., Hogness D.S. Molecular genetics of human color vision: the genes encoding blue, green, and red pigments. Science. 1986. V. 232. P. 193–202.
Neitz J. Polymorphism in normal human color vision and its mechanism. Vision RCS. 1990. V. 30 (4). P. 621–636.
Peichl L., Behrmann G., Kröger R.H.H. For whales and seals the ocean is not blue: a visual pigment loss in marine mammals. European Journal of Neuroscience. 2001.V. 13. P. 1520–1528.
Ruddock K.H. Psychophysics of inherited colour vision deficiencies. Inherited and Acquired Colour Vision Deficiencies: Fundamental Aspects and Clinical Studies. Eds D.H. Foster. 1991. V. 7. P. 4–37.
Simunovic M.P. Colour vision deficiency. Eye. 2010. V. 24 (5). P. 747–755.
Schnapf J.L., Kraft T.W., Baylor D.A. Spectral sensitivity of human cone photoreceptors. Nature. 1987. V. 325. P. 439–441.
Sharpe L.T., Stockman A., Jägle H., Nathans J. Opsin genes, cone photopigments, color vision, and color blindness. Color vision: From genes to perception. Cambridge Univ. Press, UK. 2000. P. 3–51.
Stockman A., MacLeod D.I.A., Johnson N.E. Spectral sensitivities of the human cones. J. Opt. Soc. Am. A. 1993. V. 10. P. 2491–2521.
Sumner P., Mollon J.D. Catarrhine photopigments are optimized for detecting targets against a foliage background. The Journal of Experimental Biology. 2000. V. 203. P. 1963–1986.
Viénot F., Brettel H., Ott L., Ben M’ Barek A., Mollon J.D. What do colour-blind people see? Nature. 1995. V. 376. P. 127–128.
Wright W.D. The Characteristics of Tritanopia. JOSA. 1952. V. 42 (8). P. 509–521.
Дополнительные материалы отсутствуют.
Инструменты
Сенсорные системы