Сенсорные системы, 2020, T. 34, № 1, стр. 44-56
Метод линейной регрессии, устойчивый к экстремальным стационарным помехам
Д. А. Бочаров *
Институт проблем передачи информации им. А.А. Харкевича РАН
127051 Москва, Большой Каретный пер., 19, Россия
* E-mail: bocharov.mitry@gmail.com
Поступила в редакцию 30.09.2019
После доработки 15.10.2019
Принята к публикации 29.10.2019
Аннотация
Рассматривается задача двумерной линейной регрессии для зашумленных данных. Последние представляют собой пары координат, возвращаемых пространственно-разрешающим детектором и, помимо аддитивного шума, могут содержать выбросы. В качестве основной модели выбросов рассматриваются стационарные помехи, т.е. координаты выбросов близки к фиксированному, хотя и неизвестному значению. В работе предлагается метод линейной регрессии, устойчивый к наличию экстремальной (с долей более 50% от общего объема данных) стационарной координатной помехе. Метод основан на хаф-анализе двумерной координатной гистограммы входных данных и заключается в последовательной оценке параметров угла наклона и сдвига. Основанный на данном методе алгоритм использован для локализации траекторий движения колес в интеграционном модуле системы автоматической классификации транспортных средств. Проведены эксперименты на реальных и полученных путем имитационного моделирования данных по сравнению точности предложенного метода и М-оценки Уэлша. Показано, что при той же трудоемкости алгоритмы, основанные на предложенном методе, имеют большую точность в задаче оценивания параметров траектории в условиях наличия экстремальных стационарных помех.
ВВЕДЕНИЕ
Линейные модели – один из простейших классов моделей, описывающих зависимости в данных. Несмотря на примитивность, они весьма популярны. Это связано как с распространенностью процессов, достаточно хорошо описывающихся линейным законом, так и с наличием хорошо проработанного для этого класса моделей математического аппарата. Задача оценки параметров линейной модели называется линейной регрессией. Классическим методом решения этой задачи является метод наименьших квадратов (МНК). К сожалению, этот метод не робастен, т.е. в присутствии “выбросов” во входных данных (вызванных, например, ошибками измерения) может давать сколь угодно неверный результат. Так называемые робастные методы, напротив, для выборок с долей посторонних данных, не превышающих некоторого порога (называемого асимптотической толерантностью), гарантированно не дают сколь угодно ошибочных оценок, т.е. имеют ненулевую точность в худшем случае. Примерами робастных методов линейной регрессии являются метод Тейла-Сена (Rousseeuw, Leroy, 2005), наименьших медиан квадратов (Rousseeuw, 1984), метод наименьших усеченных квадратов (Rousseeuw, Van Driessen, 2006) и группа методов робастного М-оценивания (Huber, 2011).
Очевидно, что в случаях, когда обрабатываемые данные поступают с физических сенсоров без контроля оператора, предпочтительно использовать именно робастные методы. Если при этом известно, что вероятность получения нерелевантных данных с сенсора велика, то следует рассматривать робастные методы с высокой асимптотической толерантностью. Теоретическим пределом для толерантности является 50%-ная величина, и наиболее надежным выбором кажутся методы, достигающие этого значения, тем не менее, рассуждая таким образом, можно попасть в ловушку. Действительно многие методы оценивания в некоторых случаях могут успешно справляться с долей “выбросового” шума, превышающей теоретический предел. При этом они будут обладать большей или меньшей асимптотической толерантностью, но в любом случае значение толерантности не будет превышать 50%. Такая величина характеризует лишь уровень загрязнения выборки, при котором гарантирован хоть сколько-то разумный результат. Однако для экстремально высоких уровней зашумления верный результат не может быть гарантирован в принципе. Это и делает асимптотическую толерантность слабым критерием при выборе методов, устойчивых к по-настоящему сильному шуму.
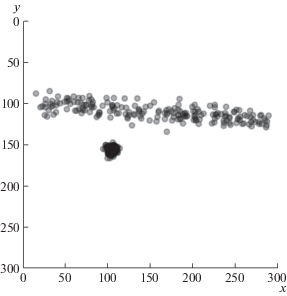
Далее будем рассматривать только случай, когда данные двумерны, т.е. каждое измерение имеет две координаты. Будем называть выбросы, имеющие раз от раза близкие значения, “стационарной помехой”; уровень выбросов, составляющий более 50% от общего объема измерений – “экстремальным”. На рис. 1 изображен набор двумерных измерений, связанных линейным законом, но подверженных шуму и загрязненных экстремальной стационарной помехой: выбросовые измерения не просто составляют более половины всех измерений, но также очень плотно сгруппированы (функция их распределения имеет малую дисперсию и центрально-симметрична). Прямая, оцененная по этим данным неробастным методом, наверняка пройдет вблизи центра кластера ошибок, что будет грубой ошибкой оценивания.
Еще раз отметим, что для произвольных экстремальных помех ни один метод не может гарантировать нахождения параметров линейной модели с ограниченной ошибкой. При этом задача оценивания в присутствии экстремальных помех встречается на практике. В качестве примера такой ситуации ниже будет рассмотрена работа подсистемы оценивания параметров траекторий движения колес транспортного средства системы автоматической классификации транспортных средств (АКТС) (Grigoryev et al., 2015). Точность этой подсистемы критична для обеспечения основной функциональности АКТС, а ее устройство не защищено от стационарных помех. Ниже мы отдельно остановимся на причинах возникновения экстремальных стационарных помех во входных данных этой подсистемы. Для обеспечения устойчивой к данному шуму оценки предлагается использовать дополнительный признак различения регулярных данных и выбросов, а именно стационарность помехи.
ОБНАРУЖЕНИЕ ТРАЕКТОРИИ ДВИЖЕНИЯ КОЛЕС В МОДУЛЕ ОЦЕНКИ КОЛИЧЕСТВА КОЛЕСНЫХ ОСЕЙ АКТС
На платных дорогах России введена в эксплуатацию система автоматической классификации транспортных средств, представляющая собой сложную систему технического зрения (Khanipov et al., 2015; Григорьев и др., 2017). Основной задачей системы является автоматическое определение класса транспортного средства, от которого зависит цена проезда по платному участку дороги. Для решения этой задачи системе необходимо оценивать количество колесных осей автомобиля, его полную высоту и высоту над первой колесной осью.
Рассмотрим принцип работы модуля АКТС, ответственного за детекцию колес и подсчет количества колесных осей. Модуль, оценивающий число колесных осей, получает на вход последовательность кадров съемки проезжающего автомобиля. Его работу можно разбить на четыре стадии.
I. Для каждого кадра проезда детектируются положения центров колес. Для описания одной детекции ${{d}_{i}}$ используются вектор ${{d}_{i}} = ({{x}_{i}},{{y}_{i}},{{t}_{i}},siz{{e}_{i}},scor{{e}_{i}})$, задающий положение $({{x}_{i}},{{y}_{i}})$ центра найденного колеса на кадре, номер кадра ${{t}_{i}}$, размер $siz{{e}_{i}}$ и значение $scor{{e}_{i}}$, характеризующие степень уверенности отклика. Результатом работы этого шага является неупорядоченное множество D срабатываний детектора на кадрах видеопоследовательности. Обозначим число таких детекций ${{N}_{d}}$.
II. С использованием пространственных координат всех детекций ${{p}_{i}} = ({{x}_{i}},{{y}_{i}})$, $i \in [1,{{N}_{d}}]$ оценивается линейная модель траектории, по которой осуществлялось движение центров образов колес автомобиля на изображениях. Результатом работы данного алгоритма является оценка параметров $\hat {k},\hat {b}$ этой прямой $(y = \hat {k}x + \hat {b})$.
III. Осуществляется фильтрация множества срабатываний D, где критерием фильтрации является степень соответствия координат срабатываний оцененной на предыдущем шаге линейной модели.
IV. По прошедшим через стадию фильтрации детекциям осуществляется подсчет числа колесных осей путем анализа распределения детекций в пространстве $(x,t)$.
Стадия I данного алгоритма выполняется так называемым детектором колес, стадии II–IV – так называемым интегратором траекторий. Данная подсистема подробно рассмотрена в работе (Grigoryev et al., 2015).
Результаты работы детектора зачастую содержат ложноположительные срабатывания, возникающие, например, на образах топливных баков автомобилей; нанесенных на кузов транспортного средства иллюстраций; отражений бликов от фар на поверхности дорожного полотна; лужах, неподвижных тенях или бликах на поверхности асфальта (рис. 2). Примеры гистограмм срабатываний детектора с многочисленными ложноположительными ошибками приведены на рис. 3.
Рис. 2.
Кадры с визуализацией ложноположительных ошибок детектора колес. Слева направо: срабатывания на образах топливных баков, иллюстрации на кузове автомобиля, фаре, отражениях освещения на поверхности асфальта.

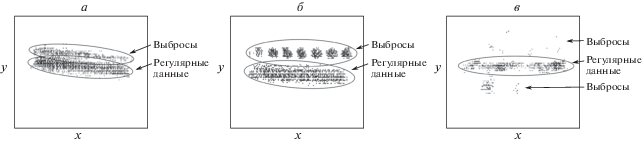
Рис. 3.
Примеры гистограмм $(x,y)$ координат срабатываний детектора колес с выраженными выбросами, возникшими на образах: а, б – иллюстраций на кузове автомобиля; в – частей кузова и неподвижной тени на поверхности дороги.
Ложноположительные ошибки детектора во многих случаях являются причиной неверной оценки количества колесных осей. В связи с этим входное множество срабатываний проходит через стадии анализа (стадия II) и фильтрации (стадия III). Алгоритм анализа и фильтрации основан на соображении, что центры образов колес автомобиля движутся на изображении по прямолинейной траектории, в то время как ложные срабатывания чаще всего ей не соответствуют. Таким образом, оценив параметры траектории движения колес, можно отфильтровать те срабатывания, которые не описываются оцененной моделью, что и выполняется на втором и третьем шаге алгоритма. Учитывая то, что ложные срабатывания слабо скоррелированны с истинноположительными, а также то, что их распределение и количество заранее неизвестны, задача локализации траектории решается как задача двумерной робастной линейной регрессии. В работе (Grigoryev et al., 2015) для ее решения предлагается алгоритм на основе вычисления М-оценки:
Большая проблема при решении задачи локализации траектории возникает, когда детектор колес выдает систематическую ложноположительную ошибку на неподвижном, попавшем в поле зрения камеры, объекте. Например, такие ошибки возникают на лужах и тенях (рис. 4). Образы таких объектов, как правило, слабо различаются между кадрами, и, как следствие, за период проезда автомобиля накапливается большое количество ложноположительных детекций. Таким образом, в пространстве $(x,y)$ формируется стационарная помеха, вес которой относительно всех данных может превышать 50%. Примеры двумерных гистограмм с подобными помехами приведены на рис. 5. При таком уровне зашумления результат вычисления М-оценки может быть сколь угодно неточным. В результате некорректной локализации траектории на этапе фильтрации может быть отбракована существенная часть хороших детекций, что может критично сказаться на качестве работы последующих стадий интегратора и классификатора в целом. В условиях повторяемости подобных ошибок детектора на нескольких проездах качество работы классификатора на данной дорожной полосе может упасть существенно ниже допустимого уровня, и тогда использование системы станет нецелесообразно.
ПРЕДЛОЖЕННОЕ РЕШЕНИЕ
Предлагаемый метод линейной регрессии основан на хаф-анализе входной двумерной гистограммы срабатываний, а именно – последовательной оценке угла наклона и сдвига.
Быстрое преобразование Хафа. В основе предлагаемого в работе метода линейной регрессии лежит быстрое преобразование Хафа – алгоритм, реализующий дискретное преобразование Радона (далее – ДПР). В отличие от классической реализации алгоритма ДПР, имеющего сложность $O({{n}^{3}})$, где n – размер стороны квадратного изображения, алгоритм БПХ обладает меньшей вычислительной сложностью – $\Theta ({{n}^{2}}{\kern 1pt} \log {\kern 1pt} n)$ (Nikolaev et al., 2008). Результатом быстрого преобразования Хафа является двумерное изображение (хаф-образ) в системе координат параметров прямых $(s,t)$ (рис. 6).
Обозначим через I квадратную гистограмму исходного множества точек с линейным размером n. Далее в работе будем рассматривать множество преимущественно горизонтальных прямых ($\left| k \right| \leqslant 1$). Обозначим через $\hat {I}$ результат свертки изображения I с гауссовским ядром, а через ${{H}_{{\hat {I}}}}$ – изображение размера $w \times h$ (хаф-образ), являющееся результатом применения БПХ от $\hat {I}$ для рассматриваемого множества прямых. Значение ${{H}_{{\hat {I}}}}(s,t)$ в точке $(s,t)$ является суммой значений пикселей вдоль прямой со сдвигом s и наклоном t, а строка ${{h}_{t}}$ – интегральной проекцией $\hat {I}$ на направление под углом ${{\phi }_{t}} = {\text{arctg}}\left( {\frac{t}{{n - 1}}} \right)$, где $t \in [ - n + 1,n - 1]$.
Определение угла наклона. Задача поиска угла наклона тесно связана с распространенной задачей коррекции угла поворота цифровых сканов документов (Hull, 1998; Amin, Fischer, 2000). Один из эффективных подходов к его определению – анализ интегральных проекций изображения (Li et al., 2007): чем ближе направление, вдоль которого проецируется изображение документа, к истинному, тем выраженнее пики проекции. В посвященных данной проблеме работах для оценки выраженности пиков используются критерии суммы квадратов значений интегральной проекции (Baird, 1987; Papandreou, Gatos, 2011), критерии, основанные на градиентах (Srihari, Govindaraju, 1989; Postl, 1988) и модификации на их основе (Stahlberg, Vogel, 2015).
Критерии оценки угла наклона могут быть вычислены по хаф-образу (Nikolaev et al., 2008). Например, в работах (Bezmaternykh et al., 2018; Limonova et al., 2017), посвященных ректификации изображений текстовых документов, предлагаются алгоритмы определения угла наклона на основе хаф-анализа. В этой работе угол наклона будем искать следующим образом:
где $F({{h}_{t}})$ – значение критерия от строки ${{h}_{t}}$.Известно, что в ($s,t$)-параметризации ортогональное расстояние между прямыми с наклоном t меньше, чем ортотропное в $\cos {{\phi }_{t}}$ раз (Ершов и др., 2017), в то же время для любого наклона сумма значений ${{h}_{t}}$ является инвариантом. Отсюда следует, что максимальное значение в строке ${{h}_{t}}$ хаф-образа круга будет в $\cos {{\phi }_{t}}$ раз меньше, чем для ${{h}_{0}}$. Будем это учитывать при определении критерев, вычисленных с использованием БПХ. Далее рассмотрим следующие критерии: суммы квадратов значений (SSV – sum of squared values), суммы модулей градиентов (SMG – sum of modules of gradients) и суммы их квадратов (SSG – sum of squares of gradients). Для строки ${{h}_{t}}$ данные критерии запишем следующим образом:
Оптимальным для М-оценки углом наклона будет тот, для которого достигается максимальное значение интегральной проекции (MOV – maximum of value):
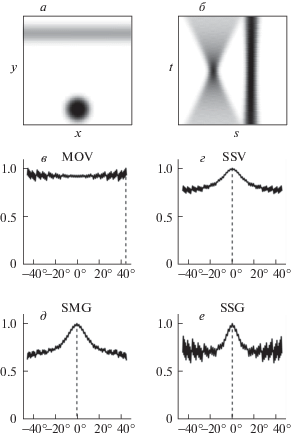
В отличие от критерия максимума, описанные ранее критерии позволяют учесть не только глобальное значение интеграла, но и форму распределения интегральной проекции, в частности, выраженность пиков. Таким образом, SSV, SMG и SSG, в отличие от MOV, не теряют чувствительности к наличию линейных объектов на изображении даже при экстремальных стационарных выбросах. Продемонстрируем это свойство на примере гистограммы со сверхтяжелым шумом. Для этого рассмотрим квадратную гистограмму со стороной, равной 64 пикселя, на котором содержатся горизонтальный и центрально-симметричный кластеры, причем масса последнего превышает массу первого (рис. 7, а). На рис. 7, б изображен хаф-образ этой гистограммы для преимущественно горизонтальных прямых, а на рис. 7, в–е – отнормированные значения MOV, SSV, SMG и SSG в зависимости от угла наклона. Видно, что значение MOV на интервале от [–40°, 40°] практически неизменно (с точностью до погрешностей дискретизации) и его максимум в данном случае достигается при угле более 40°, в то время как у SSV, SMG и SSG в нуле наблюдаются выраженные максимумы. Это и является желаемым поведением критериев.
Рис. 7.
Графики значений критериев оценки угла наклона на примере гистограммы с экстремальной помехой: а – входная гистограмма; б – ее хаф-образ; в – критерий максимального значения (MOV), г – суммы квадратов значений (SSV); д – суммы модулей градиентов (SMG); е – суммы квадратов градиентов (SSG).
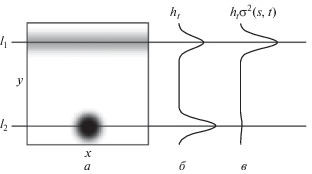
Определение сдвига. Рассмотрим интегральную проекцию гистограммы вдоль найденного направления $\hat {t}$. Для верно выбранного угла ожидается, что интегральная проекция будет характеризоваться двумя ярко выраженными пиками, соответствующими спроецированному сигналу и стационарной помехе. При экстремальном загрязнении значение в пике для помех может превышать значение, соответствующее регулярным данным, в связи с этим критерий максимума проекции даст неверный результат. Введем новый критерий, обладающий устойчивостью к подобным загрязнениям. Заметим, что дисперсия стационарной помехи значительно меньше дисперсии регулярных данных вдоль правильного направления проекции. Обозначим через ${{h}_{{{{s}_{1}},\hat {t}}}}$, ${{h}_{{{{s}_{2}},\hat {t}}}}$ отнормированные на сумму их значений одномерные гистограммы вдоль прямых ${{l}_{1}},\;{{l}_{2}}$ с наклоном $\hat {t}$ и сдвигами ${{s}_{1}},\;{{s}_{2}}$ на гистограмме $\hat {I}$ (рис. 8, а). Ожидается, что дисперсии $\sigma _{1}^{2},\;\sigma _{2}^{2}$, оцениваемые по гистограммам ${{h}_{{{{s}_{1}},\hat {t}}}},\;{{h}_{{{{s}_{2}},\hat {t}}}}$, отличаются, а именно: $\sigma _{1}^{2} > \sigma _{2}^{2}$. Таким образом, предлагается искать такой сдвиг $\hat {s}$, для которого достигается максимум значения проекции, умноженный на выборочные дисперсии вдоль прямых. Выборочную дисперсию ${{\sigma }^{2}}(s,\hat {t})$ вдоль прямой с параметрами $s,\;\hat {t}$ будем вычислять следующим образом:
Рис. 8.
Интегральные проекции вдоль правильно оцененного направления: а – гистограмма со сверхтяжелым шумом; б – исходная проекция; в – проекция, домноженная на выборочные дисперсии вдоль прямых.
Запишем предлагаемый критерий $S({{h}_{{\hat {t}}}},s)$ и оценку параметра сдвига $\hat {s}$:
На рис. 8, а приведена двумерная гистограмма с экстремальной стационарной помехой, на б и в – интегральная проекция вдоль правильного направления и домноженная на выборочные дисперсии вдоль прямых.
Предлагаемый метод. Ниже приведено описание предлагаемого метода оценки параметров линейной модели в условиях наличия стационарных помех.
Вход: двумерная квадратная гистограмма $I$ со стороной n; критерий поиска угла наклона $F({{h}_{t}})$; размер ядра свертки w.
Выход: оценки параметров линейной модели $\hat {k},\;\hat {b}$.
1) Вычислить свертку I с изотропным гауссовским ядром $\hat {I}: = I * G(w)$.
2) Вычислить БПХ от $\hat {I}$: ${{H}_{{\hat {I}}}}: = FHT(\hat {I})$.
3) Определить значение наклона $\hat {t}$:
• Инициализировать наилучшее значение критерия и параметра угла наклона ${{F}_{{\max }}}: = - 1$, $\hat {t}: = - 1$.
• Для каждого $t = 0,1, \ldots ,h - 1$:
− Вычислить значение критерия $F({{h}_{t}})$ для строки ${{h}_{t}}$.
− Если $F({{h}_{t}}) > {{F}_{{\max }}}$, то обновить значения: ${{F}_{{max}}}: = F({{h}_{t}})$, $\hat {t}: = t$
4) Определить значение сдвига $\hat {s}$:
• Инициализировать наилучшее значение критерия и параметра сдвига ${{S}_{{\max }}}: = - 1$, $\hat {s}: = - 1$.
• Для каждого $s = 0,1, \ldots ,w - 1$:
− Вычислить оценку дисперсии ${{\sigma }^{2}}(s,\hat {t})$ значений входных данных вдоль прямой с наклоном $\hat {t}$ и сдвигом s.
− Вычислить критерий $S({{h}_{{\hat {t}}}},s): = {{H}_{{\hat {I}}}}(s,\hat {t}){\kern 1pt} {{\sigma }^{2}}(s,\hat {t})$.
− Если $S({{h}_{{\hat {t}}}},s) > {{S}_{{\max }}}$, то обновить значения: ${{S}_{{\max }}}: = S({{h}_{{\hat {t}}}},s)$, $\hat {s}: = s$
5) Преобразовать параметры прямой $\hat {k}: = \hat {t}{\text{/}}(n - 1)$, $\hat {b}: = \hat {s}$.
6) Вернуть $\hat {k},\;\hat {b}$.
Иллюстрация предложенного метода приведена на рис. 9. В качестве входных данных взята гистограмма от облака точек с рис. 1, сторона квадратной гистограммы составляет 100 пикселей, для определения угла наклона выбран критерий SMG.
Рис. 9.
Стадии предложенного метода линейной регрессии на примере двумерной гистограммы данных со сверхтяжелым выбросовым шумом: 1 – гистограмма облака точек с рис. 1; 2 – результат свертки гистограммы с гауссовским ядром; 3 – хаф-образ с отображенными значениями критерия SMG и его максимумом в строке ${{t}_{a}}$; 4 – взвешенная дисперсией интегральная проекция вдоль направления под углом a; 5 – результат работы алгоритма.

Асимптотическая вычислительная сложность предложенного метода складывается из трудоемкости его этапов. Сложность вычисления БПХ (этап 2), как известно, составляет $\Theta ({{n}^{2}}{\kern 1pt} \log {\kern 1pt} n)$. В то время как сложность оценки параметров модели (этапы 3 и 4) составляет $O({{n}^{2}})$, а значит, если сложность вычисления $F({{h}_{t}})$ не превышает эту оценку, то сложность всего метода составляет $\Theta ({{n}^{2}}{\kern 1pt} \log {\kern 1pt} n)$.
ЭКСПЕРИМЕНТЫ
В данной работе проводили исследование зависимости точности алгоритмов линейной регрессии от степени загрязненности входных данных стационарной помехой. Исследовали алгоритмы на основе предложенного метода с критериями SMG, SSV, SSG и алгоритм, вычисляющий М-оценку Уэлша (далее – референтный). Также проводили сравнение оценок качества работы подсистемы подсчета количества колесных осей в зависимости от алгоритма оценки параметров траектории.
Имитационное моделирование срабатываний детектора. Выборка, на которой оценивалась точность алгоритмов, состояла из V двумерных координатных гистограмм срабатываний детектора, полученных путем имитационного моделирования. Далее будем описывать процесс создания $i$-го элемента выборки.
Рассмотрим ограниченную область в ${{\mathbb{R}}^{2}}$, $0 < x < m$, $0 < y < m$. Определим преимущественно горизонтальную прямую ${{l}_{i}}$, параметры $({{k}_{i}},{{b}_{i}})$ которой являются реализациями равномерных распределений. Пусть N – количество регулярных точек, их множество ${{D}_{i}}$ будем моделировать следующим образом:
К множеству точек ${{D}_{i}}$ будем добавлять M точек, которые имитируют стационарную помеху и K точек, моделирующих равномерно распределенные выбросы. Помеху будем моделировать двумерным нормальным распределением с фиксированными средним и дисперсией $\sigma _{c}^{2}$. Элементом выборки считается квадратное изображение ${{I}_{i}}$ со стороной n, полученное путем вычисления двумерной гистограммы точек ${{D}_{i}}$ с шагом дискретизации, равным $m{\text{/}}n$.
Метод оценки точности определения параметров модели
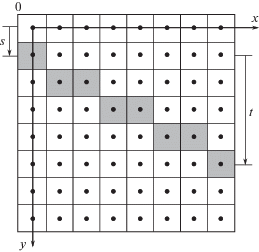
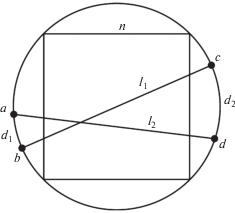
Оценку точности определения параметров сведем к задаче определения невязки между двумя прямыми на изображении. Пусть ${{l}_{1}}$ и ${{l}_{2}}$ с параметрами ${{k}_{1}},\;{{b}_{1}}$ и ${{k}_{2}},\;{{b}_{2}}$ соответственно – референтная прямая и ее оценка алгоритмом. Введем окружность C, описанную вокруг изображения I с центром в точке $(n{\text{/}}2,n{\text{/}}2)$ и радиусом $r = n\sqrt 2 {\text{/}}2$. Обозначим через $a,\;b$ и $c,\;d$ точки пересечения прямых ${{l}_{1}}$ и ${{l}_{2}}$ с окружностью C. Обозначим через ${{d}_{1}}$ дугу наименьшей длины, а через ${{d}_{2}}$ – ей противоположную. Определим погрешность оценивания параметров прямой $e({{l}_{i}},{{\hat {l}}_{i}})$ как максимальную из длин ${{d}_{1}},\;{{d}_{2}}$ (рис. 10):
Рис. 10.
В качестве значения невязки между прямыми ${{l}_{1}},\;{{l}_{2}}$ берется максимальная из длин дуг ${{d}_{1}},\;{{d}_{2}}$.
Введем пороговое значение на максимальную погрешность $T = \alpha {\kern 1pt} n$, пропорциональное линейному размеру изображения и будем считать, что прямая была оценена ошибочно, если $e({{l}_{1}},{{l}_{2}}) > T$. Таким образом, например, зафиксировав $\alpha = 0.1$, считается, что прямая определена с ошибкой, если ее невязка с референтной прямой превышает $0.1{\kern 1pt} n$ пикселей.
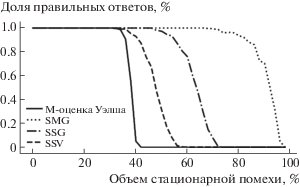
Зависимость точности линейной регрессии от величины стационарной помехи. В рамках эксперимента оценивалась точность алгоритмов, основанных на предложенном методе и алгоритма, вычисляющего М-оценку Уэлша, в зависимости от объема стационарной помехи в исходных данных. Точность алгоритма определена через долю правильно оцененных параметров прямой на выборке двумерных гистограмм. Тестовая выборка состояла из гистограмм, созданных путем моделирования и приближенных к реальным гистограммам срабатываний детектора колес в АКТС. Значения параметров моделирования и описываемого эксперимента приведены в табл. 1. Примеры получаемых описанным путем гистограмм приведены на рис. 11. На рис. 12 приведены оцененные зависимости долей правильных ответов алгоритмов от доли числа точек стационарной помехи на интервале от 0 до 98% от всех данных. Как видно из графиков, референтный алгоритм среди всех рассмотренных наименее устойчив к стационарному выбросовому шуму и при экстремальных значениях шума его точность равна нулю. Алгоритмы, основанные на предложенном методе, демонстрируют существенно большую устойчивость, причем наилучшие показатели на рассматриваемых данных наблюдаются у алгоритма с критерием суммы модулей градиентов (SMG).
Таблица 1.
Параметры имитационного моделирования и экспериментов
| Параметр | Обозначение | Значение |
|---|---|---|
| Максимальное значение x, y координат точек | m | 512 |
| Размер стороны гистограммы | n | 100 |
| Количество регулярных точек | N | 800 |
| Максимальный тангенс наклона прямой | $\left| {{{k}_{{\max }}}} \right|$ | 0.1 |
| Дисперсия аддитивного шума точек | ${{\sigma }^{2}}$ | 225 |
| Количество точек стационарной помехи | ${{M}_{{\min }}}, \ldots ,{{M}_{{\max }}}$ | 0, 16, …, 39200 |
| Дисперсия координат помехи | $\sigma _{c}^{2}$ | 100 |
| Количество равномерно распределенных выбросов | K | 5 |
| Объем выборки | V | 300 |
| Коэффициент порога на максимальную невязку прямых | α | 0.1 |
Рис. 11.
Примеры гистограмм синтезированных данных с различными степенями загрязненности стационарными помехами: а – 30% выбросов; б – 50% выбросов; в – 70% выбросов.

Рис. 12.
Зависимость точности алгоритмов линейной регрессии от доли числа точек стационарной помехи от всех данных.
Влияние алгоритмов локализации траектории движения колес на качество автоматического классификатора. Алгоритм на основе предложенного метода регрессии с критерием суммы модулей градиентов был встроен в модуль подсчета количества колесных осей системы АКТС для локализации траектории движения колес. Проводили сравнение качества определения количества осей в зависимости от алгоритма локализации траектории: алгоритма на основе М-оценки Уэлша и предложенного.
Тестовый датасет
Эксперименты по оценке качества проводили на двух выборках видео с проездами автомобилей, полученных с камер АКТС. Первая состояла из 293 видео с 4143 проездами автомобилей, записанных за длительный период с большой вариативностью условий наблюдения и классов транспортных средств. На проездах в данной выборке либо нет систематических ошибок детекторов, образующих стационарные помехи, либо они не существенны. Вторая выборка состояла из 13 проездов, на каждом из которых присутствовали стационарные помехи. В среднем приблизительная оценка доли помехи составляла около 60%, минимальное и максимальное значения – 35 и 78% соответственно. Среди доступных записанных видеопроездов с экстремальными помехами мало (единицы), однако, действительная частота воспроизведения подобных ситуаций в реальной эксплуатации, строго говоря, неизвестна. В связи с этим вторая выборка пополнялась проездами, записанными при помощи полнофункционального макета программно-аппаратного комплекса АКТС (Коптелов и др., 2014) (рис. 13, а). Для воспроизведения ситуаций со стационарными систематическими ошибками детекторов колес использовали тестовый объект радиальной формы, помещенный в поле зрения камеры. Пример кадра с камеры макета приведен на рис. 13, б. Примеры гистограмм детекций колес, получаемые на тестовых данных с систематическими ошибками, приведены на рис. 14.
Результаты экспериментов
В табл. 2 приведены количества ошибок интегратора на выборках со стационарными помехами и без. Число ошибок измерялось на подвыборке правильно детектированных системой проездов ТС (4118 и 13 для первой и второй выборок соответственно), которая идентична для версий системы с разными алгоритмами локализации траектории. Из результатов тестов можно видеть, что на выборке со стационарными помехами с алгоритмом локализации на основе М-оценки Уэлша интегратор отработал с ошибкой на 12 проездах из 13, а с использованием предложенного алгоритма число ошибок неверной оценки числа осей снизилось до двух. Стоит отметить, что в этих двух случаях траектория была локализована предложенным алгоритмом верно, а причина ошибки подсчета числа осей связана с изначально малым количеством срабатываний детектора колес на одной из осей. При этом на выборке из 4118 правильно детектированных проездов, на которых не наблюдаются стационарные помехи детектора, число ТС, для которых число колесных осей было измерено с ошибкой, также уменьшилось с 90 до 86. Данные результаты показывают, что предложенный алгоритм в отличие от референтного обладает устойчивостью к ошибкам детектора колес, образующих экстремальные стационарные помехи, при этом не приводит к ухудшению качества модуля АКТС на проездах без таких ошибок.
ЗАКЛЮЧЕНИЕ
В работе рассмотрена задача двумерной робастной линейной регрессии в условиях наличия стационарных помех. Данная задача возникает, например, на этапе локализации траектории движения колес в модуле подсчета количества колесных осей АКТС, где стационарная помеха может возникать вследствие систематических ложноположительных срабатываний детектора на статичном образе. В данной работе рассмотрено условие экстремальности стационарной помехи, т.е. такое, при котором число точек помехи превышает число регулярных данных. Предложен новый метод линейной регрессии, устойчивый к экстремальной стационарной помехе. Метод основан на хаф-анализе двумерной гистограммы входного облака точек, трудоемкость алгоритмов, основанных на данном методе и рассмотренных в работе, составляет $\Theta ({{n}^{2}}\log n)$, где n – линейный размер входной гистограммы. Результаты экспериментов показали, что алгоритмы линейной регрессии на основе предложенного метода имеют существенно большую точность регрессии в условиях наличия стационарной помехи, чем алгоритм, приближенно вычисляющий М-оценку Уэлша, при этом сохраняя асимптотическую вычислительную сложность. На выборке проездов автомобилей, на которых наблюдались ошибки детектора, формирующие экстремальные стационарные помехи, показано, что использование предложенного алгоритма для локализации траектории движения колес приводит к снижению числа ошибок подсчета количества колесных осей в сравнении с вычислением М-оценки Уэлша без потери качества на выборке проездов, где помехи не наблюдались.
Список литературы
Григорьев А., Гладилин С., Ханипов Т., Коптелов И., Бочаров Д., Мацнев Д. Архитектура системы детекции и классификации автомобилей средствами технического зрения в естественных условиях Сенсорные системы. 2017. Т. 31. № 1. С. 72–84.
Ершов Е., Асватов Е., Николаев Д. Робастная ортогональная линейная регрессия для маломерных гистограмм Сенсорные системы. 2017. Т. 31. № 4. С. 331–342.
Коптелов И., Григорьев А., Ханипов Т., Емельянов С., Николаев Д. Макет автоматического классификатора транспортных средств. ИТиС 2014 ИППИ РАН. 2014. С. 350–356.
Amin A., Fischer S. A document skew detection method using the Hough transform Pattern Analysis & Applications. 2000. T. 3. № 3. C. 243–253.
Baird H.S. The skew angle of printed documents Proceedings of SPSE 40th Symposium of Hybrid Imaging Systems. 1987. C. 739–743.
Bezmaternykh P., Nikolaev D., Arlazarov V. Textual blocks rectification method based on fast Hough transform analysis in identity documents recognition Tenth International Conference on Machine Vision (ICMV 2017). International Society for Optics and Photonics, 2018. T. 10696. C. 1069606.
Grigoryev A., Bocharov D., Terekhin A., Nikolaev D. Vision-based vehicle wheel detector and axle counter, Proc. 29th Europ. Conf. Model. Simulat., 2015. C. 521–526.
Huber P. J. Robust statistics. Springer Berlin Heidelberg, 2011. C. 1248–1251.
Hull J. J. Document image skew detection: Survey and annotated bibliography. Document Analysis Systems II. 1998. C. 40–64.
Khanipov T., Koptelov I., Grigoryev A., Kuznetsova E., Nikolaev D. Vision-based industrial automatic vehicle classifier. Seventh International Conference on Machine Vision (ICMV 2014). International Society for Optics and Photonics, 2015. T. 9445. C. 944511.
Li S., Shen Q., Sun J. Skew detection using wavelet decomposition and projection profile analysis Pattern recognition letters. 2007. T. 28. № 5. C. 555–562.
Limonova E., Bezmaternykh P., Nikolaev D., Arlazarov V. Slant rectification in Russian passport OCR system using fast Hough transform Ninth International Conference on Machine Vision (ICMV 2016). International Society for Optics and Photonics, 2017. T. 10341. C. 103410.
Nikolaev D., Karpenko S., Nikolaev I., Nikolaev P. Hough transform: Understimated tool in the computer vision field, Proc. 22th Europ. Conf. Model. Simulat., 2008. C. 238–246.
Papandreou A., Gatos B. A novel skew detection technique based on vertical projections 2011 International Conference on Document Analysis and Recognition. IEEE, 2011. C. 384–388.
Postl W. Method for automatic correction of character skew in the acquisition of a text original in the form of digital scan results. 1988. Patent No. 4,723,297. U.S.A.
Rousseeuw P. J. Least median of squares regression Journal of the American statistical association. 1984. T. 79. № 388. C. 871–880.
Rousseeuw P. J., Leroy A. M. Robust regression and outlier detection. John wiley & sons, 2005. T. 589.
Rousseeuw P. J., Van Driessen K. Computing LTS regression for large data sets Data mining and knowledge discovery. 2006. T. 12. № 1. C. 29–45.
Srihari S. N., Govindaraju V. Analysis of textual images using the Hough transform Machine vision and Applications. 1989. T. 2. № 3. C. 141–153.
Stahlberg F., Vogel S. Document skew detection based on hough space derivatives 2015 13th International Conference on Document Analysis and Recognition (ICDAR). IEEE, 2015. C. 366–370.
Дополнительные материалы отсутствуют.
Инструменты
Сенсорные системы