Сенсорные системы, 2020, T. 34, № 3, стр. 226-253

ВВЕДЕНИЕ

В статье, предлагаемой вниманию читателей, в общих чертах рассмотрены и на материале компьютерных реализаций обсуждены новые аспекты (идеи, сценарии задач и численные схемы их решения) развития темы, отраженной в цикле авторских работ по опознанию формы объекта по плоской центральной его проекции инвариантно к группе дробно линейных (проективных) преобразований картинной плоскости объекта в 3D пространстве. Объекты этого объемного исследования – кривые семейства овалов (О) – плоские гладкозамкнутые фигуры (не предполагающие формул аналитического описания, общих для семейства О, и не включающие опорных элементов контура О, традиционно используемых в распознавании фигур по особенностям их геометрии, – наподобие точек излома, перегиба, спрямления, двойного касания и проч.). Развитые технологии обработки изображений приобрели ныне статус фундаментальной науки с мощной алгоритмической базой методов обнаружения, подчеркивания и сглаживания границ, в силу чего в рамках этого текста нет необходимости в обсуждении приемов получения “продукта анализа” для данного исследования (тем более – при описании развиваемых теоретических положений, конкретно соотносимых с разделами проективной геометрии 2D кривых): собственно границы О как геометрической характеристики объекта обработки, поставляемого для “практической задачи его опознания/классификации”. В основном нас будут интересовать численно реализуемые подходы (устойчиво воспроизводимые особенности модельных экспериментов) в соотнесении аналитического задания кривой, представляющего границу фигуры, с теми способами ее обработки, что в финале должны обеспечить инвариантное описание О, т.е. к возможности классифицировать разнообразные гладкие фигуры, относя их к проективно эквивалентным выборкам, либо к формированию “эталонного образа” О для технических нужд (практических задач автономного распознавания).

Анализ данных теоретического плана, полученных на примере О в последние годы (Савчик, Николаев, 2016, теорема 1; Балицкий и др., 2017, теорема 2; Савчик, Николаев, 2018, теорема 3), в сочетании с подробно изученными особенностями T-поляры (носителя проективно инвариантных свойств композиции “О + intP”) и H-поляры (о ней – далее), обеспечил новые подходы в процедурах поиска проективно стабильных элементов О, добавив к “номенклатуре” эллиптических точек (ЭТ) (они инцидентны позициям пересечения T- и H-поляр; о свойствах ЭТ и необходимом их числе – теорема 1) новую разновидность инвариантных точек – дуальные пары (ДТ, простейшую их локализацию и минимальный набор – на прямой extL, внешней для О, – декларирует теорема 2), что и привело к построению системы универсальных процедур обработки (т.е. формирования инвариантного описания объектов) сцен, являющихся композицией овальной кривой О с фиксированной точкой intP. Реализованные схемы вычисления инвариантных функций (вурф-функций) на носителях T- и H-поляре связали характерные особенности ЭТ и ДТ, ранее предполагавшихся подчиняющимися ничем не связанным закономерностям рода необходимых признаков их существования (теорема 1 и теорема 2; о перспективных выводах “по следам” теоремы 3 будет рассказано далее, в связи со сценарием “О + extP”). Новый подход с объединением вычисления ЭТ и ДТ оказался осуществимым благодаря исследованным (в предшествующей работе цикла; Николаев, 2019) свойствам T-поляры в качестве носителя ДТ. Тем самым на эмпирическом модельном материале был расширен (за грань свойств объекта еxtL) список уже не обязательно прямолинейных носителей ДТ, гарантировавших их наличие – согласно теореме 2 – на прямой L произвольного внешнего расположения. Вместе с этим ограничением исчезла и необходимость деклараций обязательного выполнения условий коллинеарности для триады ЭТ, чтобы именно с прямой еxtL, инцидентной триаде, связывать поиск ДТ: квартет ДТ (две пары ДТ независимого положения) может принадлежать и T-поляре, т.е. наличие единственной фиксированной позиции intP в поле фигуры порождает как саму T-поляру, так и наличие дискретных “нульмерных” носителей проективно инвариантных свойств ЭТ и ДТ (в числе – не менее трех для ЭТ и в большинстве случаев – четырех для ДТ). Эволюция подходов, расширивших функции T-поляры, отражена в последних публикациях данного цикла. Перейдем к рассмотрению функциональных особенностей, обнаруженных у H-поляры, для которой удалось показать, что и она является носителем не менее двух пар ДТ.

Прежде чем перейти к описанию новых свойств H-поляры, уведомим читателя о том, что данный текст адресуется автором широкому кругу интересующихся проблемами машинного анализа формы, в том числе не сведущим в языке и задачах современной математики. Для понимания существа излагаемых проблем и результатов достаточно ориентироваться в поле представлений естественнонаучного плана (основы геометрии, гештальт-психология, физиология зрения и проч.). Авторские декларации (эвристической природы или теоремного характера) будут донесены здесь в образной геометрической форме. Исчерпывающее понимание смысла приводимых нотаций, численных схем и приемов обработки не обязательно для уяснения содержательной логики обсуждаемых тезисов. Статья не предполагает пошагового описания алгоритмов и реализующих их вычислительных программ (согласно профилю издания): текст иллюстрирован примерами результатов компьютерного моделирования (разных сценарных постановок), снабженных подробными комментариями, что должно удовлетворить неспециалистов.

1. ОВАЛ ОБЩЕГО ВИДА С ВНУТРЕННИМ ПОЛЮСОМ P И СВОЙСТВА H-ПОЛЯРЫ

Инструмент проективно инвариантного анализа кривых семейства О, названный H-полярой, детерминирует внутренняя точка P поля фигуры. Она появляется либо в качестве априори фиксированной для О общего вида, не имеющего особенностей рода скрытой симметрии (трех видов; Николаев, 2014; Николаев, 2016), либо в виде случайным образом выбранной позиции, названной “тестовым полюсом P”, – для итерационной процедуры поиска (на входной проекции О) элементов симметрии (оси симметрии с уникальной проективно инвариантной точкой на ней либо центра радиальной симметрии). Таким образом, в рамках данной статьи не возникает необходимости обсуждениия идей и численных методов, связанных с обработкой и проективно инвариантной репрезентацией О, имеющих “скрытую” либо “явную” (в виде представления О в его ортоформе) симметриями, достаточно понимания, что адекватно завершившийся поиск ее элементов (центра либо уникальной точки оси; эти процедуры подробно описаны в завершенных публикациях ведущегося цикла исследований) и есть поставщик той фиксированной для О позиции точки P, каковая образует исходный сценарий (“О + intP”) рассматриваемой здесь задачи. Итог таков: появление в поле фигуры О дополнительно заданной позиции P может иметь отнюдь не единственную реальную причину.

Алгоритм генерации H-поляры (криволинейной проективно замкнутой кривой, в дискретном случае аппроксимируемой цепью точек, уходящих в несобственную область плоскости фигуры О) таков: хорда, “по индексу n дискретно вращаемая” вокруг P (как коллинеарная триада точек, где две по разные стороны от P принадлежат контуру О) доопределяется вычислением внешней (четвертой, им коллинеарной) точки h_n согласно закону гармонического соответствия пары контурных на хорде – паре P, h_n. Цепь {h_n} и образует ломаную H-поляры (в “идеале” непрерывного представления – гладкую кривую). Если же вычислять положения в цепи “четвертых внутренних точек”, то внутри О (не соприкасаясь с его границей) будет сформирована гладкая замкнутая кривая, названная “гармоническим контуром” (HC; это второй функционально полезный “клон” H-поляры, удобный тем, что HC не простирается в несобственные области плоскости О, где велик координатный шум для процедуры вычисления образа поляры). Показано, что “внешней” H-поляре инцидентны два сорта проективно инвариантных точек (нами предложены универсальные методы их поиска): “эллиптические” (ЭТ), числом не менее трех (доказана теорема 1 их существования для произвольного расположения intP в поле фигуры, с локализацией ЭТ в позициях пересечения с T-полярой, сгенерированной для той же самой intP), и “дуальные” (была доказана теорема 2 существования для внешней фиксированой прямой extL – с числом не менее двух пар ДТ). Накопленной статистикой последующих компьютерных тестов “список источников проективно устойчивых точек” был расширен их новым потенциальным носителем: добавлением – по принадлежности H-поляре. Этому выводу предшествовали серии численных модельных демонстраций (Николаев, 2019) с “показанной эмпирически” возможной заменой прямолинейного внешнего носителя extL произвольной ориентации (что составляет содержательную часть теоремы 2) на кривую априори заданной схемы построения: на T-поляру, детерминируемую позицией полюса intP относительно координат границы О общего вида.

Требуют уточнения два обстоятельства. Понятие “дуальности” (с синонимом – двойственность) привнесено из наследия одного из творцов проективной геометрии – Плюккера, с его доктриной полюс-полярного соответствия для коник (кривых второго порядка, известным примером которых является эллипс) и фундаментальной “теоремой взаимности” для них (Глаголев, 1963; Моденов, 1969). Независимые тезисы этой теоремы (проявление дифференциально-тангенциальных свойств, присущих касательным к конике, и метрически инвариантные свойства их композиций в виде гармонизма отношений) и побудили автора к введению в аппарат анализа О двух независимых инструментов: “на языке касательных формируемую” T-поляру и подчиняющуяся законам гармонических отношений H-поляру. Зеркальная симметрия положений внутренних и внешних полюса и поляры (плюккерова прямолинейная поляра соответствует прямой, проходящей через две точки касания к эллипсу из внешней точки полюса; в силу подобной связи их позиции взаимно однозначны) в соотнесении с возможностью их сепаратного использования для описания свойств О посредством привлечения T- и H-поляр была рассмотрена в работе (Акимова и др., 2014), где показано, что для диспозиции “внешний полюс, внутренняя поляра” их однозначная связь у О общего вида сохраняется, но по полюсу внутреннего расположения вычислить для О его плюккерову поляру невозможно (формализм ее генерации, заявленный для коник, к О неприменим). Однако возможно из деклараций теоремы взаимности “вычленить такой тезис дуальности отношений”, где всеобщность связи позиций двух полюсов и двух (плюккеровых) поляр в случае с О “сузится” до связи уже уникальной: по некоторой позиции extP1 для О можно пытаться найти такую extP2, что поляра первой пройдет через extP2, при том, что полюс extP1 окажется лежащим на поляре второго полюса. Эти два полюса произвольного внешнего (для О) расположения и стали исходным носителем дуальных свойств в теореме 2: доказано, что на прямой extL произвольного положения по отношению ко всякому О обязательно существует не менее двух пар таких проективно инвариантных ДТ. Для большей внятности дальнейших описаний осталось “дать формулу” гармонического отношения, как важного частного выражения для фундаментального проективного инварианта, здесь именуемого “вурф” (в современных математических работах его чаще называют “сложным отношением четверки точек на прямой”, что является антитезой аффинному инварианту “простого отношения триады коллинеарных точек”).

Какая операция над координатами четверки точек на прямой задает на ней вурф, и среди прочих вурфов чем же замечателен “гармонический” (математики говорят более развернуто: “две пары четверки вурфа находятся в гармоническом соответствии, а пара не может быть образована соседними точками”)? Для простоты ограничимся определением вурфа через длины отрезков, на которые прямую разбивает квартет ее точек (т.е. дадим формулу вычисления модуля вурфа, где знак при численном инварианте, формируемом из ориентированных отрезков, проигнорирован). Обозначив через a, b и c длины отрезков в последовательной их маркировке (направление ее безразлично, существенно лишь, что наличествует окаймляемый отрезок b и пара “крайних”), запишем выражение сложного отношения w в виде w[a, b, c] = a*c/((a + b + c)*b), что и дает всегда “безразмерное” число при любой размерности длин. Гармоническим (в этой форме вычислений) называется вурф, удовлетворяющий условию w[a, b, c] ≡ 1, что реализуется, к примеру, радикально отличающимися композицями w[3, 1, 2] и w[x, x, ∞] с близкими и бесконечно далекой позицией одной из точек квартета (она то и называется несобственной; чтобы придать невообразимо удаленным точкам конечное численное выражение, Ю. Плюккер разработал специальную систему проективных координат, повсеместно используемую и ныне).

Далее будет показано, что каждая ЭТ H-поляры (совместное свойство с T-полярой) детерминирует на контуре О квартет (четверку) проективно инвариантных позиций. Любая пара ДТ также задает (присущий лишь ей) квартет стабильных точек на нем (свойство, монопольно реализуемое несколькими парами ДТ H-поляры). Слово квартет является для обоих случаев ключевым, поскольку понятным образом выводит на конечную цель манипуляций с проективно инвариантными точками: для решения задачи распознавания фигур семейства О необходимо получить образ О, неизменный при сменах ракурса его оптической регистрации, т.е. создать эталон, единый для класса проективно эквивалентных О. Одной из адекватных форм такой эталонной репрезентации О заявлена операция проецирования входного О на некий “стандартный 4-вершинник” (квадрат либо ромб фиксированного расположения), что просто и однозначно реализуется решением линейной системы восьми уравнений, поскольку всегда возможно координаты найденного стабильного квартета (это восемь полученных для них численных оценок; желательно не путать распределенный квартет вершин границы О с коллинеарными квартетами вурфов в их качестве вспомогательных построений по ходу решения задачи) превратить в диспозицию эталонного четырехвершинника, совершив проективное преобразование плоскости О (а оно задается восемью неизвестными независимыми коэффициентами).

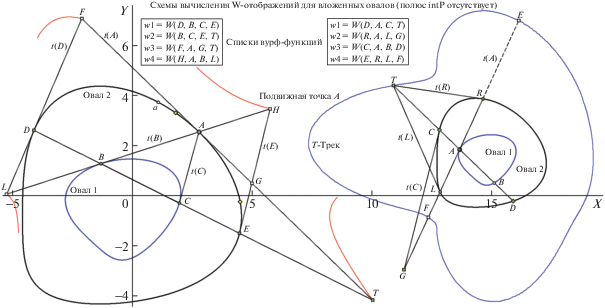
Напомним механизм генерации T-поляры в контексте использования касательных к контуру О – с целью вычисления второй формы его инвариантной репрезентации: в виде вурф-отображения (рис. 1). Любая точка A контура позволяет вычислить положение точки B, лежащей на прямой A–F по другую сторону от фиксированной F и принадлежащей контуру. T-полярой будем называть геометрическое место цепи точек пересечения пары касательных к овалу в “текущих” A и B, т.е. “дискретное вращение” хорды A-B вокруг полюса F и порождает (при сменах номера вершин аппроксимации О) цепь точек криволинейной T-поляры. T-поляра всегда расположена целиком по одну сторону от асимптоты, проходящей через F, терминально удаляется в зону несобственных значений координат и обладает свойством двойного самопокрытия, так как смена A_i позицией B_i в итоге последовательного обхода i вершин не меняет локализацию вершины T_i у T-поляры. Если для каждой T_i сделать оценку численного значения вурфа W(T_i, C_i, F, D_i) (на рис. 1 текущий квартет вычисляемого вурфа маркирован на левом О литерами T1, C, F, D), то необходимым и достаточным признаком наличия ЭТ в некой особой T_j будет условие гармоничности квартета для нее. Квартет образуют T_j, C_j, F и D_j (а C_j и D_j принадлежат контуру в пересечениях с прямой T_j-F), и условие гармоничности может быть численно выражено “в длинах отрезков” согласно правилу: │T_jC_j│*│FD_j│/(│C_jF│*│T_jD_j│) = 1. Производя для каждой i-й вершины T-поляры оценку вурфа W(T_i, C_i, F, D_i), мы сформируем в результате вурф-функцию w1(i), которая не менее трех раз (согласно теореме 1) примет значение, равное 1, фиксируя при этом каждую позицию ЭТ. Таким образом, инициирующая пара A_i, B_i контура детерминирует на нем пару C_i, D_i , входящую в квартет для функции w1(i) (в точках, не принадлежащих к разряду гармонических, w1(i) будет принимать значения, не равные 1). Для того, чтобы вычислить вурф-отображение для О, необходима, по крайней мере, еще одна вурф-функция, не зависимая от описанной выше (и имеющая массив аргументов, полностью совпадающих с массивом первой). W-отображение строится “поточечно” в декартовой системе, где координатами каждой i-й точки является пара значений (w1(i), w2(i)), т.е. вершины цепи отображения, являясь численными оценками двух независимых вурфов, принадлежащих общей для них точке контура О, образуют замкнутую ломаную (в непрерывном представлении гладкую кривую с возможно немалым числом самопересечений). Идея получения дополнительных вурф-функций по рассматриваемой здесь схеме “заодно” обеспечивает не только доступность формирования нескольких вурф-отображений V(i) (на рис. 1 в рамочке слева внизу для четырех “сконструированных” вурф-функций они фигурируют как V1, V2 и V3), но и реализует (в рамках той же процедуры) задачу поиска ЭТ и ДТ, что дает “на выбор” ряд вариантов инвариантной репрезентации О в форме эталонирования на четырехвершиннике. Рассмотрим детальнее идею и “функциональные выгоды” вычисления дополнительных вурф-функций (в краткой записи используем для них форму “W-функции”).

Рис. 1.

Схемы вычисления (для овала О с заданным полюсом F) W-функций w1(i), w2(i), w3(i) (слева) и w4(i) (справа) с показом: участков H- и T-поляр, списка структурных формул вурфов для W-функций (в рамке слева вверху) и цепи операций со служебными точками, задающими сет вурфов для i-го шага переборного процесса схем (в рамке внизу).

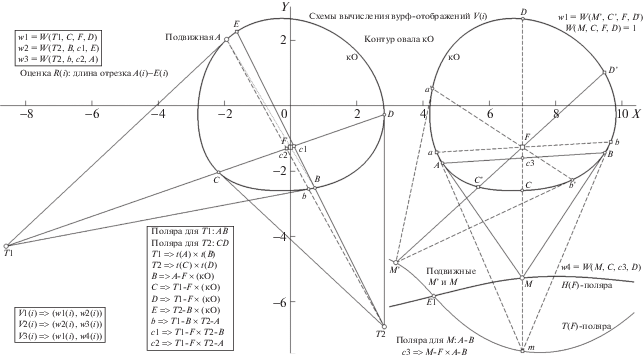
Первая и четвертая W-функции (w1(i) и w4(i)) вычисляются по правилам “обратной симметрии”: из вершин T-поляры производят оценку вурфа на луче через ее полюс F (т.е. контурная пара C, D луча из T1 “проверяется на гармонизм” относительно пары T1, F; и, как сказано выше, при выполнении условия W(T_j, C_j, F, D_j) = 1 j-я вершина T-поляры приобретает статус ЭТ), тогда как на H-поляре (показано на правом О рис. 1) вычисляется w4(i) по схеме для T-поляры (т.е. для каждой ее вершины M находят плюккерову поляру A-B и точку ее пересечения c3 с лучом M-F. Тогда для некой k-й вершины H-поляры при выполнении условия W(M_k, C_k, c3_k, D_jk) = 1 зафиксируется условие “совпадения” c3_k = F, что “даст сигнал” о статусе вершины k – тип ЭТ. Вывод из сравнительного описания для оценок w1(i) и w4(i) можно сделать такой. Если W-функции w2(i) и w3(i) (о них – ниже) в любом случае полезны для оценки (при выполнени условия w2(t) = w3(t) они маркируют все ДТ), то “разработчик системы распознавания О” вправе выбрать для подзадачи “поиск ЭТ” в альтернативе “w1(i) либо w4(i)” вычислительно более оптимальный вариант. При условии, что для системы выбран подход “репрезентация О через эталон 4-вершинник”, а не с использованием W-отображения, нет необходимости комплектовать сет из четырех W-функций, достаточно избрать эталонирование по одной паре ДТ либо по одной ЭТ (в первом случае потребуется вычислить w2(i) и w3(i), тогда как в варианте привлечения ЭТ достаточно выбрать ее носитель в виде H-поляры (новый метод) либо T-поляры (метод, ранее нами описанный). Трудность “ставки на единственную ЭТ” (не будем обсуждать детали этой задачи) в проблеме выбора из потенциального сета таковых “всегда одной и той же” ЭТ, т.е. возникает “комбинаторная громоздкость эталонирования”.

На примере “свойства T-поляры – для поиска ДТ” (рис. 1, левый О) опишем схему формирования W-функций w2(i), w3(i) (разработанный и испытанный метод для носителя H-поляры более громоздко иллюстрируется и труднее комментируется, хотя модельная итоговая разметка ДТ на H-поляре будет неоднократно фигурировать на рисунках далее). Вернемся к рис. 1, отметив, что однозначному пониманию конструктивных деталей в описании шагов вычисления W-функций могут в значительной степени поспособствовать комментарии к операциям (вынесенные в рамки), нотация для которых проста и невелика. Например, запись “T1 ⇒ t(A) × t(B)” означает “точка T1 вычисляется на пересечении касательных t в позициях A и B”, а выражение “B ⇒ A–F × (кО)” следует понимать, что позиция точки B должна быть вычислена на пересечении прямой, проходящей через A и F, с контуром О. Вместо кривой кО может “понадобиться” прямая, если описывается шаг вычисления координат точки пересечения пары прямых: “b ⇒ T1–B × T2–A”.

После разъяснения о записи операций в процедурах построения функций перейдем к непосредственному изложению последовательных шагов этого процесса. На луче T1–F (он формирует w1(i)) найдены позиции С и D контура О, для которых можно вычислить точку T2 пересечения касательных в них. Если далее “направить” из T2 луч через B и найти пересечения E с контуром и c1 с лучом T1–F, то появится коллинеарный квартет T2, B, c1, E, задающий W-функцию w2(i) (на рис. 1, в рамке слева вверху). Если же из T2 задать луч через “исходную текущую” A, то с двумя новыми пересечениями в b и c2 “укомплектуется” квартет для w3(i): {T2, b, c2, A}. Нетрудно понять, что при условии совмещния E и A (для некоторого номера “скользящей стартовой вершины” A) произойдет совмещение c1 и c2 с полюсом F (что отразит факт выполнения w2(i) = w3(i)) и возникнет композиция точек и прямых, следующая условиям “фрагмента теоремы взаимности” (в терминах плюккеровых полюсов и поляр): полюс T1 лежит на поляре для T2, и при этом поляра для T2 проходит через полюс T1. Образовавшаяся картина связей обеспечивает условие дуальности=взаимности: позиции T1 и T2 комплектуют (для этого “уникального” номера вершин О при их последовательном переборе) пару ДТ.

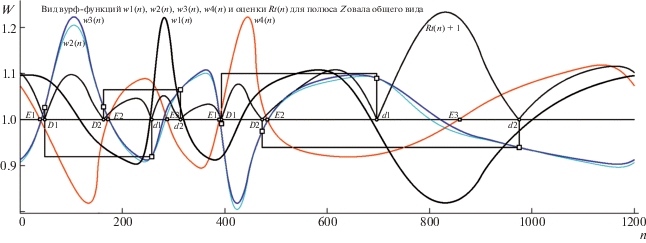
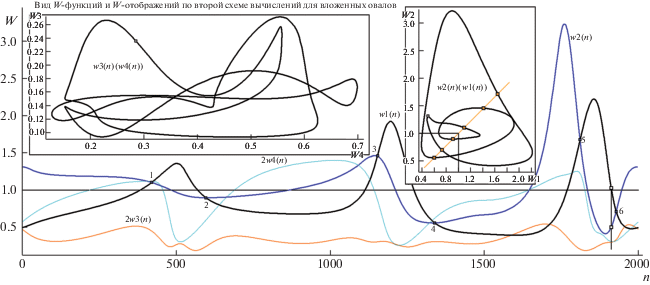
Если целью системы распознавания О заявить создание 4-эталона по паре ДТ, то не возникнет потребности в формировании самих W-функций w2(i) и w3(i). Достаточно будет “урезанной” схемы вычислений: при обходе вершин поляры=носителя делать оценку R(n) расстояния между точками контура A и E (рис. 1, левый О). Оценка R(m), близкая к 0, даст маркировку всех ДТ, причем в вершине m1 появится отсылка на дуальную m2, тогда как у m2 сформируется сигнал о m1. Таким образом, зафиксируются дуги парных связей в сете всех обнаруженных ДТ. Для полноты описания (при конкретных реализациях – возможно, избыточной) продемонстрируем вид четырех W-функций и функции R(n) + 1 (сдвиг для R(n) сделан в целях удобства масштаба общей картины) на модельном примере “О + F” по рис. 1 (рис. 2). Поскольку w2(i) и w3(i) весьма близки “по динамике”, то на рис. 2 w2(i) изображена тонкой лазурной линией, а w3(i) – утолщенной синей. Даже выбор “тонкой кривой” не дает визуально локализовать “точку” пересечения этих W-функций. Неясность легко устраняется: показ функции R(n) + 1 с высокой точностью размечает положение (номер) вершин ДТ. Для демонстрации нового метода поиска ЭТ для H-поляры нумерация вершин имеет привязку к точке M (правый О на рис. 1). Поэтому именно w4(i) фиксирует (оранжевая линия на рис. 2) ЭТ в местах ее пересечения с единичным плато. Не следует удивляться повторному размещению триады E1, E2, E3 на графике w4(i): это фактическое проявление особенности “двойное самопокрытие” (свойственной обеим криволинейным полярам), о котором было сказано выше. W-функция w1(i) (утолщенная черная линия) “не метит непосредственно” ЭТ (как это выглядит у w4(i)), поскольку нумерация ее вершин связана с “подвижной A” (О слева), а не со “скользящей M” (тот же О справа на рис. 1).

Рис. 2.

Вид четырех W-функций и кривой R(n) детекции пар ДТ для О с полюсом intF с показом связей номеров вершин ДТ в пары по условию w2(i) = w3(i) (кривые: утолщенные – черная для w1 и синяя для w3, тонкие – лазурная для w2 и черная для R+1). Остальные пояснения в тексте.

Кратко о терминологии “полюс” (он детерминирует форму обеих поляр) и “узел” (он связывает ДТ в пару) и о новом эмпирически замеченном свойстве локализации ДТ на полярах типа H и T (рис. 3, где P – это узел, а F – полюс). Не удивительно, что вурфы для квартетов {k, 8, F, 6} и {E1, 1, F, 9} гармонические: первый включает вершину k H-поляры (гармонизм – определяющее свойство ее лучей через полюс), второй – вычислен для ЭТ E1, а следовательно, также принадлежит H(F)-поляре. Интересен факт (устойчивый итог серии модельных экспериментов с разными О при вариациях положения полюса на них): ДТ близки (либо даже с машинной точностью совпадают) по номеру вершин для поляр обоих типов. На рис. 3 (врезка справа вверху) показаны графики функций Rh и Rt, задача которых – детектировать позиции ДТ на H-поляре и T-поляре соответственно. “Очевидны особенности”: пары K, D и d, k совпадают, а пары t, h и T, H “близки”. На основной карте рис. 3 эти свойства выражены позиционно: например, d и k лежат на общем луче к полюсу F, а лучи t-F и h-F (если их “мысленно провести” и сопоставить) близки расположением (тот же эффект можно заметить для лучей T–F и H–F). Авторская гипотеза относительно этого феномена такова (теорем на этот счет нами пока не доказано): “в теории” (при непрерывном, аналитическом описании поляр) “совпадения закономерны”, тогда как “неточность совпадений” – результат вычисления касательных во всех наших модельных демонстрациях по правилам, предписанным для коник (квадратичных дуг) в дискретной схеме “по пяти соседним точкам – для средней в цепочке”. Высока вероятность, что там, где кривизна дуги отличается от “квадратичной”, положения касательных определяются с погрешностью, проявляющейся в рассогласовании позиций ДТ для H- и T-поляр.

Рис. 3.

Топография пар ДТ H-поляры (h..H) и T-поляры (D..d и t..T), задающих проективно инвариантные квартеты {1÷4} и {5÷8} на контуре О, с показом кривых Rt(n), Rh(n) (для T-и H-поляр) детекции пар ДТ (на врезке вверху справа). Остальные пояснения в тексте.

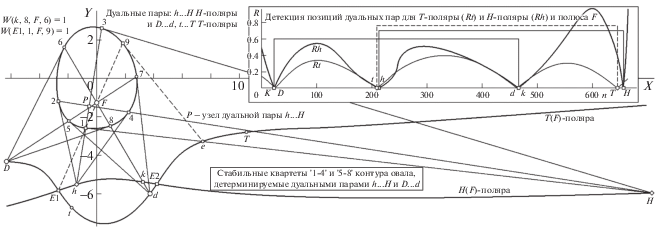
На том же рис. 3 можно проследить, как пары ДТ на H- и T-полярах задают независимые квартеты инвариантных точек контура О: у пары H, h узел P расположен на пересечении плюккеровых поляр “1–3” и “2–4” (т.е. эта пара ДТ детерминирует на О квартет {1, 2, 3, 4}), тогда как пара D, d, принадлежа T-поляре, имеет F в качестве полюса и узла, задавая квартет {5, 6, 7, 8} на плюккеровых полярах “5–7” и “6–8”. Какой квартет на контуре задает каждая ЭТ, можно понять на примере E1 (рис. 3). У E1 точки “1” и “9” принадлежат лучу, проходящему через полюс F; к ним можно добавить тангенциальную пару в виде точек внешнего касания, задающих плюккерову поляру для полюса E1.

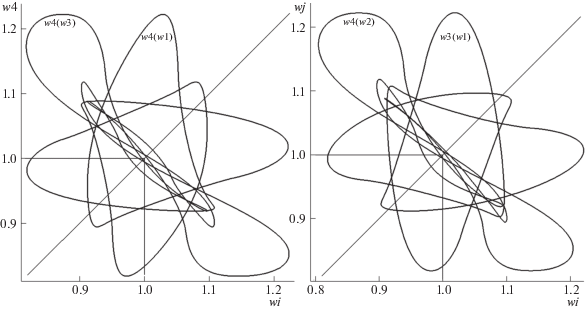
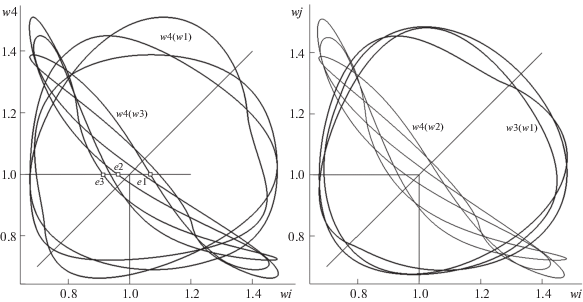
Завершим обсуждаемую тему показом картин W-отображений для двух позиций полюсов и демонстрацией вида W-функций для нового положения полюса Z, смещенного значительно (для того же О) по сравнению с уже рассмотренной позицией F. На рис. 4 изображены отображения w4(w1), w4(w3) (слева) и w4(w2), w3(w1) (справа). Показано, что номера триады ЭТ “считываются” на пересечениях кривой w4(w3) с единичной ординатой графика (что понятно: ведь w4, как было сказано выше, фиксирует оценкой “1” все ЭТ на H-поляре). W-отображения “подтверждают” также близостью формы у w4(w3) (слева) и w4(w2) (справа) малые различия W-функций w2 и w3. Рисунок 5 демонстрирует, как сильно меняется вид все той же четверки W-функций при значительном сдвиге полюса (где функция=детектор Rt(n) по-прежнему точно позиционирует все пары ДТ). Наконец, рис. 6 дает представление, как меняется форма W-отображений при смене положения полюса (он сдвинут в позицию Z, которая будет фигурировать “осмысленно” в задаче, посвященной сценарию “О + extP”). На картах рис. 6 (слева и справа) так же заметно большое сходство формы w4(w3) и w4(w2) (по той же причине близости функций w3 и w2). Перейдем теперь к обсуждению вопросов, связанных с новыми методическими предложениями в задаче инвариантного представления О с привлечением инструмента “гармонический контур”.

Рис. 4.

Вид W-отображений w4(w1), w4(w3) (слева) и w3(w1), w4(w2) (справа) с показом позиций триады ЭТ (e1, e2, e3) по единичному уровню w4. Остальные пояснения в тексте.

Рис. 5.

Вид четырех W-функций и кривой R(n) детекции пар ДТ для О с полюсом intZ с показом связей номеров вершин ДТ в пары по условию w2(i) = w3(i) (кривые: утолщенные – черная для w1 и синяя для w3, тонкие – лазурная для w2 и черная для R+1. Остальные пояснения в тексте.

Рис. 6.

Вид W-отображений w4(w1), w4(w3) (слева) и w3(w1), w4(w2) (справа), имеющх квази-радиальную симметрию (в сцене вида “О + intZ”). Остальные пояснения в тексте.

2. МЕТОДЫ ИСПОЛЬЗОВАНИЯ ИНВАРИАНТНОЙ КРИВОЙ ГАРМОНИЧЕСКИЙ КОНТУР

Рассмотрим две схемы вычисления W-функций и на их основе – W-отображений, реализующих проективно инвариантное описание объекта, представляющего собой О с полюсом P, зафиксированным в его внутреннем поле, т.е. входная сцена та же, что была нами рассмотрена в разд. 1: “О + intP”. Отличие подхода, описываемого теперь, в том, что инструментом анализа для получения репрезентации О избрана разновидность H-поляры (названная нами гармоническим контуром – HC), целиком локализуемая в поле фигуры О, а потому не обладающая при дискретном ее использовании (в технической системе) той особенностью неоднородного распределения шума квантования (связанного с падением точности вычислений при терминальном уходе в несобственную область), свойственной “внешней” H-поляре. Схем предложено и испытано две, их отличие в том, что первая три из четырех W-функций строит на внутренних пересечениях с гармоническим контуром HC, а вторая привлекает HC лишь для генерации единственной “скользящей” касательной (в виде хорды T1–T2 в точке касания a, рис. 7), так, что для оценки двух W-функций (w5 и w6) в квартеты вурфов входит по одной вершине HC (на рис. 7 она обозначена как “a”).

Рис. 7.

Схемы формирования шести W-функций (четырех слева и двух справа) с участием гармонического контура HC для полюса P и цепочки операций со служебными точками, задающими набор вурфов для i-го шага переборного процесса схем, а также и характер трех W-отображений по этим функциям (в рамках внизу). Остальные пояснения в тексте.

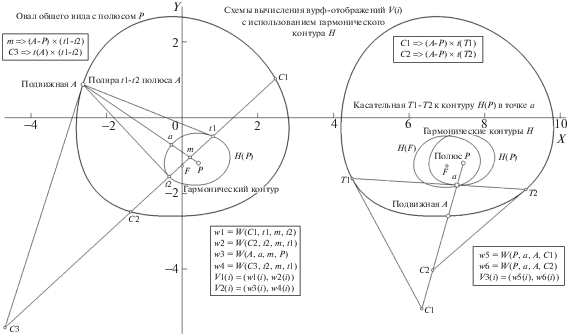
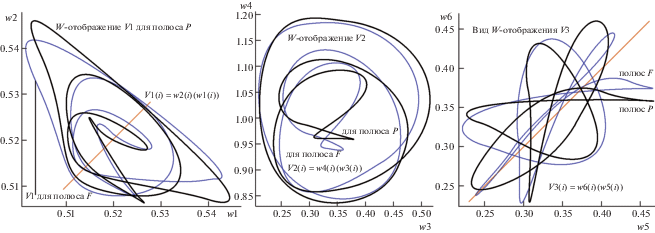
Алгоритм генерации контура HC уже был описан. Необходимо вычислить позиции четвертой внутренней точки на хорде, проходящей через P, чтобы получающийся при этом коллинеарный квартет стал гармоническим, а сама цепь “этих четвертых” (для всех вершин О на массиве хорд) – “кривой” HC. Остается лишь добавить, что форма HC не связана проективно с порождающей его кривой О, в силу чего манипуляции с вершинами HC привносят новые независимые компоненты для получения W-функций. Вернемся к рис. 7, иллюстрирующему идею и методы привлечения HC для формирования вариантов W-отображений (двух по первой схеме – V1(i) в сетке (w1(i), w2(i)) и V2(i) в сетке (w3(i), w4(i)), а по второй – V3(i) в сетке (w5(i), w6(i))). Структурные уточнения (в рамке) следуют той же нотации, что и для рис. 1 и 3. Прокомментируем первую схему (рис. 7, слева).

Для каждой A (при переборе всех вершин аппроксимации О) на HC вычисляются ее плюккеровы поляры, задающие на контуре О пару C1, C2, а на самом HC – пару t1, t2. На пересечении луча A-P с этой полярой находят m, а с самим HC – точку a. Полученный сет позиций дает возможность вычислить триаду независимых вурфов {C1, t1, m, t2}, {C2, t2, m, t1} и {A, a, m, P}, формирующих по всем i функции w1(i), w2(i) и w3(i). Четвертую w4(i) удается построить добавлением позиции C3 на пересечении хорды C1–C2 с касательной в A, что обеспечивает организацию квартета вурфа {C3, t2, m, t1} для нее. W-функция w4(i) не включает позиций C1, C2, что делает ее оценку такой же “ускоренной”, как и для w3(i).

Вторая схема имеет отличительную особенность организации, обеспечиваемую “скользящей” касательной к HC в точках пересечения a “бегущего луча” P-A с HC (рис. 7, справа). Касательная задает позиции T1, T2 на пересечениях с О, а вычисление для этой пары – касательных к О – дает возможность получения двух независимых вурф-квартетов {P, a, A, C1} и {P, a, A, C2}, используемых для оценки w5(i) и w6(i) соответственно, поскольку на луче P-A можно вычислить позиции не связанных C1 и C2 – в пересечениях внешних касательных к О. W-функции, сформированные по схеме 2 , создают возможность получения W-отображения V3 на сетке (w5(i), w6(i)) (в другой форме, по типу записи y(x), отображение можно выразить как функцию: V3(i) = w6(i) (w5(i))).

Прежде чем будет показан вид всех шести W-функций, полученных в модельных экспериментах для двух положений задаваемого внутреннего полюса (позиции P и F), нам хотелось бы коснуться темы, не отраженной (по причине ее появления пока лишь в форме идеи, требующей специального исследования) в аннотации к статье, но, вполне возможно, перспективной в плане использования для репрезентации О в форме его проецирования на 4-эталон (а также в виде малоразмерного дескриптора) и возникшей “по факту появления” (проверено на моделях сцен “О + + intP”) новых типов проективно инвариантных точек О, порождаемых наличием HC. Их можно назвать “точками симметрии”, причем у каждой из обсуждаемых схем тип таких стабильных вершин свой. Для первой схемы условием их детекции будет факт равенства (для некоторого номера s) w1(s) = w2(s); в рамках второй схемы условие их локализации (для номера t) таково: w5(t) = w6(t). Первую разновидность стабильных точек назовем “симметрично полярные” (СПТ, они из скользящего по контуру О “полюса” идентифицируются на его плюккеровой поляре к HC). Второй вид инвариантных точек можно наименовать “симметрично тангенциальные” (СТТ, так как они могут быть выявлены через равенство для триады касательных (на HC и О). На малой серии тестов наборы СПТ и СТТ исчислялись для “О + intP” магическим числом восемь.

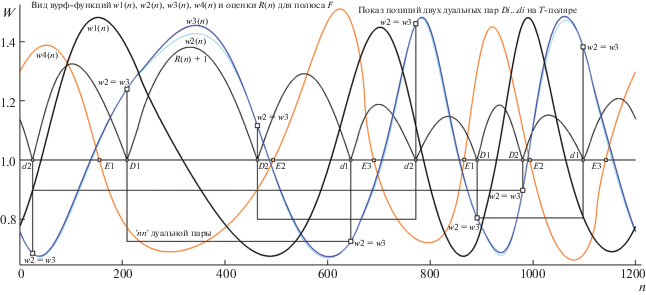
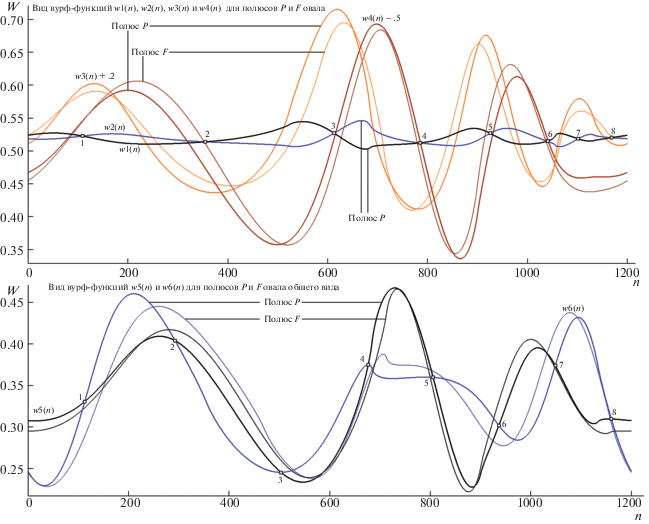
На рис. 8 объединен показ W-функций для обеих схем (по первым четырем вверху, для w5 и w6 – в нижней его части). Утолщенными линями воспроизведены функции для полюса P, тонкими – для F (позиция F показана на рис. 7). Они размечены цветом: w1 – черным, w2 – синим, w3 – оранжевым, w4 – коричневым. Для компактности изображения w3 и w4 сдвинуты по ординате: w3(n) – вверх на 0.2, w4(n) – вниз на 0.5. Отличия для w1(n) и w2(n) при переходе от P к F оказались столь малы, что показаны исключительно утолщенными линиями. W-функции w5(n) и w6(n) изображены без сдвига амплитуд, так же – линиями разной толщины (в связи с переходом от P к F), для w5(n) – черными, для w6(n) – синими. При метках “малый квадрат” (ими размечены W-функции только для случая с полюсом P) на верхней половине рис. 8 занумерован октет СПТ (в позициях восьми пересечений w1(n) и w2(n), на нижней – октет СТТ (по условию w5(n) = w6(n)). Перенеся внимание на картину W-функций для сцен, где порождающим HC является полюс F (они изображены тонкими линиями), легко убедиться, что сеты СПТ и СТТ также насчитывают по восемь проективно инвариантных точек. Остается открытым вопрос: обнаруженный на ряде модельных примеров факт – случайность или же не изученная пока закономерность?

Рис. 8.

Вид десяти W-функций в моделях сцены для двух позиций полюсов (для P и F; w3(n) и w4(n) сдвинуты для компактности картины). Остальные пояснения в тексте.

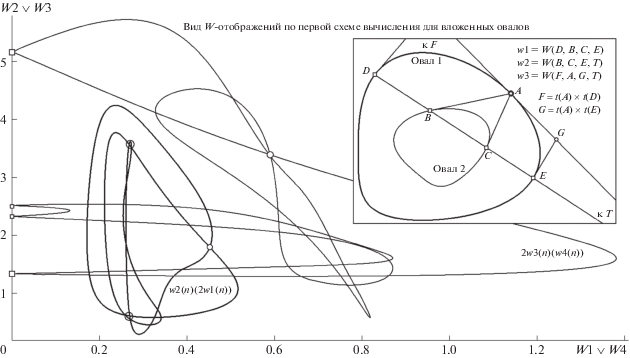
В завершение темы раздела о новых методических возможностях инструмента HC дадим наглядное представление о графическом характере W-отображений, вычисленных по шести W-функциям в той же компьютерной модели, что и все показанные выше иллюстрации. Однако исследование в направлении “привлечение HC” в задачах поиска “традиционных” ДТ выявило совершенно неожиданные решения, о чем будет сообщено в разд. 4. Сделав это предуведомление, вернемся к полученной картине W-отображений (рис. 9). Они предъявлены парами, где утолщенные линии соответствуют сцене с HC для полюса в P, а тонкие воспроизводят вид кривых для позиции F. На первой (слева) и третьей (справа) картах W-отображений тонкими оранжевыми прямыми изображены биссектрисы положительного квадранта плоскости вурфов (уравнение прямой x = y). Внимательное их прослеживание с целью подсчета числа пересечений с кривыми W-отображений дает возможность убедиться, что таковых (в том числе и у кривых, полученных для полюса F) “ровно по восемь штук”. Этой демонстрацией целевого продукта численной обработки объекта “О + intP” (проективно инвариантного описания О в форме W-отображений) закончим обсуждение новых идей и методов с привлечением контура HC. Перейдем к рассмотрению более сложных вопросов: к процедурам инвариантной обработки сцен вида “О + extP”, для чего придется “погрузиться в мир чевиан”, коснувшись сути теоремы 3.

Рис. 9.

Вид трех пар W-отображений для полюсов P и F. Остальные пояснения в тексте.

3. ПОДХОДЫ К ИНВАРИАНТНОМУ ОПИСАНИЮ СЦЕН ВИДА “О + EXTP”

Выше было замечено: в терминах плюккерового полюс-полярного соответствия для семейства О остается в силе взаимно однозначная связь (зависимость расположения) внешнего полюса extP и его поляры на О, каковой принадлежат две точки внешнего касания к О из extP. Поэтому входному сценарию “О + extP” проективно эквивалентно его описание в виде “О + intPolar”. И эту Polar без ущерба общности можно детерминировать любой парой точек, ей инцидентной (например, точками пересечения ею контура О, “чьи касательные возвращают” позицию extP, что совершенно не обязательно, ведь прямая однозначно задается произвольной парой ей принадлежащих точек).

Уже накоплен солидный набор разнообразных инвариантных элементов: “поляры прямые и кривые”, “внутренние полюса и узлы”, “стабильные вершины ЭТ и ДТ” (а “на подходе их теснят” – СПТ, СТТ,…). Тревожный сигнал: потребуется еще одно расширение рабочего инвентаря, инспирированное тезисами теоремы 3 (Савчик, Николаев, 2018). Суть возникающей проблемы не столько в “широте методических предложений” для решения задачи репрезентации О, сколько в опасениях по части их универсального характера. Надо ли слепо верить цитированным теоремам существования с их заявленной количественной гранью: “не менее n экземпляров”? Сомнения того рода, что при объединении нескольких типов стабильных точек (скажем, ЭТ и ДТ – для создания малоразмерных дескрипторов) может произойти “сбой” в гарантированном количестве элементов схемы: уже показаны (Николаев, 2019) примеры ситуаций, когда одна из ЭТ входит еще и в пару вида ДТ (т.е. оценка снизу для каждого кластера верна, хотя “пересечение множеств имеет место”).

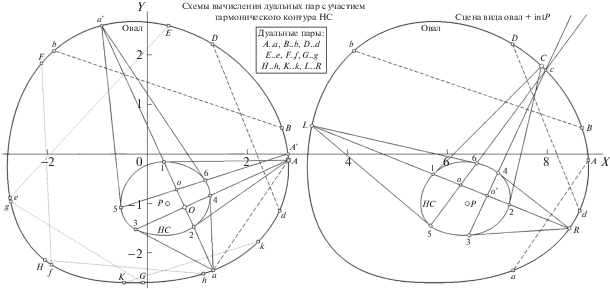
Имея в виду желательность увеличения ясности деклараций, начнем вхождение в новую тему с разбора иллюстрации методического предназначения (рис. 10). Показан О общего вида с фиксированной парой A, a на его контуре. Следовательно, эту сцену можно охарактеризовать и как принадлежащую типу “О + extP”, где в роли P (рис. 10) выступает точка E3 (о факте ее вхождении в триаду ЭТ “пока” не известно, так как о полюсе intP, задающем H-поляру, сведений также нет). Зададимся вопросом: найдется ли на поляре A-a (вне контура) точка, образующая пару типа ДТ для E3? Оказывается, таких существует больше одной. Их две, – это T и t и узел на A-a у каждой свой: это P и p соответственно.

Рис. 10.

Модель сцены с плюккеровой полярой A-a, ее полюсом E3, наличием H-поляры и двух T-поляр, заданных узлами P и p, с показом позиций пар ДТ. Комментарии в тексте.

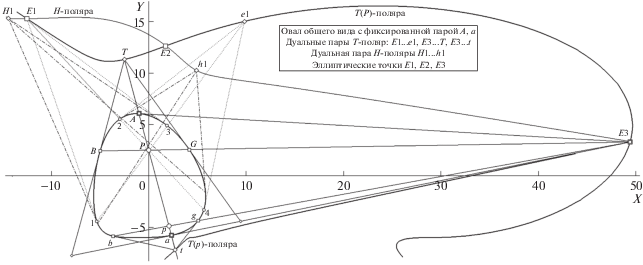
Здесь не уточняем, в каком качестве эти решения соответствуют “пороговой” декларации теоремы 3, гласящей: “если на О фиксирована пара вершин, то возможно не менее чем двумя способами дополнить такую композицию до тройки точек контура, обладающей проективно инвариантным свойством пересечения чевиан”. О природе чевиан до поры умолчим, но два квартета с общей для них парой A, a, удовлетворяющих правилам ДТ, можем указать: это {A, a, B, G} и {A, a, b, g}. Если узел P объявить полюсом для H- и T-поляры, вычислить их и произвести на них поиск пар ДТ и инвариантных точек иной природы, то итогом будет появление нескольких ансамблей. Найдется триада ЭТ (на рис. 10 – с метками “большой квадрат” и литерами E1, E2, E3 при них); на H-поляре в позициях H1, h1 зафиксируется “чистая” пара ДТ (вторая пара H2, h2 не показана на рис., поскольку расположена очень далеко от О), а также три пары ДТ “смешанной природы” на T(P)-поляре – E1, e1; E3, T и E3, t (в рамке на рис. 10 пары ДТ обозначены в форме связи “двоеточием”, а “аргумент P” в названии поляры – следствие наличия T(p)-поляры).

Этот специальным образом подобранный пример диспозиции стабильных точек должен продемонстрировать необходимость усложнения их классификации (допускающей возможность вхождения типизируемой вершины в разные кластеры): “оказывается”, две пары ДТ могут агрегироваться в триаду (T..E3..t), а ЭТ – войти в состав пары ДТ (E1..e1). При этом “эмпирические доктрины” не были опровергнуты. Действительно, две пары ДТ, объединившиеся в триаду, принадлежат разным носителям: E3..T инцидентна T(P)-поляре, тогда как E3..t дислоцирована на T(p)-поляре. В связи со сменой сценарной постановки (переход от intP к extP) новой особенностью стала структура ДТ, более не связанных с одним носителем, а получаемых для плюккеровой поляры полюса extP. Новацией стало удвоение узлов (для E3 это P и p), а “прежний квартет” стабильных вершин О заменила шестерка инвариантных точек (на рис. 10 это сет {A, G, g, a, b, B}; тем не менее, согласно старым правилам о едином носителе пара E1..e1 задает на контуре квартет {1, 2, 3, 4}, где схему ДТ компонуют пунктирные прямые). Прежде чем перейти к объединенной картине, структурирующей элементы и их отношения для О с extP, дадим определение сета чевиан, через свойство которых выражаются отношения триады стабильных точек в теореме 3.

Если вообразить для О треугольник, в который О вписан, то чевианами для этой конструкции будет являться тройка прямых, соединяющих каждую вершину треугольника с точкой касания противоположной его стороны. Поиск стабильной триады точек О в этой композиции производится подчиненно выполнению условия: три чевианы пересекаются в общей точке (внутри О, а стабильную тройку образуют, естественно, три точки касания сторон треугольника к О). На рис. 10 такую инвариантную тройку образует, например, сет {B, G, a}, в чем можно убедиться, дополнив имеющуюся картину одной вершины T для треугольника, образованного тремя касательными T–B, T–G и E3–a, двумя недостающими в пересечениях T–B и T–G с E3–a (они локализованы метками “малый ромб” без литер при них). Две чевианы из этих вершин (идущие к B и G) “обязаны” пересечься в одной точке на чевиане T–a (на рис. 10 не показано, ввиду перегрузки элементами темы ДТ).

Перейдем к обзору сводной картины инвариантных свойств композиции “О + extP” (рис. 11). Подобно обсуждавшемуся для схемы рис. 10 основной причиной возникновения у фигуры О инвариантных элементов является наличие полюса extP (который здесь имеет идентификатор C), детерминирующего позицию плюккеровой поляры A-a (названной C-полярой; уточним: метки “квадрат” для “порождающей” тройки {C, A, a} окрашены в зеленый тон). Для полюса C на его C-поляре удается найти пару позиций (T и t; имеют метки “лазурный кружок”), независимо связанных с C дуальными отношениями, иными словами, – образующих две пары ДТ (C..T и C..t). Так как прямые плюккеровых поляр B–G и b–g (они и их полюса T и t размечены лазурным тоном) проходят через C, которая со своей полярой A,a также образует дуалитет “полюс/поляра”, то C имеет вхождение в две пересекающиеся T-поляры (поименованные “T(P)-” и “T(p)-”). На C-поляре фиксируются узлы P и p (с лазурными центрами в больших кружках), каждый из которых связывает свой квартет (с общей парой A, a) на контуре О: {A, B, a, G} и {A, b, a, g} соответственно, что и обеспечивает для C детерминацию шести стабильных вершин О: {A, B, b, a, g, G}. Но помимо пары T, C на T(P)-поляре можно локализовать и пару D..d, с C не связанную и задающую свой стабильный квартет {1, 2, 3, 4} (красные метки в малых кружках).

Рис. 11.

Вид сцены с внешним полюсом C и его полярой A-a контура О с показом узлов P, p с их ДТ T, t, узла Z для решений e, q и узла z – с их чевианами. Комментарии в тексте.

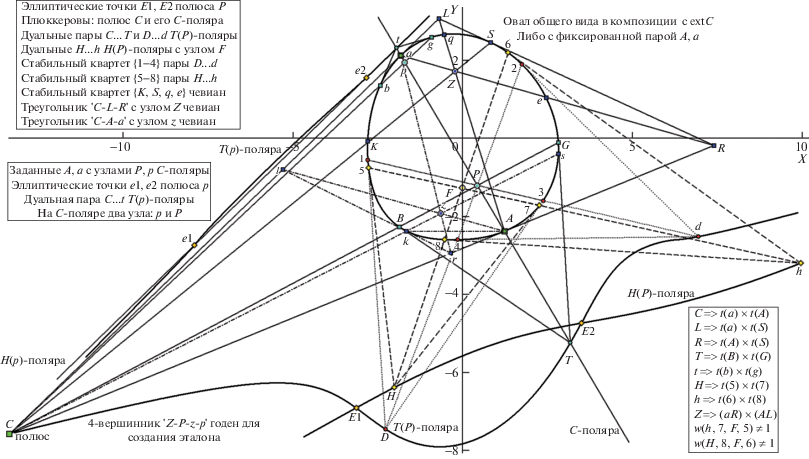
Как только определились положения полюсов P и p (узлами они являются для пар ДТ C..T и C..t, но для T(P)-поляры и T(p)-поляры они имеют статус задающих полюсов), так стало возможным вычисление H(P)-поляры и H(p)-поляры и оценка координат ДТ для них (на рис. 11 показаны желтым цветом в метках “ромб” лишь ДТ для H(P)-поляры, так как плотную сетку элементов ДТ H(p)-поляры в масштабе рис. 11 нельзя было показать “раздельно”). Вычисленные позиции ДТ пары H..h через узел F компонуют квартет {5, 6, 7, 8} (желтые малые кружки и желтый центр в большом кружке F). В поле рис. 11 удалось разместить (из-за сильной удаленности) только по паре ЭТ для полюсов P и p (E1, E2 и e1, e2, с оранжевыми метками). Заметим, что все выше сделанные комментарии для удобства ознакомления читателя со сводной схемой в отрыве от текста вынесены в рамки на полях рис. 11 (“функциональные” – слева, операционные – справа внизу). Осталось рассмотреть ситуацию с чевианами (и ими задаваемой парой стабильных квартетов на О).

Стороны описанного (вокруг О) треугольника, найденные в быстрой переборной процедуре для первого “чевианного” решения, образуют касательные в a, S и A с его тремя вершинами C, L и R. Решение (схема сканирующего перебора вершин О лучом C-S, с перевычислением касательной в S и вершин L, R в пересечениях с парой фиксированных касательных в A и a) реализует условие совместного пересечения чевиан C-S, L-A и R-a в целевой точке Z. Аналогичным образом, сканирование тем же лучом C-S, но теперь в последовательном переборе вершин О в его ближней к C точке K (с перевычислением касательной) обеспечивает для некоторой “оптимальной” вершины k формирование треугольника “l-r-s” с общей точкой z пересечения его чевиан C-s, l-A и r-a. “Фигуранты” описанной процедуры “в двух действиях” (показана реализация двух решений, наличие которых и гарантировала теорема 3) размечены синим цветом в “малых квадратах”, а два целевых узла для них (это Z и z) показаны с синим центром в “больших кружках”.

Подведем краткий итог завершенной “ревизии” накопленного материала и сделаем незамысловатые прогнозы упорядочения доложенной совокупности разноплановых идей. Была описана цепочка методов, иерархичных и ветвящихся на альтернативных вариантах. Попытаемся вычленить из нее самые новые процедурные наработки, которые, возможно, не задержались в поле внимания среди каскада усвоенных, близких по сути предложений, связанных с H- и T-полярой, как носителями инвариантных ЭТ и ДТ. Сценарий с extP дал новую постановку задачи с фиксированной парой вершин О, что открыло возможности по двум (на самом деле, – трем, но об этом – в разд. 6) направлениям технической реализации (есть новизна и в их соединении, о чем будет сообщено в конце раздела). Первый вектор развития – опора на тезис теоремы 3, дающая гарантированную возможность получать на контуре О два стабильных квартета (на рис. 11 размечена одна “синяя четверка” вершин {K, S, q, e} – для узла Z), реализуемая быстрым переборным алгоритмом, причем есть однозначная возможность оптимального выбора квартета: один (с узлом Z) – по дальней от полюса C стороне О, второй (его узел z и пара вершин – k, s – показаны) – по ближней.

Второй перспективный подход так же связан с фиксированной парой A, a (он “как бы” аналог теоремы 3, только не “чевианный”, а “дуальный”; и жаль, что пока не обрел статуса теоремы), не связан с поиском ДТ на полярах типа H и T и доставляет быстрым алгоритмом два дуальных решения B, G и b, g (в поиске полюса, дуального для C, – по разные стороны от концевых точек хорды A–a) – с однозначным выбором наилучшей модели стабильного сета: “левый квартет {b, g, a, A}”, “правый квартет {B, G, A, a}” либо “полный сет из шести вершин”. Наконец, – вкратце про объединение “чевианного” и “дуального” подходов для решения задачи инвариантной репрезентации О.

В итоге работы “чевианной” процедуры в поле фигуры (по разные стороны от фиксированной C-поляры) оказываются вычисленными узлы Z и z. “Дуальный” же поиск имеет итогом оценку позиций (на C-поляре) узлов P и p. Имеют смысл эксперименты по моделированию нового варианта репрезентации О – перепроецированием не на эталонный 4-вершинник, инцидентный границе О (как это безальтернативно предлагали мы ранее, поскольку вариант сценария с extP для задачи создания эталона не рассматривался), а на целиком внутренний 4-вершинник {Z, P, z, p}. Априорная оценка преимуществ такого подхода в том, что “информативность” кривой эталонного образа О будет распределена на этапе оценки близости классифицируемых объектов (в процедуре разделения фигур на классы проективной эквивалентности) “более изотропно”, не имея “слепых зон” вблизи четырех вершин нового эталона, более не принадлежащих контуру фигуры, как это происходило при “традиционном” перепроецировании О на квартет фиксированных (предшествующей процедурой поиска четверки проективно инвариантных точек контура О) вершин, комплектно инцидентных его границе. Повторим: это непроверенная гипотеза.

4. ГАРМОНИЧЕСКИЙ КОНТУР HC КАК ИСТОЧНИК ДВУХ ТИПОВ ДТ

Не один раз оправдавшая себя модель отношений в задаче поиска ДТ казалась единственно возможной (геометрической схемой реализации) и состояла в том, что некая наружная (по отношению к О) линия (прямая либо кривая, ограниченная в полуплоскости прямолинейной асимптотой, как это свойственно H- и T-полярам) являлась переборным поставщиком плюккеровых полюсов, прямолинейные поляры которых проверялись на наилучшее соответствие условию дуальности для некоторого удаленного полюса в ее направлении (на “периферическом” фрагменте того же носителя), что и фиксировало пару ДТ. Картина с внешним носителем полюсов – кандидатов на роль ДТ и с внутренним “полигоном” проверяемых поляр (эту роль играл контур О) натолкнула на “дикую” идею обмена ролей внешнего и внутреннего объектов переборного процесса. Так как сцена с О и контуром HC являет собой парную композицию “внешнего и внутреннего” объектов, то родилась мысль: “а не сделать ли поставщиком полюсов-кандидатов на роль ДТ саму границу О, а поведение плюккеровых поляр тестировать на овальном HC”? План инверсии ролей был успешно воспроизведен в компьютерной модели, дав два варианта реализации.

Рассмотрим схемы вычисления ДТ новых видов на примере О с заданной позицией полюса intP и контуром HC, полученным в соответствии с положением P относительно О (рис. 12). Представим в качестве плюккерова полюса проверяемую позицию A на контуре О, детерминирующую на HC его прямолинейную поляру “1–2”, пересекающую О хордой “a-a'” (левая схема на рис. 12). В итоге возникает коллизия, не имевшая прецедентов для криволинейных поляр (“тем более” невозможная для варианта с extL): на роль кандидата на статус ДТ претендуют две (!) вершины О – a и a'. Опять слом понятий – с появлением “тройной дуальности”? Большая серия модельных испытаний (разные О, с разными для них диспозициями intP) показала: “тройственная связь” вершин не под запретом, но ее вероятность близка к 0. Точность выполнения условия дуальности (гласящего: “полюс a расположен на поляре “1–2”, имеющей полюсом вершину A”; что иллюстрируется в левой половине рис. 12) у претендентов в подавляющем большинстве случаев не совпадает. Эта редчайшая ситуация не вносит “катастрофического хаоса” в процедуру поиска ДТ, поскольку решения могут быть однозначно упорядочены сепарацией на левое и правое, с протоколом альтернативного выбора. Рисунок 12 воспроизводит типовой случай: в “конкурсе на звание ДТ для A” побеждает a (тогда как поляра полюса a' “не попадает в A”, ее промах отмечен в A'). Продолжающийся последовательный перебор вершин О (на рис. 12 он идет против часовой стрелки) локализует цепь ДТ – со сменой знака ориентации по отношению к P (у A парная ей a левая, у B ее b – правая, d для D – левая; и так далее, пока не будут найдены все восемь пар ДТ – от A..a до G..g (на рис. 12 в рамке вверху перечислены все пары ДТ, в том числе и “странная” L..R нового типа, детектируемая по другому критерию, особенности которого демонстрируются на второй – правой схеме).

Рис. 12.

Схемы детекции ДТ новых типов с участием HC. Остальные пояснения в тексте.

Идея промоделированной второй схемы такова: следует искать номера вершин О, для которых поляры “3–4” и “5–6” полюсов L и R пересекаются на контуре О (в точке c на правой схеме рис. 12), при том, что сами L и R принадлежат поляре полюса С. Цепочка поиска “вторичной” пары ДТ (“L..R”) такова: некая уникальная С имеет на своей поляре “1–2” пару L, R, чьи поляры (“3–4” и “5–6”) имеют пересечение на контуре О (отнюдь не в “стартовом” полюсе С). Эта пара L, R квази-диаметрального (относительно полюса P для HC) расположения на О объявляется дуальной парой “второго типа”. Первоначально было принято именно такое решение: не принимать в “штат классификации” ни стартовую С, ни целевую c их инвариантными координатами (но с отсутствием какой-либо “зримой закономерности” расположения на контуре О). Фиксируется (по типу 2) лишь пара L..R.

Магия “октетов” продолжилась (!) – во всех наших модельных тестах сеты ДТ первого типа содержали по восемь пар (эта “норма” еще раз появится в разд. 5, посвященном свойствам ht-поляр), что отчетливо подтверждают кривые детекции R(n), приведенные на рис. 13 (по первой схеме – верхняя и нижняя – по второй). Их “двуцветность” (они либо черные, либо синие) соответствует произведенной сепарации пар на кластеры “левых” и “правых”. По той же причине показанные “ребра связи”, стартуя (по ходу заданной нумерации вершин) в точке одного цвета, финишируют (связывают) в позициях альтернативного тона. Кривые выявили неприятную особенность: допустимость позиционного квази-слияния по близкой позиции двух разных пар (что регулярно показывали карты ДТ того и другого типов). На верхнем графике рис. 13 заметен пример сближения пар E..e и g..G. На нижнем – отмечен случай почти совпавших (в окрестности одной из вершин каждой пары) пар “4..4'” и “6..6'”. Предложенные и испытанные алгоритмы детекции ДТ работали быстро и безошибочно, но исследование было продолжено, питаемое сомнениями идеологического характера: “и что с этими схемами делать в плане удобств и выгод их практической эксплуатации в задачах геометрического распознавания и проективно инвариантной классификации”? По итогам проведенной серии дополнительных экспериментов (и последовавшей за этим корректировки в постановке задачи) первая схема в ее модифицированном виде (о чем – в конце раздела) признана перспективной, вторая – оценена “неоправданно усложненной” после устранения замеченных недостатков ее функционирования, а потому – требующей дальнейшей существенной доработки.

Рис. 13.

Диаграммы детекции восьми пар ДТ по первой (вверху, для A..a, B..b,…, K..k) и второй (внизу, для 1..1', 2..2',…, 8..8') схемам с участием HC. Остальные пояснения в тексте.

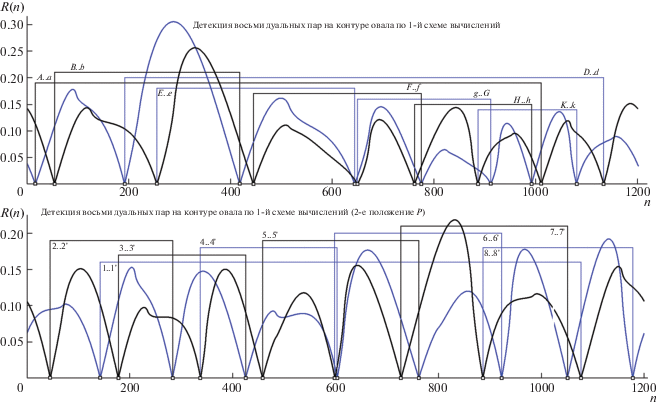
Кратко обрисуем слабые места второй схемы, переместившие ее в папку “к доработке” (соблюдая стиль конкуренции с первой, сосредоточимся на недостатках второй). Эту задачу облегчают две демонстрации рис. 14, изображающие позиционные результаты детекции (на компьютерной модели) ДТ “типа 2” для двух позиций intP с дополнительным показом карты “задающих полюсов” (то, что на рис. 12 было функцией вершины “C”, а здесь получает литерные метки P1, P2, P3,…) и кривой кросс-позиций T-трек, представляющей собой карту смены положений (при обходе контура О) “целевой точки” c пересечения поляр (на рис. 12 они помечены как “3-4” и “5-6”). Повторим: два вида точек, участвующих в процедуре (“задающие” и “ДТ-парные”) проективно инвариантные, что дает право на выбор “лучшего”. Первый вал критики, вызванный отсутствием порядка в диспозиции ДТ-пар, сместил голоса в пользу задающих. Но финальную негативную оценку варианту “быстрой доделки” обеспечил факт тестирования на модели: при первом положении P сет задающих образовали восемь вершин (слева на рис. 12), для второго – он оказался состоящим из девяти задающих позиций (правая карта). Дополнительный урон надеждам технических приложений для второй схемы внес экспериментальный факт допустимой близости участков T-трека к границе О (обратим внимание на зону у P3 и район p левой карты, на интервал от P4 до P5 – на второй), что при недостаточном разрешении позиционного описания может обернуться превращением “инвариантной точки” в “инвариантный интервал”.

Рис. 14.

Вид карт детекции пар ДТ второго типа для двух положений полюса P (слева и справа), его HC и контурах T-треков, с разным числом задающих полюсов и пар ДТ (для левой картины их восемь, тогда как для правой – девять). Остальные пояснения в тексте.

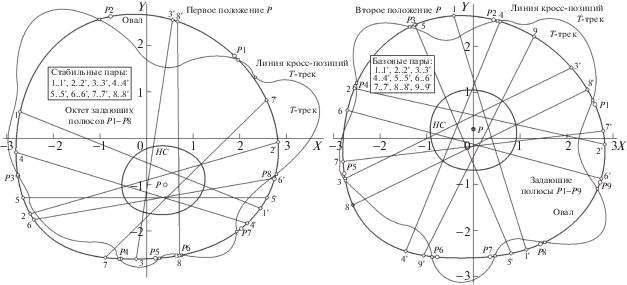
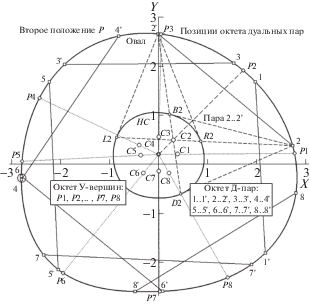
Завершим раздел описанием модификации “схемы 1 ”, превратившей ее недостаток в “потенциальное достоинство”. На рис. 15 представлены результаты компьютерного моделирования процедуры поиска стабильных элементов в сцене вида “О + intP”, привлекающий для решения этой задачи внутренний контур HC и инверсную (первого типа) схему вычисления ДТ. В правом верхнем секторе О для ДТ пары “2..2'” штриховыми прямыми воспроизведена композиция дуальных отношений плюккеровых полюсов и поляр с показом ее узловой точки C2. Факт возможного значительного (близко к пределу визуального разрешения в масштабе рис.) сближения вершин из разных пар, отмеченный на графиках функций R(n) (рис. 13), имеет место и здесь: большим кружком обведен район “перекрестного сплетения” вершин “4” и “6”, принадлежащих ДТ парам “4..4'” и “6..6'”. Если обратить внимание не на беспорядок (нарушение последовательности в привязке вершин по номеру и большую вариативность межточечных интервалов) в чередовании вершин, а на регулярное распределение октета узлов для пар ДТ (C1, C2, C3,…, C8) и на достаточно “правильное” расположение связующих пару хорд, то не выглядит нелогичным перейти от фиксации 16 стабильных точек к позиционной разметке хорд, связующих пары. Это нетрудно сделать, отмечая каждую i-ю хорду лучом из P на соответствующий ей узел Ci – до его пересечения с контуром О. В результате на нем появится “упорядоченная” цепь позиций {Pj}, которые были названы “У-вершинами”. Многочисленные модельные тесты показали, что регулярность рисунка октета У-вершин – феномен стабильный, откуда последовала рекомендация: использовать октет {Pj} для формирования малоразмерного дескриптора О (методы вычисления и применения дескрипторов для инвариантной репрезентации О описаны в работе (Николаев, 2017а)), а его “разбиение через одну точку” на два квартета (тогда получатся сеты {P1, P3, P5, P7} и {P2, P4, P6, P8}) – для организации “8-эталона” с двукратным проецированием на восьмиточечный шаблон, представляющий собой композицию двух квадратов с общим центром Q, повернутых вокруг Q на π/4 относительно друг друга. Неопределенность привязки вершины Pj к фиксированной вершине Si 8-шаблона предлагается устранить, для всех актов эталонирования О связывая выделенную вершину S1 с вершиной О из полученного октета {Pj}, имеющей некий экстремальный вурф (Wmin либо Wmax), поскольку триаду луча P-Cj-Pj легко превратить в коллинеарный квартет, добавив точку пересечения с HC.

Рис. 15.

К методу использования ДТ пар первого типа для создания распределенного октета У-вершин {P1÷P8} с привлечением сета узлов {C1÷C8}. Остальные пояснения в тексте.

5. О ПРИВЛЕЧЕНИИ ht-ПОЛЯРЫ ДЛЯ ЗАДАЧИ ПОИСКА СТАБИЛЬНЫХ ТОЧЕК О

Данный раздел включен в текст статьи в целях создания более широкой картины представлений об инструментах проективно инвариантного описания О, в данном случае, на примере роли вспомогательной кривой (структурно родственной “главной героине” повествования H-поляре), названной ht-полярой, функциональной роли которой в задачах распознавания и анализа элементов симметрии О был посвящен ряд работ (Николаев, 2011; Николаев, 2014). Имея в виду ознакомительные цели, рассказ об уже изученных возможностях ht-поляр и о планах их расширения, автор предлагает в виде кратком и фрагментарном, касающимся, главным образом, проблем инвариантного представления О в формате малоразмерного дескриптора, условно промежуточном – между “дискретным” (в виде проекции на 4-эталон) и непрерывным (в форме W-отображения), которому пока не было уделено должного внимания.

Как и для случая структурной организации H-поляры, у которой хорда, проходящая через полюс intP (и вместе с P включавшая три точки), расширяла сет своих коллинеарных точек добавлением четвертой гармонической, точно так же конструкция ht-поляры была выстроена доопределением гармонического квартета (и так же как у H-поляры, у нее есть вариант внутренней локации – наподобие HC, названный ht-контуром). Отличие ее от H-поляры в том, что четвертая точка добавлялась не к триаде таковых на хорде, а требовала вычисления на касательной к HC, у которой точка касания совершала обход всего HC. И по аналогии с H-полярой эту четвертую точку на касательной можно было вводить внутри О (получался ht-контур) или добавлять снаружи (формировалась ht-поляра). Этот вариант с внешним (относительно О) расположением представляет собой цепь из двух ветвей с набором вершин С (не менее четырех) их самопересечения, тогда как ht-контур лежит внутри О между его контуром и HС (их не касаясь), – образованный из двух замкнутых контуров с рядом точек c взаимного пересечения. Повторим: общим элементом той и другой форм является касательная в текущей точке HC, где каждой текущей касательной принадлежат три позиции: две на пересечениях с контуром О и точка касания. Для этой наличной триады и находят положение “четвертой, ей гармоничной”. Если гармоническое соответствие четвертой точки формируется по правилам для внешнего (по отношению к текущей триаде) положения, то в итоге полного обхода контура О получается ht-поляра. Если вычисление производится для внутреннего положения четвертой точки (возможны два симметричных решения – “левое” и “правое”), то формируются два “переплетенных” ht-контура (включающих не менее восьми точек c их пересечения). Далее мы будем обсуждать роль ht-поляры для инвариантного описания О (что несколько проще случая ht-контуров, свойствам которых, в том числе и их использованию в итерационных процедурах поиска элементов скрытой симметрии, много внимания уделено в работе (Николаев, 2017б)).

Рассмотрим сцену с О и с заданным intP, для которой уже вычислена ht-поляра и фиксирован на ней квартет вершин Ci (рис. 16; точка C4 не поместилась в его поле, как и третья ЭТ). Ветви ht-поляры (показаны утолщенными черными линиями – для отличия от близко расположенных тонких синих, принадлежащих H- и T-поляре) в позициях {C1, C2, C3, C4} (с меткой “оранжевый квадрат”), трактуемых как квартет плюккеровых полюсов, порождают для О четверку поляр {1–5, 2–6, 3–7, 4–8}. В акте вычисления дескриптора О квартет поляр фигурирует как октет вершин {1÷8} (неважна диспозиция хорд этих поляр, существенно свойство квази-равномерного распределения октета на контуре О). Схема вычисления дескриптора использует модифицированную (Николаев, 2017а) процедуру оценки плоскостного вурфа (Депутатов, 1926; Глаголев, 1963), когда по скользящей пятерке соседних вершин в цикле {1, 2, 3, 4, …, 8} оценивают вурф-координаты шаблона, реализующего конечноразностную модель производной Шварца (Овсиенко, Табачников, 2008)), а цепь этих координат образует на плоскости вурфов (для октета на О – в виде замкнутого цикла по сету {1÷8}) циклический граф дескриптора (врезка на рис. 16).

Рис. 16.

О роли квартета {C1÷C4} узлов ht-поляры в детекции октета {1÷8} стабильных вершин контура О, задающих циклический граф дескриптора (на врезке), со схемой (на левом О) оценки двух независимых вурфов – по пятерке вершин О. Комментарии в тексте.

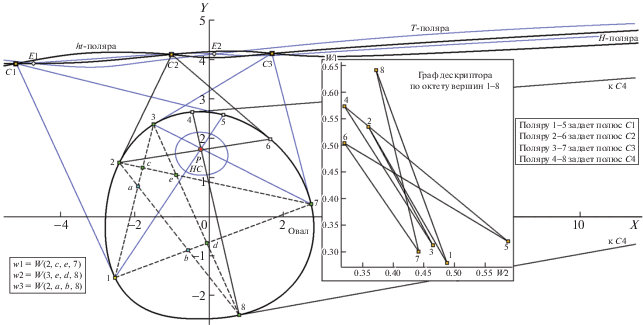
Требуется комментарий к схеме вычисления вурф-координат октета {1÷8}. На рис. 16 показано, как для вершины “1” (метка “желтый квадрат”) вычисляютя два независимых вурфа (w1 и w2; их структурные формулы для точки “1” приведены в рамке слева внизу) с использованием координат четырех ее соседей (“2”, “3”, “7” и “8”; с зелеными метками) и вспомогательного построения, добавляющего пять внутренних точек (a, b, c, d, e; пара лазурных и три зеленых). Приведен и рецепт оценки w3, но по теореме для плоскостного вурфа ((Депутатов, 1926); плоскостным вурфом называется диада независимых линейных вурфов, описывающая инвариантно каждую в композиции из пяти точек, принадлежащих выпуклой дуге) при любых вариантах его организации число независимых не превышает двух. Вычислив вурф-координаты (циклическим сдвигом “пятерки соседей”) октета {1÷8} и распределив на плоскости вурфов соответствующие им восемь точек (в порядке их соседства на О), получим искомую форму дескриптора О (врезка на рис. 16; в вершинах графа – оранжевые метки). Регулярность графа, образованного по октету {1÷8} (порождаемого, в свою очередь, сетом {Ci}), как можно заметить, состоит в том, что четные и нечетные вершины {1÷8} распределяются в плоскости графа двумя кластерами квази-симметрично относительно биссектрисы положительного квадранта W-плоскости. Рассмотренное выше представление роднит с W-отображениями принадлежность обоих декартовой плоскости вурфов, что допускает свободу в выборе альтернативных характеристик получаемого представления (заменяющих списком инвариантов 2D карту репрезентации): для картин того и другого вида функциональны такие категории меры, как угол, расстояние, площадь, центр масс и прочие (списки легче сравнивать при классификации, нежели картины).

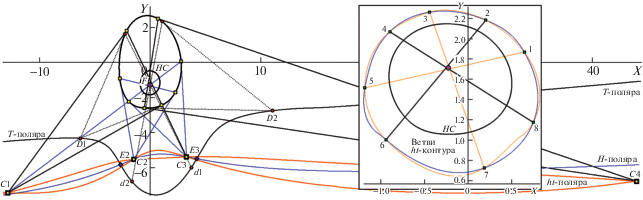
В качестве дополнительной информации о свойствах ht-поляры воспроизведем еще одну смоделированную картину сценария “О + intP” (рис. 17, где полюс intP поименован литерой F, поскольку расположен в нижней части О, не так, как для рис. 16). Показанная картина “вместила” всю четверку полюсов Ci, вид фрагментов H- и T-поляр, содержа и разметку позиций двух пар ДТ T-поляры (D1..d1 и D2..d2 с красными метками в кружках). Малоинформативная (средняя) часть рис. 17 использована для размещения (в виде врезки в другом масштабе) центрального фрагмента О с рис. 16, воспроизводящего карту ветвей ht-контура (обрамляющих HC), с распределением (метки “зеленый квадрат”) октета точек их пересечения. Дескриптор октета аналогичен полученному для ht-поляры (не показан), с той же сепарацией четных и нечетных узлов. На базовом поле рис. 17 демонстрируется характерная особенность “позиционного родства” ДТ у T-поляры и октета вершин О в их качестве плюккеровых поляр для квартета полюсов {Ci}: позиция d1 “почти инцидентна” лучу F-C3, равно как и d2 “близка” к прямой F-C2; плюккеровым полярам полюсов C1 и C4 так же присуще сближение с полярами для D1 и D2 (зеленые метки на О близки по положению к красным). В отношении родства H-поляры с ее “клоном” ht-полярой можно констатировать топографическую их близость (см. рис. 16 и 17), чего нельзя сказать о T-поляре. На этом завершим обзор проективно инвариантных свойств ht-инструментов.

Рис. 17.

Картина распределения пар ДТ на ht- H- и T-полярах, с дополнительным показом (на врезке справа) карты с октетом узлов ht-контура и кривой HC. Комментарии в тексте.

6. О ФИНАЛЬНОЙ СТАДИИ РЕПРЕЗЕНТАЦИИ ОВАЛОВ, НЕ СВЯЗАННЫХ С ПОЛЮСОМ P

Последний раздел статьи посвящен очередной попытке справиться с проблемой инвариантной репрезентации О общего вида, и имеет характер “продолжения повести”, начало которой читателю не показали, парадоксальным образом сославшись на тяжесть темы и стандартность фабулы. “Стандартность” объясняется наличием теоретического подхода, давным давно ставшего классическим (Kartan, 1933). “Неподъемность” связана с принципиальной невозможностью с помощью технических (оптических) средств достичь точностей анализа дифференциальных характеристик объекта (требуются верные оценки производных высокого порядка), декларируемых аналитически. Внятный рассказ “о вехах на тернистом пути” потребовал бы объемов, неприемлемых для статьи; и с учетом того, что победная точка в задаче “описание О, не имеющего особенностей” еще не поставлена, “хотя перспективный задел набран”, ограничимся пересказом “локальных достижений”.

В работе (Николаев, 2017а) предложен метод с привлечением чевиан, на триаду которых (в переборном процессе смены вершин О) накладывалось условие пересечения их в общей точке c, в результате чего для случайным образом выбранной позиции на контуре О вычислялся трек, состоящий из оценок координат в цепи таких c (каждая из которых была “чевианным” решением для второй вершины контура О, фиксированной на данном шаге переборного процесса, где шел поиск третьей точки по критерию для чевиан). Таким образом, для фиксированной M на контуре О вычислялся M-трек, на котором с помощью дополнительного критерия (условие по порогу для некоторого вурфа) удавалось найти пару стабильных точек (“ближнюю” и “дальнюю” относительно M, что, как потом стало понятно, было аналогом=предшественником схемы поиска точек Z и z, выше описанной по материалам рис. 11). Идеи и гипотезы упомянутой работы и привели к доказательству теоремы 3 (Савчик, Николаев, 2018). Проведенные затем серии модельных экспериментов дали импульс к обобщению задачи. Поскольку вычислительные тесты показали возможность получения для произвольной вершины M набора стабильных точек (пары внутренних на M-треке – аналогов Z, z и двух внешних – в вершинах треугольника, образованного касательными), то в добавочном внешнем цикле перебора (уже для самих точек M) для некоторых из этих стабильных точек появлялся шанс получить (при полном обходе M по контуру О) замкнутую цепь (внешнюю либо внутреннюю для О). Было бы весьма желательно, чтобы она оказалась гладкой, не прерывалась и не ветвилась.

Повторим: если требования к цепи универсально выполнимы для некоторой из найденных стабильных точек, то в итоге полного обхода границы О будет сформирован контур, который и задаст исходную композицию фигур для задачи этого раздела. Итак, полагаем, что надежный метод получения гладкого непрерывно замкнутого контура для исходной фигуры О имеется (при этом безралично, внутренний он или же окаймляющий О; главным требованием к его форме выдвигается условие принадлежности семейству О), поэтому входный сценарий меняется, сведясь к виду “О1 + О2”. Отметим, что подобная постановка нами уже рассматривалась (Николаев и др., 2018), однако акцент исследования там был сосредоточен на получении алгоритмов “быстрейшего” инвариантного описания “двуовальных композиций” – безотносительно к поиску ДТ, оценке W-отображений и прочая; существенно, что две схемы, рассматриваемые ниже, новые.

Рисунок 18 иллюстрирует идею процедур получения W-функций для композиции двух О, один из которых (левая часть рисунка) соответствует способу их оценки для варианта, когда задающая точка A совершает обход внешнего контура (“ОВАЛ 2”), другой (схема справа) предполагает перебор вершин – для внутреннего (“овал 1”). В рамках (вверху на рис.) приведены структурные формулы вычисления вурфов (по четыре экземпляра wj для каждой схемы), стереотипно идущего на каждом шаге “движения” A по контуру – в целях получения (по завершении обхода) квартета независимых W-функций, позволяющих далее сформировать необходимые W-отображения. Прокомментируем стандартный шаг i первой процедуры (рис. 18 содержит все необходимые разметки и цепь операций для него).

Рис. 18.

Схемы вычисления W-функций в сцене вида “О1 + О2”, использующие полный обход касательной в A по внешнему (слева) и внутреннему (справа) контурам О, с показом кривой T-трека и структурных формул вурфов (в рамках вверху слева и справа) для оценки двух квартетов W-функций и двух пар W-отображений. Комментарии в тексте.

Поляра B-C плюккерова полюса A задает позиции D, E на контуре, а касательная в A детерминирует T в пересечении с B-C. В итоге получен набор позиций (метки “зеленый квадрат”), достаточный для организации W-функций w1(D, B, C, E) и w2(B, C, E, T). Для расширения списка wj(i) требуется оценить позиции вспомогательных “текущих” точек: F ⇒ t(A) × t(D), G ⇒ t(A) × t(E), H ⇒ ⇒ t(E) × (A-B) и L ⇒ t(D) × (A-B). Их оценка создает возможность получения функций w3(F, A, G, T) и w4(H, A, B, L). Для наглядности (кривые поведения точек {T, H, F, L} по ходу смены шагов i) на рисунке красной тонкой линией обозначены фрагменты траекторий внешних опорных точек – при прохождении A(i) до позиции вершины, отмеченной “a”. Не будем останавливаться на подробностях, в связи с поиском ДТ, выше обсужденном на похожем (постановкой задачи и сценарием) материале рис. 7 и 12 (для схем слева), сообщив, что на левом контуре “ОВАЛ 2” метками “желтый ромб” показаны позиции одной из пар ДТ, детектированных “стандартным алгоритмом”.

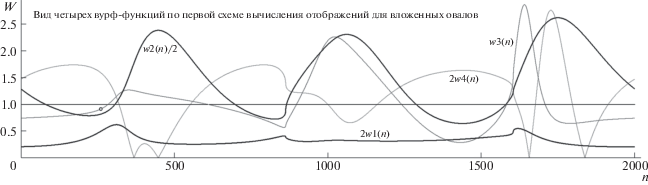
Для реализации второй схемы (зелеными метками обозначен на рис. 18 справа сет точек, требующихся для оценки w1(D, A, C, T) и w2(R, A, L, G)) в пересечениях с “овал 2” касательной в A надо найти L и R в качестве плюккеровой поляры для полюса T и оценить его расположение (т.е. T ⇒ ⇒ t(R) × t(L)). Движение A в цикле перебора вершин по i порождает кривую T-трек (изображена тонкой голубой линией), в пересечениях с которой поляры L-R определяются F и E. Для организации w1 необходимы координаты C, которая лежит в пересечении луча T-A с контуром “овала 2”. Для формирования w2 нужна оценка G ⇒ t(A) × t(C). Вычисление W-функций w3 и w4 требует оценки позиций B (пересечение лучом T-A контура “овал 1”) и пары F, E. На рис. 19 показан вид четверки W-функций для первой схемы (со сменой масштаба w1, w2 и w4 – для компактности картины): 2w1 и 2w4, 0.5w2, w3, причем график w4(n) демонстрирует особенность, связанную с разницей оценки вурфа по схеме “длин трех отрезков” (при которой игнорируется знак численного его выражения) с математически корректной процедурой, требующей для каждого отрезка учитывать его ориентацию (Глаголев, 1963). Это “пренебрежение строгостью” имеет свой “технический плюс”: фиксацию проективно инвариантных позиций для w4 (пересечение уровня смены знака для w), выражающуюся на графике зеркальным отражением участка кривой. На рис. 20 изображено, в какой форме особенность “потери знака” проявляется на карте отображения w3(w4) (показано тонкой линией). Интервалы зеркального отражения функции w4(n) фиксированы на ординате графика w3(n)(w4(n)) двумя парами меток “квадрат” (большой и малый). Дополнительная информативность рис. 20 (помимо памятки о правилах построения W-функций, вынесенной во врезку) состоит в показе тех локальных топологических черт карты W-отображений, которые могли бы обеспечить для оценки близости карт (в процедуре классификации О по их проективной эквивалентности) ускоренный режим сравнения “точечных карт” проективно инвариантных особенностей (взамен вычислительно трудоемкой процедуры оценки близости 2D кривых по схеме Фреше (Alt, Godau, 1995)): зоны “кучного” или же “точного” пересечения ветвей на отображений w2(n)(2w1(n)) и w3(n)(w4(n)) выделены “тонкими окружностями”.

Рис. 19.

Вид октета W-функций по первой схеме для вложенных О. Комментарии в тексте.

Рис. 20.

Вид двух W-отображений по первой схеме для вложенных О. Комментарии в тексте.

Рисунок 21 содержит сводную информацию по второй схеме (объект “вложенные О”), демонстрируя вид четырех W-функций (для компактности объединенной картины w3(n) и w4(n) изображены с удвоением ординат) и W-отображений (врезки вверху) w3(n)(w4(n)) и w2(n)(w1(n)). Серия модельных испытаний показала пригодность критерия w1(m) = w2(m) для маркировки кривой “ОВАЛ 2” (рис. 18, левый О) сетом шести стабильных позиций (они пронумерованы на графике W-функций, а во врезке с W-отображением w2(n)(w1(n) шесть меток “оранжевый квадрат”, расположенных на оранжевой биссектрисе положительного квадранта, локализуют эти же инвариантные позиции). Сет из шести опорных точек велик для использования в качестве 4-эталона и недостаточно представителен для дескриптора. Если вспомнить про возможность детекции пар ДТ (одна пара ДТ показана “желтыми ромбами” на внешнем О на рис. 18), то сводный их комплект можно привлечь в качестве инвариантных данных для дескриптора. Этими демонстрациями (на численных моделях) завершим рассмотрение задачи “этап анализа композиции О1 + О2 для описания О”.

Рис. 21.

Вид W-функций и W-отображений по второй схеме с двумя О. Комментарии в тексте.

ЗАКЛЮЧЕНИЕ

Доныне, не имея доказанного положения о H-поляре, как универсальном носителе двух инвариантных пар ДТ (не получено и контрпримера невозможности вычислить эти две пары, как не удалось построить пример с единственной парой ДТ), тезисы процедур, изложенных нами в этой работе, следует считать эвристическими схемами. Гипотеза о достаточных условиях, накладываемых на форму носителя ДТ, рассмотрена в работе (Николаев, 2019). Свойство дуальности присуще кривой S, имеющей особенность: “всякая прямая, пересекающая О, пересекает extS ровно в одной точке”. Нетрудно показать, что этому ограничению для extS удовлетворяет любая H-поляра, порождаемая полюсом intP (она имеет асимптоту, проходящую через P, и лежит по одну сторону от нее, не имея петель). Дополнительные результаты исследования внесли эксперименты на модели HC, показавшие надежность метода поиска ДТ нового типа (разд. 4), реализующего описание О (рис. 15) в виде эталона на четырехвершиннике (как дополнение новой схемы презентации О W-отображением; рис. 9). Перечислим и другие итоги работы по актуальной технической теме “представление О методами поиска его проективно инвариантных вершин”.

Во Введении была сформулирована постановка задачи проективно инвариантного описания О, регистрируемого в композиции с точкой P. Задача подразумевает дискретную реализацию инвариантного описания О: в виде проекции на эталон четырехвершинник либо в форме его W-отображения (интерес к вурфу – ключевому элементу производной Шварца, предложенной более века назад, до сих пор не угас у математиков (Овсиенко, Табачников, 2008)). Элементы новизны доложенного материала в том, что W-отображения не только единообразно могут быть вычислены привлечением H-поляр, но и оказались адекватной формой представления фигур в сценарии “О + extP”. Эта новая постановка связала тезисы теоремы 3 (критерий использования чевиан для поиска внешних и внутренних стабильных точек поля О по позиции плюккеровой поляры полюса extP) с новыми методами оценки ДТ на поляре для extP, итогом чего стало оригинальное предложение по вычислению “двойной проекции О на внутренний эталон восьмивершинник” (разд. 3, рис. 11).

Получены критерии применения конкурентных форм проективно инвариантного описания О методом проекции на 4-эталон с его альтернативой построения дескриптора (на сете вершин, числом более четырех, распределенных квази-равномерно по контуру О). Конструктор системы автоматического распознавания волен выбрать “более надежную” в списке возможных вариантов реализации схемы “4-эталон” с привлечением ДТ (рис. 22) в обрисованной нами совокупности семи “пригодных” схем: трех (без ДТ) для триады ЭТ и по паре для H- и T-поляры, используемых монопольно. Картина симуляции ДТ для поляр показывает очень близкое распределение задаваемых ими вершин О (D и g, T и H,…), что препятствует их совместному использованию в качестве сета “дескриптора на 16 вершин” (не рационален и вариант с дескриптором “на восемь вершин” по одной из поляр, так как две “тангенциальных” одной пары близки двум “лучевым” другой). В качестве дескрипторов “на шесть вершин для триады ЭТ” оптимальны два типа (“гармонический” и тангенциальный). Из этих же соображений схему 4-эталона рационально реализовать на любой из пар ДТ, снимая “комбинаторную вариативность” идентификацией индекса компактности пары.

Рис. 22.

О привлечении H- и T-поляр с их ЭТ и ДТ в задачах описания О в виде проекции на 4-эталон либо посредством графа дескриптора. Остальные пояснения в тексте.

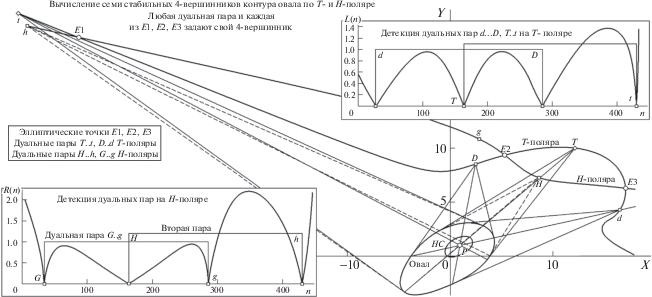
В качестве альтернативы “избыточным” инвариантным описаниям опознаваемого объекта (рода непрерывного представления W-отображением; в виде циклического графа дескриптора – по набору инвариантнных вершин контура О либо по схеме “проекция на эталон четырехвершинник”) в случае технических требований к скорости процедур опознавания О предложено использовать предельно компактные описания в виде “стэка стабильных точек и зон кучности”. Пример таковых – выборки из карт W-отображений (рис. 20).

Не один год ведущееся исследование свойств кривых семейства овалов (и аппарата проективного их анализа, в который входит H-поляра) стимулирует известная причина: дифференциальные методы оценки инвариантов для них (Картан, 1933; Faugeras, 1993) не применимы к кругу задач технического зрения (по причинам не реализуемых требований к точности вычисления производных высокого порядка на дискретных сетках для гладкой кривой). С момента предыдущей публикации цикла (Николаев, 2019) ситуация в мире не изменилась: растущая актуальность поиска решений подобного класса задач стимулирует разработку компромиссных подходов (Olver, 2001; Hann, Hickman, 2002; Musso, Nicolodi, 2009). Для численного анализа гладкой плоской кривой П. Олвер и соавт. продолжают искать полуэмпирические подходы, ведущие к оценке ее дифференциальных инвариантов и “полуинвариантов”, приемлемой для технических задач (Olver, 2011; Hoff, Olver, 2013).

Актуальность представленной работы в плане потребностей развивающихся систем автоматического распознавания подтверждается, в частности, исследованиями границ применимости проективной модели сопоставления овальных контуров водоемов для решения задачи самопозиционирования летательного аппарата, показавшими, что коррекция дисторсий с их помощью технически реальна (Savchik et al., 2018).

Вывод по доложенной теме: разработанные численные методы и схемы для задач проективно инвариантной репрезентации кривых семейства овалов – на основе поиска стабильных точек и с привлечением инструмента H-поляры – оригинальны и, можно полагать, технически перспективны. Прямые и косвенные аналоги обсуждавшихся здесь аспектов привлечения (для решения поставленной задачи) циклических дескрипторов, W-функций и W-отображений не обнаружены нами в доступных базах цитирования.

Работа выполнена при поддержке РФФИ (грант № 19-29-09075).