Сенсорные системы, 2021, T. 35, № 1, стр. 55-78

ВВЕДЕНИЕ

В данной статье описаны и на материале компьютерных реализаций обсуждены новые аспекты (сценарии задач, методы и численные схемы их решения) развития темы, отраженной в цикле авторских работ по опознанию овальной фигуры по плоской центральной ее проекции инвариантно к группе дробно линейных (иначе – проективных) преобразований плоского контура фигуры в 3D пространстве. Объект этого объемного исследования – кривые семейства овалов (о) – плоские гладкозамкнутые фигуры (не предполагающие формул аналитического описания, единых для семейства о, при том не имеющие опорных элементов контура о, традиционно используемых в распознавании фигур по особенностям их геометрии, – наподобие точек излома, перегиба, спрямления, двойного касания и проч.).

С учетом этих соображений оказываются понятными трудности, возникающие при попытках получить помехоустойчивое описание о, не зависящее от ракурса оптической регистрации о технической системой распознавания: исключительно дифференциальные методы анализа кривой, обеспечивающие ее инвариантное описание (каковые уже давно предложены теорией плоских кривых (Картан, 1933)), не пригодны для дискретных сеток входного описания о – в силу точностных требований к численной оценке локальных производных высокого порядка у “поточечно” описываемой кривой, каковые абсолютно нереализуемы практически (при любых технически возможных характеристиках камер). По вышеупомянутым причинам для инвариантной (и не затратной, как это, в принципе, реализуемо полнопереборными методами для дискретно заданной кривой) репрезентации о необходимо получить какие-то дополнительные данные о его структуре. Как показано нами ранее, ресурсно экономные методы обработки фигур этого семейства возможны в случаях задания о совместно с линейным элементом (точкой либо прямой произвольной ориентации относительно заданной фигуры (Николаев, 2011; 2019)) в плоскости кривой. Если же про о априори известно, что фигуре присущи свойства симметрии, то подобными дополнительными атрибутами ее описания могут служить элементы симметрии (ЭС) того или иного типа: пересекающая о прямая, задающая ось a, – в аксиально симметричном случае; внутренняя либо внешняя точка – при наличии центра (с локализацией в поле о, если подразумевается тип неявно радиальной либо “ротационной” симметрии) или же позиция плюккерова полюса (снаружи от о, в качестве поляры, представляющей ось a). Методы и эффективные алгоритмы детекции ЭС (полного набора вариантов) разработаны, численно промоделированы и описаны (Николаев, 2014; 2016). В статье, предлагаемой вниманию читателей, рассмотрены новые подходы к задаче поиска ЭС, что можно считать целесообразным не только из соображений “обогащения базы решений”, но и с позиций технического их уровня: обсуждаемые далее процедуры по асимптотике алгоритмической сложности не уступают самым быстрым схемам – из числа ранее разработанных.

Развитые технологии обработки изображений приобрели ныне статус дисциплины с мощной процедурной базой: с методами обнаружения, подчеркивания и сглаживания границ, в силу чего в рамках этой работы нет необходимости в обсуждении приемов получения “продукта анализа” для данного исследования – в виде “контура о” (тем более, при изложении развиваемых теоретических тезисов, конкретно соотносимых с разделами проективной геометрии плоских кривых). Таким образом, граница о, с ее инвариантными геометрическими характеристиками, и фигурирует в качестве “объекта автоматического анализа в практической задаче по его опознанию/классификации”. Далее нас будут интересовать численно реализуемые подходы (устойчиво воспроизводимые особенности модельных тестов) в соотнесении входного задания о, представляющего границу фигуры совокупностью ее вершин “оцифровки”, с теми способами дискретной обработки о, что в итоге должны дать инвариантное его описание, тем самым обеспечивая возможность успешно классифицировать разнообразные гладкие фигуры, относя их к проективно эквивалентным выборкам, либо формируя “эталонное описание” о – для последующих технических нужд (практических задач автономного распознавания объектов).

Ранее показано (Николаев, 2016; 2017), что у овалов с неявной симметрией всех возможных трех ее разновидностей (центральной=радиальной, осевой, “ротационной”) произведенная безошибочно локализация сета ЭС достаточна для получения проективно инвариантного описания каждого такого о, в любой из удобных форм репрезентации: в виде проекции на эталонный 4-вершинник; представленной гладкозамкнутой кривой 2D вурф-отображения либо посредством малоразмерного циклического графа дескриптора о. Как и в предшествующих статьях цикла, под неявной формой представительства ЭС будут подразумеваться закономерности их проявления в проективной форме, не совпадающей с вариантами поведения ЭС в рамках декартовой геометрии (где осевую симметрию можно описать правилом “хорды, перпендикулярные оси, делятся ею пополам”, а радиальную – задать через свойство: “хорды, идущие через центр, разделяются им на равные части”). В проективной геометрии неопределимы ни “перпендикулярность”, ни операция деления отрезка пополам, поэтому методы поиска ЭС, опирающиеся на проективно инвариантные их признаки, будут эффективны в широком диапазоне смены “ракурсов регистрации” о, в математической модели следуя законам лучевой оптики для камеры-обскуры. Прозрачно и утверждение, что процедуры, годные для вариантов трансформации о проективным преобразованием плоскости в 3D декартовом пространстве, не утеряют эффективности в случае ортогонального ракурса о (при котором свойства “деления хорд пополам” будут неукоснительно выполняться). Эту уникально простую разновидность проявления свойств симметрии о будем далее именовать его ортоформой. Нет причин останавливаться на деталях вычисления любой из выше перечисленных структур инвариантного описания о с симметриями, не принципиальных для основной задачи – методов детекции ЭС разных типов ее представительства, привлекающих для решения этой задачи две альтернативные идеи. “Опорные элементы” таковых – точка и отрезок на плоскости о – соответствуют схемам вычисления проективно инвариантных “дуальных пар” (ДП) точек и приемам привлечения столь же стабильных “триад чевиан” (ТЧ). Опишем кратко эволюцию идей.

Анализ данных теоретического плана, полученных для объекта о в последние годы (Балицкий и др., 2017, теорема 1; Савчик, Николаев, 2018, теорема 2), в сочетании с подробно изученными особенностями введенных нами криволинейных поляр (двух типов) позволил развить новые подходы в задаче поиска проективно стабильных элементов о, добавив очередные разновидности инвариантных точек и прямых. Ими стали сеты ДП и треугольные композиции отрезков – структуры ТЧ. Минимальный набор и порядок локализации ДП на прямой L, внешней для о, декларирует теорема 1. Опора на нее обеспечила построение универсальных процедур проективно инвариантного описания композиции “о + L”, являющейся зафиксированным внешним дополнением о прямой L (произвольной ориентации), не касающейся контура фигуры. Вторую категорию новых структурных элементов – композицию ТЧ – компонует описанный вокруг о треугольник t, в котором три отрезка, соединяющие вершины t_j с точками касания к о (в планиметрии называемые чевианами) связаны необходимым условием пересечения в одной точке.

Реализованные схемы вычисления проективно инвариантных функций, задаваемых сложным отношением квартета точек прямой (иначе – вурф-функций) на криволинейных полярах (типа T и H) связали характерные особенности эллиптических (ЭТ, порождаемых в пересечениях T- и H-поляр) и ДП точек, ранее предполагавшихся подчиняющимися независимым закономерностям рода необходимых признаков их существования. Новый подход с объединением вычисления ЭТ и ДП оказался весьма плодотворным, дав в итоге “эмпирически (до настоящего времени) справедливую”, в качестве обобщения теоремы 1, (при отсутствии контрпримера по совокупным данным модельных тестов) правомерность привлечения поляр T и H в качестве носителя ДП, с той же оценкой в виде минимального их количества (в две ДП, для поляры того и другого типа), и той же особенностью их “цепного” (закон чередования точек пары) расположения на носителе.

По ходу разворачиваемой эволюции подходов к анализу о целесообразно уточнить, что источником идей для привлечения поляр T и H, а также и ДП, стала хорошо известная “теорема взаимности” Плюккера (о симметричной полюс-полярной структуре для коник, – кривых второго порядка, являющихся «вырожденным подсемейством» для о (Акимова и др., 2014)). Теорема была декомпозирована: позиционные гармонические свойства задали структуру H-поляры, инвариантные тангенциальные особенности определили правила для формирования T-поляры, а сам характер симметричных отношений у пар плюккеровых полюсов и поляр (последние – прямолинейны, а внешний полюс P проективно однозначно задает для о поляру p по инцидентности двум точкам прикосновения касательных к нему из P), скорректированный в соответствии с требованиями для о общего вида, определил необходимые условия наличия композиции ДП. В отрыве от свойств принадлежности некому фиксированному носителю (внешней прямой L или же сформированной H-поляре) эти правила могут быть заявлены в форме, не уточняющей инцидентность двух внешних плюккеровых полюсов P1 и P2 и не меняющей детерминизма в расположении их поляр p1 и p2 при любой проективной трансформации данной композиции, а именно: “поляра p2 проходит через P1, при том что P2 принадлежит p1”. Подобное задание композиции для одиночной ДП наводит на мысль о возможности поиска для P1 дуальных полюсов P2 и P3 по разные терминальные стороны от концов хорды, которой одновременно инцидентны поляры p2 и p3. Схема вычисления этой новой дуальной композиции, где триада внешних полюсов образует две ДП вида P1..P2 и P1..P3, успешно протестирована на моделях и описана в работе (Николаев, 2020). Каким образом новый подход к ДП помогает оценить ЭС в сценариях “для о с симметриями того или иного типа”, рассмотрено в последующих разделах, а завершающую тему введения посвятим краткому комментарию к “идеологии ТЧ” и ее эволюции в задаче поиска ЭС у о с неявной симметрией разных типов.

В начале введения упомянутая теорема 2 декларирует существование не менее двух проективно инвариантных композиций ТЧ в сценах, где у о фиксирована пара точек контура (т.е. третья точка касания формируемой для о ТЧ, вычисляемая по критерию общего для них пересечения, имеет не менее двух позиционных решений), побудили к модельным экспериментам, подтверждающим гипотезу о возможности “упорядочить” два допустимых решения для ТЧ, что обеспечило бы шанс целенаправленно выбирать из них единственное по некому однозначному критерию (“искомая третья позиция принадлежит точке касания ТЧ либо контуру о со стороны противолежащей вершины t₃”). Численные результаты на старте исследования этой гипотезы приведены в статье (Николаев, 2020; см. рис. 11). Таким образом, “на эмпирическом материале сделанное уточнение=обобщение теоремы 2” обеспечило для задачи, стоящей перед нами в данной работе, процедурные подходы согласно идее: “для случайным образом выбранной точки на контуре о в ходе перебора его вершин – найти композицию ТЧ, которая удовлетворит априори известным признакам ЭС (с данным типом симметрии, что и станет критерием выбора искомой ТЧ на языке условий для неких вурф-функций) для второй и третьей точек, инцидентных ЭС”.

Подведем итог предварительного рассмотрения актуальной задачи. Общий прием при использовании структур ДП и ТЧ для поиска разнообразных ЭС состоит в задании критерия фиксации искомого позиционного решения в переборной (по вершинам о) схеме “со случайной начальной вершиной о” и варьируемыми координатами точек (из числа ДП либо ТЧ), удовлетворяющих конкретным условиям их инцидентности детектируемым ЭС.

Прежде чем перейти к рассмотрению ряда альтернативных методов поиска ЭС с привлечением структур ДП и ТЧ, уведомим читателя о том, что данный текст адресуется всем, интересующимся проблемами автоматического анализа формы (не требуя навыков профессиональной подготовки в этой сфере). Для уяснения существа излагаемых проблем и показанных модельных результатов достаточно ориентироваться в поле представлений естественно-научного плана. Авторские тезисы донесены здесь в образной геометрической форме. Исчерпывающее понимание смысла приводимых далее нотаций, схем и приемов обработки не обязательно для знакомства с содержательной логикой обсуждаемых идей. Текст иллюстрирован примерами результатов компьютерного моделирования (для разных сценариев ЭС), снабженных комментариями, что может удовлетворить неспециалистов.

1. МЕТОД ПРИВЛЕЧЕНИЯ ДП В ЗАДАЧЕ ПОИСКА НЕЯВНОЙ ОСИ СИММЕТРИИ О

Коснемся детальнее истории с генезисом ДП. Понятие “дуальности” (синоним – двойственность) привнесено из наследия одного из творцов проективной геометрии – Ю. Плюккера, с его теорией полюс-полярного соответствия для коник (известным примером которых является эллипс) и фундаментальной “теоремой взаимности” для них (Глаголев, 1963; Моденов, 1969). Тезисы теоремы (метрически инвариантные свойства композиций полюсов и вершин, инцидентных полярам, проявляющиеся в виде гармонизма отношений, и дифференциально-тангенциальные особенности, присущие касательным к конике) и побудили автора к введению в аппарат анализа о двух независимых инструментов: “на языке касательных формируемую” T-поляру и подчиняющуяся законам гармонических отношений H-поляру. Зеркальная симметрия положений внутренних и внешних полюса и поляры (напомним: плюккерова прямолинейная поляра соответствует прямой, проходящей через точки касания к эллипсу из внешнего полюса; в силу подобной связи их позиции взаимно однозначны) в соотнесении с возможностью их сепаратного использования для описания свойств о посредством привлечения поляр T и H рассмотрена в работе (Акимова и др., 2014), где показано, что для диспозиции “внешний полюс, внутренняя поляра” их однозначная связь для о общего вида неизменна при его проективных трансформациях, но по полюсу внутреннего положения вычислить для о его плюккерову поляру невозможно (так как формализм генерации кривой, верный для эллипса, к семейству о неприменим). Однако из деклараций теоремы взаимности удается вычленить “особый тезис дуальности отношений”, где гарантированная для коник всеобщность связи позиций двух полюсов и двух плюккеровых поляр в случае с о редуцируется к связи уже уникальной: по некоторой позиции extP1 для о можно искать такую extP2, что поляра p1 пройдет через extP2, при том, что полюс extP1 окажется принадлежащим поляре p2. Эти два полюса произвольного внешнего расположения и стали исходным носителем дуальных свойств в теореме 1, заявляющей, что на прямой extL произвольного расположения по отношению ко всякому о всегда существует не менее двух проективно инвариантных ДП. Для задачи, стоящей перед нами, совершенно не важна коллинеарность всего квартета (двух ДП), достаточен успех построения одной ДП с требуемыми гармоническими свойствами, а потому extL из разряда “инициирующих причин композиции” нивелируется к “неизбежным и ненужным следствиям” структуры ДП, найденной исключительно по критерию двойственности.

Для внятности описываемых далее процедурных решений, на некоторой стадии вычисления (при анализе вурф-функций) использующих понятие “гармонизма”, приведем “формулу гармонического отношения”, в качестве важнейшего частного выражения для фундаментального проективного инварианта, здесь именуемого “вурф” (в современных математических работах его чаще называют “сложным отношением четверки точек на прямой”). Для простоты дефиниций ограничимся заданием вурфа через длины отрезков, на которые прямую разбивает квартет ее точек (т.е. дадим формулу вычисления модуля вурфа, где знак при численном инварианте, формируемом из ориентированных отрезков, нами проигнорирован). Обозначив через a, b и c длины отрезков в последовательной их маркировке, запишем выражение вурфа w в виде w[a, b, c] ≡ a*c/((a + b + c)*b), что и дает всегда “безразмерное” число при любой размерности длин. Гармоническим (в этой форме задания) называется вурф, следующий условию w[a, b, c] = 1, что реализуется, к примеру, радикально отличающимися композицями w[3, 1, 2 ] и w[x, x, ∞] с близкими и бесконечно далекой позицией одной из точек квартета (ее называют несобственной). В нашем случае «прыжки из бесконечности» в окрестность о будут характерной особенностью сцен при переходе от явного задания свойств симметрии (ортоформой) к неявному их выражению (при технических реализациях процедуры поиска ЭС – в итоге смены оптического ракурса регистрации о от ортогональной к произвольной неортогональной). Перейдем к описанию модельных (компьютерных) процедур, форма о для которых задавалась непосредственно цепью вершин аппроксимации с управляемой плотностью представительства на контуре).

Рассмотрим аксиально симметричный о в неортогональной проекции, для которого требуется найти положение неявной оси L-R, привлекая аппарат поиска ДП в переборном процессе ее детекции, идущей с вычислением вурф-функций, проверяемых на исполнение условий гармонизма для искомой диспозиции всех элементов варьируемой конфигурации (четверок точек на лучах перебираемых направлений, касательных к контуру с позициями их пересечений и проч.; рис. 1). Для большей ясности идеи поиска справа внизу на малой врезке показана ортоформа о. На ее примере нагляно демонстрируется, что у произвольно выбранной позиции A всегда найдется симметричная ей точка b, при том что хорду A-b ось поделит на две равные части, а сама хорда всегда будет параллельна паре касательных у терминальных точек оси – в L и R. На языке проективных (а не декартовых особеностей ортоформы) это условие трансформируется к виду “хорда и пара касательных пересекутся в несобственной точке P'”, что при переходе к неявной форме задания о с его осью можно выразить заменой соотношения w[x, x, ∞] ≡ w(A, c, b, P ') = 1 (x = A-c = c-b, а |∞| ≡ b-P '; при этом вторая форма нотации вурфа “через квартет коллинеарных точек” использует круглые скобки вместо квадратных, избранных для его задания “в отрезках”) на запись w(A, c, b, P) = 1, теперь уже адекватной для полюса P (детерминируемого плюккеровой полярой L-R) в его качестве позиции пересечения луча A-P с касательными t(L) и t(R) (что отражено на врезке рис. 1 вверху слева структурной формулой “P => t(L) × t(R)”; знак × имеет смысл “точка пересечения”, а запись t(A) истолковывается как “касательная в точке A”). Итог именно этого «вброса плюккерова полюса P ' из бесконечности в окрестность о», совершающийся при переходе от представления о ортоформой к неявным проявлениям для ЭС, демонстрирует общий план о на поле рис. 1 слева. Прочие формулы для T, P ', t1, t2, помогая понять их генезис, также размещены на врезке вверху слева.

Рис. 1.

Метод детекции образа оси симметрии с привлечением композиции одиночной ДП (дуальной пары P..T) и подход к выбраковке ложных решений – с помощью контрольных W-функций w(E(n)) и w(G(n)) – в комплекте с основной w(b(n)) (на врезке справа вверху). Остальные пояснения в тексте.

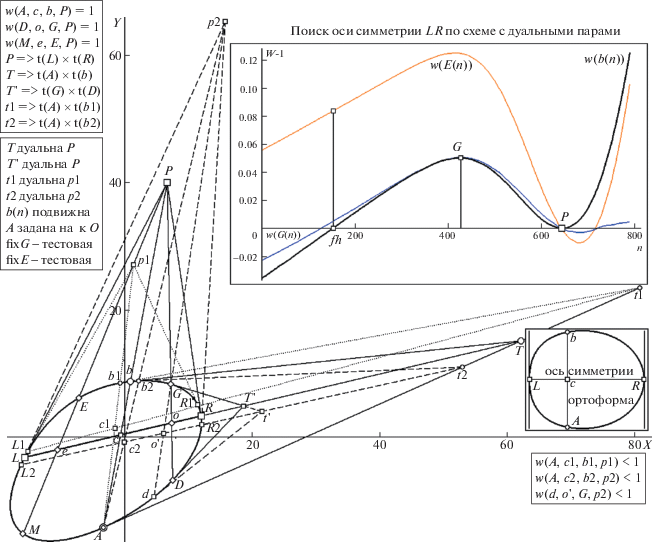
До рассмотрения процедуры поиска оси L-R кратко коснемся финальных этапов (не обсуждаемых в рамках “укороченной” постановки задачи) инвариантного представления о, достаточных для целей распознавания=классификации. Понятно, что любая ДП задает (присущий лишь ей) квартет стабильных точек на о (в нашем случае это четверка A, L, b, R). Слово квартет тут ключевое, поскольку понятным образом выводит на конечную цель манипуляций с проективно инвариантными точками: для решения задачи опознания фигур семейства о необходимо получить образ о, неизменный при сменах оптического ракурса его регистрации, создав эталон, единый для класса проективно эквивалентных о. Одной из адекватных форм такой репрезентации о нами заявлена операция проецирования входного о на некоторый стандартный 4-вершинник (например, квадрат фиксированного расположения), что просто и однозначно реализуется решением линейной системы восьми уравнений (Николаев, 2011), так как позиции некой стабильной четверки вершин контура о всегда возможно трансформировать в диспозицию эталонного 4-вершинника, совершив проективное преобразование плоскости исходного о (его задают восемь неизвестных независимых коэффициентов, доставляемых решением системы) перепроецированием на квадрат эталона – при условии совмещения найденной стабильной четверки с вершинами эталона. Идея проецирования на вершины эталона, скорее всего, ясна. Однако наличный квартет A, L, b, R не годится на роль однозначно “стабильной четверки”, так как позиция A выбрана на контуре о рандомно. Указанное препятствие легко преодолимо: нами описан (Николаев, 2017) алгоритм обнаружения уникальной точки C на стабильной хорде L-R, использующий некоторое экстремальное условие для вурфа на “скользящей касательной в b(i)” (по i идет перебор вершин о), которое для луча P-C в пересечениях с контуром о обеспечивает однозначную оценку координат уникальной пары B, A' (на рис. 1 эта пара не показана). В итоге, для дальнейшего эталонирования о будет получен квартет {A', L, B, R}. Вернемся к идее поиска неявной оси и требуемым шагам ее реализации – в переборном процессе детекции вершин L и R, задающих позицию оси симметрии о.

Случай осевой симметрии вносит коррективу в правило взаимной однозначности отношений для “фигурантов” ДП. Действительно, точке T, принадлежащей продолжению хорды L-R (т.е. искомой оси), однозначно дуальна позиция плюккерова полюса P (рис. 1). Но и у T  ', с ее полярой D-G, ДП для нее окажется та же самая P. Вывод: некой позиции на внешних продолжениях хорды L-R дуальна P, однозначно задающая искомую ось, тогда как “в обратном прочтении” дуализм проявляется в неоднозначном виде: “уникальному полюсу P двойственно линейное семейство позиций внешних фрагментов оси”. Подобная асимметрия отношений, не мешая организации процедуры детекции, даже помогает найти единственно верное решение, создавая возможность проверок гармоничности вурфов на лучах из P, тем самым и обеспечивая отбраковку ложных решений. Поясним подробнее.

Как указано на врезках рис. 1, лучом из случайным образом фиксированной точки A производится дискретное сканирование вершин о, где “скользящая” (перебираемая по номеру n вершин аппроксимации о) точка b(n) детерминирует пошагово формирование поляр A-b(n), для каждой из которых вычисляются позиции ее “текущей” ДП – в виде полюсов t(n) и p(n) совместно с полярой L(n)-R(n) для неподвижной A. На рис. 1 показаны положения b1 и b2, обрамляющие искомую позицию b, с размеченными полярами L1-R1 и L2-R2 для них и их полюсами в виде двух ДП: p1..t1 и p2..t2. Для искомой диспозиции с хордой оси L-R помечены (большими “кружком” и “квадратом”) дуальные полюса T и P. И, поскольку на каждом шаге переборного процесса можно вычислить точку пересечения c(n) дуальных поляр, то появляется возможность сформировать основную вурф-функцию процедуры по дискретным оценкам вурфа w(A, c(n), b(n), p(n)) (показана вверху справа на врезке рис. 1, помеченная как “w(b(n))”). На шаге максимально возможного (что зависит от плотности реализованной аппроксимации вершин) совпадения b(n) с b оценка w(b(n)) по критерию w(b) = 1 (признак гармоничности вурфа) будет сигналом завершения поиска, в итоге будут выделены все адекватные компоненты композиции: полюса P, T и хорда=ось L-R. Если опираться единственно на ход функции w(b(n)), то адекватность решения будет зависеть от правильности выбора между двумя вариантами – истинным (метка “большой квадрат” у литеры P, врезка справа вверху) и ложным (позиция “фальшь-гармонизм fh”). Функция w(b(n)) – 1 для “P” имеет минимум, а в “fh” пересекает оценку w(b) – 1 = 0. На контуре меткой “малый зачерненный квадрат” (между R1 и G) показана позиция для b(n), где основная вурф-функция (далее будем использовать сокращенную форму W-функция) предлагает ложное решение “fh”. Возникла ситуация альтернативы, где оба варианта – равноправные кандидаты на целевую композицию. Выход из тупика требует независимую проверку=контроль, что и возлагается на рандомную пару G, E.

Проверка идет параллельно на каждом шаге перебора, не требуя каких-либо оценок дуализма. Из текущего полюса p(n) вычисляются два вурфа в направлении G и E. На рис. 1 показано, что для G из “неверного” полюса p2 формируется оценка w(d, o', G, p2) < 1 (на врезке справа внизу приведено это уклонение от гармонического значения), тогда как луч “из P на G” дает гармоническую оценку w(D, o, G, P) = 1 (она помещена на верхней врезке слева). Эта проверка показывает, что позиция G удовлетворяет гипотезе о полюсе оси (на большой врезке W-функция w(G(n)) принимает единичное значение для того же номера n вершины, что и основная w(b(n)), при том, что у вершины с меткой “fh” не равна 1 (хотя и близка к гармонической). Для большей уверенности в правильности отбраковки номера при “fh” производится вторая проверка по W-функции на луче p(n)-E. Она подтверждает истинность выбора P в качестве полюса оси, “безкомпромиссно отвергая версию решения для fh” (W-функция w(E(n)) по этому номеру выдает оценку, весьма отличную от 1, что и показывает ордината w(E(n)) у “малого квадрата”). Структурные формулы, фиксирующие условие гармонизма для искомой конфигурации элементов на лучах из P в направлении на “рандомно контрольные”, G и E приведены слева на верхней врезке рис. 1.

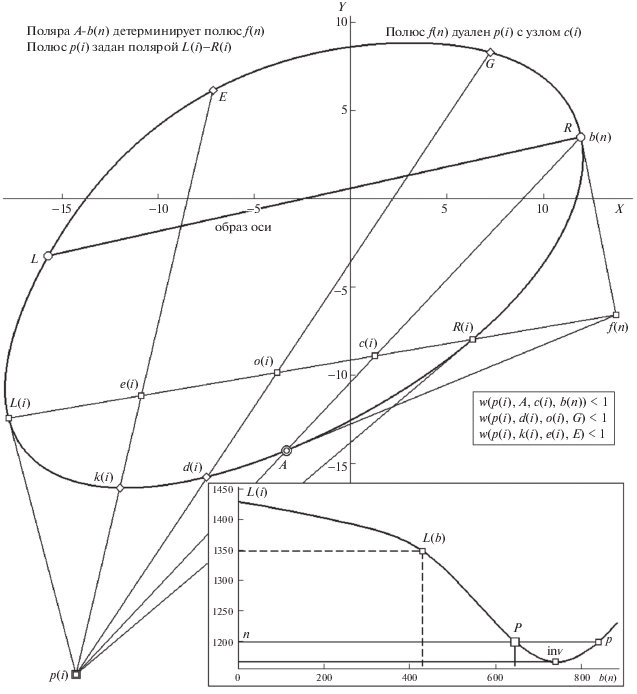
Как себя ведут вурф-оценки по ходу пошагового формирования позиций ДП (т.е. как для “подвижного” луча A-b(n) в роли плюккеровой поляры, варьируемого в диапазоне номеров от R до L, вычисляются его дуальная поляра L(n)-R(n) и ДП полюсов f(n) и p(i)), помогает уяснить рис. 2. Его поле изображает картину связей плюккеровых элементов на шаге n, соответствующем направлению луча сканирования из A на вершину R, каковая подразумевается в обозначении b(n). Этот луч детерминирует полюс f(n), который в свою очередь задает его ДП в виде p(i), – с полярой L(i)-R(i) (и узлом c(i) в пересечении поляр), весьма позиционно далекой от искомого положения хорды L-R в качестве «образа оси». Основной вурф w(p(i), A, c(i), b(i)), также как и пара “проверочных” – w(p(i), d(i), o(i), G), w(p(i), k(i), e(i), E) характеризуют ситуацию, как отличную от гармонической (эти оценки вынесены на малую врезку справа). Дополнительную информацию привносит показ связи между текущим номером “скользящей” вершины b(n) и номером концевой точки L(i) луча f(n)-L(i) (кривая на большой врезке справа внизу). Функциональная зависимость номеров такова, что номер b(n) (метка “большой квадрат”), фиксирующий позицию P (проективно симметричную A), не уникален для “правильной” L(i), каковая образует шаблон ДП и для номера при литере “p”, фиксирующего ложное решение. При этом номер для вершины inv явлется точкой инверсии направления перебора номеров для L(i) при монотонном росте номеров у b(n). Таким образом, проверки шаблонов ДП по лучам на G и E необходимы.

На материале проведенного недетализированного описания процесса вычислений, формирующих ДП для каждой позиции b(n), можно сделать общий (предварительного характера) вывод: последовательно по номеру n формируемые списки оценок вурфов, которые по завершении процесса должны образовать массивы W-функций (основной и пары контрольных) оперируют пошаговыми данными, где изменяемому положению b(n) ставится в однозначное соответствие им детерминируемая композиция ДП. Но сама эта композиция не может быть вычислена (по “априорной исчерпывающей формуле”), как функция координат b(n), ее требуется “построить”, сообразуясь с дуальными принципами отношений поляр. Идея построения проста: для поляры A-b(n), однозначно задающей полюс f(n), требуется выбрать такое положение поляры L(i)-R(i) (рис. 2), чтобы ее полюс p(i) стал инцидентен лучу A-b(n). Следовательно, без независимого перебора по i для L(i) (либо для R(i), что “для идеи” безразлично, и выбирается из соображений оптимума по точности для операции “p(i) – наиближайшая к A-b(n)”) не обойтись, и это означает, что в процедуре должен быть продуман и программно реализован поиск дуального положения поляры L(i)-R(i). Вывод: комбинаторный процесс получения W-функций – двухуровневый (дискретные аргументы W-функций образуют ряд перебора по n, а реализация критерия дуальности для полюса p(n) требует выбора его позиции через вариации по переменной i). Ограничимся этим комментарием функционального характера, упреждая читателя о более развернутом описании двупараметрического перебора вершин, столь же необходимого и по той же схеме работающего, но уже на примере аппарата ТЧ (разд. 2).

Рис. 2.

Формирование ДП f(n)..p(i) во внутреннем цикле (i) переборной процедуры поиска оси L-R лучом обхода из фиксированной A в b(n) (с контрольными E и G) и демонстрация функции позиционной связи L(i) c b(n) (на врезке внизу). Остальные пояснения в тексте.

Дополнительно заметим, что специфика дуальных отношений для подсемейства осесимметричных овалов такова (в том числе, в связи с неоднозначностью вариантов ДП по линии их поиска “от P к массиву t(n)”, обсуждавшуюся выше), что “в целях экономии вычислительного ресурса” нами был выбран путь решения поставленной частной задачи несколько более простой (более “быстрый”), нежели описанный во введении в разряде новаций: метод, рассмотренный нами в данном разделе, не потребовал привлечения более громоздкой численной схемы с формированием тройственных структур ДП вида P1..P2, P1..P3, поскольку решение доставляла “минимальная” ДП (P1..P2). Вариант тройственной организации ДП в процедуре поиска ЭС использован для случая радиальной симметрии о и будет рассмотрен далее в разд. 3. Этим комментарием завершим обсуждение подхода с привлечением аппарата ДП в целях обнаружения неявной оси o, переходя к обсуждению новых переборных методов теперь уже с использованием композиций ТЧ для решения той же обратной задачи – на компьютерных моделях аксиально симметричного o.

2. МЕТОДЫ ИСПОЛЬЗОВАНИЯ КОМПОЗИЦИЙ ТЧ В ЗАДАЧЕ ПОИСКА ОСИ СИММЕТРИИ О

Объект проективно инвариантного анализа и обработки – тот же, что и в разд. 1. Не изменились ни целевая установка (поиск неявной оси), ни метод работы с объектом (тесты на моделях численных схем, где контур o генерируется в виде замкнутой цепи вершин его аппроксимации – с регулируемой плотностью презентации и целенаправленно меняемыми “проекциями оптической регистрации”, имитируемыми сменой сета 8 коэффициентов проективного преобразования плоскости o), ни концепция двупараметрического перебора вершин o в алгоритме поиска оси. Меняется “детектирующий инструмент” поиска. Теперь миссия позиционной оценки возложена на инвариантную композицию “ТЧ”, где схема “текущих метаморфоз” ТЧ устроена по уже оправдавшему себя (на примере аппарата ДП) сценарию: последовательно (комбинаторно) перевычисляемые структуры композиций ТЧ порождают на каждом шаге процедуры коллинеарные квартеты «точек», что позволяет сформировать сет W-функций, для которых заранее определены и согласно теоретическим критериям “считываются” оценки, однозначно выявляющие целевую конфигурацию.

Еще один нюанс: для того, чтобы объемы разделов не очень сильно различались, однотипный материал перераспределен в соответствии с меняющейся акцентацией (без нежелательных потерь в его связности и ясности). В текущем – уделено больше внимания двумерному перебору вершин о, т.е. идее алгоритма, имеющего внутренний и внешний циклы (в них и идут вычисления со сменой номеров вершин). В разд. 1 акцент выделил геометрические (“лучи”, хорды, касательные, гармонические вурфы) и “изографические” (ход W-функций) аспекты метода, чем закамуфлировал якобы прозрачную идею перебора. Этот важный момент, структурно общий с организацией процедуры перебора для ДП, будет обсужден здесь на примере ТЧ, “по авторским ожиданиям”, не слишком увеличивая сложность восприятия текста – с минимальным уклоном в программирование.

Перед нами – снова та же фигура о с неявной осью симметрии L-R и случайным образом фиксированной позицией A (рис. 3). Вспомогательные построения, методически иллюстрирующие подход, имеют элементами касательные с точками их пересечения, что на трех врезках слева комментируется: в виде структурных формул их идентификации (на нижней; в той же нотации, что и на рис. 1, 2 ), в стиле “словесно выраженного” критерия целевых соотношений (на средней врезке) и в специфике организации квартета вурфов, по рецептам для которых и формируется четверка основных W-функций {w1, w2, w3, w4} (вверху). Все вспомогательные построения соответствуют финальной картине поиска оси L-R: найден ее полюс P, т.е. на прямой P-A уже известно целевое положение подвижной B, следовательно, определена и позиция T согласно правилу T => t(A) × t(B). Изображенная композиция наглядно показывает, какие именно две ТЧ детерминируют искомую картину. Левая ТЧ образована чевианами T-L, t4-A, t2-B с узлом o1 (так мы будем называть общую точку ТЧ); правую – компонуют T-R, t3-A, t1-B с их узлом o2 (т.е. чевиана T-R является концевым участком T-L для “поляры симметрии” L-R, общей этим двум ТЧ). Критерий получения целевой композиции теперь не связан с условиями гармонизма для квартетов вершин и пересечений, как это требовалось в работе с ДП. Их заменили проверки на попарное равенство ординат W-функций, что для целевой позиции выражается оценками w1_B = w2_B, w3_B = w4_B, где w1 ≡ W(A, o1, a, t4), w2 ≡ W(B, o1, b, t2), w3 ≡ ≡ W(B, o2, b', t1) и w4 ≡ W(A, o2, a', t3). На каждом шаге вычисления W-функций именно новая позиция b(n) задает всю ею детерминируемую композицию ТЧ. Шаг n процедуры перебора фиксирует пару A, b(n), в итоге из элементов формируемой ТЧ оказывается заданной единственно f(n) (рис. 4; в роли плюккерова полюса поляры A-b(n), в финальной диспозиции рис. 3 – “под именем T”). Появление остальных элементов зависит от выбора положения для вершины e, реализующего критерий общего узла. Требуется найти такую позицию для “подвижной вершины e” (той, что в финале поиска получит “имя” L), чтобы касательная t(e) (вводимая к уже имеющимся t(A) и t(b)) “уникальным образом замкнула треугольную конструкцию” для о (он должен быть вписан в треугольник из касательных), итогом чего чевианы, соединившие вершины t_j треугольника с точками касания A, b и e, “максимально кучно сошлись бы в узле” (в идеале – пересеклись в одной точке). Следовательно, выбор вершин необходим двойной: для n-го шага, задавшего b(n), требуется, варьируя вершины по i, подобрать адекватное критерию положение для e(i). Логика “двух степеней свободы для организации шаблона (конструкции) ТЧ” обусловила требования к численной схеме: компьютерная программа поиска оси должна иметь внешний цикл, задающий координаты b(n), и цикл внутренний (“вложенный”), путем перебора по i реализующий (согласно критерию общего узла для ТЧ) наилучшее положение для вершины e(i). Внутренний цикл поставляет внешнему на каждом n-ом шаге сет необходимых данных для вычисления четырех вурф-квартетов {w1, w2, w3, w4}, из которых по завершении работы внешнего цикла оказываются скомпанованными четыре W-функции, требуемые для окончательного выбора целевой конфигурации, т.е. появления адекватных координатных оценок вершин L и R. Поведение этой четверки W-функций (с показом меткой «ромб» номера вершины для B) демонстрирует правая (вверху) врезка на рис. 3. Для номера, безошибочно оценившего позицию B, попарные равенства значений для квартета W-функций выполнены, однако у пары w3, w4 найдена еще одна вершина (помечена литерой “b”) с равенством вурфов, что сигнализирует (аналогично особенностям W-функций в схеме с шаблоном ДП) о критерии попарного равенства как необходимом, но не принадлежащем разряду достаточных. Этот пример демонстрирует необходимость введения контрольных проверок в алгоритм.

Рис. 3.

Вид целевой композиции переборного процесса поиска оси L-R с привлечением схемы ТЧ (триад чевиан) и модель поведения W-функций {w1(n)÷w4(n)}, выполняющих поиск вершины B и отбраковку ложного позиционного решения b (врезка вверху справа). Показ функции связи вершин L(i) и B(n) (на врезке внизу). Остальные пояснения в тексте.

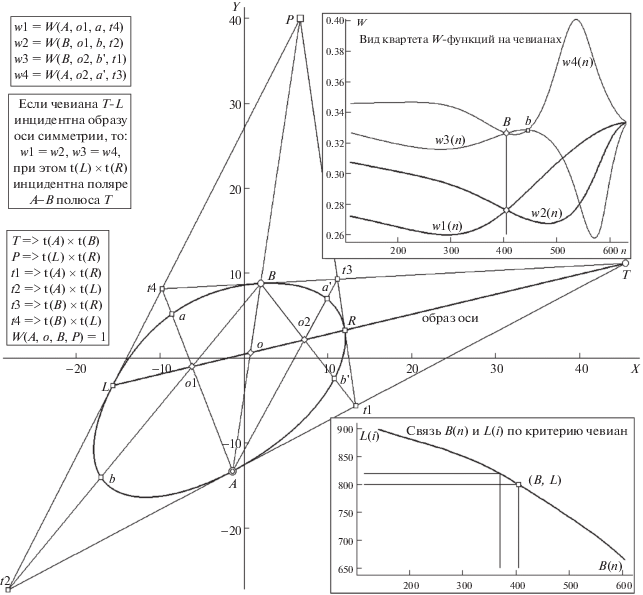
Рис. 4.

Демонстрация этапа переборного процесса (локализации на о его неявной оси L-R), идущего с участием ТЧ {A-a, B-b, f-e}, обеспечивающей на чевианах вычисление квартета W-функций, а на луче A-B(n) – получение оценок N(n) (врезка вверху слева) и F(n) (врезка в середине справа), отсекающих ложные решения для “b” и “b'”. Структурные формулы, задающие композицию, показаны на врезке справа вверху. Остальные пояснения в тексте.

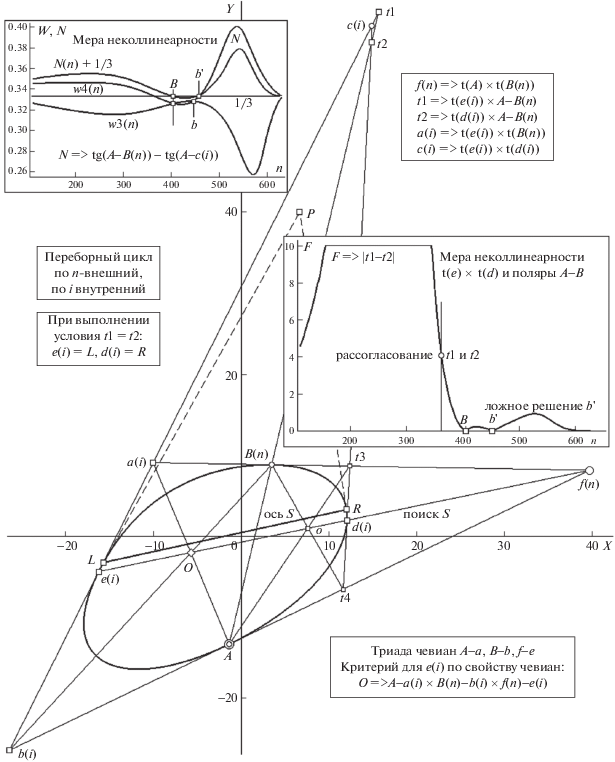
На рис. 4 показан фиксированный (по n во внешнем цикле) шаг процедуры поиска оси L-R для “ожидаемой” позиции B(n) и ошибочных координатах для e(i) в переборе по i во вложенном цикле (на этом этапе e(i) является плохой позиционной оценкой для L). На врезках (слева вверху и справа в середине рис. 4) дана сводка модельных тестов по ряду проверочных приемов. Учет оценок, получаемых в итоге их включения, позволяет избрать верное решение. Реализации возможных проверок альтернативны и затратно близки, а идея – общая и чрезвычайно простая. Описав ее, перечислим кратко приемы контроля.

Идея комбинирует триаду проективно инвариантных свойств: однозначную связь плюккеровых внешнего полюса P и поляры для осесимметричного о; ненарушаемую ее особенность гармонической вурф-оценки для любого луча P-A с квартетом {P, B, o, A} (рис. 3) и тезис теоремы 2 об обязательном существовании шаблона ТЧ для любой пары вершин, фиксированных на контуре о. Первое свойство гарантирует для касательных t(L) и t(R) в концевых вершинах хорды=оси обязательность их пересечения на луче P-A, тогда как третий тезис утверждает для любой пары B(n), A возможность построения шаблона ТЧ (даже двух, но достаточно и одного). Следствиями “свойства три” будут: гарантированная возможность построения для любой ложной гипотезы “e(i)-d(i)” о положении оси на луче f(n)-e(i) (где полюс f(n) задан “ложной” полярой A-B(n), не совпадающей с целевой A-B) шаблона ТЧ с “наверняка” не выполняемой инцидентностью полюса c(i) (для его поляры d(i)-e(i); рис. 4) прямой A-B(n). Таким образом, процесс обработки о по всему диапазону перебора по n единообразно формирует шаблоны ТЧ, причем имеется возможность на каждом шаге n произвести оценку отклонения полюса c(n) от прямой A-B(n) (если шаблон построен, c(i) логично обозначить как c(n)). Эти оценки можно делать по-разному (врезки на рис. 4). Наконец, универсальное “свойство два” поможет в ситуации (в этой статье, не описываемой отдельным разделом по причине лимита на объем), когда объектом анализа являются частные представители семейства о – из подсемейства кривых Ламе (игнорируя генезис, их еще называют “суперэллипсами”), у которых две оси симметрии, а стало быть, возможна ситуация (когда ложная ось для ортоформы параллельна истинной) отсутствия отклонения c(n) от второй оси, где отбраковке гипотезы поможет оценка W(P, B, o, A) ≠ 1.

Вернемся к методам контроля неверных гипотез о положении оси (рис. 4). Помимо непосредственного вычисления расстояния от точки c(n) до прямой A-B(n), на рис. 4 не показанного из-за перегруженности данными сходного типа, целесообразно производить оценку F расстояния между точками t1 и t2 в пересечениях с прямой A-B(n) касательных t(d(i)) и t(e(i)) (средняя врезка справа на рис. 4; для шага внешнего цикла эти вершины правильнее обозначить d(n) и e(n)). Аналогом степени неколлинеарности на врезке слева вверху показан ход оценки N, вычисляемой в виде разности тангенсов углов наклона (в любой прямоугольной системе декартовых координат) прямых A-B(n) и A-c(n). Врезка с функционалом N демонстрирует возможность дать сигнал о выбраковке ложных решений для позиций “b” и “b'”, не совпадающих по номеру для N(n) и сравниваемой пары w3(n), w4(n). Картина с привлечением оценки F (на средней врезке справа) показывает второе нулевое отклонение “b'” для F, не совпадающее по номеру вершины с ложным номером для пары w3(n), w4(n). Наконец, добавим замечание относительно значимой оптимизации процедуры поиска оси, связанной с эмпирически показанным отсутствием необходимости участия в ней шаблона “ТЧ-2”, вычисляемого по правой триаде чевиан A-t3, B-t4, f-d.

Все проведенные тесты (числом около полусотни для разных ортоформ задания о и вариаций позиции A) показали, что в рамках тезиса “выбрать в качестве e(i) вершину на дальней от f(n) стороне контура о”, второе (всегда существующее согласно теореме 2) позиционное решение в виде “ТЧ-2” не может нарушить тезиса однозначности в оценке координат c(n) – при построении для ближней стороны о на прямой f(n)-e(i'). На рис. 4 намеренно показаны полюса t4, t3 и узел o, единый для чевиан {A-t3, B-t4, f-d} в ситуации ложной гипотезы d(i)-e(i) о позиции оси. Этот результат, обязательный (по соображениям симметрии) для целевой конфигурации, в продемонстрированном на рис. 4 примере не может быть обоснован теоретически. В других позициях по n для B(n) условие единого узла в “ТЧ-2” может нарушиться (но быть перестроеным по i в режим выполнения для вершин d(i') – за счет неисполнения критерия для e(i') в “ТЧ-1”). Сделанный комментарий завершает обзор методических приемов и модельных испытаний – с применением аппаратов ДП и ТЧ для овалов с неявной аксиальной симметрией – в рамках общей задачи поиска ЭС гладкой чисто выпуклой кривой.

3. ИДЕИ И СХЕМЫ ПОИСКА ЦЕНТРА РАДИАЛЬНОЙ СИММЕТРИИ МЕТОДОМ ДП

Объектом анализа становится теперь о, ортоформа которого обладает радиальной симметрией (в качестве синонима используется термин центральная). Как и в случае с о, имеющим осевую симметрию, описываемые далее методы обнаружения центра о так же подразумевают работу с объектом в любом ракурсе его регистрации. По этой причине нет резона строить процесс поиска центра O в опоре на декартов признак ортоформы: “любая хорда, проходящая через O, делится этой точкой пополам”. В общем случае этот закон не адекватен, в итоге требуется привлечь проективно инвариантные признаки данного типа (неявной) симметрии. Формулировка обобщенного признака радиальной симметрии для о, представленного ортоформой, включает два независимых свойства ЭС: “для любой хорды h, проходящей через центр O, две касательные в ее концевых точках A, B (на контуре о) пересекаются в несобственной точке Pt, принадлежащей проективной прямой p; хорда h в пересечении Ph с p образует гармонический квартет {A, O, B, Ph}”. При неортогональной регистрации о (в форме неявного проявления ЭС) прямая p, “живущая в бесконечности”, передислоцируется в окрестность о, где бывшую p именуют теперь «линией горизонта» HL, каковой инцидентны T и H, для ортоформы заявленные как Pt и Ph соответственно. Если вспомнить аналогичные определения для осесимметричного о, нетрудно усмотреть «плюккерову взаимность» проявления ЭС в диаде типов симметрии: прямой оси дуален ее полюс, тогда как точке O центра дуальна прямая HL. Перейдем к обсуждению свойств ЭС и идей их переборно процедурной детекции на иллюстративном материале рис. 5.

С той же методической целью, что и при компоновке рис. 1, законы проявления свойств радиальной симметрии – применительно к схеме привлечения ДП в двух формах презентации (общего вида и в качестве ортоформы) демонстрирует рис. 5. Процесс поиска O строится в той же стартовой постановке со случайным выбором вершины A, что и в уже описанных ранее вычислительных подходах. Структурные формулы, помогающие понять “логику” композиции, образуемой в процедуре, приведены на врезке слева и используют типовую нотацию. Начнем рассмотрение особенностей включения ДП в процесс поиска O на модели целевой композиции, реализуемой на примере ортоформы (врезка справа).

Рис. 5.

Метод переборного поиска центра O для о радиальной симметрии с привлечением схемы “тройственных дуальных пар” (ДП: T..U и T..F). Аналог финальной конфигурации для варианта ортоформы показан на врезке справа внизу. Остальные пояснения в тексте.

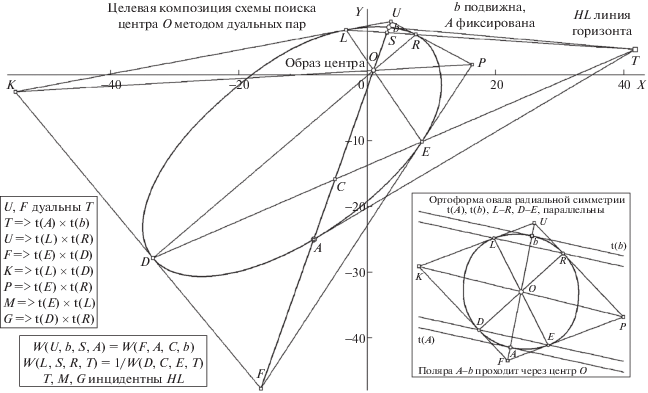
Признаки радиальной симметрии, сформулированные выше, выражаются для случая ортоформы, в основном, через свойства параллельности касательных и хорд. Предъявлен случай финальной композиции, когда номер вершины b задает хорду A-b, проходящую через искомую O. При этом из несобственной точки T  ', где “пересекаются параллельные” касательные t(A) и t(b), вычислены направления прямых L-R и D-E такие, что полюс U в пересечении t(L) и t(R), как и F на пересечении t(D) и t(E), образуют (в полюсах U и F, по отношению к T  ') два шаблона ДП, т.е. U является полюсом для плюккеровой поляры L-R, F  играет ту же роль для D-E, а поляра A-b с ее полюсом T  ' являются элементом, дуальным для обеих ДП. Описанная конфигурация имеет проективно инвариантные свойства, учет которых детерминирует список позиционных критериев целевой картины, пригодный как для ортоформы (врезка), так и для презентации в общем виде (в скрытой форме для ЭС).

Следствием того, что T  ' детерминирут проективный пучок лучей T  '-A, T  '-b, T  '-R-L и T  '-E-D для ортоформы, а в целевой картине неортогонального ракурса эта конфигурация из полюса T (с конечными координатами окрестности о, и исключительно из одних лишь соображений симметрии) выглядит пучком лучей в направлении A, b, R и E, реализуются выполненными следующие закономерности: 1) прямая, соединяющая точки P и K (их структурные формулы “P => t(E) × t(R)” и “K => t(D) × t(L)” приведены на врезке слева), проходит через центр O; 2) на хорде U-F вурфы W(U, b, S, A) и W(F, A, C, b), где S и C – инцидентны A-b в пересечениях с T-L и T-D, имеют равные значения; 3) значения вурфов W(L, S, R, T) и W(D, C, E, T) обратно пропорциональны; 4) триада T, M, G лежит на линии горизонта HL, при том, что M задает операция t(E) × t(L), а G определяется по “t(D) × t(R)”.

Условие 1 фиксирует позицию O на A-b. Независимые закономерности 2÷4 логично привлечь (в разных комбинациях) либо для критерия достижения (варьируемой позицией b(n)) целевой конфигурации, либо для отбраковки ложных решений. Позицию O можно вычислить (не прибегая к оценке координат P и K, предваряемой формированием квартета касательных) через решение линейного уравнения W(F, A, O, b) = W(U, b, O, A). Указанная “пластичность” в привлечении теоретических положений для оптимальной организации процедуры детекции O, а также “априорная избыточность” их списка (т.е. отсутствие “нужды в дублировании” проверочных оценок, диктуемое на уровне теории), при работе над техническими реализациями могут способствовать переходу предлагаемых подходов из квалификационной аттестации “модель” в категорию “автоматическая система”.

Перейдем к обсуждению реализованной модели поиска O. Концепцию организации процедуры можно назвать уже стандартной: во внешнем цикле обработки (переменная n) происходит дискретная смена ориентаций хорды A-b(n), так что вершина A, позиционно фиксированная случайным образом, совместно с текущим положением вершины b(n) на каждом шаге n задают (итогом операции “T(n) => t(A) × t(b(n))”) позицию полюса T(n), из которого луч сканирования (по переменной i во внутреннем цикле численной схемы) для терминальных фрагментов A-b(n) находит перебором сначала для R(i) искомое положение R(n) такое, что поляра R(n)-L(n) детерминирует через терминальные касательные позицию полюса U(n), располагающегося максимально близко к поляре A-b(n), после чего такой же поиск со стороны A перебором вершин по i приводит к формированию второго шаблона ДП, где луч из T на E(i) задает в финальной позиции E(n) текущую композицию ДП в виде полюса F(n) для поляры E(n)-D(n) (рис. 6, где полюс F не показан из-за его локализации вне избранного поля рисунка). Позиционные итоги шага n должны быть далее проверены на соответствие заранее заданным и процедурно введенным критериям целевой картины.

Опишем функции контрольных оценок, использованных нами в модельных тестах. В качестве одного из показателей отклонения текущей конфигурации от искомой работала оценка r(n), вычисляемая в виде расстояния между точками c1 и c2 (позиции первой и второй задаются формулами c1(n) => A-b(n) × P(n)-K(n) и c2(n) => L(n)-E(n) × R(n)-D(n) соответственно, означающими вычисление координат пересечений прямых, заданных парой точек), целесообразность чего является следствием особенности 1, свойственной целевой композиции. Ход этой функции в виде кривой r(n), где позиция “B” соответствует искомому расположению вершины B(n), показан на правой нижней врезке рис. 6. На той же врезке воспроизведено поведение 10-кратно увеличенной оценки u(n), равной модулю разности W-функций W(U, b, S, A) и W(b, C, A, F), равенство которых для целевой картины декларирует свойство 2. Наконец, там же демонстрируется поведение функции f(T, M, G), оценивающей степень “неколлинеарности” триады {T(n), M(n), G(n)}, в целевой картине имеющими согласно признаку 4 обязательную инцидентность линии горизонта HL (что и проиллюстрировал общий вид “не-целевой” композиции – с уклонением M от прямой G-T (рис. 6)). Врезка слева вверху показывает ход оценки степени “не-инцидентности” полюса F(n) относительно “главной” поляры A-b(n) при “почти круговом” сканировании вершин о (от правой окрестности L до левой окрестности R – через D, A, E), где L и D ведут себя (согласно радиально симметричным особенностям расположения вершин на ортоформе, что “убеждающее” демонстрирует врезка на рис. 5) симметрично паре E, R относительно фиксированной A. Стандартным оказался и “расклад”: ложные решения, фигурирующие на массиве вычисляемой разности W-функций u(n) (ложные решения при метках “ромб”, на врезке рис. 6 обрамляющие позицию “B”, где u(n) = |W(U, B, S, A) – W(F, A, C, b)|), однозначно отвергаются системой проверочных оценок r(n), f(T, M, G) и N(n). Степень уверенности в адекватности итогового решения (по причинам целесообразности создания “запаса робастности” в ситуации наличия значительного уровня координатного шума, что реально при гипотетической технической реализации развитых здесь подходов) может быть увеличена благодаря дополнительному включению в процедуру поиска о деклараций тезиса 3 (в опоре на свойства W-функций, независимые от сформулированных для u(n), что не показано на рис. 6 по причине перегруженности иллюстративными данными, мало отличающимися по характеру поведения). Этими прогностическими соображениями мы заканчиваем описание метода оценки координат O, представляющего центр радиальной симметрии о, переходя к рассмотрению той же задачи переборного характера, но теперь реализуемой не посредством тройственной схемы ДП, а с привлечением инструмента ТЧ.

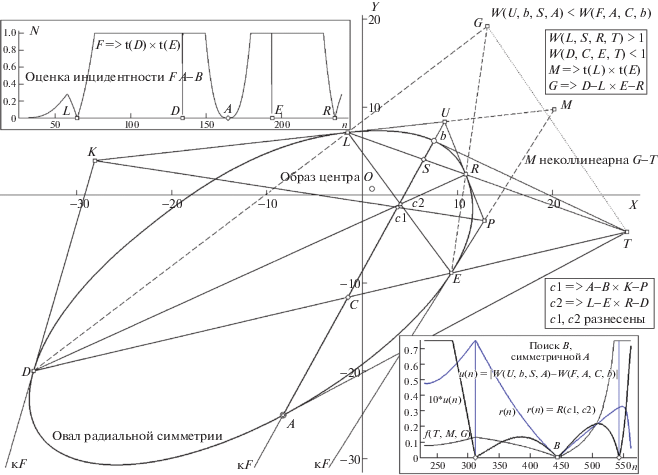
Рис. 6.

Этап переборной процедуры поиска O у о радиальной симметрии методом “ДП” с использованием финального критерия W(U, b, S, A) = W(F, A, C, b) для основной функции u(n) и при участии контрольных r(n), f(T, M, G) (графики на врезке справа внизу) и R(n), в финале фиксирующей {L, D, A, E, R} (врезка слева вверху). Остальные пояснения в тексте.

4. О МЕТОДАХ ПОИСКА ЦЕНТРА РАДИАЛЬНОЙ СИММЕТРИИ О НА ОСНОВЕ СХЕМ ТЧ

Общая структурная организация обсуждаемой процедуры обработки о на примере привлечения “инструмента детекции в виде тройственных ДП”, оставаясь неизменной на уровне идеи двупараметрического перебора вершин и роли контрольных проверок для отсева неадекватных позиционных гипотез – при переходе от осесимметричного объекта к фигуре с центральной симметрией (и при смене “приема детекции” ЭС), с точки зрения количества теоретически приемлемых вариантов реализации переборного процесса – по итогам модельных тестов демонстрирует их заметное увеличение в случае о радиальной симметрии. Предпринятый нами предварительный анализ вариативности реализаций при переходе к ТЧ-схемам выявил еще большее количество “работающих версий” (в рамках сохраняющейся вышеупомянутой общей концепции), в сравнении с применением схемы ДП. Эти обстоятельства повлияли на акцентацию в подаче материала по заявленной теме. Больше внимания при рассмотрении схем ТЧ будет уделено “инвариантным блокам”, из которых “можно конструировать процедуру обработки”, нежели ей самой, из конкретных блоков заданным образом собранной. Оптимальным вхождением в тему представляется сравнительное (о общего вида и его ортоформа) описание элементов и композиций, в построениях с ТЧ обладающих проективно инвариантными характеристиками (рис. 7).

Рисунок 7 организован по той же методике, что и рис. 5: основная часть картины дает детализированное представление о трансформациях построений с участием ТЧ, которые происходят при переходе от презентации ортоформой (на врезках) к проекции о общего вида, при том, что изображается целевая композиция (завершившегося поиска O). Врезка (нижняя, справа) на модели о радиальной симметрии изображает структуру двух ТЧ для рандомно фиксированной позиции A (относительно центра O, заданного явным образом). Список структурных формул в стандартной нотации, позволяющий проследить логику последовательного построения “каркаса для вурфов”, размещен во врезке справа вверху (запись вида “U => A-L × B-F” означает, что координаты U вычислены в пересечении прямых, которым парно инцидентны A, L и B, F). Структура ряда вурфов, порождаемых гармоническими квартетами в целевой композиции, приведена на левой врезке внизу. Как это свойственно презентации о в ортоформе, пары параллельных хорд, фиксируемые в ней по законам симметричных отношений, имеют полюсами “пересечения” несобственные точки, принадлежащие несобственной прямой. В неортогональной проекции общего вида они приобретают конечные координаты, что упрощает “запись и восприятие их участия” в организации коллинеарных квартетов для структур вурфов.

Рис. 7.

Искомая конфигурация вершин и полюсов в процедуре детекции центра O (для о радиальной симметрии, с рандомно заданной A) с привлечением аппарата “ТЧ” и целевых критериев коллинеарности {T, E, c2, O, c1, G}, {T, K, H, U} в презентации общего вида и на примере ортоформы о (врезки справа внизу и слева вверху). Комментарии в тексте.

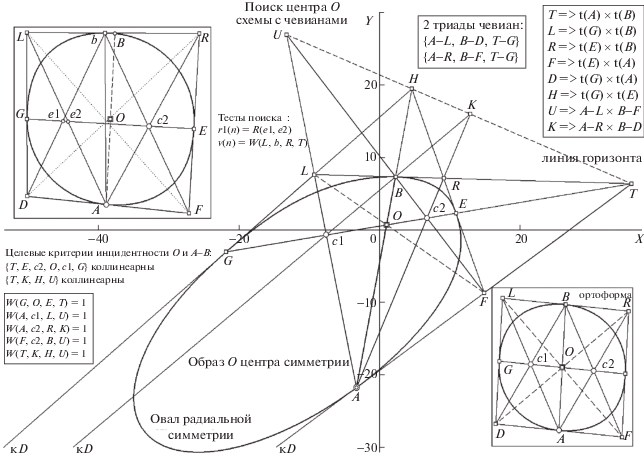
Проследим последовательность задания элементов при формировании требуемой композиции на ортоформе. Для случайно выбранной A задана симметричная ей вершина B (AO = OB). Согласно теореме 2, для фиксированной пары A, B обязательно существуют два решения по схеме “ТЧ”. Для конкретного задания геометрии о найдено положение такой хорды G-E (проходящей через O), что на пересечениях касательных в A, E, B и G из сета полюсов {D, L, R, F} образуется “каркас=параллелограмм”, позволяющий указать положения двух композиций ТЧ. Правую образуют A-R, B-F и хорда G-E, продолженная до несобственной T' (после перепроецирования к виду с неявным ЭС обозначаемая уже как T на основном поле рис. 7). Левая ТЧ составлена из пары A-L, B-D и той же, “до T  ' расширенной” G-E. Из условий обязательной параллельности пар {A-R, B-D}, {A-L, B-F} (с их несобственными K' и U') следует, что при неявном представлении о линии горизонта HL будут инцидентны {T, K, H, U}, а вхождение H в HL – следствие параллельности D-L и R-F. Если заметить, что квартет {T, K, H, U} является проекцией коллинеарной четверки {T, R, B, L} из вершины A, то станет ясна аргументация гармонического и “неочевидного” свойства W(T, K, H, U) = 1, зафиксированного в нижнем ряду списка на левой врезке, ибо квартет {T, R, B, L} для ортоформы имеет вид {T ', R, B, L}, где отрезки R-B и B-L из тех же соображений симметрии должны быть равной длины (что возвращает нас к обсужденному примеру гармонической композиции w[x, x, ∞] ≡ 1, а “документальным примером триады w[2, 1, 3 ] ≡ 1 выступает” коллинеарный квартет {F, c2, B, U}). Подобные компарации позволяют без затруднений “доказать внушительный ряд утверждений” (шире списка из пяти уравнений, приведенных на левой врезке) о гармонических свойствах коллинеарных квартетов, извлекаемых из картины отношений линейных элементов (показанных на рис. 7 общего плана), желательных для включения в конструируемую процедуру обработки (с целью ее оптимизации) – на ролях данных для основной W-функции (в переборной схеме детекции O) либо для организации массива {R_k(n)} независимых проверок на интервале n, отсекающих ложные оценки “по факту несовпадения искомых номеров в разных R_k(n)”.

Прояснению моментов, связанных с утратой гармонических свойств для текущих композиций ТЧ в их “поисковом виде”, может помочь вид ортоформы о на этапе перебора с несимметричной (относительно A) позицией b, показанный на верхней врезке слева. На численных моделях получена устойчивая альтернатива: во внутреннем цикле перебора, на этапе поиска шаблонов, не удается сформировать две композиции ТЧ с общим носителем G-E “в соосном варианте – для пары чевиан из разных комплектов”, реализуемого для финальной конфигурации (нижняя врезка справа). Единообразно выбирая по отношению к полюсу T либо дальнюю, либо ближнюю часть контура о, одну композицию ТЧ (на врезке – правую) стабильно=надежно использовать в качестве контрольно эталонной, где все три чевианы пересекаются в “c2”, тогда как вторую, с ее нереализуемым критерием пересечения пары чевиан на хорде G-E, привлекать в качестве “индикатора сближения с искомой картой отношений” (с ситуацией двух ТЧ с общей хордой), где мерой сближения избрано, например, расстояние между “рассогласованными” узлами “e1” и “e2”. Условие этой проверки вынесено на поле рис. 7 в качестве одной из контрольных функций r1(n), к числу которых отнесено и вычисление v(n) = W(L(n), b(n), R(n), T(n)) – 1. Эту $v(n)$ можно аттестовать и как “основную”, но для сета функций от n не так важна принадлежность к W-функциям, как общая задача для них: найти номер вершины с максимальным числом совпадений по всему их списку. Роль “контрольной можно назначить” оценке расстояния между позициями “A-b(n) × G(n)-T(n)” и “L(n)-F(n) × D(n)-R(n)”, поскольку обе “обязаны” совместиться на целевой конфигурации в искомой O (правая врезка “зримо подтверждает это”). Таким образом, подобный функционал, не будучи W-функцией и не требуя затрат на оценку позиций дополнитльных касательных и полюсов, не только укажет “истинный номер вершины B”, но и задаст искомые координаты неявного центра симметрии.

Была предпринята тест=проверка тезиса о произвольности выбора в альтернативе: “создав правый шаблон ТЧ, по левой композиции – оценить разброс e (r1(i) = R(e1, e2))” либо “левый шаблон ТЧ построив, по данным правой композиции дать оценку для диады o (r2(i) = R(o1, o2))”. Итоги численной модели (на том же о, что изображен на рис. 7), для шага внешнего цикла с фиксированной верной позицией B и варьируемым положением оптимизируемой вершины G(i)), демонстрируются на рис. 8. Показано поведение обеих контрольных функций r1(i) и r2(i) (совместно с рядом других, – с тем же функциональным назначением). Помимо “динамики оппонентных” кривых r1(i) и r2(i) рис. 8 воспроизводит ход функций r3(i) и r4(i): для сета полюсов T, H и “точек схода” U, K функции оценивают степень неколлинеарности триад {T, H, U} и {T, K, H}. Для каждой триады вычисляются угловые (через тангенс) отклонения хорд, инцидентных комбинируемым парам точек в триаде. При условии, что луч T-G(i) включает центр O, финальная диспозиция четверки на прямой HL должна обеспечить их гармонический порядок. На том же графике отражено поведение кривой w(i) = 1 – W(G(i), O(i), E(i), T), для которой гипотеза о расположении центра задается вычислением пересечения O(i) => A-B × T-G(i). Поскольку в окрестности G отклонение от 0 у трех функций {r3(i), r4(i), w(i)} весьма незначительное, на малую врезку в поле рисунка вынесен фрагмент их сета с удесятеренной амплитудой. Да и сама W-функция w(i) настолько мала в масштабе величин угловых отклонений r3(i), r4(i), что ее ординаты на основном графике пришлось “поднять множителем 25×”.

Рис. 8.

Роль контрольных функций {r1(i)÷r4(i)} (во вложенном цикле схемы перебора по i, на шаге с фиксированной полярой A-B и варьируемой вершиной G(i)) и W-функции w(i), подтверждающих гипотезу о B(n), как симметричной A. Остальные пояснения в тексте.

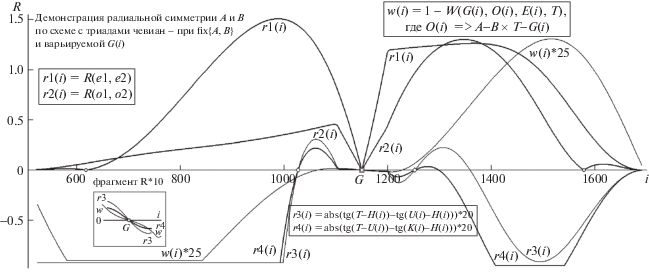
Завершим тему “участия ТЧ в задаче поиска O” демонстрацией поведения функций r1(n), r2(n), r3(n) и $v(n)$ во внешнем переборном цикле численного эксперимента с тем же центрально симметричным о (и не измененной позицией вершины A) при условии, что все оптимизации для ТЧ благополучно завершены (критерий общего узла для ТЧ на каждом шаге n соблюден; рис. 9). Напомним, что $v(n)$ = W(L(n), b(n), R(n), T(n)) (и уменьшение на единицу ординат W-функции целесообразно для отображения нулевым уровнем всех ее абсцисс с гармоническим значением, что обеспечивает единообразие их представления в совместном показе с функциональными оценками rj(n), выделяющими именно уровень 0). Иллюстрация воспроизводит ход оценок в диапазоне перебора по n, соответствующем фрагменту контура о в секторе поиска между лучами R-A и L-A (с примерно центральным расположением на нем целевой позиции B). На графике “двойным квадратом” помечен номер вершины “B”, на который “указывает весь квартет функций”, в то время как для ложных решений максимальное совпадение номеров наблюдается лишь у пары оценок (“$v(n)$ – 1”, r3(n); номера совпадений для них маркированы меткой “малый кружок”), что логично расценить “приемлемой адекватностью критерия совпадений” для однозначной сепарации искомого позиционного решения. Этой демонстрацией завершим рассмотрение методов поиска ЭС и результатов моделирования по ряду сценариев для них (с привлечением композиций “ДП” и “ТЧ”), переходя от вариантов осевой и радиальной симметрии к новому ее типу – ротационному (будет описан частный случай R3).

5. О МЕТОДАХ ПОИСКА ЭС С ИСПОЛЬЗОВАНИЕМ “АППАРАТА ТЧ” ДЛЯ О ТИПА R3

Тип симметрии вращения проще всего определить через операцию, порождающую ортоформу о. Положим существующим угловой фрагмент выпуклой дуги длиной 2π/n такой, что n его дискретных поворотов вокруг точки центра, гладко сопрягающих “начало одной дуги” с концевой точкой следующей, образуют замкнутую кривую, являющуюся о с типизацией Rn, в которой n назовем индексом вращения. Легко понять, что при четном n фигуры будут относиться к радиально симметричным, а при осевой симметрии самого порождающего фрагмента – к аксиально симметричным с n осями. В этой таксономии о радиального типа удовлетворяет номинации R2, поскольку его ортоформа, разрезанная любой центральной хордой, одним поворотом дуги=половинки на π восстанавливает свою целостность. Естественно, что генерации, порождающие “Rn” через поворот (при n > 1) не могут быть признаком для проективно инвариантного описания таких о. В рамках этой задачи единственно разумной остается идея опоры на ансамбль корреспонденции (АК, представляющий собой упорядчный сет n вершин о, с произвольной точки разбивающих и n-кратным поворотом воссоздающих ортоформу), для детекции которого и дальнейшего привлечения АК в поиске центра и создания проективно инвариантного эталона, были разработаны универсальные алгоритмы обработки (Николаев, 2016). Наименее сложной и наиболее часто встречаемой в “технологичном социуме” разновидностью Rn является о R3 (“сглаженный треугольник”; цепь касательных к любому АК ортоформы представляет собой описанный вокруг о правильный треугольник). Идею и проективно инвариантные методы поиска O (образа центра о “R3”) – “с участием ТЧ” – мы и рассмотрим далее.

Рис. 9.

График функции $v(n)$ – 1 ($v(n)$ = W(L(n), b(n), R(n), T(n)) наряду с контрольными {r1(i)÷r3(i)}, “единогласно голосующими” за безошибочную позицию B (метка “двойной квадрат”), отвергая ложные гипотезы (метка “малый кружок”) сообразно критерию “не максимального числа их подтверждений”. Остальные пояснения в тексте.

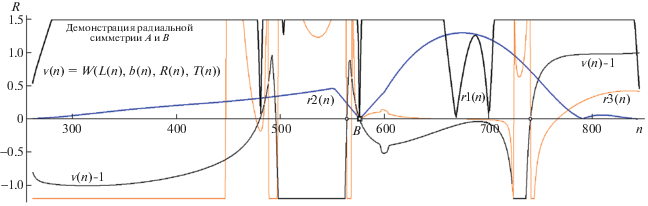
Данный раздел тематически нарушает сценарий описания разработанных методов детекции ЭС с последовательной “сменой инструментария – от ДП к ТЧ” в рубрике тип симметрии о. Причина отсутствия раздела “роль аппарата ДП в процедурах поиска ЭС для о типа R3” состоит в нецелесообразности рассмотрения алгоритмов, не имеющих, по авторской оценке, реального шанса технической реализации. Проведенные нами тесты на моделях с включением ДП показали, что для о ротационного типа (при случайном выборе стартовой вершины A) велик процент случаев, когда узел одной из ДП настолько сближен с границей о, что возможный уровень координатного шума при оценке позиции полюса по данным для касательных может лишить достоверности последующие вычисления ЭС.

Для аппарата ТЧ набранная статистика тестов получилась “не внушающей тревог в плане робастности”, что делает осмысленным описание идей решения стоящей задачи и модельных итогов по ней, к чему мы и переходим. Начнем с того, что “универсальная пригодность схем ТЧ на ролях детектора АК”, несмотря на ее кажущуюся “очевидность”, является тезисом ложным. Рассмотрим левую схему рис. 10, где на модели ортоформы показано, что лишь при условии совмещения стартовой A* со следом одной из трех осей симметрии о композиция ТЧ будет иметь узлом образ центра о, что должен подтверждать критерий равенства вурфов на чевианах A*-D*, B*-U* и G*-E* (условие равенства вурфов – на левой врезке внизу). Вероятность такого совпадения близка к 0. В случае задания A' вне выделенных шести вершин о гипотеза об аппроксимации образа центра позицией узла o' оказывается ложной вкупе с нарушением равенства значений вурфов на чевианах данного расположения (та же нижняя врезка воспроизводит нотацию неравенства W(A', o', e', E') ≠ W(R', o', h', H') ≠ W(L', o', f   ', F')). Таким образом, надежды на тривиальное решение задачи не оправдываются, и надо предлагать действительно универсальный подход к проблеме.

Идея метода с необходимой всеобщностью применения достаточно проста: для A (с ее случайным расположением) требуется найти позиции двух точек, симметричных по отношению к двум осям (тогда третью ось легко локализовать, хотя для оценки позиции O достаточно безошибочной оценки и двух). На правой схеме рис. 10 показано необходимое построение по этой процедуре (на верхней врезке справа дан список структурных формул, позволяющих уяснить логику в задании операций и функциональность картины). Итогом переборного процесса должно стать формирование двух композиций ТЧ: триада A-D, B-U и G-K обеспечивает инцидентность узла с1 оси “1” (g-K), тогда как ТЧ {A-E, H-R, F-L} со своим узлом с2 задает на h-R ось “2”. При адекватном исполнении всех “установочных и проверочных” требований преобразуемая конфигурация согласуется с правой схемой рис. 10, что позволяет воспользоваться условием идентификации оси “3” (по паре пересечений “t(h) × t(g)” и “h-L × g-R”, ей инцидентных, что показано на верхней врезке справа).

Рис. 10.

Новый подход к задаче поиска неявного центра O (у о типа R3) привлечением аппрата ТЧ: для рандомно заданной A идет поиск B, симметричной к A относительно “оси 1” K-g, совместно с детекцией L, симметричной – по “оси 2” R-h (правая схема). Схема слева показывает “неуспех прямого участия ТЧ” в поиске O. Комментарии в тексте.

Рис. 11.

Роль W-функций в переборном поиске вершин R, B на о R3 (верхний график) и отсечение ложных гипотез “r” и “b” контрольной r(n) согласно критерию: “истинную позицию фиксирует максимум числа голосов” (внизу). Остальные пояснения в тексте.

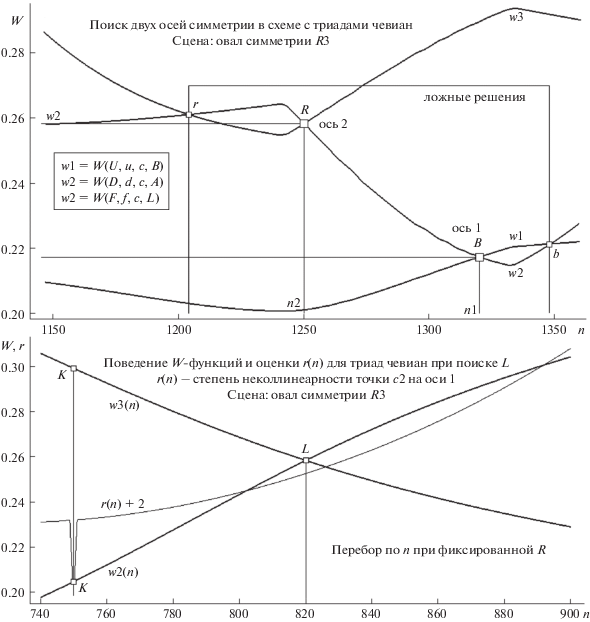
Опишем детальнее процесс детекции O и его установки. Поскольку основание всех перевычисляемых (по n) треугольных каркасов ТЧ – это фиксированная касательнная t(A), то перебор во внутреннем цикле (по i), формирующий ТЧ по критерию общего узла, не вызывает “срыва программы” к вычислению альтернативного для ТЧ решения: все для n вычисляемые треугольники (о в них вписан) монотонно меняют позиции второй своей стороны (образованной второй касательной, скользящей от f до d – c обходом около 1/3 периметра контура). При этом, поскольку схема ТЧ для каждого n реализуется, то наличие оценки узла c(n) позволяет вычислить триаду вурфов {w1, w2, w3}, обеспечивающих в финале обхода формирование W-функций W(U(n), u(n), c(n), B(n)), W(D(n), d(n), c(n), A) и W(F(n), f(n), c(n), L(n)). Из целевой установки для ЭС (детекция осей “1” и “2”) следует: на шаге n1, реализующем условия симметрии A и B относительно оси “1”, должно быть выполненным равенство w1(n1) = = w2(n1); на шаге n2, который обеспечивает оценку R(n2) в роли позиции, симметричной A относительно оси “2”, справедлив закон w2(n2) = w3(n2); что и демострирует рис. 11 (верхний график). Таким образом, для чевиан при переходе от B(n1) к R(n2) (обозначим B => R) происходят смены: D => E, L => K, H => U, G => F. “Не стоит удивляться”: и в этом случае для однозначного выбора целевой конфигураци нужны контрольные оценки, поскольку единственно условий w1(n1) = w2(n1), w2(n2) = w3(n2) не достаточно из-за наличия ложных гипотез (дублирующих решение R ложной r, а кроме истинной B предлагающих вариант b). На нижнем графике рис. 11 показан прием, дающий верный выбор для B при идентификации оси “1” (т.е. отсекающий ложную гипотезу “b”) и подтверждающий истинность оценки c2 для оси “2”. Однозначность финальных оценок достигается введением функции r(n, i), вычисляющей расстояние от c2(i) до прямой F-L(i) при зафиксированной по n позиции R (при “L => K” r(i) => 0, что фиксирует выбор “K”). На этом завершим краткий обзор темы “приемы ТЧ-поиска образа центра у о типа R3”, отметив, что новый подход оптимальней ранее предложенного (Николаев, 2016), так как, непосредственным образом локализуя O, не требует этапа предварительной детекции АК.

ЗАКЛЮЧЕНИЕ

В исследовании методов проективно инвариантной репрезентации фигур семейства о немало работ посвящено имеющим особенность скрытой симметрии различных типов (Николаев, 2014; 2016; 2017; 2019). Во Введении была сформулирована постановка одной из задач проективно инвариантного описания гладких выпуклых фигур, имеющих те или иные ЭС и “регистрируемых массивом вершин в произвольном ракурсе” (моделируемая оптика камер задана плоской центральной проекцией). Такая постановка подразумевает быстрое вычисление дискретного описания (устойчивого к трансформирующим влияниям проективного преобразования плоскости о) – в виде вурф-отображения либо посредством получения графа дескриптора (Николаев, 2016; 2019), формирование которых привлекает концепцию плоскостного вурфа (Депутатов, 1926). Интерес к вурфу, по сути ключевому элементу производной Шварца, рассмотренной более века назад, до сих пор интересен математикам (Овсиенко, Табачников, 2008). Элемент новизны доложенного материала – в том, что не только W-функции единообразно “нашли себе место” в переборном процессе поиска ЭС, выполняя роль позиционных маркеров искомой конфигурации, но и модельно протестированные инструменты детекции ЭС – схемы ДП и ТЧ-композиции – столь же органично вписались в концепцию разработанного подхода: все процедуры берут старт, вовлекая позицию случайным образом заданной вершины A контура о в “двухуровневый” комбинаторный процесс, где во внешнем цикле перебора формируются требуемые (для данного типа ЭС и “применямого инструмента”) W-функции, тогда как внутренний цикл обеспечивает построение “инструмента поиска” сообразно критериям его рабочей схемы.

Критерием формирования схем ДП (промоделированных версий – “одинарной” для случая осевой симметрии о и “тройственной” – для радиальной) заявлен и программно реализован аспект теоремы взаимности Плюккера (Акимова и др., 2014), в нашем случае (когда объект анализа не коника, а представитель семейства о), косвенно подкрепляемый теоремой 1 (о существовании двух ДП у прямой extL), “эвристически уточненной нами” – с отрывом от требований наличия для ДП внешнего носителя extL (при “гарантированной возможности для любого полюса, детерминируемого его плюккеровой полярой, построить второй, а по необходимости – и третий, дуальный/ные первому”). Эта “подвижная поляра A-b(n)”, варьируемая во внешнем цикле переборной процедуры, также является звеном, общим для обоих испытанных “инструментов детекции ЭС”. Аналогичный ситуации с ДП “прогресс применения” можно констатировать и для шаблона “ТЧ”. Теорема 2 о наличии двух позиционных решений в виде ТЧ для пары случайным образом заданных вершин о “эмпирически уточнена” тезисом о возможности эти решения однозначно упорядочить (Николаев, 2020), при том, что в роли “подвижной поляры A-b(n)” выступает теперь «пара вершин» из Теоремы 2. Превращение эвристических схем в универсальные (“апдэйтом” теорем “1” и “2”) зависит ныне от энтузиазма молодых творцов науки Computer Science.

Полезно повторить тезис введения, что классические дифференциальные методы оценки инвариантов для дуг о (Картан, 1933; Faugeras, 1993) не приложимы к задачам технического зрения (по причинам практически не реализуемых требований к точности вычисления производных высокого порядка на дискретных сетках для гладкой кривой). Востребованность задач автоматического опознания объектов типа о побуждает искать приемлемые подходы с предложениями различных “полуинвариантов” (Olver, 2001; Hann, Hickman, 2002; Musso, Nicolodi, 2009; Hoff, Olver, 2013). Следует отметить, что в этих работах схемы и методы детекции проективно устойчивых свойств симметрии выпуклой гладкой кривой не рассматриваются. Свойства симметрии плоских гладких фигур если и исследуются, то, как правило, это относится к кривым заданного аналитического порядка. В качестве примера приведем работы (Itenberg, Itenberg, 2004) по исследованию аспектов симметрии у алгебраических объектов шестого порядка и (Brugalle, 2007), где обсуждены свойства и особенности кривых седьмого порядка. Интересны и современные работы по параметризации и нормализации кривых ротационной симметрии (Lebmeir, Jurgen, 2008), а также – по разработке теоретических подходов и реализации задач попарного сравнения аффинно и проективно эквивалентных симметричных кривых (Hauer, Jüttler, 2018). Все процитированые работы не имели объектом иcследования представителей семейства о.

Сформулируем выводы по рассмотренной теме Новые функции и задачи для ранее предложенных инструментов обработки о – схем “ДП” и “ТЧ”. Разработаны и испытаны в сериях модельных тестов численные методы решения задач детекции ЭС (скрытых осей и центров) в проективно инвариантной моде поиска, с однотипной структурой алгоритмов целевой реализации. Предложенные приемы обработки кривых семейства о и полученные по ним модельные результаты оригинальны и, можно надеяться, технически актуальны. Прямые и косвенные аналоги описанных выше аспектов привлечения дуальных схем и композиций с триадами чевиан не обнаружены нами в доступных базах цитирования.

Работа выполнена при поддержке РФФИ (грант № 19-29-09075).