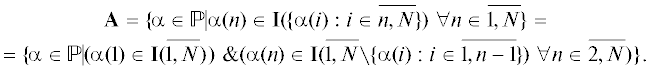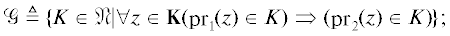Известия РАН. Теория и системы управления, 2019, № 1, стр. 117-130

Введение. В статье используются сокращения: АЭС – атомная электростанция, ДП – динамическое программирование, ДР – допустимое решение, ЗК – задача коммивояжера, ОЗМ – основная задача маршрутизации, п/м – подмножество, УП – упорядоченная пара, ЧПУ – числовое программное управление.

Проблемы маршрутизации, имеющие своим прототипом известную труднорешаемую ЗК [1–4], возникают в различных сферах практической деятельности и, в частности, во многих инженерных задачах. Однако для их решения обычно используются эвристические алгоритмы, что обусловлено соображениями сложности вычислений и достаточно большой размерностью. Кроме того, в прикладных задачах, связанных с маршрутизацией, обычно присутствуют разнообразные ограничения, среди которых, в частности, выделяются так называемые условия предшествования (условия типа “одно после другого”). В этой связи, наряду с вычислительными, возникают (особенно при поиске оптимальных решений) трудности качественного характера. Это касается, в частности, аппарата ДП, теоретическая проработка которого представляется важной прежде всего для понимания структуры оптимальных решений. В то же время в маршрутных задачах большой размерности метод ДП в непосредственном виде нереализуем даже при использовании мощной вычислительной техники. Можно, однако, попытаться применять ДП при построении вставок в глобальный маршрут; эти вставки будем далее именовать беллмановскими. По ряду причин [5, § 4.9] упомянутые вставки оказываются достаточно эффективными при наличии условий предшествования (см. [6, 7]); последние удается использовать “в положительном направлении” в смысле проблемы сложности вычислений [5, § 4.9; 8]. При этом условия предшествования локального оптимизационного блока “вырезаются” из глобальных условий предшествования; соответствующая процедура должна обеспечить надлежащее их согласование.

Еще одно осложняющее обстоятельство, возникающее при формализации инженерных задач с элементами маршрутизации, связано с возможной зависимостью стоимостей элементарных перемещений от списка заданий, которые не выполнены на текущий момент (в других случаях, напротив, может возникать зависимость от списка уже выполненных заданий). Примером такой ситуации может служить задача о демонтаже энергоблока АЭС, выведенного из эксплуатации: речь идет о снижении дозовой нагрузки участников бригады, занимающейся последовательным демонтажом излучающих элементов. По самому смыслу данной задачи радиационное воздействие на работников оказывают те и только те элементы, которые на данный момент еще не демонтированы.

Следовательно, для задачи с упомянутой особенностью при формировании вставки важно обеспечить нужную трансформацию зависимости от списка заданий при переходе от глобальной задачи к локальному оптимизационному блоку. Теоретические вопросы, связанные с упомянутой трансформацией, подробно исследовались в [9], где на идейном уровне была также намечена схема построения итерационного алгоритма, рассмотрению которого и посвящена настоящая статья.

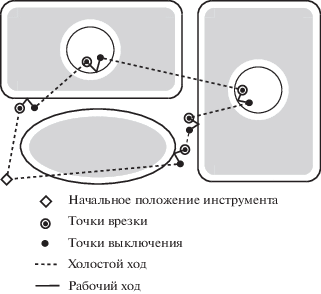
Заметим, что многие прикладные задачи, возникающие при автоматизации технологического проектирования, могут быть интерпретированы в терминах математических моделей дискретной оптимизации. К таким задачам, в частности, относится задача проектирования управляющей программы для машин фигурной листовой резки с ЧПУ. Управляющая программа разрабатывается на основе спроектированной раскройной карты и содержит информацию о маршруте движения (траектории) режущего инструмента, дополненную необходимыми технологическими командами (включения и выключения процесса резки, задания скорости рабочего хода инструмента и пр.). Все технологии листовой резки (лазерная, плазменная, газовая, гидроабразивная и др.) предполагают, что для сохранения требуемой геометрии детали траектория движения режущего инструмента задается с учетом некоторого припуска на рез, т.е. определяется некоторой эквидистантой соответствующего контура. В управляющей программе также необходимо определить точки включения режущего инструмента (точки врезки), где осуществляется предварительная пробивка листового материала и точки выключения. При проектировании маршрута инструмента приходится учитывать и некоторые другие технологические требования резки, в частности условия предшествования, возникающие при наличии отверстий в вырезаемых деталях, и технологические рекомендации по выбору точек врезки и выбору последовательности резки деталей (см., например, [10–12]). На рис. 1 показан пример маршрута инструмента машины с ЧПУ при резке трех деталей с использованием техники резки “по замкнутому контуру”.

На практике используются и другие техники резки, при которых контур может вырезаться в несколько шагов или несколько контуров без выключения инструмента. В любом случае задачи оптимизации маршрута резки (например, задачи минимизации времени и стоимости резки) для вычисления целевой функции требуют одних и тех же данных: информацию о точках врезки и точках выключения инструмента, последовательности их прохождения, а также о длине рабочего и холостого хода. При резке по замкнутому контуру в некоторых случаях необходимо также знать направление резки. Как нетрудно видеть, такие задачи относятся к классу задач непрерывной оптимизации из-за континуальности множества возможных наборов точек врезки.

Вместе с тем если во множестве допустимых точек врезки рассматривать только некоторое конечное число элементов, то задачи маршрутизации инструмента машин фигурной листовой резки с ЧПУ могут быть сведены к обобщенной задаче коммивояжера (GTSP) с дополнительными ограничениями. Такие постановки и методы решения задач маршрутизации рассмотрены, например, в [11–15]. Ряд других эвристических алгоритмов решения GTSP, разработанных зарубежными исследователями специально для маршрутизации инструмента машин листовой резки, описан в [16–18]. Следует отметить, что в зарубежных публикациях отсутствует описание точных алгоритмов, позволяющих получать оптимальные решения для задач небольшой размерности, а также не учитываются многие технологические требования термической резки. Отечественные исследования в области оптимизация маршрута инструмента технологического оборудования с ЧПУ для фигурной листовой резки ограничиваются работами, в которых все точки врезки определены заранее [19, 20], что существенно снижает практическую значимость таких исследований, так как они сводятся по существу только к рассмотрению модели классической задачи коммивояжера, используемой для минимизации холостого хода инструмента.

В данной статье применяется известная математическая модель мегаполисов [5], которая позволяет учитывать множественность возможных точек врезки для каждого контура и на основе которой разработаны некоторые точные и приближенные алгоритмы. Помимо возможности гарантированного нахождения оптимального решения за приемлемое время при резке небольшого числа контуров, упомянутая модель значительно упрощает учет условий предшествования и дополнительных технологических ограничений, а также позволяет сократить время получения рациональных вариантов маршрута в задачах большой размерности.

1. Общие определения и обозначения. Будем использовать стандартную теоретико-множественную символику: кванторы, связки, $\emptyset $ – пустое множество; через $ \triangleq $ обозначаем равенство по определению, def заменяет фразу “по определению”. Семейством называем множество, все элементы которого – множества.

Если p и q – произвольные объекты, то $\{ p;q\} $ есть def (единственное) множество, содержащее $p$ и $q$ и не содержащее никаких других элементов. Тогда всякому объекту y сопоставляется синглетон $\{ y\} \triangleq \{ y;y\} $, его содержащий. Учитывая, что каждое множество – объект, полагаем, следуя [21, с. 67], что для всяких объектов $\alpha $ и $\beta $ $(\alpha ,\beta ) \triangleq \{ \{ \alpha \} ;\{ \alpha ;\beta \} \} $; получаем УП с первым элементом $\alpha $ и вторым элементом $\beta $. Если же $z$ – какая-либо УП, то через $\mathop {pr}\nolimits_1 (z)$ и $\mathop {pr}\nolimits_2 (z)$ обозначаем соответственно первый и второй элементы $z$, однозначно определяемые условием $z = (\mathop {pr}\nolimits_1 (z),\mathop {pr}\nolimits_2 (z))$. Для любых трех объектов $\alpha ,\beta $ и $\gamma $ определен триплет $(\alpha ,\beta ,\gamma ) \triangleq ((\alpha ,\beta ),\gamma )$, являющийся, строго говоря, УП специального вида. Как обычно [22, с. 17], для любых трех множеств A, B и C полагаем $A \times B \times C \triangleq (A \times B) \times C$.

Через $\mathcal{P}(T)$ обозначаем семейство всех п/м множества $T$ (булеан $T$), а через ${\text{Fin}}(T)$ – семейство всех конечных множеств из $\mathcal{P}'(T) \triangleq \mathcal{P}(T){\backslash }\{ \emptyset \} ;$ если $T$ – непустое конечное множество, то ${\text{Fin}}(T) = \mathcal{P}'(T)$.

Если $A$ и $B$ – множества, то ${{B}^{A}}$ есть def множество всех отображений из множества $A$ в $B$ (при $g \in {{B}^{A}}$ и $a \in A$ в виде $g(a) \in B$ имеем значение функции $g$ в точке a); если $C \in \mathcal{P}'(A)$ и $h \in {{B}^{A}}$, то ${{h}^{1}}(C) \triangleq \{ h(\alpha ):\alpha \in C\} \in \mathcal{P}'(B)$ есть образ множества $C$ при действии $h$.

Для произвольных непустых множеств $P$ и $Q$ через $({\text{Bi}})[P;Q]$ обозначаем множество (возможно пустое) всех биекций [22, с. 87] множества $P$ на $Q$ (разумеется, ${{\varphi }^{1}}(P) = Q\,\forall \varphi \in ({\text{Bi}})[P;Q]$). Если $S$ и $T$ – непустые множества, а $\psi \in ({\text{Bi}})[S;T],$ то ${{\psi }^{{ - 1}}} \in ({\text{Bi}})[T;S]$ есть def биекция, обратная к $\psi :$ $(\psi ({{\psi }^{{ - 1}}}(t)) = t\;\forall t \in T)\,{\& }\,({{\psi }^{{ - 1}}}(\psi (s)) = s\;\forall s \in S).$ В виде $({\text{Bi}})[A;A]$ имеем [22, с. 87] множество всех перестановок непустого множества $A$. Если $\mathbb{A},\;\mathbb{B}$ и $\mathbb{C}$ – непустые множества, $g \in {{\mathbb{B}}^{\mathbb{A}}}$ и $h \in {{\mathbb{C}}^{\mathbb{B}}},$ то $h \circ g \in {{\mathbb{C}}^{\mathbb{A}}}$ есть композиция $g$ и $h$ : $(h \circ g)(x) \triangleq h(g(x))\;\;\forall x \in A$; при $g \in ({\text{Bi}})[\mathbb{A};\mathbb{B}]$ и $h \in ({\text{Bi}})[\mathbb{B};\mathbb{C}]$ имеем, конечно, $h \circ g \in ({\text{Bi}})[\mathbb{A};\mathbb{C}]$.

Отметим некоторые соглашения в части обозначений для функций нескольких переменных. Если A, B и C – непустые множества, $s \in {{C}^{{A \times B}}},a \in A$ и $b \in B$, то, как обычно, $s(a,b)$ отождествляется с $s(z)$, где $z = (a,b)$. Заметим также, что при всяком выборе непустых множеств $P,\;Q,\;R$ и T, отображения $e \in {{T}^{{P \times Q \times R}}}$, а также элементов $\alpha \in P \times Q$ и $\beta \in R$ определено значение $e(\alpha ,\beta ) \in T$, которое при ${{\alpha }_{1}} \triangleq \mathop {{\text{pr}}}\nolimits_1 (\alpha )$ и ${{\alpha }_{2}} \triangleq \mathop {{\text{pr}}}\nolimits_2 (\alpha )$ записывается в виде $e({{\alpha }_{1}},{{\alpha }_{2}},\beta )$, т.е. $e({{\alpha }_{1}},{{\alpha }_{2}},\beta ) \triangleq e(\alpha ,\beta )$.

Как обычно, $\mathbb{R}$ есть вещественная прямая, $\mathbb{N} \triangleq \{ 1;2; \ldots \} $ – натуральный ряд, ${{\mathbb{N}}_{0}} \triangleq \{ 0\} \cup \mathbb{N}$ = {0; 1; 2; ...} и $\overline {p,q} \triangleq \{ i \in {{\mathbb{N}}_{0}}{\text{|}}(p \leqslant i)\& (i \leqslant q)\} \in \mathcal{P}({{\mathbb{N}}_{0}})$ $\forall p \in {{\mathbb{N}}_{0}}$ $\forall q \in {{\mathbb{N}}_{0}}$ (отметим, что $\overline {1,0} = \emptyset $; это свойство используется ниже без дополнительных пояснений). Каждому непустому конечному множеству K сопоставляется его мощность $\left| K \right| \in \mathbb{N}$ и непустое множество $({\text{bi}})[K] \triangleq ({\text{Bi}})\left[ {\overline {1,\left| K \right|} ;K} \right]$ всевозможных биекций “промежутка” $\overline {1,\left| K \right|} $ на K; $\left| \emptyset \right| \triangleq 0$. Если $n \in \mathbb{N}$, то ${\text{|}}\overline {1,n} {\text{|}} = n$ и $({\text{bi}})[\overline {1,n} ] = ({\text{Bi}})[\overline {1,n} ;\overline {1,n} ]$ есть множество всех перестановок множества $\overline {1,n} $. Наконец, условимся, что для всякого непустого множества T через ${{\mathcal{R}}_{ + }}[T]$ обозначается множество всех функций из T в $[0,\infty [\; \triangleq \{ \xi \in \mathbb{R}{\text{|}}0 \leqslant \xi \} ;$ итак, ${{\mathcal{R}}_{ + }}[T]$ есть множество всех неотрицательных вещественнозначных функций на T.

2. Специальные понятия и обозначения. В настоящем разделе излагаются понятия и обозначения, относящиеся к задаче маршрутизации, рассматриваемой ниже в качестве основной (неявно предполагается, что данная задача имеет достаточно большую размерность, что не позволяет напрямую использовать точные методы для ее решения). Сама эта задача будет обсуждаться здесь на содержательном уровне. Фиксируем непустое множество X, точку ${{{\mathbf{x}}}_{0}} \in X$ (база процесса), число ${\mathbf{n}} \in \mathbb{N}$, ${\mathbf{n}} \geqslant 2$, множества

именуемые далее мегаполисами, а также (непустые) отношения определяющие каждые возможные варианты выполнения работ, связанных с посещением соответствующего мегаполиса. Постулируем, что

Полагаем, что ${\mathbf{P}} \triangleq ({\text{bi}})[\overline {1,{\mathbf{n}}} ]$, получая (в виде P) множество всех перестановок $\overline {1,{\mathbf{n}}} $, именуемых ниже маршрутами. Мы рассматриваем далее перемещения

где $\beta \in {\mathbf{P}}$ и кортеж $({{z}_{1}}, \ldots ,{{z}_{{\mathbf{n}}}})$ (с соблюдением условий (2.4)) могут выбираться исследователем. Из (2.4) видно, что при $\beta \in {\mathbf{P}}$ сам процесс может определяться неединственным образом; в этой связи логично ввести множество всех таких возможных при данном $\beta $ процессов (трасс) или соответствующий пучок траекторий. Однако предварительно отметим, что элементы УП, составляющих трассу или траекторию в (2.4), непременно реализуются в множестве (при $t \in \overline {1,{\mathbf{n}}} $ имеют место включения ${\text{p}}{{{\text{r}}}_{1}}({{z}_{t}}) \in \mathfrak{X}$ и ${\text{p}}{{{\text{r}}}_{2}}({{z}_{t}}) \in \mathfrak{X}$; разумеется, ${{{\mathbf{x}}}_{0}} \in \mathfrak{X}$). С учетом этого введем (объемлющее) множество $\tilde {\mathfrak{Z}}$ всех кортежей ${{({{z}_{i}})}_{{i \in \overline {0,{\mathbf{n}}} }}}:\overline {0,{\mathbf{n}}} \to \mathfrak{X} \times \mathfrak{X}.$ Среди упомянутых кортежей будем особо выделять трассы (траектории). При этом осуществляем несущественное преобразование начального состояния: элемент x₀ в (2.4) заменяется УП $({{{\mathbf{x}}}_{0}},{{{\mathbf{x}}}_{0}})$. Тогда при $\beta \in {\mathbf{P}}$есть множество всех возможных вариантов развития процесса в (2.4).

Для введения условий предшествования зафиксируем множество $\mathfrak{K} \in \mathcal{P}(\overline {1,{\mathbf{n}}} \times \overline {1,{\mathbf{n}}} )$, элементами которого являются УП индексов из $\overline {1,{\mathbf{n}}} $, именуемые адресными (случай $\mathfrak{K} = \emptyset $ отвечает отсутствию условий предшествования). Постулируем, что

Тогда [5, ч. 2] получаем, что множество

всех $\mathfrak{K}$-допустимых (по предшествованию) маршрутов непусто: $\mathcal{A} \in \mathcal{P}'({\mathbf{P}})$. Итак, допустимые по предшествованию маршруты (в рассматриваемом случае (2.7)) существуют и составляют непустое конечное множество. Тогда рассматриваем как множество всех ДР формулируемой ниже задачи.

Полагаем, что ${\mathbf{N}} \triangleq \mathcal{P}'(\overline {1,{\mathbf{n}}} )$; элементы ${\mathbf{N}}$ называем списками (заданий). Фиксируем кортеж $({{{\mathbf{c}}}^{\natural }},c_{1}^{\natural },\; \ldots ,\;c_{{\mathbf{n}}}^{\natural },{{f}^{\natural }})$, для которого

Функция ${{{\mathbf{c}}}^{\natural }}$ позволяет оценивать внешние перемещения (перемещения между мегаполисами, а также из x₀ к мегаполисам); при $j \in \overline {1,{\mathbf{n}}} $ для оценивания работ, связанных с мегаполисом ${{{\mathbf{L}}}_{j}}$, используем $c_{j}^{\natural }$, а ${{f}^{\natural }}$ применяем для оценивания терминального состояния (элемент $\mathop {{\text{pr}}}\nolimits_2 ({{z}_{{\mathbf{n}}}})$ в (2.4)). Данные функции по методическим соображениям считаем максимально продолженными, что не составляет труда (отметим, например, что при $j \in \overline {1,{\mathbf{n}}} $ значения $c_{j}^{\natural }(x,y,K)$ потребуются, на самом деле, только при $(x,y) \in {{\mathbb{L}}_{j}}$ и $K \in {\mathbf{N}}$, для которых $j \in K$; см. (2.4)).

Если $\beta \in {\mathbf{P}}$ и ${{({{z}_{i}})}_{{i \in \overline {0,{\mathbf{n}}} }}} \in \tilde {\mathfrak{Z}}$, то полагаем, что

Для наших целей (2.10) существенно при $\beta \in \mathcal{A}$ и ${{({{z}_{i}})}_{{i \in \overline {0,{\mathbf{n}}} }}} \in {{\mathfrak{Z}}_{\beta }}$. С учетом (2.8) ОЗМ определяем в следующем виде:

Отметим, что в [8, 23–25] для решения (2.11) использовался экономичный вариант метода ДП, являющийся развитием процедуры [5, § 4.9]. Мы полагаем, однако, сейчас, что n достаточно велико, а потому непосредственное применение упомянутого варианта ДП затруднено.

Замечание. Отметим, что в исходной содержательной задаче возможен случай, когда в (2.10) вместо соответствующих значений функций (2.9) используются значения некоторых других функций, в которых имеется зависимость не от списка “оставшихся” заданий, а, напротив, присутствует подобная зависимость от списка уже выполненных заданий (такая ситуация складывается, в частности, в маршрутных задачах для станков с ЧПУ). Это соответствует случаю, когда ${{{\mathbf{c}}}^{\natural }},c_{1}^{\natural },\; \ldots ,\;c_{N}^{\natural }$ заменены функциями ${{{\mathbf{\tilde {c}}}}^{\natural }},\tilde {c}_{1}^{\natural }, \ldots ,\tilde {c}_{{\mathbf{n}}}^{\natural }$, определенными на $\mathfrak{X} \times \mathfrak{X} \times \mathcal{P}(\overline {1,{\mathbf{n}}} )$, а в (2.10) реально применяются при $t \in \overline {1,{\mathbf{n}}} $ значения 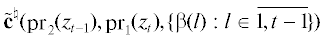и 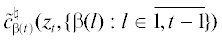, где $\beta \in {\mathbf{P}}$. Однако данный случай легко сводится к (2.10) при следующем варианте выбора ${{{\mathbf{c}}}^{\natural }},c_{1}^{\natural },\; \ldots ,\;c_{{\mathbf{n}}}^{\natural }$: ${{{\mathbf{c}}}^{\natural }}(z,K)$ = ${{{\mathbf{\tilde {c}}}}^{\natural }}(z,\overline {1,N} {\backslash }K),c_{1}^{\natural }(z,K)$ = $\tilde {c}_{1}^{\natural }(z,\overline {1,N} {\backslash }K),\; \ldots ,\;c_{{\mathbf{n}}}^{\natural }(z,K) = \tilde {c}_{{\mathbf{n}}}^{\natural }(z,\overline {1,N} {\backslash }K)$ при $z \in \mathfrak{X} \times \mathfrak{X}$ и $K \in {\mathbf{N}}$.

3. Беллмановские вставки; общая схема. В настоящем разделе кратко излагаются основные положения [9], связанные с построением беллмановских вставок. В целях сокращения обозначений фиксируем какое-либо ДР $\delta \triangleq (\lambda ,{{({{{\mathbf{h}}}_{i}})}_{{i \in \overline {0,{\mathbf{n}}} }}}) \in {\mathbf{\tilde {D}}}$ задачи (2.11), для которого определено значение ${{\mathfrak{C}}_{\lambda }}[{{({{{\mathbf{h}}}_{i}})}_{{i \in \overline {0,{\mathbf{n}}} }}}] \in [0,\infty [.$

Кроме того, в настоящем разделе фиксируем $N \in \overline {2,{\mathbf{n}} - 1} $, а также $\nu \in \overline {0,{\mathbf{n}} - (N + 1)} $. В этих терминах вводим отображение $\Lambda \triangleq {{(\lambda (\nu + s))}_{{s \in \overline {1,N} }}}$, действующее из $\overline {1,N} $ в $\overline {1,{\mathbf{n}}} $, после чего вводим $\Gamma \triangleq \{ \Lambda (s):s \in \overline {1,N} \} \in \mathcal{P}'(\overline {1,{\mathbf{n}}} )$ (образ $\overline {1,N} $ при действии Λ). Ясно, что $\Gamma = \{ \lambda (\nu + s):s \in \overline {1,N} \} $, $\left| \Gamma \right| = N$ и $\Lambda \in ({\text{bi}})[\Gamma ]$. Определяем далее $Q \triangleq \{ z \in \mathfrak{K}{\kern 1pt} {\text{|}}{\kern 1pt} (\mathop {{\text{pr}}}\nolimits_1 (z) \in \Gamma )$ & $(\mathop {{\text{pr}}}\nolimits_2 (z) \in \Gamma )\} $ и, наконец, множество

определяющее условия предшествования оптимизационного блока (вставки). Известно [6, 7, 9], что (следствие (2.7)) $\forall {{{\mathbf{K}}}_{0}} \in \mathcal{P}'({\mathbf{K}})\;\exists {{z}_{o}} \in {{{\mathbf{K}}}_{0}}:\mathop {{\text{pr}}}\nolimits_{\text{1}} ({{z}_{0}}) \ne \mathop {{\text{pr}}}\nolimits_{\text{2}} (z)\;\forall z \in {{{\mathbf{K}}}_{0}}$. Тогда при $\mathbb{P} \triangleq ({\text{bi}})[\overline {1,N} ]$есть множество всех локальных маршрутов, K-допустимых по предшествованию (в дальнейшем (3.1), (3.2) будут использоваться в режиме итераций). Мы фиксируем на трассе, отвечающей решению δ, точку которая будет играть роль базы локального процесса, для определения которого полагаем $\forall s \in \overline {1,N} $

Ясно, что при $t \in \overline {1,N} $ ${{\mathbb{M}}_{t}} \in \mathcal{P}'({{M}_{t}} \times {{M}_{t}})$ и ${{{\mathbf{M}}}_{t}} \triangleq \{ \mathop {{\text{pr}}}\nolimits_{\text{2}} (z):z \in {{\mathbb{M}}_{t}}\} \in \mathcal{P}'({{M}_{t}})$. Кроме того,

(множества ${\mathbf{X}},{{{\mathbf{M}}}_{1}},\; \ldots ,\;{{{\mathbf{M}}}_{N}}$ существенны при построении локальных версий ДП в духе [8, 25]). Теперь мы создаем локальную маршрутную задачу, в которой x⁰ (3.3) играет роль базы, а $\mathbb{X}$ – роль фазового пространства. Полагая, что $\mathbb{Z}$ – множество всех кортежей ${{({{z}_{i}})}_{{i \in \overline {0,N} }}}:\overline {0,N} \to \mathbb{X} \times \mathbb{X}$, имеем при $\alpha \in \mathbb{P}$, что

Рассматриваем ${\mathbf{D}} \triangleq \{ (\alpha ,{\mathbf{z}}) \in {\mathbf{A}} \times \mathbb{Z}{\kern 1pt} |{\kern 1pt} {\mathbf{z}} \in {{Z}_{\alpha }}\} $ как множество всех ДР локальной задачи, D ∈ ${\text{Fin}}({\mathbf{A}} \times \mathbb{Z})$.

Локализация функций стоимости. При $\mathfrak{N} \triangleq \mathcal{P}'(\overline {1,N} )$ и $K \in \mathfrak{N}$ имеем ${{\Lambda }^{1}}(K) \in \mathcal{P}'(\Gamma )$ и Λ¹(K) ∪ ${{\lambda }^{1}}(\overline {\nu + N + 1,{\mathbf{n}}} )$ ∈ N. С учетом этого введем функции стоимости оптимизационного блока: определяем ${\mathbf{c}} \in {{\mathcal{R}}_{ + }}[\mathbb{X} \times \mathbb{X} \times \mathfrak{N}]$ правилом

при $j \in \overline {1,N} $ полагаем, что функция ${{c}_{j}} \in {{R}_{ + }}[\mathbb{X} \times \mathbb{X} \times \mathfrak{N}]$ такова, что наконец, $f \in {{\mathcal{R}}_{ + }}[\mathbb{X}]$ вводим по правилу

Посредством (3.4)–(3.8) построен кортеж $({\mathbf{c}},{{c}_{1}},\; \ldots ,\;{{c}_{N}},f)$, позволяющий ввести (локальный) аддитивный критерий: если $\alpha \in \mathbb{P}$ и ${{({{z}_{i}})}_{{i \in \overline {0,N} }}} \in \mathbb{Z}$, то

В (3.9) cледуем [8, 23, 25]. В (3.9) можно, в частности, использовать $\alpha \in {\mathbf{A}}$ и ${{({{z}_{i}})}_{{i \in \overline {0,N} }}} \in {{Z}_{\alpha }}$. С учетом этого приходим к локальной задаче

для решения которой используем вариант ДП, изложенный в [8, 23–25]. Как обычно, ДР $({{\alpha }^{0}},{{{\mathbf{z}}}^{0}})$ ∈ D называем оптимальным, если

Мы полагаем здесь, что размерность локальной задачи (3.10) умеренна и данная задача разрешима посредством ДП в духе [8, 23–25]. Отметим, что для тривиального маршрута ${\mathbf{e}} \in \mathbb{P}$, формируемого условием

реализуется [6, замечание 7.1] свойство ${\mathbf{e}} \in {\mathbf{A}}$.

Теперь рассмотрим схему вставки [9], начиная с вопроса о “вклеивании” локального маршрута в глобальный. Начнем с общего свойства, полагая при $\alpha \in \mathbb{P}$, что

задается следующими правилами: $(\alpha - sew)[\lambda ;\nu ](t) \triangleq \lambda (t)$ при $t \in \overline {1,{\mathbf{n}}} {\backslash }\overline {\nu + 1,\nu + N} $, $(\alpha - sew)[\lambda ;\nu ](\tau )$ = = $(\Lambda \circ \alpha )(\tau - \nu )$ при $\tau \in \overline {\nu + 1,\nu + N} .$ Тогда, в частности [9, (3.10), предложение 3.3], ((α – sew)[λ; $\nu ] \in \mathcal{A}\;\forall \alpha \in {\mathbf{A}}){\& }(({\mathbf{e}} - sew)[\lambda ;\nu ]$ = λ). Фиксируем оптимальное ДР локальной задачи: пусть $({{\alpha }^{0}},{{{\mathbf{z}}}^{0}}) \in {\mathbf{D}}$ таково, что ${{\mathfrak{C}}_{{{{\alpha }^{0}}}}}[{{{\mathbf{z}}}^{0}}] \leqslant {{\mathfrak{C}}_{\alpha }}[{\mathbf{z}}]\;\forall (\alpha ,{\mathbf{z}}) \in {\mathbf{D}}$. Далее, введем локализацию исходной трассы “большой” задачи: полагаем $({{{\mathbf{\tilde {h}}}}_{0}} \triangleq ({{x}^{0}},{{x}^{0}}))$ & $({{{\mathbf{\tilde {h}}}}_{t}} \triangleq {{{\mathbf{h}}}_{{\nu + t}}}\;\forall t \in \overline {1,N} )$; легко видеть, что ${{({{{\mathbf{\tilde {h}}}}_{i}})}_{{i \in \overline {0,N} }}} \in {{Z}_{{\mathbf{e}}}}$, а тогда из (3.11) имеем неравенство

Отметим, что значение ${{\mathfrak{C}}_{{\mathbf{e}}}}[{{({{{\mathbf{\tilde {h}}}}_{i}})}_{{i \in \overline {0,N} }}}]$ достаточно просто выражается в терминах исходного ДР “большой” задачи:

При этом для $t \in \overline {\nu + 1,\nu + N} $ имеем по определению $\Lambda $, что ${{\Lambda }^{1}}(\overline {t - \nu ,N} )$ = {λ(ν + s) : 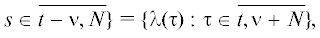а потому

Из (3.14) и (3.15) вытекает, что

Таким образом, ${{\mathfrak{C}}_{{\mathbf{e}}}}[{{({{{\mathbf{\tilde {h}}}}_{i}})}_{{i \in \overline {0,N} }}}]$ есть “часть” суммы, реализующей значение ${{\mathfrak{C}}_{\lambda }}[{{({{{\mathbf{h}}}_{i}})}_{{i \in \overline {0,{\mathbf{n}}} }}}]$, которое оценивает качество ДР $\delta $ “большой” задачи. В [9] показано, что $\kappa $ (3.13) определяет не только локальное, но и глобальное улучшение качества. Сейчас ограничимся описанием конструкции [9], используя то, что

и конструируя кортеж ${{({{{\mathbf{\hat {h}}}}_{t}})}_{{t \in \overline {0,{\mathbf{n}}} }}} \in \tilde {\mathfrak{Z}}$ по правилу

Легко видеть, что ${\mathbf{\hat {h}}} \triangleq {{({{{\mathbf{\hat {h}}}}_{t}})}_{{t \in \overline {0,{\mathbf{n}}} }}} \in {{\mathfrak{Z}}_{\eta }}$. Итак, $(\eta ,{\mathbf{\hat {h}}})$ есть ДР в ОЗМ (2.11) и сформировано значение $\mathfrak{C}_{\eta }^{\natural }[{\mathbf{\hat {h}}}] \in [0,\infty [.$ При этом [9, теорема 5.1]

Итак, преобразование $(\delta = (\lambda ,{{({{{\mathbf{h}}}_{i}})}_{{i \in \overline {0,{\mathbf{n}}} }}})) \to (\eta ,{\mathbf{\hat {h}}})$ сопровождается улучшением критерия ОЗМ на величину $\varkappa ,\varkappa \geqslant 0$.

4. Комбинированный итерационный метод. В настоящем разделе рассматривается один из подходов к применению процедуры разд. 2 в итерациoнном режиме (см. Заключение работы [9]). Напомним, что, согласно разд. 2, мы полагали заданными ДР $\delta $, а также числа $N \in \overline {2,{\mathbf{n}} - 1} $ и $\nu \in \overline {0,{\mathbf{n}} - (N + 1)} $. При фиксации триплета $(\delta ,N,\nu )$ (в разд. 3) была указана процедура, приводящая к (3.18). Разумеется, ДР $(\eta ,{\mathbf{\hat {h}}})$, получаемое в результате ее применения, снова можно принять за начальное, т.е. можно заменить $\delta $ на $(\eta ,{\mathbf{\hat {h}}})$, с целью повторения преобразования разд. 3. Возникает, однако, вопрос о выборе N и $\nu $ (число n задано по условиям ОЗМ).

В этой связи допустим сначала возможность выбора в разд. 3 двух вариантов $N:{{N}_{1}} \in \overline {2,{\mathbf{n}} - 1} $ и ${{N}_{2}} \in \overline {2,{\mathbf{n}} - 1} $. Будем считать при этом, что ${{N}_{1}} < {{N}_{2}}$ (примерные диапазоны выбора N₁ и N₂ на сегодняшний день таковы: ${{N}_{1}} \in \overline {10,16} $, ${{N}_{2}} \in \overline {25,30} $). Целью выбора N₁ является реализация процедуры разд. 3 для всевозможных значений $\nu \in \overline {0,{\mathbf{n}} - ({{N}_{2}} + 1)} $, а именно, используем в построениях беллмановских вставок (при фиксированном $\delta $) условие N = N₁ при переборе всех $\nu $ из вышеупомянутого диапазона. Тогда для каждого такого значения $\tilde {\nu }$ будет определена (при условии $\nu = \tilde {\nu }$) своя неотрицательная величина $\varkappa $ (3.13), которую сейчас обозначим ${{\varkappa }_{1}}(\tilde {\nu })$ (имеем в виду случай “коротких” вставок с началом в “момент” $\tilde {\nu }$). Затем выбираем $\nu \in \overline {0,{\mathbf{n}} - ({{N}_{2}} + 1)} $ так, что

Данное значение $\nu $ со свойством (4.1) используем теперь в процедуре разд. 2 при N = N₂, конструируя беллмановскую вставку более ощутимой размерности; итогом ее применения будет соответствующий вариант (3.18), где $\varkappa $ определяется посредством (3.13) при N = N₂.

Таким образом построен шаг планируемой итерационной процедуры, включающий два этапа: 1) своеобразное “зондирование” на основе (4.1) (предполагается, что при достаточно малом значении N₁ нам удастся “быстро” прорешать все “короткие” локальные подзадачи для определения ${{\varkappa }_{1}}(\tilde {\nu }),\tilde {\nu } \in \overline {0,{\mathbf{n}} - ({{N}_{2}} + 1)} $ и последующей оптимизации в смысле (4.1)) с целью выбора начала основной вставки, при котором фрагмент исходного ДР $\delta $ оказывается, по нашим представлениям, наиболее “податливым” к улучшению; 2) рабочее воздействие в виде более ощутимой вставки с известным началом. Именно после второго этапа получаем ДР в ОЗМ, которое в разд. 2 обозначено как $(\eta ,{\mathbf{\hat {h}}})$.

Этим ДР $(\eta ,{\mathbf{\hat {h}}})$ мы заменяем $\delta $, т.е. используем преобразования

После этого процедура разд. 2 снова повторяется в двухэтапном варианте при заменах (4.2).

5. Динамическое программирование (алгоритм на функциональном уровне). В настоящем разделе излагается “алгоритмический” вариант процедуры ДП, детально исследуемой в [8, 23]. Речь идет о решении задачи (3.10), для соответствующей беллмановской вставки. Однако сначала приведем сводку необходимых определений. Так, в частности, следуя [5, (2.2.27), (2.2.28)], вводим отображение I, действующее в N, по правилу ${\mathbf{I}}(K) \triangleq K{\backslash }\{ \mathop {{\text{pr}}}\nolimits_{\text{2}} (z):z \in \Xi [K]\} ,$ где $\Xi [K] \triangleq \{ z \in {\mathbf{K}}{\text{|}}(\mathop {{\text{pr}}}\nolimits_{\text{1}} (z) \in K)\,{\& }\,(\mathop {{\text{pr}}}\nolimits_{\text{2}} (z)$ ∈ K)} (здесь $K \in \mathfrak{N}$). Тогда (см. (3.2); [23, (3.17)])

Далее излагаем алгоритм на функциональном уровне, реализуемый в виде последовательного исполнения приводимых ниже этапов.

Шаг 1. Существенные списки заданий. Вводим семейство

множества – элементы (5.2) – называем существенными списками (заданий) и ранжируем по мощности: полагаем ${{\mathcal{G}}_{s}} \triangleq \{ K \in \mathcal{G}{\text{|}}s = \left| K \right|\} \;\;\forall s \in \overline {1,N} $. Легко находятся семейства ${{\mathcal{G}}_{N}} = \{ \overline {1,N} \} $ (синглетон) и ${{\mathcal{G}}_{1}} = {\{ }\{ t\} :t \in \overline {1,N} {\backslash }{{{\mathbf{K}}}_{1}}\} $, где ${{{\mathbf{K}}}_{1}} \triangleq \{ \mathop {{\text{pr}}}\nolimits_{\text{1}} (z):z \in {\mathbf{K}}\} $ (см. (3.1)). Наконец,

Посредством (5.3) определена рекуррентная процедура ${{\mathcal{G}}_{N}} \to {{\mathcal{G}}_{{N - 1}}} \to \ldots \to {{\mathcal{G}}_{1}}:{{\mathcal{G}}_{N}}$ известно, а (5.3) реализует преобразование ${{\mathcal{G}}_{s}} \to {{\mathcal{G}}_{{s - 1}}}$ при $s \in \overline {2,N} $.

Шаг 2. Слои пространства позиций. Конструируем множества ${{D}_{0}},{{D}_{1}},$ …, ${{D}_{N}}$ (слои), для которых ${{D}_{j}} \subset {\mathbf{X}} \times \mathcal{P}(\overline {1,N} )\;\;\forall j \in \overline {0,N} $ (X введено в разд. 3). При этом ${{D}_{N}} \triangleq \{ ({{x}^{0}},\overline {1,N} )\} $ (синглетон) и ${{D}_{0}} \triangleq \{ (x,\emptyset ):x \in \mathfrak{M}\} $, где $\mathfrak{M}$ есть объединение всех множеств ${{{\mathbf{M}}}_{i}},i \in \overline {1,N} {\backslash }{{{\mathbf{K}}}_{1}}$, определяются непосредственно.

Рассмотрим построение ${{D}_{1}}, \ldots ,{{D}_{{N - 1}}}$. Если $s \in \overline {1,N - 1} $ и $K \in {{\mathcal{G}}_{s}}$, то полагаем, что ${{\mathcal{J}}_{s}}(K) \triangleq \{ t \in \overline {1,N} {\backslash }K{\text{|}}\{ t\} \cup K \in {{\mathcal{G}}_{{s + 1}}}\} $, получая непустое множество: ${{\mathcal{J}}_{s}}(K) \in \mathfrak{N};$ формируем ${{\mathcal{M}}_{s}}[K]$ в виде объединения всех множеств ${{{\mathbf{M}}}_{j}},j \in {{\mathcal{J}}_{s}}(K)$, и на этой основе – клетку пространства позиций

При $s \in \overline {1,N - 1} $ слой D_s вводим в виде

Слои D₀ и D_N определяются непосредственно. Дальнейшее построение соответствует (5.4), (5.5): на s-элементные существенные списки “навешиваются” слева состояния из X. Получающаяся система $({{D}_{0}},{{D}_{1}},\; \ldots ,\;{{D}_{N}})$ обладает свойством

Шаг 3. Слои функции Беллмана. Рекуррентно определяются функции ${{v}_{0}} \in {{\mathcal{R}}_{ + }}[{{D}_{0}}]$, ${{v}_{1}} \in {{\mathcal{R}}_{ + }}[{{D}_{1}}]$, ..., ${{v}_{N}} \in {{\mathcal{R}}_{ + }}[{{D}_{N}}].$ Функция ${{\text{v}}_{0}}$ задается условием ${{v}_{0}}(x,\emptyset ) \triangleq f(x)\;\forall x \in \mathfrak{M}$. Преобразование ${{v}_{{s - 1}}} \to {{v}_{s}}$ при $s \in \overline {1,N} $ с учетом (5.6) вводится в виде

На основе (5.7) реализуется процедура ${{v}_{0}} \to {{v}_{1}} \ldots \to {{v}_{N}}$, для которой

есть глобальный экстремум задачи (3.10).

Шаг 4. Оптимальные ДР. Полагаем ${{{\mathbf{z}}}^{0}} \triangleq ({{x}^{0}},{{x}^{0}}) \in \mathbb{X} \times {\mathbf{X}}$. С учетом (5.7), (5.8) выбираем ${{{\mathbf{j}}}_{1}} \in {\mathbf{I}}(\overline {1,N} )$ и ${{{\mathbf{z}}}^{{(1)}}} \in {{\mathbb{M}}_{{{{{\mathbf{j}}}_{1}}}}}$ так, что

где, согласно (5.6), $(\mathop {{\text{pr}}}\nolimits_{\text{2}} ({{{\mathbf{z}}}^{{(1)}}}),\overline {1,N} {\backslash }\{ {{{\mathbf{j}}}_{1}}\} ) \in {{D}_{{N - 1}}}.$ Последнее означает, что (см. (5.7))

С учетом (5.10) выбираем ${{{\mathbf{j}}}_{2}} \in {\mathbf{I}}(\overline {1,N} {\backslash }\{ {{{\mathbf{j}}}_{1}}\} )$ и ${{{\mathbf{z}}}^{{(2)}}} \in {{\mathbb{M}}_{{{{{\mathbf{j}}}_{2}}}}}$ так, что при этом

где, согласно (5.6), $(\mathop {{\text{pr}}}\nolimits_2 ({{{\mathbf{z}}}^{{(2)}}}),\overline {1,N} {\backslash }\{ {{{\mathbf{j}}}_{1}};{{{\mathbf{j}}}_{2}}\} ) \in {{D}_{{N - 2}}}.$ Теперь из (5.9) и (5.11) вытекает, что справедливо равенство

Процедуру выбора экстремальных элементов, подобную (5.9), (5.11), следует продолжать вплоть до исчерпывания (полного) списка $\overline {1,N} $. В результате будет построено ДР $(\eta ,{{({{{\mathbf{z}}}^{{(i)}}})}_{{i \in \overline {0,N} }}}),$ $\eta = {{({{{\mathbf{j}}}_{t}})}_{{t \in \overline {1,N} }}} \in {\mathbf{A}}$, ${{({{{\mathbf{z}}}^{{(i)}}})}_{{i \in \overline {0,N} }}} \in {{Z}_{\eta }}$ со свойством ${{C}_{\eta }}[{{({{{\mathbf{z}}}^{{(i)}}})}_{{i \in \overline {0,N} }}}] = V$, т.е. оптимальное в задаче (3.10) ДР (при N = 2 вывод об оптимальности данного ДР извлекается из (5.12) непосредственно).

Отметим одно полезное обстоятельство, связанное с построениями разд. 3: при выборе конкретного начала $\nu $ соответствующей беллмановской вставки (случай N = N₁; см.(4.1)) не требуется выполнение шага 4 (построение локального оптимального ДР). Это связано с тем, что согласно (3.13) и (5.8), справедливо равенство $\kappa = {{\mathfrak{C}}_{{\mathbf{e}}}}[{{({{{\mathbf{\tilde {h}}}}_{i}})}_{{i \in \overline {0,N} }}}] - V,$ поскольку в силу (3.11) локальное ДР $({{\alpha }^{0}},{{{\mathbf{z}}}^{0}}) \in {\mathbf{D}}$ оптимально в задаче (3.10). Поэтому при N = N₁ в режиме поиска начала рабочей вставки можно ограничиться шагами 1–3.

6. Управление движением инструмента при листовой резке на станках с ЧПУ. В настоящем разделе приводится детализация общей конструкции, ориентированная на применение в конкретной инженерной задаче. Полагаем, что X есть прямоугольник на плоскости: $X = [0,{\mathbf{a}}] \times [0,{\mathbf{b}}]$, где ${\mathbf{a}} > 0$ и ${\mathbf{b}} > 0$. В прямоугольнике X размещены заготовки деталей; упомянутое размещение достигнуто на этапе раскроя, который здесь не рассматривается. Итак, ${{{\mathbf{D}}}_{1}}, \ldots ,{{{\mathbf{D}}}_{n}}$, где $n \in \mathbb{N}$, суть данные заготовки, т.е. плоские множества, которые для простоты будем называть деталями; ${{{\mathbf{D}}}_{1}} \subset X, \ldots ,{{{\mathbf{D}}}_{n}} \subset X$, причем каждое из множеств ${{{\mathbf{D}}}_{j}},j \in \overline {1,n} $, непусто, ограничено, замкнуто и имеет внутренние точки. Множества ${{{\mathbf{D}}}_{1}}, \ldots ,{{{\mathbf{D}}}_{n}}$ полагаем попарно непересекающимися. Если $j \in \overline {1,n} $, то также полагаем, что граница ${{\Gamma }_{j}}$ детали D_j является объединением попарно непересекающихся непустых ограниченных и замкнутых множеств ${{\Gamma }_{{j,1}}}, \ldots ,{{\Gamma }_{{j,{{{\mathbf{n}}}_{j}}}}}$, где ${{{\mathbf{n}}}_{j}} \in \mathbb{N}$; каждое из множеств ${{\Gamma }_{{j,k}}},k \in \overline {1,{{{\mathbf{n}}}_{j}}} $, в данном построении предполагается замкнутой кривой, отвечающей либо внешнему, либо одному из внутренних контуров, ограничивающих саму деталь D_j. Внешний контур является при этом выделенным и соответствующим завершению резки D_j. Множества ${{\Gamma }_{{j,k}}},k \in \overline {1,{{{\mathbf{n}}}_{j}}} ,$ именуем контурами D_j. Считаем при этом, что возле каждого контура Γ_{j, k}, $j \in \overline {1,n} ,k \in \overline {1,{{{\mathbf{n}}}_{j}}} ,$ задана замкнутая кривая ${{\Omega }_{{j,k}}}$, расположенная с внешней по отношению к контуру (и к самой детали) стороны и называемая эквидистантой; эквидистанта “копирует” контур и служит для непосредственной резки (с запасом). Разумеется, ${{\Omega }_{{j,k}}} \cap {{{\mathbf{D}}}_{j}} = \emptyset \;\;\forall j \in \overline {1,n} \;\;\forall k \in \overline {1,{{{\mathbf{n}}}_{j}}} $. Каждая эквидистанта есть непустое, ограниченное и замкнутое множество. Полагаем также, что

пусть n > 2, что соответствует невырожденной задаче. Всю совокупность эквидистант Ω_{1, 1}, ..., ${{\Omega }_{{1,{{{\mathbf{n}}}_{1}}}}},{{\Omega }_{{2,1}}}, \ldots ,{{\Omega }_{{2,{{{\mathbf{n}}}_{2}}}}}, \ldots ,{{\Omega }_{{n,1}}}, \ldots ,{{\Omega }_{{n,{{{\mathbf{n}}}_{n}}}}}$ занумеруем подряд, получая ${{\Omega }^{{(1)}}}, \ldots ,{{\Omega }^{{({\mathbf{n}})}}}$ (см. (6.1)) и выделяя, следовательно, всю совокупность эквидистант. Возле каждой эквидистанты ${{\Omega }^{{(j)}}},j \in \overline {1,{\mathbf{n}}} $, размещаем теперь мегаполис L_j (непустое конечное п/м X), точки которого сгруппированы в пары, отвечающие возможной врезке и выключению инструмента; считаем, что точки L_j находятся с внешней по отношению к ${{\Omega }^{{(j)}}}$ стороны в смысле соответствующей исходной детали. Мы считаем, конечно, что множества ${{{\mathbf{L}}}_{1}}, \ldots ,{{{\mathbf{L}}}_{N}}$ попарно не пересекаются (в нашем построении мегаполисы суть дискретизации некоторых “вторичных” эквидистант). Каждое из отношений ${{\mathbb{L}}_{j}},j \in \overline {1,N} $, определяем теперь в виде совокупности всех упорядоченных пар, составленных всякий раз из намеченных заранее точек врезки и выключения инструмента (две упомянутые точки близки). Таким образом, реализуется конкретная версия (2.1)–(2.3) и можно рассматривать процессы (2.4).

Принимая (2.5), получаем пучки трасс (2.6), развивающихся в $\mathfrak{X}$ и, в частности, в X. Точку x⁰ совмещаем с началом координат: ${{x}^{0}} \triangleq (0,0)$.

Пример. Вычисления производились на персональной электронно-вычислительной машине с процессором Intel i5-2400 с 4 Гб оперативной памяти, работающей под управлением Windows 7 (64-bit). Точки начала и завершения движения совпадают с началом координат. Вычисления производились в многопоточном режиме (с использованием всех четырех ядер процессора).

Рассматривается прямоугольник $X = [0,{\mathbf{a}}] \times [0,{\mathbf{b}}]$ с размерами a = 2000 и b = 1000. Точка начала и завершения движения есть x⁰ = (0, 0).

Требуется обойти 45 контуров ${{\Gamma }_{{1,1}}},\;...,$ ${{\Gamma }_{{1,{{{\mathbf{n}}}_{1}}}}},\;...,$ ${{\Gamma }_{{n,1}}},\;...,$ ${{\Gamma }_{{n,{{{\mathbf{n}}}_{n}}}}}$, которые нумеруются подряд. Получающиеся после дискретизации “вторичных” эквидистант мегаполисы ${{{\mathbf{L}}}_{j}},j \in \overline {1,45} $, имеют от 1 до 29 пар точек врезки и выключения инструмента. Количество адресных пар 36. Вычисления производились комбинированным методом. Именно сначала производились вычисления приближенным итерационным алгоритмом, изложенным в [26–28]. Речь идет о задаче управления режущим инструментом, рассматриваемой во Введении (имеется в виду резка “по замкнутому контуру” на машинах с ЧПУ). Оптимизируется общее время реализации раскройного плана при условиях предшествования следующего типа: для каждой детали резка внутренних контуров должна предшествовать резке внешнего контура; аналогичное соглашение действует и в отношении “внутренних” деталей (деталей, расположенных внутри других деталей). Количество контуров предполагалось достаточно большим (в примерах [27, разд. 8] n = 60) с точки зрения “прямого” использования ДП для поиска оптимального решения глобальной задачи. В [27] рассматривались варианты организации итерационных алгоритмов, из которых сейчас (по соображениям объема) остановимся только на одном (см. [27, разд. 8]), имея в виду итерации со случайной реализацией вставок.

Итак, начальное приближение в [27, разд. 8] определялось жадным алгоритмом при соблюдении условий предшествования (исследовался также вариант с улучшением жадного алгоритма, подробно описанный в [28, разд. 6]). Далее производилось случайное испытание по реализации начала вставки (параметр $\nu $), доставляющее ${{\nu }_{1}}$, после чего применялось ДП для вставки с началом ${{\nu }_{1}}$. В результате получается улучшенный вариант “начального” решения, для которого на основе случайного испытания формируется новое значение ν = ν₂; реализуется новая вставка на основе ДП при ν = ν₂. Далее процедура повторяется. При этом на каждом этапе используется эвристика, полученная при посредстве оптимизирующей вставки на предыдущем этапе. В [27, разд. 8] приведен конкретный пример решения со случайным механизмом генерации вставок (в [27, разд. 7] предложен также детерминированный вариант итерационной процедуры, в основе которого находится идея использования условий предшествования).

Ниже рассматривается детерминированный вариант процедуры (в духе разд. 4 применяются короткие “зондирующие” вставки с целью выбора локализации вставок большей размерности для осуществления рабочего воздействия на эвристику), реализуемый в режиме итераций, которые осуществляются всякий раз для “своей” локализации вставки. Как уже отмечалось, исследуется вариант листовой резки “по замкнутому контуру” при наличии условий предшествования и функцией стоимости с зависимостью от списка заданий (разработанный метод решения применим, следовательно, в условиях общей постановки разд. 2; в частности, он может применяться (см. [29]) в задаче о демонтаже радиоактивного оборудования, отмеченной во Введении). Общее количество итераций в эвристическом алгоритме составляет 10000, количество итераций в одном цикле – 30. Затем использовался приведенный в данной статье итерационный алгоритм улучшения решения с применением беллмановских вставок. Количество итераций равно 3. Размер малого окна N₁ = 10, размер большого окна N₂ = 25.

Стоимость в данном примере имеет характер времени движения. Для определения этого времени используются скорость холостого хода ${{\text{v}}_{{idling}}}$ и скорость реза ${{\text{v}}_{{cut}}}$. Именно в примере ${{v}_{{idling}}} = 100$, а ${{v}_{{cut}}} = 2$.

В описании функций стоимости через $\rho (x,y)$ обозначаем евклидово расстояние между точками x и y на плоскости.

Функция ${{{\mathbf{c}}}^{\natural }}$ задается следующим образом: если $x \in \mathfrak{X}$, $y \in \mathfrak{X}$ и $K \subset \overline {1,{\mathbf{n}}} $, $K \ne \emptyset $, то

Теперь введем существенный фрагмент функции $c_{s}^{\natural }$, $s \in \overline {1,{\mathbf{n}}} $, где ${\mathbf{n}} = 45$: если $x \in {{{\mathbf{L}}}_{s}}$, $y \in {{{\mathbf{L}}}_{s}}$, $a = a_{{x,y}}^{{(s)}}$ – точка начала реза на эквидистанте и $K \subset \overline {1,{\mathbf{n}}} $, $K \ne \emptyset $, то

где ${{\tilde {D}}_{s}}$ – функция, определяющая зависимость стоимости внутренних работ в мегаполисе L_s от списка $\overline {1,{\mathbf{n}}} {\backslash }K$ выполненных на данный момент заданий. Если $K = \overline {1,{\mathbf{n}}} $, то ${{\tilde {D}}_{s}}(K) \triangleq 0$. Для определения ${{\tilde {D}}_{s}}(K)$ в случае $K \ne \overline {1,{\mathbf{n}}} $ введем следующее обозначение: $r_{{{\text{min}}}}^{s}(K)$ – минимальное из всех расстояний от геометрического центра мегаполиса L_s до аналогичных центров уже посещенных мегаполисов (описываемых множеством $\overline {1,{\mathbf{n}}} {\backslash }K$). Если при этом $r_{{{\text{min}}}}^{s}(K) \leqslant 250$, то ${{\tilde {D}}_{s}}(K) \triangleq $ ((250 – $r_{{{\text{min}}}}^{s}(K)){\text{/}}250)100$, иначе ${{\tilde {D}}_{s}}(K) \triangleq 0$. Далее следует учитывать замечание из разд. 2.

Терминальная функция ${{f}^{\natural }}$ задается следующим способом: при $x \in \mathfrak{X}$

Результат, достигаемый на первой итерации эвристического алгоритма, есть 20377.3, а результат работы итерационного эвристического алгоритма совпадает с 20112.5. Наконец, результат работы улучшающего алгоритма на основе беллмановских вставок есть 20013.4. Время счета составляет 5 мин 46 с. Результат счета показан на рис. 2.

Заключение. Использование вставок на основе ДП представляется естественным вариантом локального улучшения результатов, доставляемых эвристическими решениями. Особенностью процедуры, применяемой в настоящей работе, является то, что исходная маршрутная задача существенно усложнена; в частности, она содержит ограничения в виде условий предшествования, а соответствующие функции стоимости могут включать зависимость от списка заданий. Данные особенности мотивируются потребностями актуальных прикладных задач и требуют специального теоретического исследования. Постановка осложняется достаточно большой размерностью, что важно в задачах маршрутизации и требует применения эффективных эвристических алгоритмов. В работе указан подход к построению оптимизирующих вставок на основе ДП, реализуемых в режиме итераций, что позволяет ощутимо улучшить результат, доставляемый эвристическими алгоритмами.