Известия РАН. Теория и системы управления, 2019, № 1, стр. 109-116

Введение. В ходе исследований была решена проблема о приведении в состояние покоя за конечное время двумерной мембраны с помощью ограниченного по абсолютной величине управляющего силового воздействия, приложенного к границе рассматриваемой мембраны. В постановке задачи управления на функции начальных данных (смещение и скорость) наложены условия гладкости и некоторые граничные условия. Граничное силовое воздействие определяется неоднородным условием Неймана. Заметим, что условия гладкости начальных данных, приведенные в данной работе, существенно более слабые, чем в [1].

Решение задачи делится на два этапа. На первом этапе производится стабилизация решения в достаточно малую окрестность состояния покоя с помощью трения, введенного на границе области. При этом достаточная малость величины управления достигается за счет выбора близкого к нулю значения коэффициента трения. В данном случае используются результаты работ [2–4], посвященные стабилизации энергии мембран посредством граничных условий специального вида. На втором этапе управления производится полное успокоение колебаний мембраны. Здесь существенную роль играет метод продолжения начальных данных на некоторую ограниченную область и рассмотрение некоторой специальной начально-краевой задачи для двумерного волнового уравнения в этой области. Тогда управлением является производная по нормали к границе исходной области, занимаемой мембраной, взятая от решения указанной начально-краевой задачи. Заметим, что способ управления на данном этапе фактически определяется способом продолжения начальных данных на упомянутую ограниченную область. Решающую роль в подобной конструкции играет обратимость классического волнового уравнения по времени. Управление такого рода использовалось в работах многих авторов 70–90-х гг.В данном случае ограничение на абсолютную величину управляющего силового воздействия выполняется в силу того, что решение исходной задачи было приведено в достаточно малую окрестность по норме некоторого соболевского пространства на первом этапе. Точные математические определения будут даны ниже.

Заметим, что изложенный в данной работе метод доказательства может быть применен в случае любой размерности, но мы рассматриваем плоский случай для простоты изложения.

Возможность полной остановки за конечное время в случае распределенного управления доказывается в [5]. Там же дана оценка сверху для оптимального времени управления.

Ранее вопрос об управлении колебаниями плоской мембраны c помощью граничных сил рассматривался многими авторами (например, обзорные статьи [2, 6], а также приведенная в них литература). В монографии [7] описывается задача об остановке колебаний ограниченной струны с помощью граничного управления, доказывается, что возможно за конечное время полностью остановить колебания струны при ограничении на абсолютную величину управляющего воздействия и дается оценка времени, необходимого для полной остановки колебаний. В [8] рассматриваются задачи оптимального управления системами с распределенными параметрами и формулируются условия оптимальности, аналогичные принципу максимума Л.С. Понтрягина для систем с конечным числом степеней свободы. При этом указанные условия далеко не всегда приводят к конструктивному способу построения оптимального управления. В [6] приводится задача о полной остановке движения мембраны, доказывается существование такого граничного управления и оценивается время, необходимое для полной остановки колебаний. Здесь авторы во многих постановках задач отказываются от требований оптимальности управления и рассматривают только проблему управляемости, что существенно облегчает исследование. В работе не берутся задачи с ограничением на абсолютную величину управляющих сил, а также нет явных выражений для управляющих воздействий, а только доказываются теоремы существования.

Постановка задачи данной статьи существенно отличается от представленной в [2, 6], так как величина управляющего силового воздействия на границе области должна удовлетворять условию ${\text{|}}u(t,x){\text{|}} \leqslant \varepsilon $. Заметим также, что мы ищем здесь не оптимальное, а некоторое допустимое (удовлетворяющее исходным ограничениям) управление.

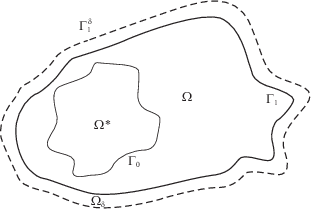
1. Постановка задачи. Пусть $\Omega $ – ограниченная область в ${{R}^{2}}$ с бесконечно гладкой границей, $\nu $ – внешняя единичная нормаль к границе области $\Omega $, $\Sigma $ – боковая поверхность цилиндра ${{Q}_{T}} = (0,T) \times \Omega $. Пусть также граница $\Omega $ состоит из двух частей ${{\Gamma }_{0}}$ и ${{\Gamma }_{1}}$, т.е.

Предположим дополнительно, что

Таким образом, ${{\Gamma }_{0}}$ должна быть также границей некоторой ограниченной области $\Omega {\text{*}}$, такой, что $\Omega \cap \Omega {\text{*}} = \emptyset $ (рисунок).

Обозначим

Рассмотрим начально-краевую задачу для уравнения колебаний мембраны:

Пусть $\varepsilon > 0$ – произвольное число. Ставится задача построить такое управляющее воздействие u, удовлетворяющее неравенству

что соответствующее решение $w$ и его первая производная по t обращаются в нуль в некоторый момент времени $T$, т.е. $w(T,x) = 0,$ ${{w}_{t}}(T,x) = 0$ для всех $x \in \Omega $. Если данная задача имеет решение, то систему (1.1)–(1.3) будем называть управляемой.

Рассмотрим пространство

Следующая теорема является главным результатом данной работы.

Теорема. Пусть дополнительно граница $\Omega $ удовлетворяет условию: существует точка ${{x}_{0}} \in {{R}^{2}}$, такая, что:

1) $(x - {{x}_{0}}) \cdot \nu \leqslant 0$, $x \in {{\Gamma }_{0}}$,

2) $(x - {{x}_{0}}) \cdot \nu \geqslant \beta > 0$, $x \in {{\Gamma }_{1}}$,

кроме того, $(\varphi (x),\psi (x)) \in \mathcal{H}_{0}^{3}(\Omega )$ и

Тогда система (1.1)–(1.3) управляема.

Доказательство теоремы состоит из двух этапов. На первом этапе рассматриваемое решение и его первая производная по времени приводятся в достаточно малую окрестность нуля по норме $\mathcal{H}_{0}^{3}(\Omega )$, а на втором этапе из малой окрестности система приводится в полный покой.

Заметим, что на начальные данные в задаче управления накладываются условия достаточно большой гладкости. Это связано с тем, что в процессе доказательства будет использоваться теорема С.Л. Соболева о вложении для перехода от соболевской нормы к норме в пространстве гладких функций. В этом случае будет происходить потеря порядка гладкости.

2. Первый этап управления. На первом этапе поставим задачу приведения решения системы (1.1)–(1.4) и ее первой производной по переменной t в сколь угодно малую окрестность нуля по норме пространства $\mathcal{H}_{0}^{3}(\Omega )$. При этом на управляющее воздействие наложено ограничение (1.5).

Для этого воспользуемся результатами работ [3, 4]. Суть этих результатов состоит в том, что на ${{\Gamma }_{1}}$ вводится трение, заданное первой производной от $w(t,x)$ по переменной t, т.е. рассматривается начально-краевая задача (1.1)–(1.3) с краевым условием

где $k > 0$ – коэффициент трения. Опишем коротко вопросы разрешимости данной начально-краевой задачи и регуляризации ее решения.

Введем следующие обозначения:

где

В пространстве $V \times H$ определим неограниченный оператор

c областью определения

Известно, что квадрат нормы в пространстве $D(\mathfrak{A})$ может быть задан следующим образом:

Рассмотрим систему дифференциальных уравнений:

где $\bar {w} = ({{w}_{1}},{{w}_{2}})$,

Известно (см., например, [4] и цитируемую там работу [9]), что оператор $\mathfrak{A}$ – производящий оператор сжимающей полугруппы ${{e}^{{t\mathfrak{A}}}}$, т.е. такой полугруппы, для которой

Заметим также, что оператор $\mathfrak{A}$ является диссипативным. Действительно, для любого $\bar {v} \in D(\mathfrak{A})$ имеем

что и означает диссипативность.

Из теории непрерывных полугрупп известно, что если пара начальных данных $(\varphi ,\psi )$ является элементом пространства $D({{\mathfrak{A}}^{k}})$, $k = 0,1,2,\;...$, то для соответствующего решения системы (2.3) верно включение

Предположим, что $(\varphi ,\psi ) \in V \times H$. Доказано (см. [3] или [4], но для более слабых условий на границу области), что для энергии системы верно неравенство

где – энергия системы и положительные постоянные M и $\gamma $ не зависят от начальных данных.

Пусть $(\varphi ,\psi ) \in D(\mathfrak{A})$ и $({{w}_{1}}(t),{{w}_{2}}(t))$ – соответствующее этим начальным данным решение. Подействуем на уравнение (2.3) и начальные условия (1.2) оператором $\mathfrak{A}$. Следовательно, получим

Заметим, что

Тогда из (2.4) и (2.5) имеем

Объединяя (2.2), (2.4) и (2.6), получим:

Пусть начальные данные являются элементом $D(\mathfrak{A})$, тогда для соответствующего решения из теории эллиптических краевых задач (см. [10, с. 98]) верна оценка

где константа N₁ не зависит от выбора w₁. Из последней оценки, а также из (2.4) и (2.6) следует, что ${{w}_{1}}(t)$ стремится к нулю при $t \to + \infty $ по норме в ${{H}^{2}}(\Omega )$, так как w₁ закреплено на части границы.

Следствием этих оценок и рассуждений является эквивалентность норм в пространствах $D(\mathfrak{A})$ и ${{H}^{2}} \times {{H}^{1}}$.

Перейдем теперь к рассмотрению пространства $D({{\mathfrak{A}}^{2}})$. Как и прежде, используя теорию разрешимости эллиптических краевых задач, данное пространство можно эффективно описать следующим образом:

Пусть $({{w}_{1}}(t),{{w}_{2}}(t))$ – решение задачи (1.1)–(1.3), (2.1), тогда оно принадлежит пространству $C([0,T];D({{\mathfrak{A}}^{2}}))$. Имеем

Из (2.9) и [4] следует:

Объединяя (2.7) и (2.10), получим

Применяя теорию эллиптических граничных задач (см. [10, с. 98]), можно написать

где константы ${{N}_{2}}$ и ${{N}_{3}}$ не зависят от выбора $({{w}_{1}},{{w}_{2}})$.

Из (2.6) и (2.10) получаем, что $\Delta {{w}_{1}}(t)$ стремится к нулю (при $t \to + \infty $) по норме в ${{H}^{1}}(\Omega )$. Следовательно, по теореме С.Л. Соболева о следах $\Delta {{w}_{1}}(t)$ будет стремиться к нулю и по норме ${{H}^{{\frac{1}{2}}}}({{\Gamma }_{1}})$. Тогда, используя также (2.4), (2.13) и снова (2.10), получаем, что ${{w}_{2}}(t)$ стремится к нулю (при $t \to + \infty $) по норме в ${{H}^{2}}(\Omega )$. Таким образом из оценки (2.12) вытекает, что ${{w}_{1}}(t)$ стремится к нулю при $t \to + \infty $ по норме в ${{H}^{3}}(\Omega )$, так как ${{w}_{1}}$ закреплено на части границы.

Следствием этих оценок и рассуждений является эквивалентность норм в пространствах $D({{\mathfrak{A}}^{2}})$ и ${{H}^{3}} \times {{H}^{2}}$.

При заданных начальных условиях решим задачу (1.1)–(1.3), (2.1), затем данное решение подставим только в правую часть равенства (2.1), получим краевое условие (1.5) для начально-краевой задачи (1.1)–(1.4). Другими словами, управляющее воздействие в задаче (1.1)–(1.4) на первом этапе мы положим равным

на ${{\Gamma }_{1}}$. Здесь $w_{1}^{0}$ – решение задачи (1.1)–(1.3), (2.1).

Следовательно, доказано, что, управляя достаточно долго, можно сделать величину

сколь угодно малой в некоторый момент времени $t = {{T}_{1}}$. Заметим, что для функций $\phi (x)$, $\psi (x)$ должны выполняться следующие условия:

Посредством (1.6) условие (2.14) выполнено для любого k.

Покажем теперь, что граничное управляющее воздействие $u(t,x)$ можно сделать также достаточно малым, т.е. удовлетворить ограничению (1.5). Для этого заметим, что в силу сжимаемости полугруппы, порожденной оператором $\mathfrak{A}$, верно равенство

Следовательно, можно написать

Таким образом, используя теоремы С. Л. Соболева о вложении и (2.13), получим

Так как коэффициент k можно выбрать сколь угодно близким к нулю, то в силу последней оценки величина ${{\left\| {{{w}_{2}}(t)} \right\|}_{{C(\overline \Omega )}}}$ ограничена. Также заметим, что в силу краевых условий (1.6) начальные данные $(\varphi ,\psi )$ будут элементом пространства $D({{\mathfrak{A}}^{2}})$ при любом k. Выбирая коэффициент трения k достаточно малым, получим, что условие (1.5) выполнено.

3. Второй этап управления. Поставим теперь задачу о приведении рассматриваемой системы в полный покой. Функции ${{\left. w \right|}_{{t = 0}}} = w({{T}_{1}},x)$ и ${{\left. {{{w}_{t}}} \right|}_{{t = 0}}} = {{w}_{t}}({{T}_{1}},x)$ будем считать новыми начальными данными в задаче (1.1)–(1.4). Напомним, что, согласно доказанному выше, эти начальные условия (пара функций) достаточно малы по норме пространства $\mathcal{H}_{0}^{3}(\Omega )$.

Рассмотрим область ${{\Omega }_{\delta }}$, которая по определению является $\delta $-окрестностью области $\Omega $ без точек множества $\bar {\Omega }{\text{*}}$ (рисунок). Область ${{\Omega }_{\delta }}$ построим так, чтобы внешний контур ее границы (назовем его $\Gamma _{1}^{\delta }$) удовлетворял п. 2$)$ условия, которое содержится в формулировке теоремы. Пусть также ${{\nu }_{\delta }}$ – внешняя единичная нормаль к границе области ${{\Omega }_{\delta }}$.

Определим пространство

Рассмотрим также произвольную пару функций

из пространства $\mathcal{H}_{0}^{3}(\Omega )$. Продолжим эту пару к нулю (линейный оператор продолжения существует и ограничен) на область ${{\Omega }_{\delta }}$ с сохранением гладкости. Конструкция оператора продолжения E хорошо известна и подробно описана в [11].

Продолженные таким образом функции начальных данных будем, следуя Д.Л. Расселу, обозначать соответственно ${{f}^{e}}(x)$ и ${{g}^{e}}(x)$.

Рассмотрим начально-краевую задачу для уравнения колебания мембраны в области ${{\Omega }_{\delta }}$:

Для решения задачи (3.1)–(3.4) аналогично предыдущему разделу имеет место оценка

где

Далее будем использовать метод (в измененном виде), описанный в [2] и примененный в задачах граничного управления для волнового уравнения.

Пусть имеются некоторые начальные условия $f(x)$ и $g(x)$, $x \in \Omega $. Продолжим их на ${{\Omega }_{\delta }}$ с помощью линейного ограниченного оператора E. Тогда $({{f}^{e}},{{g}^{e}}) = E(f,g)$. Получаем начально-краевую задачу (3.1)–(3.4). Пусть ${{w}^{s}}(t,x)$ – решение данной задачи. Для области ${{\Omega }_{\delta }}$ рассмотрим оператор ${{\mathfrak{A}}_{\delta }}$, который строится совершенно аналогично оператору $\mathfrak{A}$ для области $\Omega $. Тогда выполнена оценка

А в силу эквивалентности норм верно

Рассмотрим достаточно большой момент времени $t = {{T}_{2}}$ и ограничение решения и его производной по времени в момент ${{T}_{2}}$ на область $\Omega $. Очевидно, что для $t = {{T}_{2}}$ в силу (3.7) и непрерывности оператора $E$ верна оценка

Пусть по определению

Приведем теперь начально-краевую задачу в обратном времени (т.е. при $t\;\leqslant \;{{T}_{2}}$) для уравнения (остается неизменным)

с краевым условием на $\Gamma _{1}^{\delta }$условием (3.3) на ${{\Gamma }_{0}}$ и начальными условиями

Пусть $(w_{1}^{i}(t),w_{2}^{i}(t))$ – решение начально-краевой задачи (3.3), (3.9), (3.10) (3.11) в обратном времени. Аналогично предыдущему выполнена оценка

Рассмотрим сумму решений в прямом и обратном времени, ограниченную на область $\Omega $:

Эта сумма удовлетворяет уравнению (1.1), а в качестве искомого граничного управляющего воздействия $u(t,x)$ можно взять ограничение производной по внешней нормали от $w(t,x)$ на боковую поверхность цилиндра.

Очевидно, что решение (3.13) с начальными условиями вида

(индекс $r$ означает ограничение на $\Omega $) тождественно равно нулю в $\Omega $ вместе со своей первой производной по t в момент времени $t = {{T}_{2}}$. Заметим, что значение соответствующего решения начально-краевой задачи с начальными условиями (3.14) на границе области $\Omega $ и определяет искомое управление.

Пара $(w_{1}^{{i,r}}(0,x),w_{2}^{{i,r}}(0,x))$ получается из пары $(f(x),g(x))$ применением некоторого линейного непрерывного оператора, назовем его L с нормой, меньшей единицы (следствие оценок (3.8) и (3.12)). Очевидно, что суммы в правых частях (3.14) дают все элементы пространства $\mathcal{H}_{0}^{3}(\Omega )$. Действительно, (3.14) можно записать как

где I – тождественный оператор. Следовательно, так как $\left\| L \right\| < 1$, то оператор $I + L$, действующий из $\mathcal{H}_{0}^{3}(\Omega )$ в себя, обратим.

Теперь представим искомую функцию управления (на втором этапе) в следующем виде:

$x \in {{\Gamma }_{1}}$, где R – оператор ограничения из ${{\Omega }_{\delta }}$ на область $\Omega $, ${{S}_{ + }}(t)$, ${{S}_{ - }}({{T}_{2}} - t)$ – разрешающие операторы диссипативной задачи в прямом и обратном времени соответственно, P – проекция: $(a,b) \mapsto a$ и

Таким образом, доказана возможность приведения в покой системы с произвольными гладкими начальными данными. Покажем теперь, что, выбирая начальные данные достаточно малыми, можно привести систему в покой малым по модулю граничным управлением.

Пусть пара $({{\left. w \right|}_{{t = 0}}},{{\left. {{{w}_{t}}} \right|}_{{t = 0}}})$ достаточно мала по норме пространства $\mathcal{H}_{0}^{3}(\Omega )$. Из формулы (3.16) автоматически следует достаточная малость управления ${{u}^{{(2)}}}(t,x)$, так как все операторы, входящие в эту формулу, непрерывны.

Следовательно, ограничение нормальной производной от решения начально-краевой задачи на границу области $\Omega $ (условие Неймана в задаче управления) будет меньше наперед заданного $\varepsilon $ по абсолютной величине, если время управления на первом этапе выбрать достаточно большим. Последнее и означает, что выполнено требуемое ограничение на управляющее воздействие $u(t,x)$. Теорема доказана.

Заключение. Доказано существование граничного управления, приводящего колебания мембраны в покой за конечное время. При этом на само управляющее воздействие наложено ограничение по абсолютной величине. В формулировке основной теоремы начальное смещение, начальная скорость и геометрия границы мембраны удовлетворяют некоторым условиям.