Известия РАН. Теория и системы управления, 2019, № 1, стр. 166-176
РЕШЕНИЕ ЗАДАЧИ ОПТИМАЛЬНОГО ПРОГРАММНОГО ТЕРМИНАЛЬНОГО УПРАВЛЕНИЯ РАСХОДОМ ТОПЛИВА РАКЕТЫ-НОСИТЕЛЯ
В. И. Калёв 1, *, А. Ф. Шориков 1, **
1 ФГАОУ ВО “УрФУ имени первого Президента России Б.Н. Ельцина”,
АО “НПО автоматики имени академика Н.А. Семихатова”
Екатеринбург, Россия
* E-mail: v.i.kalev@urfu.ru
** E-mail: afshorikov@mail.ru
Поступила в редакцию 27.02.2018
После доработки 23.11.2018
Аннотация
Предлагается способ решения задачи оптимального программного терминального управления расходом топлива ракеты-носителя. Исходная нелинейная дифференциальная модель объекта управления линеаризуется вдоль опорной траектории и аппроксимируется линейной дискретной динамической системой. Предполагается, что множества ограничений фазового состояния и управления являются выпуклыми, замкнутыми и ограниченными многогранниками с конечным числом вершин. Для сформированной системы решается задача оптимального программного терминального управления с учетом заданных ограничений на векторы состояния и управления. При решении задачи оптимального программного терминального управления используется аппарат построения прямых и обратных областей достижимости. Эффективность предлагаемого алгоритма решения рассматриваемой задачи демонстрируется на примере численного моделирования.
Введение. На большинстве современных отечественных ракет-носителей (РН), оснащенных жидкостными реактивными двигателями, решаются четыре основные задачи управления: навигации, стабилизации, наведения и управления расходом топлива.
Задача оптимизации управления расходом топлива жидкостной двигательной установки (ДУ) РН заключается в регулировании текущих запасов компонентов топлива в баках с целью обеспечения номинального режима работы ДУ. При этом номинальный (опорный) режим работы ДУ РН представляет собой расчетные значения параметров изменения тяги и массы компонентов топлива в баках ДУ РН в зависимости от времени [1, 2], а также предписывает момент времени, в который должно произойти разделение ступеней РН. Эти данные формируются в результате решения соответствующей задачи наведения фазовой траектории движения РН на заданную опорную траекторию. Тогда в задаче оптимизации терминального управления ДУ РН критерий качества для рассматриваемого процесса управления должен оценивать отклонение значений основных параметров состояния этого процесса (массовые расходы и масса компонентов топлива в баках) от их номинальных (опорных) значений в финальный (терминальный) момент времени (момент выключения ДУ при разделении ступеней РН) при соблюдении в этом процессе управления ограничений на значения фазового вектора ДУ РН, обеспечивающих реализацию номинального (опорного) закона изменения ее параметров с заданной точностью. Таким образом, основной целью в задаче оптимизации терминального управления расходом топлива ДУ РН является нахождение такого управляющего воздействия, которое минимизирует выбранный критерий качества и, следовательно, обеспечивает синхронизацию и полное израсходование рабочих запасов компонентов топлива в баках к заданному моменту времени разделения ступеней РН. Тогда достижение этой цели при решении задачи оптимизации терминального управления ДУ РН обеспечивает соответствующую реализацию фазовой траектории движения РН вблизи требуемой опорной фазовой траектории ее движения в предположении, что системы наведения, навигации и стабилизации движения РН работают достаточно точно.
За последние 40 лет решению задачи терминального управления расходом топлива уделялось большое внимание, и полученные результаты широко представлены в научной литературе. Основным трудом в этом направлении является монография Б.Н. Петрова [3], в которой намечены пути решения задачи терминального управления расходом топлива РН как задачи стохастического оптимального управления. Результаты длительного исследования по разработке, а также внедрению систем управления на отечественные РН изложены в недавней публикации [4].
В настоящее время хорошо изучены задачи оптимизации терминального управления динамическими системами, в которых считаются известными вероятностные характеристики априори неопределенных параметров. Однако реальная ситуация такова, что для сложных систем, какими являются объекты ракетно-космической техники, очень часто оказывается невозможным провести большое количество испытаний, позволяющих определить вероятностные характеристики для априори неопределенных параметров. В связи с этим информация о вероятностных характеристиках априори неопределенных параметров может отсутствовать или быть недостоверной [5, 6]. Это обстоятельство мотивирует разработчика алгоритмов управления рассматривать неопределенность параметров в качестве ограниченного множества их возможных значений.
В данной работе для решения задачи оптимального программного терминального управления расходом топлива РН используется исходная нелинейная модель объекта, описанная в [7]. Указанная модель линеаризуется, и полученные линеаризованные уравнения динамики объекта управления приводятся к дискретному виду. Предполагается, что ограничения на неопределенные априори параметры рассматриваемого процесса – начальное состояние объекта и управляющее воздействие – являются выпуклыми, замкнутыми и ограниченными многогранниками (с конечным числом вершин) в соответствующих конечномерных векторных пространствах. После этого для сформированной линейной дискретной динамической системы решается задача оптимизации программного терминального управления и полагается, что найденное оптимальное программное управление будет близким к оптимальному программному управлению относительно того же самого терминального критерия качества для аналогичной задачи, в которой динамика объекта описывается исходной нелинейной системой.
Предлагаемый в работе подход к решению задачи оптимизации программного терминального управления базируется на применении аппарата построения и анализа точных областей достижимости линейной дискретной динамической системы. В связи с этим в данной статье взят за основу изложенный в работах [5, 8] общий рекуррентный алгебраический алгоритм построения областей достижимости для линейных дискретных динамических систем с некоторыми его модификациями.
1. Постановка задачи. На промежутке времени $[{{t}_{0}},{{t}_{1}}]$ в качестве управляемого объекта рассматривается нелинейная модель [7], описывающая установившийся режим работы ДУ первой ступени РН в совокупности с двумя топливными баками (здесь ${{t}_{0}}$ – время выхода на режим и ${{t}_{1}}$ – время выключения ДУ первой ступени РН). Управляющее воздействие $u(\theta )$ осуществляется с помощью смены положения исполнительного органа – дросселя, установленного в трубопроводе горючего, что позволяет изменять секундные расходы компонентов топлива из баков.
Текущие значения массовых расходов компонентов топлива из баков могут быть вычислены из следующих алгебраических соотношений:
(1.1)
$\begin{gathered} {{m}_{о }}(\theta ) = \frac{{(P + {{c}_{2}}{{{(\Delta {{K}_{{д р }}} + {{c}_{1}}u(\theta ))}}^{2}} + {{c}_{3}}(\Delta {{K}_{{д р }}} + {{c}_{1}}u(\theta )))(K + \Delta {{K}_{{д р }}} + {{c}_{1}}u(\theta ))}}{{(I + {{c}_{4}}{{{(\Delta {{K}_{{д р }}} + {{c}_{1}}u(\theta ))}}^{2}} + {{c}_{5}}(\Delta {{K}_{{д р }}} + {{c}_{1}}u(\theta )))(1 + K + \Delta {{K}_{{д р }}} + {{c}_{1}}u(\theta ))}}, \\ {{m}_{г }}(\theta ) = \frac{{P + {{c}_{2}}{{{(\Delta {{K}_{{д р }}} + {{c}_{1}}u(\theta ))}}^{2}} + {{c}_{3}}(\Delta {{K}_{{д р }}} + {{c}_{1}}u(\theta ))}}{{(I + {{c}_{4}}{{{(\Delta {{K}_{{д р }}} + {{c}_{1}}u(\theta ))}}^{2}} + {{c}_{5}}(\Delta {{K}_{{д р }}} + {{c}_{1}}u(\theta )))(1 + K + \Delta {{K}_{{д р }}} + {{c}_{1}}u(\theta ))}}, \\ \end{gathered} $Текущие значения масс окислителя и горючего в топливных баках зависят от значений их массовых расходов (1.1) и могут быть вычислены следующим образом:
(1.2)
$\begin{gathered} {{M}_{о }}(\theta ) = M_{о }^{{н о м }} + \Delta {{M}_{о }} - \int\limits_{{{t}_{0}}}^t {{{m}_{о }}(\theta )d\theta } , \\ {{M}_{г }}(\theta ) = M_{г }^{{н о м }} + \Delta {{M}_{г }} - \int\limits_{{{t}_{0}}}^t {{{m}_{г }}(\theta )d\theta } , \\ \end{gathered} $Исходная нелинейная модель объекта управления, описываемая системой соотношений (1.1), (1.2), линеаризуется вдоль опорного закона изменения массы компонентов топлива:
(1.3)
$\left\{ {\begin{array}{*{20}{c}} {m_{о }^{{о п о р }}(\theta ) = \frac{{PK}}{{I + IK}}} \\ {m_{г }^{{о п о р }}(\theta ) = \frac{P}{{I + IK}}} \end{array},\quad \left\{ {\begin{array}{*{20}{c}} {M_{о }^{{о п о р }}(\theta ) = M_{о }^{{н о м }} - \frac{{PK}}{{I + IK}}\theta ,} \\ {M_{г }^{{о п о р }}(\theta ) = M_{г }^{{н о м }} - \frac{P}{{I + IK}}\theta ,} \end{array}} \right.} \right.$Опишем теперь систему соотношений для сформированной упрощенной модели управляемого объекта, динамика которого рассматривается на заданном целочисленном промежутке времени $\overline {0,T} $.
Текущие значения массовых расходов окислителя и горючего определяются из рекуррентных дискретных соотношений:
(1.4)
$\begin{gathered} {{m}_{о }}(t + 1) = {{m}_{о }}(t) + \alpha u(t),\quad {{m}_{о }}(0) = m_{о }^{{н о м }} + \alpha \Delta {{K}_{{д р }}}, \\ {{m}_{г }}(t + 1) = {{m}_{г }}(t) + \beta u(t),\quad {{m}_{г }}(0) = m_{г }^{{н о м }} + \beta \Delta {{K}_{{д р }}}, \\ \end{gathered} $Дискретные рекуррентные уравнения, позволяющие определить значения текущей массы компонентов топлива в топливных баках, имеют вид
(1.5)
$\begin{gathered} {{M}_{о }}(t + 1) = {{M}_{о }}(t) - \Delta T(t){{m}_{о }}(t),\quad {{M}_{о }}(0) = M_{о }^{{н о м }} + \Delta {{M}_{о }}, \\ {{M}_{г }}(t + 1) = {{M}_{г }}(t) - \Delta T(t){{m}_{г }}(t),\quad {{M}_{г }}(0) = M_{г }^{{н о м }} + \Delta {{M}_{г }}, \\ \end{gathered} $Динамические уравнения объекта (1.4), (1.5) могут быть записаны в рекуррентном векторно-матричном виде:
где t – дискретный момент времени; x(t) – фазовый вектор системы, $x(t) \in {{\mathbb{R}}^{4}}$ (здесь и далее, ${{\mathbb{R}}^{n}}$ – n-мерное векторное пространство векторов-столбцов); $x(0) = {{x}_{0}}$ – заданное начальное значение фазового вектора; $u(t)$ – управляющее воздействие, $u(t) \in {{\mathbb{R}}^{1}}$; $A(t)$ – матрица состояния системы, $A(t) \in {{\mathbb{R}}^{{4 \times 4}}}$; предполагается, что для всех $t \in \overline {0,T - 1} $ для матрицы $A(t) \in {{\mathbb{R}}^{{4 \times 4}}}$ существует обратная ей матрица ${{A}^{{ - 1}}}(t) \in {{\mathbb{R}}^{{4 \times 4}}}$; $B(t)$ – матрица управления, $B(t) \in {{\mathbb{R}}^{{4 \times 1}}}$.Для дальнейшего рассмотрения решения задачи оптимизации терминального программного управления линейной дискретной системой (1.6) с использованием методов построения и анализа областей достижимости [5, 8] в данной работе делаются следующие предположения.
Предположение 1. Начальное фазовое состояние системы $x(0) = {{x}_{0}}$ фиксировано, а на фазовый вектор системы (1.6) наложены геометрические ограничения:
где ${\mathbf{X}}(t)$ – выпуклый, компактный многогранник (с конечным числом вершин). Ограничения (1.7) обусловлены требованиями к безаварийной работе ДУ РН и реализации только допустимых значений ее параметров, близких к опорным (номинальным) значениям в процессе терминального управления с заданной точностью.Предположение 2. Управляющее воздействие стеснено геометрическим ограничением:
где ${\mathbf{U}}(t)$ – выпуклый, компактный многогранник (с конечным числом вершин). Отметим, что в пространстве ${{\mathbb{R}}^{1}}$ выпуклым, компактным многогранником считается отрезок.Рассматриваемый процесс управления оценивается выпуклым терминальным функционалом $\Phi $: ${{\mathbb{R}}^{4}} \to {{\mathbb{R}}^{1}}$, определенным на возможных реализациях фазового вектора $x(T) \in {{\mathbb{R}}^{4}}$ объекта (1.6) на финальном шаге T, значения которого определяются как
где $x(T) \in {{\mathbb{R}}^{4}}$ – финальное фазовое состояние движения (траектории) $\bar {x}(T;\overline {0,T} ,{{x}_{0}},{{\{ u(t)\} }_{{t \in \overline {0,T - 1} }}})$ системы (1.6), соответствующего паре $({{x}_{0}},{{\{ u(t)\} }_{{t \in \overline {0,T - 1} }}}) = ({{x}_{0}},u(\, \cdot \,))$; ${{x}_{d}}$ – вектор, определяющий желаемое финальное фазовое состояние системы (1.6), ${{x}_{d}} \in {{\mathbb{R}}^{4}}$; $||\, \cdot \,{\text{|}}{{{\text{|}}}_{4}}$ – евклидова норма в пространстве ${{\mathbb{R}}^{4}}$. Функционал (1.9) оценивает отклонение параметров расхода топлива ДУ РН от соответствующих значений, рассчитанных для опорного закона изменения массы компонентов топлива, в финальный (терминальный) момент времени (выключения ДУ и последующее разделение ступеней РН) при условии выполнения фазового ограничения (1.7), обеспечивающего реализацию опорного закона функционирования ДУ РН с заданной точностью. Минимизация этого отклонения обеспечит полное расходование рабочих запасов компонентов топлива и синхронность их окончания в финальный момент времени.Тогда можно сформулировать следующую задачу оптимального программного терминального управления.
Для дискретной динамической системы (1.6)–(1.9) требуется найти такое допустимое программное управление
(1.10)
${{u}^{{(e)}}}(\, \cdot \,) = {{\{ {{u}^{{(e)}}}(t)\} }_{{t \in \overline {1,T - 1} }}} \in {{\mathbb{R}}^{{1 \times T - 1}}},\quad \forall t \in \overline {1,T - 1} :{{u}^{{(e)}}}(t) \in {\mathbf{U}}(t),$Предлагаемый в данной работе подход к решению поставленной задачи применяет аппарат построения и анализа областей достижимости. Основные положения по поводу используемого в данной работе метода построения областей достижимости для линейной дискретной динамической системы предложены в следующем разделе.
2. Области достижимости линейной дискретной динамической системы. В настоящее время применение аппарата построения и анализа областей достижимости динамических систем для решения задач управления имеет широкое распространение в теоретических и прикладных задачах [2, 5, 8–17]. В первую очередь нам необходимо ввести определения областей достижимости линейных дискретных динамических систем.
Определение 1. Прямой областью достижимости фазовых состояний линейной дискретной динамической системы (1.6)–(1.8) (в пространстве ${{\mathbb{R}}^{4}}$) на момент времени $\vartheta \in \overline {\tau + 1,T} $, соответствующей паре $(\tau ,X(\tau )) \in \overline {0,T - 1} \times {{2}^{{{{\mathbb{R}}^{4}}}}}$ (здесь и далее для любого множества $X$ символом ${{{\mathbf{2}}}^{X}}$ обозначается множество всех подмножеств множества $X$), называется множество, определяемое соотношением
Определение 2. Обратной областью достижимости фазовых состояний линейной дискретной динамической системы (1.6)–(1.8) (в пространстве ${{\mathbb{R}}^{4}}$) на момент времени τ, соответствующей паре $(\vartheta ,X(\vartheta )) \in \overline {1,T} \times {{2}^{{{{\mathbb{R}}^{4}}}}}$, называется множество, определяемое соотношением:
Необходимо отметить, что обратная область достижимости в нашем случае может быть вычислена напрямую, поскольку матрица $A(t)$ считается невырожденной для всех $t \in \overline {0,T - 1} $ (а это всегда так, поскольку уравнения динамики (1.6) были получены посредством дискретизации непрерывной линейной системы, соответствующей исходному объекту (см. [10])).
В силу принятых предположений о том, что множества ограничений (1.7), (1.8) относятся к классу выпуклых компактных многогранников, в работе [5] было показано, что множества, описывающие прямые и обратные области достижимости такой динамической системы, будут также принадлежать к классу выпуклых компактных многогранников.
Известно [8, 18–20], что любой выпуклый, замкнутый и ограниченный многогранник $P \in {{\mathbb{R}}^{n}}$ может быть представлен двумя способами: как выпуклая оболочка системы векторов и как множество решений системы линейных неравенств.
Определение 3. Множество из $k \in \mathbb{N}$ крайних точек, задаваемых набором векторов ${{v}_{i}} \in {{\mathbb{R}}^{n}}$, $i = \overline {1,k} $, выпуклая оболочка которых является многогранником $P \in {{\mathbb{R}}^{n}}$, называется вершинным описанием (V-Rep) этого многогранника:
(2.1)
$P = conv({{v}_{1}},{{v}_{2}}, \ldots ,{{v}_{k}}),\quad {{v}_{i}} \in {{\mathbb{R}}^{n}},\quad i = \overline {1,k} .$Определение 4. Система из $m \in \mathbb{N}$ линейных неравенств, определяющая многогранник $P \in {{\mathbb{R}}^{n}}$, называется фасетным описанием (H-Rep) этого многогранника:
(2.2)
$P = \{ x \in {{\mathbb{R}}^{n}}{\text{|}}Ax \leqslant b\} ,\quad A \in {{\mathbb{R}}^{{m \times n}}},\quad b \in {{\mathbb{R}}^{m}}.$Приведем теперь описание общего рекуррентного алгебраического метода [5, 8] построения областей достижимости с некоторыми его модификациями, направленными по большей части на повышение быстродействия работы алгоритма.
В основе метода [5, 8] лежит полугрупповое (эволюционное) свойство областей достижимости:
где $X(t) = {{{\mathbf{G}}}_{ + }}(0,X(0);t)$, $\forall t \in \overline {1,T - 1} $. Из этого свойства следует рекуррентная конструкция алгоритмов метода (см. рис. 1), заключающаяся в решении последовательности одношаговых задач по построению прямых и обратных областей достижимости. В предлагаемом методе при построении областей достижимости используются оба способа описания многогранников V-Rep (2.1) и H-Rep (2.2). Применение двойственного описания многогранников необходимо для реализации определенных операций над множествами (например, H-Rep используется для пересечения многогранных множеств и поиска экстремума функции на множестве, а V-Rep применяется для линейных преобразований, геометрической суммы множеств и поиска выпуклой оболочки множества).Операция $conv(\, \cdot \,)$ в алгоритмах, приведенных на рис. 1, обозначает решение задачи нахождения крайних точек приведенного внутри скобок множества точек и решается как задача линейного математического программирования способом, предложенным в [21]. Операции суммирования и вычитания множеств в данных алгоритмах понимаются как суммы Минковского этих множеств. Операции формирования двойственного описания множества достижимости V-Rep ↔ H-Rep и H-Rep ↔ V-Rep реализуются в данной работе с помощью модификации метода двойного описания [12], предложенной в [20], с фиксированным порядком неравенств lexmin.
Используя все вышесказанное, перейдем к описанию предлагаемого способа решения задачи оптимального программного терминального управления расходом топлива РН.
3. Алгоритм решения задачи. На основании сделанных построений и результатов работ [5, 8] можно показать, что решение поставленной задачи оптимального программного терминального управления линейной дискретной динамической системой (1.6)–(1.8) сводится к решению следующей последовательности подзадач:
1) построение последовательности прямых областей достижимости ${{{\mathbf{G}}}_{ + }}\left( {0,{{x}_{0}};t} \right)$, $\forall t \in \overline {1,T} $;
2) оптимизация выпуклого функционала $\Phi (x(T)) = {\text{||}}x(T) - {{x}_{d}}{\text{|}}{{{\text{|}}}_{4}}$ на множестве ${{{\mathbf{G}}}_{ + }}(0,{{x}_{0}};T)$, а именно определение множества ${\mathbf{G}}_{\Phi }^{{(e)}}(T) \subset {{\mathbb{R}}^{4}}$ финальных фазовых состояний рассматриваемой системы (1.5)–(1.7) из решения следующей задачи выпуклого математического программирования:
3) построение последовательности обратных областей достижимости ${{{\mathbf{G}}}_{ - }}(T,{\mathbf{G}}_{\Phi }^{{(e)}}(T);t)$, $\forall t \in \{ T - 1,T - 2, \ldots ,2,1\} $;
4) построение следующей последовательности множеств:
5) решение на промежутке $\overline {0,T} $ двухточечных краевых задач для динамической рекуррентной системы (1.6)–(1.8) при краевых условиях $x(0) = {{x}_{0}}$ и $x(T) = {{x}^{{(e)}}}(T) \in {\mathbf{G}}_{\Phi }^{{(e)}}(T)$, т.е. нахождение следующего множества оптимальных программных управлений:
(сводится к решению задач линейного программирования в прямых и обратных конструкциях общего рекуррентного алгебраического метода [5]).
Из результатов работ [5, 8] следует, что сформированное множество допустимых программных управлений ${{{\mathbf{U}}}^{{(e)}}}(\overline {0,T} ,x(0),{\mathbf{G}}_{\Phi }^{{(e)}}(T))$ есть множество всех допустимых программных управлений, являющихся решением рассматриваемой задачи оптимального программного терминального управления.
4. Численный пример. Продемонстрируем эффективность предлагаемого подхода на численном примере, в котором моделируется решение задачи оптимального программного терминального управления расходом топлива первой ступени РН “Союз-2-1в” [7, 23]. Исходная нелинейная система описывается на промежутке времени $\left[ {0,\;{{t}_{1}}} \right]$ уравнениями (1.1), (1.2), значения параметров которых приведены в табл. 1.
Таблица 1.
Значения параметров нелинейной системы
| I, с | P, кг | K | $M_{о }^{{н о м }}$, кг | $M_{г }^{{н о м }}$, кг | ΔMо, кг | ΔMг, кг |
|---|---|---|---|---|---|---|
| 320 | 528 000 | 8/3 | 120 000 | 45 000 | –500 | 300 |
| ΔKдр | c1 | c2 | c3 | c4 | c5 | t1, с |
| 8/75 | 8/75 | –1675 | 2250 | –15 | –12 | 100 |
В соответствие исходной нелинейной модели поставлена сформированная линейная система, полученная посредством линеаризации вдоль опорной траектории (1.3), и последующей дискретизации. Таким образом, система векторно-матричных линейных рекуррентных соотношений, описывающая динамику системы, соответствует уравнениям (1.4), (1.5) и имеет вид
здесь $x(t) = \{ {{x}_{1}}(t),{{x}_{2}}(t),{{x}_{3}}(t),{{x}_{4}}(t)\} \in {{\mathbb{R}}^{4}}$; ${{x}_{1}}(t)$ – массовый расход окислителя; ${{x}_{2}}(t)$ – масса окислителя в баке; ${{x}_{3}}(t)$ – массовый расход горючего; ${{x}_{4}}(t)$ – масса горючего в баке; $u(t) \in {{\mathbb{R}}^{1}}$ – скалярное допустимое управляющее воздействие; $x(0) = {{x}_{0}} = {{(1216.904,\;119500,\;438.787,\;45300)}^{{\text{т }}}}$; матрицы A(t) и B(t) являются стационарными:На фазовый вектор на протяжении всего движения наложены ограничения, отражающие условие безаварийной работы двигательной установки РН:
Качество процесса управления в данной задаче оценивается значением выпуклого терминального функционала на финальном шаге T = 16 (соответствует моменту времени t1 = 100 с для исходной нелинейной системы):
Для решения задачи оптимального программного терминального управления линейной дискретной динамической системой использовался описанный в предыдущем разделе алгоритм, результатом реализации которого стало сформированное множество оптимальных программных управлений ${{U}^{{(e)}}}(\, \cdot \,) = {{\{ {{u}^{{(e,j)}}}(\, \cdot \,)\} }_{{j \in \overline {1,k} }}}$, $\forall j \in \overline {1,k} \,:{{u}^{{(e,j)}}}(\, \cdot \,) = {{\{ {{u}^{{(e,j)}}}(t)\} }_{{t \in \overline {1,15} }}}$. Найденное множество управлений ${{U}^{{(e)}}}(\, \cdot \,)$ = = ${{\{ {{u}^{{(e,j)}}}(\, \cdot \,)\} }_{{j \in \overline {1,k} }}}$ порождает оптимальные траектории ${{x}^{{(e,j)}}}(\, \cdot \,)$ = $\tilde {x}(\, \cdot \,;\overline {0,16} ,{{x}_{0}},{{u}^{{(e,j)}}}(\, \cdot \,))$, $j \in \overline {1,k} $, финальное состояние которых ${{x}^{{(e,j)}}}(16) = \tilde {x}(16;\overline {0,16} ,{{x}_{0}},{{u}^{{(e,j)}}}(\, \cdot \,))$ есть для каждого $j \in \overline {1,k} $ один и тот же фазовый вектор ${{x}^{{(e,j)}}}(16) = {{x}^{{(e)}}}(16)$ = ${{(1200.7,\; - 22.929,\;450.2,\; - 7.709)}^{T}}$, доставляющий минимум вышеуказанному терминальному функционалу $\Phi $, т.е. искомое оптимальное значение этого функционала ${{\Phi }^{{(e)}}} = \Phi ({{x}^{{(e)}}}(16)) = {\text{30}}{\text{.899}}$. Каждое найденное управление ${{u}^{{(e,j)}}}(\, \cdot \,) \in {{U}^{{(e)}}}(\, \cdot \,)$, $j \in \overline {1,k} $, далее подставляется в исходную нелинейную модель объекта (1.1), (1.2) и сравнивается с управлением $u{\text{*}}(\, \cdot \,) = {{\{ u{\text{*}}(t)\} }_{{t \in \overline {0,15} }}}$, полученным с помощью терминального регулятора с замороженными коэффициентами [3, 4]. В табл. 2 сведены значения терминального функционала, которые он принимает в линеаризованной системе и исходной нелинейной системе при использовании трех различных оптимальных управлений ${{u}^{{(e,j)}}}$, $j \in \overline {1,3} $, т.е. при $k = 3$, и одного “неоптимального” $u{\text{*}}(t)$, а также значение функционала $\Phi (x(16))$ на опорной траектории. Проекции фазовых траекторий линейной и нелинейной системы при действии всех указанных управлений изображены на рис. 2–4.
Таблица 2.
Результаты решения задачи оптимального программного терминального управления
| Система | Управление | x1(T), кг/c | x2(T), кг | x3(T), кг/c | x4(T), кг | Ф(x(T)) |
|---|---|---|---|---|---|---|
| Опорная траектория | $u(t) \equiv 0$ | 1200 | 0 | 450 | 0 | 0 |
| Нелинейная система | $u{\text{*}}(t)$ | 1190.4 | 101.7 | 455.12 | –72.817 | 368.45 |
| ${{u}^{{(e,1)}}}(t)$ | 1200.5 | –2.695 | 449.72 | 10.556 | 41.855 | |
| ${{u}^{{(e,2)}}}(t)$ | 1200.5 | 0.50887 | 449.72 | 17.561 | 65.874 | |
| ${{u}^{{(e,3)}}}(t)$ | 1200.5 | –6.366 | 449.72 | –1.475 | 7.922 | |
| Линейная система | ${{u}^{{(e,j)}}}(t)$, $j \in \overline {1,3} $ | 1200.7 | – 22.929 | 450.2 | – 7.709 | 30.899 |
Рис. 2.
Проекции фазовых траекторий в линейной и нелинейной системах (${{u}^{{(e,1)}}}(\, \cdot \,)$):  проекции прямых областей достижимости;
проекции прямых областей достижимости;  проекция траектории линейной системы (оптимальное управление);
проекция траектории линейной системы (оптимальное управление);  проекция траектории нелинейной системы (оптимальное управление);
проекция траектории нелинейной системы (оптимальное управление);  проекция траектории нелинейной системы (неоптимальное управление);
проекция траектории нелинейной системы (неоптимальное управление);  проекция опорной траектории
проекция опорной траектории
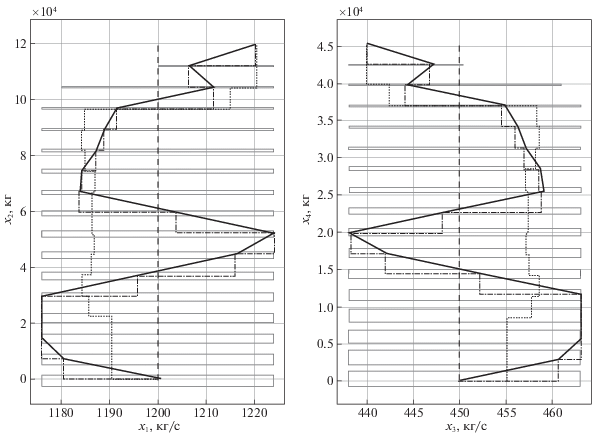
Рис. 3.
Проекции фазовых траекторий в линейной и нелинейной системах (${{u}^{{(e,2)}}}(\, \cdot \,)$): проекции прямых областей достижимости;
проекции прямых областей достижимости;  проекция траектории линейной системы (оптимальное управление);
проекция траектории линейной системы (оптимальное управление);  проекция траектории нелинейной системы (оптимальное управление);
проекция траектории нелинейной системы (оптимальное управление);  проекция траектории нелинейной системы (неоптимальное управление);
проекция траектории нелинейной системы (неоптимальное управление);  проекция опорной траектории
проекция опорной траектории
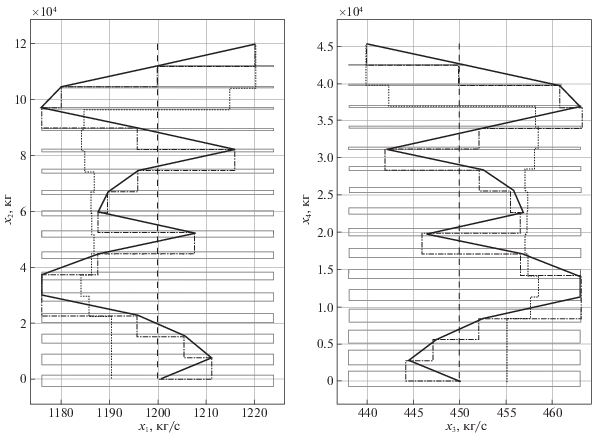
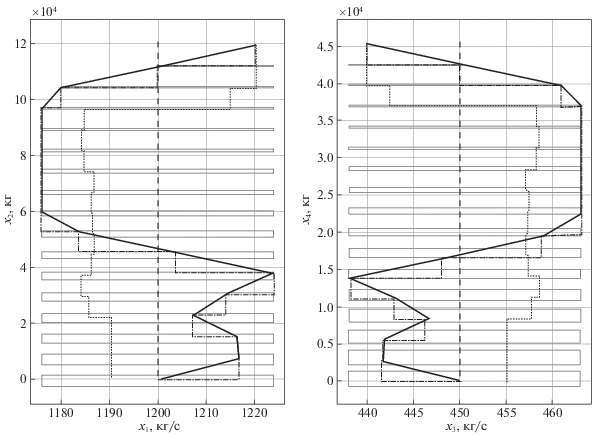
Рис. 4.
Проекции фазовых траекторий в линейной и нелинейной системах (${{u}^{{(e,3)}}}(\, \cdot \,)$): проекции прямых областей достижимости;
проекции прямых областей достижимости;  проекция траектории линейной системы (оптимальное управление);
проекция траектории линейной системы (оптимальное управление);  проекция траектории нелинейной системы (оптимальное управление);
проекция траектории нелинейной системы (оптимальное управление);  проекция траектории нелинейной системы (неоптимальное управление);
проекция траектории нелинейной системы (неоптимальное управление);  проекция опорной траектории
проекция опорной траектории
Численное моделирование проводилось в программной среде MATLAB R2014a на персональном компьютере с процессором Intel© Core™ i7-3770 CPU @ 3.4 GHz, оперативной памятью 8 Gb и с видеокартой NVIDIA GeForce GT 730. Визуализация построения областей достижимости осуществлена с использованием библиотеки инструментов MPT Toolbox для MATLAB [24]. Время решения задачи составило 0.4 с. Построенное множество оптимальных программных управлений ${{{\mathbf{U}}}^{{(e)}}}(\, \cdot \,)$ формирует множество оптимальных фазовых траекторий, проходящих через все вершины пересечений прямых и обратных областей достижимости. Всевозможные линейные комбинации таких движений также будут являться оптимальными в смысле функционала $\Phi $.
Из результатов моделирования можно заключить, что множество оптимальных программных управлений ${{{\mathbf{U}}}^{{(e)}}}(\, \cdot \,)$, сформированное для линеаризованной дискретной системы с помощью общего рекуррентного алгебраического метода [5, 8], при подстановке его в уравнения динамики исходной нелинейной системы дает достаточно близкие к опорной (желаемой) траектории характеристики в финальный момент времени. Также результаты моделирования подтверждают хорошее качество аппроксимации исходной нелинейной системы с помощью линейной дискретной системы.
Заключение. Приведено описание нелинейной динамической системы, отражающей динамику расхода топлива первых ступеней жидкостных РН. Задача терминального управления расходом топлива сформулирована как задача оптимального программного терминального управления линейной дискретной динамической системой. В работе подробно описан предлагаемый алгоритм решения задачи оптимизации программного терминального управления расходом топлива РН. Многошаговая оптимизационная задача решается путем решения конечной последовательности только одношаговых задач линейного и выпуклого математического программирования. На основе описанного метода решения задачи оптимального программного терминального управления была разработана программная система моделирования ее решения, в которой были получены результаты численных расчетов для модельного примера терминального управления расходом топлива первой ступени РН.
Результаты моделирования показали применимость общего рекуррентного алгебраического метода [5, 8] для решения задачи оптимального программного терминального управления расходом топлива первых ступеней жидкостных РН.
Предложенный алгоритм может быть применен для решения задачи оптимизации программного терминального управления расходом топлива ДУ РН, осуществляемой, например, непосредственно перед реализацией полетного задания. Использование данного алгоритма для оптимизации управления по принципу обратной связи в полете (в реальном времени) на борту РН является теоретически и практически возможным, что составит предмет дальнейших исследований авторов.
Список литературы
Аппазов Р.Ф., Сытин О.Г. Методы проектирования траекторий носителей и спутников Земли. М.: Наука, 1987. 440 с.
Лазарев Ю.Н. Управление траекториями аэрокосмических аппаратов. Самара: Самар. науч. центр РАН, 2007. 274 с.
Петров Б.Н., Портнов-Соколов Ю.П., Андриенко А.Я., Иванов В.П. Бортовые терминальные системы управления (принципы построения и элементы теории). М.: Машиностроение, 1983. 200 с.
Андриенко А.Я., Иванов В.П. Вопросы теории и практики создания бортовых терминальных систем жидкостных ракет-носителей // АиТ. 2013. № 3. С. 401–412.
Тюлюкин В.А., Шориков А.Ф. Алгоритм решения задачи терминального управления для линейной дискретной системы // АиТ. 1993. № 4. С. 115–127.
Ширяев В.И., Подивилова Е.О. Об аппроксимации информационных множеств в задаче гарантированного оценивания состояния линейных динамических систем // Сб. тр. XII Всероссийск. совещ. по проблемам управления ВСПУ-2014. М., 2014. С. 2132–2140.
Шориков А.Ф., Калёв В.И. Формирование линейной дискретной динамической модели для решения задачи оптимального терминального управления расходом топлива ракеты-носителя // Тр. 5-й Междунар. науч. конф. Информационные технологии и системы. Челябинск, 2016. С. 61–66.
Шориков А.Ф. Минимаксное оценивание и управление в дискретных динамических системах. Екатеринбург: Изд-во Урал. ун-та, 1997. 242 с.
Брайсон А., Хо Ю-Ши. Прикладная теория оптимального управления. М.: Мир, 1972. 544 с.
Красовский Н.Н. Теория управления движением. М.: Наука, 1968. 476 с.
Красовский Н.Н., Субботин А.И. Позиционные дифференциальные игры. М.: Наука, 1974. 456 с.
Моцкин Т.С., Райфа Х., Томпсон Д.Л., Тролл Р.М. Метод двойного описания // Матричные игры. М.: Физматгиз, 1961. 280 с.
Alam A., Gattami A., Johansson K.H., Tomlin C.J. Guaranteeing Safety for Heavy Duty Vehicle Platooning: Safe Set Computations and Experimental Evaluations // Control Engineering Practice. 2014. V. 24. P. 33–41.
Kostousova E.K. Control Synthesis via Parallelotopes: Optimization and Parallel Computations // Optimization Methods and Software. 2001. V. 14. P. 267–310.
Kurzhanski A.B. Valyi I. Ellipsoidal Calculus for Estimation and Control. Boston: Birkhäuser, 1997. 320 p.
Kurzhanski A.B., Varaiya P. On Ellipsoidal Techniques for Reachability Analysis // Optimization Methods and Software. 2002. V. 17. P. 177–207.
Kurzhanskiy A.A., Varaiya P. Reach Set Computation and Control Synthesis for Discrete-time Dynamical Systems with Disturbances // Automatica. 2011. № 47. P. 1414–1426.
Бастраков С.И., Золотых Н.Ю. Использование идей алгоритма Quickhull в методе двойного описания // Вычислительные методы и программирование. 2011. Т. 12. С. 232–237.
Циглер Г. Теория многогранников. М.: МЦНМО, 2014. 586 с.
Fukuda K., Prodon A. Double Description Method Revisited // Lecture Notes in Computer Science. 1996. V. 1120. P. 91–111.
Булаев В.В., Шориков А.Ф. Модификация общего рекуррентного алгебраического метода построения областей достижимости линейных дискретных управляемых систем // Тр. 6-й Междунар. науч. конф. Информационные технологии и системы. Челябинск, 2017. С. 47–52.
Зойтендейк Г. Методы возможных направлений. М.: Изд-во иностр. лит., 1963. 176 с.
Калёв В.И., Шориков А.Ф. Моделирование задачи терминального управления расходом топлива жидкостных ракет // Изв. вузов. Физика. 2016. Т. 59. № 8 (2). С. 45–48.
Kvasnica M., Grieder P., Baotic M., Morari M. Multi-Parametric Toolbox (MPT), http://control.ee.ethz.ch/~mpt/.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления



