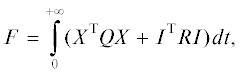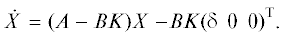Известия РАН. Теория и системы управления, 2019, № 2, стр. 145-153

СИНТЕЗ НАБЛЮДАТЕЛЯ В ЗАДАЧЕ СТАБИЛИЗАЦИИ ОБРАТНОГО МАЯТНИКА С УЧЕТОМ ОШИБКИ В ДАТЧИКАХ ПОЛОЖЕНИЯ

С. В. Арановский^1, 2, А. Э. Бирюк³, Е. В. Никульчев^4, *, И. В. Рядчиков³, Д. В. Соколов⁵

¹ CentraleSupelec-IETR
Cesson-Sévigné, France

² Университет ИТМО
Санкт-Петербург, Россия

³ Кубанский государственный ун-т
Краснодар, Россия

⁴ МИРЭА – Российский технологический ун-т
Москва, Россия

⁵ Université de Lorraine
Nancy, France

^* E-mail: nikulchev@mail.ru

Поступила в редакцию 28.10.2018
После доработки 09.11.2018
Принята к публикации 26.11.2018

DOI: 10.1134/S0002338819020021

Полный текст (PDF)

Аннотация

Задача стабилизации обратного маятника является модельным приближением перемещения центра масс при ходьбе двуногих шагающих роботов. Статья посвящена синтезу линейного наблюдателя в задаче стабилизации обратного маятника с помощью маховика, закрепленного на его конце в условиях систематической ошибки показаний датчиков положения. Маховик представляет собой инерционный диск, на который воздействует управляющий момент двигателя. Рассматривается постановка задачи стабилизации в условиях, когда датчики положения имеют некоторое постоянное, но неизвестное смещение. Важность рассматриваемой постановки определяется практической значимостью синтеза управления, обеспечивающего компенсацию ошибок и независимость реализации от калибровки датчика положения. Приведены теоретические и экспериментальные результаты разработки линейного регулятора для стабилизации конструкции в вертикальном положении и линейный наблюдатель для оценки неизвестного смещения в датчике положения.

Введение. Шагающие робототехнические системы широко применяются для перемещения по труднопроходимым поверхностям, такие, как преодоления препятствий, большие углы разворота, преодоление пересеченной местности или неизвестных ландшафтов [1]. Перемещение шагающих роботов характеризуется периодическим отрывом ног от ее поверхности [2], которое происходит, вне зависимости от количества ног и типа ходьбы, перемещением центра масс объекта с изменением количества точек опоры. Одним из подходов к моделированию и стабилизации шагающих роботов выступает модель обратного маятника [3, 4]. Центр масс обратного маятника расположен выше точки опоры, что является модельным приближением механической конфигурации двуногих шагающих роботов в задаче динамической компенсации отклонения корпуса робота от положения равновесия, возникающего при ходьбе устройства.

Исследование математических моделей стабилизации обратного маятника и синтез регуляторов осуществляются вычислительными [5, 6] и имитационными методами [7, 8] на основе анализа дифференциальных уравнений движения. К достоинствам методов, использующих адекватные модели в форме дифференциальных уравнений, можно отнести высокую точность и вычислительную надежность получающихся решений [9], возможность исследовать поведение характеристик системы при варьировании ее параметров. Найденные аналитические выражения решения могут применяться в дальнейшем для параметрической идентификации системы.

В настоящее время конструкции управляющих устройств позволяют реализовать нечеткие алгоритмы, методы искусственного интеллекта, что определило исследования в области решения задачи стабилизации перевернутого маятника с использованием искусственных нейронных сетей [10], систем нечеткого и нейронечеткого управления [11], на основе эволюционных вычислений [12] и других эвристических методов. Особенностями этих решений являются зависимость от объема и качества эмпирических выборок обучающих данных, а также невозможность оперативного пересчета управляющих воздействий при значительном изменении условий функционирования, приводящего к невязкам модели с реальными данными.

Статья посвящена решению задачи стабилизации одномерного обратного маятника с маховиком, имеющего систематическую ошибку в показаниях датчика положения. Стабилизация осуществляется за счет синтеза LQR-регулятора на основе анализа уравнений движения. Для коррекции систематической ошибки датчика положения предложено использовать линейный наблюдатель. К достоинствам данного наблюдателя относится то, что он работает при достаточно произвольных траекториях движения обратного маятника в отличие от решений, работающих только в стационарной точке [13].

Проведенные на опытном образце эксперименты показывают эффективность выбранного наблюдателя.

1. Экспериментальная установка и постановка задачи. На рис. 1 приведено изображение экспериментальной установки, на которой проведено тестирование регулятора и разработанного наблюдателя. Маховик приводится в движение бесколлекторным двигателем постоянного тока мощностью 70 Вт (Maxon EC 45), который управляется с помощью контроллера (Maxon EPOS2 50/5) в режиме крутящего момента. Контроллер двигателя измеряет ток, а также угол поворота ротора. В качестве основного вычислительного устройства использован микроконтроллер STM32F407, который взаимодействует с контроллером двигателя по протоколу CANopen. Угол маятника измеряется оптическим инкрементным датчиком разрешением 2500 отсчетов на оборот.

Рис. 1.

Экспериментальная установка (обратный маятник)

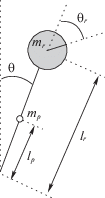
На рис. 2 представлена схема экспериментальной установки. При выводе уравнений движения используются следующие физические параметры установки: m_p – масса маятника; m_r – масса ротора; l_p – расстояние от шарнира до центра масс маятника; l_r – расстояние от шарнира до центра масс ротора; I_p – момент инерции маятника при вращении вокруг центра масс; J_r – момент инерции ротора; θ – угол маятника относительно вертикали; θ_r – угол ротора относительно маятника; τ – момент, прикладываемый к ротору.

Рис. 2.

Схема обратного маятника

Конкретные значения параметров установки следующие: m_p = 0.58 кг, l_p = 0.10 м, J_p = 3.8 × × 10^–3 кг · м², m_r = 0.35 кг, l_r = 0.22 м, J_r = 12.48 × 10^–4 кг · м². Трение в шарнире маятника и в роторе достаточно мало, поэтому им пренебрегаем.

Для того чтобы найти лагранжиан системы, запишем выражения для кинетической и потенциальной энергии системы.

По теореме Кенига, кинетическая энергия стержня маятника (без маховика) представляется как

${{T}_{p}} = \frac{1}{2}({{m}_{p}}l_{p}^{2} + {{J}_{p}})\quad{{\dot {\theta }}^{2}}.$

Аналогично кинетическая энергия маховика имеет следующее выражение:

${{T}_{r}} = \frac{1}{2}{{m}_{r}}l_{r}^{2}{{\dot {\theta }}^{2}} + \frac{1}{2}{{J}_{r}}{{({{\dot {\theta }}_{r}} + \dot {\theta })}^{2}}.$

Потенциальную энергию запишем следующим образом:

$P = ({{m}_{p}}{{l}_{p}} + {{m}_{r}}{{l}_{r}})g\cos \theta .$

Лагранжиан имеет вид

$\mathcal{L} = {{T}_{p}} + {{T}_{r}} - P.$

Для упрощения выражений введем следующие обозначения:

$J = {{J}_{p}} + {{m}_{p}}l_{p}^{2} + {{m}_{r}}l_{r}^{2},\quad m = {{m}_{p}} + {{m}_{r}},\quad l = ({{m}_{p}}{{l}_{p}} + {{m}_{r}}{{l}_{r}}){\text{/}}m.$

Тогда лагранжиан запишется как

$\mathcal{L} = \frac{1}{2}J{{\dot {\theta }}^{2}} + \frac{1}{2}{{J}_{r}}{{({{\dot {\theta }}_{r}} + \dot {\theta })}^{2}} - mlg\cos \theta .$

Для удобства выпишем все частные производные:

$\frac{{\partial{ \mathcal{L}}}}{{\partial {{{\dot {\theta }}}_{r}}}} = {{J}_{r}}({{\dot {\theta }}_{r}} + \dot {\theta }),\quad \frac{\mathcal{L}}{{\partial {{\theta }_{r}}}} = 0,$

$\frac{{\partial{ \mathcal{L}}}}{{\partial{ \dot {\theta }}}} = (J + {{J}_{r}})\dot {\theta } + {{J}_{r}}{{\dot {\theta }}_{r}},\quad \frac{{\partial{ \mathcal{L}}}}{{\partial \theta }} = mlg\sin \theta .\quad$

Напомним, что уравнения Лагранжа имеют следующий вид:

$\frac{d}{{dt}}\left( {\frac{{\partial{ \mathcal{L}}}}{{\partial {{{\dot {q}}}_{i}}}}} \right) - \frac{{\partial{ \mathcal{L}}}}{{\partial {{q}_{i}}}} = {{\tau }_{i}},$

где q_i – обобщенная координата, τ_i – соответствующая ей обобщенная сила. В нашем случае q₁ = θ_r, q₂ = θ, поэтому уравнения движения примут следующий вид:

$\left\{ \begin{gathered} {{J}_{r}}{{{\ddot {\theta }}}_{r}} + {{J}_{r}}\ddot {\theta } = \tau , \hfill \\ (J + {{J}_{r}})\ddot {\theta } + {{J}_{r}}{{{\ddot {\theta }}}_{r}} - mlg\sin \theta = 0, \hfill \\ \end{gathered} \right.$

где τ – момент двигателя.

Преобразовав уравнения к нормальному виду, т.е. разрешив уравнения относительно старших производных, получим

(1.1)

$\left\{ {\begin{array}{*{20}{l}} {{{{\ddot {\theta }}}_{r}} = \frac{{J + {{J}_{r}}}}{{J{{J}_{r}}}}\tau - \frac{{mlg}}{J}{\text{sin}}\theta ,} \\ {\ddot {\theta } = - \frac{\tau }{J} + \frac{{mlg}}{J}{\text{sin}}\theta .} \end{array}} \right.$

Задача состоит в синтезе наблюдателя, обеспечивающего стабилизацию системы (1.1) в условиях систематической ошибки показаний датчиков положения.

2. Синтез линейного регулятора. Будем считать, что усилитель и контур тока позволяют управлять моментом напрямую и компенсируют противо-ЭДС (электродвижущая сила). Тогда в модели системы (1.1) положим τ = kI, где сила тока I – сигнал управления.

Линеаризованная система с контуром тока имеет вид

(2.1)

$\dot {X} = AX + BI,$

где, пренебрегая вязким трением,

$X = \left( {\begin{array}{*{20}{c}} \theta \\ {\dot {\theta }} \\ {{{{\dot {\theta }}}_{r}}} \end{array}} \right),\quad A = \left( {\begin{array}{*{20}{c}} 0&1&0 \\ {\frac{{mlg}}{J}}&0&0 \\ { - \frac{{mlg}}{J}}&0&0 \end{array}} \right),\quad B = \quad\left( {\begin{array}{*{20}{c}} 0 \\ { - \frac{k}{J}} \\ {\frac{{(J + {{J}_{r}})k}}{{J\quad{{J}_{r}}}}} \end{array}} \right).$

Найдем линейный регулятор вида I = –KX, где K = (k₁, k₂, k₃), который будет минимизировать следующий функционал:

сделаем это, воспользовавшись LQR-алгоритмом [14]. Матрицы Q и R выберем единичными размером 3 × 3 и 1 × 1 соответственно. Для параметров рассматриваемой установки

$K{\;} = ( - 378, - 55, - 1).$

Зафиксировав найденное LQR-методом значение K, система (3.1) с регулятором I = –KX принимает вид X = (A – BK)X. Метод LQR гарантирует, что вещественные части собственных чисел матрицы A – BK отрицательны.

3. Влияние ошибки калибровки датчика положения. В случае неправильной юстировки датчика угла маятника имеет место искажение его показаний на некоторое постоянное смещение δ. Тогда вместо правильного управления система на вход будет получать сигнал I = –KX – K(δ 0 0 )^T. В этом случае система (2.1) принимает следующий вид:

Найдем стационарную точку этой системы:

$0 = (A - BK)X - BK{{(\begin{array}{*{20}{l}} \delta &0&0 \end{array})}^{{{\rm T}}}} \Rightarrow X = {{(A - BK)}^{{ - 1}}}BK{{(\begin{array}{*{20}{l}} \delta &0&0 \end{array})}^{{{\rm T}}}} = {{\left( {\begin{array}{*{20}{l}} 0&0&{ - \delta \frac{{{{k}_{1}}}}{{{{k}_{3}}}}} \end{array}} \right)}^{{{\rm T}}}}.$

Поскольку все собственные значения матрицы (A – BK) имеют отрицательную вещественную часть, то найденная стационарная точка является глобально асимптотически устойчивой. Это означает, что при плохо откалиброванном датчике система сойдется к нулевому углу маятника, но ненулевой скорости маховика, причем скорость пропорциональна ошибке калибровки.

4. Синтез наблюдателя. В рассматриваемой механической системе можно непосредственно измерять угол маятника, но в системе нет датчика угловой скорости. В то же время для синтеза управления необходимо знать угловую скорость маятника. Кроме того, качество управления зависит от точности калибровки датчиков, калибровки датчиков неидеальны, что в реальности не всегда так. Рассмотрим случай, в котором данные, получаемые с датчика положения маятника, имеют постоянное неизвестное смещение δ. Другими словами, вместо истинного значения угла θ датчик выдает значение θ + δ.

Таким образом, возникает необходимость синтезировать наблюдатель, задачей которого является определение истинного значения угла θ, угловой скорости $\dot {\theta }$ и смещения δ с точностью, достаточной для стабилизации.

Как было показано в разд. 3, величину δ можно определить в установившемся режиме. Однако в постановку задачи входит определение величины δ вдоль произвольных траекторий системы, что позволит избежать автоколебаний и может сократить время стабилизации.

Для решения поставленной задачи будем использовать тот факт, что управляющее воздействие силы тока известно за все прошедшие моменты времени. Будет построена вспомогательная система обыкновенных дифференциальных уравнений, решения которой асимптотически стремятся к решениям исходной системы. Текущее положение в фазовом пространстве вспомогательной системы и будет выходными данными наблюдателя.

Зная силу тока I как функцию времени, а следовательно, и крутящий момент двигателя τ = kI, можем проводить анализ второго уравнения системы (1.1):

(4.1)

$x\ddot {\theta } = - \frac{{kI}}{J} + \frac{{mlg}}{J}{\text{sin}}\theta $

независимо от первого с целью синтеза наблюдателя.

Обозначим текущие показания датчика угла маятника y = θ + δ (при истинном состоянии системы θ) и введем следующие обозначения:

$x = \left[ {\begin{array}{*{20}{c}} \theta \\ {\dot {\theta }} \\ \delta \end{array}} \right],\quad \hat {x} = \left[ {\begin{array}{*{20}{c}} {\hat {\theta }} \\ {\widehat {\dot {\theta }}} \\ {\hat {\delta }} \end{array}} \right],$

где x – вектор истинных состояний, а $\hat {x}$– вектор оценок (выходные данные наблюдателя). Также определим вектор ошибок оценивания $\tilde {x}$ = $\hat {x}$ – x. Добавим к уравнению (4.1) уравнение $\dot {\delta }$ = 0 и перепишем полученную систему в матричном виде, используя координаты x (x₁ = θ, x₂ = $\dot {\theta }$, x₂ = δ):

(4.2)

$\dot {x} = \quad\left[ {\begin{array}{*{20}{c}} {{{x}_{2}}} \\ {a\sin {{x}_{1}} + bI} \\ 0 \end{array}} \right]\quad,\quad y = Cx,{\;\;}$

где a = mlg/J, b = –k/J, C = [1 0 1].

В этих условиях имеют место равенства

$\theta = {{x}_{1}} = y - {{x}_{3}} = y - {{\hat {x}}_{3}} + {{\tilde {x}}_{3}}.$

Поскольку ошибка юстировки датчика достаточно мала, тогда

${\text{sin(}}{{x}_{1}}{\text{)}} = \sin (y - {{\hat {x}}_{3}} + {{\tilde {x}}_{3}}) \approx {\text{sin(}}y - {{\hat {x}}_{3}}{\text{)}} + {\text{cos(}}y - {{\hat {x}}_{3}}{\text{)}}{{\tilde {x}}_{3}}.$

Вспомогательные уравнения на вектор оценок $\hat {x}$ запишем в следующем виде:

(4.3)

$\dot {\hat {x}} = \left[ {\begin{array}{*{20}{c}} {{{{\hat {x}}}_{2}}} \\ {a\sin (y - {{{\hat {x}}}_{3}}) + bI} \\ 0 \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{{l}_{1}}} \\ {{{l}_{2}}} \\ {{{l}_{3}}} \end{array}} \right]\tilde {y},\quad \hat {y} = C\hat {x}{\;\;},$

где $\tilde {y}$ = $\hat {y}$ – y = $C\tilde {x}$, а вектор L = [l₁ l₂ l₃]^T определим позднее. Вычтя из (4.3) уравнение (4.2), получим уравнение, описывающее динамику ошибки оценивания

(4.4)

$\dot {\tilde {x}} = \dot {\hat {x}} - \dot {x} = \left[ {\begin{array}{*{20}{c}} 0&1&0 \\ 0&0&{ - a\cos (y - {{{\hat {x}}}_{3}})} \\ 0&0&0 \end{array}} \right]\tilde {x} - LC\tilde {x}.$

Получена линейная система дифференциальных уравнений относительно $\tilde {x}$ с переменными коэффициентами. В точках cos(y – ${{\hat {x}}_{3}}$) = 0 она становится ненаблюдаемой. Обозначим для краткости z = y – ${{\hat {x}}_{3}}$,

$A(z) = \left[ {\begin{array}{*{20}{c}} 0&1&0 \\ 0&0&{ - a\cos (z)} \\ 0&0&0 \end{array}} \right].$

Тогда уравнения (5.4) примут вид

$\dot {\tilde {x}} = (A(z) - LC)\tilde {x}.$

Задача сводится к исследованию устойчивости для всех z этой системы. Выписав характеристические полиномы матрицы A(z) – LC для случаев cos(y₁ – ${{\hat {x}}_{3}}$) = ±1:

${{s}^{3}} + ({{l}_{1}} + {{l}_{3}}){{s}^{2}} + {{l}_{2}}s \pm a{{l}_{3}},$

можно видеть, что не существует такого постоянного вектора L = [l₁ l₂ l₃]^T, при котором матрица A(z) – LC была бы Гурвицева, как при cos(y₁ – ${{\hat {x}}_{3}}$), так и при cos(y₁ – ${{\hat {x}}_{3}}$) = –1. Другими словами, наблюдатель с постоянными коэффициентами не будет работать вдоль траекторий, где маятник пересекает горизонтальное положение.

Для построения наблюдателя введем следующее допущение: пусть начальное положение маятника и траектория движения таковы, что сам маятник остается в верхнем полукруге, т.е. выполняется |z| ≤ σ₀, где π/2 > σ₀ > 0. Это допущение не является ограничивающим для рассматриваемой задачи управления, так как в случае решения задачи стабилизации маятник находится вблизи вертикального положения, а при отклонении от него на угол, превышающий π/2, маятник окажется в зоне, где линеаризованная модель оказывается недостоверной и стабилизация маятника становится невозможной.

Таким образом, можем предполагать, что сигнал y удовлетворяет требуемым допущениям. Касательно сигнала ${{\hat {x}}_{3}}$ отметим, что с точки зрения технического смысла решаемой задачи систематическая ошибка датчика угла также ограничена и существенно меньше величины π/2, что и позволяет сформулировать ограничения на сигнал z.

С учетом введенного допущения задача построения наблюдателя может быть сформулирована как задача решения системы линейных матричных неравенств вида

$P = {{P}^{{\text{T}}}} > 0,$

${{(A(0) - LC)}^{{\text{T}}}}P + P(A(0) - LC) < 0,$

${{(A({{\sigma }_{0}}) - LC)}^{{\text{T}}}}P + P(A({{\sigma }_{0}}) - LC) < 0.$

Действительно, если возможно найти L, для которой указанная система уравнений имеет решения, то матрица P будет весовой матрицей квадратичной функции Ляпунова для ошибки оценивания. Производная по времени этой функции Ляпунова будет отрицательна для всех значений z, что следует из выполнения второго и третьего неравенств.

Решение линейной системы матричных неравенств для рассматриваемой в работе системы было получено как

$L = {{[\begin{array}{*{20}{l}} {546}&{1100}&{ - 508} \end{array}]}^{{{\rm T}}}},$

обеспечивающее в системе время переходного процесса на уровне 0.5 с.

5. Экспериментальное исследование. Приведем результаты двух экспериментов с установкой, изображенной на рис. 1. В обоих экспериментах предустановили заранее известное смещение δ = 0.1 рад. Первый эксперимент проводится без использования наблюдателя, а второй – с разработанным наблюдателем.

Результаты экспериментальных исследований приведены на рис. 3–5 .

Рис. 3.

Положение маятника в реальном эксперименте: 1 – эксперимент без оценки смещения, 2 – эксперимент с оценкой смещения

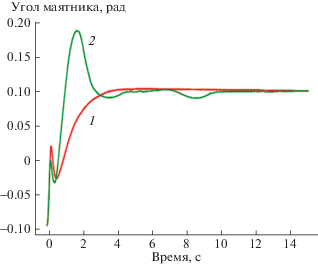
Рис. 4.

Скорость вращения маховика в реальном эксперименте: 1 – эксперимент без оценки смещения, 2 – эксперимент с оценкой смещения

Рис. 5.

Показания наблюдателя: 1 – оценка реального угла маятника, 2 – оценка ошибки юстировки

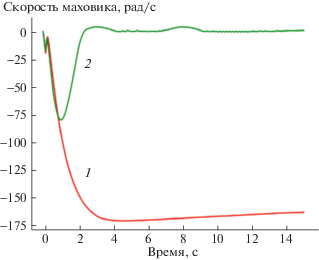
Согласно рис. 3, маятник стабилизируется в вертикальном положении в обоих экспериментах. В то же время из рис. 4 видно, что скорость вращения маховика в эксперименте с использованием наблюдателя практически равна нулю в отличие от эксперимента без оценки смещения, где скорость вращения маховика достаточно высока, порядка 170 рад/с, что согласуется с полученными теоретическими результатами. Уменьшение абсолютной угловой скорости вращения маховика, наблюдаемое в первом эксперименте после выхода в стационарное положение, объясняется влиянием противо-ЭДС. Как видно, это влияние сравнительно небольшое.

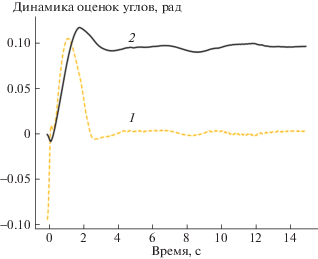
На рис. 5 показана динамика поведения наблюдателя (во втором эксперименте). Из графика видно, что оценка ошибки юстировки сходится к эталонному значению δ = 0.1, а оценка угла маятника – к нулю.

Таким образом, эксперименты, проведенные на стенде, полностью согласуются с теоретическими результатами. Разработанный регулятор с наблюдателем реализованы в конструкции шагающего робота [15].

Заключение. В статье рассматривался синтез линейного наблюдателя в задаче стабилизации обратного маятника с помощью маховика в условиях, когда датчики положения имеют некоторое постоянное, но неизвестное смещение. Важность приведенной постановки определяется практической значимостью синтеза управления, обеспечивающего компенсацию ошибок и независимость реализации от калибровки датчика положения.

Найден способ определения смещения в показаниях датчика положения маятника не только в стационарном положении, но и при движении маятника по достаточно произвольной траектории.

Предложенный способ при использовании совместно с линейным регулятором, стабилизирующим в верхней стационарной точке, не приводит к появлению автоколебаний, что подтверждается как теоретически, так и экспериментально.

Полученные результаты также могут быть применены для удешевления конструкций типа “обратного маятника” за счет отказа от датчиков угловой скорости маятника, вместо которого можно использовать соответствующий наблюдатель.

Список литературы

Брискин Е.С., Калинин Я.В., Малолетов А.В., Шурыгин В.А. Об оценке эффективности шагающих роботов на основе многокритериальной оптимизации их параметров и алгоритмов движения // Изв. РАН. ТиСУ. 2017. № 2. С. 168–176.
Савин С.И., Ворочаева Л.Ю. Методы управления движением шагающих внутритрубных роботов // Cloud of Science. 2018. Т. 5. № 1. 163–195.
Гришин А.А., Ленский А.В., Охоцимский Д.Е., Панин Д.А., Формальский А.М. О синтезе управления неустойчивым объектом. Перевернутый маятник // Изв. РАН. ТиСУ. 2002. № 5. С. 14–24.
Решмин C.А., Черноусько Ф.Л. Оптимальное по быстродействию управление перевернутым маятником в форме синтеза // Изв. РАН. ТиСУ. 2006. № 3. С. 51–62.
Franco E., Astolfi A., Baena F.R. Robust Balancing Control of Flexible Inverted-Pendulum Systems // Mechanism and Machine Theory. 2018. V. 130. P. 539–551.
Hua Y., Yang Z. Simple Rotary Inverted Pendulum and the Control Device // Applied Mechanics & Materials. 2016. V. 851. P. 445–448.
Chen X., Yu R., Huang K., Zhen S., Sun H., Shao K. Linear Motor Driven Double Inverted Pendulum: A Novel Mechanical Design as a Testbed for Control Algorithms // Simulation Modelling Practice and Theory. 2018. V. 81. P. 31–50.
Sánchez J., Dormido S., Pastor R., Morilla F. A Java/MATLAB-based Environment for Remote Control System Laboratories: Illustrated with an Inverted Pendulum // IEEE Transactions on Education. 2004. V. 47. № 3. P. 321–329.
Chatterjee S., Das S.K. An Analytical Formula for Optimal Tuning of the State Feedback Controller Gains for the Cart-Inverted Pendulum System // IFAC-PapersOnLine. 2018. V. 51. № 1. P. 668–672.
Rubio J.J. Discrete Time Control Based in Neural Networks for Pendulums // Applied Soft Computing. 2018. V. 68. P. 821–832.
Bellino A., Fasana A., Gandino E., Garibaldi L., Marchesiello S. A time-varying inertia pendulum: Analytical modelling and experimental identification // Mechanical Systems and Signal Processing. 2014. V. 47. № 1–2. P. 120–138.
Ping Z., Huang J. Approximate Output Regulation of Spherical Inverted Pendulum by Neural Network Control // Neurocomputing. 2012. V. 85. P. 38–44.
Gajamohan M., Merz M., Thommen I., D’Andrea, R. The Cubli: A Cube That Can Jump up and Balance // 2012 IEEE/RSJ Intern. Conf. on Intelligent Robots and Systems (IROS). Piscataway: IEEE Publ., 2012. P. 3722–3727.
Anderson B.D.O., Moore J.B. Optimal Control: Linear Quadratic Methods. Mineola: Dover Publ. Inc., 2007.
Ryadchikov I., Sechenev S., Nikulchev E., Drobotenko M., Svidlov A., Volkodav P., Vishnykov R. Control and Stability Evaluation of the Bipedal Walking Robot Anywalker // International Review of Automatic Control. 2018. V. 11. №. 4. P. 160–165.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал