Известия РАН. Теория и системы управления, 2019, № 2, стр. 14-29
РАЗБИЕНИЕ СИСТЕМЫ БУЛЕВЫХ ФУНКЦИЙ НА ПОДСИСТЕМЫ “СВЯЗАННЫХ” ФУНКЦИЙ
П. Н. Бибило *
Объединенный ин-т проблем информатики НАН Белоруссии
Минск, Белоруссия
* E-mail: bibilo@newman.bas-net.by
Поступила в редакцию 10.07.2018
После доработки 22.11.2018
Принята к публикации 26.11.2018
Аннотация
Предлагаются алгоритмы разбиения системы булевых функций на подсистемы связанных функций для таких форм представления функций, как таблицы истинности, системы дизъюнктивных нормальных форм, диаграммы двоичного выбора. “Связанность” функций заключается в наличии одинаковых частей в областях определения функций системы. Алгоритмы являются эвристическими и предназначены для использования в системах автоматизированного проектирования при решении задач практической размерности, когда число аргументов функций достигает нескольких десятков, а число функций системы – сотен. Проведенные эксперименты показывают эффективность применения такого разбиения при логической оптимизации системы булевых функций на основе разложения Шеннона с учетом возможности использования инверсий подфункций.
Введение. Синтез логических схем из библиотечных элементов выполняется по оптимизированным двухуровневым либо многоуровневым представлениям систем булевых функций. Двухуровневыми (И-ИЛИ) представлениями называют в литературе представления функций в виде дизъюнктивных нормальных форм (ДНФ), многоуровневыми – различные формы функциональных разложений [1–4]. Идея использовать связанность (общность) областей определений булевых функций при синтезе многовыходных комбинационных схем предложена давно [5, 6]. В [6] рассматривается связанность (там она называется “связность”) неполностью определенных булевых функций, заданных наборами значений булевых переменных. Показывается, что выделение связанных функций позволяет находить доопределения таких функций до полностью определенных, а общие части в областях определения задают подфункции в совместных дизъюнктивных и конъюнктивных разложениях.
“Хорошая” связанность функций существенно влияет на появление одинаковых структурных частей (конъюнкций, алгебраических выражений, подфункций и т.д.) в оптимизированных двухуровневых либо многоуровневых формах представления функций, по которым и строятся логические схемы в том или ином технологическом базисе. Чем более связанные функции, тем скорее можно ожидать, что в представлениях таких функций будет больше одинаковых подвыражений и синтезированные схемы будут менее сложными. По существу, выделение связанных функций является одним из приемов логической оптимизации многоуровневых представлений систем функций. Для связанных подсистем функций более эффективно решаются задачи логической оптимизации, например оптимизации в классе ДНФ [2, 3], оптимизации BDD-представлений [4, 7–9] (BDD – Binary Decision Diagram – диаграмма двоичного выбора) и декомпозиции различных видов, например при построении совместных функциональных разложений [10]. В русскоязычной литературе BDD называют также диаграммами двоичных решений, бинарными диаграммами решений, двоичными решающими диаграммами и т.д. Представления булевых функций в виде BDD соответствуют многоуровневым представлениям на базе разложения Шеннона [4].
В данной работе формулируются понятия связанности булевых функций (и связанности с точностью до инверсии) и предлагаются алгоритмы выделения связанных подсистем функций для различных форм представления систем полностью определенных функций. Алгоритмы являются эвристическими и ориентированы на большую размерность задач – десятки булевых переменных и сотни функций в системах, представления которых требуется оптимизировать. Проведенные эксперименты по выделению связанных подсистем функций показали, что данную процедуру целесообразно выполнять перед BDD-оптимизацией, являющейся в настоящее время наиболее распространенным методом логической минимизации при синтезе логических схем из библиотечных элементов. Для одних систем функций предпочтительнее совместные BDD, для других – раздельные [11]. Выделение связанных функций позволяет объединить в одну подсистему те функции, которые целесообразно минимизировать на основе совместных BDD.
1. Основные определения и формы задания систем булевых функций. Пусть задана система f(x) = $({{f}^{1}}(x), \ldots ,{{f}^{m}}(x))$ булевых функций, через x обозначен вектор $x = ({{x}_{1}},{{x}_{2}}, \ldots ,{{x}_{n}})$ аргументов ${{x}_{1}}$, ${{x}_{2}}$, …, ${{x}_{n}}$. Характеристическим множеством $M_{{{{f}^{i}}}}^{1}$ компонентной функции ${{f}^{i}}(x)$ системы $f(x)$ называется множество наборов булева пространства, на которых функция ${{f}^{i}}(x)$ принимает единичное значение. Через $M_{{{{f}^{i}}}}^{0}$ обозначим множество наборов нулевых значений функции ${{f}^{i}}(x)$.
Далее под связанностью булевых функций будет пониматься совпадение подобластей в областях определения функций. Обозначим через ${\text{|}}A{\text{|}}$ мощность множества А. Система функций $f(x)$ называется ${{S}_{p}}$-связанной, если $p_{{\max }}^{n} \geqslant p$, где
Иначе говоря, имеются p наборов n-мерного булева пространства, на которых все компонентные функции ${{f}^{i}}(x)$ системы одновременно принимают значение 1 либо 0. Очевидно, что для заданной системы булевых функций, зависящих от n переменных, параметр $p_{{\max }}^{n}$ задает максимальное значение p. Если система функций является ${{S}_{p}}$-связанной, то она будет ${{S}_{q}}$-связанной для всех q, удовлетворяющих условию 0 < q < p. Число $p_{{\max }}^{n}$ назовем весом связанности системы функций. Для одной булевой функции, зависящей от n переменных, вес связанности – это число, равное сумме мощностей множеств $M_{{{{f}^{i}}}}^{1}$, $M_{{{{f}^{i}}}}^{0}$, иначе говоря, это число ${{2}^{n}}$ элементов булева пространства, построенного над переменными булева вектора $x = ({{x}_{1}},{{x}_{2}}, \ldots ,{{x}_{n}})$. Элементами этого пространства являются n-компонентные наборы (векторы) $x{\text{*}}$ нулей и единиц.
Мерой (долей) связанности ${{\rho }^{n}}({{f}^{1}}, \ldots ,{{f}^{m}})$ системы функций $f(x)$ назовем отношение
Очевидно, что мера связанности ограничена:
Если система функций включает одну компонентную функцию ${{f}^{1}}$ (либо если все компонентные функции равны), то ${{\rho }^{n}}({{f}^{1}}) = 1$. Если же система функций состоит, например, из пары ${{f}^{1}}$, ${{\bar {f}}^{1}}$ взаимно инверсных функций, то ${{\rho }^{n}}({{f}^{1}},{{\bar {f}}^{1}}) = 0$, очевидно, что это не единственный пример системы функций с нулевой мерой связанности, такие системы будем называть также несвязанными. Примеры будут приведены позже.
Введем в рассмотрение m-компонентный булев вектор $\alpha = ({{\alpha }^{1}},{{\alpha }^{2}}, \ldots ,{{\alpha }^{m}})$, называемый далее вектором поляризации для компонентных функций ${{f}^{i}}(x)$. Обозначим ${{\alpha }^{i}} = 1$, если рассматривается функция ${{f}^{i}}$, и ${{\alpha }^{i}} = 0$, если берется инверсия ${{\bar {f}}^{i}}$ функции ${{f}^{i}}$. Система $f(x)$ функций называется $S_{p}^{\alpha }$-связанной, если найдется хотя бы один вектор $\alpha = ({{\alpha }^{1}},{{\alpha }^{2}}, \ldots ,{{\alpha }^{m}})$ поляризации, для которого соответствующая данному вектору система функций является ${{S}_{p}}$-связанной. Понятие $S_{p}^{\alpha }$-связанности соответствует связанности функций с точностью до инверсии компонентных функций системы.
Системы булевых функций могут быть заданы в различной форме. В качестве форм задания систем функций далее будут рассматриваться матричные формы – таблицы истинности (табл. 1) и системы ДНФ (табл. 2), а также представления систем функций алгебраическими формулами, задающими разложения Шеннона (BDD-представления). Для системы функций (табл. 1) мера связанности ${{\rho }^{4}}({{f}^{1}},{{f}^{2}},{{f}^{3}},{{f}^{4}}) = 0$, так как нет ни одного набора значений переменных вектора x = = $({{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}})$, на котором значения всех четырех компонентных функций одновременно равны 1 либо 0. Позже будет показано, что данная система содержит подсистемы связанных функций.
Таблица 1.
Система полностью определенных булевых функций
| ${{x}_{1}}$ ${{x}_{2}}$ ${{x}_{3}}$ ${{x}_{4}}$ | ${{f}^{1}}$ ${{f}^{2}}$ ${{f}^{3}}$ ${{f}^{4}}$ |
|---|---|
| 0 0 0 0 | 0 0 1 1 |
| 0 0 0 1 | 1 1 0 0 |
| 0 0 1 0 | 1 0 0 0 |
| 0 0 1 1 | 1 1 0 0 |
| 0 1 0 0 | 0 0 1 1 |
| 0 1 0 1 | 1 1 0 0 |
| 0 1 1 0 | 0 1 1 1 |
| 0 1 1 1 | 1 1 1 0 |
| 1 0 0 0 | 0 0 1 1 |
| 1 0 0 1 | 1 0 0 0 |
| 1 0 1 0 | 1 1 0 0 |
| 1 0 1 1 | 1 1 0 0 |
| 1 1 0 0 | 0 0 1 1 |
| 1 1 0 1 | 1 0 1 1 |
| 1 1 1 0 | 0 0 0 1 |
| 1 1 1 1 | 1 0 1 0 |
Таблица 2.
Система ДНФ булевых функций
| ${{T}^{x}}$ | ${{B}^{f}}$ |
|---|---|
| ${{x}_{1}}$ ${{x}_{2}}$ ${{x}_{3}}$ ${{x}_{4}}$ | ${{f}^{1}}$ ${{f}^{2}}$ ${{f}^{3}}$ ${{f}^{4}}$ |
| – 0 1 – | 1 0 0 0 |
| 0 1 1 – | 0 1 1 0 |
| – – – 1 | 1 0 0 0 |
| 1 0 1 – | 0 1 0 0 |
| 1 1 0 – | 0 0 1 1 |
| – 1 – 0 | 0 0 0 1 |
| – 1 1 1 | 0 0 1 0 |
| 0 – – 1 | 0 1 0 0 |
| – – 0 0 | 0 0 1 1 |
В матричной форме система ДНФ (табл. 2) задается парой матриц: строки троичной матрицы ${{T}^{x}}$ представляют элементарные конъюнкции (троичные векторы – интервалы булева пространства [3]), а единичные значения элементов в булевой матрице ${{B}^{f}}$ отмечают вхождения соответствующих конъюнкций в ДНФ функций:
Заметим, данная система ДНФ представляет ту же систему булевых функций, которая приведена в табл. 1. Если в элементарной конъюнкции отсутствуют q литералов, то в представляющем ее троичном векторе имеется q неопределенных элементов “–”. Весом троичного вектора, содержащего q неопределенных элементов, назовем число ${{2}^{q}}$. Другими словами, вес троичного вектора – это число двоичных векторов, получающихся всевозможными заменами неопределенных элементов троичного вектора на определенные элементы 0 либо 1.
Системы ДНФ обычно минимизируются [2, 3], при этом стремятся уменьшить число элементарных конъюнкций и (или) число литералов в конъюнкциях. В получаемых минимизированных системах ДНФ элементарные конъюнкции (троичные векторы) находятся в различных отношениях. Далее будет использоваться отношение ортогональности. Если все троичные векторы матрицы ${{T}^{x}}$ попарно ортогональны, то система ДНФ называется ортогонализованной [12]. Троичные векторы $a = (x_{1}^{a}, \ldots ,x_{n}^{a})$, $b = (x_{1}^{b}, \ldots ,x_{n}^{b})$ ортогональны, если найдется хотя бы одна компонента i ∈ {1, …, n}, что $x_{i}^{a}$, $x_{i}^{b}$ определены и не равны. Например, троичные векторы a = (0–10), b = (–100) ортогональны, так как для i = 3 выполняется условие ортогональности: $x_{3}^{a} = 1$, $x_{3}^{b} = 0$. Если троичные векторы ортогональны, то конъюнкция (логическое произведение) соответствующих им элементарных конъюнкций равна нулю: $a\& b = ab = {{\bar {x}}_{1}}{{x}_{3}}{{\bar {x}}_{4}}{\& }{{{\text{x}}}_{2}}{{\bar {x}}_{3}}{{\bar {x}}_{4}} = 0$.
BDD являются графовыми представлениями булевых функций. Как показано в [4], таким представлениям соответствуют задания каждой из компонентных функций ${{f}^{i}}(x)$ в виде пары ортогонализованных ДНФ. Одна из таких ДНФ задает область $M_{{{{f}^{i}}}}^{1}$ единичных значений компонентной функции, вторая ДНФ – область $M_{{{{f}^{i}}}}^{0}$ нулевых значений функции. Компактность BDD-представления системы функций в виде графа обеспечивается тем, что задание графа более компактно, чем перечисление всех путей из корневых вершин к листовым вершинам 0; 1. Для упрощения графа листовые вершины обычно дублируются. Каждому пути из корневой вершины BDD, помеченной функцией ${{f}^{i}}$, к листовой вершине 1 соответствует элементарная конъюнкция, включающая дуги-литералы ${{x}_{i}}$, ${{\bar {x}}_{i}}$ на этом пути. При этом дуге, помеченной символом 0, соответствует отрицательный литерал ${{\bar {x}}_{i}}$, дуге, помеченной символом 1, соответствует положительный литерал ${{x}_{i}}$, а всем путям между указанными вершинами соответствует дизъюнкция получаемых элементарных конъюнкций, образующая ортогонализованную ДНФ $D_{{{{f}^{i}}}}^{1}$. Пути из корневой вершины ${{f}^{i}}$ к листовой вершине 0 задают ортогонализованную ДНФ $D_{{{{f}^{i}}}}^{0}$.
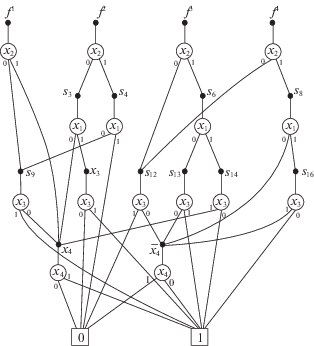
На рис. 1 показана BDD, представляющая ту же систему булевых функций, которая задана в табл. 1 и 2. В табл. 3–6 даны ортогонализованные ДНФ, полученные по графовому BDD-представлению (рис. 1). Каждой функциональной вершине BDD соответствует формула разложения Шеннона. Например, функциональной вершине ${{f}^{1}}$ соответствует формула ${{f}^{1}} = {{\bar {x}}_{2}}{{s}_{9}} \vee {{x}_{2}}{{x}_{4}}$, функциональной вершине ${{s}_{{13}}}$ – формула ${{s}_{{13}}} = {{\bar {x}}_{3}}{{\bar {x}}_{4}} \vee {{x}_{3}}$ и т.д. Поэтому часто функциональные вершины не изображаются на графе, а пометки 0, 1 на дугах заменяются различными изображениями линий, например, если дуга помечена символом 0, то соответствующая линия рисуется прерывистой [8, 9]. Всему графу BDD соответствует 13 формул (1.1)–(1.4), которые включают 29 логических операций дизъюнкции, конъюнкции:
(1.1)
${{f}^{1}} = {{\bar {x}}_{2}}{{s}_{9}} \vee {{x}_{2}}{{x}_{4}};\quad {{f}^{2}} = {{\bar {x}}_{2}}{{s}_{3}} \vee {{x}_{2}}{{s}_{4}};\quad {{f}^{3}} = {{\bar {x}}_{2}}{{s}_{{12}}} \vee {{x}_{2}}{{s}_{6}};$(1.2)
${{f}^{4}} = {{\bar {x}}_{2}}{{s}_{{12}}} \vee {{x}_{2}}{{s}_{8}};\quad {{s}_{9}} = {{\bar {x}}_{3}}{{x}_{4}} \vee {{x}_{3}};\quad {{s}_{3}} = {{\bar {x}}_{1}}{{x}_{4}} \vee {{x}_{1}}{{x}_{3}};\quad {{s}_{4}} = {{\bar {x}}_{1}}{{s}_{9}};$(1.3)
${{s}_{{12}}} = {{\bar {x}}_{3}}{{\bar {x}}_{4}};\quad {{s}_{6}} = {{\bar {x}}_{1}}{{s}_{{13}}} \vee {{x}_{1}}{{s}_{{14}}};\quad {{s}_{8}} = {{\bar {x}}_{1}}{{\bar {x}}_{4}} \vee {{x}_{1}}{{s}_{{16}}};\quad {{s}_{{13}}} = {{\bar {x}}_{3}}{{\bar {x}}_{4}} \vee {{x}_{3}};$(1.4)
${{s}_{{14}}} = {{\bar {x}}_{3}} \vee {{x}_{3}}{{x}_{4}};\quad {{s}_{{14}}} = {{\bar {x}}_{3}} \vee {{x}_{3}}{{x}_{4}};\quad {{s}_{{16}}} = {{\bar {x}}_{3}} \vee {{x}_{3}}{{\overline x }_{4}}.$Таблица 3.
Задание функции ${{f}^{1}}$ ортогонализованными ДНФ
| ДНФ | ${{x}_{1}}$ ${{x}_{2}}$ ${{x}_{3}}$ ${{x}_{4}}$ | ${{f}^{1}}$ |
|---|---|---|
| $D_{{{{f}^{1}}}}^{0}$ | – 0 0 0 | 0 |
| – 1 – 0 | 0 | |
| $D_{{{{f}^{1}}}}^{1}$ | – 1 – 1 | 1 |
| – 0 1 – | 1 | |
| – 0 0 1 | 1 |
Таблица 4.
Задание функции ${{f}^{2}}$ ортогонализованными ДНФ
| ДНФ | ${{x}_{1}}$${{x}_{2}}$${{x}_{3}}$${{x}_{4}}$ | ${{f}^{2}}$ |
|---|---|---|
| $D_{{{{f}^{2}}}}^{0}$ | 1 0 0 – | 0 |
| 0 0 – 0 | 0 | |
| 0 1 0 0 | 0 | |
| 1 1 – – | 0 | |
| $D_{{{{f}^{2}}}}^{1}$ | 1 0 1 – | 1 |
| 0 1 1 – | 1 | |
| 0 0 – 1 | 1 | |
| 0 1 0 1 | 1 |
Таблица 5.
Задание функции ${{f}^{3}}$ ортогонализованными ДНФ
| ДНФ | ${{x}_{1}}$${{x}_{2}}$${{x}_{3}}$${{x}_{4}}$ | ${{f}^{3}}$ |
|---|---|---|
| $D_{{{{f}^{3}}}}^{0}$ | – 0 1 – | 0 |
| – 0 0 1 | 0 | |
| 0 1 0 1 | 0 | |
| 1 1 1 0 | 0 | |
| $D_{{{{f}^{3}}}}^{1}$ | 0 1 1 – | 1 |
| – 0 0 0 | 1 | |
| 1 1 0 – | 1 | |
| 0 1 0 0 | 1 | |
| 1 1 1 1 | 1 |
Таблица 6.
Задание функции ${{f}^{4}}$ ортогонализованными ДНФ
| ДНФ | ${{x}_{1}}$${{x}_{2}}$${{x}_{3}}$${{x}_{4}}$ | ${{f}^{4}}$ |
|---|---|---|
| $D_{{{{f}^{4}}}}^{0}$ | – 0 1 – | 0 |
| 0 1 – 1 | 0 | |
| 1 1 1 1 | 0 | |
| – 0 0 1 | 0 | |
| $D_{{{{f}^{4}}}}^{1}$ | 1 1 0 – | 1 |
| 0 1 – 0 | 1 | |
| 1 1 1 0 | 1 | |
| – 0 0 0 | 1 |
2. Проверка связанности системы булевых функций.
Задача 1. Задана система $f(x) = ({{f}^{1}}{\text{(}}x{\text{)}}, \ldots ,{{f}^{m}}(x))$ булевых функций и параметр p, где 0 < p < ${{2}^{n}}$. Требуется проверить, является ли она ${{S}_{p}}$-связанной.
Задача 2. Задана система $f(x) = ({{f}^{1}}{\text{(}}x{\text{)}}, \ldots ,{{f}^{m}}(x))$ булевых функций, вектор поляризации α = $({{\alpha }^{1}},{{\alpha }^{2}}, \ldots ,{{\alpha }^{m}})$ и параметр p, где $0 < p < {{2}^{n}}$. Требуется проверить, является ли она $S_{p}^{\alpha }$-связанной.
В случае задания функций системы ${{2}^{n}}$-разрядными булевыми векторами значений функций на всех наборах булева пространства (вектор-столбцами значений функций в таблицах истинности) может быть успешно применена для проверки связанности систем функций техника булевых вычислений, предложенная в работе [13]. Проверка ${{S}_{p}}$-связанности заданной подсистемы функций (табл. 7) сводится к следующим операциям: операции “сложение по модулю 2” вектор-столбцов значений функций, входящих в подсистему, и подсчету числа единичных значений в результирующем векторе. Проверка $S_{p}^{\alpha }$-связанности требует предварительного инверсирования тех вектор-столбцов функций, которым соответствуют нулевые значения компонент в векторе поляризации.
Таблица 7.
Подсистемы булевых функций
| ${{x}_{1}}$${{x}_{2}}$${{x}_{3}}$${{x}_{4}}$ | ${{f}^{1}}$${{f}^{2}}$ | ${{f}^{1}}$${{\overline f }^{2}}$ |
|---|---|---|
| 0 0 0 0 | 0 0 | 0 1 |
| 0 0 0 1 | 1 1 | 1 0 |
| 0 0 1 0 | 1 0 | 1 1 |
| 0 0 1 1 | 1 1 | 1 0 |
| 0 1 0 0 | 0 0 | 0 1 |
| 0 1 0 1 | 1 1 | 1 0 |
| 0 1 1 0 | 0 1 | 0 0 |
| 0 1 1 1 | 1 1 | 1 0 |
| 1 0 0 0 | 0 0 | 0 1 |
| 1 0 0 1 | 1 0 | 1 1 |
| 1 0 1 0 | 1 1 | 1 0 |
| 1 0 1 1 | 1 1 | 1 0 |
| 1 1 0 0 | 0 0 | 0 1 |
| 1 1 0 1 | 1 0 | 1 1 |
| 1 1 1 0 | 0 0 | 0 1 |
| 1 1 1 1 | 1 0 | 1 1 |
| Вес связанности | 11 | 5 |
| Мера связанности | 11/16 | 5/16 |
Заметим, что таблице истинности булевой функции соответствует совершенная ДНФ (СДНФ), в которую входят полные элементарные конъюнкции, являющиеся взаимно ортогональными.
Проиллюстрируем решение задач 1, 2 на примере некоторых подсистем системы функций, заданных таблицей истинности (табл. 1), в виде ДНФ (табл. 2) и BDD-представления (рис. 1), которому соответствуют формулы (1.1)–(1.4).
2.1. Проверка связанности систем ДНФ функций. В случае задания функций в виде системы ДНФ задача 1 переформулируется в виде задачи 1а.
Задача 1а. Задана система ДНФ $D(x) = ({{D}^{1}}(x), \ldots ,{{D}^{m}}(x))$, представляющая систему булевых функций $f(x) = ({{f}^{1}}{\text{(}}x{\text{)}}, \ldots ,{{f}^{m}}(x))$, зависящих от n переменных. Требуется определить, задает ли $D(x)$ ${{S}_{p}}$-связанную систему булевых функций.
Если система функций дана в виде ДНФ на общем множестве элементарных конъюнкций, то для проверки ${{S}_{p}}$-связанности данной системы целесообразно сначала провести ортогонализацию данной системы либо обобщенную ортогонализацию. Алгоритмы ортогонализации описаны в [12] и обобщенной ортогонализации – в [14].
Проведем ортогонализацию системы ДНФ (табл. 2) и получим ее ортогонализованную форму (табл. 8), т.е. такую, в которой все пары троичных векторов ортогональны. Ортогонализованные ДНФ являются более компактными по сравнению с таблицами истинности, в рассматриваемом примере табл. 8 содержит 12 строк, а табл. 1–16 строк, однако минимизированные ДНФ (табл. 2) являются более компактными по сравнению с ортогонализованными системами ДНФ – табл. 2 содержит девять строк. По табл. 8 легко определить, что для каждого троичного вектора (элементарной конъюнкции) в правой части таблицы, т.е. в векторе вхождений конъюнкций в ДНФ, имеется нуль. Следовательно, $p_{{{\text{max}}}}^{n} = 0$ и система функций является несвязанной. Для ортогонализованной формы (как и для таблиц истинности либо систем СДНФ) легко найти вес $p_{{{\text{max}}}}^{n}$-cвязанности для подсистем функций в прямой форме (табл. 9). В данном примере нет наборов из области определения функций, на которых все функции равны 0, однако проверка и вычисление такой области является важным при проверке $S_{p}^{\alpha }$-связанности. Нахождение $S_{p}^{\alpha }$-связанных подсистем требует нахождения областей, на которых все компонентные функции равны 0. Эта область может быть “большой” и представление ее в явной форме (в виде ДНФ) может быть затруднено в силу большой сложности соответствующей ДНФ. Ортогонализованные формы также могут быть громоздкими – содержать много элементарных конъюнкций. Чтобы сократить число элементарных конъюнкций, целесообразно задать систему функций на множестве попарно ортогональных ДНФ ${{П }^{i}}$ (дизъюнктивном базисе). Такое представление в [14] называется обобщенно-ортогонализованной формой, там же представлено решение задачи нахождения обобщенно-ортогонализованной формы для системы ДНФ, которое сводится к операциям перемножения и инверсирования ДНФ, представляющих области единичных и нулевых значений компонентных функций системы.
Таблица 8.
Ортогонализованная система ДНФ
| Вес троичного вектора | ${{x}_{1}}$ ${{x}_{2}}$ ${{x}_{3}}$ ${{x}_{4}}$ | ${{f}^{1}}$ | ${{f}^{2}}$ | ${{f}^{3}}$ | ${{f}^{4}}$ |
|---|---|---|---|---|---|
| 2 | 0 – 0 0 | 0 | 0 | 1 | 1 |
| 2 | 1 – 0 0 | 0 | 0 | 1 | 1 |
| 2 | 0 0 - 1 | 1 | 1 | 0 | 0 |
| 1 | 0 1 0 1 | 1 | 1 | 0 | 0 |
| 2 | 1 0 1 – | 1 | 1 | 0 | 0 |
| 1 | 0 0 1 0 | 1 | 0 | 0 | 0 |
| 1 | 1 0 0 1 | 1 | 0 | 0 | 0 |
| 1 | 0 1 1 0 | 0 | 1 | 1 | 1 |
| 1 | 0 1 1 1 | 1 | 1 | 1 | 0 |
| 1 | 1 1 0 1 | 1 | 0 | 1 | 1 |
| 1 | 1 1 1 0 | 0 | 0 | 0 | 1 |
| 1 | 1 1 1 1 | 1 | 0 | 1 | 0 |
Таблица 9.
Подсистемы ортогонализованной системы ДНФ
| Вес троичного вектора | ${{x}_{1}}$${{x}_{2}}$${{x}_{3}}$${{x}_{4}}$ | ${{f}^{1}}$${{f}^{2}}$ | ${{f}^{1}}$${{\overline f }^{2}}$ |
|---|---|---|---|
| 2 | 0 – 0 0 | 0 0 | 0 1 |
| 2 | 1 – 0 0 | 0 0 | 0 1 |
| 2 | 0 0 – 1 | 1 1 | 1 0 |
| 1 | 0 1 0 1 | 1 1 | 1 0 |
| 2 | 1 0 1 – | 1 1 | 1 0 |
| 1 | 0 0 1 0 | 1 0 | 1 1 |
| 1 | 1 0 0 1 | 1 0 | 1 1 |
| 1 | 0 1 1 0 | 0 1 | 0 0 |
| 1 | 0 1 1 1 | 1 1 | 1 0 |
| 1 | 1 1 0 1 | 1 0 | 1 1 |
| 1 | 1 1 1 0 | 0 0 | 0 1 |
| 1 | 1 1 1 1 | 1 0 | 1 1 |
| Вес связанности | 11 | 5 | |
| Мера связанности | 11/16 | 5/16 | |
Таблица 10.
Минимальный дизъюнктивный базис для системы ДНФ
| $S({{П }^{i}})$ | ${{П }^{i}}$ | ${{x}_{1}}$${{x}_{2}}$${{x}_{3}}$${{x}_{4}}$ |
|---|---|---|
| 4 | ${{П }^{1}}$ | – – 00 |
| 5 | ${{П }^{2}}$ | 0 0 – 1 |
| 0 1 0 1 | ||
| 1 0 1 – | ||
| 2 | ${{П }^{3}}$ | 0 0 1 0 |
| 1 0 0 1 | ||
| 1 | ${{П }^{4}}$ | 0 1 1 0 |
| 1 | ${{П }^{5}}$ | 0 1 1 1 |
| 1 | ${{П }^{6}}$ | 1 1 0 1 |
| 1 | ${{П }^{7}}$ | 1 1 1 0 |
| 1 | ${{П }^{8}}$ | 1 1 1 1 |
Таблица 11.
Обобщенно-ортогонализованная форма системы ДНФ
| $S({{П }^{i}})$ | ${{П }^{i}}$ | ${{f}^{1}}$${{f}^{2}}$${{f}^{3}}$${{f}^{4}}$ |
|---|---|---|
| 4 | ${{П }^{1}}$ | 0 0 1 1 |
| 5 | ${{П }^{2}}$ | 1 1 0 0 |
| 2 | ${{П }^{3}}$ | 1 0 0 0 |
| 1 | ${{П }^{4}}$ | 0 1 1 1 |
| 1 | ${{П }^{5}}$ | 1 1 1 0 |
| 1 | ${{П }^{6}}$ | 1 0 1 1 |
| 1 | ${{П }^{7}}$ | 0 0 0 1 |
| 1 | ${{П }^{8}}$ | 1 0 1 0 |
Таблица 12.
Связанность подсистем при задании системы ДНФ обобщенно-ортогонализованной формой
| $S({{П }^{i}})$ | ${{П }^{i}}$ | ${{f}^{1}}$${{f}^{2}}$ | ${{f}^{1}}$${{\overline f }^{2}}$ |
|---|---|---|---|
| 4 | ${{П }^{1}}$ | 0 0 | 0 1 |
| 5 | ${{П }^{2}}$ | 1 1 | 1 0 |
| 2 | ${{П }^{3}}$ | 1 0 | 1 1 |
| 1 | ${{П }^{4}}$ | 0 1 | 0 0 |
| 1 | ${{П }^{5}}$ | 1 1 | 1 0 |
| 1 | ${{П }^{6}}$ | 1 0 | 1 1 |
| 1 | ${{П }^{7}}$ | 0 0 | 0 1 |
| 1 | ${{П }^{8}}$ | 1 0 | 1 1 |
| Вес связанности | 11 | 5 | |
| Мера связанности | 11/16 | 5/16 | |
Таблица 13.
Связанность подсистемы {${{f}^{1}}$, ${{f}^{2}}$}, полученной по BDD-представлению функций ${{f}^{1}}$, ${{f}^{2}}$ (рис. 1)
| ДНФ | ${{x}_{1}}$${{x}_{2}}$${{x}_{3}}$${{x}_{4}}$ | ${{f}^{1}}$${{f}^{2}}$ |
|---|---|---|
| $D_{{{{f}^{1}}}}^{0}$$D_{{{{f}^{2}}}}^{0}$ | 1 0 0 0 | 0 0 |
| 0 0 0 0 | 0 0 | |
| 0 1 0 0 | 0 0 | |
| 1 1 – 0 | 0 0 | |
| $D_{{{{f}^{1}}}}^{0}$$D_{{{{f}^{2}}}}^{1}$ | 0 1 1 0 | 0 1 |
| $D_{{{{f}^{1}}}}^{1}$$D_{{{{f}^{2}}}}^{0}$ | 1 1 – 1 | 1 0 |
| 0 0 1 0 | 1 0 | |
| 1 0 0 1 | 1 0 | |
| $D_{{{{f}^{1}}}}^{1}$$D_{{{{f}^{2}}}}^{1}$ | 0 1 – 1 | 1 1 |
| 1 0 1 – | 1 1 | |
| 0 0 1 1 | 1 1 | |
| 0 0 0 1 | 1 1 | |
| Вес связанности | 11 | |
| Мера связанности | 11/16 | |
Таблица 14.
Связанность подсистемы {${{f}^{1}}$, ${{\overline f }^{2}}$}, полученной по BDD-представлению функций ${{f}^{1}}$, ${{\overline f }^{2}}$ (рис. 1)
| ДНФ | ${{x}_{1}}$ ${{x}_{2}}$ ${{x}_{3}}$ ${{x}_{4}}$ | ${{f}^{1}}$ ${{\overline f }^{2}}$ |
|---|---|---|
| $D_{{{{f}^{1}}}}^{0}$ $D_{{{{{\overline f }}^{2}}}}^{1}$ | 1 0 0 0 | 0 1 |
| 0 0 0 0 | 0 1 | |
| 0 1 0 0 | 0 1 | |
| 1 1 – 0 | 0 1 | |
| $D_{{{{f}^{1}}}}^{0}$ $D_{{{{{\overline f }}^{2}}}}^{0}$ | 0 1 1 0 | 0 0 |
| $D_{{{{f}^{1}}}}^{1}$ $D_{{{{{\overline f }}^{2}}}}^{1}$ | 1 1 – 1 | 1 1 |
| 0 0 1 0 | 1 1 | |
| 1 0 0 1 | 1 1 | |
| $D_{{{{f}^{1}}}}^{1}$ $D_{{{{{\overline f }}^{2}}}}^{0}$ | 0 1 – 1 | 1 0 |
| 1 0 1 – | 1 0 | |
| 0 0 1 1 | 1 0 | |
| 0 0 0 1 | 1 0 | |
| Вес связанности | 5 | |
| Мера связанности | 5/16 | |
Таблица 15.
Веса связанности подсистем, состоящих из пар функций
| Компонентные функции | ${{f}^{2}}$ | ${{f}^{3}}$ | ${{f}^{4}}$ |
|---|---|---|---|
| ${{f}^{1}}$ | 11 | 4 | 1 |
| ${{f}^{2}}$ | 5 | 4 | |
| ${{f}^{3}}$ | 13 |
Таблица 16.
Веса связанности подсистем, состоящих из пар функций (с учетом инверсий функций)
| Компонентные функции | ${{f}^{2}}$ | ${{\overline f }^{2}}$ | ${{f}^{3}}$ | ${{\overline f }^{3}}$ | ${{f}^{4}}$ | ${{\overline f }^{4}}$ |
|---|---|---|---|---|---|---|
| ${{f}^{1}}$ | 11 | 5 | 4 | 12 | 1 | 15 |
| ${{\overline f }^{1}}$ | 5 | 11 | 12 | 4 | 15 | 1 |
| ${{f}^{2}}$ | 5 | 11 | 4 | 12 | ||
| ${{\overline f }^{2}}$ | 11 | 5 | 12 | 4 | ||
| ${{f}^{3}}$ | 13 | 3 | ||||
| ${{\overline f }^{3}}$ | 3 | 13 |
Для системы ДНФ (табл. 2) минимальный – состоящий из минимального числа ДНФ – дизъюнктивный базис включает восемь ДНФ ${{П }^{i}}$ (табл. 10). Матричное представление обобщенно-ортогонализованной формы
системы ДНФ (табл. 2) дано в табл. 11. В табл. 10 приведены также веса ДНФ. Весом $S({{П }^{i}})$ ДНФ ${{П }^{i}}$ назовем число полных элементарных конъюнкций в СДНФ, равной ДНФ ${{П }^{i}}$. Например, вес ДНФ ${{П }^{1}}$ равен четырем, так как ДНФ ${{П }^{1}} = {{\bar {x}}_{3}}{{\bar {x}}_{4}}$ содержит одну элементарную конъюнкцию, которая представляет четыре полных элементарных конъюнкции:Аналогично могут быть подсчитаны веса других ДНФ из табл. 10. Если обобщенно ортогонализованная форма для системы функций построена, то проверка ${{S}_{p}}$-связанности подсистем не вызывает затруднений и аналогична проверке связанности для ортогонализованной формы. Например, в табл. 12 заданы две подсистемы и для них легко считается вес связанности. Напомним, что в этом примере нет области булева пространства входных переменных, на которой значения всех функций равны 0, поэтому легко получить инверсию компонентной функции по столбцу ее значений на интервалах булева пространства ДНФ ${{П }^{i}}$.
2.2. Проверка связанности систем функций, заданных диаграммам и двоичного выбора. Логические операции над булевыми функциями, заданными BDD-представлениями, описаны в [4] и используют универсальную операцию получения ортогонализованной ДНФ системы, состоящей из двух функций, по ортогонализованным ДНФ функций, участвующих в операции. Такой подход может быть использован для построения ортогонализованной формы подсистемы функций. Легко также учесть вектор поляризации и инверсию функции при формировании подсистемы.
Получение ортогонализованной формы подсистемы по ортогонализованным формам компонентных функций заключается в перемножении $D_{{{{f}^{i}}}}^{\alpha }$ на $D_{{{{f}^{j}}}}^{\alpha }$, где $\alpha \in \{ 0,1\} $.
Вычислим ортогонализованную форму подсистемы$\{ {{f}^{1}},{{f}^{2}}\} $, произведя перемножения ДНФ. Построенная ортогонализованная форма задана в табл. 13. Для случая подсистемы {${{f}^{1}}$, ${{\bar {f}}^{2}}$} следует учесть $D_{{{{f}^{2}}}}^{0} = D_{{{{{\overline f }}^{2}}}}^{1}$, $D_{{{{f}^{2}}}}^{1} = D_{{{{{\overline f }}^{2}}}}^{0}$, тогда легко получить представление данной подсистемы на четырех попарно ортогональных ДНФ (табл. 14).
При программной реализации для BDD-представлений систем функций могут быть использованы структуры данных и эффективные алгоритмы выполнения логических операций над ними, описанные в работе [15]. Базовой операцией при проверке связанности формируемой подсистемы BDD-представления системы функций по BDD-представлениям отдельных функций является операция ◊ “слияния” двух BDD [15, с. 259].
3. Постановка задачи и алгоритм выделения связанных подсистем.
Задача 3. Задан параметр $p$ ($0 < p < {{2}^{n}}$) и система $f(x) = ({{f}^{1}}{\text{(}}x{\text{)}}, \ldots ,{{f}^{m}}(x))$ булевых функций, зависящих от n переменных. Требуется разбить систему $f(x)$ на минимальное число подсистем, каждая из которых является ${{S}_{p}}$-связанной.
Точное решение задачи 3 может быть сведено к:
нахождению всех максимальных по мощности ${{S}_{p}}$-связанных подсистем функций;
построению булевой матрицы R вхождения компонентных функций в подсистемы – каждой подсистеме соответствует строка матрицы R;
нахождению кратчайшего строчного покрытия матрицы R, методы решения этой задачи подробно изложены в [3];
обеспечению взаимной непересекаемости подсистем, вошедших в кратчайшее покрытие, путем удаления некоторых функций из соответствующих подсистем.
Точное решение задачи 3 может быть найдено для систем булевых функций, состоящих из ограниченного числа компонентных функций, зависящих, например, от не более чем двух десятков переменных. Рассмотрим алгоритмы решения задачи 3 для различных форм представления систем булевых функций, которые могут быть программно реализованы и использованы в системах логической оптимизации, таких, как, например, FLC [16].
Эвристический алгоритм решения задачи 3 состоит в последовательном формировании (на каждой итерации) очередной подсистемы ${{S}_{p}}$-связанных функций по текущей (остаточной) системе функций. На первой итерации текущую систему функций образуют функции исходной системы.
На каждой итерации выполняются шаги 1–3.
Шаг 1. Рассмотреть $C_{m}^{2}$ неупорядоченных пар функций {${{f}^{i}},{{f}^{j}}$}, i ≠ j, $m > 1$, текущей системы и найти такую пару L функций, которые являются ${{S}_{q}}$-связанными с максимальным значением параметра q, причем $q \geqslant p$; если таких пар функций несколько, то выбирается любая из таких пар (эвристика EVR1). Если указанной пары L функций нет, то решением задачи 3 являются подсистемы, каждая из которых включает только одну функцию текущей системы.
Шаг 2. Составить из функций найденной на первом шаге пары L функций формируемую подсистему из двух связанных функций, исключив выбранную пару функций из текущей системы, и добавлять в формируемую подсистему поочередно те функции, которые находятся с помощью эвристики EVR2.
Эвристика EVR2: “из множества функций текущей системы выбирается та функция, которая обеспечивает наибольшее возможное значение параметра q для формируемой ${{S}_{q}}$-связанной подсистемы. Если таких функций несколько, то выбирается любая из них”.
Шаг 3. Если нельзя включить ни одну из функций текущей системы в формируемую ${{S}_{q}}$-связанную ($q \geqslant p$) подсистему без нарушения ограничения $q \geqslant p$, то закончить формирование подсистемы и объявить не входящие в нее функции текущей подсистемой, перейти на шаг 1 (формировать следующую подсистему).
Шаг 4. Формирование подсистем заканчивается, когда все функции текущей системы включены в формируемые подсистемы, т.е. когда текущая система становится пустой. Конец алгоритма.
Эвристический алгоритм позволяет получить точное решение задачи 3 гарантированно в двух случаях: (1) когда все функции исходной системы образуют одну подсистему связанных функций, (2) когда в каждую из подсистем связанных функций входит только одна функция исходной системы.
Задача 4. Задан параметр $p$ ($0 < p < {{2}^{n}}$) и система $f(x) = ({{f}^{1}}{\text{(}}x{\text{)}}, \ldots ,{{f}^{m}}(x))$ булевых функций, зависящих от n переменных. Требуется разбить систему $f(x)$ на минимальное число подсистем, каждая из которых является $S_{p}^{\alpha }$-связанной.
Очевидно, что задача 3 является частным случаем задачи 4. Решение задачи 4 надо искать в классе связанных с точностью до инверсии подсистем функций.
Точное решение задачи 4 аналогично точному решению задачи 3 и требует нахождения всех максимальных по мощности связанных (с учетом инверсий функций) подсистем, что приводит каждый раз к перебору ${{2}^{{{{m}_{i}}}}}$ векторов $\alpha = ({{\alpha }^{1}},{{\alpha }^{2}},\; \ldots ,\;{{\alpha }^{{{{m}_{i}}}}})$ поляризации для каждой из формируемых подсистем, состоящих из ${{m}_{i}}$ функций, и является трудоемким для задач практической размерности – десятки и сотни функций системы.
Эвристический алгоритм решения задачи 4 имеет следующие отличия от предложенного эвристического алгоритма решения задачи 3.
Текущую систему функций образуют как функции исходной системы, так и их инверсии.
На шаге 1 каждая из функций ${{f}^{i}}$ рассматривается как в прямой ${{f}^{i}}$, так и инверсной ${{\overline f }^{i}}$ форме, перебираются $C_{{2m}}^{2} - m$, $m > 1$, всевозможных неупорядоченных пар функций текущей системы (пары {${{f}^{i}}$, ${{f}^{i}}$}, {${{\bar {f}}^{i}}$, ${{\bar {f}}^{i}}$}, {${{f}^{i}}$, ${{\bar {f}}^{i}}$} не рассматриваются) и находится такая пара функций, которая является $S_{q}^{\alpha }$-связанной с максимальным значением ${{q}_{{{\text{max}}}}}$ параметра q, $q \geqslant p$. Если таких пар функций несколько, то выбирается любая из таких пар (эвристика EVR3). Формируется вектор $\alpha = ({{\alpha }^{1}},{{\alpha }^{2}})$ поляризации для подсистемы из двух функций.
На шаге 2 при добавлении очередной функции из текущей системы функций в формируемую подсистему используется эвристика EVR4.
Эвристика EVR4: “из множества функций и инверсий функций текущей системы выбирается та функция (либо ее инверсия), которая обеспечивает наибольшее возможное значение параметра q для формируемой $S_{p}^{\alpha }$-связанной подсистемы. Если таких функций несколько, то выбирается любая из них”.
Эвристики EVR1, EVR2 ориентированы на нахождение на каждой итерации подмножества связанных функций возможно большей мощности и тем самым на уменьшение числа подсистем, которые являются ${{S}_{p}}$-связанными (задача 3). Аналогично и для эвристик EVR3, EVR4 при решении задачи 4.
4. Пример выделения ${{S}_{p}}$-связанных подсистем функций. Требуется разбить систему функций (табл. 1) на минимальное число ${{S}_{{11}}}$-связанных подсистем функций (p = 11).
Итерация 1. Формирование первой подсистемы связанных функций.
Шаг 1. В табл. 15 заданы веса связанности пар функций системы. Пару функций с максимальным значением параметра $q = 13$ образует пара {${{f}^{3}}$, ${{f}^{4}}$}.
Шаг 2. Образуем первую ${{S}_{{13}}}$-связанную подсистему {${{f}^{3}}$, ${{f}^{4}}$} и будем поочередно добавлять в нее функции, не вошедшие в данную подсистему. Легко видеть, что для подсистемы {${{f}^{1}}$, ${{f}^{3}}$, ${{f}^{4}}$} значение 1 функции принимают только на одном наборе 1101 значений переменных (q = 1) и данная подсистема является ${{S}_{1}}$-связанной. Добавим в подсистему {${{f}^{3}}$, ${{f}^{4}}$} функцию ${{f}^{2}}$ и проверим, для какого значения параметра q она является ${{S}_{q}}$-связанной. Так как имеется только три набора, на котором все функции подсистемы {${{f}^{2}}$, ${{f}^{3}}$, ${{f}^{4}}$} принимают значение 1 либо 0, поэтому подсистема {${{f}^{1}}$, ${{f}^{2}}$, ${{f}^{4}}$} является ${{S}_{3}}$-связанной и, очевидно, не является ${{S}_{{11}}}$-связанной. Формирование первой подсистемы закончено. В качестве текущей подсистемы функций далее рассматривается подсистема {${{f}^{1}}$, ${{f}^{2}}$}.
Итерация 2. Формирование второй подсистемы связанных функций.
Шаг 1. Подсистема {${{f}^{1}}$, ${{f}^{2}}$} является ${{S}_{{11}}}$-связанной. Конец алгоритма.
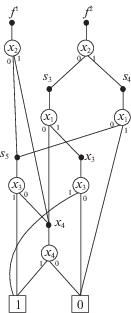
Проведем отдельную BDD-оптимизацию каждой из полученных подсистем. Совместная BDD для {${{f}^{1}}$, ${{f}^{2}}$} (рис. 2) описывается пятью уравнениями (4.1), (4.2), которые содержат 12 логических операций дизъюнкции, конъюнкции:
(4.1)
${{f}^{1}} = {{\bar {x}}_{2}}{{s}_{5}} \vee {{x}_{2}}{{x}_{4}};\quad {{f}^{2}} = {{\bar {x}}_{2}}{{s}_{3}} \vee {{x}_{2}}{{s}_{4}};\quad {{s}_{5}} = {{\bar {x}}_{3}}{{x}_{4}} \vee {{x}_{3}};$(4.2)
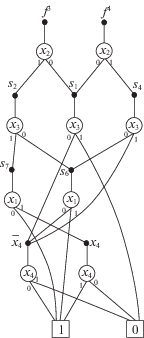
${{s}_{3}} = {{\bar {x}}_{1}}{{x}_{4}} \vee {{x}_{1}}{{x}_{3}};\quad {{s}_{4}} = {{\bar {x}}_{1}}{{s}_{5}}.$Совместная BDD для {${{f}^{3}}$, ${{f}^{4}}$} (рис. 3) описывается семью уравнениями (4.3), (4.4), которые содержат 15 логических операций дизъюнкции, конъюнкции:
(4.3)
${{f}^{3}} = {{\bar {x}}_{2}}{{s}_{1}} \vee {{x}_{2}}{{s}_{2}};\quad {{f}^{4}} = {{\bar {x}}_{2}}{{s}_{1}} \vee {{x}_{2}}{{s}_{4}};\quad {{s}_{1}} = {{\bar {x}}_{3}}{{\bar {x}}_{4}};\quad {{s}_{2}} = {{\bar {x}}_{3}}{{s}_{6}} \vee {{x}_{3}}{{s}_{7}};$(4.4)
${{s}_{4}} = {{\bar {x}}_{3}}{{s}_{6}} \vee {{x}_{3}}{{\bar {x}}_{4}};\quad {{s}_{6}} = {{\bar {x}}_{1}}{{\bar {x}}_{4}} \vee {{x}_{1}};\quad {{s}_{7}} = {{\bar {x}}_{1}} \vee {{x}_{1}}x{}_{4}.$5. Пример выделения $S_{p}^{\alpha }$-связанных подсистем функций. Требуется разбить систему функций (табл. 1) на минимальное число подсистем $S_{{11}}^{\alpha }$-связанных функций (p = 11).
Итерация 1. Формирование первой подсистемы связанных функций.
Шаги 1–3. В табл. 16 заданы веса связанности пар функций системы. Пару функций с максимальным значением параметра $q = 15$ образует пара {${{f}^{1}}$, ${{\overline f }^{4}}$}, вектор поляризации $\alpha = ({{\alpha }^{1}},{{\alpha }^{4}}) = (1,0)$. Добавление в подсистему {${{f}^{1}}$, ${{\overline f }^{4}}$} любой функции из множества {${{f}^{2}}$, ${{\overline f }^{2}}$, ${{f}^{3}}$, ${{\overline f }^{3}}$} не позволяет получить требуемую $S_{{11}}^{\alpha }$-связанность расширенной подсистемы.
Итерация 2. Формирование второй подсистемы связанных функций.
Шаг 1. Второй подсистемой является {${{\overline f }^{2}}$, ${{f}^{3}}$}, которая является $S_{{11}}^{\alpha }$-связанной подсистемой, вектор поляризации $\alpha = ({{\alpha }^{2}},{{\alpha }^{3}}) = (0,1)$. Конец алгоритма.
После BDD-оптимизации исходной системы (без выделения подсистем связанных функций) и проведения синтеза в базисе библиотечных КМОП-элементов в полученной схеме все элементы схемы содержали в сумме 68 транзисторов. После разбиения исходной системы на две подсистемы и BDD-оптимизации [4] подсистем (результаты такой оптимизации показаны на рис. 2, 3 соответственно) число транзисторов в схеме сократилось до 66. Если же использовать BDDI-оптимизацию [17] полученных подсистем, то разбиение на подсистемы {${{f}^{1}}$,${{\overline f }^{4}}$}, {${{\overline f }^{2}}$, ${{f}^{3}}$} связанных функций приводит к лучшему решению – схема содержит 62 транзистора. Под BDDI (Binary Decision Diagram with Inverse cofactors) в работе [17] понимаются представления систем булевых функций на основе разложений Шеннона с учетом возможности использования инверсий подфункций, получаемых при таких разложениях.
6. Результаты эксперимента. Для проверки эффективности влияния процедуры выделения связанных подсистем функций на сложность (площадь) логических схем был проведен вычислительный эксперимент.
Примеры систем функций взяты из набора тестовых примеров [18] и для каждого них были построена таблица истинности, представленная в формате SDF системы логической оптимизации FLC [16]. Для каждого примера синтезировались три варианта схемы, используя различные программы предварительной логической оптимизации.
Вариант 1. Совместная BDDI-оптимизация, конвертация минизированного BDDI-описания в VHDL-описание и схемная реализация.
Вариант 2. Раздельная BDDI-оптимизация, конвертация минизированных BDDI-описаний в VHDL-описания и схемная реализация.
Вариант 3. Выделение связанных подсистем функций, совместная BDDI-оптимизация каждой из подсистем, устранение иерархии описания, конвертация в VHDL-описание и схемная реализация.
Для формирования связанных подсистем использовались примерно одни и те же значения параметра ${{\rho }^{n}}({{f}^{1}},\; \ldots ,\;{{f}^{m}})$, выраженные в процентах к общему числу ${{2}^{n}}$ наборов соответствующего булева пространства. Для системы функций P82 ${{\rho }^{n}}({{f}^{1}},\; \ldots ,\;{{f}^{m}}) = 60$ % (табл. 17) это означает, что $p = \left\lceil {0.6 \times 32} \right\rceil = 20$ наборов булева пространства, на которых функции связанной подсистемы должны принимать одинаковые значения, здесь $\left\lceil a \right\rceil $ – наименьшее целое число, большее либо равное $a$. Заметим, что для этого примера n = 5, а число наборов булева пространства равно 32.
Таблица 17.
Результаты эксперимента
| Пример | Параметры системы функций | Вариант 1. Совместные BDDI | Вариант 2. Раздельные BDDI | Вариант 3. Разбиение на подсистемы связанных функций и совместные BDDI для подсистем |
|||
|---|---|---|---|---|---|---|---|
| n | m | ${{S}_{{ASIC}}}$ | ${{S}_{{ASIC}}}$ | ${{\rho }^{n}}({{f}^{1}}, \ldots ,{{f}^{m}})\,\,\% $ | Число подсистем связанных функций | ${{S}_{{ASIC}}}$ | |
| P82 | 5 | 14 | 19 988 | 18 481 | 60 | 2 | 21 282 |
| Z5XP1 | 7 | 10 | 18 442 | 19 296 | 50 | 1 | 18 665 |
| M2 | 8 | 16 | 45 064 | 46 532 | 60 | 1 | 45 064 |
| M3 | 8 | 16 | 52 580 | 58 456 | 60 | 3 | 52 781 |
| ROOT | 8 | 5 | 26 109 | 27 113 | 65 | 4 | 26 092 |
| ADDM4 | 9 | 8 | 80 782 | 77 210 | 55 | 3 | 87 154 |
| MP2D | 11 | 14 | 17 471 | 17 666 | 60 | 1 | 18 018 |
| ADD6 | 12 | 7 | 12 806 | 20 518 | 55 | 6 | 21 929 |
| T3 | 12 | 8 | 17 276 | 17 170 | 60 | 4 | 16 941 |
| TIAL | 14 | 8 | 255 531 | 441 523 | 60 | 5 | 295 043 |
| B12 | 15 | 9 | 18 358 | 16 266 | 55 | 2 | 17 934 |
| INTB | 15 | 7 | 273 532 | 248 338 | 55 | 3 | 221 688 |
| M181 | 15 | 9 | 18 849 | 16 344 | 60 | 2 | 17 549 |
| IN0 | 15 | 11 | 94 620 | 93 655 | 60 | 3 | 130 706 |
| B2 | 16 | 17 | 192 655 | 313 925 | 60 | 1 | 192 655 |
| Число лучших решений | 7 | 5 | – | – | 5 | ||
Для построения совместных BDDI применялась программа BDD_Builder [17], использующая эвристику – “минимальное число различных (с точностью до инверсии) подфункций” при выборе очередной переменной разложения. Построение BDDI в варианте 2 осуществляется в системе FLC с помощью комбинированного маршрута, включающего последовательное выполнение программы выделения связанных подсистем и последующим выполнением стратегий “BDDI-оптимизация листьев проекта”, “Устранение иерархии” и конвертации полученных оптимизированных описаний в VHDL-описания. Синтез схем из библиотечных КМОП-элементов по VHDL-описаниям во всех случаях выполнялся в системе LeonardoSpectrum [19] при одних и тех же режимах (установках) синтеза.
Результаты эксперимента представлены в табл. 17, где n – число переменных; m – число функций системы; ${{S}_{{ASIC}}}$ – площадь логической схемы, выраженная в суммарном числе условных единиц площадей логических элементов, из которых состоит схема. Жирным шрифтом в табл. 17 выделены лучшие решения – схемы меньшей площади. Если формировалась одна подсистема связанных функций (примеры Z5XP1, M2, MP2D, B2) в варианте 3, а площадь схемы изменилась по сравнению с вариантом 1, то это означает, что некоторые функции исходной системы были инвертированы (см. пример Z5XP1), поэтому и результат синтеза для этого примера получился другим по сравнению с результатом, полученным из варианта 1.
Эксперимент показал, что для исследованного набора тестовых примеров систем булевых функций выделение связанных подсистем может оказаться эффективной процедурой при логической оптимизации многоуровневых BDDI-представлений, так как при последующем синтезе схемы получаются схемы меньшей площади. Если функции системы являются “сильно” связанными, то лучший результат дает оптимизация на основе совместных BDDI, если “слабо” связанными, то на основе раздельных BDDI. Преимущества разбиения системы функций на подсистемы связанных функций основываются именно на данных характеристиках выделяемых подсистем функций. Эксперимент показал также, что при практическом использовании соответствующих программ возникает задача выбора значения параметра “мера связанности”, которая требует отдельного рассмотрения.
Заключение. Логическая оптимизация многоуровневых представлений систем булевых функций большой размерности является актуальной проблемой, возникающей при сокращении площади функциональных блоков заказных сверхбольших интегральных схем. Сокращение площади (уменьшение числа транзисторов в схемах) положительно влияет на снижение энергопотребления логических схем. Во многих случаях выделение подсистем связанных функций и оптимизация BDDI-представлений подсистем позволяют уменьшать сложность функциональных описаний и тем самым сокращать площадь и энергопотребление логических схем, синтезированных по оптимизированным функциональным описаниям.
Список литературы
Брейтон Р.К., Хэчтел Г.Д., Санджованни-Винчентелли А.Л. Синтез многоуровневых комбинационных логических схем // ТИИЭР. 1990. Т. 78. № 2.
Brayton K.R., Hactel G.D., McMullen C.T., Sangiovanni-Vincentelli A.L. Logic Minimization Algorithm for VLSI Synthesis. Kluwer Acad. Publ., 1984.
Закревский А.Д., Поттосин Ю.В., Черемисинова Л.Д. Логические основы проектирования дискретных устройств. М.: Физматлит, 2007.
Бибило П.Н. Применение диаграмм двоичного выбора при синтезе логических схем. Минск: Беларус. навука, 2014.
Гаврилов М.А. Композиция и декомпозиция комбинационных автоматов // Теория автоматов. М.: Наука, 1976.
Гаврилов М.А., Девятков В.В., Пупырев Е.И. Логическое проектирование дискретных автоматов. М.: Наука, 1977.
Кузнецов О.П. О программной реализации логических функций и автоматов // АиТ. 1977. № 7.
Bryant R.E., Meinel C. Ordered Binary Decision Diagrams // Logic synthesis and verification / Eds. S. Hassoun, T. Sasao, R.K. Brayton: Kluwer Acad. Publ., 2002.
Yang S., Ciesielski M. BDS: a BDD-based Logic Optimization System // IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. 2002. V. 21. № 7.
Бибило П.Н. Декомпозиция булевых функций на основе решения логических уравнений. Минск: Беларус. навука, 2009.
Бибило П.Н., Кириенко Н.А., Ланкевич Ю.Ю. Логическая оптимизация многоуровневых представлений систем булевых функций на основе блочного разбиения и разложения Шеннона // Информатика. 2018. Т. 15. № 3.
Поттосин Ю.В., Шестаков Е.А. Ортогонализация системы полностью определенных булевых функций // Логическое проектирование: Сб. науч. тр. Минск: Ин-т техн. кибернетики НАН Беларуси, 2000. Вып. 5.
Закревский А.Д. Вычисления в многомерном булевом пространстве. Минск: ОИПИ НАН Беларуси, 2011.
Бибило П.Н. Синтез комбинационных ПЛМ-структур для СБИС. Минск: Наука и техника, 1992.
Кнут Д.Э. Искусство программирования. Т. 4, А. Комбинаторные алгоритмы. Ч. 1 / Пер. с англ. М.: Вильямс, 2013.
Бибило П.Н., Романов В.И. Логическое проектирование дискретных устройств с использованием продукционно-фреймовой модели представления знаний. Минск: Беларус. навука, 2011.
Бибило П.Н., Ланкевич Ю.Ю. Использование полиномов Жегалкина при минимизации многоуровневых представлений систем булевых функций на основе разложения Шеннона // Программная инженерия. 2017. № 3.
Jeong C. Computer-Aided Design of Digital Systems // Department of Computer Science. http://www1.cs.columbia.edu/~cs6861/sis/espresso-examples/ex.
Бибило П.Н., Авдеев Н.А. VHDL. Эффективное использование при проектировании цифровых систем. М.: СОЛОН-Пресс, 2006.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления