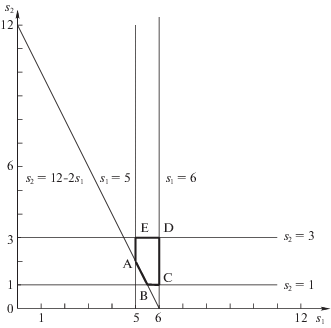Известия РАН. Теория и системы управления, 2019, № 2, стр. 41-46

Введение. Задача построения допустимых многопроцессорных расписаний является одной из основных задач при разработке математического и программного обеспечения многопроцессорных вычислительных систем реального времени. Эти системы находят широкое применение при разработке и эксплуатации сложных технических объектов (самолеты, ядерные реакторы, системы экологического и экономического мониторинга, конвейерные системы и др.). Задачам построения расписаний с прерываниями посвящено большое число работ. Отметим, например, такие работы, как [1] (идентичные процессоры), [2] (произвольные процессоры, одинаковые директивные интервалы), [3–5] (произвольные процессоры, произвольные директивные интервалы). В некоторых случаях аналогичные задачи сводятся к минимаксным и сетевым задачам, методы решения которых приведены в [6–9]. В настоящей статье рассматривается своего рода обратная задача по отношению к перечисленным выше, а именно задача нахождения таких производительностей процессоров, при которых допустимое расписание существует. При этом предполагается, что директивные интервалы фиксированы, а объемы работ в одном случае также фиксированы, а во втором – линейно зависят от количества выделенных работ дополнительных ресурсов. Кроме того, приведена задача, когда на производительности процессоров накладываются ограничения сверху и снизу.

1. Задача с фиксированными объемами работ. Рассматривается задача нахождения допустимых производительностей процессоров при заданных директивных интервалах и объемах работ. Результаты, полученные в этом разделе, основаны на результатах работ [4, 10].

1.1. Постановка задачи. Описывается вычислительная система, состоящая из m процессоров. Каждый процессор  j характеризуется производительностью ${{s}_{j}}$, $j = \overline {1,m} $. Имеется набор работ (заданий) $N = \{ \overline {1,n} \} $, подлежащих выполнению. При выполнении заданий допускаются прерывания и переключения с одного процессора на другой. Предполагается, что прерывания и переключения не сопряжены с временны́ми затратами. В фиксированный момент времени каждый процессор может выполнять не более одной работы, а каждая работа выполняется не более чем одним процессором. Каждое задание $i \in N$ характеризуется своим директивным интервалом $({{b}_{i}},{{f}_{i}}]$ (работа i может быть начата после момента времени ${{b}_{i}}$ и должна быть завершена не позднее момента времени ${{f}_{i}}$) и объемом ${{Q}_{i}}$ работы процессоров по его выполнению (суммарный объем работы процессоров по выполнению задания i должен быть равен ${{Q}_{i}}$). Если суммарная длительность работы процессора  j по выполнению работы i составляет ${{\tau }_{{ij}}}$, $i \in N$, $j = \overline {1,m} $, то

Требуется определить множество ${{s}_{1}},{{s}_{2}},\; \ldots ,{{s}_{m}}$ производительностей процессоров, для которых существует допустимое расписание (т.е. расписание, при котором каждая работа полностью выполняется в своем директивном интервале).

1.2. Построение области допустимых производительностей процессоров. Без ограничения общности будем находить производительности процессоров, которые удовлетворяют неравенствам

Введем следующие обозначения: ${{S}_{k}} = \;{{s}_{{\text{1}}}}\; + \;{{s}_{{\text{2}}}}\; + \;... + \;{{s}_{k}}$,  $k = \overline {1,m} $; ${{y}_{0}} < {{y}_{1}} < \; \ldots \; < {{y}_{p}}$, $p < 2n$, – все разные по величине значения ${{b}_{i}}$, ${{f}_{i}}$, $i \in N$; ${{I}_{l}} = ({{y}_{{l - 1}}},{{y}_{l}}]$, $l = \overline {1,p} $; ${{\delta }_{l}} = {{y}_{l}} - {{y}_{{l - 1}}}$ – длина интервала ${{I}_{l}}$. Очевидно, что для любых двух интервалов ${{I}_{l}}$ и $({{b}_{i}},{{f}_{i}}]$ либо ${{I}_{l}} \subseteq ({{b}_{i}},{{f}_{i}}]$, либо ${{I}_{l}} \cap ({{b}_{i}},{{f}_{i}}] = \emptyset $. Директивный интервал $({{b}_{i}},{{f}_{i}}]$ каждой работы $i \in N$является объединением некоторых интервалов ${{I}_{l}}$.

Будем говорить, что работа $i \in N$ доступна в интервале ${{I}_{l}}$, если ${{I}_{l}} \subseteq ({{b}_{i}},{{f}_{i}}]$, т.е. работа i может выполняться в интервале ${{I}_{l}}$. Без ограничения общности можно считать, что в каждом интервале ${{I}_{l}}$, $1 \leqslant l \leqslant p$, доступна хотя бы одна работа $i \in N$, поскольку интервалы ${{I}_{l}}$, которые не удовлетворяют этому условию, можно исключить из дальнейшего рассмотрения, а оставшиеся интервалы перенумеровать.

Как следует из [4], допустимое расписание в поставленной задаче существует тогда и только тогда, когда для любого подмножества $\tilde {N} \subseteq N$ выполнено неравенство

где $k(l,\tilde {N}) = \min (m,m{\text{'}})$, $m{\text{'}}$ – число работ $\tilde {N} \subseteq N$, доступных в интервале I_l. По аналогии с тем, как это сделано в [1] для случая идентичных процессоров, число подмножеств $\tilde {N}$, для которых следует выполнять проверку условия (1.2), в некоторых случаях можно существенно сократить. Предположим, что множество работ N можно разбить на $r \geqslant 2$ непересекающихся подмножеств, $N = {{N}_{{{{l}_{1}}{{l}_{2}}}}} \cup {{N}_{{{{l}_{3}}{{l}_{4}}}}} \cup \; \ldots \; \cup {{N}_{{{{l}_{{2r - 1}}}{{l}_{{2r}}}}}}$, ${{N}_{{{{l}_{{2u - 1}}}{{l}_{{2u}}}}}} \cap {{N}_{{{{l}_{{2v - 1}}}{{l}_{{2v}}}}}} = \emptyset $ при $u \ne v$, таких, что где

Докажем следующее утверждение.

Лемма 1. Для существования допустимого расписания необходимо и достаточно, чтобы для любой пары ${{l}_{{2u - 1}}}$, ${{l}_{{2u}}}$, $u = \overline {1,r} $, и любого подмножества ${{\tilde {N}}_{u}} \subseteq {{N}_{{{{l}_{{2u - 1}}}{{l}_{{2u}}}}}}$ выполнялось неравенство

Доказательство. Необходимость. Если допустимое расписание существует, то неравенство (1.2) справедливо для всех подмножеств $\tilde {N} \subseteq N$ и, в частности, для подмножеств ${{\tilde {N}}_{u}} \subseteq {{N}_{{{{l}_{{2u - 1}}}{{l}_{{2u}}}}}}$, $u = \overline {1,r} $.

Достаточность. Пусть неравенство (1.3) справедливо для любого подмножества ${{\tilde {N}}_{u}} \subseteq {{N}_{{{{l}_{{2u - 1}}}{{l}_{{2u}}}}}}$, $u = \overline {1,r} $. Выберем произвольное подмножество $\tilde {N} \subseteq N$. Его можно представить в виде следующего объединения непересекающихся подмножеств:

где ${{\tilde {N}}_{u}} \subseteq {{N}_{{{{l}_{{2u - 1}}}{{l}_{{2u}}}}}}$, $u = \overline {1,r} $, ${{\tilde {N}}_{u}} \cap {{\tilde {N}}_{v}} = \emptyset $ при $u \ne v$. Для каждого ${{\tilde {N}}_{u}}$, $u = \overline {1,r} $, неравенство (1.3) справедливо. Складывая неравенства (1.3) для всех $u = \overline {1,r} $, получаем (1.2) и, следовательно, допустимое расписание существует. Лемма доказана.

Доказанная лемма 1 позволяет выполнять проверку условия (1.2) не для всех подмножеств $\tilde {N} \subseteq N$, а только для подмножеств вида ${{\tilde {N}}_{u}} \subseteq {{N}_{{{{l}_{{2u - 1}}}{{l}_{{2u}}}}}}$, $u = \overline {1,r} $ (условие (1.3)), число которых может быть существенно меньше, чем число всех подмножеств множества N, т.е. ${{2}^{n}}$. Перепишем неравенство (1.3) в следующем виде:

где а неравенство (1.4) перепишем в виде где ${{G}_{{uj}}} = {{H}_{{u1}}} + {{H}_{{u2}}} + \; \ldots \; + {{H}_{{uj}}}$, $j = \overline {1,m - 1} $. Теперь задача заключается в нахождении производительностей ${{s}_{1}},{{s}_{2}},\; \ldots ,\;{{s}_{m}}$ процессоров, удовлетворяющих системе линейных неравенств с m переменными (1.1), (1.5) для любой пары ${{l}_{{2u - 1}}}$, ${{l}_{{2u}}}$, $u = \overline {1,r} $, и любого подмножества ${{\tilde {N}}_{u}} \subseteq {{N}_{{{{l}_{{2u - 1}}}{{l}_{{2u}}}}}}$.

Отметим, что наряду с предположениями, сделанными в этом разделе, дополнительно можно предполагать, что на производительности процессоров накладываются ограничения сверху и снизу:

где h_j и  g_j  – заданные величины. В этом случае неравенства (1.6) добавляются к неравенствам (1.1), (1.5).

Величины s₁, s₂, …, s_m можно также искать, ограничившись неравенствами (1.4). Для этого будем использовать следующее утверждение [10].

Лемма 2. Для того, чтобы по заданным величинам ${{S}_{1}},{{S}_{2}},\; \ldots ,\;{{S}_{m}}$ можно было определить величины ${{s}_{1}},{{s}_{2}},\; \ldots ,\;{{s}_{m}}$, удовлетворяющие неравенствам (1.1), необходимо и достаточно выполнения неравенств

Доказательство. Необходимость. Справедливость (1.7) следует из определения величин S_k, $k = \overline {1,m} $. Кроме того, 2S₁ – S₂ = 2s₁ – (s₁ + s₂) = s₁ – s₂, откуда в силу (1.1) следует (1.9), и 2S_r – (S_r – 1 + S_{r + 1}) = 2(s₁ + … + s_r) – (s₁ + … + s_r – 1) – (s₁ + … + s_r + 1) = s_r – s_r + 1, откуда в силу (1.1) вытекает (1.8).

Достаточность. Пусть величины S₁, …, S_m удовлетворяют неравенствам (1.7)–(1.9). Определим величины s₁, …, s_m следующим образом:

Тогда ${{s}_{r}} \geqslant 0$, $r = \overline {1,m} $, в силу (1.7). В силу (1.8), (1.9) имеем

откуда следует (1.1). Лемма доказана.

Таким образом, величины ${{S}_{1}},{{S}_{2}},\; \ldots ,\;{{S}_{m}}$, по которым можно определить производительности ${{s}_{1}},{{s}_{2}},\; \ldots ,\;{{s}_{m}}$ процессоров, должны удовлетворять системе линейных неравенств (1.4), (1.7)–(1.9) с m переменными. Как показано в лемме 2, по величинам ${{S}_{1}},{{S}_{2}},\; \ldots ,\;{{S}_{m}}$ производительности ${{s}_{1}},{{s}_{2}},\; \ldots ,\;{{s}_{m}}$ процессоров вычисляются по формулам (1.10).

Отметим также, что в рассматриваемой задаче можно потребовать выполнение ряда дополнительных условий, как, например: 1) суммарная производительность процессоров должна быть минимальной, т.е. ${{s}_{1}} + {{s}_{2}} + \; \ldots \; + {{s}_{m}} \to \min $; 2) производительность самого быстрого процессора должна быть минимальной, т.е. ${{s}_{1}} \to \min $, а также других условий. В этом случае получаем задачу линейного программирования с целевой функцией соответственно ${{s}_{1}} + {{s}_{2}} + \; \ldots \; + {{s}_{m}}$ и s₁ и ограничениями (1.1), (1.5), (1.6).

1.3. Парето-оптимальные решения. Рассмотрим задачу поиска парето-оптимального вектора $(s_{1}^{0},s_{2}^{0},\; \ldots ,\;s_{m}^{0})$ с точки зрения минимизации производительностей процессоров. Будем предполагать, что выполнены неравенства ${{g}_{1}} \geqslant {{g}_{2}} \geqslant \; \ldots \; \geqslant {{g}_{m}}$. Пусть $\Delta $ – это множество векторов $(s_{1}^{{}},s_{2}^{{}},\;...,\;s_{m}^{{}})$, удовлетворяющих неравенствам (1.5). Опишем процедуру поиска вектора $(s_{1}^{0},s_{2}^{0},\; \ldots ,\;s_{m}^{0}) \in \Delta $, для которого не существует такого вектора $(s_{1}^{{}},s_{2}^{{}},\; \ldots ,\;s_{m}^{{}}) \in \Delta $, что ${{s}_{j}}\; \leqslant s_{j}^{0}$ при всех  $j = \overline {1,m} $ и хотя бы для одного ${{j}_{1}}$, $1 \leqslant {{j}_{1}} \leqslant m$, ${{s}_{{{{j}_{1}}}}} < s_{{{{j}_{1}}}}^{0}$.

Все неравенства (1.5), записанные для каждой пары ${{l}_{{2u - 1}}}$, ${{l}_{{2u}}}$, $u = \overline {1,r} $, и каждого подмножества ${{\tilde {N}}_{u}} \subseteq {{N}_{{{{l}_{{2u - 1}}}{{l}_{{2u}}}}}}$, занумеруем от 1 до некоторого T и будем рассматривать их в следующем виде:

Будем предполагать, что при ${{s}_{j}} = g_{j}^{{}}$, $j = \overline {1,m} $, неравенства (1.11) выполняются при всех  $t = \overline {1,T} $. В противном случае,  как следует, из леммы 1, решения не существует. Найдем минимальное значение s_m, при котором $(g_{1}^{{}},g_{2}^{{}},\; \ldots ,\;{{g}_{{m - 1}}},s_{m}^{{}}) \in \Delta $. В силу (1.11) и леммы 1 ${{s}_{m}} \geqslant ({{a}_{t}} - {{c}_{{t1}}}{{g}_{1}} - {{c}_{{t2}}}{{g}_{2}} - \; \ldots \; - {{c}_{{t,m - 1}}}{{g}_{{m - 1}}}){\text{/}}{{c}_{{tm}}}$ при всех $t = \overline {1,T} $. Тогда полагаем $s_{m}^{0}\, = \,{\text{max}}({\text{min}}(\bar {s}_{m}^{0},{{g}_{m}}),{{h}_{m}})$, где $\bar {s}_{m}^{0} = {{\max }_{{t = \overline {1,T} }}}({{a}_{t}} - {{c}_{{t1}}}{{g}_{1}} - {{c}_{{t2}}}{{g}_{2}} - \; \ldots \; - {{c}_{{t,m - 1}}}{{g}_{{m - 1}}}){\text{/}}{{c}_{{tm}}}$. Очевидно, что вектор $(g_{1}^{{}},g_{2}^{{}},\; \ldots ,\;{{g}_{{m - 1}}},s_{m}^{0})$ удовлетворяет неравенствам (1.1), (1.6), (1.11) и в силу выбора $s_{m}^{0}$ вектор $(g_{1}^{{}},g_{2}^{{}},\; \ldots ,\;{{g}_{{m - 1}}},s_{m}^{{}}) \notin \Delta $ при ${{s}_{m}} < s_{m}^{0}$, так как для него не выполнены некоторые из неравенств (1.11). Тем более, $(s_{1}^{{}},s_{2}^{{}},\; \ldots ,\;{{s}_{{m - 1}}},s_{m}^{{}}) \notin \Delta $ при ${{s}_{j}} < g_{j}^{{}}$, $j = \overline {1,m - 1} $, и ${{s}_{m}} < s_{m}^{0}$.

В общем случае, предположим, что уже определены значения $s_{{v + 1}}^{0}, \ldots ,s_{m}^{0}$, $1 \leqslant v \leqslant m - 1$. Найдем минимальное значение ${{s}_{v}}$, при котором $({{g}_{1}}, \ldots ,{{g}_{{v - 1}}},{{s}_{v}},s_{{v + 1}}^{0},s_{m}^{0}) \in \Delta $. В силу (1.11) и леммы 1 ${{s}_{v}} \geqslant ({{a}_{t}} - {{c}_{{t1}}}{{g}_{1}} - {{c}_{{t2}}}{{g}_{2}} - \ldots - {{c}_{{t,v - 1}}}{{g}_{{v - 1}}},{{c}_{{t,v + 1}}}s_{{v + 1}}^{0} - \ldots - {{c}_{{tm}}}s_{m}^{0}){\text{/}}{{c}_{{tv}}}$ при всех $t = \overline {1,T} $. Тогда полагаем $s_{v}^{0} = \max (\min (\bar {s}_{v}^{0},{{g}_{v}}),s_{{v + 1}}^{0},{{h}_{v}})$, где $\bar {s}_{v}^{0} = {{\max }_{{t = \overline {1,T} }}}({{a}_{t}} - {{c}_{{t1}}}{{g}_{1}} - {{c}_{{t2}}}{{g}_{2}} - \ldots - {{c}_{{t,v - 1}}}{{g}_{{v - 1}}},{{c}_{{t,v + 1}}}s_{{v + 1}}^{0} - \ldots - {{c}_{{tm}}}s_{m}^{0}){\text{/}}{{c}_{{tv}}}$. Очевидно, что $({{g}_{1}}, \ldots ,{{g}_{{v - 1}}},s_{v}^{0},s_{{v + 1}}^{0},s_{m}^{0})$ удовлетворяет неравенствам (1.1), (1.6), (1.11) и в силу выбора $s_{v}^{0}$ вектор $({{g}_{1}}, \ldots ,{{g}_{{v - 1}}},{{s}_{v}},s_{{v + 1}}^{0},s_{m}^{0}) \notin \Delta $ при ${{s}_{v}} < s_{v}^{0}$, так как для него не выполнены некоторые из неравенств (1.11). Тем более, $({{g}_{1}}, \ldots ,{{g}_{{v - 1}}},{{s}_{v}},s_{{v + 1}}^{0},s_{m}^{0}) \notin \Delta $ при ${{s}_{j}} < g_{j}^{{}}$, $j = \overline {1,v - 1} ,$ и ${{s}_{v}} < s_{v}^{0}$. Следовательно, вектор $(s_{1}^{0},s_{2}^{0},\; \ldots ,\;s_{m}^{0})$ является парето-оптимальным в смысле минимизации производительностей процессоров, так как ни одну из величин $s_{j}^{0}$ нельзя уменьшить без увеличения некоторых величин $s_{v}^{0}$, $v = \overline {1,m} $, $v \ne j$, оставаясь при этом во множестве $\Delta $.

2. Задача с нефиксированными объемами работ. В этом разделе наряду с предположениями, сделанными в разд. 1, дополнительно будем предполагать, что помимо процессоров в системе имеется K типов дополнительных ресурсов невозобновляемого типа. Суммарное количество k-го типа этого ресурса составляет R_k, $k = \overline {1,K} $. Если заданию $i \in N$ выделено ${{r}_{{ik}}}$ единиц дополнительного ресурса k-го типа, $i \in N$; $k = \overline {1,K} $, то объем работы процессоров по выполнению задания $i$ составляет

где ${{a}_{{ik}}}$, ${{d}_{i}}$, ${{\bar {r}}_{{ik}}}$ – заданные величины, ${{a}_{{ik}}} \geqslant 0$, ${{d}_{i}} > 0$, ${{\bar {r}}_{{ik}}} \geqslant 0$, ${{d}_{i}}$ – объем работы процессоров по выполнению задания i в случае, если ей дополнительных ресурсов не выделено. Требуется найти такое распределение ресурсов $r_{{ik}}^{0}$, $i \in N$, $k = \overline {1,K} $, и производительности ${{s}_{1}},{{s}_{2}},\; \ldots ,\;{{s}_{m}}$ процессоров, при которых существует допустимое расписание. При этом указанное распределение ресурсов должно удовлетворять ограничениям (2.1, 2.2). Примеры подобных задач содержатся в [11, 12]. В этом случае неравенство (1.5) преобразуется в неравенство для любой пары ${{l}_{{2u - 1}}}$, ${{l}_{{2u}}}$, $u = \overline {1,r} $, и любого подмножества ${{\tilde {N}}_{u}} \subseteq {{N}_{{{{l}_{{2u - 1}}}{{l}_{{2u}}}}}}$. Таким образом, решение поставленной задачи сведено к решению системы линейных ограничений (1.1), (2.1)–(2.3) с m + nK переменными.

Пример. Рассмотрим пример, когда n = 3, $N = \{ 1,\;2,\;3\} $, m = 2, b₁ = 0,  f₁ = 2, b₂ = 1,  f₂ = 2, b₃ = 2, f₃ = 4, Q₁ = 8, Q₂ = 4, Q₃ = 10, h₁ = 4, g₁ = 6, h₂ = 1, g₂ = 3. В этом случае y₀ = 0, y₁ = 1, y₂ = 2, y₃ = 4, I₁ = (0, 1], I₂ = (1, 2], I₃ = (2, 4], ${{\delta }_{1}} = 1$, ${{\delta }_{2}} = 1$, ${{\delta }_{3}} = 2$, $N = {{N}_{{12}}} \cup {{N}_{{33}}}$, $N_{{12}}^{{}} = \{ 1,\;2\} $, ${{N}_{{33}}} = \{ 3\} $, ${{I}_{{12}}} = {{I}_{1}} \cup {{I}_{2}}$, ${{I}_{{33}}} = {{I}_{3}}$. Система неравенств (1.4) выглядит следующим образом:

Запишем систему неравенств (1.1), (1.5), (1.6):

На рисунке выделенная область (пятиугольник ABCDE) определяет допустимые пары значений производительностей процессоров s₁, s₂. Так, например, точка A имеет координаты s₁ = 5, s₂ = 2, а точка B – координаты s₁ = 5.5, s₂ = 1. Обе эти точки (а также их выпуклые линейные комбинации) определяют парето-оптимальные решения (вектора производительностей процессоров): (5; 2), (5.5; 1).

Заключение. Исследована задача синтеза вычислительной системы, заключающаяся в нахождении производительностей процессоров при построении допустимых расписаний с прерываниями и директивными интервалами. Рассмотрена постановка с фиксированными объемами заданий, а также задача распределения дополнительных ресурсов, влияющих на длительности выполнения работ. Разработан метод нахождения парето-оптимальных решений. Предложенные алгоритмы основаны на построении системы линейных неравенств.