Известия РАН. Теория и системы управления, 2019, № 2, стр. 154-165

ОТСЛЕЖИВАНИЕ ПРИВОДАМИ МАНИПУЛЯТОРА ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНОЙ СТРУКТУРЫ ПРОГРАММНЫХ ПЕРЕМЕЩЕНИЙ РАБОЧЕГО ОРГАНА

Н. С. Воробьева^1, *, В. В. Жога², И. А. Несмиянов¹

¹ Волгоградский государственный аграрный ун-т
Волгоград, Россия

² Волгоградский государственный технический ун-т
Волгоград, Россия

^* E-mail: vgsxa@mail.ru

Поступила в редакцию 07.05.2018
После доработки 29.10.2018
Принята к публикации 26.11.2018

DOI: 10.1134/S0002338819020185

Полный текст (PDF)

Аннотация

Разработаны методы синтеза программных перемещений исполнительных цилиндров манипулятора последовательно-параллельной структуры, обеспечивающих реализацию требуемых траекторий рабочего органа манипулятора. Программные перемещения исполнительных цилиндров интерполируются конечным набором сплайнов третьего и четвертого порядков. Конфигурация манипулятора в каждой точке траектории рабочего органа определяется решением оптимизационной задачи из условия минимума критерия обобщенной энергии.

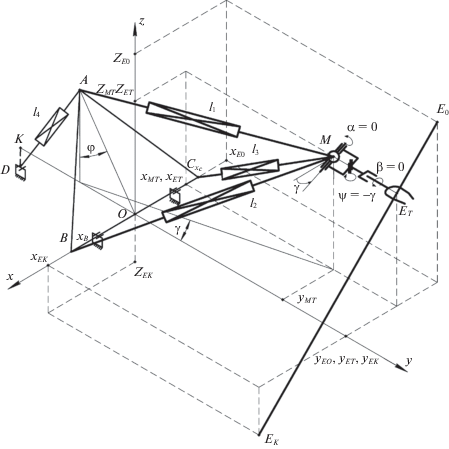
0. Введение. Рассматривается манипулятор параллельно-последовательной структуры [1] (рис. 1). Манипулятор состоит из пространственного механизма в виде треугольной пирамиды со звеньями переменной длины AM, BM, CM. Одни концы этих звеньев соединяются с основанием ABC, а другие концы соединены между собой в точке M специальным шарниром [2]. Конструкция шарнира обеспечивает пересечение геометрических осей исполнительных приводов в точке. Такое соединение исключает передачу изгибающих моментов на звенья манипулятора от внешних нагрузок и увеличивает жесткость конструкции.

Рис. 1.

Манипулятор параллельно-последовательной структуры

Звенья исполнительных цилиндров связаны кинематическими парами V класса. Применение в качестве приводных звеньев цилиндров с кинематическими звеньями V класса исключает запутывание энергоподводящих проводов. В точках крепления A, B, C исполнительные цилиндры связаны с основанием двухподвижными шарнирами. Тогда при числе подвижных звеньев n = 11, числе кинематических пар пятого класс p₅ = 12 и третьего класса p₃ = 1 механизм без избыточных связей и местных подвижностей имеет число степеней подвижности, равное трем. Основание имеет возможность изменять угол φ наклона к горизонту (рис. 1) за счет изменения длины звена AD, что позволяет увеличить рабочую зону манипулятора [3].

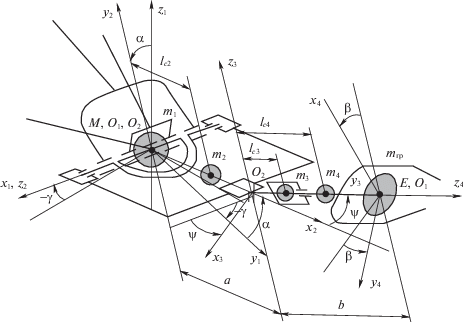
Для повышения манипулятивности рабочего органа в точке M к специальному шарниру присоединен трехзвенный механизм – захватное устройство с рабочим органом. В качестве захватного устройства используется манипулятор последовательной структуры с тремя степенями свободы (рис. 2).

Рис. 2.

Кинематическая схема захвата с тремя степенями свободы

Для определения пространственного положения манипулятора и рабочего органа захвата вводятся пять систем координат, абсолютная система Oxyz (рис. 1) и подвижные системы координат O_jx_jy_jz_j, $j = \overline {{\text{1,4}}} $. Ось O_jz_j каждого звена направлена по оси относительного вращения этого звена (рис. 2). Конструкция манипулятора обеспечивает связи между длинами исполнительных звеньев, координатами x_M(t), y_M(t), z_M(t) точки M и углом поворота φ основания ABC:

$\begin{gathered} {{l}_{1}}(t) = \sqrt {x_{M}^{2} + {{{({{y}_{M}} + О А \sin \varphi )}}^{2}} + {{{({{z}_{M}} - OA\cos \varphi )}}^{2}}} , \\ {{l}_{2}}(t) = \sqrt {{{{({{x}_{M}} - OB)}}^{2}} + y_{M}^{2} + z_{M}^{2}} ,\quad {{l}_{3}}(t) = \sqrt {{{{({{x}_{M}} + OB)}}^{2}} + y_{M}^{2} + z_{M}^{2}} , \\ {{l}_{4}}(t) = \sqrt {{{{(OK - О А \sin \varphi )}}^{2}} + {{{(OA\cos \varphi + DK)}}^{2}}} . \\ \end{gathered} $

Параметр γ(t) манипулятора (рис. 1) определяется выражением [4]

${tg\gamma } = \frac{{ - {{x}_{M}}}}{{{{y}_{M}} + OA\sin {\varphi }}}.$

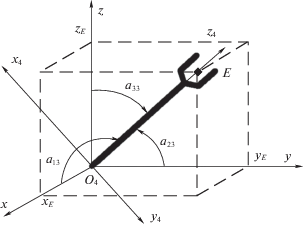
1. Постановка задачи. Заданы законы перемещения характерной точки рабочего органа манипулятора (рис. 1) E[x_E(t), y_E (t), z_E (t)] и его направляющих косинусов a_pq(t) (рис. 2, 3 ).

Требуется найти законы изменения обобщенных координат манипулятора l_k(t), $k = \overline {{\text{1,4}}} $, α(t), ψ(t), β(t), обеспечивающих выполнение законов перемещения рабочего органа. Принимаем, что скорости и ускорения равны нулю в начальной и конечной точках траектории и непрерывно изменяются в промежуточных точках.

Число обобщенных координат манипулятора равно семи – длины исполнительных звеньев l_k(t), $k = \overline {{\text{1,4}}} $, и углы поворота звеньев захватного устройства α(t), ψ(t), β(t). Число обобщенных координат рабочего органа равно шести – декартовы координаты характерной точки E[x_E(t), y_E(t), z_E(t)] и углы Эйлера [5], задающие его ориентацию в пространстве. т.е. маневренность манипулятора равна единице [6]. В этом случае задача построения закона изменения управляющих перемещений исполнительных звеньев допускает множество решений. Положению рабочего органа соответствует множество конфигураций манипулятора. Для выбора из этого множества единственного решения можно использовать некоторый критерий оптимальности [5–7].

Сформировать законы изменения обобщенных координат манипулятора l_k(t), $k = \overline {{\text{1,4}}} $, α(t), ψ(t), β(t) в реальном масштабе времени затруднительно из-за высокой размерности задачи и ограниченной вычислительной мощности контроллеров приводного уровня. Так как системы управления строятся по иерархическому принципу, то рационально для каждого заданного движения рабочего органа заранее определить аналитические законы изменения обобщенных координат исполнительных приводов. Процесс выполнения любой технологической операции состоит из последовательного выполнения заданных программных движений рабочего органа [8]. Причем количество программных движений манипулятора, последовательное исполнение которых обеспечивает выполнение технологического процесса, ограничено [9]. Для эффективного выполнения технологических операций захват манипулятора необходимо перемещать с заданной скоростью по гладкой траектории, которая соединяет целевые точки. Необходимость движения по гладким траекториям обусловлена также требованиями ограничения максимальных значений ускорений звеньев манипулятора [10, 11].

Таким образом, необходимо разработать методику, позволяющую сформировать базу знаний, элементы которой аппроксимируют траектории рабочего органа, функциями изменения обобщенных координат исполнительных цилиндров в виде сплайнов.

2. Метод решения. Считаем, что в начальный момент времени конфигурация манипулятора известна, т.е. заданы значения обобщенных координат манипулятора l_k(0) = l_k0, $k = \overline {{\text{1,4}}} $, α(0) = α₀, ψ(0) = ψ₀, β(0) = β₀. В конкретный момент времени t_i положение рабочего органа в пространстве определяется произведением матриц перехода M_j–1,j, описывающих положение j звена захватного устройства (рис. 2), относительно (j – 1) [12]:

(2.1)

${{M}_{{04}}} = {{M}_{{01}}}{{M}_{{12}}}{{M}_{{23}}}{{M}_{{34}}}.$

Связь между координатами точек X_j в j-й и X_j _{– 1} в (j – 1)-й системах координат осуществляется последовательным выполнением операций X_j _{– 1} = M_j _{– 1,}_jX_j с помощью матриц перехода M_j–1,j :

(2.2)

$\left[ \begin{gathered} {{х }_{{j - 1}}} \\ {{y}_{{j - 1}}} \\ {{z}_{{j - 1}}} \\ 1 \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {\cos ({{x}_{{j - 1}}},{{x}_{j}})}&{\cos ({{x}_{{j - 1}}},{{y}_{j}})}&{\cos ({{x}_{{j - 1}}},{{z}_{j}})}&\vline & {{{х }_{{j - 1,j}}}} \\ {\cos ({{y}_{{j - 1}}},{{x}_{j}})}&{\cos ({{y}_{{j - 1}}},{{y}_{j}})}&{\cos ({{y}_{{j - 1}}},{{z}_{j}})}&\vline & {{{y}_{{j - 1,j}}}} \\ {\cos ({{z}_{{j - 1}}},{{x}_{j}})}&{\cos ({{z}_{{j - 1}}},{{y}_{j}})}&{\cos ({{z}_{{j - 1}}},{{z}_{j}})}&\vline & {{{z}_{{j - 1,j}}}} \\ \hline 0&0&0&\vline & 1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{х }_{j}}} \\ {{{y}_{j}}} \\ {{{z}_{j}}} \\ 1 \end{array}} \right],$

где X_j = [x_j, y_j, z_j]^T – вектор-столбец координат точки в j-й системе; X_i _{– 1}, _i = [x_j _{– 1,}_j, y_j _{– 1,}_j, z_j _{– 1,}_j]^T – вектор-столбец координат начала j-й системы в (j – 1)-й системе координат. Верхняя левая подматрица размером [3 × 3], образованная направляющими косинусами, определяет поворот j-й системы относительно (j – 1)-й.

При последовательном переходе по цепочке шарнирно-соединенных звеньев захватного устройства от системы координат O₄x₄y₄z₄ к системе O₁x₁y₁z₁, применяя выражения (2.1) и (2.2), получаем

(2.3)

${{М }_{{{\mathbf{04}}}}} = \left. {\left[ {\left. {\begin{array}{*{20}{c}} {{{a}_{{11}}}}&{{{a}_{{12}}}}&{{{a}_{{13}}}} \\ {{{a}_{{21}}}}&{{{a}_{{22}}}}&{{{a}_{{23}}}} \\ {{{a}_{{31}}}}&{{{a}_{{32}}}}&{{{a}_{{33}}}} \\ \hline 0&0&0 \end{array}} \right|} \right.\begin{array}{*{20}{c}} {{{x}_{M}} - b\sin {\psi }\cos {\gamma } - (a + b\cos {\psi })\cos {\alpha }\sin {\gamma }} \\ {{{y}_{M}} - b\sin {\psi }\sin {\gamma } + (a + b\cos {\psi })\cos {\alpha }\cos {\gamma }} \\ {{{z}_{M}} + (a + b\cos {\psi })\sin {\alpha }} \\ 1 \end{array}} \right],$

где a_pq – направляющие косинусы, определяющие ориентацию рабочего органа захватного устройства в пространстве:

${{a}_{{11}}} = {\text{sin}}\beta ({\text{cos}}\gamma {\text{cos}}\psi --{\text{sin}}\gamma {\text{cos}}\alpha {\text{sin}}\psi ) + {\text{sin}}\gamma {\text{cos}}\beta {\text{sin}}\alpha ;$

${{a}_{{12}}} = {\text{cos}}\beta ({\text{cos}}\gamma {\text{cos}}\psi --{\text{sin}}\gamma {\text{cos}}\alpha {\text{ sin}}\psi )--{\text{sin}}\gamma {\text{sin}}\beta {\text{sin}}\alpha ;$

${{a}_{{13}}} = --{\text{cos}}\gamma {\text{ sin}}\psi --{\text{sin}}\gamma {\text{cos}}\psi {\text{cos}}\alpha ;$

(2.4)

${{a}_{{21}}} = {\text{sin}}\beta ({\text{sin}}\gamma {\text{cos}}\psi + {\text{cos}}\gamma {\text{cos}}\alpha {\text{sin}}\psi )--{\text{cos}}\gamma {\text{cos}}\beta {\text{sin}}\alpha ;$

${{a}_{{22}}} = {\text{cos}}\beta ({\text{sin}}\gamma {\text{cos}}\psi + {\text{cos}}\gamma {\text{cos}}\alpha {\text{ sin}}\psi ) + {\text{cos}}\gamma {\text{sin}}\beta {\text{sin}}\alpha ;$

${{a}_{{23}}} = {\text{cos}}\gamma {\text{cos}}\psi {\text{cos}}\alpha --{\text{sin}}\gamma {\text{sin}}\psi ;$

${{a}_{{31}}} = {\text{cos}}\beta {\text{cos}}\alpha + {\text{sin}}\psi {\text{sin}}\beta {\text{sin}}\alpha ;$

${{a}_{{32}}} = {\text{cos}}\beta {\text{sin}}\psi {\text{sin}}\alpha --{\text{cos}}\alpha {\text{sin}}\beta ;$

${{a}_{{33}}} = {\text{cos}}\psi {\text{sin}}\alpha .$

Тогда из (2.3) и (2.4) следует

(2.5)

$\left\{ \begin{gathered} {{x}_{E}} = {{x}_{M}} + b{{a}_{{13}}} - a\cos \alpha \sin \gamma , \hfill \\ {{y}_{E}} = {{y}_{M}} + b{{а }_{{23}}} + a\cos \alpha \cos \gamma , \hfill \\ {{z}_{E}} = {{z}_{M}} + b{{а }_{{33}}} + a\sin \alpha , \hfill \\ {{а }_{{33}}} = \cos \psi \sin \alpha , \hfill \\ {{а }_{{23}}} = \cos \gamma \cos \psi \cos \alpha - \sin \gamma \sin \psi , \hfill \\ \end{gathered} \right.$

где a, b – геометрические параметры захватного устройства (рис. 2).

Из выражений (2.5) видно, что координаты точки E [x_E(t), y_E(t), z_E(t)] не зависят от угла β. Закон изменения угла β собственного вращения рабочего органа зависит от вида технологического процесса.

Программную траекторию точки E разбиваем на n участков через интервалы времени Δτ. Значения координат x_E(t_i), y_E(t_i), z_E(t_i) точки E рабочего органа захвата и направляющих косинусов α_pq(t_i) в момент времени ${{t}_{i}} = i \times \Delta \tau $, $i = \overline {0,n} $, известны.

Необходимо найти значения обобщенных координат l_k(t_i), $k = \overline {{\text{1,4}}} $, манипулятора-трипода и обобщенных координат α(t_i), ψ(t_i) захватного устройства в моменты времени t_i. С этой целью из системы (2.5) определяем координаты точки M – x_M(t_i), y_M(t_i), z_M(t_i), углы поворота звеньев манипулятора захватного устройства α(t_i), ψ(t_i) и конструктивный угол γ(t_i).

По методике, изложенной в работе [13], задаемся углом γ' (0.2). В первом приближении принимаем $\gamma {\text{'}} = {\text{arctg(}} - {{x}_{E}}({{t}_{i}}){\text{/}}{{y}_{E}}({{t}_{i}}){\text{)}}$. Затем из уравнений (2.2) и (2.3) системы (2.5) по формулам

(2.6)

${{\Psi }_{{1,2}}} = {\text{arcsin(}}--{{a}_{{23}}}{\text{sin}}\gamma \pm {{a}_{{13}}}{\text{cos}}\gamma {\text{)}},\quad \alpha = {\text{arcsin(}}{{a}_{{33}}}{\text{/cos}}\psi {\text{)}}$

определяем углы ψ и α, а из первых трех уравнений системы (2.5) находим координаты $x_{M}^{'}$, $y_{M}^{'}$, $z_{M}^{'}$ точки M.

Для исключения неоднозначности определения конфигурации манипулятора-трипода для заданного положения захвата вводятся критерии качества управления движением манипулятора [5–7]. В [6] отмечается, что оптимизационная постановка обратной задачи о положении звеньев манипулятора часто является условной. Оптимизация нужна для разработки алгоритма, позволяющего определить конфигурацию манипулятора из множества допустимых. Можно считать рациональным подход к выбору критерия качества, позволяющий достаточно быстро вычислить обобщенные координаты манипулятора, возможность учитывать ограничения на подвижность звеньев и наличия в его выражении весовых коэффициентов [5]. В данной статье предлагается угол φ_i поворота основания манипулятора-трипода находить из условия минимума критерия обобщенной энергии [5, 7] в виде квадратичной функции

(2.7)

$\Phi ({{\varphi }_{i}}) = {{c}_{1}}{{[{{l}_{{1i}}}({{\varphi }_{i}}){\text{ }} - {{l}_{{10}}}]}^{2}} + {{c}_{4}}{{[{{l}_{{4i}}}({{\varphi }_{i}}) - {{l}_{{40}}}]}^{2}}$

с ограничениями в виде неравенств

(2.8)

${{\varphi }_{{\min }}} \leqslant \varphi _{i}^{'} \leqslant {{\varphi }_{{\max }}},$

где l_1i(φ_i), l_4i(φ_i) – значения длин исполнительных звеньев в момент времени t_i; c₁, c₄ – весовые коэффициенты; φ_min, φ_max – минимальное и максимальное допустимые значения угла поворота основания манипулятора – трипода (рис. 1); $\varphi _{i}^{'}$ – оптимальное значение угла поворота.

Условия (2.8) накладывают ограничения на максимальное и минимальное значения длины исполнительного звена l₄. Значения весовых коэффициентов c₁, c₄ следует выбирать так, чтобы обобщенным координатам l₁(φ), l₄(φ), усилия в которых большие, соответствовали и большие значения весовых коэффициентов. Результаты исследований показывают [10], что в манипуляторе–триподе звенья l₁ и l₄ нагружены приблизительно одинаково. Однако в процессе функционирования манипулятора выбором значений весовых коэффициентов можно добиться наиболее выгодного критерия. В нижеприведенном примере расчета значения весовых коэффициентов приняты равными единице.

Целевая функция Лагранжа имеет вид [14]

(2.9)

$\Phi {\text{*}} = {{c}_{1}}{{({{l}_{{1i}}} - {{l}_{{10}}})}^{2}} + {{c}_{4}}{{({{l}_{{4i}}} - {{l}_{{40}}})}^{2}} + {{\lambda }_{1}}(u_{1}^{2} + {{\varphi }_{i}} - {{\varphi }_{{\max }}}) + {{\lambda }_{2}}(u_{2}^{2} + {{\varphi }_{{\min }}} - {{\varphi }_{i}}),$

где $u_{1}^{2}$, $u_{2}^{2}$ – вспомогательные переменные; λ₁, λ₂ – множители Лагранжа.

Необходимые условия минимума функции (2.7) записываются в форме [14]

(2.10)

$\frac{{\partial \Phi {\text{*}}}}{{\partial \varphi }} = {{c}_{1}}\frac{{\partial {{{({{l}_{{1i}}} - {{l}_{{10}}})}}^{2}}}}{{\partial \varphi }} + {{c}_{4}}\frac{{\partial {{{({{l}_{{4i}}} - {{l}_{{40}}})}}^{2}}}}{{\partial \varphi }} + {{\lambda }_{1}} - {{\lambda }_{2}} = 0,$

(2.11)

$\begin{gathered} {{\lambda }_{1}} = 0\quad {\text{п р и }}\quad \varphi _{i}^{'} < {{\varphi }_{{\max }}};\quad {{\lambda }_{2}} = 0\quad {\text{п р и }}\quad \varphi _{i}^{'} > {{\varphi }_{{{\text{min}}}}}; \\ {{\lambda }_{1}} > 0\quad {\text{п р и }}\quad \varphi _{i}^{'} = {{\varphi }_{{\max }}};\quad {{\lambda }_{2}} > 0\quad {\text{п р и }}\quad \varphi _{i}^{'} = {{\varphi }_{{{\text{min}}}}}. \\ \end{gathered} $

Так как функция Лагранжа (2.9) выпуклая, а множители ${{\lambda }_{{\text{1}}}} \geqslant 0$, ${{\lambda }_{{\text{2}}}} \geqslant 0$, то необходимые условия (2.10), (2.11) являются достаточными.

Конкретная форма кривой (2.7) зависит от координат начальной и конечной точек захвата (0.1). Расчеты показали, что для конкретного манипулятора [3, 4] при значениях конечной координаты захвата по оси Oy, близкой к нулю, эффективным становится ограничение на максимальный угол поворота основания λ₁ > 0, λ₂ = 0. А при значениях конечной координаты захвата по оси Oz, меньше –420 мм, эффективным становится ограничение на минимальный угол поворота основания λ₂ > 0, λ₁ = 0.

Определив из (2.10), (2.11) угол $\varphi _{i}^{'}$, из (0.2) находим конструктивный угол $\gamma _{i}^{*}$.

Найденное значение угла $\gamma _{i}^{*}$ принимается за новое начальное значение, и расчет повторяется в последовательности, начиная с выражения (2.6), до тех пор, пока |$\gamma _{{p + 1,i}}^{*}$ – $\gamma _{{p,i}}^{*}$| ≤ ε, p = 0, 1, 2… Здесь ε > 0 – выбранная точность вычисления. По окончательным значениям углов φ_i и γ_i вычисляются координаты точки M(x_M, y_M, z_M,) (2.5) и длины звеньев l_ki, $k = \overline {{\text{1,4}}} $, выражения (0.1). Результаты последних вычислений и определяют искомую конфигурацию l_ki,, φ_i, α_i, Ψ_i манипулятора (рис. 2) в заданный момент времени t_i.

Разбивая заданную траекторию точки E на n участков через интервалы времени Δτ, по вышеизложенной методике находится последовательность значений обобщенных координат l_k(t_i), манипулятора–трипода и обобщенных координат α(t_i), Ψ(t_i) захватного устройства. Зная значения обобщенных координат в моменты времени t_i, можно для каждой обобщенной координаты, для каждого отрезка провести интерполяцию сплайнами [15], т.е. построить полином, выражающий обобщенную координату как функцию времени. Полиномиальная интерполяция является наиболее простой. Ее эффективно применять для монотонных траекторий в тех случаях, когда на основе малого числа заданных точек необходимо быстро получить приемлемый результат. Задача сплайновой интерполяции сводится к решению двух подзадач: расчет коэффициентов сплайна и последующая аппроксимация значений функции в заданные моменты времени.

Для любого отрезка функций l_k(t), α(t), Ψ(t) на каждом конце имеются граничные условия. Граничные условия на значения скорости и ускорения являются условиями непрерывности для каждого из промежуточных участков соответствующих функций времени. Для каждого из крайних участков имеются граничные условия на перемещение, скорость и ускорение. В этом случае первый и последний отрезки траектории интерполируются полиномами четвертого порядка, а промежуточные отрезки – полиномами третьего порядка [16].

Рассмотрим отрезок траектории, описываемый многочленом

(2.12)

${{\theta }_{i}}(\tau ) = {{A}_{{i4}}}{{\tau }^{4}} + {{A}_{{i3}}}{{\tau }^{3}} + {{A}_{{i2}}}{{\tau }^{2}} + {{A}_{{i1}}}\tau + {{A}_{{i0}}},\quad\quad\quad\quad$

где θ_i(τ) – одна из обобщенных координат манипулятора как функция времени τ на i-участке изменения функции; $\tau = t{\text{/}}{{T}_{i}}$ – безразмерное время, т.е. 1 ≥ τ ≥ 0; T_i – время перемещения на i-участке изменения функции θ_i(τ); A_0i…A_i4 – коэффициенты полинома для i-участка изменения функции θ_i(τ).

Из выражения (2.12) следуют соотношения, связывающие коэффициенты полиномов со значениями обобщенной координаты θ_i(τ) и ее производных ${{\dot {\theta }}_{i}}(\tau )$, ${{\ddot {\theta }}_{i}}(\tau )$ в (n + 1) узловых точках $i = \overline {{\text{0,}}n} $.

Для первого отрезка траектории, подставляя значение τ = 0, получим

(2.13)

${{A}_{{10}}} = {{\theta }_{1}}(0) = {{\theta }_{{10}}},\quad {{A}_{{11}}} = {{\dot {\theta }}_{1}}(0) = {{\dot {\theta }}_{{10}}} = 0,\quad {{A}_{{12}}} = {{\ddot {\theta }}_{1}}(0) = {{\ddot {\theta }}_{{10}}} = 0.$

При τ = 1 имеем на правом конце

(2.14)

$\Delta {{\theta }_{1}}(0) = {{\theta }_{1}}(1) - {{\theta }_{1}}(0) = {{A}_{{14 + }}}{{A}_{{13}}},$

(2.15)

${{T}_{1}}{{\dot {\theta }}_{1}}(1) = 4{{A}_{{14}}} + 3{{A}_{{13}}},$

(2.16)

$T_{1}^{2}{{\ddot {\theta }}_{1}}(1) = 12{{A}_{{14}}} + 6{{A}_{{13}}}.$

Для i-го промежуточного участка закона изменения θ_i(τ) полином (2.12) принимает вид

(2.17)

${{\theta }_{i}}(\tau ) = + {{A}_{i}}_{3}{{\tau }^{3}} + {{A}_{i}}_{2}{{\tau }^{2}} + {{A}_{i}}_{1}\tau + {{A}_{i}}_{0}.$

С учетом граничных условий на скорость и ускорение, определяющих условия непрерывности функции времени θ_i(τ), получаем

(2.18)

${{\theta }_{i}}(0) = {{\theta }_{{i - 1}}}(1) = {{A}_{i}}_{0},$

(2.19)

$\Delta {{\theta }_{i}}(\tau ) = {{\theta }_{i}}(1) - {{\theta }_{{i - }}}_{1}(0) = {{A}_{i}}_{3}{{A}_{i}}_{2}{{A}_{i}}_{1},$

(2.20)

${{T}_{i}}{{\dot {\theta }}_{{i - 1}}}(1) = {{A}_{{i1}}},$

(2.21)

$T_{i}^{2}{{\ddot {\theta }}_{{i - 1}}}(1) = 2{{A}_{{i2}}},$

(2.22)

${{T}_{i}}{{\dot {\theta }}_{i}}(1) = 3{{A}_{{i3}}} + 2{{A}_{{i2}}} + {{A}_{{i1}}},$

(2.23)

$T_{i}^{2}{{\ddot {\theta }}_{i}}(1) = 6{{A}_{{i3}}} + 2{{A}_{{i2}}}.$

Для последнего отрезка закона изменения ${{\theta }_{n}}(\tau )$ полином определяем как функцию

(2.24)

${{\theta }_{n}}(\tau ) = {{A}_{n}}_{4}{{\tau }^{4}} + {{A}_{n}}_{3}{{\tau }^{3}} + {{A}_{n}}_{2}{{\tau }^{2}} + {{A}_{n}}_{1}\tau + {{A}_{n}}_{0}.$

Подставляя значение τ = 0, получим

(2.25)

${{A}_{{n0}}} = {{\theta }_{n}}(0) = {{\theta }_{{n - 1}}}(1) = {{A}_{{n0}}},\quad {{\dot {\theta }}_{n}}(0) = {{\dot {\theta }}_{{n - 1}}}(1) = {{T}_{n}}{{A}_{{n1}}},\quad {{\ddot {\theta }}_{n}}(0) = {{\ddot {\theta }}_{{n - 1}}}(1) = T_{n}^{2}2{{A}_{{n2}}}.$

При τ = 1 имеем на правом конце

(2.26)

${{\theta }_{n}} = {{A}_{n}}_{4} + {{A}_{n}}_{3} + {{A}_{n}}_{2} + {{A}_{n}}_{1} + {{A}_{n}}_{0},$

(2.27)

${{\theta }_{n}}(1) = 4{{A}_{n}}_{4} + 3{{A}_{n}}_{3} + 2{{A}_{n}}_{2} + {{A}_{n}}_{1} = 0,$

(2.28)

${{\theta }_{n}}\left( 1 \right) = 12{{A}_{n}}_{4} + 6{{A}_{n}}_{3} + 2{{A}_{n}}_{2} = 0.$

3. Пример реализации метода. Анализ технологических операций показывает, что одним из распространенных перемещений рабочего органа является прямолинейное поступательное перемещение с заданной ориентацией в пространстве. Задаемся законом перемещения точки E рабочего органа по прямой линии из начальной точки, с координатами x_E(0) = –316.4 мм, y_E(0) = = 1437 мм, z_E(0) = 740 мм в конечную точку с координатами x_E(T) = 300 мм, y_E(T) = 1437 мм, z_E(T) = –100 мм, т.е. перемещение точки происходит в плоскости, параллельной неподвижной плоскости Oxz, y = const, за время T = 12 c. Угол поворота основания может изменяться в пределах от –0.323 до 0.53 рад. Закон изменения дуговой координаты принимаем в форме [6], который обеспечивает равенство нулю скоростей и ускорений в начальной и конечной точках траектории:

(3.1)

$S(t) = (10 - 15t{\text{/}}T + 6{{t}^{2}}{\text{/}}{{T}^{2}})\frac{{{{t}^{3}}}}{{{{T}^{3}}}}{{S}_{e}},\quad T \geqslant t \geqslant 0,$

где ${{S}_{e}} = \sqrt {{{{({{x}_{E}}(T) - {{x}_{E}}(0))}}^{2}} + {{{({{y}_{E}}(T) - {{y}_{E}}(0))}}^{2}} + {{{({{z}_{E}}(T) - {{z}_{E}}(0))}}^{2}}} $ – длина траектории.

Скорости и ускорения точки E в начальной и конечной точках траектории равны нулю. На рис. 1 показана траектория точки E.

Пространственное положение рабочего органа задаем направляющими косинусами a₂₃ = 1, a₃₃ = 0, a₁₃ = 0 подвижной системы координат O₄x₄y₄z₄ рабочего органа относительно неподвижной системы координат Oxyz (рис. 3). Из (2.6) следует, что при выбранном программном перемещении рабочего органа во все время движения α = 0, Ψ = –γ. Выбор количества и расположения узловых точек зависит от вида программного перемещения захвата, технологического процесса и от требуемой точности отслеживания программной траектории. В рассматриваемом примере разбиваем весь отрезок длиной S_e на три части, n = 3 – число отрезков. Число узловых точек рассматриваем четыре: $m = \overline {0,3} $. Через равный интервал Δt = T/3 находим координаты второй и третьей узловых точек (координаты начальной и конечной точек известны) [17]:

(3.2)

$\begin{gathered} {{x}_{E}}({{t}_{i}}) = S({{t}_{i}}){\text{/}}{{K}_{X}} + {{x}_{E}}(0),\quad {{y}_{E}}({{t}_{i}}) = {{y}_{E}}(0),\quad {{z}_{E}}(\Delta t) = S({{t}_{i}}){\text{/}}{{K}_{Z}} + {{z}_{E}}(0); \\ {{K}_{X}} = \sqrt {1 + K_{1}^{2} + K_{2}^{2}} ;\quad {{K}_{Y}} = \sqrt {1 + 1{\text{/}}K_{1}^{2} + K_{3}^{2}} ;\quad {{K}_{Z}} = \sqrt {1 + 1{\text{/}}K_{2}^{2} + 1{\text{/}}K_{3}^{2}} ; \\ {{K}_{1}} = \Delta y{\text{/}}\Delta x;\quad {{K}_{2}} = {{\Delta z} \mathord{\left/ {\vphantom {{\Delta z} {\Delta x}}} \right. \kern-0em} {\Delta x}};\quad {{K}_{3}} = \Delta z{\text{/}}\Delta y; \\ \Delta x = {{x}_{E}}(T) - {{x}_{E}}(0),\quad \Delta y = {{y}_{E}}(T) - {{y}_{E}}(0),\quad \Delta z = {{z}_{E}}(T) - {{z}_{E}}(0). \\ \end{gathered} $

Рис. 3.

Ориентация в пространстве рабочего органа захвата манипулятора

Определяем [13] конфигурацию манипулятора в начальный момент времени l_k(0) = l_k0, $k = \overline {{\text{1,4}}} $, α(0) = 0, Ψ(0) = Ψ₀ = –γ₀. Затем, воспользовавшись методикой (2.5)–(2.11), находим конфигурацию манипулятора во второй, третьей и четвертой узловых точках. Таким образом, в моменты времени t_i = 0, T/3, 2T/3, T известны координаты точки M(x_M, y_M, z_M), угол φ(t_i) поворота основания манипулятора-трипода и угол Ψ(t_i) = –γ(t_i). Тогда выражения (0.1), (0.2) позволяют в эти моменты времени найти длины исполнительных цилиндров l_k(t_i), $k = \overline {{\text{1,4}}} $. Полученные значения используются для интерполяции законов перемещения приводов манипулятора. Воспользовавшись выражениями (2.13)–(2.28), получаем систему линейных алгебраических уравнений относительно коэффициентов A_i0…A_i4 полиномов типа (2.12) и (2.17):

(3.3)

$\left\{ \begin{gathered} {{A}_{{10}}} = {{l}_{{k1}}}(0), \hfill \\ {{A}_{{14}}} + {{A}_{{13}}} = {{l}_{{k1}}}(1) - {{l}_{{k1}}}(0), \hfill \\ 4{{A}_{{14}}} + 3{{A}_{{13}}} - {{A}_{{21}}}\frac{{{{T}_{1}}}}{{{{T}_{2}}}} = 0, \hfill \\ 6{{A}_{{14}}} + 3{{A}_{{13}}} - {{A}_{{22}}}\frac{{T_{1}^{2}}}{{T_{2}^{2}}} = 0, \hfill \\ {{A}_{{20}}} = {{l}_{{k2}}}(0) = {{l}_{{k1}}}(1), \hfill \\ {{A}_{{23}}} + {{A}_{{22}}} + {{A}_{{21}}} = {{l}_{{k2}}}(1) - {{l}_{{k2}}}(0), \hfill \\ 3{{A}_{{23}}} + 2{{A}_{{22}}} + {{A}_{{21}}} - {{A}_{{31}}}\frac{{{{T}_{2}}}}{{{{T}_{3}}}} = 0, \hfill \\ 3{{A}_{{23}}} + {{A}_{{22}}} - {{A}_{{32}}}\frac{{T_{2}^{2}}}{{T_{3}^{2}}} = 0, \hfill \\ {{A}_{{30}}} = {{l}_{{k3}}}(0) = {{l}_{{k2}}}(1), \hfill \\ {{A}_{{34}}} + {{A}_{{33}}} + {{A}_{{32}}} + {{A}_{{31}}} + {{A}_{{30}}} = {{l}_{{k3}}}(1), \hfill \\ 4{{A}_{{34}}} + 3{{A}_{{33}}} + 2{{A}_{{32}}} + {{A}_{{31}}} = 0, \hfill \\ 12{{A}_{{34}}} + 6{{A}_{{33}}} + 2{{A}_{{32}}} = 0. \hfill \\ \end{gathered} \right.$

Решение системы (3.3) для каждых значений l_k(t_i), $k = \overline {{\text{1,4}}} $ определяет три полинома (2.12), (2.17), которые интерполируют законы изменения длин исполнительных цилиндров непрерывными функциями времени l_k(t_i). Для нахождения непрерывной функции изменения угла $\psi (t)$ в системе (3.3) значения l_k(t_i) заменяются значениями Ψ(t_i). В результате решения этой системы получим коэффициенты A_i0…A_i4 трех полиномов типа (2.12), (2.17), которые интерполируют функцию Ψ(t). В рассматриваемом примере принято T₁ = T₂ = T₃.

В результате расчетов получено для каждых значений l_k(t_i), Ψ(t_i) значения трех полиномов для первого, промежуточного и последнего отрезков траектории:

${{l}_{1}}(t) = \left\{ \begin{gathered} 43.84{{\tau }^{4}} + ( - 50.28{{\tau }^{3}}) + 1400, \hfill \\ - 72.78{{\tau }^{3}} + 112.23{{\tau }^{2}} + 24.54\tau + 1393.57, \hfill \\ 137.22{{\tau }^{4}} + ( - 355.688){{\tau }^{3}} + 243.76{{\tau }^{2}} + 30.67\tau + 1457.56; \hfill \\ \end{gathered} \right.$

${{l}_{2}}(t) = \left\{ \begin{gathered} 130.21{{\tau }^{4}} + ( - 259.243{{\tau }^{3}}) + 1500, \hfill \\ 31.38{{\tau }^{3}} + 3.53{{\tau }^{2}} + ( - 256.89)\tau + 1370.97, \hfill \\ 119.24{{\tau }^{4}} + ( - 369.87){{\tau }^{3}} + 394.16{{\tau }^{2}} + ( - 155.68)\tau + 1148.99; \hfill \\ \end{gathered} \right.$

(3.4)

${{l}_{3}}(t) = \left\{ \begin{gathered} 129.88{{\tau }^{4}} + ( - 206.35){{\tau }^{3}} + 1352, \hfill \\ - 95.40{{\tau }^{3}} + 160.25{{\tau }^{2}} + ( - 99.515)\tau + 1275.53, \hfill \\ 242.35{{\tau }^{4}} + ( - 668.00){{\tau }^{3}} + 549.91{{\tau }^{2}} + ( - 65.22)\tau + 1240.87; \hfill \\ \end{gathered} \right.$

${{l}_{4}}(t) = \left\{ \begin{gathered} 45.51{{\tau }^{4}} + ( - 52.701){{\tau }^{3}} + 911.89, \hfill \\ - 74.95{{\tau }^{3}} + 114.91{{\tau }^{2}} + 23.89\tau + 904.69, \hfill \\ 140.14{{\tau }^{4}} + ( - 364.1){{\tau }^{3}} + 251.42{{\tau }^{2}} + 28.86\tau + 968.55; \hfill \\ \end{gathered} \right.$

$\psi (t) = - \gamma (t) = \left\{ \begin{gathered} - 0.046{{\tau }^{4}} + 0.13{{\tau }^{3}} - 0.214, \hfill \\ - 0.072{{\tau }^{3}} + 0.115{{\tau }^{2}} + 0.206\tau - 0.13, \hfill \\ 0.099{{\tau }^{4}} + ( - 0.16){{\tau }^{3}} - 0.022{{\tau }^{2}} + 0.219\tau + 0.119. \hfill \\ \end{gathered} \right.$

Для оценки точности отслеживания приводами манипулятора заданных программных перемещений захвата манипулятора строятся траектория и закон перемещения характерной точки E[x_E(t), y_E(t), z_E(t)] рабочего органа манипулятора (рис. 1) по интерполяционным (3.4) законам изменения длин исполнительных цилиндров. С этой целью, решая прямую задачу о положениях, определяем координаты точки M(x_M, y_M, z_M) через обобщенные координаты манипулятора l_k(t), $k = \overline {{\text{1,4}}} $ [18]:

(3.5)

$\left\{ {\begin{array}{*{20}{l}} {{{x}_{M}} = \frac{{l_{3}^{2} - l_{2}^{2}}}{{4OB}},} \\ {{{y}_{M}} = {{{\left[ {l_{1}^{2} - \frac{{{{{(l_{3}^{2} - l_{2}^{2})}}^{2}}}}{{16O{{B}^{2}}}} - \frac{{(A - O{{B}^{2}} - z_{A}^{2})}}{{4z_{A}^{2}}}} \right]}}^{{\frac{1}{2}}}}\cos {\varphi } - \left( {\frac{{A - O{{B}^{2}} + z_{A}^{2}}}{{2{{z}_{A}}}}} \right)\sin {\varphi },} \\ {{{z}_{M}} = {{{\left[ {l_{1}^{2} - \frac{{{{{(l_{3}^{2} - l_{2}^{2})}}^{2}}}}{{16O{{B}^{2}}}} - \frac{{(A - O{{B}^{2}} - z_{A}^{2})}}{{4z_{A}^{2}}}} \right]}}^{{\frac{1}{2}}}}\sin {\varphi } + \left( {\frac{{A - O{{B}^{2}} + z_{A}^{2}}}{{2{{z}_{A}}}}} \right)\cos {\varphi },} \end{array}} \right.$

где

$\begin{gathered} \varphi = \arcsin \frac{{O{{K}^{2}} + D{{K}^{2}} + O{{A}^{2}} - l_{4}^{2}(t)}}{{2OA\sqrt {D{{K}^{2}} + O{{K}^{2}}} }} + \nu , \\ A = - l_{1}^{2}(t) + 0.5l_{2}^{2}(t) + 0.5l_{3}^{2}(t), \\ \nu = \arcsin \frac{{DK}}{{\sqrt {D{{K}^{2}} + O{{K}^{2}}} }},\quad {{z}_{A}} = OA\cos \varphi . \\ \end{gathered} $

Затем, воспользовавшись выражениями (2.5), находим законы изменения координат точки E[x_E(t), y_E(t), z_E(t)] и строим уравнение ее траектории z_E(x_E) и закон перемещения по траектории (3.2)

$S{\text{*}}(t) = {{K}_{X}}[{{x}_{E}}(t) - {{x}_{E}}(0)].$

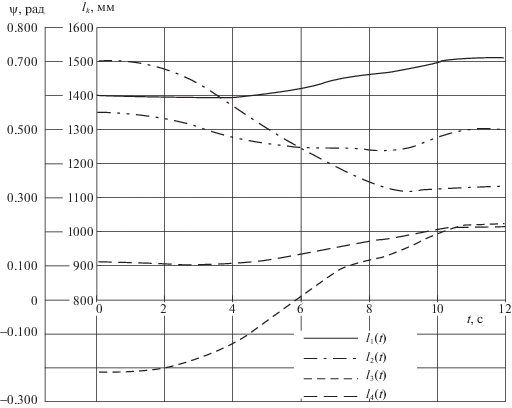
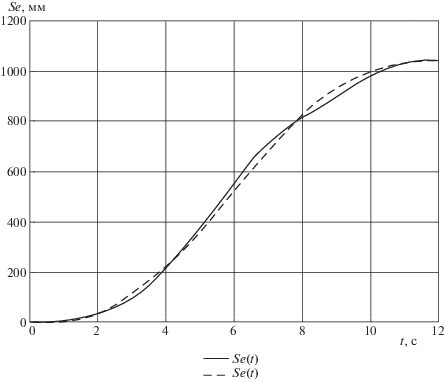
На рис. 4 приведены зависимости (3.4) длин исполнительных органов и угла Ψ(t) от времени, на рис. 5 представлены функции времени изменения координат точки E[x_E(t), y_E(t), z_E(t)], построенные по заданным программным перемещениям и по законам, полученным в результате интерполяции, а на рис. 6 – программный закон изменения дуговой координаты (3.1) и реализуемый при изменении длин исполнительных цилиндров по выражениям (3.5).

Рис. 4.

Зависимости длин исполнительных органов l(t) и угла Ψ(t) от времени

Рис. 5.

Траектории точки E xe, ye, ze, построенные по интерполяционным законам и по заданным программным перемещениям

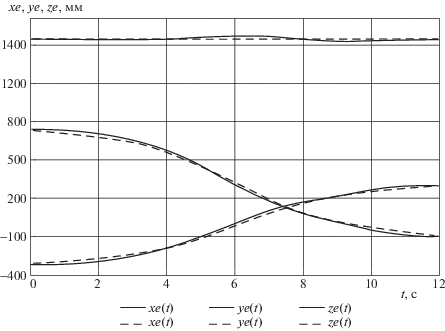
Рис. 6.

Программный закон изменения дуговой координаты Se, построенный по интерполяционным законам и по заданным программным перемещениям

Точность аппроксимации программной траектории (рис. 5) при формировании управляющих перемещений исполнительных цилиндров интерполяционными полиномами возможно оценить отношением абсолютного отклонения от траектории к длине траектории:

$\quad\delta = \max {\text{|}}\Delta z{\text{|/}}K\,\,({\text{в р а с с м о т р е н н о м п р и м е р е }}\,\delta \,{\text{ = }}\,{\text{0}}{\text{.001}}).$

Если полученная точность не удовлетворяет требованиям качественного выполнения технологического процесса, необходимо увеличить число узловых точек на программной траектории. Скорость и ускорение захватного устройства по траектории определяются как первая и вторая производные сформированных полиномов.

Заключение. Предложенная методика расчета аналитических зависимостей законов изменения длин управляющих исполнительных звеньев манипулятора параллельно-последовательной структуры интерполяционными полиномами позволяет сформировать базу знаний лингвистического аппроксиматора [8], базу динамических моделей [19] и разработать программную и позиционную с обратными связями по положению системы управления, обеспечивающие отслеживание программных траекторий [20, 21]. Задающий сигнал для каждого исполнительного звена манипулятора получается в результате вычисления полиномов соответствующих участков траектории для заданных интервалов времени.

Расчеты показывают, что при полиноминальной интерполяции закон изменения скорости перемещения захвата по траектории не соответствует программному. Увеличение числа узловых точек не позволяет обеспечить монотонное изменение скорости вследствие неизбежного наличия локальных экстремумов кривой изменения дуговой координаты [16].

Список литературы

Глазунов В.А., Колискор А.Ш., Крайнев А.Ф. Пространственные механизмы параллельной структуры. М.: Наука, 1991. 95 с.
Герасун В.М., Пындак В.И., Несмиянов И.А., Дяшкин-Титов В.В., Павловский В.Е. Манипуляторы для мобильных роботов. Концепции и принципы проектирования: Препринты ИПМ им. М.В. Келдыша. 2012. № 44. 24 с.
Герасун В.М., Жога В.В., Несмиянов И.А., Воробьева Н.С., Дяшкин-Титов В.В. Определение зоны обслуживания мобильного манипулятора-трипода // Машиностроение и инженерное образование. 2013. № 3. С. 2–8.
Жога В.В., Дяшкин-Титов В.В., Дяшкин А.В., Воробьева Н.С., Несмиянов И.А., Иванов А.Г. Манипулятор-трипод параллельно-последовательной структуры: Пат. 2616493 Российская Федерация, МПК В66С 23/44. Опубл. 17.04.2017. Бюл. № 11.
Кобринский А.А., Кобринский А.Е. Манипуляционные системы роботов. М.: Наука, 1985. 343 с.
Коловский М.З., Слоущ А.В. Основы динамики промышленных роботов. М.: Наука. Физматлит, 1998. 240 с.
Динамика управления роботами роботы / Под ред. Е.И. Юревича, В.В. Козлова, В.П. Макарычева и др. М.: Наука. Физматлит, 1984. 336 с.
Интеллектуальные роботы / Под ред. Е.И. Юревича, И.А. Каляева, В.М. Лохина, И.М. Макарова и др. М.: Машиностроение, 2007. 360 с.
Шипилевский Г.Б., Викторов А.И. Автоматизация мобильных сельскохозяйственных агрегатов // Механизация и электрификация сельского хозяйства. 2001. № 3. С. 28–29.
Zhoga V., Gavrilov A., Gerasun V., Nesmianov I., Pavlovsky V., Skakunov V., Bogatyrev V., Golubev D., Dyashkin-Titov V., Vorob’eva N. Walking Mobile Robot with Manipulator-Tripod // Proc. Romansy 2014 XX CISM-IFToMM Sympos. on Theory and Practice of Robots and Manipulators – Series: Mechanisms and Machine Science. V. 22. Moscow: Springer International Publishing Switzerland, 2014. P. 463–471.
Жога В.В., Герасун В.М., Несмиянов И.А., Воробьева Н.С., Дяшкин-Титов В.В. Динамический синтез оптимальных программных движений манипулятора-трипода // Проблемы машиностроения и надежности машин. 2015. № 2. С. 85–92.
Корендясев А.И., Саламандра Б.Л., Тывес Л.И. Теоретические основы робототехники: в 2-х кн. Кн. 1. М.: Наука, 2006. 383 с.
Жога В.В., Дяшкин-Титов В.В., Несмиянов И.А., Воробьева Н.С. Задача позиционирования манипулятора параллельно-последовательной структуры с управляемым захватным устройством // Мехатроника, автоматизация, управление. 2016. № 8. Т. 17. С. 525–530.
Брайсон А., Хо Ю-ши. Прикладная теория оптимального управления. М.: Мир, 1972. 544 с.
Зенкевич С.Л., Ющенко А.С. Основы управления манипуляционными роботами. М.: МГТУ им. Н.Э. Баумана, 2004. 449 с.
Пол Р. Моделирование, планирование траекторий и управление движением робота-манипулятора / Пер. с англ. М.: Наука. Физматлит, 1976. 104 с.
Воробьева Н.С., Дяшкин-Титов В.В., Жога В.В., Несмиянов И.А. Динамика параллельно-последовательной структуры на основе трипода // Машиностроение и инженерное образование. 2017. № 3. С. 32–41.
Несмиянов И.А., Жога В.В., Скакунов В.Н., Воробьева Н.С., Дяшкин-Титов В.В., Бочарников В.С. О неустойчивых режимах работы электропривода манипулятора // Проблемы машиностроения и надежности машин. 2017. № 3. С. 18–25.
Воробьева Н.С., Жога В.В., Дяшкин-Титов В.В., Дяшкин А.В. Разработка базы моделей манипулятора параллельно-последовательной структуры // Изв. ЮФУ. Технические науки. 2017. № 9 (194). С. 143–152.
Крутько П.Д., Лакота Н.А. Метод обратных задач динамики в теории конструирования алгоритмов управления манипуляционных роботов. Осуществление назначенных траекторий // Изв. АН СССР. Техн. кибернетика. 1987. № 4.
Nesmiyanov I., Zhoga V., Skakunov V., Terekhov S., Vorob’eva N., Dyashkin-Titov V., Fares Ali Hussein Al-hadsha. Synthesis of Control Algorithm and Computer Simulation of Robotic Manipulator-Tripod // Communications in Computer and Information Science. Volgograd: Springer International Publishing Switzerland, 2015. P. 392–404.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал