Известия РАН. Теория и системы управления, 2019, № 3, стр. 34-47
МЕТОД ПАРАМЕТРИЧЕСКОЙ ОПТИМИЗАЦИИ НЕЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ СОВМЕСТНОГО ОЦЕНИВАНИЯ И УПРАВЛЕНИЯ
Л. Г. Давтян a, А. В. Пантелеев a, *
a МАИ (национальный исследовательский ун-т)
Москва, Россия
* E-mail: avpanteleev@inbox.ru
Поступила в редакцию 26.11.2018
После доработки 25.01.2019
Принята к публикации 28.01.2019
Аннотация
Рассматривается задача синтеза оптимального в среднем управления пучком траекторий нелинейной детерминированной динамической системы, исходящим из заданного множества начальных состояний, по результатам оценок вектора состояния, вырабатываемых нелинейным наблюдателем состояния по поступающим измерениям. Законы управления моделью объекта управления и наблюдателем находятся одновременно путем решения задачи параметрической оптимизации одним из метаэвристических алгоритмов. Предложенный алгоритм решения задачи проиллюстрирован на двух примерах управления трехмерными хаотическими нелинейными динамическими системами.
Введение. Прикладные задачи синтеза нелинейных детерминированных систем совместного оценивания и управления, как правило, решаются посредством линеаризации в окрестности опорной траектории и применения принципа разделения для линейных систем с квадратичным критерием качества, заключающегося в независимом нахождении оптимального линейного регулятора и асимптотического наблюдателя состояния полного или низкого порядка [1, 2]. Другим путем решения задачи является поиск такого ограниченного класса нелинейных систем управления, для которого принцип разделения остается справедливым, а также можно построить асимптотические наблюдатели и соответствующие стабилизирующие управления [3–5]. При этом коэффициенты усиления наблюдателей задаются либо постоянными функциями, либо функциями времени. Для общего случая нелинейных систем проблема нахождения наблюдателей состояния пока не решена. Предлагается структура нелинейного наблюдателя с матрицей коэффициентов усиления, зависящих не только от времени, но и от вырабатываемых оценок вектора состояния. Как правило, задачи синтеза оптимального управления и синтеза наблюдателя решаются независимо. Представляется логичным совместить процесс решения этих задач в рамках единой процедуры оптимизации и моделирования без применения линеаризации нелинейной системы. При этом законы управления объектом и процессом наблюдения ищутся в виде функций одних и тех же переменных: времени и оценок координат вектора состояния.
Рассматривается поведение нелинейной непрерывной детерминированной модели объекта управления, поведение которой описывается системой обыкновенных дифференциальных уравнений. На управление наложены параллелепипедные ограничения. Начальные условия заданы компактным множеством положительной меры, т.е. имеется априорная информация, характеризующая множество возможных начальных состояний. По информации, поступающей с нелинейной модели измерительной системы, предлагается восстановить полный вектор состояния, используя нелинейный наблюдатель. Предполагается, что при управлении объектом используется информация, получаемая на выходе наблюдателя (оценка вектора состояния) с учетом доступной априорной информации и выхода измерительной системы. Минимизация погрешностей оценивания обеспечивается выбором управления наблюдателем, зависящим от времени и полученных оценок. Качество управления отдельной траекторией оценивается величиной функционала Больца, а пучка траекторий – его средним значением по множеству начальных состояний. Ставится задача нахождения управлений объектом и наблюдателем, минимизирующих значение функционала качества управления пучком.
Различные задачи поиска оптимального программного управления и управления с обратной связью пучками траекторий рассматривались в [6–8], в том числе с помощью различных метаэвристических алгоритмов глобальной оптимизации в [9, 10], где предложен подход для нахождения управления, зависящего от части координат вектора состояния, доступной измерению. В данной работе по неполной информации, поступающей с модели измерительной системы, предлагается восстановить значения всех координат вектора состояния (получить их оценки) и строить управление, зависящее от полученных оценок. Метаэвристические алгоритмы подтвердили свою эффективность при решении различных прикладных задач оптимизации, хотя и не гарантируют нахождения точки глобального условного экстремума, но позволяют надеяться на нахождение хорошего приближения к нему за приемлемое с практической точки зрения время [11–15].
В статье предлагается прямой метод решения поставленной задачи на основе параметрической оптимизации. Искомое управление с обратной связью по оцениваемым координатам вектора состояния ищется в классе функций с насыщением, учитывающим наличие ограничений на управление, с помощью систем базисных функций, применяемых в спектральном методе анализа и синтеза нелинейных систем управления [16]. Для решения сформулированной задачи управления пучком траекторий предлагается использовать метод “серых волков” [17, 18], имитирующий охоту волчьей стаи за жертвой. Он относится к методам роевого интеллекта [14, 15], в которых используется иерархия лидерства в стае и особый механизм охоты, заключающийся в отслеживании и приближении к жертве, ее последующем окружении и финальном нападении.
Предлагается алгоритм параметрической оптимизации нелинейных детерминированных систем управления, эффективность которого демонстрируется на решении двух модельных примеров управления нелинейными динамическими системами [19–21].
1. Постановка задачи. Поведение нелинейной непрерывной детерминированной модели объекта управления описывается уравнением
где t – непрерывное время, $t \in T = [{{t}_{0}};{{t}_{1}}]$, моменты ${{t}_{0}}$ начала процесса и ${{t}_{1}}$ окончания процесса управления считаются заданными; $x$ – вектор состояния системы, $x \in {{R}^{n}}$; $u$ – вектор управления, $u \in U(t) \subseteq {{R}^{q}}$; $U(t)$ – множество допустимых значений управления, для каждого момента времени t представляющее собой прямое произведение отрезков $[{{a}_{j}}(t),{{b}_{j}}(t)]$, $j\, = \,\overline {1,q} ;f(t,x,u)$ = = ${{({{f}_{1}}(t,x,u), \ldots ,{{f}_{n}}(t,x,u))}^{{\text{т }}}}$ – непрерывно дифференцируемая вектор-функция.Начальные условия заданы компактным множеством Ω положительной меры с кусочно-гладкой границей:
где множество Ω характеризует неопределенность задания начальных условий.Предполагается, что при управлении используется информация, поступающая с модели измерительной системы, описываемой соотношением
где $z \in {{R}^{m}}$– вектор измерений, $h\left( {t,x} \right)$ – непрерывная вектор-функция.Предполагается, что по поступающей с модели измерительной системы информации можно получить оценку вектора состояния, используя нелинейный наблюдатель вида
(1.4)
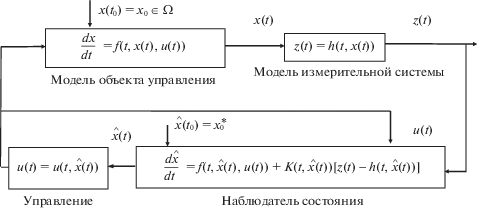
$\frac{{d\hat {x}}}{{dt}} = f\left( {t,\hat {x}(t),u(t,\hat {x}(t))} \right) + K(t,\hat {x}(t))[z(t) - h(t,\hat {x}(t))],$Управление моделью объекта, применяемое в каждый момент времени t, имеет вид управления с обратной связью по оценке вектора состояния: $u(t) = u(t,\hat {x}(t))$ (рис. 1). Множество допустимых управлений $U$ образуют такие функции $(u(t,\hat {x}),K(t,\hat {x}))$, что $\forall t \in T$ управление моделью объекта $u(t) = u\left( {t,\hat {x}(t)} \right) \in U(t)$ кусочно-непрерывно, управление $K(t) = K(t,\hat {x}(t)) \in {{R}^{{n \times m}}}$ наблюдателем непрерывно, а функция $f\left( {t,\hat {x},u(t,\hat {x})} \right)$ такова, что решение системы уравнений (1.1), (1.4) с начальными условиями (1.2), (1.5) с учетом (1.3) существует и единственно.
Определим функционал качества управления отдельной траекторией
(1.6)
$I\left( {{{x}_{0}},u(t,\hat {x}(t)),K(t,\hat {x}(t))} \right) = \int\limits_{{{t}_{0}}}^{{{t}_{1}}} {{{f}^{0}}\left( {t,x(t),u(t,\hat {x}(t)),K(t,\hat {x}(t))} \right)} dt + F\left( {x({{t}_{1}})} \right)$,Каждому допустимому управлению $(u(t,\hat {x}),K(t,\hat {x})) \in {\mathbf{U}})$ и множеству $\Omega $ поставим в соответствие пучок (ансамбль) [6] траекторий системы уравнений (1.1), (1.4):
Качество управления пучком траекторий предлагается оценивать величиной функционала
(1.7)
$J\left[ {u(t,\hat {x}),K(t,\hat {x})} \right] = \int\limits_\Omega {I\left( {{{x}_{0}},u(t,\hat {x}(t)),K(t,\hat {x}(t))} \right)} d{{x}_{0}}{\text{/mes}}\;\Omega ,$Требуется найти такое управление $(u{\text{*}}(t,\hat {x}),K{\text{*}}(t,\hat {x})) \in {\mathbf{U}}$, что
(1.8)
$J\left[ {u{\text{*}}(t,\hat {x}),K{\text{*}}(t,\hat {x})} \right] = \mathop {\min }\limits_{(u\left( {t,\hat {x}} \right),K(t,\hat {x})) \in U} J\left[ {u(t,\hat {x}),K(t,\hat {x})} \right].$Искомое управление называется оптимальным в среднем, поскольку минимизируется среднее значение функционала (1.6) на множестве начальных состояний $\Omega $.
Зависимость управления $K(t,\hat {x})$ наблюдателем от всех координат вектора оценок $\hat {x}$ дает возможность построить наблюдатель с $n$ обратными связями по оцениваемым переменным, что позволяет надеяться на улучшение качества оценивания. С целью упрощения структуры наблюдателя можно последовательно сокращать число оцениваемых координат, используемых в управлении, в предельном случае получая зависимость только от текущего времени t. При этом, наряду с упрощением процедуры синтеза наблюдателя, возможна потеря точности оценивания.
2. Стратегия поиска решения. Предлагаемый подход к решению заключается в переходе от задачи (1.8) к задаче конечномерной оптимизации, т.е. проблеме поиска наилучших значений неопределенных элементов, задающих структуру управления моделью объекта управления (1.1) и наблюдателем состояния (1.4). В этой структуре учитывается наличие ограничений на управление моделью объекта.
Далее будем использовать математический аппарат из [10] и следующие предположения.
1. Множество начальных состояний $\Omega $ представляет собой параллелепипед, определенный прямым произведением отрезков $\left[ {{{\alpha }_{i}};{{\beta }_{i}}} \right]$, $i = \overline {1,n} $, т.е. $\Omega = \left[ {{{\alpha }_{1}};{{\beta }_{1}}} \right] \times \cdots \times \left[ {{{\alpha }_{n}};{{\beta }_{n}}} \right]$. Все отрезки с помощью шага $\Delta {{x}_{i}}$ разбиваются на ${{N}_{i}}$ отрезков, а параллелепипед $\Omega $ делится на $N = {{N}_{1}} \cdots {{N}_{n}}$ элементарных непересекающихся подмножеств ${{\Omega }_{k}}$, $k = \overline {1,N} $. В каждом элементарном подмножестве ${{\Omega }_{k}}$ задается начальное состояние $x_{0}^{k}$ (центр параллелепипеда ${{\Omega }_{k}}$).
2. Известна оценка множества возможных состояний, которая представляется прямым произведением $Q = [\underline {{{x}_{1}}} ,\overline {{{x}_{1}}} ] \times \cdots \times [\underline {{{x}_{n}}} ,\overline {{{x}_{n}}} ]$, где $\underline {{{x}_{i}}} ,\overline {{{x}_{i}}} $, $i = \overline {1,n} $, – нижняя и верхняя границы по каждой координате соответственно, определяемые физическим смыслом решаемой задачи. Поэтому можно считать, что искомые оценки вектора состояния должны удовлетворять условиям ${{\hat {x}}_{1}} \in [\underline {{{x}_{1}}} ,\overline {{{x}_{1}}} ]$, ..., ${{\hat {x}}_{n}} \in [\underline {{{x}_{n}}} ,\overline {{{x}_{n}}} ]$.
3. Компоненты закона управления моделью объекта $u\left( {t,\hat {x}} \right) = {{\left( {{{u}_{1}}\left( {t,\hat {x}} \right),\; \ldots ,\;{{u}_{q}}\left( {t,\hat {x}} \right)} \right)}^{{\text{T}}}}$ находятся в виде
(2.1)
${{u}_{j}}\left( {t,\hat {x}(t)} \right) = {\text{sat}}\underbrace {\left\{ {{{g}_{j}}\left( {t,{{{\hat {x}}}_{1}}(t),\; \ldots ,\;{{{\hat {x}}}_{n}}(t)} \right)} \right\}}_{{{\text{v}}_{j}}(t)},\quad j = \overline {1,q} ,$(2.2)
$sat\;{{\text{v}}_{j}}(t) = \left\{ \begin{gathered} {{\text{v}}_{j}}(t),\quad {{a}_{j}}\left( t \right) < {{\text{v}}_{j}}(t) < {{b}_{j}}\left( t \right), \hfill \\ {{a}_{j}}\left( t \right),\quad {{\text{v}}_{j}}(t) \leqslant {{a}_{j}}\left( t \right), \hfill \\ {{b}_{j}}\left( t \right),\quad {{\text{v}}_{j}}(t) \geqslant {{b}_{j}}\left( t \right), \hfill \\ \end{gathered} \right.$(2.3)
${{g}_{j}}\left( {t,{{{\hat {x}}}_{1}}, \ldots ,{{{\hat {x}}}_{n}}} \right) = \sum\limits_{{{i}_{0}} = 0}^{{{L}_{0}} - 1} {\sum\limits_{{{i}_{1}} = 0}^{{{L}_{1}} - 1} { \cdots \sum\limits_{{{i}_{n}} = 0}^{{{L}_{n}} - 1} {u_{{{{i}_{0}},{{i}_{1}}, \ldots ,{{i}_{n}}}}^{j} \times q\left( {{{i}_{0}},t} \right){{p}_{1}}({{i}_{1}},{{{\hat {x}}}_{1}}) \cdots {{p}_{n}}\left( {{{i}_{n}},{{{\hat {x}}}_{n}}} \right)} ,} } $(2.4)
${{k}_{{ij}}}(t,\hat {x}) = \sum\limits_{{{i}_{0}} = 0}^{{{L}_{0}} - 1} {\sum\limits_{{{i}_{1}} = 0}^{{{L}_{1}} - 1} { \cdots \sum\limits_{{{i}_{n}} = 0}^{{{L}_{n}} - 1} {k_{{{{i}_{0}},{{i}_{1}}, \ldots ,{{i}_{n}}}}^{{ij}}q\left( {{{i}_{0}},t} \right){{p}_{1}}({{i}_{1}},{{{\hat {x}}}_{1}}) \cdots {{p}_{n}}\left( {{{i}_{n}},{{{\hat {x}}}_{n}}} \right)} ,} } \quad i = \overline {1,n} ;\quad j = \overline {1,m} ,$Известно [22], что если система функций $\{ q({{i}_{0}},t)\} _{{{{i}_{0}} = 0}}^{\infty }$ является базисом пространства ${{L}_{2}}(T)$, а системы $\{ {{p}_{1}}({{i}_{1}},{{\hat {x}}_{1}})\} _{{{{i}_{1}}}}^{\infty },\;. \ldots ,\;\{ {{p}_{n}}\left( {{{i}_{n}},{{{\hat {x}}}_{n}}} \right)\} _{{{{i}_{n}}}}^{\infty }$ представляют собой базисы пространств ${{L}_{2}}([\underline {{{x}_{1}}} ,\overline {{{x}_{1}}} ])$, ..., ${{L}_{2}}([\underline {{{x}_{n}}} ,\overline {{{x}_{n}}} ])$, соответственно, то система функций, образованных произведениями, $\{ q({{i}_{0}},t){{p}_{1}}({{i}_{1}},{{\hat {x}}_{1}}) \cdots {{p}_{n}}({{i}_{n}},{{\hat {x}}_{n}})\} _{{{{i}_{0}},{{i}_{1}},...,{{i}_{n}} = 0}}^{\infty }$ также образует базис пространства ${{L}_{2}}(T \times Q)$. Тогда любую функцию $g(t,\hat {x}) \in {{L}_{2}}(T \times Q)$ можно представить в виде ряда по функциям этой системы:
Для нахождения приближенного решения берут конечное число членов ряда, т.е. задаются числа ${{L}_{0}},{{L}_{1}},\; \ldots ,\;{{L}_{n}}$ (масштабы усечения), определяющие количество неопределенных коэффициентов разложения и используемых элементов базисной системы. Таким образом, обосновывается структура управления наблюдателем (2.4). При поиске управления моделью объекта учитывается наличие параллелепипедных ограничений на величину управляющего воздействия, для автоматического выполнения которых в (2.1) применяется функция насыщения.
В качестве базисных функций $q\left( {{{i}_{0}},t} \right)$${{p}_{k}}\left( {{{i}_{k}},{{{\hat {x}}}_{k}}} \right)$, $k = \overline {1,n} $, можно взять, например:
а) полиномы Лежандра:
б) косинусоиды:
Стратегия решения задачи заключается в поиске наилучших значений коэффициентов $u_{{{{i}_{0}},{{i}_{1}}, \ldots ,{{i}_{n}}}}^{j}$, $k_{{{{i}_{0}},{{i}_{1}}, \ldots ,{{i}_{n}}}}^{{ij}}$, образующих структуру управления (2.1), (2.4). Для формализации задачи определения коэффициентов предлагается использовать вектор
(2.5)
$u = {{(u_{{{{i}_{0}},{{i}_{1}}, \ldots ,{{i}_{n}}}}^{1},\; \ldots ,\;u_{{{{i}_{0}},{{i}_{1}}, \ldots ,{{i}_{n}}}}^{q})}^{{\text{T}}}},$Для решения задачи поиска коэффициентов $u_{{{{i}_{0}},{{i}_{1}}, \ldots ,{{i}_{n}}}}^{j}$, $k_{{{{i}_{0}},{{i}_{1}}, \ldots ,{{i}_{n}}}}^{{ij}}$ и, как следствие, управления $u\left( {t,\hat {x}} \right)$, $K\left( {t,\hat {x}} \right)$ предлагается применить метод “серых волков” поиска глобального условного экстремума функций многих переменных (см. разд. 4). В качестве решения задачи выбираются наилучшие коэффициенты $u_{{{{i}_{0}},{{i}_{1}}, \ldots ,{{i}_{n}}}}^{{*j}}$, $k_{{{{i}_{0}},{{i}_{1}}, \ldots ,{{i}_{n}}}}^{{*ij}}$ и определяемые ими управления $u{\text{*}}\left( {t,\hat {x}} \right)$, $K{\text{*}}\left( {t,\hat {x}} \right)$, которым соответствует наименьшее значение критерия (1.7). Поскольку решение ищется в рамках фиксированной структуры, получаемое управление является субоптимальным.
3. Алгоритм решения задачи. Описанная стратегия поиска решения реализуется следующим пошаговым алгоритмом.
Шаг 1. Генерация множества $\Omega \subset {{R}^{n}}$.
1.1. Задать множество $\Omega $ как прямое произведение отрезков $\left[ {{{\alpha }_{1}};{{\beta }_{1}}} \right]$, $i = \overline {1,n} $; значения шага по каждой координате $\Delta {{x}_{1}},\; \ldots ,\;\Delta {{x}_{n}}$; векторы $\underline x = (\underline {{{x}_{1}}} , \ldots ,\underline {{{x}_{n}}} ),\bar {x} = (\overline {{{x}_{1}}} , \ldots ,\overline {{{x}_{n}}} )$ и масштабы усечения ${{L}_{0}},{{L}_{1}},\; \ldots ,\;{{L}_{n}}$.
1.2. Найти число промежутков ${{N}_{1}} = ({{\beta }_{1}} - {{\alpha }_{1}}){\text{/}}\Delta {{x}_{1}},\; \ldots ,\;{{N}_{n}} = ({{\beta }_{n}} - {{\alpha }_{n}}){\text{/}}\Delta {{x}_{n}}$ и число элементарных подмножеств ${{\Omega }_{k}}:N = {{N}_{1}} \cdots {{N}_{n}}$.
Шаг 2. Определить целевую функцию, т.е. задать правило $h:(u(t,\hat {x}),\;K(t,\hat {x})) \to \text{v}$, ставящее в соответствие каждому набору коэффициентов $u_{{{{i}_{0}},{{i}_{1}}, \ldots ,{{i}_{n}}}}^{j}$, $k_{{{{i}_{0}},{{i}_{1}}, \ldots ,{{i}_{n}}}}^{{ij}}$ некоторое число $\text{v}$ – значение целевой функции.
2.1. Найти решение ${{x}^{k}}(t)$, ${{\hat {x}}^{k}}(t)$ системы уравнений (1.1), (1.4) с управлениями вида (2.1), (2.4) и начальным условием $x({{t}_{0}}) = x_{0}^{k}$ и (1.5), т.е. четверку $({{x}^{k}}(t),{{\hat {x}}^{k}}(t),\;{{u}^{k}}(t,{{\hat {x}}^{k}}(t)),\;{{K}^{k}}(t,{{\hat {x}}^{k}}(t)))$, $k = \overline {1,N} $. Для этого применить один из методов численного решения обыкновенных дифференциальных уравнений.
2.2. Подсчитать значение функционала (1.6): $I\left( {{{x}_{0}},u(t,\hat {x}(t)),K(t,\hat {x}(t))} \right)$, $k = \overline {1,N} $. Величину интегрального члена функционала можно подсчитать в п. 2.1, если к системе уравнений добавить уравнение ${{\dot {x}}_{{n + 1}}}(t) = {{f}^{0}}\left( {t,x(t),u(t,\hat {x}(t)),K(t,\hat {x}(t))} \right)$, ${{x}_{{n + 1}}}({{t}_{0}}) = 0$.
2.3. Найти приближенное значение критерия (1.7), полагая
Процесс последовательной минимизации и моделирования замкнутой системы завершается, когда дальнейшие итерации метода “серых волков” не приводят к улучшению решения либо по истечении заданного максимального числа итераций. В результате определяются наилучшие значения коэффициентов $u_{{{{i}_{0}},{{i}_{1}}, \ldots ,{{i}_{n}}}}^{j}$, $k_{{{{i}_{0}},{{i}_{1}}, \ldots ,{{i}_{n}}}}^{{ij}}$ и, как следствие, искомое управление $u{\text{*}}(t,\hat {x})$, $K{\text{*}}(t,\hat {x})$.
4. Метод “серых волков”. Поскольку применение классических численных методов поиска локального и глобального экстремума многоэкстремальных функций со сложным рельефом поверхностей уровня может быть малоэффективным, для решения задачи оптимизации на шаге 3 предлагается использовать метаэвристические методы оптимизации, которые позволяют получить приближенное решение за приемлемое время [13–15]. Одним из таких методов является метод “серых волков”, который имитирует охоту стаи серых волков за жертвой [17, 18] и служит для решения следующей задачи, в которой дана целевая функция $f(x) = f\left( {{{x}_{1}},{{x}_{2}},\; \ldots ,\;{{x}_{n}}} \right)$, определенная на множестве допустимых решений $D \subseteq {{R}^{n}}$. Требуется найти глобальный минимум функции $f(x)$ на множестве $D$, т.е. такую точку $x* \in D$, что $f(x*) = \mathop {\min }\limits_{x \in D} f(x)$, где $x = {{\left( {{{x}_{1}},{{x}_{2}},\; \ldots ,\;{{x}_{n}}} \right)}^{{\text{T}}}}$, D = = $\{ x|{{x}_{i}} \in [{{a}_{i}},{{b}_{i}}],\;i = \overline {1,n} \} $.
Метод имитирует охоту стаи серых волков за жертвой. Он относится к методам роевого интеллекта, в которых используется иерархия лидерства в стае и особый механизм охоты, заключающийся в отслеживании и приближении к жертве, ее последующем окружении и финальном нападении.
В начале работы метода случайным образом, используя предположение о равномерном распределении, на множестве допустимых решений D генерируется некоторый набор начальных точек (“волков в стае”) $I = \{ {{x}^{j}} = {{(x_{1}^{j},x_{2}^{j}, \ldots ,x_{n}^{j})}^{{\text{T}}}},\;j = \overline {1,NP} \} \subset D$, где ${{x}^{j}}$ – вектор координат положения волка с номером j, NP – количество волков в стае. Поскольку в процессе охоты положение жертвы точно неизвестно вследствие ее постоянного движения (а в задаче оптимизации неизвестно положение точки экстремума), то члены стаи ориентируются на лидеров, полагая, что они обладают большей информацией о положении жертвы (точке экстремума). В стае волков, где каждый волк характеризуется своей позицией в области допустимых решений, выбираются три последовательно лучшие $\left( {\alpha ,\;\beta ,\;\gamma } \right)$ по величине целевой функции $f(x):{{x}^{\alpha }},{{x}^{\beta }},{{x}^{\gamma }}$. Все волки в стае меняют свое положение с учетом сравнения своей текущей позиции с этими тремя наилучшими:
Алгоритм решения задачи.
Шаг 1. Генерация начальной популяции.
1.1. Задать параметры метода: число элементов в популяции NP; максимальное число итераций K; положить $k = 1$ (счетчик числа итераций).
1.2. Используя равномерный закон распределения на множестве D, сгенерировать начальную популяцию ${{I}_{k}} = \{ {{x}^{j}}(k) = (x_{1}^{j}(k), \ldots ,x_{n}^{j}(k)),j = \overline {1,NP} \} \subset D$.
1.3. Для каждого волка в стае вычислить соответствующее значение целевой функции: $f({{x}^{1}}(k)), \ldots ,f({{x}^{{NP}}}(k))$.
1.4. Среди сгенерированных частиц найти три наилучших решения, которым соответствуют наименьшие значения целевой функции: ${{x}^{\alpha }} = \mathop {\arg \min }\limits_{j \in \left\{ {1, \ldots ,NP} \right\}} f({{x}^{j}}(k))$ – лучшее решение; ${{x}^{\beta }}$ – второе по величине функции; ${{x}^{\gamma }}$ – третье по величине функции.
Шаг 2. Вычисление параметров.
Для каждого волка в стае с номером j найти:
a – вектор с одинаковыми компонентами ${{a}_{j}} = 2\left( {1 - (k{\text{/}}K)} \right)$, $j = \overline {1,n} $, или ${{a}_{j}} = 2(1 - ({{k}^{2}}{\text{/}}{{K}^{2}}))$, $j = \overline {1,n} $; ${{A}_{\alpha }}$, ${{A}_{\beta }}$, ${{A}_{\gamma }}$ – векторы, определяемые по правилу ${{A}_{m}} = 2a \circ {{r}_{1}} - a$, $m = \alpha ,\beta ,\gamma $; где ${{r}_{1}}$ – n-мерный вектор, каждая компонента которого описывается равномерным распределением на отрезке [0, 1]; ${{C}_{\gamma }}$, ${{C}_{\alpha }}$, ${{C}_{\beta }}$ – векторы, определяемые по правилу ${{C}_{m}} = 2{{r}_{2}}$, $m = \alpha ,\beta ,\gamma $; ${{r}_{2}}$ – n-мерный вектор, каждая компонента которого описывается равномерным распределением на отрезке [0; 1].
Ш а г 3. Генерация новой популяции.
3.1. Найти новые положения элементов популяции:
3.2. Для каждой частицы в популяции вычислить соответствующее ей значение целевой функции: $f({{x}^{1}}(k + 1)), \ldots ,f({{x}^{{NP}}}(k + 1))$.
3.3. Найти новые три наилучшие решения, которым соответствуют наименьшие значения целевой функции:
${{x}^{\alpha }} = \mathop {\arg \min }\limits_{j \in \left\{ {1, \ldots ,NP} \right\}} f({{x}^{j}}(k))$ – лучшее решение; xβ – второе по величине функции; xγ – третье по величине функции.
Шаг 4. Проверка условия завершения поиска.
Если k = K, то процесс поиска завершить, перейти к шагу 5, иначе положить $k = k + 1$ и перейти к шагу 2.
Шаг 5. Выбор решения из последней популяции.
Закончить работу алгоритма. В качестве решения (приближенного) задачи $f\left( {x{\text{*}}} \right) = \mathop {\min }\limits_{x \in D} f(x)$ выбрать волка с положением xα, которому соответствует наименьшее значение целевой функции.
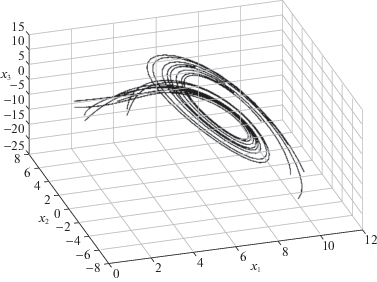
5. Решение модельных примеров. Пример 1. Поведение нелинейной непрерывной детерминированной модели объекта управления описывается следующей системой [19]:
(5.1)
$\begin{gathered} {{{\dot {x}}}_{1}}(t) = {{x}_{2}}, \\ {{{\dot {x}}}_{2}}(t) = {{x}_{3}}, \\ {{{\dot {x}}}_{3}}(t) = a{{x}_{1}} - b{{x}_{2}} - {{x}_{3}} - x_{1}^{2} + {{10}^{{ - 3}}}u, \\ \end{gathered} $Предполагается, что при управлении используется информация, поступающая с модели измерительной системы, описываемой соотношением
где $z \in R$ – измерения.Предлагаемое уравнение наблюдателя:
(5.2)
$\begin{gathered} {{{\dot {\hat {x}}}}_{1}}(t) = {{{\hat {x}}}_{2}}(t), \\ {{{\dot {\hat {x}}}}_{2}}(t) = {{{\hat {x}}}_{3}}(t), \\ {{{\dot {\hat {x}}}}_{3}}(t) = a{{{\hat {x}}}_{1}}(t) - b{{{\hat {x}}}_{2}}(t) - {{{\hat {x}}}_{3}}(t) - \hat {x}_{1}^{2}(t) + {{10}^{{ - 6}}}K(t,\hat {x}(t))(x_{3}^{3}(t) - \hat {x}_{3}^{3}(t)) + {{10}^{{ - 3}}}u(t,\hat {x}(t)). \\ \end{gathered} $Требуется синтезировать систему управления, обеспечивающую выполнение условия ${{x}_{3}}(t) = 1$, т.е. отслеживание заданной величины координаты x3.
Предлагаемая структура управления моделью объекта и наблюдателем:
(5.3)
$u(t,\hat {x}) = {\text{sat}}\sum\limits_{{{i}_{0}} = 0}^{{{L}_{0}} - 1} {\sum\limits_{{{i}_{1}} = 0}^{{{L}_{1}} - 1} {\sum\limits_{{{i}_{2}} = 0}^{{{L}_{2}} - 1} {\sum\limits_{{{i}_{3}} = 0}^{{{L}_{3}} - 1} {u_{{{{i}_{0}},{{i}_{1}},{{i}_{2}},{{i}_{3}}}}^{j}q\left( {{{i}_{0}},t} \right)p\left( {{{i}_{0}},{{{\hat {x}}}_{1}}} \right)p\left( {{{i}_{2}},{{{\hat {x}}}_{2}}} \right)p\left( {{{i}_{3}},{{{\hat {x}}}_{3}}} \right)} } } } ,$Величины шагов $\Delta {{x}_{1}} = 2$, $\Delta {{x}_{2}} = 2$, $\Delta {{x}_{3}} = 2$, векторы $\underline x = \left( {0.5;0.5;0.5} \right)$, $\bar {x} = \left( {3.5;3.5;3.5} \right)$. Число промежутков ${{N}_{1}} = 2$, ${{N}_{2}} = 2$, ${{N}_{3}} = 2$, а число элементарных подмножеств ${{\Omega }_{k}}:N = 8$. Вектор оценки начального состояния $\hat {x}_{0}^{k} = \left\{ {2,2,2} \right\}$.
В качестве базисных функций используются косинусоиды:
Зададим функционал качества управления отдельной траекторией:
Приближенное значение функционала качества управления пучком траекторий находится по формуле
(5.4)
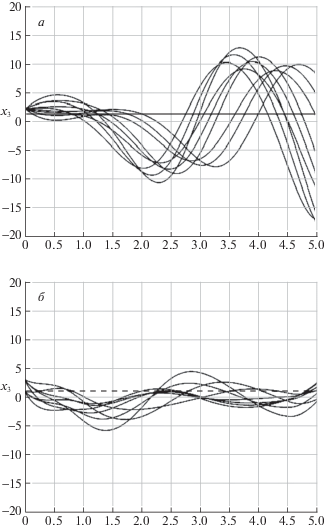
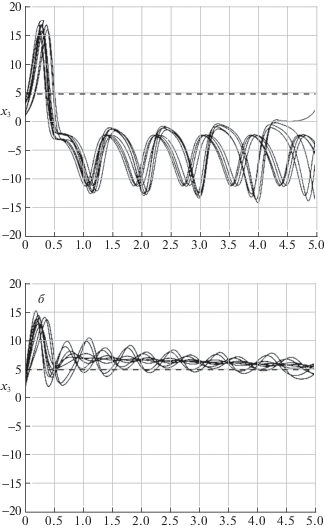
$\text{v} = J\left[ {u\left( {t,\hat {x}} \right),K\left( {t,\hat {x}} \right)} \right] = (1{\text{/}}N)\sum\limits_{k = 1}^N {I(x_{0}^{k},{{u}^{k}}(t,\hat {x}(t)),{{K}^{k}}(t,\hat {x}(t)))} $.Параметры метода “серых волков”: число элементов в популяции NP = 50; максимальное число итераций K = 50. Для численного решения системы уравнений (5.1), (5.2) применялся метод Рунге-Кутты 4-го порядка. Значение функционала (5.4) при нулевых управлениях объектом и наблюдателем $\text{v} = 7.7 \times {{10}^{4}}$. Зависимость координаты ${{x}_{3}}(t)$ без воздействия управления представлена на рис. 3, а, где выделено желаемое значение ${{x}_{3}} = 1$. Как видно из рисунка, только одна траектория пучка приходит в область желаемого результата, а на протяжении всего времени наблюдения ни одна траектория не находится близко к желаемому результату.
Рис. 3.
График изменения координаты ${{x}_{3}}(t)$ при отсутствии управления (а) и под действием управления (б)
В табл. 1 приведены значения функционала в зависимости от изменения масштабов усечения ${{L}_{0}}$, ${{L}_{1}}$, ${{L}_{2}}$, ${{L}_{3}}$, а также времени решения (используемый процессор Intel Core i5 2.9 GHz). Лучшее значение функционала $\text{v} = 425.8$ получено при масштабах усечения ${{L}_{0}} = 2$; ${{L}_{1}} = {{L}_{2}} = {{L}_{3}} = 3$.
Таблица 1.
Наилучшие значения критерия (5.4) при различных масштабах усечения в примере 1
| № | L0 | L1 | L2 | L3 | $\text{v}$ | t, с |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 3 | 3 | 425.8 | 71.3 |
| 2 | 1 | 2 | 2 | 2 | 1141.4 | 60.5 |
| 3 | 2 | 2 | 2 | 2 | 1334.7 | 60.7 |
| 4 | 2 | 3 | 1 | 1 | 1151.3 | 55.2 |
| 5 | 2 | 1 | 1 | 3 | 1238.9 | 57.1 |
Зависимость координаты ${{x}_{3}}(t)$ под действием найденного управления представлена на рис. 3, б. Из графика видно, что на протяжении всего отрезка времени и в конечный момент траектории проходят близко к желаемому результату по сравнению с рис. 3, а.
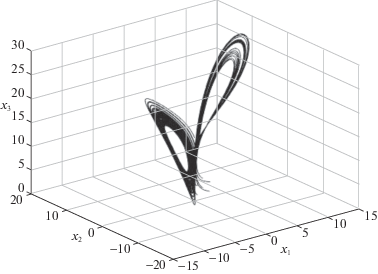
Пример 2. Поведение нелинейной непрерывной детерминированной модели объекта управления описывается системой [20]
(5.5)
$\begin{gathered} {{{\dot {x}}}_{1}}(t) = a({{x}_{2}} - {{x}_{1}}), \\ {{{\dot {x}}}_{2}}(t) = b{{x}_{1}} - {{x}_{1}}{{x}_{3}} + 5 \times {{10}^{{ - 3}}}u, \\ {{{\dot {x}}}_{3}}(t) = c{{x}_{3}} + {{x}_{1}}{{x}_{2}}, \\ \end{gathered} $Предполагается, что при управлении используется информация, поступающая с модели измерительной системы, описываемой соотношением
где $z \in R$ – измерения.Предлагаемое уравнение наблюдателя имеет вид:
(5.7)
$\begin{gathered} {{{\dot {\hat {x}}}}_{1}}(t) = a({{{\hat {x}}}_{2}}(t) - {{{\hat {x}}}_{1}}(t)), \\ {{{\dot {\hat {x}}}}_{2}}(t) = b{{{\hat {x}}}_{1}}(t) - {{{\hat {x}}}_{1}}(t){{{\hat {x}}}_{3}}(t) + 5 \times {{10}^{{ - 7}}}(x_{2}^{3}(t) - \hat {x}_{2}^{3}(t))K(t,\hat {x}(t)) + 5 \times {{10}^{{ - 3}}}u(t,\hat {x}(t)), \\ {{{\dot {\hat {x}}}}_{3}}(t) = c{{{\hat {x}}}_{3}}(t) + {{{\hat {x}}}_{1}}(t){{{\hat {x}}}_{2}}(t). \\ \end{gathered} $Требуется синтезировать систему управления, обеспечивающую выполнение условия ${{x}_{2}}(t) = 5$, т.е. отслеживание заданной величины координаты ${{x}_{2}}$.
Предлагаемая структура управления моделью объекта и наблюдателем совпадает с используемой в примере 1. Шаги $\Delta {{x}_{1}} = 2$, $\Delta {{x}_{2}} = 2$, $\Delta {{x}_{3}} = 2$, векторы $\underline x = \left( {0.5;0.5;0.5} \right)$, $\bar {x} = \left( {3.5;3.5;3.5} \right)$. Число промежутков ${{N}_{1}} = 2$, ${{N}_{2}} = 2$, ${{N}_{3}} = 2$, а число элементарных подмножеств ${{\Omega }_{k}}:N = 8$. Вектор оценки начального состояния $\hat {x}_{0}^{k} = \left\{ {2,2,2} \right\}$.
В качестве базисных функций взяты полиномы Лежандра:
Зададим функционал качества управления отдельной траекторией:
Приближенное значение функционала качества управления пучком траекторий находится по формуле (5.4).
Параметры метода “серых волков”: число элементов в популяции NP = 50; максимальное число итераций K = 50. Значение функционала (5.4) при нулевом управлении $\text{v} = 1.7 \times {{10}^{5}}$. Зависимость координаты ${{x}_{2}}(t)$ при отсутствии управления представлена на рис. 5, а, где выделено желаемое значение ${{x}_{2}} = 5$. Траектории пучка находятся достаточно далеко от желаемого результата.
Рис. 5.
График изменения координаты ${{x}_{2}}(t)$ при отсутствии управления (а) и под действием управления (б)
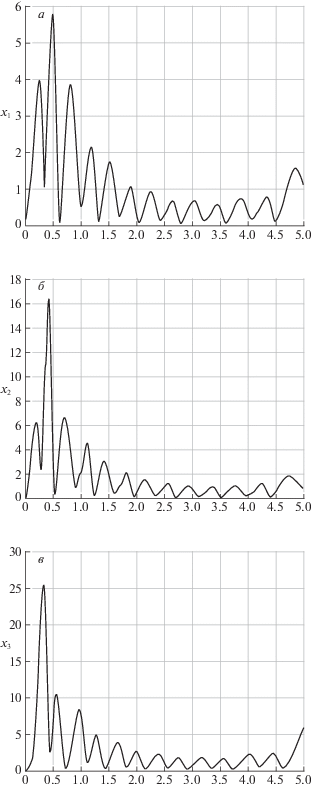
В табл. 2 приведены значения функционала в зависимости от используемых масштабов усечения ${{L}_{0}}$, ${{L}_{1}}$, ${{L}_{2}}$, ${{L}_{3}}$, а также времени решения (процессор Intel Core i5 2.9 GHz). Лучшее значение функционала $\text{v} = 677.9$ получено при масштабах усечения L0 = 2; ${{L}_{1}} = {{L}_{2}} = {{L}_{3}} = 3$. Зависимость координаты ${{x}_{2}}(t)$ под действием управления представлена на рис. 5, б, где выделено желаемое значение ${{x}_{2}} = 5$. Из графика видно, что на протяжении всего отрезка времени траектории проходят близко к желаемому результату по сравнению с рис. 5, а. На рис. 6, а–в представлены графики изменения среднеквадратического отклонения ошибки оценивания на отрезке [0; 5]. В целом, можно сделать вывод, что ошибка оценивания принимает приемлемые значения для обеспечения приближенного решения достаточно хорошего качества.
Таблица 2.
Наилучшие значения критерия (5.4) при различных масштабах усечения в примере 2
| № | L0 | L1 | L2 | L3 | $\text{v}$ | t, с |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 3 | 3 | 677.9 | 193.1 |
| 2 | 1 | 2 | 2 | 2 | 1782.9 | 172.4 |
| 3 | 2 | 2 | 2 | 2 | 1732.5 | 173.9 |
| 4 | 2 | 3 | 1 | 1 | 1945.3 | 159.3 |
| 5 | 2 | 1 | 3 | 1 | 1538.9 | 163.6 |
Рис. 6.
Среднеквадратическое отклонение ошибки оценивания координат: ${{x}_{1}}(t)$ (а), ${{x}_{2}}(t)$ (б), ${{x}_{3}}(t)$ (в)
Заключение. Разработана стратегия и алгоритм приближенного решения задачи поиска оптимального управления нелинейными непрерывными детерминированными динамическими системами совместного оценивания и управления в условиях неопределенности задания начальных условий. Приведенный алгоритм апробирован на двух модельных примерах.
Список литературы
Филипс Ч., Харбор Р. Системы управления с обратной связью. М.: Лаборатория Базовых знаний, 2001.
Квакернаак Х., Сиван Р. Линейные оптимальные системы управления. М.: Мир, 1977.
Голубев А.Е., Крищенко А.П., Ткачев С.Б. Стабилизация нелинейных динамических систем с использованием оценки состояния системы асимптотическим наблюдателем (обзор) // А и Т. 2005. № 7. С. 3–42.
Старков К.Е. Наблюдатели для полиномиальных систем: алгебраические методы построения // А и Т. 1993. № 12. С. 43–53.
Ткачев С.Б. Стабилизация неминимально фазовых аффинных систем методом виртуальных выходов. М.: МГТУ им. Н.Э. Баумана, 2010.
Куржанский А.Б. Управление и наблюдение в условиях неопределенности. М.: Наука, 1977.
Овсянников Д.А. Математические методы управления пучками. Л.: Изд-во ЛГУ, 1980.
Пантелеев А.В., Бортаковский А.С. Теория управления в примерах и задачах. М.: ИНФРА–М, 2016.
Пановский В.Н., Пантелеев А.В. Метаэвристические интервальные методы поиска оптимального в среднем управления нелинейными детерминированными системами при неполной информации о ее параметрах // Изв. РАН. ТиСУ. 2017. № 1. С. 53–64.
Пантелеев А.В., Письменная В.А. Применение меметического алгоритма в задаче оптимального управления пучками траекторий нелинейных детерминированных систем с неполной обратной связью // Изв. РАН. ТиСУ. 2018. № 1. С. 27–38.
Гладков В.А., Курейчик В.В. Биоинспирированные методы в оптимизации. М.: Физматлит, 2009.
Карпенко А.П. Современные алгоритмы поисковой оптимизации. Алгоритмы, вдохновленные природой. М.: Изд-во МГТУ им. Н.Э. Баумана, 2014.
Пантелеев А.В., Метлицкая Д.В., Алешина Е.А. Методы глобальной оптимизации. Метаэвристические стратегии и алгоритмы. М.: Вузовская книга, 2013.
Encyclopedia of Optimization / Eds. C.A. Floudas, P.M. Pardalos. N.Y.: Springer, 2009.
Gendreau M. Handbook of Metaheuristics. N.Y.: Springer, 2010.
Пантелеев А.В., Рыбаков К.А. Методы и алгоритмы синтеза оптимальных стохастических систем управления при неполной информации. М.: Изд-во МАИ, 2012.
Mirjalili S. Grey Wolf Optimizer // Advances in Engineering Software. 2014. V. 69. P. 46–61.
Mittal N., Singh U., Sohi B.S. Modified Grey Wolf Optimizer for Global Engineering Optimization // Applied Computational Intelligence and Soft Computing. 2016. V. 2016. Article ID 7950348.
Pan L., Xu D., Zhou W. Controlling a Novel Chaotic Attractor Using Linear Feedback // J. Information and Computing Science. 2010. V. 5. P. 117–124.
Sundarapandian V. Output Regulation of the Pan System // ISRN Applied Mathematics. 2011. V. 2011. Article ID 983136.
Sundarapandian V. Output Regulation of the Sprott-D System // International Journal of Computer Information Systems. 2011. V. 2. № 6. P. 27–31.
Пугачев В.С. Лекции по функциональному анализу. М.: Изд-во МАИ, 1996.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления