Известия РАН. Теория и системы управления, 2019, № 3, стр. 66-76
Энергоэффективное планирование в распределенных вычислительных системах реального времени
А. М. Грузликов a, Н. В. Колесов a, *, Д. В. Костыгов a, В. В. Ошуев a
a ГНЦ РФ АО “Концерн “ЦНИИ “Электроприбор”
Санкт-Петербург, Россия
* E-mail: kolesovnv@mail.ru
Поступила в редакцию 13.08.2018
После доработки 28.12.2018
Принята к публикации 28.01.2019
Аннотация
Исследуется проблема планирования в многоканальных распределенных системах обработки информации. Проблема решается в отношении систем на кристалле и рассматривается в расширенной постановке, когда процедуру планирования предваряет этап определения архитектуры системы с позиций энергоэффективности.
Введение. Проблема планирования каких-либо действий возникает в разных приложениях и в разнообразных постановках. Среди возможных приложений – планирование бизнес-процессов, технологических процессов, движения транспорта, вычислительных процессов, учебных занятий и т.п. Нередко рассматриваемые в различных приложениях математические постановки задачи оказываются близки или даже идентичны, что способствует перетеканию предлагаемых решений из одной прикладной области в другую. Вопросам планирования в современной научной литературе уделяется большое внимание. При этом разнообразие представленных задач весьма велико. Среди них можно выделить планирование вычислений как в центрах коллективного пользования [1, 2], так и в бортовых системах [3–7]. В настоящей статье обсуждается второе направление, а именно планирование вычислений в распределенных системах реального времени (СРВ). Если быть более точными, то в фокусе данной работы лежит планирование распределенных вычислений в многоядерной системе на кристалле. Под планированием вычислений обычно понимают определение для каждой решаемой задачи из заданного множества временного интервала исполнения на выделенном для нее процессоре. При этом если на одном процессоре оказываются две или более задач, не связанных отношением предшествования, попутно возникает вопрос об очередности их выполнения, которая определяется наилучшим образом с точки зрения заданного критерия. Таковыми могут быть, например, минимум общего времени выполнения или минимум максимального отклонения от заданных директивных сроков. Данными критериями, конечно, не исчерпываются важные аспекты проектирования вычислительных систем. В частности, одной из ключевых проблем при проектировании вычислительных систем всегда было снижение энергопотребления. В последние десятилетия ей уделяется особое внимание, в том числе в связи с обсуждением ее в отношении систем на кристалле [8–10], когда снижение энергопотребления (рассеиваемой мощности) достигается за счет снижения тактовой частоты и напряжения питания. О признании практической значимости этого направления свидетельствует и тот факт, что разработчики процессоров в целях снижения энергопотребления стали предусматривать в своих проектах встроенные средства для варьирования тактовой частотой и напряжением питания. Ниже минимум рассеиваемой мощности будет одним из критериев, на основании которых будут планироваться вычисления.
Можно выделить два универсальных подхода при решении проблемы планирования – одноэтапный и двухэтапный. В первом случае на каждом шаге используемого алгоритма планирования для очередной задачи из заданного множества определяется и исполняющий процессор, и интервал решения. Во втором случае решение проблемы планирования распадается на два этапа. На первом этапе со всеми задачами соотносятся исполняющие их процессоры (процедура назначения), после этого на втором этапе на каждом процессоре производится упорядочение назначенных на него задач (процедура планирования). Далее будем придерживаться второго подхода, рассматривая широко обсуждаемую в литературе проблему (flow shop)-планирования, в качестве практической интерпретации которой часто называют обработку информации в многоканальных системах. В предлагаемом алгоритме планирования на первом этапе будет использоваться критерий минимума рассеиваемой мощности, а на втором – минимум общего времени выполнения плана. Заметим, что для систем реального времени при решении задачи планирования дополнительно должно учитываться ограничение, вызванное периодичностью входного потока данных [5] и требующего учета производительности процессоров и пропускной способности каналов обмена на периоде. Оптимальное решение проблемы планирования может быть получено в рамках любого из обозначенных подходов переборными алгоритмами [3, 4], однако все они характеризуются экспоненциальной вычислительной сложностью, и в силу этого их применение в целом ряде приложений оказывается невозможным. По этой причине широкое распространение на практике получили субоптимальные алгоритмы, среди которых алгоритмы с конструктивными эвристиками [11–15] и ненаправленного поиска [6]. В настоящей статье обсуждается первая группа алгоритмов.
В разд. 1 рассматривается постановка задачи, в разд. 2 – предварительные сведения об алгоритмах (flow shop)-планирования, в разд. 3 – математическая модель мощности рассеивания в распределенной вычислительной системе и энергоэффективный алгоритм назначения задач на процессоры, в разд. 4 – алгоритм гибридного (flow shop)-планирования и, наконец, в разд. 5 – результаты моделирования.
1. Постановка задачи. Сначала приведем традиционную постановку задачи (flow shop)-планирования в распределенной
вычислительной системе. На практике случай flow shop обычно возникает в многоканальных
системах обработки информации, когда в распределенной системе выполняется совокупность
алгоритмов, каждый из которых использует информацию со своего набора датчиков. Система
включает множество $C = \{ {{C}_{i}}|i = \overline {1,n} \} $ процессоров (ядер), имеющих индивидуальную память для хранения кода программ и обменивающихся
информацией через каналы передачи данных. Предполагается, что рассматриваемое множество
задач разбито на независимые группы задач (далее задания), связанных отношением предшествования.
Планированию подлежат m независимых равноприоритетных заданий 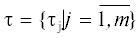 , обрабатывающих входные данные, которые поступают с периодом T. Каждое j-е задание состоит из n задач ${{\tau }_{{j,i}}}$ длительностью ${{e}_{{j,i}}}$, $i = \overline {1,n} $. Будем предполагать, что значения длительностей известно точно. С практической точки
зрения это означает, что мы используем, например, верхние границы этих длительностей.
Все процессоры системы имеют одинаковую производительность. При (flow shop)-планировании
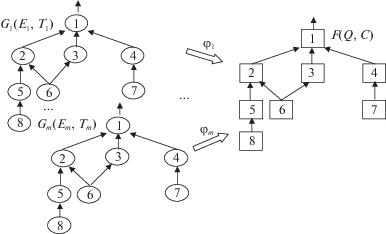
предполагается, что проблема назначения уже решена [5, 11–15]. В данной работе это означает, что имеется m изоморфизмов ${{\varphi }_{j}}{\text{:}}{{G}_{j}}({{E}_{j}},{{T}_{j}}) \to F(Q,C)$, $j = \overline {1,m} $, где ${{G}_{j}}({{E}_{j}},{{T}_{j}})$ – граф межзадачных связей j-го задания, ${{E}_{j}}$ – множество ребер, ${{T}_{j}}$ – множество вершин (задач), $F(Q,C)$ – граф межпроцессорных связей, $Q$ – множество ребер, C – множество процессоров (рис. 1). Процессор ${{C}_{i}}$ будем называть i-й стадией системы. Заметим, что в простейшем случае граф ${{G}_{j}}({{E}_{j}},{{T}_{j}}{\text{)}}$ является линейным, т.е. представляет собой цепочку. В этом случае система будет конвейером,
а процессор ${{C}_{i}}$ – его стадией.
, обрабатывающих входные данные, которые поступают с периодом T. Каждое j-е задание состоит из n задач ${{\tau }_{{j,i}}}$ длительностью ${{e}_{{j,i}}}$, $i = \overline {1,n} $. Будем предполагать, что значения длительностей известно точно. С практической точки
зрения это означает, что мы используем, например, верхние границы этих длительностей.
Все процессоры системы имеют одинаковую производительность. При (flow shop)-планировании
предполагается, что проблема назначения уже решена [5, 11–15]. В данной работе это означает, что имеется m изоморфизмов ${{\varphi }_{j}}{\text{:}}{{G}_{j}}({{E}_{j}},{{T}_{j}}) \to F(Q,C)$, $j = \overline {1,m} $, где ${{G}_{j}}({{E}_{j}},{{T}_{j}})$ – граф межзадачных связей j-го задания, ${{E}_{j}}$ – множество ребер, ${{T}_{j}}$ – множество вершин (задач), $F(Q,C)$ – граф межпроцессорных связей, $Q$ – множество ребер, C – множество процессоров (рис. 1). Процессор ${{C}_{i}}$ будем называть i-й стадией системы. Заметим, что в простейшем случае граф ${{G}_{j}}({{E}_{j}},{{T}_{j}}{\text{)}}$ является линейным, т.е. представляет собой цепочку. В этом случае система будет конвейером,
а процессор ${{C}_{i}}$ – его стадией.
Все введенные графы являются направленными, ациклическими, содержащими в общем случае не один путь между любыми выделенными вершинами. Графы характеризуются выделенным подмножеством входных вершин и одной выходной вершиной. Далее для рассматриваемой системы будем использовать обозначение $S(C,\tau )$.
Предполагается, что при назначении задач на процессоры было выполнено условие, гарантирующее независимость обработки разных порций входной информации. В этом случае исключается образование растущих очередей на процессоры из-за незавершенности обработки предыдущей порции входной информации. Следующая позиция постановки проблемы требует, чтобы передача и прием данных между задачами одного задания, выполняемыми на смежных процессорах, осуществлялась без дополнительных задержек по их готовности.
В настоящей работе рассматривается расширенная проблема (flow shop)-планирования, которую назовем проблемой энергоэффекивного (flow shop)-планирования. Отличие будет состоять в том, что если традиционно задачи любой i-й стадии решаются на одном процессоре, то в предлагаемом подходе число процессоров i-й стадии определяется, исходя из соображений энергоэффективности, и может принимать значения от 1 до m. В результате на этапе назначения задач будет варьироваться архитектура A системы с одновременным изменением тактовой частоты и напряжения питания процессоров с целью минимизации потребляемой мощности P :
Таким образом, традиционная однокритериальная задача фактически превращается в двухкритериальную, подход к решению которой, хотя и хорошо известен, но непрост [16]. Однако, исходя из практических соображений о существенной предпочтительности, по мнению авторов, критерия энергоэффективности, в настоящей работе принят подход, при котором данная двухкритериальная задача формулируется как две последовательно решаемые на разных этапах проектирования однокритериальные задачи.
2. Предварительные сведения. Основой для предлагаемых решений являются известные эффективные алгоритмы (flow shop)-планирования, а именно NEH-алгоритм (Nawaz, Enscore, Ham) [13] и разработанный авторами РКС-алгоритм (алгоритм разрешимых классов систем) [14, 15]. По возможности коротко опишем эти алгоритмы.
NEH-алгоритм. Этот алгоритм достаточно прост и основывается на ограниченном переборе возможных вариантов упорядочивания заданий. Суть его заключается в следующем. Предварительно список планируемых заданий упорядочивается, например, по возрастанию их длительностей. Далее в формируемом плане на первой позиции размещается первое задание из упорядоченного списка. Далее второе задание из этого списка размещается в плане сначала на первой позиции, а затем на второй. Для обоих вариантов вычисляется значение критерия (общее время выполнения плана), а затем принимается вариант с минимальным значением критерия. На следующем шаге действия аналогичны, т.е. для третьего задания из исходного списка оцениваются варианты с размещением его на первой, второй и третьей позициях, среди которых выбирается наилучший и т.д. до исчерпания исходного списка. Этот алгоритм обрел большую популярность на практике и в литературе в силу своей вычислительной простоты.
РКС-алгоритм. Следующий из рассматриваемых алгоритмов основан на использовании разрешимых классов распределенных (flow shop)-систем. Вводится отношение доминирования на множестве $C = \{ {{C}_{i}}|i = \overline {1,n} \} $ процессоров.
Определение 1. Процессор ${{C}_{q}}$ доминирует над процессором ${{C}_{r}}$ (${{C}_{q}} > {{C}_{r}}$), если $\mathop {\min }\limits_j {{e}_{{j,q}}}\, \geqslant \,\mathop {\max }\limits_j {{e}_{{j,r}}}$, $j = \overline {1,m} $.
Общее свойство рассматриваемых далее разрешимых классов распределенных систем состоит в следующем: для любого задания, реализуемого в системе, критический путь единственен и проходит по одним и тем же процессорам ${{C}_{1}},{{C}_{2}},\; \ldots ,\;{{C}_{{n*}}}$, $n{\text{*}}$ – число процессоров критического пути. Далее звездочкой (*) будем отмечать параметры системы, связанные с критическим путем. Теперь приведем определяющие свойства для каждого из разрешимых классов.
Определение 2 (класс 1). Множество процессоров критического пути представляет собой последовательность ${{C}_{1}} > {{C}_{2}} > \ldots > {{C}_{{n*}}}$, убывающую по отношению доминирования.
Определение 3 (класс 2). Множество процессоров критического пути представляет собой последовательность ${{C}_{1}} < {{C}_{2}} < \ldots < {{C}_{{n*}}}$, возрастающую по отношению доминирования.
Определение 4 (класс 3). Множество процессоров критического пути представляет собой пару соединенных последовательностей
Для всех разрешимых классов известны [14, 15] алгоритмы (flow shop)-планирования, которые получаются в результате исследования на экстремум выражений для длительностей ${{E}_{1}}(\pi )$, ${{E}_{2}}(\pi )$, ${{E}_{3}}(\pi )$ выполнения плана $\pi $ в системах из этих классов.
Эти алгоритмы отличает существенная простота, поскольку в них отсутствует перебор вариантов плана. Минимальная длительность плана гарантируется размещением на определенном месте в плане всего лишь одного (для классов 1 и 2) или двух (для класса 3) заданий. В каждом из приведенных алгоритмов требуется выделение заданий, характеризующихся минимальным значением некоторых сумм. Сложность этой операции и, как следствие, каждого из этих алгоритмов является линейной – O(m).
Очевидно, что на практике для распределенной системы общего вида, описанной в постановке проблемы, жесткие условия ее принадлежности к тому или иному разрешимому классу чаще всего не выполняются. В частности, могут не совпадать критические пути разных заданий, может нарушаться отношение доминирования между процессорами, а если оно и выполняется, то может не быть характерных для разрешимых классов упорядоченных по этому отношению цепочек процессоров. В результате исчезают гарантии оптимальности упомянутых выше алгоритмов, и теряет силу справедливый для разрешимых классов факт независимости качества плана от варианта упорядоченности некрайних заданий. В связи с этим предлагается пусть приближенный, но справедливый для любой из рассматриваемых систем рекурсивный алгоритм планирования (РКС-алгоритм), выполняемый за число шагов, не большее, чем число заданий. На каждом шаге рекурсии определяется некоторый аналог критического пути, называемый псевдокритическим. Далее используется алгоритм планирования, соответствующий тому разрешимому классу, к которому наиболее близка рассматриваемая на данном шаге система $S{\text{'}} = \{ C,\tau {\text{'}}\} $, где $\tau {\text{'}}$ – множество неразмещенных заданий ($\tau {\text{'}} \subseteq \tau $). При этом выбранные задания занимают обе крайние позиции из интервала свободных позиций формируемого плана или одну из них. После размещения эти задания исключаются из исходного множества и осуществляется переход к следующему шагу рекурсии, реализуемому уже для оставшегося множества заданий на множестве свободных позиций плана. В результате алгоритм последовательно размещает в плане все рассматриваемые задания в направлении от крайних заданий плана к центру.
РКС-алгоритм.
Шаг 1. Системе S ' присвоить S.
Шаг 2. Поиск псевдокритического пути:
вычислить для каждого процессора ${{C}_{i}}$ системы $S{\text{'}} = (C,\tau {\text{'}})$ (на первом шаге $\tau {\text{'}} = \tau $) медиану ${{\bar {e}}_{i}}$ на множестве длительностей решаемых на нем задач;
найти в системе $S{\text{'}} = (C,\tau {\text{'}})$ псевдокритический вычислительный путь ${{p}_{k}}$, который характеризуется наибольшим значением суммы медиан для множеств времен решения задач
Шаг 3. На основе поясняемого ниже эвристического классификационного правила с использованием выделенного псевдокритического вычислительного пути определить, к какому классу наиболее близка рассматриваемая на данном шаге система $S{\text{'}} = (C,\tau {\text{'}})$.
Шаг 4. Найти с использованием соответствующего известного алгоритма [4, 6] для интервала свободных позиций плана одно из крайних (первое или последнее) заданий будущего плана (классы 1 и 2) либо оба крайних задания (класс 3). Исключить из множества $\tau {\text{'}}$ размещенные на данном шаге задания. Если множество $\tau {\text{'}}$ непусто, то перейти к шагу 2, иначе конец.
Классификация на шаге 3 алгоритма осуществляется на основе эвристического правила геометрического характера [14, 15]. Оно выделяет на множестве процессоров псевдокритического пути рассматриваемой системы определяющий признак – наличие убывающей последовательности (класс 1) либо наличие возрастающей последовательности (класс 2), либо наличие состыкованных возрастающей и убывающей последовательностей (класс 3). При этом анализируется зависимость медианы ${{\bar {e}}_{i}}$ от номера процессора.
3. Энергоэффективный алгоритм назначения задач на процессоры. Сначала обсудим соотношения, описывающие потребляемую системой мощность P, поскольку именно она будет составлять основу критерия оптимизации (1.1) на этапе назначения задач. Сразу отметим, что случай с минимизацией энергии вместо мощности аналогичен рассматриваемому ниже, поскольку энергия, потребляемая системой, равна произведению мощности на время работы системы. Известно [8], что мощность имеет две составляющие – динамическую ${{P}_{d}}$ и статическую ${{P}_{s}}$. Выражения, описывающие эти составляющие без излишней для данного изложения детализации, имеют вид
где a, b – коэффициенты пропорциональности, зависящие от свойств кристалла, N – число процессоров в системе, V – напряжение питания, f – тактовая частота. Поскольку вклад статической мощности в суммарную потребляемую мощность невелик, далее будем учитывать лишь динамическую составляющую. Для ее анализа полезна приближенная формула, определяющая задержку, вносимую схемой при напряжении питания V [8]: где c – коэффициент пропорциональности, зависящий от свойств кристалла.При снижении частоты тактовых импульсов в обратной пропорции возрастает их период, ограничивающий допустимое время для переходных процессов, возникающих в системе при каждом срабатывании. При исходном значении напряжения питания фактическое время переходных процессов будет мало по отношению к новому увеличенному значению периода, а значит, возникает возможность пропорционально снизить напряжение питания с увеличением задержки в рамках периода тактовых импульсов в соответствии с (3.2). В результате выполнения этих двух шагов может быть достигнуто существенное снижение потребляемой мощности (3.1). Действительно, пусть как частота, так и напряжение питания снижены в k раз. Тогда, в соответствии с (3.1), динамическая мощность снижается в ${{k}^{3}}$ раз. При этом, правда, и время работы ядра увеличивается в k раз. Если для сохранения его на прежнем уровне увеличить в k раз число ядер, а вычислительную нагрузку разделить между всеми ядрами поровну, то в результате потребляемая мощность по отношению к исходному варианту уменьшится ${{k}^{2}}$ раз. Описанный факт положен в основу предлагаемого подхода к определению архитектуры системы.
Суть подхода состоит в последовательном определении для каждой стадии числа реализующих ее процессоров. Причем предполагается, что все процессоры стадии работают на одной частоте и при одном напряжении питания, а также что для системы известен допустимый исходный вариант значений параметров ${{f}_{0}}$, ${{V}_{0}}$. Безусловно, проектируя систему на кристалле, разработчик всегда ограничен не только по потребляемой мощности, но по площади ${{s}_{0}}$ кристалла, отведенной для реализации вычислительной системы:
по напряжению питания: и частоте:Зная размер площади ${{s}_{k}}$, занимаемой одним ядром, можно пересчитать ограничение по площади кристалла в допустимое число ${{n}_{d}}$ дополнительных ядер:
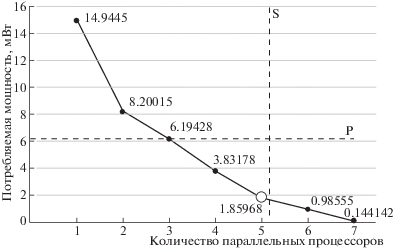
Пример 1. Пусть система содержит одно ядро. Определим количество ядер в одной стадии (flow shop)-системы, исполняющей семь заданий (в одной стадии – семь задач). Длительности задач из рассматриваемой стадии, заданные в условных единицах, имеют значения {10, 11, 12, 20, 21, 23, 12}. Ограничение по площади кристалла для данной стадии составляет 107 мкм2.
На рис. 2 представлена зависимость потребляемой стадией динамической мощности от числа используемых ядер, рассчитанная с учетом понижения частоты и напряжения в соответствии с выражением
где $\alpha $ – активность схемы стадии, ${{C}_{{tech}}}$ – емкость схемы стадии (суммарная емкость в моделях всех транзисторов схемы стадии). Здесь также штриховыми линиями отражены ограничения по площади и потребляемой мощности. Таким образом, наилучшему решению соответствует использование в стадии пяти ядер.В общем случае, когда стадий несколько, возникает вопрос о том, как наилучшим образом с точки зрения минимизации потребляемой мощности распорядиться дополнительными ядрами (запасом по площади) в рамках ограничений (3.4) и (3.5). На этот вопрос отвечает приводимый ниже алгоритм определения энергоэффективной архитектуры. Будем называть ядра исходной реализации системы “исходными”, процесс добавления в i-ю стадию ${{n}_{{d,i}}}$ дополнительных ядер – “расщеплением i-го исходного ядра”, а образованное в результате этого расщепления множество ядер – “расщепленным множеством i-го ядра”. Кроме того, будем считать расщепленное множество i-го ядра предельным, если исключение из него одного ядра делает его среднюю по множеству потребляемую мощность максимальной среди стадий системы. Интуитивно, по-видимому, ясно, что экономия мощности будет максимальной, если разгружаться будут наиболее загруженные ядра, а распределение нагрузки между ядрами в расширенном множестве будет осуществляться сбалансированным образом, т.е. равномерно. По этому принципу работает предлагаемый алгоритм. В дальнейшем этот принцип будет обоснован. Заметим, что идеальная сбалансированность при распределении нагрузки, когда нагрузка делится на равные части между ядрами стадии, на практике в общем случае невозможна. В связи с этим речь идет лишь о приближенной сбалансированности. Архитектуру системы представим вектором состава A = = $(\begin{array}{*{20}{c}} {{{a}_{1}}}&{{{a}_{2}}}& \ldots &{{{a}_{n}}} \end{array})$, где ${{a}_{i}}$ – число ядер в расщепленном множестве i-го ядра, и вектором средней потребляемой мощности $\bar {P} = (\begin{array}{*{20}{c}} {{{{\bar {P}}}_{1}}}&{{{{\bar {P}}}_{2}}}& \ldots &{{{{\bar {P}}}_{n}}} \end{array})$, где ${{\bar {P}}_{i}}$ – средняя по расщепленному множеству i-го ядра потребляемая мощность. Итак, предлагается следующий простой алгоритм.
Алгоритм 1 (определение энергоэффективной архитектуры).
Шаг 1. Сделать начальные присвоения: $M = {{n}_{d}}$ (допустимое число дополнительных ядер), $A = (\begin{array}{*{20}{c}} 1&1& \ldots &1 \end{array})$, $\bar {P} = (\begin{array}{*{20}{c}} {{{{\bar {P}}}_{1}}}&{{{{\bar {P}}}_{2}}}& \ldots &{{{{\bar {P}}}_{n}}} \end{array})$.
Шаг 2. Выбрать в $\bar {P} = (\begin{array}{*{20}{c}} {{{{\bar {P}}}_{1}}}&{{{{\bar {P}}}_{2}}}& \ldots &{{{{\bar {P}}}_{n}}} \end{array})$ компоненту с максимальным значением ${{\bar {P}}_{{\max }}}$. Пусть ее номер равен l. Ввести дополнительное ядро в l-ю стадию. Произвести между ядрами l-й стадии приближенно сбалансированное перераспределение нагрузки. Пересчитать параметры алгоритма: $\bar {P}$, ${{a}_{l}}: = {{a}_{l}} + 1$, $M: = M - 1$. Если $M \ne 0$, то повторить шаг 2, иначе конец.
Проведем качественный анализ приведенного алгоритма. Нестрогость дальнейшего анализа связана с предположением о делимости нагрузки стадий при расщеплении ядер на необходимое для реализации шагов алгоритма число частей. В результате ниже мы сможем говорить о возможности строго сбалансированного назначения задач при расщеплении ядер.
Утверждение 1. Если упорядочить стадии системы по убыванию потребляемой мощности, то соответствующая оптимальная последовательность, составленная из постадийных мощностей множеств используемых ядер, будет невозрастающей.
Доказательство. Запишем выражение для значения $\Delta P$ сэкономленной мощности:
Поскольку уменьшаемое в этом выражении, представляющее мощность безызбыточной системы,
задано, для максимизации $\Delta P$ следует минимизировать вычитаемое. Эту сумму можно рассматривать как произведение
двух числовых последовательностей 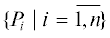 и $\{ 1{\text{/}}n_{i}^{2}|i = \overline {1,n} \} $.
и $\{ 1{\text{/}}n_{i}^{2}|i = \overline {1,n} \} $.
Упорядочим первую последовательность по убыванию значений. Тогда известно [17, 18], что рассматриваемая сумма будет минимальной, если соответствующая вторая последовательность будет неубывающей. Неубывание членов последовательности означает в данном случае невозрастание мощности множеств ядер, используемых на разных стадиях.
Данное утверждение подтверждает направленность предложенного алгоритма на разгрузку наиболее загруженных ядер.
Утверждение 2. Алгоритм 1 является “жадным”, а именно каждый его шаг будет оптимальным по критерию $A* = \arg \mathop {\min }\limits_A P(A)$.
Доказательство. Покажем, что получаемый на каждом шаге алгоритма 1 вклад в сэкономленную мощность будет максимальным. Запишем выражение для сэкономленной мощности $\Delta {{P}_{i}}$:
Перейдем от дискретной функции ${{P}_{i}}{\text{/}}{{(n_{i}^{{}} + 1)}^{2}}$ к непрерывной и воспользуемся для ее представления двумя первыми слагаемыми из разложения в ряд Тейлора:
(3.6)
$\Delta {{P}_{i}} \cong \frac{{{{P}_{i}}}}{{n_{i}^{2}}} - \frac{{{{P}_{i}}}}{{n_{i}^{2}}} + 2\frac{{{{P}_{i}}}}{{n_{i}^{2}}}\frac{1}{{n_{i}^{{}}}} = 2\frac{{{{P}_{i}}}}{{n_{i}^{2}}}\frac{1}{{n_{i}^{{}}}}.$Из выражения (3.6) видно, что прирост сэкономленной мощности равен удвоенной удельной мощности стадии. Следовательно, выбор по максимуму удельной мощности соответствует жадному выбору по максимуму сэкономленной мощности.
Утверждение 3. Алгоритм 1 поставляет архитектуру, оптимальную по критерию A* = = $\arg \mathop {\min }\limits_A P(A)$ при заданном ограничении на число дополнительных ядер ${{n}_{d}} \leqslant {{n}_{{d0}}}$.
Доказательство. Прежде всего, заметим, что в оптимальной архитектуре все расщепленные множества системы являются предельными, кроме, возможно, множества с максимальной удельной мощностью. Действительно, предположим противное, а именно что в оптимальной архитектуре существует непредельное расщепленное множество с немаксимальной удельной мощностью. Тогда из этой стадии можно исключить одно ядро и перенести его в стадию с максимальной удельной мощностью. При этом сэкономленная мощность увеличится, а, значит, предположение о существовании такой оптимальной архитектуры неверно. Очевидно, что алгоритм 1 на каждом шаге поставляет архитектуру, в которой все расщепленные множества системы являются предельными, кроме, возможно, множества с максимальной удельной мощностью. При этом он осуществляет перебор всех возможных таких архитектур в рамках заданного ограничения на ${{n}_{d}} \leqslant {{n}_{{d0}}}$, который в конце концов приведет к оптимальному решению.
Поскольку приведенный алгоритм оперирует не с абсолютными значениями мощностей, а с их соотношением, то с инженерной точки зрения возможен переход к оперированию не потребляемыми в стадиях мощностями, а их вычислительными сложностями. Итак, пусть планируется m заданий $\{ {{\tau }_{j}}|j = \overline {1,m} \} $, каждое j-е из которых включает n задач $\{ {{\tau }_{{j,i}}}|i = \overline {1,n} \} $. Введем понятие вычислительной сложности ${{\Psi }_{j}}$ задания ${{\tau }_{j}}$, под которой будем понимать число составляющих это задание операций. В относительных расчетах, проводимых далее в примере, в качестве оценок можно использовать его исходную длительность (до снижения частоты). Аналогично введем вычислительную сложность ${{\Psi }_{{j,i}}}$ для задачи ${{\tau }_{{j,i}}}$, а также вычислительную сложность ${{\Psi }^{i}}$ для стадии i. При этом
Выбирая в расщепленном множестве каждого i-го исходного ядра ядро с максимальной нагрузкой $\Psi _{{\max }}^{i}$, рассчитываем для стадии минимальную тактовую частоту как пропорциональную вычислительной сложности:
Далее в той же пропорции снижается напряжение питания:
Подчеркнем, что выбор варианта размещения задач стадии целесообразно делать в пользу сбалансированного назначения, поскольку в этом случае вычислительная сложность максимального блока будет минимальной, а значит, и минимальной будет выбираемая тактовая частота стадии (3.7). Рассмотрим иллюстративный пример.
Пример 2. Пусть система содержит три ядра, на которых выполняются четыре задания ${{\tau }_{1}}$, ${{\tau }_{2}}$, ${{\tau }_{3}}$, ${{\tau }_{4}}$, имеющие длительности стадий, выраженные в условных единицах и приведенные в таблице.
В нижней строке таблицы приведены суммарные длительности для всех задач каждой из стадий. Далее они будут использованы как оценки вычислительной сложности и оценки потребляемой на каждой стадии мощности в условных единицах. Необходимо определить наилучшее расщепление для каждого ядра при условии, что запас по площади позволяет добавить в систему четыре ядра (${{n}_{d}} = 4$). Для решения задачи воспользуемся вышеприведенным алгоритмом с анализом длительностей стадий.
1. Делаем начальные присвоения M = 4, $A = (\begin{array}{*{20}{c}} 1&1&1 \end{array})$, $\bar {P} = (\begin{array}{*{20}{c}} {11}&5&4 \end{array})$.
2. Расщепляем ядро первой стадии, вводя два дополнительных ядра. Распределяем нагрузку примерно равномерно между тремя ядрами: {5, 3, 3}. Вычисляем среднюю мощность, потребляемую ядрами расщепленного множества 1-й стадии: ${{\bar {P}}_{1}} = 3.6 < 5$. Вычисляем количество запасных ядер ${{n}_{d}} = 2 \ne 0$. Переходим к следующему шагу расщепления.
3. Расщепляем ядро второй стадии, вводя одно дополнительное ядро. Распределяем нагрузку примерно равномерно между двумя ядрами: {3, 2}. Вычисляем среднюю нагрузку ядер расщепленного множества 2-й стадии: ${{\bar {P}}_{2}} = 2.5 < 3.6$. Вычисляем количество запасных ядер ${{n}_{d}} = 1 \ne 0$. Переходим к следующему шагу расщепления.
4. Расщепляем ядро третьей стадии, вводя одно дополнительное ядро. Распределяем нагрузку равномерно между двумя ядрами: {2, 2}. Вычисляем среднюю мощность, потребляемую ядрами расщепленного множества 3-й стадии: ${{\bar {P}}_{3}} = 2$. Вычисляем количество запасных ядер ${{n}_{d}} = 0$. Конец.
Таким образом, результирующая система содержит семь ядер и характеризуется следующим вектором средних нагрузок для стадий: $\bar {P} = (\begin{array}{*{20}{c}} {3.6}&{2.5}&2 \end{array})$. Оценим приближенно достигаемое при этом снижение потребляемой мощности. В качестве оценки мощности в условных единицах, потребляемой исходной системой, будем использовать, как уже отмечалось:
При этом для преобразованной системы выражение будет иметь вид
где коэффициент ${{k}_{i}}$ снижения частоты (напряжения питания) определяется выражением ki = = ${{\bar {P}}_{{\Sigma ,i}}}{\text{/}}{{\bar {P}}_{{i,\max }}}$, ${{\bar {P}}_{{i,\max }}}$ – наибольшая средняя мощность, потребляемая ядрами расщепленного множества j-й стадии. В результате снижение мощности выражается величиной $l = {{P}_{0}}{\text{/}}P = 5.3$.Безусловно, реальный выигрыш будет меньше, поскольку в проведенных вычислениях не учтено ограничение (2.4) по напряжению питания.
4. Алгоритм (flow shop)-планирования. Теперь опишем предлагаемый алгоритм (flow shop)-планирования, названный авторами “гибридным”, что объясняется использованием комбинации РКС- и NEH-алгоритмов. При этом предлагается процедура, порождающая алгоритм планирования с заданными характеристиками производительности и качества планирования в смысле принятого критерия. В качестве критерия оптимальности при этом будем рассматривать минимум общего времени выполнения плана.
Используемые здесь алгоритмы в каком-то смысле составляют альтернативу друг другу. Действительно, РКС-алгоритм характеризуется большей производительностью, но и более низким качеством поставляемого плана, нежели NEH-алгоритм, и соответственно наоборот. Предлагается при построении плана применять оба эти алгоритма в рамках следующей двухэтапной процедуры, в которой предполагается, что, во-первых, выходная стадия (flow shop)-системы реализуется на одном ядре и, во-вторых, в ней используется расширенная модификация РКС-алгоритма, описанная в [19]. Эта модификация работает не только в отношении (flow shop)-системы, определенной в разд. 1, но и в случае, когда в некоторых стадиях системы не все выполняемые задания представлены своими задачами. В [19] показано, что эта проблема сводится к проблеме (flow shop)-планирования путем введения фиктивных задач нулевой длительности.
Алгоритм планирования (гибридный).
Шаг 1. Упорядочить множество заданий по убыванию времени выполнения.
Шаг 2. Разбить все множество заданий на k групп и при помощи РКС-алгоритма составим частные расписания для каждой из групп.
Шаг 3. Составить общий план для всех заданий при помощи NEH-алгоритма, последовательно размещая очередное задание из каждой группы в общем плане, не нарушая их последовательность относительно частных расписаний.
В случае, когда (flow shop)-система имеет несколько выходов, которые могут быть в ней априори или появиться в результате расщепления выходной вершины, разбиение множества заданий на группы оказывается фиксированным. При этом задания, соотнесенные с одним и тем же выходом, принадлежат одной группе. В других случаях, варьируя числом групп, можно варьировать характеристики получаемого алгоритма планирования. Причем при числе групп, равном мощности исходного множества, получаем NEH-алгоритм, а при числе групп, равном единице, – РКС-алгоритм. Во всех промежуточных ситуациях порождаются алгоритмы планирования с промежуточными значениями характеристик.
5. Результаты моделирования. На рис. 3 приведены результаты моделирования задачи планирования при использовании предложенного подхода. При этом применялась случайная генерация как графов заданий, так и длительностей составляющих их задач. Примеры генерировались с числом заданий 20, 40, 60, 80, 120, 140, 160 (по 500 примеров для каждой из этих точек). При формировании любого задания сначала производилось построение ациклического направленного графа, содержащего заданное число вершин (n = 10) при заданном числе базовых циклов в ненаправленном аналоге. В общем случае этот граф содержит не один путь между любыми выделенными вершинами. Далее для каждой задачи полученного графа путем случайной генерации формировались длительности выполнения как реализации случайной величины, равномерно распределенной в некотором интервале. В каждом из сформированных примеров расщеплялись вершины с введением 50% дополнительных вершин (${{n}_{d}} = 5$). После этого по отношению к примеру применялся алгоритм планирования, описанный в предыдущем разделе. На рис. 3 представлены величины проигрыша гибридных алгоритмов по отношению к оценке Тейларда [20] длительности планов в примерах большой размерности, на рис. 4 – графики для времени построения планов при использовании анализируемых алгоритмов.
Рис. 3.
Зависимости величины проигрыша алгоритмов планирования по отношению к оценке Тейларда от числа заданий в плане
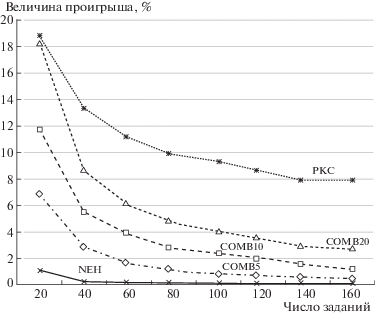
Рис. 4.
Зависимости времени построения планов при использовании анализируемых алгоритмов от числа заданий в плане
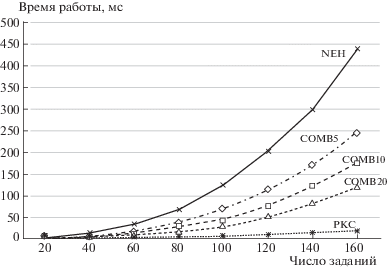
Видно, что, меняя число групп, можно варьировать характеристики получаемого алгоритма планирования, а именно время работы алгоритма и близость получаемого результата к оптимальному. Причем при числе групп, равном мощности исходного множества, получаем NEH-алгоритм, а при числе групп, равном единице, – РКС-алгоритм. В промежуточных ситуациях при размерах групп 5, 10 и 20 порождаются алгоритмы планирования с промежуточными значениями характеристик (COMB5 – COMB20).
Заключение. В статье предложен и исследован алгоритм энергоэффективного (flow shop)-планирования, который отличают две особенности. Во-первых, введен этап определения архитектуры системы с целью минимизации потребляемой системой мощности. Во-вторых, предлагается для получаемой архитектуры использовать алгоритм планирования, основанный на комбинации двух известных и наиболее эффективных, но обладающих разными достоинствами алгоритмов (flow shop)-планирования – NEH (качество плана)- и РКС-алгоритма (быстродействие). Результаты моделирования показали, что применение в рамках гибридного подхода этих двух алгоритмов позволяет получать различные компромиссные с точки зрения отношения времени работы алгоритма к его результативности реализации расписания. Это особенность позволяет обеспечить большую адаптивность алгоритма планирования к требованиям конкретного приложения.
Список литературы
Голосов П.Е., Козлов М.В., Малашенко Ю.Е., Назарова И.А., Ронжин А.Е. Анализ управления специализированными вычислительными заданиями в условиях неопределенности // Изв. РАН. ТиСУ. 2012. № 1. С. 50–66.
Малашенко Ю.Е., Назарова И.А. Управление ресурсоемкими разнородными вычислительными заданиями с директивными сроками окончания // Изв. РАН. ТиСУ. 2012. № 5. С. 15–22.
Liu J.W.S. Real-Time Systems. N.J.: Prentice Hall, Englewood Cliffs, 2000. 600 p.
Drozdowski M. Scheduling for Parallel Processing. London: Springer, 2009.
Колесов Н.В., Толмачева М.В., Юхта П.В. Системы реального времени. Планирование, анализ, диагностирование. СПб.: ОАО “Концерн “ЦНИИ “Электроприбор”, 2014. 185 с.
Зорин Д.А., Костенко В.А. Алгоритм синтеза архитектуры вычислительной системы реального времени с учетом требований к надежности // Изв. РАН. ТиСУ. 2012. № 2. С. 45–54.
Xu R., Melhem R., Moss D. Energy-Aware Scheduling for Streaming Applications on Chip Multiprocessors // 28th IEEE Intern.l Real-Time Systems Sympos. Tucson, 2007. P. 25–38.
Panda P. R., Shrivastava A., Silpa B.V.N., Gummidipudi K. Power-efficient System Design. N.Y.: Springer, 2010. 260 p.
Sun H., He Y., Hsu W.-J. Energy-Efficient Multiprocessor Scheduling for Flow Time and Makespan // Theoretical Computer Science. 2014. V. 550. P. 1–20.
Rudek A., Rudek R. On Flowshop Scheduling Problems with the Aging Effect and Resource Allocation // Intern. J. Adv. Manuf. Technol. 2012. V. 62. № 1. P. 135–145.
Bocewicz G., Banaszak Z.A. Declarative Approach to Cyclic Steady State Space Refinement: Periodic Process Scheduling // Intern. J. Adv. Manuf. Technol. 2013. V. 67. № 1–4. P. 137–155.
Korytkowski P., Rymaszewski S., Wiśniewski T. Ant Colony Optimization for Job Shop Scheduling Using Multi-Attribute Dispatching Rules // Intern. J. Adv. Manuf. Technol. 2013. V. 67. № 1–4. P. 231–241.
Nawaz M., Enscore E.E., Jr., Ham I. A Heuristic Algorithm for the m-Machine, n-Job Flow-shop Sequencing Problem // Omega – Intern. J. Management Science. 1983. V. 11. № 1. P. 91–95.
Колесов Н.В., Толмачева М.В., Юхта П.В. Планирование вычислительного процесса в распределенных системах реального времени с неопределенными временами решения задач // Изв. РАН. ТиСУ. 2012. № 4. С. 39–50.
Gruzlikov A.M., Kolesov N.V., Skorodumov Iu.M., Tolmacheva M.V. Using Solvable Classes in Flowshop Scheduling // Intern. J. Adv. Manuf. Technol. 2017. V. 88. P. 1535–1546.
Штойер Р. Многокритериальная оптимизация. Теория, вычисления и приложения. М.: Радио и связь, 1992. 504 с.
Харди Г.Г., Литтльвуд Дж.Е., Полиа Г. Неравенства. М.: Изд-во иностр. лит., 1948. 456 с.
Конвей Р.В., Максвелл В.Л., Миллер Л.В. Теория расписаний. М.: Наука, 1975. 282 с.
Колесов Н.В., Грузликов А.М., Скородумов Ю.М., Толмачева М.В. Смешанное планирование заданий в распределенных системах реального времени // Вестник компьютерных и информационных технологий. 2016. № 5. С. 34–40.
Taillard E. Benchmarks for Basic Scheduling Problems // Europ. J. Operational Research. 1993. V. 64. № 2. P. 278–285.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления